Приборы и техника эксперимента, 2019, № 4, стр. 132-135
ОПРЕДЕЛЕНИЕ ПРОВОДИМОСТИ ИНДИВИДУАЛЬНЫХ УГЛЕРОДНЫХ НАНОТРУБОК НА ОСНОВЕ АНАЛИЗА ПРОФИЛЯ ИЗОБРАЖЕНИЙ ЭЛЕКТРОСТАТИЧЕСКОЙ СИЛОВОЙ МИКРОСКОПИИ
Н. А. Давлеткильдеев a, b, *, Д. В. Соколов a, **, Е. Ю. Мосур a, b, В. В. Болотов a, b, И. А. Лобов a
a Омский научный центр СО РАН
644024 Омск, просп. Карла Маркса, 15, Россия
b Омский государственный университет им. Ф.М. Достоевского
644077 Омск, просп. Мира, 55а, Россия
* E-mail: nadim@obisp.oscsbras.ru
** E-mail: stezko@obisp.oscsbras.ru
Поступила в редакцию 16.11.2018
После доработки 28.01.2019
Принята к публикации 03.02.2019
Аннотация
Предложена методика оценки электрической проводимости индивидуальных углеродных нанотрубок (у.н.т.) на основе сопоставления профилей их изображений, полученных методом электростатической силовой микроскопии (э.с.м.) с моделированными профилями. В результате моделирования определен параметр, характеризующий проводимость индивидуальной нанотрубки, – напряжение между зондом э.с.м. и у.н.т. Выявлена положительная корреляционная связь между данным напряжением и удельной проводимостью индивидуальных у.н.т.
ВВЕДЕНИЕ
Возможность применения индивидуальных углеродных нанотрубок (у.н.т.), как активных и пассивных элементов наноэлектроники, определяет необходимость разработки и усовершенствования методов контроля их электрических параметров [1, 2]. Традиционно электрическую проводимость нанотрубок оценивают посредством контактных электрофизических измерений, выполненных на массивах у.н.т. Данный подход имеет существенный недостаток – невозможность определения проводимости у.н.т. вследствие значительного вклада в измеряемые величины контактных явлений на границах между нанотрубками [3]. Технологическая сложность создания электрических контактов к индивидуальным у.н.т. не позволяет обеспечить серийность измерений их проводимости. Достоинства, свойственные электростатической силовой микроскопии (э.с.м.), такие как бесконтактность измерений, высокое разрешение, чувствительность к изменению локальных электрических свойств, обуславливают перспективность данного метода для определения электрических параметров индивидуальных у.н.т. [4–6]. При этом необходимо отметить, что интерпретация особенностей наблюдаемого контраста и количественный анализ получаемых э.с.м.-изображений представляют собой неординарные задачи [7, 8].
Поэтому целью данной работы является развитие метода э.с.м. для бесконтактного определения электрической проводимости индивидуальных у.н.т.
МЕТОДИКА ЭКСПЕРИМЕНТА
В работе использовались многостенные у.н.т., легированные азотом, которые синтезировались методом химического газофазного осаждения. Методика синтеза и характеристики синтезированных у.н.т. описаны ранее в [9].
Образцы для измерения проводимости индивидуальных у.н.т. готовились следующим образом. Очищенные от частиц катализатора у.н.т. диспергировались ультразвуком в дихлорметане в течение 1 ч. Из полученной суспензии у.н.т. осаждались на золотые микроэлектродные матрицы, фотолитографически сформированные на подложке – слое SiO2 толщиной 430 нм на пластине n-Si с удельным сопротивлением 4.5 Ом·см. Непосредственно перед измерениями все образцы выдерживались при температуре 150°С в течение 10 мин для удаления слоя водного адсорбата с поверхности подложки и формирования более тесного контакта между у.н.т. и золотым электродом.
Измерения методами проводящей атомно-силовой микроскопии (п.а.с.м.) и э.с.м. выполнялись на атомно-силовом микроскопе MFP-3D SA (Asylum Research) в Омском региональном центре коллективного пользования СО РАН. Для исключения образования водного адсорбата и его влияния на проводимость все измерения проводились в атмосфере сухого азота при относительной влажности не более 5%. Для измерений использовались проводящие кантилеверы серии ETALON HA_FM (NT-MDT SI) с Pt-покрытием, с резонансной частотой порядка 100 кГц и радиусом закругления зонда 35 нм. Для каждой нанотрубки в обоих методах применялся один и тот же кантилевер.
На подготовленных образцах с использованием а.с.м. выделялись индивидуальные нанотрубки, расположенные одновременно на двух соседних микроэлектродах. Сканирование выделенной у.н.т. методом э.с.м. проводилось по двухпроходной методике в области расположения нанотрубки на подложке между микроэлектродами. На первом проходе зонд сканирует поверхность образца в полуконтактном режиме для получения топографического изображения, на втором – зонд движется по траектории первого прохода на постоянной высоте от поверхности образца, равной 50 нм. На втором проходе к зонду прикладывалось постоянное смещение +5 В.
Величина продольного электрического сопротивления у.н.т. определялась с помощью п.а.с.м. На один из микроэлектродов через предусилитель в модуле головки а.с.м. подавалось линейно-модулированное напряжение в пределах от –1 до +1 В, к другому микроэлектроду прижимался кантилевер с постоянной силой 21 нН (среднее значение силы, начиная с которого величина тока не меняется с ростом силы прижатия) и проводилась регистрация вольт-амперной характеристики (в.а.х.) контакта “электрод–нанотрубка–электрод–зонд”.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
В качестве примера на рис. 1 показано 3D а.с.м.-изображение у.н.т. ∅27 нм, расположенной на двух соседних микроэлектродах. В.а.х. контакта “электрод–нанотрубка” для всех исследованных у.н.т. в диапазоне напряжений –1…+1 В имеют линейный вид, что свидетельствует об омическом характере контакта. Из полученных в.а.х. на основе данных по длине и диаметру у.н.т. (полученных при анализе а.с.м.-изображений) и с учетом вклада контактного сопротивления (оцененного с использованием результатов работы [3]) определялось продольное электрическое сопротивление и рассчитывалась удельная проводимость индивидуальных у.н.т. (данные представлены в табл. 1). При расчете удельной проводимости в качестве площади поперечного сечения у.н.т. бралась площадь поперечного сечения внешней стенки нанотрубки, так как именно она обеспечивает доминирующий вклад в проводимость многостенной у.н.т. [10]. Это обусловлено тем, что внешняя стенка имеет непосредственный контакт с микроэлектродами, и проводимость вдоль стенки на два–три порядка превышает проводимость между стенками у.н.т. [11]. Адекватный учет вклада внутренних стенок у.н.т. при расчете удельной проводимости невозможен в силу отсутствия достоверной информации о степени вовлеченности внутренних стенок в обеспечение проводимости нанотрубки, а также из-за необходимости учета особенностей структуры и состава дефектов у.н.т. Необходимо отметить, что при измерениях методом э.с.м. внешнее электрическое поле практически не проникает внутрь нанотрубки из-за ее высокой проводимости, и э.с.м.-сигнал в основном формируется при электростатическом взаимодействии зонда с ее внешней стенкой.
Таблица 1.
Средние значения морфологических и электрических параметров у.н.т.
| № образца | Сопротивление, кОм | Диаметр, нм | Длина, мкм | Удельная проводимость, См/см |
|---|---|---|---|---|
| 1 | 245 | 7 | 3.1 | 1.9 · 104 |
| 2 | 350 | 27 | 2.5 | 2.8 · 103 |
| 3 | 153 | 38 | 3.3 | 5.9 · 103 |
| 4 | 1500 | 62 | 3.2 | 3.6 · 102 |
| 5 | 118 | 66 | 4 | 5.3 · 103 |
На рис. 2 представлены типичное э.с.м.-изображение у.н.т. и соответствующий данному изображению профиль. Контраст э.с.м.-изображений указывает на проводящий характер у.н.т. Вокруг нанотрубок на изображении присутствует светлый контраст (увеличение э.с.м.-сигнала), который возникает вследствие установления емкостной связи между зондом и нанотрубкой, обусловленный наличием в у.н.т. свободных носителей заряда. Темный контраст (уменьшение э.с.м.-сигнала) связан с экранированием проводящей у.н.т. емкостной связи между зондом и подложкой в тот момент, когда зонд находится непосредственно над нанотрубкой [12]. Э.с.м.-профиль представляет собой зависимость сдвига фазы колебаний зонда от его продольной координаты. В представленном примере асимметрия экспериментального профиля э.с.м.-сигнала объясняется отличием формы зонда от идеальной полусферы.
Рис. 2.
Э.с.м.-изображение у.н.т. с внешним диаметром 27 нм и соответствующие экспериментальный и модельный профили поперечного сечения.

Для анализа профиля э.с.м.-сигнала у.н.т. использовалась модель, рассматривающая емкостные связи “зонд–подложка”, ”зонд–нанотрубка”, “нанотрубка–подложка” [8, 12]. В результате моделирования определялся параметр, характеризующий электрическую проводимость индивидуальной у.н.т., – напряжение “зонд–у.н.т.”. Данная величина лимитируется плотностью заряда, локализованного на поверхности у.н.т. непосредственно под зондом. Плотность заряда, в свою очередь, определяется концентрацией и подвижностью свободных носителей заряда, т.е. проводимостью у.н.т. [9].
Траектория движения зонда при сканировании нанотрубки, определяющая модельные емкости “зонд–подложка” и “зонд–нанотрубка”, описывалась движением шара радиусом R (радиус зонда) по поверхности шара радиусом r (радиус у.н.т.).
Фазовый сдвиг колебаний зонда может быть рассчитан по формуле вида [9]:
(1)
$\Phi (x) = {\text{arctg}}\left[ {\left( {\frac{Q}{{2k}}} \right)\frac{{{{\partial }^{2}}{{C}_{1}}(x)}}{{\partial {{x}^{2}}}}U_{1}^{2} + \left( {\frac{Q}{{2k}}} \right)\frac{{{{\partial }^{2}}{{C}_{2}}(x)}}{{\partial {{x}^{2}}}}U_{2}^{2}} \right],$При моделировании э.с.м.-профилей использовались реальные параметры кантилевера (Q = = 350, k = 6.6 Н/м), радиуса зонда (35 нм), диэлектрической проницаемости и толщины подложки (3.9 и 430 нм соответственно), контактной разности потенциалов между зондом и подложкой (+0.15 В), радиусов и длин нанотрубок.
Подгонка теоретического э.с.м.-профиля к экспериментальному осуществлялась с помощью метода наименьших квадратов. Критерием, которому должно соответствовать решение, является минимум суммы квадратов отклонений теоретического фазового сдвига от экспериментального:
(2)
$\sum\limits_{i = 1}^n {(\Phi ({{x}_{i}}) - {{\Phi }_{{{\text{э к с п }}}}}} ({{x}_{i}}){{)}^{2}} = \min ,$В качестве примера результатов моделирования на рис. 2 приведены экспериментальный и рассчитанный э.с.м.-профили. При моделировании профиля использовался пик с наибольшим значением сдвига фаз [9]. Ниже представлены следующие усредненные значения напряжения U2, которые получены при моделировании профилей э.с.м.-изображений, построенных в различных точках вдоль каждой у.н.т.:
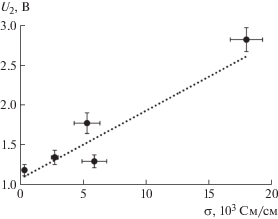
Для определения связи напряжения в зазоре “зонд–у.н.т.” с удельной проводимостью у.н.т. была построена корреляционная зависимость среднего значения напряжения U2 и удельной проводимости индивидуальной у.н.т. (рис. 3). Полученная зависимость демонстрирует сильную положительную корреляционную связь между напряжением U2 и удельной проводимостью σ с коэффициентом корреляции Пирсона, близким к единице (0.91). Наличие данной связи показывает, что величина напряжения в зазоре “зонд–у.н.т.”, полученная из анализа профилей э.с.м.-изображений, действительно характеризует проводимость у.н.т. Полученный результат для индивидуальных у.н.т. хорошо согласуется с результатами, полученными для слоев у.н.т. [13].
ЗАКЛЮЧЕНИЕ
В работе продемонстрирована возможность применения метода э.с.м. для определения параметра, характеризующего проводимость индивидуальных у.н.т. (разности потенциалов между зондом и у.н.т.). Установлена корреляционная зависимость между величиной напряжения в зазоре “зонд–у.н.т.” и удельной проводимостью индивидуальной у.н.т. На основе данной зависимости может быть построен градуировочный график для экспресс-оценки проводимости индивидуальных нанотрубок по величине разности потенциалов между зондом и у.н.т. для заданных значений прикладываемого смещения на зонде.
БЛАГОДАРНОСТИ
Авторы выражают благодарность Ю.А. Стенькину за синтез у.н.т.
ФИНАНСИРОВАНИЕ РАБОТЫ
Работа выполнена по государственному заданию Омского научного центра СО РАН в соответствии с Программой ФНИ ГАН на 2013–2020 годы (номер госрегистрации проекта в системе ЕГИСУ НИОКТР АААА-А17-117041210227-8), при частичной поддержке гранта РФФИ № 18-48-550009 р_а.
Список литературы
Dmitriev V., Gomes F., Nascimento C. // J. Aerospace Technology and Management. 2015. V. 7. P. 53. https://doi.org/10.5028/jatm.v7i1.358
Hou P.X., Du J., Liu C., Ren W., Kauppinen E.I., Cheng H.M. // MRS Bulletin. 2017. V. 42. P. 825. https://doi.org/10.1557/mrs.2017.238
An L., Friedrich C.R. // Nucl. Instrum. and Methods in Phys. Res. B. 2012. V. 272. P. 169. https://doi.org/10.1016/j.nimb. 2011.01.058
Jespersen T.S., Nygård J. // Appl. Phys. A. 2007. V. 88. P. 309. https://doi.org/10.1007/s00339-007-3927-7
Barboza A.P.M., Gomes A.P., Chacham H., Neves B.R.A. // Carbon. 2010. V. 48. P. 3287. https://doi.org/10.1016/j.carbon. 2010.05.028
Zdrojek M., Mélin T., Diesinger H., Stiévenard D., Gebicki W., Adamowicz L. // J. Appl. Phys. 2006. V. 100. P. 114326-1. https://doi.org/10.1063/1.2392674
Bede P., Dias R.A., Almeida C.A., Achete C.A., Fragneaud B. // Carbon. 2016. V. 102. P. 367. https://doi.org/10.1016/ j.carbon.2016.02.062
Staii C., Johnson Jr. A.T., Pinto N.J. // Nano Lett. 2004. V. 4. P. 859. https://doi.org/10.1021/nl049748w
Davletkildeev N.A., Stetsko D.V., Bolotov V.V., Stenkin Y.A., Korusenko P.M., Nesov S.N. // Material Lett. 2015. V. 161. P. 534. https://doi.org/10.1016/j.matlet.2015.09.045
Skakalova V., Kaiser A. B., Woo Y.-S., Roth S. // Phys. Rev. B. 2006. V. 74. P. 085403. https://doi.org/10.1103/PhysRevB. 74.085403
Agrawal S., Raghuveer M.S., Li H., Ramanath G. // Appl. Phys. Lett. 2007. V. 90. P. 193104. https://doi.org/10.1063/ 1.2737127
Давлеткильдеев Н.А., Соколов Д.В., Лобов И.А., Болотов В.В.// Письма в ЖТФ. 2014. Т. 40. № 21. С. 63.
Давлеткильдеев Н.А., Соколов Д.В., Лобов И.А., Болотов В.В. // Письма в ЖТФ. 2017. Т. 43. № 4. С. 47. https://doi.org/10.21883/PJTF.2017.04.44297.16489
Дополнительные материалы отсутствуют.
Инструменты
Приборы и техника эксперимента