Приборы и техника эксперимента, 2020, № 2, стр. 13-20
ИССЛЕДОВАНИЕ ФОРМЫ СИГНАЛОВ В 3He-СЧЕТЧИКЕ ПРИ РЕГИСТРАЦИИ НЕЙТРОНОВ
И. А. Васильев a, Р. М. Джилкибаев a, *, Д. В. Хлюстин a
a Институт ядерных исследований РАН
117312 Москва, просп. 60-летия Октября, 7а, Россия
* E-mail: rmd@inr.ru
Поступила в редакцию 17.09.2019
После доработки 17.09.2019
Принята к публикации 23.09.2019
Аннотация
Представлены результаты исследования формы сигналов в 3He-счетчике при регистрации тепловых нейтронов. Разработана электроника, состоящая из зарядово-чувствительного предусилителя и усилителя-формирователя сигналов счетчика. Проведено сравнение измеренной формы сигналов с результатами моделирования сигналов в 3He-счетчике при регистрации нейтронов. Предложен новый метод определения давления 3He в счетчике, основанный на измерении эффективности сбора полного заряда и максимальной эффективной ширины сигналов в счетчике. Данный метод хорошо согласуется с прямым измерением давления 3He в счетчике методом пропускания.
1. ВВЕДЕНИЕ
Данная работа связана с разработкой элементов установки ИНЕС по измерению полных и парциальных (n, γ) сечений на импульсном источнике нейтронов РАДЭКС Центра коллективного пользования ИЯИ РАН [1]. Установка ИНЕС использует времяпролетную (TOF – Time of Flight) методику для измерения сечений и состоит из сцинтилляционного γ-детектора, мониторных и пучковых нейтронных 3He-счетчиков СНМ-18-1. Пропорциональные счетчики, заполненные 3He, широко используются для регистрации нейтронов в ядерной физике [2, 3]. Счетчик нейтронов СНМ-18-1 представляет собой цилиндрическую тонкостенную латунную камеру длиной 310 мм и диаметром 32 мм. В центре камеры расположен анод диаметром 100 мкм. Камера заполнена газовой смесью 3He (97%) + Ar (3%) с давлением, равным 4 атм на момент изготовления счетчика. Имеющиеся в нашем распоряжении счетчики нейтронов СНМ-18-1 изготовлены в 1982 г. Поскольку давление 3He в счетчике со временем падает, нами предложен метод определения его давления в счетчике, основанный на измерении эффективности сбора полного заряда и максимальной эффективной ширины сигналов в счетчике.
2. ОПИСАНИЕ РАБОТЫ 3He-СЧЕТЧИКОВ
3He имеет большое сечение (5330 б) захвата тепловых нейтронов в реакции 3He + n– > 3H + p с выделением полной энергии, равной 764 кэВ. В результате 2-частичной реакции захвата в конечном состоянии появляются протон с энергией 573 кэВ и тритон (3H) с энергией 191 кэВ, имеющие одинаковые импульсы и разлетающиеся в противоположные стороны. В 3He с давлением 2.5 атм протоны и тритоны имеют средний пробег, равный 15.2 и 5.8 мм соответственно [4]. При этом протоны и тритоны образуют прямолинейные треки в газовой среде счетчика с разной плотностью ионизации вдоль соответствующего трека.
Пропорциональный режим работы счетчика задается выбором напряжения между анодом и катодом порядка ∼1000 В. Этот режим работы предполагает, что небольшое газовое усиление (∼100) вблизи анода позволяет пренебречь искажением электрического поля в этой области из-за пространственного заряда. Электроны ионизации, образованные вдоль трека, дрейфуют в электрическом поле счетчика к аноду, и на расстоянии нескольких длин свободного пробега электронов (∼10 мкм) от анода, в области сильного (∼30 кВ/см) электрического поля, происходит лавинообразное размножение электронов. При этом в газовом счетчике время образования лавины составляет ∼1 нс.
В зависимости от расположения трека относительно анода будет меняться временная картина прихода электронов ионизации к аноду. В результате 3He-счетчик будет работать как одномерная времяпроекционная камера (1D Time Projection Chamber). Для трека, параллельного аноду, все электроны ионизации достигнут анода практически одновременно, и анодный сигнал будет иметь самое короткое время нарастания. Поскольку ширина трека пренебрежимо мала, это эквивалентно событию с первоначальной ионизацией в точке. Импульс с анода счетчика от событий с точечной ионизацией будет иметь время нарастания, обусловленное временем дрейфа ионов из лавины от анода, и время спада, связанное с временем дифференцирования усилителя. Для трека, расположенного непараллельно аноду, форма импульса будет определяться как суперпозиция импульсов с точечной ионизацией в счетчике по времени прихода электронов ионизации трека к аноду. Для треков, расположенных перпендикулярно аноду, разница времен прихода первых и последних (наиболее удаленных) электронов ионизации будет максимальной, в результате чего импульс с анода будет иметь наиболее широкую и двугорбую форму. Регистрация формы импульсов с анода счетчика позволит оценить максимальное время дрейфа электронов ионизации, которое в свою очередь зависит от давления газа 3He в счетчике.
3. ЭЛЕКТРОНИКА 3He-СЧЕТЧИКА
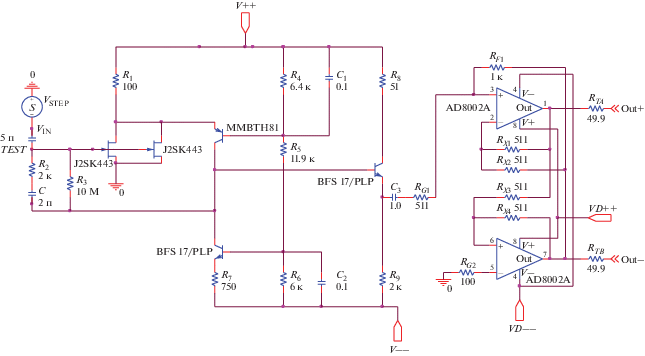
Для измерений формы импульсов с 3He-счетчиков СНМ-18-1 была разработана электроника, состоящая из зарядово-чувствительного предусилителя и усилителя-формирователя. Предусилители устанавливались в непосредственной близости от детектора СНМ-18-1 для уменьшения шумов. Аналоговые парафазные сигналы с выхода предусилителя передавались по длинному (≈10 м) кабелю (UTP Cat. 5E) на входы усилителя-формирователя. Питание предусилителей ±6 В осуществлялось по этому же кабелю. Для предусилителя выбрана стандартная схема [5, 6] зарядово-чувствительного усилителя с полевыми транзисторами на входе. Для уменьшения шумов применялись два малошумящих полевых транзистора J2SK443, соединенных параллельно. Принципиальная схема зарядово-чувствительного предусилителя с парафазным выходом показана на рис. 1.
Усилитель-формирователь имеет дифференциальный вход, усиливающий разность сигналов на входе. Шумы от наводки внешних сигналов на кабель дают сигналы одной полярности на входе усилителя-формирователя, поэтому результирующий сигнал от шумов наводки будет компенсироваться. Материнская плата на 8 измерительных каналов включает в себя двухпороговые дискриминаторы и усилители для передачи цифровых и аналоговых парафазных сигналов по согласованной длинной линии UTP (≈150 м) в измерительную комнату. Усилитель-формирователь состоит из дифференциального усилителя на входе, электронного фильтра Sallen–Key [7] и дифференциального выхода. Принципиальная схема усилителя-формирователя показана на рис. 2. Фильтр Sallen–Key реализован на основе операционного усилителя (AD828, U2A) и обеспечивает форму выходного сигнала, близкую к оптимальной [8], при которой достигается наилучшее отношение сигнал/шум при измерении амплитуды сигнала.
4. ИЗМЕРЕНИЯ СИГНАЛОВ В 3He-СЧЕТЧИКЕ
Измерения формы сигналов счетчика при регистрации тепловых нейтронов проводились с помощью 12-битного 4-канального аналого-цифрового преобразователя CAEN DT5720 (waveform digitizer) [9]. Устройство работало на частоте 250 МГц, амплитуда сигналов измерялась в 4096 точках с интервалом 4 нс.
Трек частиц состоит из протонного и 3Н участков длиной 38 мм/Р и 14.5 мм/Р соответственно, где Р – давление 3He в счетчике, измеренное в атмосферах [4].
Зависимость амплитуды типового сигнала на выходе усилителя с анода счетчика от времени показана на рис. 3а. Распределение собранного заряда при регистрации нейтронов в счетчике, полученное интегрированием амплитуды сигналов в интервале 4–16 мкс, приведено на рис. 3б.
Рис. 3.
а – амплитуда типового сигнала на выходе усилителя с анода счетчика; б – гистограмма собранного заряда при регистрации нейтронов в счетчике, полученная интегрированием амплитуды сигналов в интервале 4–16 мкс.

Узкий пик в распределении собранного заряда аппроксимируется функцией Гаусса со средним зарядом и дисперсией, соответственно равными 2413 и 37.7 и выраженными в условных единицах. Относительная ширина пика равна 3.7% (FWHM). На распределении (см. рис. 3б) можно выделить три граничных значения (600, 1800 и 2400) собранного заряда, при которых начинается резкое увеличение числа событий в распределении. Первые два граничных значения (600, 1800) связаны с событиями реакции захвата нейтронов и образования треков вблизи катода счетчика, в которых регистрируется только один 3Н-трек (191 кэВ) или протонный (574 кэВ) трек соответственно. Другая часть трека поглощается катодом. События, в которых оба трека находятся в газовом объеме счетчика, имеют энерговыделение 765 кэВ и дают узкий пик с суммарным зарядом в районе 2400. Таким образом, граничные значения (600, 1800 и 2400) собранного заряда находятся в линейной зависимости от энерговыделения треков (191, 574 и 765 кэВ), следовательно, счетчик работает в линейном режиме. Эффективность регистрации полного заряда определяется как отношение площади под распределением Гаусса к полной площади и составляет ∼31%.
Общая длина трека равна 52.5 мм/Р [4]. Отсюда следует, что при давлении меньше 3.4 атм общая длина трека от протона и тритона будет превышать радиус счетчика, и максимальное время дрейфа электронов будет определяться радиусом счетчика.
Моделирование методом Монте-Карло использовалось для определения зависимости эффективности собирания полного заряда трека, эквивалентного энерговыделению 764 кэВ, от давления 3He в счетчике. Длина треков в счетчике однозначно определяется давлением 3Не в счетчике при регистрации тепловых нейтронов. При этом полагается, что трек в объеме счетчика равномерен и изотропен и не достигает стенки счетчика. Такие события дают узкий пик (см. рис. 3б) в распределении сигналов в счетчике при регистрации нейтронов в зависимости от собранного заряда. Эффективность сбора полного заряда зависит от геометрии счетчика и длины треков.
Результаты моделирования зависимости эффективности собирания полного заряда от давления 3Не в счетчике представлены на рис. 4. Измеренная эффективность собирания полного заряда, равная ∼31%, находится в хорошем согласии с вычисленной величиной при условии, что давление в счетчике составляет 2.5 атм. Согласно рис. 4, ошибка 1% при измерении эффективности сбора полного заряда приводит к ошибке измерения давления 0.05 атм. Таким образом, по результатам измерения эффективности сбора полного заряда счетчиком можно определить давление 3Не как 2.5 ± 0.05 атм.
Программа LTspice [10] использовалась при моделировании формы сигналов для событий с треком, параллельным аноду, в электронной схеме, состоящей из предусилителя и усилителя-формирователя. Для трека, параллельного аноду, все электроны ионизации достигнут анода практически одновременно, и тем самым анодный сигнал будет иметь минимальное время нарастания. При этом полагается, что основной вклад в импульс с анода дает сигнал от движения ионной компоненты лавины вблизи анода счетчика, имеющий логарифмическую зависимость от времени: V(t) = Q/Cln(1 + t/T0) [11], где Q – заряд лавины, C – емкость анода, T0 – характерное время, определяемое давлением газа, диаметром анода, подвижностью ионов в газе и составляющее ∼30 нс.
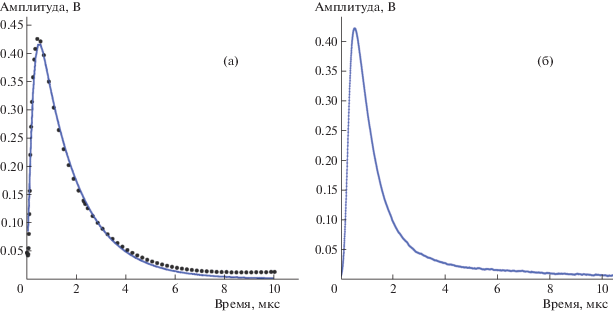
Смоделированная форма импульса на выходе усилителя-формирователя, определяемая вкладом движения ионов лавины вблизи анода счетчика, показана точками на рис. 5а. Эта форма импульса хорошо аппроксимируется произведением функций erf и exp: Aerf(t/t0)exp(–t/t1), где A – амплитуда, t0 – время нарастания сигнала и t1 – время спада сигнала. Результирующая кривая с параметрами фита, равными: A = 0.62, t0 = 0.4 мкс, t1 = = 1.6 мкс, показана на рис. 5а. При этом аппроксимирующая кривая хорошо описывает форму импульса с анода, за исключением плавного спада во времени. Наличие этого спада в импульсах обусловлено логарифмической зависимостью от времени входного сигнала. Смоделированная форма импульса хорошо согласуется с измеренной формой импульса (рис. 5б) счетчика СНМ-18-1. При этом отбирался импульс с минимальным временем нарастания и полным зарядом, который лежит в узком интервале (2350–2500) под пиком (см. рис. 3б).
Рис. 5.
а – смоделированная форма импульса на выходе усилителя-формирователя (точки) для событий с треком, параллельным аноду, сплошная кривая – аппроксимация зависимостью Aerf(t/t0)exp(-t/t1); б – измеренная форма импульса счетчика с минимальным временем нарастания.
Время дрейфа электронов ионизации, образованных вдоль трека, зависит от расстояния до анода и скорости дрейфа электронов в газовой среде счетчика СНМ-18-1. При этом скорость дрейфа электронов будет в основном определяться 3He, ввиду того что его парциальное давление много больше, чем Ar. Реальное соотношение остаточных парциальных давлений газов в счетчике можно оценить в предположении, что Ar практически не вытекает из счетчика и его парциальное давление в счетчике не меняется. Исходя из этого, первоначальная примесь Ar (3%) в счетчике увеличится до 4.6% при давлении 3He, равном 2.5 атм.
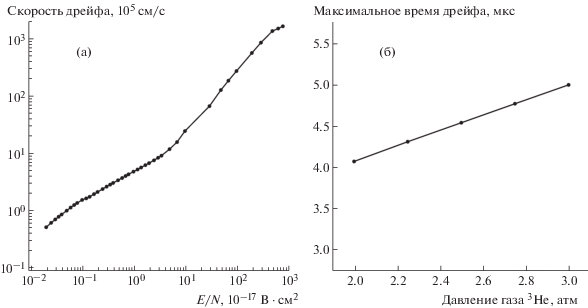
Напряженность, В/см, электрического поля в счетчике в точке, расположенной на расстоянии r от анода, равна Е = V/r/ln(R/a), где V, В – напряжение на аноде, R = 1.55 см – внутренний радиус счетчика, a = 0.005 см – радиус анода. Таким образом, напряженность поля в точке, удаленной от анода на расстояние 1 см, равна Е = 190 В/см при рабочем напряжении на счетчике 1100 В. Зависимость скорости дрейфа электронов ионизации в 4He от величины E/N, где E – напряженность электрического поля, а N – плотность газа, показана на рис. 6а [12]. Удельная плотность N, атом/см3, газа зависит от давления P, Торр, и температуры T, К, газа следующим образом: N = = 2.69 ⋅ 1019 ⋅ (P/760) ⋅ (273/T). При давлении 3Не 2.5 атм общая длина трека от протона и тритона превышает радиус счетчика, и максимальное время дрейфа электронов будет определяться радиусом счетчика. Можно оценить максимальную разницу времен прихода первых и последних электронов ионизации к аноду счетчика как время дрейфа электрона от катода к аноду. Детальный расчет времени дрейфа электрона ионизации от катода к аноду при давлении 3Не 2.5 атм дает значение 4.5 мкс. На рис. 6б приведена зависимость вычисленного времени дрейфа электронов ионизации, образованных вблизи катода, от давления 3Не в счетчике. Эта зависимость имеет линейный характер и не зависит от длины трека, поскольку общая длина трека больше радиуса счетчика.
Рис. 6.
а – зависимость скорости дрейфа электронов ионизации в 4He от величины E/N, где E – напряженность электрического поля, а N – плотность газа; б – зависимость вычисленного времени дрейфа электронов ионизации, образованных вблизи катода, от давления 3Не в счетчике.
Разница времен прихода ближайших к аноду и наиболее удаленных электронов ионизации будет максимальной для треков, расположенных перпендикулярно к аноду, в результате чего импульс с анода будет иметь наиболее широкую и двугорбую форму. Второй пик во временной зависимости амплитуды сигнала связан с тем, что в конце трека протона или тритона резко возрастает число электронов ионизации на единицу длины трека. События с двугорбой формой имеют четкую сигнатуру и несут информацию о длине трека. Регистрация формы импульсов с анода счетчика позволит определить максимальное время дрейфа электронов ионизации, которое зависит от давления 3He в счетчике, и тем самым оценить давление в счетчике.
Для определения эффективной ширины импульса двугорбой формы использовался алгоритм поиска пиков в программе TSpectrum [13]. Для корректной работы программы амплитуды сигналов инвертировались. При этом поиск пиков проводился для событий с полным зарядом в узком интервале (2350–2500) под пиком (см. рис. 3б). Для таких событий треки протона и тритона, образованные в результате реакции захвата нейтрона ядром 3Не, полностью находятся внутри газового объема и не касаются стенок счетчика.
Двугорбая форма сигнала на выходе усилителя, имеющего максимальную эффективную ширину импульса 4.5 мкс, показана на рис. 7.
Рис. 7.
Зависимость амплитуды сигнала на выходе усилителя с анода счетчика от времени для события, имеющего максимальную эффективную ширину импульса 4.5 мкс.

Эффективная ширина сигнала определялась как разница во времени между положением максимума второго пика и началом первого пика с порогом, равным 5% от максимума пика.
Гистограмма распределения отобранных событий с двугорбой формой и полным зарядом в узком интервале 2350–2500 под пиком (см. рис. 3б) в зависимости от эффективной ширины сигнала с анода счетчика представлена на рис. 8а. В этом распределении максимальная эффективная ширина сигнала составила 4.5 ± 0.1 мкс. Как было отмечено выше, при длине трека больше радиуса счетчика максимальная разница времен прихода первых и последних электронов ионизации к аноду счетчика вычисляется как время дрейфа электрона от катода к аноду. По результатам моделирования зависимости времени дрейфа электронов ионизации, образованных вблизи катода, от давления 3Не в счетчике (см. рис. 6б) можно оценить давление 3Не в счетчике как 2.5 ± 0.1 атм.
Рис. 8.
а – гистограмма распределения отобранных событий с полным зарядом в узком интервале под пиком в зависимости от эффективной ширины сигнала с анода счетчика; б – зависимость эффективности пропускания тепловых нейтронов от давления газа 3Не в счетчике.

Этот результат находится в хорошем согласии с величиной 2.5 ± 0.05 атм, полученной путем измерения эффективности сбора полного заряда счетчиком. Таким образом, можно заключить, что два метода анализа формы сигналов – измерение эффективности собирания полного заряда и максимальной эффективной ширины сигнала – хорошо согласуются и позволяют определить давление 3Не в счетчике.
Другой, хорошо известный метод, основанный на методе пропускания [14], использовался для независимого измерения давления 3Не в счетчике. Метод пропускания основан на определении эффективности пропускания тепловых нейтронов через исследуемый счетчик. Для этого использовалась простая установка, состоящая из коллимированного источника тепловых нейтронов, мониторного нейтронного счетчика и исследуемого нейтронного счетчика. При этом эффективность мониторного счетчика не влияет на определение эффективности пропускания тепловых нейтронов через исследуемый счетчик. Источник тепловых нейтронов выполнен в форме закрытого куба из борированного полиэтилена размером 600 × 600 × 600 мм и с толщиной стенок 100 мм, внутри которого помещен источник 252Cf. Для создания пучка тепловых нейтронов размером, сравнимым со счетчиком СНМ-18-1, с внешней стороны куба размещались с образованием щели 32 × 400 мм листы из Cd (толщиной 1 мм), поглощающие тепловые нейтроны. Напротив щели на расстоянии 100 мм помещался исследуемый счетчик, а за ним – мониторный счетчик СНМ-17 диаметром 18 мм и длиной 200 мм. Исследуемый счетчик геометрически полностью перекрывал поток прямых тепловых нейтронов, попадающих в мониторный счетчик. Таким образом, в мониторный счетчик попадали прямые и фоновые тепловые нейтроны. Для определения эффективности пропускания (eff) тепловых нейтронов через исследуемый счетчик проводилось три измерения:
1) без счетчика СНМ-18-1 монитор регистрировал счет (N1) прямых (n) и фоновых (n0) нейтронов: N1 = n0 + n;
2) при подавленном потоке прямых нейтронов и закрытой листом Cd щели монитор регистрировал счет (N2) фоновых нейтронов: N2 = n0;
3) с счетчиком СНМ-18-1 монитор регистрировал счет (N3) прямых ослабленных (n ⋅ eff) и фоновых (n0) нейтронов: N3 = n0 + n ⋅ eff.
В результате получено три уравнения с тремя неизвестными, решение которых относительно eff будет имеет вид: eff = (N3 – N2)/(N1 – N2). Проведенные измерения со счетчиком СНМ-18-1 дали следующий результат: eff = (405 – 219)/(700 – 219) = = 0.38 ± 0.02.
Эффективность пропускания тепловых нейтронов зависит от длины трека нейтрона, пересекающего исследуемый счетчик, от сечения взаимодействия нейтрона с 3Не с учетом теплового размытия по энергии нейтрона и от давления газа в счетчике. Тепловое размытие скорости V нейтрона моделировалось с учетом того, что функция плотности вероятности по скорости равна p(x) = = x2exp(–x2). Здесь х = V/Vp – относительная скорость; Vp – наиболее вероятная скорость нейтронов, находящихся в тепловом равновесии при температуре Т: $V_{p}^{2}$ = 2kT/m, где k – постоянная Больцмана и m – масса нейтрона. Программа GEANT4 [15] использовалась для вычисления зависимости эффективности пропускания тепловых нейтронов от давления 3Не в счетчике, которая представлена на рис. 8б. Измеренная и вычисленная эффективности пропускания согласуются при условии, что давление в счетчике составляет 2.4 ± ± 0.2 атм. Это находится в хорошем согласии со значениями, ранее полученными путем измерения эффективности сбора полного заряда и максимальной эффективной ширины сигналов в счетчике.
5. ЗАКЛЮЧЕНИЕ
Представлены результаты исследования формы сигналов в 3He-счетчике при регистрации тепловых нейтронов. Разработана электроника, состоящая из зарядово-чувствительного предусилителя и усилителя-формирователя сигналов счетчика. Проведено сравнение измеренной формы сигналов с результатами моделирования сигналов в 3He-счетчике при регистрации нейтронов. Предложен новый метод определения давления 3He в счетчике, основанный на измерении эффективности сбора полного заряда и максимальной ширины сигналов в счетчике. Проведенные измерения давления 3He с использованием независимого метода пропускания показали результаты, которые хорошо согласуется с предложенным методом.
Список литературы
Бенецкий Б.А., Вахетов Ф.З., Грачев М.И., Даньшин С.Н., Емельянов В.В., Жуков Ю.Н., Заикин Д.А., Копте-лов Э.А., Кутузов В.А., Лебедев С.Г., Мордовской М.В., Рябов Ю.В., Сазанов В.Н., Скоркин В.И., Соболевский Н.М. и др. Препринт ИЯИ-1058/2001. М.: 2001.
Mazeda D., Mameri S., Giolini R. // Radiation Measurements. 2012. V. 47. P. 577. https://doi.org/10.1016/j.radmeas.2012.06.002
Langford T.J., Bass C.D., Beise E.J., Breuer H., Erwin D.K., Heimbach C.R., Nico J.S. // Nucl. Instrum. and Methods in Physics Research. 2003. V. A717. P. 51. https://doi.org/10.1016/j.nima.2013.03.062
Ziegler J.F., Biersack J.P. SRIM2000. The Stopping and Range of Ions in Matter. Version 0.06. 2000. www.srim.org
Santiard J. CERN/EP/JCS/ef. 7 October 1976.
Radeka V. // Ann. Rev. Nucl. Sci. 1988. V. 38. P. 217.
Sallen R., Key L. // IRE Trans. Circuit Theory. 1955. V. CT-2. P. 74.
Цитович А.П. Ядерная электроника. М.: Энергоатомиздат, 1984.
CAEN DT5720. 4 channel 12 bit waveform digitizer. http://www.caen.it
LTspice. Analog electronic circuit simulator. http://www.analog.com
Sauli F. Report CERN 77-09. Geneva: CERN, 1977.
Физические величины. Справочник / Под ред. И.С. Григорьева, Е.З. Мейлихова. М.: Энергоатомиздат, 1991.
Brun R., Rademakers F. // Nucl. Instrum. and Methods in Physics Research. 1977. V. A389. P. 81. https://doi.org/10.1016/S0168-9002(97)00048-X
Абрамов А.И., Казанский Ю.А., Матусевич Е.С. Основы экспериментальных методов ядерной физики. М.: Атомиздат, 1970.
Geant4 Collaboration Agostinelli S. et al. // Nucl. Instrum. and Methods in Physics Research. 2003. V. A506. P. 250. https://doi.org/10.1016/S0168-9002(03)01368-8
Дополнительные материалы отсутствуют.
Инструменты
Приборы и техника эксперимента