Приборы и техника эксперимента, 2020, № 3, стр. 30-39
ИЗМЕРЕНИЕ ЭМИТТАНСА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ В малогабаритных линейных ускорителях
И. А. Каньшин a, *, **, А. А. Солодовников a
a ВНИИ автоматики им. Н.Л. Духова
127055 Москва, Сущевская ул., 22, Россия
* E-mail: ilia.kanshin2011@yandex.ru
** E-mail: iliakanshin1991@gmail.com
Поступила в редакцию 07.11.2019
После доработки 05.12.2019
Принята к публикации 16.12.2019
Аннотация
Разработана и апробирована методика “бесконтактного” измерения эмиттанса корпускулярного потока, экстрагируемого из пеннинговского ионного источника малогабаритного линейного ускорителя заряженных частиц. Вычисление эмиттанса достигается в ходе минимизации разности между теоретически рассчитанными и экспериментально измеренными размерами пучка в ионно-оптической системе ускорителя. Измерение размеров выполнялось в ходе фоторегистрации светящегося в ионно-оптической системе следа корпускулярного потока. Представлены результаты применения “бесконтактного” метода измерения эмиттанса пучка корпускулярного потока.
ВВЕДЕНИЕ
При разработке малогабаритных линейных ускорителей (м.л.у.), конструкция которых включает пеннинговский источник ионов (п.и.и.) и ионно-оптическую систему (и.о.с., рис. 1), уделяется особое внимание электропрочности прибора [1–4]. Ее снижение приводит к пробоям по поверхности изолятора и выходу прибора из строя. Снижение электропрочности связано, в частности, с запылением внутренней поверхности высоковольтного изолятора и.о.с. продуктами взаимодействия пучка ионов с ее электродами [4].
Рис. 1.
Принципиальная схема м.л.у. 1 – газоразрядная плазма в п.и.и.; 2 – заземленная выходная апертура п.и.и.; 3 – высоковольтный изолятор и.о.с.; 4 – ускоряющий электрод и.о.с.; 5 – экстрагируемый из п.и.и. пучок ионов; 6 – распыленный материал ускоряющего электрода и.о.с.; 7 – напыление на поверхности изолятора и.о.с.

К распылению приводит бомбардировка ускоряющего электрода и.о.с. ионами экстрагируемого из п.и.и. пучка. Это обусловлено рассогласованной работой п.и.и. и и.о.с., являющейся следствием несогласованности эмиттанса пучка и аксептанса и.о.с. [5]. Поэтому при разработке м.л.у. актуальной является задача экспериментального определения эмиттанса пучка, как на этапах стендовых исследований, так и на этапах макетирования готовых (отпаянных) изделий.
Обычно подобные измерения проводят с помощью систем щелей и экранов [6, 7], проволочных коллекторов тока пучка [8, 9], pepper-pot сканеров [10, 11], квадруполей [12, 13], триплетов [14], соленоидов [15], отклоняющих пластин [16]. Однако во всех указанных выше случаях перечисленные диагностические элементы размещаются на пути пучка, и происходит либо их прямое взаимодействие (pepper-pot, экраны), либо косвенное за счет воздействия на пучок магнитных (квадруполи, соленоиды) и электрических (отклоняющие пластины) полей. В свою очередь, размещение диагностических элементов внутри готового (отпаянного) м.л.у. затруднительно. Более того, при прямом взаимодействии происходит искажение пучка, и его дальнейшее использование в отпаянном м.л.у. по предназначению невозможно.
В данной статье описывается “бесконтактная” методика измерения эмиттанса экстрагируемого из п.и.и. пучка, при использовании которой не требуется размещать диагностические элементы внутри м.л.у. Вычисление эмиттанса достигается в ходе минимизации разности между размерами пучка, теоретически рассчитанными и экспериментально измеренными по его фотографическому изображению в и.о.с.
ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЯ ЭМИТТАНСА
Описываемый в статье метод базируется на восстановлении значения эмиттанса ε и параметров Твисса α, β, γ [17, 18] в фиксированной поперечной движению пучка плоскости в системе его транспортировки. Используя эти величины в качестве коэффициентов в нижеследующем уравнении, можно построить фазовую диаграмму эмиттанса в плоскости поперечных координат частиц пучка x и их углов вылета $x{\text{'}}$, имеющую форму эллипса (центр эллипса совмещен с осью пучка):
Рассмотрим принцип измерения эмиттанса экстрагируемого из п.и.и. пучка в м.л.у. (рис. 2). Примем, что эмиттанс восстанавливается в фиксированной плоскости на выходе из п.и.и.
Рис. 2.
Схематичное изображение плоскостей измерения размеров пучка в м.л.у. 1 – газоразрядная плазма в п.и.и.; 2 – заземленная выходная апертура п.и.и.; 3 – плоскость вычисления эмиттанса; 4 – высоковольтный изолятор и.о.с.; 5 – ускоряющий электрод и.о.с.; 6 – пучок ионов; di – измеряемые экспериментально поперечные размеры пучка на расстоянии Li от плоскости измерения эмиттанса.

К ускоряющему электроду и.о.с. 5 прикладывается отрицательный относительно земли потенциал (ускоряющее напряжение), что приводит к экстракции из п.и.и. 2 и ускорению в и.о.с. пучка положительно заряженных ионов 6. В ускорительном зазоре в i-х поперечных движению пучка плоскостях, располагающихся на расстояниях Li от плоскости вычисления эмиттанса, последовательно измеряются поперечные размеры пучка di = $2r_{i}^{{{\text{эксп}}}}$ и вычисляется величина осевого потенциала Ui относительно плоскости измерения эмиттанса 3 (например, посредством численного моделирования).
Движение пучка в направлении Z через любой оптический элемент (дрейфовый или ускоряющий промежуток, квадруполь и т.д.) можно описать с помощью известной матрицы перехода [18, 19]:
(2)
${{M}_{{{\text{transf}}}}} = \left( {\begin{array}{*{20}{c}} C&S \\ {C{\text{'}}}&{S{\text{'}}} \end{array}} \right),$(3)
$r_{i}^{{\text{Т}}} = \sqrt {C_{i}^{2}\beta \varepsilon - 2{{C}_{i}}{{S}_{i}}\alpha \gamma + S_{i}^{2}\gamma \varepsilon } ,$Согласно [19], матрица перехода (2) ускорительного зазора выглядит следующим образом:
(4)
$M_{{{\text{transf}}}}^{{{\text{accel}}}} = \left( {\begin{array}{*{20}{c}} 1&{2{{L}_{i}}{\text{/}}(\sqrt {{{U}_{i}}{\text{/}}{{U}_{1}}} + 1)} \\ 0&{\sqrt {{{U}_{1}}{\text{/}}{{U}_{i}}} } \end{array}} \right),$Для восстановления эмиттанса и параметров Твисса в плоскости 3 (рис. 2) выполняется минимизация разности между n экспериментально измеренными размерами пучка $r_{i}^{{{\text{эксп}}}}$ и теоретически вычисленными по формуле (3) $r_{i}^{{\text{T}}}$ [7, 14]:
(5)
${{\chi }^{2}} = \sum\limits_{i = 1}^n {{{{({{{(r_{i}^{{\text{T}}})}}^{2}} - {{{(r_{i}^{{{\text{эксп}}}})}}^{2}})}}^{2}}} = \min .$Экстремум функционала (5), являющийся его минимумом [14, 17], определяется равенством нулю частных производных $\frac{{\partial {{\chi }^{2}}}}{{\partial (\alpha \varepsilon )}}$ = 0, $\frac{{\partial {{\chi }^{2}}}}{{\partial (\beta \varepsilon )}}$ = 0, $\frac{{\partial {{\chi }^{2}}}}{{\partial (\gamma \varepsilon )}}$ = 0, что выражается следующей системой уравнений в матричном виде [14, 17]:
(6)
$\begin{gathered} \left( {\begin{array}{*{20}{c}} {\beta \varepsilon } \\ {\alpha \varepsilon } \\ {\gamma \varepsilon } \end{array}} \right) = {{\left( {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^n {C_{i}^{4}} }&{ - 2\sum\limits_{i = 1}^n {C_{i}^{3}{{S}_{i}}} }&{\sum\limits_{i = 1}^n {C_{i}^{2}S_{i}^{2}} } \\ { - 2\sum\limits_{i = 1}^n {C_{i}^{3}{{S}_{i}}} }&{4\sum\limits_{i = 1}^n {C_{i}^{2}S_{i}^{2}} }&{ - 2\sum\limits_{i = 1}^n {{{C}_{i}}S_{i}^{3}} } \\ {\sum\limits_{i = 1}^n {C_{i}^{2}S_{i}^{2}} }&{ - 2\sum\limits_{i = 1}^n {{{C}_{i}}S_{i}^{3}} }&{\sum\limits_{i = 1}^n {S_{i}^{4}} } \end{array}} \right)}^{{ - 1}}} \times \\ \, \times \left( {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^n {C_{i}^{2}{{{(r_{i}^{{{\text{эксп}}}})}}^{2}}} } \\ { - 2\sum\limits_{i = 1}^n {{{C}_{i}}{{S}_{i}}{{{(r_{i}^{{{\text{эксп}}}})}}^{2}}} } \\ {\sum\limits_{i = 1}^n {S_{i}^{2}{{{(r_{i}^{{{\text{эксп}}}})}}^{2}}} } \end{array}} \right). \\ \end{gathered} $Разрешение данной системы совместно с условием $\beta \gamma - {{\alpha }^{2}} = 1$ [17] позволяет вычислить искомые эмиттанс ε и параметры Твисса α, β, γ. По полученным данным, исходя из (1), строится фазовая диаграмма эмиттанса.
Измерение поперечных размеров пучка di = $2r_{i}^{{{\text{эксп}}}}$ выполняется на этапе обработки фотографий его светящегося следа, возникающего при транспортировке пучка ионов вследствие его взаимодействия с газовой средой. Движущийся через газ ионный пучок передает часть своей энергии на возбуждение и ионизацию молекул и атомов газовой среды. Возбуждение внутренних уровней энергии снимается испусканием фотонов [21, 22], благодаря чему возможна визуализация следа первичного пучка ионов.
В результате ионизации появляются медленные электроны [21, 22], которые, как сказано в [22], при взаимодействии с газовой средой могут также вызывать ее возбуждение. В этом случае испускание фотонов возбужденными атомами и молекулами может нарушать след первичного пучка ионов и приводить к искажению его реальной формы и, как следствие, некорректному определению его поперечных размеров. Поэтому целесообразно иметь представление о том, какой процесс позволяет визуализировать след пучка ионов в и.о.с. м.л.у.
Для этого воспользуемся приведенными в [23] оценками сечений взаимодействия. В качестве газовой среды будем рассматривать молекулярный водород, выступавший рабочим газом при проведении экспериментов. Поскольку в работе используется источник ионов Пеннинга, то из него экстрагируются преимущественно молекулярные ионы ${\text{H}}_{2}^{ + }$, а доля атомарных ионов H+ составляет не более 10% [2]. Таким образом, при рассмотрении сечений учитываем только процессы ионизации и возбуждения молекулярного водорода его молекулярным ионом, а также возбуждения молекулярного водорода электроном.
Как показывают зависимости, представленные в [23], до момента достижения первичным пучком ионов энергии 30 кэВ превалирующим в и.о.с. будет являться процесс возбуждения газовой среды. По достижении 30 кэВ наиболее вероятным становится процесс ионизации газовой среды первичным ионным пучком с образованием медленных электронов, которые могут также вызывать возбуждение газовой среды.
При этом во всем рассматриваемом диапазоне энергий частиц (от 0.1 до 90 кэВ) сечение возбуждения газовой среды молекулярными ионами водорода не менее чем на порядок выше соответствующего сечения электронами. Исходя из этого, можно сделать вывод, что наиболее вероятным процессом, приводящим к появлению светящегося следа в и.о.с., является возбуждение молекул нейтральной газовой среды первичным ионным пучком.
Выясним, как процесс возбуждения молекул влияет на рост эмиттанса. Для этого оценим уширение поперечного профиля пучка, которое происходит за время релаксации возбужденных атомов водорода.
В [24, 25] сказано, что из возбужденного состояния в основное атомы возвращаются за промежуток времени порядка 10–8 с. Согласно [18], средняя скорость частиц в плазме равна $\bar {V}$ = $\sqrt {8kT{\text{/}}\pi m} $, где k = = 1.38 ⋅ 10–23 Дж/К – постоянная Больцмана, T – температура плазмы, m – масса частиц. В используемом в данном м.л.у. источнике Пеннинга электронная температура плазмы равна ~5 эВ [26], поэтому, согласно [27], ионная температура плазмы на порядок ниже электронной и может составлять около 0.5 эВ.
Подставляя в формулу для средней скорости частиц в плазме вместо T ионную температуру 0.5 эВ, выраженную в градусах Кельвина, и вместо m – массу протона, получим, что скорость ионов в поперечном направлении составляет около 1.2 ⋅ 104 м/с.
Скорость возбужденной молекулы рабочего газа, очевидно, будет меньше скорости налетающего иона ввиду передачи части его энергии на возбуждение. Однако для приводимых здесь оценок примем допущение, что скорость возбужденной молекулы равна скорости возбуждающего ее иона, т.е. 1.2 ⋅ 104 м/с. Произведение скорости возбужденной молекулы и времени релаксации атома равно примерно 0.1 мм. Таким образом, за время высвечивания атома молекула в поперечном оси Z направлении переместится на величину порядка десятых долей миллиметра. Однако эту величину превосходит случайная погрешность измерений размера пучка, составляющая не более 0.5 мм. Поэтому влияние процесса возбуждения молекул рабочего газа на рост эмиттанса в работе не учитывалось.
ОПИСАНИЕ ИССЛЕДОВАТЕЛЬСКОГО СТЕНДА И ПОСТАНОВКА ЭКСПЕРИМЕНТА
На рис. 3 показан внешний вид диагностического стенда TPS-compact, предназначенного для исследования разборных м.л.у. и размещенных внутри него п.и.и. и и.о.с.
Рис. 3.
Внешний вид стенда для исследования разборных м.л.у. (а) и размещенных внутри вакуумной камеры п.и.и. и и.о.с. разборного м.л.у. (б: 1 – высоковольтный ввод питания п.и.и.; 2 – вакуумная камера; 3 – направляющие шпильки и оправка для крепления п.и.и.; 4 – п.и.и.; 5 – выходная апертура п.и.и.; 6 – высоковольтный изолятор и.о.с.; 7 – ускоряющий электрод и.о.с.).

Рабочий газ – водород – вырабатывался в генераторе водорода. Давление в вакуумной камере поддерживалось турбомолекулярным насосом в режиме непрерывной откачки и составляло 1 мТорр (рабочее давление рассматриваемого в статье типа м.л.у.). Подача рабочего газа регулировалась с помощью прецизионного натекателя. Перед напуском рабочего газа вакуумная камера стенда откачивалась до давления остаточных газов (5–7) ⋅ 10–7 Торр. Поэтому влияние остаточного газа на рост эмиттанса в ускоряющем промежутке при проведении экспериментов не учитывалось. Контроль давления и управление источниками высокого напряжения осуществлялись с помощью персонального компьютера и специально разработанного приложения в среде LabVIEW. Более подробно исследовательский стенд TPS-compact описан в работе [1].
В вакуумной камере размещался п.и.и. 4 разборного м.л.у. (рис. 3б). На его анод через высоковольтный ввод 1 подавалось постоянное напряжение положительной полярности 1 кВ. Напряжение отрицательной полярности подавалось на ускоряющий электрод и.о.с. 7 и варьировалось от –1 до –5 кВ. Ток экстрагируемого из п.и.и. ионного пучка составлял 100–110 мкА (рабочий ток рассматриваемого в статье типа м.л.у.).
Выходная апертура 5 п.и.и. и ускоряющий электрод и.о.с. 7 гальванически развязаны посредством металлостеклянного изолятора 6 (рис. 3б). Его конструкция позволяла регистрировать светящийся след корпускулярного потока в и.о.с. с помощью дистанционно управляемой фотокамеры. Полученные в ходе эксперимента фотографии светящегося следа пучка автоматически обрабатывались с помощью программного обеспечения, написанного в среде LabVIEW.
Приведем более подробное описание процесса обработки фотографий следа пучка в и.о.с. и автоматического вычисления эмиттанса.
При измерении эмиттанса важно различить ореол пучка, т.е. область, где интенсивность свечения низка по сравнению с остальной частью пучка [18]. Например, в [17] сказано, что для пучка, имеющего гауссово распределение плотности тока в поперечном сечении, 10% и ниже от ее максимума соответствует ореолу пучка. С учетом ореола значение эмиттанса пучка завышается, что приводит к ошибке при его согласовании с аксептансом и.о.с. Поэтому в данной работе с целью выявления ореола пучка процесс вычисления эмиттанса был циклическим. Для этого при определении поперечного размера пучка di в каждой i‑й поперечной движению пучка плоскости (см. рис. 2) строился профиль интенсивности свечения пучка I(x), который аппроксимировался функцией Гаусса (рис. 4). Адекватность применимости такой функции была проверена с помощью критерия Пирсона [28].
Рис. 4.
а – фотографическое изображение светящегося следа пучка ионов в ускорительном зазоре и.о.с. с указанием области измерения профиля интенсивности свечения; б – профиль интенсивности свечения и его аппроксимация функцией Гаусса.
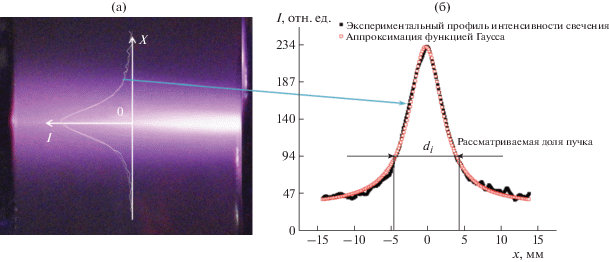
Затем размеры пучка di поочередно определялись на уровнях от 0.2σ (доля пучка 0.14%) до 3σ (доля пучка 99.7%), где σ – среднеквадратическое отклонение (с.к.о.) в аппроксимирующей функции Гаусса. На каждом уровне формировался массив из размеров пучка di, и одновременно в программу передавался массив значений осевого потенциала Ui в плоскостях, где измерялись размеры пучка. Массив значений осевого потенциала, в свою очередь, определялся в ходе численного моделирования распределения электрического поля в рассматриваемой геометрии и.о.с. в программе COMSOL Multiphysics 5.3. В итоге автоматически формировалась и решалась система уравнений (6), в результате чего вычислялись эмиттанс и параметры Твисса. Цикл процесса вычислений, блок-схема которого представлена на рис. 5, завершался по достижении уровня 3σ.
Также результатом вычислений являлся график зависимости эмиттанса от рассматриваемой доли пучка. На рис. 6 представлен его типичный для проведенных экспериментов вид, для которого характерны две ветви: пологая (до 80–85%) и крутая (свыше 90%). Первая ветвь демонстрирует монотонное возрастание эмиттанса пучка с увеличением его рассматриваемой доли. По достижении уровня 80–85% наблюдается переход ко второй ветви зависимости, демонстрирующей резкое изменение наклона графика. Это объясняется тем, что в основной части пучка, характеризуемой наибольшей интенсивностью свечения, по мере увеличения рассматриваемой доли пучка с.к.о., определяющее поперечный размер, растет медленно.
В области ореола пучка по мере увеличения его доли значение с.к.о. растет быстрее, что связано с появлением “хвостов” в профиле интенсивности. Таким образом, крутая ветвь принадлежит ореолу пучка, а пологая – основной его части. Поэтому значения эмиттанса и параметров Твисса, соответствующих координате точки, в которой меняется наклон графика и происходит переход от основной части пучка к его ореолу, являются искомыми значениями. Чтобы определить эту координату, необходимо найти точку пересечения двух прямых, одна из которых соответствует крутой ветви зависимости, а другая – пологой (рис. 6).
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ
Эмиттанс измерялся в плоскости выходной апертуры п.и.и., на расстоянии 20 мм от которой находился ускоряющий электрод и.о.с. (рис. 7а). Измерение эмиттанса выполнялось для случаев, когда напряжение на ускоряющем электроде Uaccel составляло 0, –1, –4 и –5 кВ.
Рис. 7.
Светящийся след корпускулярного потока в и.о.с. (а, 1 – выходная апертура п.и.и., 2 – ускоряющий электрод и.о.с.), карта распределения потенциала в и.о.с. (б), зависимость осевого потенциала от продольной координаты в ускорительном зазоре и.о.с. (в). Напряжение на ускоряющем электроде –1 кВ.

В качестве примера на рис. 7 показаны светящийся след пучка в и.о.с. (рис. 7а) при значении ускоряющего напряжения Uaccel = –1 кВ, а также смоделированные в среде COMSOL Myltiphysics 5.3 для данного случая распределение потенциала в и.о.с. (рис. 7б) и зависимость осевого потенциала от продольной координаты в и.о.с. (рис. 7в). Стоит отметить, что в плоскости измерения эмиттанса так же, как в плоскости входной апертуры ускоряющего электрода, происходит “провисание” поля в полости соответствующих электродов. Поэтому в точках графика, которые лежат в этих плоскостях, осевой потенциал Uax не равен потенциалам электродов.
В каждой плоскости, удаляющейся от плоскости вычисления эмиттанса вдоль оси Z системы, с шагом в 1.5 мм измерялись размеры пучка, и фиксировалось значение осевого потенциала. Таким образом, формировались коэффициенты для решения системы (6).
Ниже приведены полученные в результате вычислений значения эмиттанса и параметров Твисса:
| Uaccel, кВ | ε, π · мм · рад | α | β, мм/рад | γ, рад/мм |
| 0 | 2.12 ± 0.18 | –0.19 | 10.1 | 0.10 |
| –1 | 0.81 ± 0.15 | –0.1 | 25.2 | 0.04 |
| –4 | 0.41 ± 0.08 | 0.25 | 43.1 | 0.02 |
| –5 | 0.37 ± 0.06 | 0.51 | 34.9 | 0.04 |
На рис. 8 показаны фазовые диаграммы эмиттанса пучка, полученные “бесконтактным” методом для выбранных величин ускоряющего напряжения.
Рис. 8.
Диаграммы эмиттанса пучка, полученные при величинах ускоряющего напряжения 0 и –1 кВ (а), –4 и –5 кВ (б).
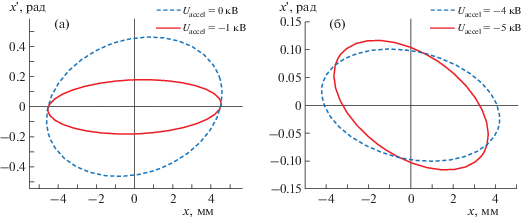
Из этого рисунка видно, что при величинах ускоряющего напряжения 0 и –1 кВ пучок является расходящимся (диаграммы занимают преимущественно квадранты I и III). По мере увеличения ускоряющего напряжения пучок принимает сходящуюся форму (диаграммы “проворачиваются” по часовой стрелке и занимают преимущественно квадранты II и IV). Таким образом, увеличение по модулю величины ускоряющего напряжения приводит к усилению фокусирующих свойств и.о.с., что также прослеживается на фотографических изображениях светящегося следа ионного пучка (рис. 9).
Рис. 9.
Фотографическое изображение светящегося следа пучка ионов в ускорительном зазоре и.о.с. при различных значениях ускоряющего напряжения. 1 – выходная апертура п.и.и., 2 – ускоряющий электрод и.о.с.

Также из рис. 8 видно, что уменьшается поперечный размер пучка при увеличении по модулю величины ускоряющего напряжения. Попытаемся объяснить это следующим образом. Известно, что максимальный размер пучка связан с эмиттансом и β-параметром Твисса соотношением xmax = $\sqrt {\varepsilon \beta } $ [14, 17]. При этом по результатам проведенных экспериментов также зафиксировано уменьшение эмиттанса пучка с увеличением модуля укоряющего напряжения (рис. 10 и вышеприведенные вычисленные значения эмиттанса). Отсюда, согласно представленному выражению для размера пучка, следует его уменьшение.
Рис. 10.
Зависимость эмиттанса пучка и максимального угла вылета из п.и.и. частиц пучка от ускоряющего напряжения.

В свою очередь, уменьшение эмиттанса с ростом ускоряющего напряжения можно связать с уменьшением угла вылета частиц пучка x'. Известно, что под числовым значением эмиттанса понимается уменьшенная в π раз площадь фазовой диаграммы (1), т.е. ${{\varepsilon }_{х}} = \frac{1}{\pi }\int {dxdx{\text{'}}} $ [18], из чего следует, что величина эмиттанса пропорциональна, в частности, углу вылета частиц пучка x'. Максимальный угол вылета частиц связан с эмиттансом и γ-параметром Твисса выражением $x_{{\max }}^{'}$ = $\sqrt {\varepsilon \gamma } $ [14, 17, 18]. Вычисленные по полученным экспериментальным данным максимальные углы вылета частиц демонстрируют уменьшение с ростом ускоряющего напряжения (рис. 10), что и объясняет одновременное уменьшение эмиттанса пучка.
Уменьшение угла вылета частиц с ростом ускоряющего напряжения можно объяснить, воспользовавшись результатами работы [29], где моделировались траектории пучка в и.о.с. По мнению авторов [29], угол вылета частиц пучка на выходе из п.и.и. пропорционален отношению их поперечной составляющей энергии к продольной и выражается как $x{\text{'}} = \sqrt {\frac{{k{{T}_{{{\text{ion}}}}}}}{{e{{U}_{{{\text{аx}}}}}}}} $, где k = 1.38 ⋅ 10–23 Дж/K – постоянная Больцмана, Tion– ионная температура, e – элементарный заряд, Uax – величина осевого потенциала в плоскости измерения эмиттанса. Ионная температура определяется только параметрами п.и.и. (анодное напряжение, конфигурация, магнитное поле и т.д.), поэтому при неизменных его параметрах в фиксированной плоскости измерения эмиттанса она существенно не меняется. При отсутствии ускоряющего потенциала в и.о.с. продольная энергия пучка определяется приобретенной им энергией в п.и.и. При наличии в и.о.с. ускоряющего потенциала пучок к приобретенной им в п.и.и. продольной компоненте энергии получает дополнительно энергию, определяемую градиентом потенциала в ускоряющей и.о.с. Поэтому при увеличении ускоряющего напряжения и, соответственно, потенциала в плоскости измерения эмиттанса увеличивается продольная энергия экстрагируемых из п.и.и. ионов и, как следствие, уменьшается эмиттанс пучка.
На рис. 11а приведены зависимости эмиттанса пучка от продольной координаты Z внутри ускоряющего промежутка, а на рис. 11б – фазовые диаграммы, восстановленные непосредственно перед входной апертурой ускоряющего электрода и.о.с. На график рис. 11а не нанесена зависимость для ускоряющего напряжения 0 кВ, поскольку при отсутствии ускоряющего поля пучок движется в дрейфовом пространстве, где его первоначальный эмиттанс 2.12 ± 0.18 π⋅мм⋅рад сохраняется.
Рис. 11.
Зависимость эмиттанса от продольной координаты внутри ускоряющего промежутка (а) и фазовые диаграммы перед входной апертурой ускоряющего электрода и.о.с. (Z = 17 мм) (б).

Для получения результатов, представленных рис. 11а, плоскость восстановления эмиттанса и параметров Твисса перемещалась вдоль оси Z и фиксировалась на расстояниях 5, 10 и 17 мм от плоскости выходной апертуры п.и.и. При каждом значении координаты Z в плоскостях, удаляющихся в направлении оси Z от новой плоскости вычисления эмиттанса, с шагом 1 мм измерялись размеры пучка, и фиксировалось значение осевого потенциала. Таким образом, формировались коэффициенты для решения системы (6).
Из рис. 11а видно, что по мере перемещения в направлении оси Z по ускоряющему промежутку плоскости измерения эмиттанса последний уменьшается, что связано с увеличением энергии ионов под действием осевого потенциала (см. рис. 7в).
Из рис. 11б видно, что при величинах напряжения –4 и –5 кВ удается обеспечить сходящуюся форму пучка на входе в ускоряющий электрод и.о.с. При этом при ускоряющем напряжении –5 кВ достигается наименьший для данной серии экспериментов размер пучка, составляющий 4 мм. Сравнение его с диаметром входной апертуры ускоряющего электрода и.о.с., равным 12 мм, позволяет заключить, что в данном случае пучок согласован с апертурой. Поэтому можно ожидать, что бомбардировка поверхности ускоряющего электрода ионами экстрагируемого пучка и, следовательно, ее распыление будут сведены к минимуму.
ЗАКЛЮЧЕНИЕ
Предложен метод “бесконтактного” измерения эмиттанса корпускулярного потока, экстрагируемого из п.и.и. м.л.у. Вычисление эмиттанса выполняется посредством минимизации разности между поперечными размерами пучка в и.о.с., рассчитанными теоретически и экспериментально определенными по фотографическим изображениям следа пучка. Для автоматизации процесса обработки фотографических изображений следа пучка в и.о.с., определения его поперечных размеров и вычисления эмиттанса и параметров Твисса разработано программное обеспечение в среде LabVIEW. Представлены результаты применения “бесконтактного” метода измерения эмиттанса пучка ионов, экстрагируемого из п.и.и. Зафиксировано уменьшение эмиттанса с ростом величины ускоряющего напряжения.
Представленный в статье “бесконтактный” метод измерения эмиттанса был использован ранее в работе [4] при проведении факторного анализа влияния геометрических параметров и.о.с. на эмиттанс ускоренного пучка ионов.
Список литературы
Мамедов Н.В., Прохорович Д.Е., Юрков Д.И., Каньшин И.А., Солодовников А.А., Колодко Д.В., Соро-кин И.А. // ПТЭ. 2018. № 4. С. 62. https://doi.org/10.1134/S0032816218030242
Mamedov N.V., Kolodko D.V., Sorokin I.A., Kanshin I.A., Sinelnikov D.N. // IOP Conf. Series: J. Physics Conf. Series. 2017. V. 830. P. 012063. https://doi.org/10.1088/1742-6596/830/1/012063
Рачков Р.С., Пресняков А.Ю., Юрков Д.И. // Атомная энергия. 2019. Т. 126. Вып. 6. С. 334.
Каньшин И.А. // Технологии ЭМС. 2018. № 3 (66). С. 26.
Бердников А.С., Галль Л.Н., Хасин А.Ю. // Научное приборостроение. 2001. Т. 11. № 4. С. 28.
Sarstedt M., Lee Y., Leung K.N., Perkins L.T., Pickard D.S., Weber M., Williams M.D. // Rev. Sci. Instrum. 1996. V. 67. № 3. P. 1249. https://doi.org/10.1063/1.1146688
Вальков А.Е., Зайченко А.К., Устинов А.И. // Ядерная физика и энергетика. 2010. Т. 11. № 2. С. 199.
Roychowdhury P., Kewlani H., Mishra L., Gharat S., Rajawat R.K. // Nucl. Instrum. and Methods in Phys. Res. A. 2015. V. 795. P. 45. https://doi.org/10.1016/j.nima.2015.05.043
Быков Т.А., Касатов Д.А., Колесников Я.А., Кошкарев А.М., Макаров А.Н., Остреинов Ю.М., Соко-лова Е.О., Сорокин И.Н., Таскаев С.Ю., Щудло И.М. // ПТЭ, 2018. № 5. С. 90. https://doi.org/10.1134/S003281621805018X
Alexandrov V.S., Donets E.E., Nyukhalova E.V., Kaminsky A.K., Sedykh S.N., Tuzikov A.V., Philippov A.V. // Physics of particles and nuclei letters. 2016. V. 13. № 7. P. 767. https://doi.org/10.1134/S1547477116070025
Barabin S., Kozlov A., Kulevoy T., Liakin D., Lukashin A., Selesnev D. // Proceedings of 26th Russian Particle Accelerator Conference RUPAC2018. Protvino, Russia. 2018. THPSC17. P. 440.
Dong Hyun An, Garam Hahn, Chawon Park // J. Korean Physical Society. 2015. V. 66. № 3. P. 323. https://doi.org/10.3938/jkps.66.323
Pandit S., Sarma P.R., Bhattacharya S., Bhandari R.K. // Meas. Sci. Technol. 1997. V. 8. P. 1085. https://doi.org/10.1088/0957-0233/8/10/008
Khiary F.Z., Abdel-Aal R.E., Muhammad R. // Nucl. Instrum. and Methods in Phys. Res. A. 1994. V. 343. P. 383. https://doi.org/10.1016/0168-9002(94)90215-1
Mäder J., Roßbach J., Maimone F., Spädtke P., Tinschert K., Lang R., Sun L., Cao Y., Zhao H. // Rev. Sci. Instrum. 2010. V. 81. P. 02B720. https://doi.org/10.1063/1.3272891
Stockli M.P., Blokland W., Gorlov T., Han B., Long C., Pennisi T., Assadi S. // Proceedings of PAC09. Vancouver, BC, Canada. 2009. TH6REP012. P. 3974.
Stockli Martin // AIP Conference Proceedings 2006. V. 868. P. 25. https://doi.org/10.1063/1.2401393
Браун Я. Физика и технология источников ионов. М.: Мир, 1998.
Liebl H. Applied Charged Particle Optics. Springer, 2007. P. 131. https://doi.org/10.1007/978-3-540-71925-0_3
Курнаев В.А., Протасов Ю.С., Цветков И.В. Введение в пучковую электронику: Уч. пособие. М.: МИФИ, 2008.
Мешков И.Н., Парфенов А.Н., Бровко О.И. Патент на изобретение 2212690 РФ // Опубл. 20.09.2003. Бюл. № 26.
Голубев А.А., Гурьева Е.В., Канцырев А.В., Королёв В.А., Марков Н.В., Рудской И.В., Смирнов Г.Н., Туртиков В.И., Фертман А.Д., Худомясов А.В., Шарков А.В. // ПТЭ. 2009. № 3. С. 13.
Janev R.K., Langer W.D., Evans Jr.K. , Post Jr. D.E. Elementary Processes in Hydrogen-Helium Plasmas. Berlin Heidelberg: Springer-Verlag, 2019. dol: https://doi.org/10.1007/978-3-642-71935-6
Ободовский И.М. Физические основы радиационных технологий: Уч. пособие. Долгопрудный: Издательский дом “Интеллект”, 2014.
Пенинг Ф. Электрические разряды в газах. Изд-во иностр. лит., 1960.
Долгов А.Н., Марков В.Г., Окулов А.А., Прохорович Д.Е., Садилкин А.Г., Юрков Д.И. // Успехи прикладной физики. 2013. Т. 1. № 6. С. 739.
Hooper Jr. E.B. A Review of Reflex and Penning Discharges. Department of Engineering and Applied Science Yale University. New Haven, Connecticut, USA. 1969. V. 27. P. 295–343.
Гмурман В.Е. Теория вероятностей и математическая статистика: Уч. пособие для вузов. М.: Высшая школа, 2003.
Soliman B.A., Abdelrahman M.M., Helal A.G., Abdelsalam F.W. // Chinese Physics C. 2011. V. 35. № 1. P. 83. https://doi.org/10.1088/1674-1137/35/1/017
Дополнительные материалы отсутствуют.
Инструменты
Приборы и техника эксперимента




