Приборы и техника эксперимента, 2021, № 3, стр. 68-74

ВВЕДЕНИЕ

Несмотря на большое количество разнообразных монохроматоров, анализаторов энергии электронов и электронных спектрометров потребность в создании новых типов таких приборов остается актуальной. Эти приборы на протяжении многих десятилетий широко используются в исследованиях рассеяния моноэнергетических электронов на атомах и молекулах, взаимодействия электронов с поверхностью твердых тел, а также резонансных явлений при столкновениях электронов с атомами, молекулами и положительными ионами.

Наиболее распространенные из них это 127-градусный цилиндрический электростатический конденсатор Юза–Рожанского [1] и 180-градусный сферический энергоанализатор [2]. Уникальным по своим свойствам является трохоидальный электронный монохроматор, разработанный Шульцем и Стоматовичем [3], который широко используется для изучения возбуждения атомов сверхмоноэнергетическими (порядка 10 мэВ) электронами [4].

Некоторые результаты практического использования указанных выше приборов для исследования процессов взаимодействия моноэнергетических электронов с атомами и молекулами изложены в [5, 6]. В настоящее время появляются новые работы и по расчетам различных электронных систем, которые могут быть успешно использованы для получения первичных моноэнергетических электронных пучков и анализа энергий рассеянных электронов [7, 8].

Цель данной работы состояла в разработке нового электронного спектрометра – спиратрона, диспергирующим элементом которого является коаксиальный электростатический цилиндрический конденсатор. Важным было изучение его характеристик и демонстрация возможностей при использовании для исследований рассеяния медленных электронов на атомах и молекулах, в том числе для рассеяния “вперед” на угол 0°.

АНАЛИЗАТОР ЭЛЕКТРОНОВ

Прежде чем перейти к описанию разработанного нами электростатического электронного спектрометра остановимся на основных электронно-оптических свойствах цилиндрического конденсатора, электроны в котором движутся вдоль эквипотенциальных поверхностей по траекториям, близким к круговым. Отметим, что теоретические расчеты дисперсионных и фокусирующих характеристик цилиндрического конденсатора впервые использованы в анализирующем элементе электростатического спектрометра электронов в работе [1]. Впоследствии дисперсионные и фокусирующие свойства поля конденсатора исследованы многими авторами, в том числе и в нашей лаборатории [9, 10].

127-градусный цилиндрический электростатический конденсатор

Перпендикулярно оси в конденсатор (см. рис. 1) через отверстие в диафрагме D входит слаборасходящийся пучок электронов радиусом r с углом полураствора α. Радиус внешней стороны внутреннего цилиндра равен R₁, а радиус внутренней стороны внешнего цилиндра – R₂. Электроны вводятся в зазор между цилиндрами на расстоянии R₀ = (R₁ + R₂)/2 под углом γ = 45° относительно оси цилиндров. Если к цилиндрам приложена разность потенциалов, которая создает напряженность электрического поля между цилиндрами, равную Е₀, то создается аксиально-симметричное электростатическое поле, которое отклоняет электроны к оси цилиндров при выполнении условия

(1)

$e{{Е}_{0}} = (m{v}_{0}^{2}){\text{/}}{{R}_{0}},~$

где е, m, ${{v}_{0}}$ – заряд, масса и скорость электрона.

Рис. 1.

Схема траекторий прохождения электронов в поле 127°-ного цилиндрического конденсатора [10].

Таким образом, исходя из уравнения (1), электроны будут описывать спиральные траектории радиусом R₀ и двигаться в направлении оси цилиндров со скоростью ${{v}_{0}}$.

Движение электронов в поле такого конденсатора детально аналитически рассмотрено в монографии [11]. Установлено, что при повороте электронов на азимутальный угол $\varphi = \pi {\text{/}}\sqrt 2 $ имеет место их фокусировка первого порядка по этому углу φ. При повороте на угол $\varphi = 2\pi {\text{/}}\sqrt 2 $ происходит двойная фокусировка. В этом случае по углу α осуществляется фокусировка второго, а по углу Δγ – фокусировка третьего порядка (при γ = π/4, γ – угол между осью пучка и осью конденсатора, см. рис. 2). При этом происходит монокинетизация заряженных частиц по энергии. Таким образом, если на входе конденсатора установить диафрагму S₁ (рис. 1), а на выходе диафрагму S₂, сместив их относительно друг друга на угол $2\pi {\text{/}}\sqrt 2 $ и установив расстояние между ними вдоль оси цилиндров, равное $L = {{R}_{0}}(2\pi {\text{/}}\sqrt 2 )$, то на выходе конденсатора можно получить моноэнергетический пучок электронов. Изменяя (сканируя) энергию пучка электронов на входе в конденсатор, можно измерять распределение электронов по энергиям. Таким образом, рассматриваемый конденсатор может служить и как монохроматор энергии пучка электронов, и как анализатор их энергии.

Рис. 2.

Ввод электронов в поле коаксиального цилиндрического электростатического конденсатора [11].

Как показано в [11], увеличивая расстояние между входной и выходной щелями в n раз (где n = 2, 3, … ∝), можно улучшить энергетическое разрешение прибора. Для рассмотренной выше геометрии энергоанализатора его разрешающая сила равна

(2)

$W = (\sqrt 2 \pi {{r}_{0}}){\text{/}}[(0.37\pi {\text{/}}(\sqrt 2 {{r}_{0}}{{\alpha }^{4}})\, + \,M{{s}_{1}}\, + \,{{s}_{2}}\, + \,Q\, + \,d],$

где Q – расширение линии изображения за счет пространственного заряда исследуемого пучка, d – расширение изображения из-за технологических погрешностей, допущенных при изготовлении прибора, М – коэффициент увеличения, s₁ и s₂ – размеры входной S₁ и выходной S₂ диафрагм, r₀ – расстояние между цилиндрами.

Коаксиальный цилиндрический электростатический конденсатор

Это определенная модификация 127-градусного электростатического конденсатора. Специфика этого конденсатора заключается в том, что при вхождении электронов в его поле при определенном соотношении между их энергией и отклоняющим напряжением они движутся в направлении оси цилиндров, описывая спиральные траектории (рис. 2). Когда слаборасходящийся пучок электронов входит в поле цилиндрического конденсатора, то при определенной разности потенциалов между цилиндрами создается аксиально-симметричное поле с радиальной составляющей напряженности Е₀. Полярность разности потенциалов такова, что электроны отклоняются к оси цилиндров, и при условии

(3)

$е{{Е}_{0}} = (m{v}_{0}^{2}{{\sin }^{2}}\gamma ){\text{/}}{{R}_{0}}$

центральные электроны пучка описывают спиральные траектории с радиусом R₀. В уравнении (3) Е₀– радиальная составляющая напряженности поля на расстоянии R₀ от оси цилиндров, ${{v}_{0}}$ – скорость электронов, задаваемая ускоряющим напряжением V₀, γ – угол между осью пучка электронов и осью конденсатора (рис. 2).

Для нахождения траекторий прохождения электронов через коаксиальный цилиндрический электростатический конденсатор необходимо решить систему уравнений движения [7, 8]. Решение этих уравнений позволяет сделать выводы относительно фокусирующих свойств коаксиального цилиндрического электростатического конденсатора, которые практически совпадают со сделанными выше для 127-градусного цилиндрического конденсатора.

Нами были проведены численные расчеты уравнений движения электронов в поле коаксиального цилиндрического электростатического конденсатора для широкого диапазона параметров. Наилучшая фокусировка пучка получена для среднего радиуса R₀ = 5 мм, при этом радиусы цилиндров R₁ = 3 мм и R₂ = 7 мм, а угол влета электронов в конденсатор γ = 45°.

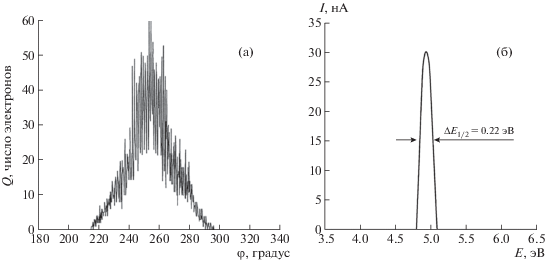
В качестве примера на рис. 3 приведены результаты расчета распределения электронов в поле коаксиального цилиндрического конденсатора с указанными выше параметрами R₀, R₁, R₂ и при Е = 2 ± 0.25 эВ, z = 44 мм, γ = 45 ± 5°. Как видно, наибольшее число электронов сосредоточено в интервале углов 240–270°, а максимум достигается при φ_max ~ 254° (рис. 3a). Расчет ширины распределения электронов по энергиям (рис. 3б) дает, без учета влияния аберрации, величину у основания ΔЕ = 0.44 эВ. При этом полная ширина этого распределения на половине высоты (FWHM) – стандартный термин для обозначения моноэнергетичности [2], получилась равной ΔЕ_1/2 = 0.22 эВ.

Рис. 3.

Результаты расчетов распределения электронов в поле коаксиального цилиндрического конденсатора. Распределения электронов: a – угловое, б – по энергиям.

Таким образом, теоретические расчеты подтверждают ранее сделанный вывод о том, что при указанных выше параметрах анализатора на выходе происходит фокусировка электронов второго порядка при азимутальном угле, равном $2\pi {\text{/}}\sqrt 2 $.

СПЕКТРОМЕТР И ЕГО ХАРАКТЕРИСТИКИ

Учитывая изложенные выше особенности фокусировки электронных пучков в цилиндрическом электростатическом поле и используя приведенные выше расчеты, нами был изготовлен коаксиальный цилиндрический электростатический спектрометр электронов, который был назван “спиратроном”. Он имеет рассчитанный оптимальный средний радиус R₀ = 5 мм, а источником электронов была пятиэлектродная электронная пушка с системой фокусировки пучка на входную щель анализатора.

На рис. 4a представлена схема спектрометра. Все электроды изготовлены из немагнитной нержавеющей стали, их толщина 1 мм, диаметр отверстий для прохождения пучка 1.0–1.2 мм. Спектрометр состоит из электронной пушки (катод 1 и электроды 2, 3, 5), входной и выходной диафрагм (электроды 6, 10), коаксиального конденсатора (электроды 7, 9) с радиусами R₀ = 5 мм, R₁ = 3 мм, R₂ = 7 мм и коллектора электронов (электрод 11). Камера столкновений 4 выполнена в виде полого параллелепипеда, куда из нагреваемого резервуара 12 подавались пары исследуемого вещества. Это позволяет изучать рассеяние электронов на атомах или молекулах. Заметим, что такое расположение электронной пушки и анализатора дает возможность изучать рассеяние электронов “вперед”, т.е. на угол 0°, и на твердотельных мишенях.

Рис. 4.

Схема спиратрона (a) и блок-схема системы управления (б). 1 – катод; 2, 3, 5 – вытягивающий, фокусирующий и ускоряющий электроды; 4 – камера столкновений; 6, 10 – входная и выходная диафрагмы; 7, 9 – внешний и внутренний цилиндры; 8 – траектория движения электронов; 11 – коллектор электронов; 12 – капсула с исследуемым веществом.

Конструктивно пучок электронов вводится в энергоанализатор под углом 45° через выполненный в виде призмы электрод 6, в котором просверлен канал ∅2 мм. Диаметр входной щели равен 1 мм, а выходной – 1.2 мм. Длина цилиндров 7, 9 такова, что пучок электронов при прохождении конденсатора описывает траекторию 8, поворачивается на угол $4\pi {\text{/}}\sqrt 2 $, обеспечивая двукратное повышение разрешения по энергиям. Это подтверждается приведенными на рис. 3 расчетами.

Рис. 4б иллюстрирует автоматизированную систему управления экспериментом. Нами использованы прецизионные блоки питания катода и электродов анализатора, что позволяло устанавливать все потенциалы с точностью 0.01%. Управление блоками питания осуществлялось персональным компьютером через цифроаналоговый преобразователь и генератор ступенчатого напряжения. Система регистрации полезного сигнала на коллектор вольтметр-электрометр В7-30 и аналогоцифровой преобразователь, сигнал с которого поступал в персональный компьютер. Специальная компьютерная программа позволяла непосредственно контролировать процесс управления экспериментом в режиме онлайн.

Спектрометр собран на рабочем фланце, который устанавливается в цилиндрическую вакуумную камеру из нержавеющей стали. Для исключения влияния внешнего магнитного поля камера защищена многослойным экраном из пермаллоя. Откачка вакуумной камеры осуществлялась двумя магниторазрядными насосами НОРД-100, что обеспечивало рабочий вакуум в процессе измерений порядка 10^–5 Па.

Для проверки работы прибора в реальных условиях эксперимента нами были проведены исследования по рассеянию электронов на атомах кадмия. Этот хорошо изученный элемент со сложной электронной структурой (электронная конфигурация [Kr]4d¹⁰5s²¹S₀ [12]) является привлекательным и надежным объектом для тестовых экспериментальных исследований процессов столкновений.

Методика эксперимента заключалась в предварительном прогреве всей установки, в том числе и спиратрона, при высоком вакууме в течение 20 ч. Затем проводилась настройка параметров спиратрона, которая заключалась в подборе оптимальных потенциалов на электродах спектрометра с целью получения максимальной моноэнергетичности электронного пучка и регистрации серии спектров, характерных для частиц остаточных газов, возбуждаемых при рассеянии электронов.

На рис. 5 приведена энергетическая зависимость интенсивности рассеяния электронов на молекулах остаточного газа после прогрева спиратрона.

Рис. 5.

Энергетическая зависимость интенсивности рассеяния электронов на молекулах остаточного газа при давлении порядка 10^–5 Па.

На представленной кривой интенсивный пик в области нулевых энергий электронов соответствует прохождению первичного пучка. Поскольку основным компонентом остаточных газов является молекула азота, на полученной зависимости отчетливо прописывается характерный пик, максимум которого лежит при энергии ~1.98 эВ. Этот пик соответствует долгоживущему состоянию отрицательного иона ${\text{N}}_{2}^{ - }$(²Π_g). В экспериментах по упругому рассеянию он используется для калибровки шкалы энергий в области малых энергий [13, 14].

После проведения этих подготовительных процедур включался прогрев капсулы (12 на рис. 4а), что позволяло заполнить парами кадмия камеру столкновений 4. Концентрация атомов в области столкновений составляла ~10¹² cм^–3. При разных энергиях падающих электронов сканировался спектр тех электронов, которые взаимодействовали с атомами. Такой спектр должен состоять из пика первичного электронного пучка при нулевом потенциале на электроде 5. Далее, с увеличением ускоряющего потенциала, появляются пики упруго и неупруго рассеянных электронов на атомах или молекулах.

Предложенная конструкция спектрометра позволяет следующее: изучать энергетические зависимости интенсивности тока упруго рассеянных электронов; исследовать спектры постоянных остаточных энергий, в том числе почти нулевых (пороговые спектры); регистрировать спектры энергетических потерь. Спектры энергетических потерь исследовались нами при различных энергиях возбуждающих электронов (от 10 до 25 эВ с шагом 0.5 эВ) и температурах паров кадмия (от 80 до 240°С с шагом 10°С). Контроль температуры капсулы с кадмием и вакуумной камеры осуществлялся двумя термопарами. Это позволяло для предотвращения конденсации кадмия на электродах спектрометра поддерживать градиент температур нагрева спектрометра и камеры столкновений в 20°С. При температуре паров кадмия <200°С спектры характеризуются уменьшением интенсивности тока с увеличением энергии электронов и не имеют видимых особенностей. При температуре >200°С на спектрах появляется структура.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Перейдем к рассмотрению результатов измерений. После активации катода и установки потенциалов на электродах 2, 3, 5 спектрометра (см. рис. 4), при разности потенциалов на обкладках 7, 9 цилиндрического конденсатора 2–4 эВ, был получен ток порядка (0.3–7) ⋅ 10^–8 А на коллектор электронов 11. Заметим, что напряжение питания на обкладках конденсатора относительно входной диафрагмы было асимметричным.

Для анализа характеристик спиратрона проводились измерения распределения по энергиям потока электронов на коллектор 11 при разных потенциалах на электродах. Необходимо было определить как влияет на моноэнергетичность электронного пучка радиальная составляющая напряженности поля Е₀, ускоряющее напряжение V₀ и энергия электронов на входе в анализатор. Сканирование энергии электронов осуществлялось с шагом 0.03 эВ.

В результате этих измерений получен большой набор распределений электронов по энергиям при разных потенциалах пропускания и потенциалах входа в анализатор. Как видно из рис. 6, с увеличением энергии электронов на входе формы распределений подобны, но наблюдается некоторое уширение кривой распределения с ростом энергии пропускания. Так, при энергии 4 эВ FWHM равна 0.2 эВ, а при 12 эВ – 0.28 эВ. Такое увеличение уширения связано с разрешающей силой самого конденсатора.

Рис. 6.

Распределение электронов по энергии ΔE_1/2 при потенциале на входе в анализатор Е = 6 В и разных энергиях входящего электронного пучка Е₀, эВ: 7 (а), 10 (б), 12 (в), 14 (г).

Как показали проведенные измерения, распределение электронов по энергии ΔE_1/2 (FWHM) при энергии пропускания Е = 4–12 эВ изменяется в пределах 0.20–0.28 эВ. При энергии пропускания <4 эВ дальнейшего уменьшения полуширины функции распределения не наблюдается. Это связано, очевидно, с тем, что при эмиссии электронов с катода их разброс по энергии составляет ~0.2 эВ.

Анализ проведенных нами расчетов для данного прибора показывает, что при определенных конструктивных изменениях его можно использовать в качестве монохроматора электронов. Если сделать входную диафрагму ∅0.5 мм, а выходную – ∅1.5 мм, то в интервале энергий 1–6 эВ можно получить на входе анализатора моноэнергетический пучок электронов с полушириной распределения по энергиям ΔЕ_1/2 = 0.06–0.1 эВ при токе порядка 10^–8 А. Усовершенствованный таким образом прибор является электростатическим электронным спектрометром, позволяющим проводить широкий класс прецизионных экспериментальных исследований рассеяния медленных электронов на атомах и молекулах.

Результаты контрольных экспериментов по исследованию энергетической зависимости интенсивности пучка электронов, прошедших через пары кадмия в интервале энергий 0–10 эВ, приведены на рис. 7. Эта зависимость связана с полным сечением рассеяния. Как видим, на кривой имеется целый ряд ярко выраженных максимумов. В области нулевых энергий наблюдается интенсивный пик, который соответствует прохождению первичного пучка и является первым калибровочным репером шкалы энергий.

Рис. 7.

Энергетическая зависимость интенсивности рассеяния электронов на атомах кадмия.

Далее, вблизи упругого пика наблюдается максимум (E = 0.36 эВ), связанный с резонансом формы 5s²εp ²P_1/2. Энергия этого резонанса с точностью 0.03 эВ совпадает с известными данными [13]. Второй максимум при Е = 1.96 эВ соответствует пику рассеяния на молекуле N₂. Он имеет малую величину, поскольку концентрация молекул азота значительно меньше концентрации паров кадмия.

Остальные наблюдаемые особенности соответствуют прохождению неупругих процессов. В области энергий 3.84–3.99 эВ, за порогом возбуждения резонансной линии λ 326.1 нм, это переход ${{5}^{1}}{{S}_{0}}{\kern 1pt} - {\kern 1pt} {{5}^{3}}P_{1}^{{^{ \circ }}}$, энергия возбуждения которого равна Е_в = 3.80 эВ. В интервале энергий 5.35–7.45 эВ находятся возбужденные синглетные и триплетные уровни с переходом электрона в s-, p-, d-состояния с главными квантовыми числами n = 5, 6 [12].

ЗАКЛЮЧЕНИЕ

В работе проведен анализ работы коаксиального цилиндрического электростатического энергоанализатора электронов, предложена простая конструкция и изготовлен прибор. Экспериментально показано, что параметры спектрометра согласуются с расчетными. Спиратрон может быть использован как для получения моноэнергетического, до ~0.2 эВ, электронного пучка, так и для анализа электронов по энергиям в экспериментах по рассеянию медленных (0–10 эВ) электронов на атомах, молекулах и поверхности твердых тел.

Измеренные энергетические зависимости интенсивности электронов, рассеянных на атомах кадмия, обнаружили максимумы (пики), которые соответствуют известным электронным состояниям этого атома. Это подтверждает возможность успешного применения спиратрона для исследования электронной структуры атомов и молекул. Полученные результаты, по нашему мнению, позволяют рассматривать предложенный электронный спектрометр после определенной модификации как перспективный и для исследования процессов взаимодействия медленных электронов с конденсированными системами.