Приборы и техника эксперимента, 2023, № 2, стр. 122-128
ИЗМЕРЕНИЕ МАЛЫХ ПОТЕРЬ НА ПОЛЯРИЗАЦИЮ ПОЛУПРОВОДНИКОВОГО МАТЕРИАЛА В ГОТОВЫХ ДИОДАХ
Э. В. Семенов a, *, О. Ю. Малаховский b
a Томский государственный университет систем управления и радиоэлектроники
634050 Томск, просп. Ленина, 40, Россия
b АО “Научно-исследовательский институт полупроводниковых приборов”
634034 Томск, Красноармейская ул., 99а,
Россия
* E-mail: edwardsemyonov@narod.ru
Поступила в редакцию 25.05.2022
После доработки 03.06.2022
Принята к публикации 05.08.2022
- EDN: PWDAME
- DOI: 10.31857/S0032816223010226
Аннотация
Рассмотрен способ измерения потерь на поляризацию полупроводникового материала в области пространственного заряда готового диода. Показано, что измерение может быть выполнено методом сравнения с мерой емкостной добротности при помощи измерителей импеданса общего применения в лабораториях без стабилизации микроклимата и экранирования электромагнитных полей. Для исключения дрейфовой погрешности в этих условиях предлагается многократное регулярное переключение объекта измерения и меры. В результате тангенс угла потерь на поляризацию величиной 1.9 ⋅ 10–4 удалось измерить с погрешностью ±16%.
1. ВВЕДЕНИЕ
Для ряда применений полупроводниковых приборов важен учет потерь энергии в режиме обратного смещения (например, для варикапов, умножительных диодов, защитных диодов). Обычно учитывают два фактора, обусловливающие потери энергии: rs – последовательное сопротивление потерь областей прибора вне p–n-перехода (сопротивления p- и n-областей вне области пространственного заряда, подложки, омических контактов и выводов) и Rj – сопротивление p–n-перехода (рис. 1).
Рис. 1.
Используемая эквивалентная схема варикапа. rs – сопротивление областей прибора вне p–n-перехода; Rj – параллельное сопротивление p–n-перехода; rj – последовательное сопротивление, эквивалентное в части вносимых потерь сопротивлению Rj; rp – сопротивление, отражающее потери на поляризацию в ОПЗ; C − емкость варикапа.

Таков, в частности, классический подход к расчету добротности варикапов [1]. При этом можно построить частотную зависимость добротности варикапа, имеющую характерный максимум [1], так как последовательное сопротивление rs снижает добротность на верхних частотах, а параллельное сопротивление Rj – на нижних частотах. Значение максимальной добротности, рассчитанное таким образом, часто получается сильно завышенным (иногда до 14 000 [2]) по отношению к результатам измерений.
Такая ситуация указывает на то, что остается неучтенным еще некоторый фактор потерь. Физическая природа этого фактора становится очевидной, если учесть, что материалы для изготовления полупроводниковых приборов (например, кремний, арсенид галлия) имеют относительную диэлектрическую проницаемость в пределах 11–12. Это значит, что энергия накапливается не столько в виде заряда в p- и n-областях, сколько в виде поляризации полупроводника в области пространственного заряда (ОПЗ). Процесс поляризации и деполяризации сопровождается потерями энергии, которые характеризуются тангенсом угла потерь [3].
Измерению тангенса угла потерь собственно полупроводниковых материалов (подложек) посвящено большое число работ [4–5]. Есть и работы, в которых исследуются потери уже легированных полупроводников [5]. Однако в готовом диоде легирование различно в p- и n-областях, и даже внутри одной области может присутствовать градиент концентрации примеси. Кроме того, могут присутствовать еще и паразитные примеси (глубокие центры), например избыточный мышьяк в GaAs или кислород. Количество примесей и дефектов может также отличаться от проектных или средних значений. В итоге результаты измерения потерь в исходном полупроводниковом материале позволяют оценить поляризационные потери в ОПЗ готового диода лишь весьма приближенно.
Таким образом, было бы полезно иметь метод для измерения поляризационных потерь в ОПЗ готового диода. Рассмотрению такого метода посвящена настоящая работа.
2. ОБЪЕКТ ИЗМЕРЕНИЯ
В качестве примера для изложения предлагаемого подхода будем использовать арсенид-галлиевый варикап разработки АО “НИИПП” (г. Томск).
Варикап выполнен как бескорпусный с размещением кристалла на кристаллодержателе. Кристалл варикапа изготовлен по мезатехнологии (диаметр мезы ~100 мкм). Для увеличения коэффициента перекрытия до 3.5 (отношение емкостей варикапа при напряжениях –2 и –12 В) концентрация примесей в активном слое имеет обратный (отрицательный) градиент: в окрестности p–n-перехода концентрация примесей увеличена [6]. Номинальная емкость варикапа при напряжении смещения –4 В составляет 2–3 пФ.
3. СЕЛЕКЦИЯ ПОЛЯРИЗАЦИОННЫХ ПОТЕРЬ
Для того чтобы селективно измерить потери на поляризацию в готовом диоде, нужно либо учесть вклад потерь двух других видов (последовательного сопротивления пассивной части диода и электропроводности ОПЗ), либо выбрать режим измерения так, чтобы этими двумя видами потерь можно было пренебречь.
Последовательное сопротивление rs достаточно легко поддается измерению, если в диоде не наблюдается выраженный скин-эффект. На рис. 2 приведена вещественная часть rΣ импеданса вышеуказанного варикапа в диапазоне частот 50–400 МГц (кривая 1) при напряжении смещения ‒9.18 В. Сопротивление rΣ характеризует совокупное действие всех факторов потерь и измерено с использованием предложений, приведенных ниже, в разд. 4 настоящей статьи. Можно видеть, что в области частот выше 150 МГц rΣ практически постоянно. Это означает, что скин-эффектом в данном варикапе можно пренебречь. При выполнении данного условия rs рационально измерять в области верхних частот (в данном случае на частоте 400 МГц). Во-первых, в этой области добротность варикапа Q минимальна (кривая 2 на рис. 2), что обусловит меньшую погрешность измерения. Во-вторых, на верхних частотах основным фактором потерь является последовательное сопротивление пассивной части диода rs, т.е. rs = rΣ. На нижних частотах (50 МГц в данном случае) становится заметным влияние других факторов потерь, и rΣ увеличивается (см. рис. 2). На частотах ниже 50 МГц относительный вклад rs в общие потери становится еще меньше, однако проводить измерения там для выбранного варикапа нерационально, поскольку его добротность на частотах ниже 50 МГц превышает (1.5–2) ⋅ 103 и погрешность измерения потерь возрастает.
Параллельное сопротивление p–n-перехода Rj сказывается в области нижних частот и может быть измерено как дифференциальное сопротивление диода на постоянном токе (точнее, на частотах, где реактанс диода много больше Rj) при заданном смещении. Рассматривать частотную зависимость Rj не имеет смысла, так как уменьшающийся с увеличением частоты реактанс емкости варикапа C (см. рис. 1) нивелирует влияние Rj на верхних частотах. Далее целесообразно пересчитать данное сопротивление в эквивалентное ему (в части вносимых потерь) последовательное сопротивление rj (см. рис. 1). Это можно сделать, если известен сусцептанс диода ωC, где C – емкость диода. Тогда находим адмиттанс p–n-перехода, учитывающий потери на электропроводность: $Y\, = \,1{\text{/}}{{R}_{j}}\, + \,j\omega C$. Далее вычисляем импеданс Z = 1/Y, и определяем rj как его вещественную часть: ${{r}_{j}} = \operatorname{Re} (Z)$. Окончательно
Если вычесть из rΣ сопротивления rs и rj, оставшееся последовательное сопротивление rp (см. рис. 1) будет характеризовать потери на поляризацию в ОПЗ: Представление поляризационных потерь в виде эквивалентного последовательного сопротивления является логически правильным, так как параллельное к емкости сопротивление привело бы к уменьшению сопротивления диэлектрика на постоянном токе, что не соответствует поляризационному характеру потерь.Тангенс угла потерь на поляризацию находится далее как
Отсчитывать значение тангенса угла потерь на поляризацию нужно на частоте, выбираемой из компромиссных соображений. С одной стороны, она должна быть достаточно низкой, чтобы потери на поляризацию были заметны на фоне последовательного сопротивления пассивной части диода rs, с другой – добротность объекта измерения не должна быть слишком большой (для используемого метода и средства измерения не более 2 ⋅ 103). Для выбранного варикапа этому условию удовлетворяет частота порядка 50 МГц.
В принципе, однако, можно измерить rp на сетке частот, а из полученной информации о частотной зависимости rp делать выводы о конкретных механизмах наблюдаемых поляризационных потерь.
4. ОБЕСПЕЧЕНИЕ ПРИЕМЛЕМОЙ ПОГРЕШНОСТИ ИЗМЕРЕНИЯ
Основная проблема при измерении потерь на поляризацию используемых полупроводниковых материалов состоит в том, что относительная величина этих потерь (порядка 10–4) лежит за пределами диапазона измерения современных измерительных приборов. Например, измеритель импеданса Keysight E4991A, в соответствии с данными производителя, для добротности объекта измерения 300 имеет погрешность измерения уже ±20%.
Высокоточные измерения малых потерь в емкостных объектах можно выполнить с использованием резонансных камер [4, 5, 7], но такие измерения технически реализуемы только от частот примерно 2.5 ГГц. В принципе существует и коаксиальный резонатор большой длины [8], на котором можно выполнять измерения на частотах выше 130 МГц. Однако из рис. 2 ясно, что поляризационные потери заметны на фоне потерь в пассивной части диода на частотах ниже 130 МГц.
На частотах порядка 100 МГц и ниже можно использовать резонаторы на сосредоточенных элементах, но их калибровка выполняется с использованием мер емкостной добротности или конденсаторов с малыми потерями [9]. Однако для сравнения меры добротности с объектом измерения можно использовать и обычный измеритель импеданса [10]. Поскольку далее потери в объекте измерения вычисляются относительно потерь в мере (простым вычитанием), минимальная погрешность измерения будет обеспечена при одинаковых для меры и объекта систематических погрешностях измерения.
Для того чтобы систематическая погрешность измерителя импеданса была одинаковой и для объекта измерения, и для меры, будем выбирать емкости объекта измерения и меры одинаковыми. Таким образом, например, удается на два порядка расширить вниз диапазон измерения потерь прибора Keysight E4991A [10]. Для обратносмещенных диодов достаточно, чтобы емкость меры укладывалась в диапазон изменения емкости диода при допустимом изменении обратного смещения. Окончательно равенство емкостей диода и меры обеспечивается регулировкой смещения диода таким образом, чтобы его емкость вместе с емкостью присоединительных устройств была равна емкости меры. Практика измерений показывает, что достижимо различие емкостей меры и объекта измерения порядка сотых долей процента, что позволяет считать систематическую погрешность измерения исключенной из результатов измерений.
Кроме того, воспользуемся известным из литературы [11] приемом уменьшения остаточной (после выполнения калибровки) систематической погрешности измерения потерь емкостных объектов. Этот подход состоит в том, что для калибровки измерителя импеданса используется не классический набор мер (холостой ход, короткое замыкание, согласованная нагрузка), а набор, в котором мера короткого замыкания (наиболее далекая по свойствам от емкостных объектов) заменяется конденсатором с малыми потерями. В частности, из декларируемых производителем прибора Keysight E4991A данных следует, что при такой калибровке погрешность измерения добротности объекта емкостью 2 пФ на частоте 1 ГГц уменьшается в 15 раз.
Наши исследования, однако, показали, что вышеперечисленных мер недостаточно для достижения приемлемой погрешности измерения поляризационных потерь порядка 10–4. На рис. 3 представлены результаты измерения тангенса угла потерь D меры емкостной добротности из набора мер Keysight 16195В на частоте 50 МГц. Для минимизации случайной погрешности измерения каждый результат измерения получен усреднением 8000 наблюдений. Видно, что эта погрешность по большей части относительно медленно меняется (дрейфует) без выраженной закономерности. Измерения выполнялись в одном из помещений АО “НИИПП” без кондиционирования воздуха, экранирования и дополнительной стабилизации напряжения питания измерительного прибора. Наибольшая скорость дрейфа (в пересчете на тангенс потерь) в этой реализации составляет 0.65 ⋅ 10–4/мин. Для измерения с заданным усреднением и заменой объекта измерения (конденсатор с малыми потерями/диод с измерительным столиком) требуется время около 70 с. Следовательно, дрейфовая погрешность в этих условиях может составлять до 0.76 ⋅ 10–4.
Рис. 3.
Зависимость от времени погрешности измерения тангенса угла потерь меры емкостной добротности на частоте 50 МГц.

Для снижения дрейфовой погрешности измерения воспользуемся методикой на основе динамической калибровки. Проблема компенсации дрейфа (динамического смещения) измерительных приборов часто возникает в различных измерительных задачах [12–14]. При этом используются различные методы компенсации, которые, по сути, являются вариациями динамической калибровки [15, 16]. Для рассматриваемой задачи наиболее подходящим методом представляется регулярное переключение меры и объекта измерения. Такой подход используется, например, в радиометрах [17] для устранения погрешности дрейфа усилителей и смесителей. Во-первых, это позволит контролировать скорость дрейфа погрешности и исключить временные интервалы с быстрым дрейфом из обработки. Во-вторых, расчет текущей дрейфовой погрешности может быть выполнен путем интерполяции между погрешностями измерения как до, так и после измерения исследуемого объекта. Это позволит использовать в дальнейших расчетах оценку значения дрейфовой погрешности в момент измерения потерь в объекте. В-третьих, поскольку такой подход позволяет исключить медленно изменяющуюся составляющую погрешности путем аппроксимации, остаточную погрешность (невязку аппроксимации) можно априори считать нормально распределенной. Для нескольких таких измерений мы можем оценить доверительный интервал результата измерения, используя коэффициент Стьюдента.
5. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЯ ПОЛЯРИЗАЦИОННЫХ ПОТЕРЬ ДЛЯ ВЫБРАННОГО ОБЪЕКТА
Реализация предложенного метода измерения применительно к выбранному диоду имеет несколько особенностей.
В принципе калибровка с использованием конденсатора с малыми потерями вместо меры короткого замыкания уже предусмотрена штатно в приборе Keysight E4991A (в комплект калибровочных мер Keysight 16195В входит конденсатор с малыми потерями), однако в программном обеспечении прибора она используется только на частотах выше 400 МГц. Поскольку измерения поляризационных потерь выполняются на частоте 50 МГц, измерения проводились прибором Keysight E4991A с отключенной штатной калибровкой. Внесение поправок в результат измерения на основе калибровки выполнялось при обработке результатов измерения.
Варикап для проведения измерений устанавливался в измерительный столик Keysight 16192A. Поскольку измерения проводились без использования штатных средств калибровки, компенсация передаточных свойств столика выполнялась также по завершении измерений. Использованная модель столика включает в себя параллельную емкость на входе для подключения к измерителю (разъем APC-7) величиной 0.679 пФ и индуктивность пружинного вывода для подключения объекта измерения (4.5 нГн). Этот вывод также обладает существенным сопротивлением, которое зависит от частоты по закону скин-эффекта как $0.12\sqrt {f{\text{/}}200\;{\text{МГц}}} $ Ом.
Для реализации динамической калибровки в качестве меры емкостной добротности использован конденсатор с малыми потерями из набора калибровочных мер Keysight 16195В. Емкость данной меры составляет 1.91 пФ на частоте 50 МГц и 1.92 пФ на частоте 400 МГц (рост действующей емкости с частотой связан с влиянием индуктивности обкладок и выводов конденсатора).
На рис. 4 позицией 1 обозначены измерения последовательного сопротивления потерь r(t) столика с варикапом как функции времени. Измерения последовательного сопротивления потерь меры с малыми потерями (т.е., фактически, дрейфовая погрешность измерения Δr(t)) обозначены позицией 2. Между этими измерениями выполнена интерполяция кубическим сплайном (сплошная кривая). Текущее значение дрейфовой погрешности Δr определено по этой интерполяции в момент времени, когда выполнено измерение r. На рис. 4 пунктирной линией показан пример для четвертого по счету измерения r(t4). Измерения выполнены на частоте 50 МГц.
Рис. 4.
Последовательное сопротивление r столика с варикапом (1), погрешность измерения Δr последовательного сопротивления меры емкостной добротности (2) и ее аппроксимация (сплошная линия) на частоте 50 МГц.

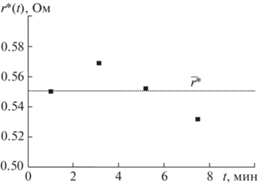
Измерение с исключенной дрейфовой погрешностью обозначим как r*: $r{\kern 1pt} {\text{*}}(t) = r(t) - \Delta r(t)$. На рис. 5 приведены четыре значения r*, полученные в разные моменты времени. Пунктирной линией обозначен результат измерения последовательного сопротивления потерь $\bar {r}{\text{*}}$ (среднее арифметическое четырех наблюдений). Получается, что на частоте 50 МГц $r{\kern 1pt} * = 0.551$ Ом. С учетом емкости столика с варикапом (она равна емкости меры 1.91 пФ) пересчитаем измеренный импеданс к точке подключения варикапа (с учетом модели столика): получим емкость варикапа 1.23 пФ и последовательное сопротивление потерь $r_{\Sigma }^{*} = 1.263$ Ом.
Рис. 5.
Последовательное сопротивление потерь r* столика с варикапом с исключенной дрейфовой погрешностью (частота 50 МГц). Пунктирной линией показан результат измерения последовательного сопротивления потерь $\bar {r}{\text{*}}$ (среднее арифметическое четырех наблюдений).
Аналогичные измерения потерь столика с варикапом на частоте 400 МГц представлены на рис. 6, 7. Последовательное сопротивление потерь $\bar {r}{\text{*}}$ составляет 0.388 Ом, а пересчет к точке подключения варикапа с учетом модели столика дает значение 0.758 Ом. Как описано в разд. 3, это измерение понимается как измерение rs.
Рис. 6.
Последовательное сопротивление r столика с варикапом (1), погрешность измерения Δr последовательного сопротивления меры емкостной добротности (2) и ее аппроксимация (сплошная линия) на частоте 400 МГц.

Рис. 7.
Последовательное сопротивление потерь r* столика с варикапом с исключенной дрейфовой погрешностью (частота 400 МГц). Пунктирной линией показан результат измерения последовательного сопротивления потерь $\bar {r}{\text{*}}$ (среднее арифметическое четырех наблюдений).

Параллельное (дифференциальное) сопротивление p–n-перехода Rj определено измерителем импеданса Keysight E4980A при постоянном смещении –9.18 В и напряжении тестового синусоидального сигнала 1 В. Частота тестового сигнала выбрана минимально возможной для указанного прибора (20 Гц) с целью уменьшения шунтирующего действия емкости варикапа. Получено, что кондуктанс варикапа составляет 1.408 нСм. Вычислив обратную величину, найдем параллельное сопротивление варикапа на нижних частотах Rj = 710 МОм. В соответствии с формулой (1) и с учетом емкости варикапа (1.24 пФ) получаем эквивалентное последовательное сопротивление p–n-перехода на частоте 50 МГц, равное ${{r}_{j}} = 9.28$ мОм.
Далее по формуле (2) находим последовательное сопротивление, характеризующее потери на поляризацию, ${{r}_{p}} = 0.496$ Ом, а по формуле (3) – тангенс угла потерь на поляризацию в ОПЗ – ${{D}_{p}} = 1.92 \cdot {{10}^{{ - 4}}}$.
Для получения погрешности измерения Dp нужно учесть погрешность измерения всех слагаемых в формуле (2). Доверительные границы погрешности для $\bar {r}_{\Sigma }^{*}$ и $\bar {r}_{s}^{*}$, вычисленные из среднего квадратического отклонения $r_{\Sigma }^{*}$ и $r_{s}^{*}$ (см. рис. 5 и 7) с учетом коэффициента Стьюдента (для доверительной вероятности 0.95), равны соответственно ±0.058 и ±0.011 Ом. Основной составляющей погрешности измерения rj является аддитивная к кондуктансу объекта измерения погрешность. Постоянная систематическая составляющая этой погрешности устраняется при калибровке, а дрейфовая, как показывают наблюдения, не усматривается на фоне случайной. Случайная погрешность при использованных условиях измерения (режим “long” с усреднением 256 отсчетов (настройки Keysight E4980A) с дальнейшим усреднением 19 наблюдений) составила ±0.09 мОм.
Погрешности измерения rΣ, rs и rj являются случайными, нормально распределенными, поэтому общую погрешность измерения rp находим как корень квадратный из суммы их квадратов. Окончательно имеем ${{r}_{p}} = 0.50 \pm 0.06$ Ом или Dp = = $(1.9 \pm 0.3) \cdot {{10}^{{ - 4}}}$.
6. ЗАКЛЮЧЕНИЕ
Классический подход к расчету добротности обратносмещенных p–n-переходов учитывает лишь два фактора потерь – потери в пассивной части диода и потери, связанные с проводимостью p–n-перехода. Однако существенное значение имеет и третий фактор потерь – потери на поляризацию полупроводникового материала в ОПЗ.
Измерения потерь на поляризацию в готовых диодах встречают большие технические трудности в связи с их малой величиной (порядка 10–4), а также с одновременным наличием двух других упомянутых источников потерь. Кроме того, вклад потерь на поляризацию в диодах существен до частот порядка 100 МГц, что исключает применение для точного измерения потерь высокодобротных резонансных камер или коаксиальных линий. Единственным подходящим методом, как представляется, является метод сравнения с мерами емкостной добротности, в частности, с конденсаторами с малыми потерями.
Эксперименты показывают, что приемлемую погрешность измерения (около ±16%) можно получить, если использовать для сравнения меры и объекта измерители импеданса общего применения (например, Keysight E4991A), проводя измерения в обычных лабораториях, но при этом потребуется регулярное многократное переключение объекта и меры для исключения дрейфовой погрешности.
Полученное значение тангенса угла потерь на поляризацию легированного арсенида галлия (1.9 ± 0.3) ⋅ 10–4 на частоте 50 МГц, является, по нашим сведениям, первым селективным измерением поляризационных потерь в данном частотном диапазоне для готового диода.
Отметим, что ничто в данном методе не связано с конкретными особенностями конструкции варикапа, поэтому метод применим для самых разных варикапов, в том числе с различными емкостями. Единственное, что принципиально требуется для реализации данного метода, – это мера емкостной добротности с емкостью, входящей в диапазон перестройки емкости варикапа.
Результаты селективного (на фоне других факторов) измерения потерь на поляризацию в готовых диодах могут иметь двоякое применение. Во-первых, они могут быть использованы на этапе проектирования диодов для более точного предсказания их добротности. Во-вторых, такие измерения могут использоваться для диагностики качества изготовления диодов. Повышенное значение этого вида потерь может свидетельствовать о наличии неприемлемых дефектов (в том числе латентных) в окрестности границ p- и n-областей.
Список литературы
Norwood M.H., Shatz E. // Proc. IEEE. 1968. V. 56. № 5. P. 788. https://doi.org/10.1109/PROC.1968.6408
Barrera J.S., Curby R.C., DeFevere D.C., Kwan F.S., Nevin L.J., Solomon R. // 6th European Microwave Conference. Rome, Italy, 14–17 September 1976. P. 14. https://doi.org/10.1109/EUMA.1976.332237
Poplavko Y.M. Electronic Materials. Principles and Applied Science. Oxford, United Kingdom: Elsevier, 2019. https://doi.org/10.1016/C2017-0-03281-0
Krupka J., Mouneyrac D., Hartnett J.G., Tobar M.E. // IEEE Trans. Microwave Theory and Techniques. 2008. V. 56. № 5. P. 1201. https://doi.org/10.1109/TMTT.2008.921652
Courtney W.E. // IEEE Trans. Microwave Theory and Techniques. 1977. V. 25. № 8. P. 697.
Малаховский О.Ю., Гущин С.М., Фотина Л.В., Скотников Н.В., Скробов Е.В. Патент РФ 165025 U1, МПК H01L 29/93 // Опубл. 27.09.2016. Бюл. № 27. https://new.fips.ru/Archive4/PAT/2016FULL/2016.09.27/DOC/RUNWU1/000/000/000/165/025/DOCUMENT.PDF
Baker-Jarvis J., Geyer R.G., Grosvenor J.H., Jr., Janezic M.D., Jones C.A., Riddle B., Weil C.M., Krupka J. // IEEE Trans. Dielectrics and Electrical Insulation. 1998. V. 5. № 4. P. 571.
Resonant Coaxial-Line. Model 34A. Instruction Manual. Boonton Electronics Corp. Parsippany, New Jersey, USA, 2002. http://ftb.ko4bb.com/manuals/23.106.56.14/ Boonton_34A_Resonant_Coaxial_Line_Manual.pdf
ГОСТ 18986.19–73. Варикапы. Метод измерения добротности. М.: ИПК Изд-во стандартов, 2004.
Семенов Э.В., Малаховский О.Ю. // Докл. Томск. гос. ун-та систем управления и радиоэлектроники. 2018. Т. 21. № 4. С. 11. https://doi.org/10.21293/1818-0442-2018-21-4-11-16
Yonekura T. // 10th IEEE Instrumentation and Measurement Technology Conference. Hamamatsu, Japan, 10–12 May 1994. P. 1004. https://doi.org/10.1109/IMTC.1994.351935
Shi L., He Y., Li B., Wu Y., Huang Y., Cheng T. // IEEE Trans. Instrumentation and Measurement. 2019. V. 68. № 9. P. 3244. https://doi.org/10.1109/TIM.2018.2878073
Zhang L., Zhang D. // IEEE Trans. Instrumentation and Measurement. 2015. V. 64. № 7. P. 1790. https://doi.org/10.1109/TIM.2014.2367775
Wang C. // IEEE Trans. Instrumentation and Measurement. 2015. V. 64. № 7. P. 1994. https://doi.org/10.1109/TIM.2014.2377991
Zakrzewski J., Wróbel K. // IEEE Trans. Instrumentation and Measurement. 2002. V. 51. № 6. P. 1358. https://doi.org/10.1109/TIM.2002.808030
Morawski R.Z., Podgórski A., Sutkowski K. // IEEE Trans. Instrumentation and Measurement. 1992. V. 41. № 6. P. 881. https://doi.org/10.1109/19.199426
Janik D. // IEEE Trans. Instrumentation and Measurement. 1983. V. 32. № 1. P. 232. https://doi.org/10.1109/TIM.1983.4315048
Дополнительные материалы отсутствуют.
Инструменты
Приборы и техника эксперимента



