1. На главную
  2. Электронные версии
  3. Электрохимия
  4. T. 59, № 12, 2023

Электрохимия, 2023, T. 59, № 12, стр. 834-842

Термодинамическое исследование Ag8GeТe6 и твердых растворов Ag8GeТe6 –xSex методом ЭДС с твердым Ag+-проводящим электролитом

А. Дж. Амирасланова a, А. Т. Мамедова a, С. З. Имамалиева b, *, И. Дж. Алвердиев a, Ю. А. Юсибов a, М. Б. Бабанлы b, c

a Гянджинский государственный университет
Гянджа, Азербайджан

b Институт катализа и неорганической химии
Баку, Азербайджан

c Бакинский государственный университет
Баку, Азербайджан

* E-mail: samira9597a@gmail.com

Поступила в редакцию 11.02.2023
После доработки 12.05.2023
Принята к публикации 18.05.2023

Полный текст (PDF)

Аннотация

Измерением ЭДС концентрационных относительно серебряного электрода цепей с твердым электролитом Ag4RbI5 в интервале температур 300–400 К изучены термодинамические свойства соединения Ag8GeTe6 и твердых растворов Ag8GeТe6 –xSex. Из данных измерений ЭДС вычислены парциальные термодинамические функции серебра в сплавах. На основании данных по твердофазным равновесиям в системе Ag–Ge–Se–Te определены потенциалобразующие реакции, ответственные за эти парциальные молярные функции и вычислены стандартные термодинамические функции образования и стандартные энтропии соединения Ag8GeТe6 и твердых растворов составов Ag8GeTe5Se, Ag8GeTe4Se2, Ag8GeTe3Se3, Ag8GeTe2Se4 и Ag8GeTeSe5.

Ключевые слова: теллурид серебра-германия, фазовая диаграмма, твердые растворы, термодинамические функции, метод ЭДС, твердый электролит Ag4RbI5

1. ВВЕДЕНИЕ

Сложные халькогениды на основе серебра и меди находятся в центре внимания исследователей как экологически безопасные функциональные материалы, обладающие термоэлектрическими, фотоэлектрическими, оптическими и др. свойствами [1–6]. Среди этих материалов важное место занимают соединения семейства аргиродитов с общей формулой Ag8AIVX6 (AI – Cu, Ag; BIV – Si, Ge, Sn; X – S, Se, Te) и фазы на их основе [7‒13], которые помимо указанных свойств также обладают ионной проводимостью по катионам Cu+ и Ag+ и могут быть использованы в качестве электрохимических сенсоров, электродов или электролитных материалов в устройствах электрохимического превращения энергии – в твердотельных батареях, дисплеях и др. [14–21]. По мнению авторов [19–21], наличие смешанной электронно-ионной проводимости является одним из весомых факторов, положительно влияющих на термоэлектрические характеристики указанных материалов.

Эффективное решение вопросов разработки методов направленного синтеза сложных фаз требует глубокого термодинамического анализа этих процессов и проведения соответствующих термодинамических расчетов. Для обеспечения этих расчетов важно наличие надежных взаимосогласованных комплексов термодинамических данных для веществ, участвующих в рассматриваемых процессах [22, 23].

Для термодинамического исследования неорганических систем широко применяется метод электродвижущих сил (ЭДС), который, являясь равновесным методом химической термодинамики, позволяет органически сочетать исследование фазовых равновесий и термодинамических свойств [23–26]. Различные модификации этого метода успешно используются при термодинамических исследованиях сложных халькогенидов металлов [23–30]. Термодинамические данные, полученные методом ЭДС, помимо внутренней согласованности в рамках отдельной фазы, характеризуются также взаимосогласованностью их значений для всех фаз системы и с фазовой диаграммой [23, 24].

Наличие суперионных проводников с чистой Cu+- и Ag+-проводимостью открывает широкие возможности для термодинамического исследования сложных халькогенидов серебра и меди методом ЭДС с твердым электролитом [24–26]. В работах [31–40] представлены результаты подобных исследований ряда сложных халькогенидов меди и серебра.

В данной работе представлены результаты термодинамического исследования методом ЭДС с твердым электролитом Ag4RbI5 соединения Ag8GeTe6 и твердых растворов Ag8GeТe6 – xSex, представляющих значительный интерес как экологически безопасные термоэлектрики и смешанные ионно-электронные проводники [8, 16].

2. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Для термодинамического исследования соединения Ag8GeТe6 и твердых растворов Ag8GeТe6 – xSex нами были составлены концентрационные цепи типа

(1)
$\left( {\text{--}} \right){\text{ Ag}}\left( {{\text{тв}}} \right){\text{/A}}{{{\text{g}}}_{{\text{4}}}}{\text{Rb}}{{{\text{I}}}_{{\text{5}}}}\left( {{\text{тв}}} \right){\text{/}}\left( {{\text{Ag в сплаве}}} \right)\left( {{\text{тв}}} \right)\,\left( {\text{ + }} \right),$
в которых электролитом служил твердый супер-ионный проводник Ag4RbI5, обладающий высокой ионной проводимостью уже при комнатной температуре [26].

Твердый электролит Ag4RbI5 синтезировали из химически чистых RbI и AgI по методике, описанной в [24, 38]: стехиометрическую смесь исходных йодидов расплавили в кварцевой ампуле в вакууме (~10–2 Па) и затем быстро охлаждали до комнатной температуры. При охлаждении расплав кристаллизуется в мелкозернистое и микроскопически однородное тело. Последующий отжиг при 400 К в течение 200 ч приводит к полной гомогенизации Ag4RbI5.

Однофазность синтезированного соединения проверяли методом порошковой рентгенографии. Порошковые дифрактограммы снимали на приборе Bruker D2 Phaser с CuKα1-излучением. Индицирование рентгенограмм проводили с помощью программного обеспечения Topas V3.0.

Как видно из рис. 1, дифракционная картина синтезированного образца идентична с литературными данными, а вычисленный период кубической решетки (a = 1.1238 нм, пр. гр. P4132) практически совпадает с результатами [41]. Затем из цилиндрического слитка (диаметр ~1 см) синтезированного Ag4RbI5 вырезали таблетки толщиной 4–6 мм, которые использовали как твердый электролит в цепях типа (1). В качестве электрода сравнения использовали пластинку из металлического серебра высокой степени чистоты, а анодов – равновесные сплавы системы Ag–Ge–Se–Тe. Составы сплавов-анодов, а также условия их синтеза и термического отжига выбирали, исходя из данных по фазовым равновесиям в указанной системе.

Рис. 1.

Порошковая дифрактограмма соединения Ag4RbI5.

На рис. 2 представлен фрагмент схематической диаграммы твердофазных равновесий системы Ag–Ge–Se–Te, построенный с учетом данных [6, 42–45]. Согласно [42], в системе Ge–Se–Te диселенид германия имеет коннодные связи с GeTe и элементарным теллуром. С другой стороны, бинарная система Te–Se характеризуется образованием непрерывного ряда твердых растворов [44] (на рис. 1, α-фаза). Таким образом, в системе Ge–Se–Te имеются трехфазная GeTe + + GeSe2 + Te (зеленая область) и двухфазная GeSe2 + α (синяя область) области. Прямая 1–7 отражает разрез Ag8GeТe6–Ag8GeSe6, на котором образуется непрерывный ряд твердых растворов Ag8GeТe6 – xSex (δ-фаза) [45]. Промежуточные точки 2, 3, …, 6 на этой прямой соответствуют различным составам δ-фазы.

Рис. 2.

Фрагмент диаграммы твердофазных равновесий системы Ag–Ge–Se–Te при комнатной температуре. Окрашенные плоскости – фазовые области GeSe2–Te–Se (синий цвет), GeSe2–GeTe–Te (зеленый цвет), Ag8GeTe6–Ag8GeSe6–GeSe2–GeTe (розовый цвет). Красные прямые – лучевые линии от угла Ag, проходящие через различные составы.

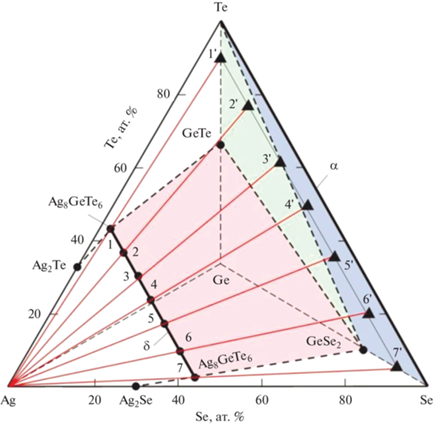
Известно [24–26], что при термодинамических исследованиях фаз в гетерогенных системах методом ЭДС в качестве анодов используются, как правило, сплавы из определенных гетерогенных областей на фазовой диаграмме. С учетом этого, составы сплавов-анодов выбраны нами таким образом, чтобы они находились на лучевых прямых, исходящих из угла Ag (левый электрод цепей типа (1)) концентрационного тетраэдра и проходящих через определенные составы δ-фазы (точки на прямой 1–7).

Учитывая вышеизложенное, для приготовления сплавов – анодов цепей типа (1) нами из предварительно синтезированных и идентифицированных соединений Ag8GeТe6 и Ag8GeSe6 были синтезированы образцы δ-фазы различных составов с добавлением 2–3 ат. % избытка элементарных селена и теллура высокой степени чистоты. При этом селен и теллур взяты в таких соотношениях, чтобы составы образцов находились на указанных лучевых линиях вблизи точек 1–6. Методика синтеза и результаты РФА исследуемых сплавов приведены в нашей предыдущей работе [45], посвященной синтезу и идентификации твердых растворов Ag8GeТe6 – xSex.

Синтез проводили сплавлением в вакуумированных (∼10–2 Па) кварцевых ампулах при температурах, на ∼50 K превышающих температуры ликвидуса [45]. Полученные литые негомогенизированные образцы подвергали длительному ступенчатому термическому отжигу при 700 К (500 ч) и 400 К (100 ч).

Для приготовления анодов отожженные сплавы перетирали в порошок, а затем запрессовывали в виде таблеток массой ∼0.5 г. Была собрана электрохимическая ячейка конструкции [24, 38], которую вакуумировали, наполнили аргоном до давления ∼ 40 кПа и поместили в специально изготовленную трубчатую печь сопротивления, где она термостатировалась при температуре ~380 К в течение 3 суток. Температуру ячейки измеряли хромель-алюмельевыми термопарами и ртутным термометром с точностью ±0.5°C.

ЭДС измеряли с помощью цифрового вольтметра марки Keithley 2100 6½ в интервале температур 300–400 К. Первые равновесные значения были получены после термостатирования ячейки в вышеуказанных условиях, а последующие – через каждые 4 ч после установления определенной температуры. Равновесными считали те значения ЭДС, которые при неоднократном измерении при данной температуре отличались друг от друга не более, чем на 0.5 мВ, независимо от направления изменения температуры.

Обратимость составленных концентрационных цепей типа (1) и воспроизводимость результатов контролировали методом РФА, а также измерением масс электродов и электролита до и после измерений ЭДС. При этом составы и массы электродов в ходе эксперимента оставались практически постоянными, что потверждает отсутствие взаимодействия между электролитом и электродами.

3. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

На рис. 3 представлены данные измерений ЭДС цепей типа (1). Как видно, численые значения ЭДС увеличиваются с повышением концентрации селена в твердых растворах и для каждого образца температурная зависимость ЭДС носит линейный характер. Учитывая это, для проведения термодинамических расчетов экспериментальные данные были обработаны методом наименьших квадратов и получены линейные уравнения типа

(2)
$E = a + bT \pm t{{\left[ {(S_{{\text{E}}}^{2}{\text{/}}n) + S_{b}^{2}{{{(T - \bar {T})}}^{2}}} \right]}^{{1/2}}},$
рекомендованного в современной термодинамической литературе [25, 26]. В уравнении (2) n – число пар значений E и T; SE и Sb – дисперсии отдельных измерений ЭДС и коэффициента b соответственно; $\overline T $ – средняя абсолютная температура, t-критерий Стьюдента. При доверительном уровне 95% и числе экспериментальных точек n ≥ 20 критерий Стьюдента t ≤ 2.

Рис. 3.

Температурная зависимость ЭДС для δ-фазы различных составов в интервале температур 300–400 К. 1 – Ag8GeTe6; 2 – Ag8GeTe5Se; 3 – Ag8GeTe4Se2; 4 – Ag8GeTe3Se3; 5 – Ag8GeTe2Se4; 6 – Ag8GeTeSe5.

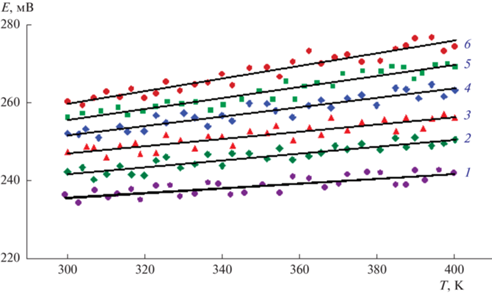
Полученные уравнения типа (2) приведены в табл. 1.

Таблица 1.

Уравнения температурных зависимостей ЭДС для фаз Ag8GeТe6 –xSex различных составов в интервале температур 300–400 К

Фаза E, мВ =а+bТ± 2${{\tilde {S}}_{{\text{E}}}}$(Т)
Ag8GeTe6 $217.59 + 0.0608T \pm 2{{\left[ {\frac{{2.02}}{{30}} + 7.3 \times {{{10}}^{{ - 5}}}{{{(T - 349.8)}}^{2}}} \right]}^{{1/2}}}$
Ag8GeTe5Se $214.87 + 0.0896T \pm 2{{\left[ {\frac{{1.62}}{{30}} + 5.8 \times {{{10}}^{{ - 5}}}{{{(T - 350.0)}}^{2}}} \right]}^{{1/2}}}$
Ag8GeTe4Se2 $213.53 + 0.1120T \pm 2{{\left[ {\frac{{1.80}}{{30}} + 6.5 \times {{{10}}^{{ - 5}}}{{{(T - 350.1)}}^{2}}} \right]}^{{1/2}}}$
Ag8GeTe3Se3 $216.29 + 0.1186T \pm 2{{\left[ {\frac{{2.01}}{{30}} + 7.2 \times {{{10}}^{{ - 5}}}{{{(T - 349.7)}}^{2}}} \right]}^{{1/2}}}$
Ag8GeTe2Se4 $213.54 + 0.1404T \pm 2{{\left[ {\frac{{1.92}}{{30}} + 7.0 \times {{{10}}^{{ - 5}}}{{{(T - 352.9)}}^{2}}} \right]}^{{1/2}}}$
Ag8GeTeSe5 $211.24 + 0.1617T \pm 2{{\left[ {\frac{{2.14}}{{30}} + 7.7 \times {{{10}}^{{ - 5}}}{{{(T - 350.0)}}^{2}}} \right]}^{{1/2}}}$

Из данных табл. 1 по термодинамическим соотношениям [25, 26]

(3)
$\Delta {{\overline G }_{{{\text{Ag}}}}} = - zFE,$
(4)
$\Delta {{\overline H }_{{{\text{Ag}}}}} = - z\left[ {E - T{{{\left( {\frac{{\partial E}}{{\partial T}}} \right)}}_{P}}} \right] = - zFa,$
(5)
$\Delta {{\bar {S}}_{{{\text{Ag}}}}} = zF{{\left( {\frac{{\partial E}}{{\partial T}}} \right)}_{P}} = zFb$
вычислены относительные парциальные свободная энергия Гиббса, энтальпия и энтропия серебра в сплавах (табл. 2).

Таблица 2.

Парциальные молярные функции серебра в сплавах Ag8GeТe6 –xSex при 298 К

Фаза $ - \Delta {{\overline G }_{{{\text{Ag}}}}}$ $ - \Delta {{\overline H }_{{{\text{Ag}}}}}$ $\Delta {{\overline S }_{{{\text{Ag}}}}}$, Дж К–1 моль–1
кДж моль–1
Ag8GeTe6 22.74 ± 0.05 21.00 ± 0.29 5.84 ± 0.82
Ag8GeTe5Se 23.31 ± 0.04 20.73 ± 0.26 8.64 ± 0.74
Ag8GeTe4Se2 23.83 ± 0.05 20.60 ± 0.27 10.81 ± 0.78
Ag8GeTe3Se3 24.28 ± 0.05 20.87 ± 0.29 11.44 ± 0.82
Ag8GeTe2Se4 24.64 ± 0.05 20.60 ± 0.29 13.54 ± 0.81
Ag8GeTeSe5 25.04 ± 0.05 20.38 ± 0.30 15.61 ± 0.85

Для расчета интегральных термодинамических функций соединения Ag8GeТe6 и фаз Ag8GeТe6 –xSex различных составов нами использован фрагмент диаграммы твердофазных равновесий системы Ag–Ge–Te–Se (рис. 1). Как видно из рис. 1, парциальные молярные величины серебра в Ag8GeТe6 являются термодинамическими функциями потенциалобразующей реакции [26]

$8{\text{Ag(тв}}{\text{.)}} + {\text{GeТe(тв}}{\text{.}}) + {\text{5Тe(тв}}{\text{.}}) = {\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeТ}}{{{\text{e}}}_{{\text{6}}}}{\text{\;(тв}}{\text{.}}).$

Тогда стандартные свободная энергия Гиббса образования и энтальпия образования соединения Ag8GeТe6 могут быть вычислены по соотношению

(6)
${{\Delta }_{f}}{{Z}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{6}}}}) = 8\Delta {{\overline Z }_{{{\text{Ag}}}}} + {{\Delta }_{f}}{{Z}^{0}}({\text{GeTe}}),$
где $Z$ ≡ G, H, а стандартная энтропия по

(7)
$\begin{gathered} {{S}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{6}}}}) = 8[\Delta {{\overline S }_{{{\text{Ag}}}}} + {{S}^{0}}({\text{Ag)}}] + \\ + \,\,5{{S}^{0}}({\text{Te}}) + {{S}^{0}}({\text{GeTe}}). \\ \end{gathered} $

Результаты расчетов по уравнениям (6) и (7) приведены в табл. 3.

Таблица 3.

Стандартные интегральные термодинамические функции соединений GeSe2, GeТe, Ag8GeТe6 и твердых растворов Ag8GeТe6 –xSex

Фаза ${{\Delta }_{f}}{{G}^{0}}(298\,{\text{K}})$ ${{\Delta }_{f}}{{H}^{0}}(298\,{\text{K}})$ ${{\Delta }_{f}}{{S}^{0}}\,(298\,{\text{K}})$ ${{S}^{0}}\,(298\,{\text{K}})$ Источник
кДж моль–1 Дж К–1 моль–1
GeТe 52.87 ± 0.09 49.5 ± 0.4 11.3 ± 1.0 91.1 ± 1.4 [47]
GeSe2 101.3 ± 2.9 102.3 ± 2.6 – 112.6 ± 3.4 [46] [53]
Ag8GeТe6 234.8 ± 0.5 217.5 ± 2.7 58.0 ± 7.6 726.0 ± 10.0 Наст. раб.
266 ± 2 221 ± 1 150 ± 2 – [37]
Ag8GeTe5Se 263.6 ± 1.9 241.7 ± 3.6 73.5 ± 8.5 734.2 ± 10.2 Наст. раб.
Ag8GeTe4Se2 291.9 ± 3.3 267.1 ± 4.8 83.2 ± 10.1 737.5 ± 11.5 Наст. раб.
Ag8GeTe3Se3 301.1 ± 3.4 269.3 ± 4.9 106.7 ± 10.2 753.7 ± 11.8 Наст. раб.
Ag8GeTe2Se4 305.3 ± 3.4 267.1 ± 5.0 128.1 ± 10.2 767.2 ± 11.7 Наст. раб.
Ag8GeTeSe5 307.2 ± 3.4 265.4 ± 5.0 140.2 ± 10.8 772.8 ± 12.5 Наст. раб.
β-Ag8GeSe6 304.9 ± 3.6 270.7 ± 4.2 114.7 ± 12.1 740.9 ± 13.8 [39]

С другой стороны, согласно рис. 1, сплавы, находящиеся по составу на лучевой линии 2–2ꞌ, имеют фазовый состав Ag8GeТe5Se + GeTe + + GeSe2 + Te, а на линии 3–3ꞌ – фазовый состав Ag8GeТe4Se2 + GeSe2 + Te. Сплавы на линиях 4–4ꞌ, 5–5ꞌ и 6–6ꞌ трехфазны: δ + GeSe2 + α. Указанные равновесные фазовые составы сплавов позволяют составить уравнения потенциалобразующих реакций для δ-твердых растворов соответствующих составов:

(8)
$\begin{gathered} {\text{8Ag}} + 0.5{\text{GeS}}{{{\text{e}}}_{2}} + 0.{\text{5GeTe}} + 4.5{\text{Te}} = \\ = {\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{5}}}}{\text{Se}}, \\ \end{gathered} $
(9)
$8{\text{Ag}} + {\text{GeS}}{{{\text{e}}}_{2}} + 4{\text{Te}} = {\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{4}}}}{\text{S}}{{{\text{e}}}_{{\text{2}}}},$
(10)
$8{\text{Ag}} + {\text{GeS}}{{{\text{e}}}_{2}} + 4{\text{T}}{{{\text{e}}}_{{{\text{0}}{\text{.75}}}}}{\text{S}}{{{\text{e}}}_{{{\text{0}}{\text{.25}}}}} = {\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{3}}}}{\text{S}}{{{\text{e}}}_{{\text{3}}}},$
(11)
$8{\text{Ag}} + {\text{GeS}}{{{\text{e}}}_{{\text{2}}}} + 4{\text{T}}{{{\text{e}}}_{{{\text{0}}{\text{.5}}}}}{\text{S}}{{{\text{e}}}_{{0.5}}} = {\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{2}}}}{\text{S}}{{{\text{e}}}_{4}},$
(12)
$8{\text{Ag}} + {\text{GeS}}{{{\text{e}}}_{2}} + 4{\text{T}}{{{\text{e}}}_{{{\text{0}}{\text{.25}}}}}{\text{S}}{{{\text{e}}}_{{0.75}}} = {\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeTeS}}{{{\text{e}}}_{5}}.$

Согласно уравнениям (8)–(12), стандартные термодинамические функции образования твердых растворов вычислены по соотношениям

(13)
$\begin{gathered} {{\Delta }_{f}}{{Z}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{5}}}}{\text{Se}}) = \\ = \,\,8\Delta {{\overline Z }_{{{\text{Ag}}}}} + 0.5{{\Delta }_{f}}{{Z}^{0}}({\text{GeS}}{{{\text{e}}}_{{\text{2}}}}) + 0.5{{\Delta }_{f}}{{Z}^{0}}({\text{GeTe}}), \\ \end{gathered} $
(14)
${{\Delta }_{f}}{{Z}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{4}}}}{\text{S}}{{{\text{e}}}_{{\text{2}}}}) = 8\Delta {{\overline Z }_{{{\text{Ag}}}}} + {{\Delta }_{f}}{{Z}^{0}}({\text{GeS}}{{{\text{e}}}_{2}}),$
(15)
$\begin{gathered} {{\Delta }_{f}}{{Z}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{3}}}}{\text{S}}{{{\text{e}}}_{3}}) = 8\Delta {{\overline Z }_{{{\text{Ag}}}}} + \\ + \,\,{{\Delta }_{f}}{{Z}^{0}}({\text{GeS}}{{{\text{e}}}_{{\text{2}}}}) + 4{{\Delta }_{f}}{{Z}^{0}}({\text{T}}{{{\text{e}}}_{{{\text{0}}{\text{.75}}}}}{\text{S}}{{{\text{e}}}_{{{\text{0}}{\text{.25}}}}}{\text{),}} \\ \end{gathered} $
(16)
$\begin{gathered} {{\Delta }_{f}}{{Z}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{2}}}}{\text{S}}{{{\text{e}}}_{{\text{4}}}}) = 8\Delta {{\overline Z }_{{{\text{Ag}}}}} + \\ + \,\,{{\Delta }_{f}}{{Z}^{0}}({\text{GeS}}{{{\text{e}}}_{2}}) + 4{{\Delta }_{f}}{{Z}^{0}}({\text{T}}{{{\text{e}}}_{{{\text{0}}{\text{.5}}}}}{\text{S}}{{{\text{e}}}_{{{\text{0}}{\text{.5}}}}}), \\ \end{gathered} $
(17)
$\begin{gathered} {{\Delta }_{f}}{{Z}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeTeS}}{{{\text{e}}}_{{\text{5}}}}) = 8\Delta {{\overline Z }_{{{\text{Ag}}}}} + \\ + \,\,{{\Delta }_{f}}{{Z}^{0}}({\text{GeS}}{{{\text{e}}}_{{\text{2}}}}) + 4{{\Delta }_{f}}{{Z}^{0}}({\text{T}}{{{\text{e}}}_{{{\text{0}}{\text{.25}}}}}{\text{S}}{{{\text{e}}}_{{0.75}}}), \\ \end{gathered} $
а стандартные энтропии –

(18)
$\begin{gathered} {{S}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{5}}}}{\text{Se}}) = 8\Delta {{\overline S }_{{{\text{Ag}}}}} + 8{{S}^{0}}({\text{Ag}}) + \\ + \,\,4.5{{S}^{0}}({\text{Te}}) + {{S}^{0}}({\text{GeS}}{{{\text{e}}}_{2}}) + 0.5{{S}^{0}}({\text{GeTe}}), \\ \end{gathered} $
(19)
$\begin{gathered} {{S}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{4}}}}{\text{S}}{{{\text{e}}}_{{\text{2}}}}) = 8\Delta {{\overline S }_{{{\text{Ag}}}}} + 8S_{{}}^{0}(Ag) + \\ + \,\,4{{S}^{0}}({\text{Te}}) + {{S}^{0}}({\text{GeS}}{{{\text{e}}}_{{\text{2}}}}), \\ \end{gathered} $
(20)
$\begin{gathered} {{S}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{3}}}}{\text{S}}{{{\text{e}}}_{{\text{3}}}}) = 8\Delta {{\overline S }_{{{\text{Ag}}}}} + 8S_{{}}^{0}({\text{Ag}}) + \\ + \,\,{{S}^{0}}({\text{GeS}}{{{\text{e}}}_{{\text{2}}}}) + 4{{S}^{0}}({\text{T}}{{{\text{e}}}_{{{\text{0}}{\text{.75}}}}}{\text{S}}{{{\text{e}}}_{{{\text{0}}{\text{.25}}}}}), \\ \end{gathered} $
(21)
$\begin{gathered} {{S}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeT}}{{{\text{e}}}_{{\text{2}}}}{\text{S}}{{{\text{e}}}_{{\text{4}}}}) = 8\Delta {{\overline S }_{{{\text{Ag}}}}} + 8{{S}^{0}}({\text{Ag}}) + \\ + \,\,{{S}^{0}}({\text{GeS}}{{{\text{e}}}_{{\text{2}}}}) + 4{{S}^{0}}({\text{T}}{{{\text{e}}}_{{{\text{0}}{\text{.5}}}}}{\text{S}}{{{\text{e}}}_{{{\text{0}}{\text{.5}}}}}), \\ \end{gathered} $
(22)
$\begin{gathered} {{S}^{0}}({\text{A}}{{{\text{g}}}_{{\text{8}}}}{\text{GeTeS}}{{{\text{e}}}_{5}}) = 8\Delta {{\overline S }_{{Ag}}} + 8{{S}^{0}}({\text{Ag}}) + \\ + \,\,{{S}^{0}}({\text{GeS}}{{{\text{e}}}_{2}}) + 4{{S}^{0}}({\text{T}}{{{\text{e}}}_{{{\text{0}}{\text{.25}}}}}{\text{S}}{{{\text{e}}}_{{{\text{0}}{\text{.75}}}}}). \\ \end{gathered} $

При расчетах по уравнениям (6), (7), (13)–(22) были использованы рекомендуемые в современной справочной литературе значения стандартных энтропий серебра и теллура (S0(Ag) = = 42.55 ± 0.13 Дж моль–1 K–1; ${{S}^{0}}({\text{Te}}) = 49.50 \pm $ ± 0.21 Дж моль–1 K–1) [46], а также стандартные термодинамические функции соединений GeТе и GeSe2 (табл. 3). Для GeTe были использованы стандартные термодинамические функции, определенные недавно методом ЭДС [47], которые хорошо согласуются с данными более ранних работ [48, 49] и рекомендованными в справочниках [50–52]. Стандартные теплота образования и энтропия соединения GeSe2 заимствованы из [53] и [46] соответственно, а его стандартная свободная энергия Гиббса образования рассчитана нами на основании этих данных по уравнению Гиббса–Гельмгольца.

В потенциалобразующих реакциях (10)–(12) участвуют α-твердые растворы составов Te0.75Se0.25, Te0.5Se0.5 и Te0.25Se0.75. Согласно [54], теплота смешения этих твердых растворов с точностью ±1 кДж равна нулю, т.е. они близки к идеальному. Поэтому при расчетах по соотношениям (15)–(17) и (20)–(22) энтропия и свободная энергия Гиббса смешения α-фазы вычислены по соотношениям

(23)
$\Delta {{S}_{{{\text{mix}}}}} = - R\left[ {x\ln x + \left( {1 - x} \right)\ln \left( {1 - x} \right)} \right],$
(24)
$\Delta {{G}_{{{\text{mix}}}}} = RT\left[ {x\ln x + \left( {1 - x} \right)\ln \left( {1 - x} \right)} \right].$

При расчетах погрешности вычислены методом накопления ошибок.

В табл. 3 также представлены значения стандартных термодинамических функций Ag8GeТe6 [37], полученные методом со стеклообразным твердым электролитом с Ag+-проводимостью и β‑Ag8GeSe6 [39]. Как видно, наши данные по свободной энергии Гиббса образования Ag8GeТe6 отличаются от [37] на 12%, а по энтальпии образования – практически совпадают. В то же время значения энтропии образования существенно отличаются. По нашему мнению, эти расхождения связаны с тем, что в [37] и нами при расчетах использованы различные термодинамические данные для GeТe. Авторы [37] использовали значение ${{\Delta }_{f}}{{S}^{0}}\,(298\,{\text{K}})$ = 19.4 Дж К–1 моль–1, полученное ими косвенным путем из данных измерений ЭДС в системе Ag–Ge–Te. Это значение существенно выше использованных нами (табл. 3) и рекомендованных в современных справочниках [46, 50, 51].

ЗАКЛЮЧЕНИЕ

В работе представлены новые взаимосогласованные комплексы термодинамических данных для соединения Ag8GeTe6 и твердых растворов Ag8GeТe6 – xSex различных составов, полученные методом ЭДС с твердым электролитом Ag4RbI5. Из данных измерений ЭДС вычислены относительные парциальные свободная энергия Гиббса, энтальпия и энтропия серебра в сплавах. На основании литературных данных был построен фрагмент диаграммы твердофазных равновесий системы Ag–Ge–Тe–Se, который позволил определить потенциалобразующие реакции, ответственные за указанные парциальные молярные величины. С использованием полученных уравнений потенциалобразующих реакций вычислены стандартные термодинамические функции образования и стандартная энтропия соединения Ag8GeТe6 и твердых растворов Ag8GeТe6 –xSex различных составов, представляющих интерес как потенциальные термоэлектрики и смешанные ионно-электронные проводники.

Список литературы

  1. Applications of Chalcogenides: S, Se, and Te. Ed. by Ahluwalia, G.K. Cham, Switzerland, Springer, 2016, 461 p.

  2. Chalcogenides: Advances in Research and Applications. Ed. Woodrow P. New-York. Nova, 2018. 111 p.

  3. Chalcogenide. From 3D to 2D and Beyond. Ed. By Liu, X., Lee, S., Furdyna, J.K., Luo, T., and Zhang, Y-H. Elsevier, 2019. 385 p.

  4. Scheer, R. and Schock, H-W., Chalcogenide Photovoltaics: Physics, Technologies, and Thin Film Devices. Wiley-VCH, 2011. 384 p.

  5. Alonso-Vante, N., Chalcogenide Materials for Energy Conversion: Pathways to Oxygen and Hydrogen Reactions. Springer Cham, 2018. 226 p.

  6. Бабанлы, М.Б., Юсибов, Ю.А., Абишев, В.Т. Трехкомпонентные халькогениды на основе меди и серебра, Баку: изд.БГУ, 1993. 342 с. [Babanly, M.B., Yusibov Yu.A., and Abishev, V.T., Ternary chalcogenides on the base of copper and silver (In Russian), Baku: BGU, 1993. 342 p.]

  7. Lin, S., Li, W., and Pei, Y., Thermally insulative thermoelectric argyrodites, Materials Today, 2021, vol. 48, p.198. https://doi.org/10.1016/j.mattod.2021.01.007

  8. Fujikane, M., Kurosaki, K., Muta, H., and Yamanaka, Sh., Thermoelectric properties of Ag8GeTe6, J. Alloys Compd., 2005, vol. 396 (1–2), p. 280. https://doi.org/10.1016/j.jallcom.2004.12.038

  9. Jiang, Q., Li,S., Luo, Y., Xin, J., Li, S., Li, W., and Yang, J., Ecofriendly highly robust Ag8SiSe6-based thermoelectric composites with excellent performance near room temperature, ACS Appl. Mater. Interfaces, 2020, vol. 12(49), p. 54653. https://doi.org/10.1021/acsami.0c15877

  10. Fan, Y., Wang, G., Wang, R., Zhang, B., Shen, X., Jiang, P., Zhang, X., Gu, H., Lu, X., and Zhou, X., Enhanced thermoelectric properties of p-type argyrodites Cu8GeS6 through Cu vacancy, J. Alloys Compd., 2020, vol. 822, p. 153665. https://doi.org/10.1016/j.jallcom.2020.153665

  11. Semkiv, H., Ilchuk, N., and Kashuba, A., Photoluminescence of Ag8SnSe6 argyrodite, Low Temp. Phys., 2022, vol. 48 (1), p. 12. https://doi.org/10.1063/10.0008957

  12. Yeh, L-Y and Cheng, K-W., Modification of Ag8SnS6 Photoanodes with Incorporation of Zn Ions for Photo-Driven Hydrogen Production, Catalysts, 2021, vol. 11(3), p. 363. https://doi.org/10.3390/catal11030363

  13. Yang, M., Shao, G., Wu, B., Jiang, J., Liu, S., and Huimin, L., Irregularly Shaped Bimetallic Chalcogenide Ag8SnS6 Nanoparticles as Electrocatalysts for Hydrogen Evolution, ACS Appl. Nano Mater., 2021, vol. 4(7), p. 6745. https://doi.org/10.1021/acsanm.1c00769

  14. Иванов-Шиц, А.К., Мурин, И.В. Ионика твердого тела, Т. 1. изд. С.-Петерб. ун-та: 2000, 616 с. [Ivanov-Shits, A.K. and Murin, I.V., Solid State Ionics (In Russian), vol. 1, Sankt-Petersburg, 2000, 616 p.]

  15. Li, L., Liu, Y., Dai, J., Hong, A, Zeng, M., Yan, Z., Xu, J., Zhang, D., Shan, D., Liu, S., Ren, Zh., and Liu, J-M., High thermoelectric performance of superionic argyrodite compound Ag8SnSe6, J. Mater. Chem. C, 2016, vol. 4, p. 5806. https://doi.org/10.1039/C6TC00810K

  16. Sardarly, R.M., Ashirov, G.M., Mashadiyeva, L.F., Aliyeva, N.A., Salmanov, F.T., Agayeva, R.Sh., Mamedov, R.A., and Babanly, M.B., Ionic conductivity of the Ag8GeSe6 compound, Mod. Phys. Lett. B, 2022. https://doi.org/10.1142/S0217984922501718

  17. Studenyak, I.P., Pogodin, A.I., Studenyak, V.I., Izai, V.Y., Filep, M.J., Kokhan, O.P., and Kúš, P., Electrical properties of copper- and silver-containing superionic (Cu1 − xAgx)7SiS5I mixed crystals with argyrodite structure, Solid State Ion., 2020, vol. 345, p. 115183. https://doi.org/10.1016/j.ssi.2019.115183

  18. Lin, Y., Fang, S., Su, D., and Brinkman, K.S. Enhancing grain boundary ionic conductivity in mixed ionic–electronic conductors, Nat. Commun., 2015, vol. 6(1), p. 1. https://doi.org/10.1038/ncomms7824

  19. Heep, B.K., Weldert, K.S., Krysiak, Y., Day, T.W., Zeier, W.G., Kolb, U., Snyder, G.J., and Tremel, W., High electron mobility and disorder induced by silver ion migration lead to good thermoelectric performance in the argyrodite Ag8SiSe6, Chem. Mater., 2017, vol. 29 (11), p. 4833. https://doi.org/10.1021/acs.chemmater.7b00767

  20. Li, W., Lin, S., Ge, B., Yang, J., Zhang, W., and Pei, Y., Low Sound Velocity Contributing to the High Thermoelectric Performance of Ag8SnSe6, Adv. Sci., 2016, vol. 3(11), p. 1600196. https://doi.org/10.1002/advs.201600196

  21. Weldert, K.S., Zeier, W.G., Day, T.W., Panthofer, M., Snyder, G.J., and Tremel, W., Thermoelectric transport in Cu7PSe6 with high copper ionic mobility, J. Amer. Chem. Soc., 2014, vol. 136, 12035. https://doi.org/10.1021/ja5056092

  22. Matsushita, T. and Mukai, K. Chemical Thermodynamics in Materials Science: From Basics to Practical Applications, 2018, Singapore: Springer, 257 p.

  23. Babanly, M.B., Mashadiyeva, L.F., Babanly, D.M., Imamaliyeva, S.Z., Tagiyev, D.B., and Yusibov, Yu.A., Some aspects of complex investigation of the phase equilibria and thermodynamic properties of the ternary chalcogenid systems by the EMF method, Russ. J. Inorg. Chem., 2019, vol. 64(13), p. 1649. https://doi.org/10.1134/S0036023619130035

  24. Babanly, M.B., Yusibov, Y.A., and Babanly, N.B., The EMF method with solid-state electrolyte in the thermodynamic investigation of ternary Copper and Silver Chalcogenides / Electromotive force and measurement in several systems. Ed. Kara, S., Intechweb.Org. 2011, p. 57.

  25. Морачевский, А.Г., Воронин, Г.Ф., Гейдерих, В.А., Куценок, И.Б. Электрохимические методы исследования в термодинамике металлических систем. М.: ИЦК “Академкнига”, 2003. 334 с. [Morachevsky, A.G., Voronin, G.F., Geiderich, V.A., and Kutsenok, I.B. Electrochemical methods of research in the thermodynamics of metal systems (in Russian), M.: ICC “Akademkniga”, 2003, 334 p.].

  26. Бабанлы, М.Б., Юсибов, Ю.А. Электрохимические методы в термодинамике неорганических систем. Баку, Элм, 2011, с.306. [Babanly, M.B. and Yusibov, Yu.A., Electrochemical methods in the thermodynamics of inorganic systems (in Russian), Baku: Elm, 2011, p. 306.]

  27. Osadchii, E.G., Korepanov, Ya.I., and Zhdanov, N.N., A multichannel electrochemical cell with glycerin-based liquid electrolyte, Instrum. Exp. Tech., 2016, vol. 59, no. 2, p. 302. https://doi.org/10.1134/S0020441216010255

  28. Kristavchuk, A.V., Zabolotskaya, A.V., Voronin, M.V., Chareev, D.A., and Osadchii, E.G., Temperature dependence of tellurium fugacity for the kotulskite (PdTe)–merenskyite (PdTe2) equilibrium determined by the method of a solid-state galvanic cell, Phys. Chem. Miner., 2021, vol. 48, p. 16. https://doi.org/10.1007/s00269-021-01141-x

  29. Hasanova, G.S., Aghazade, A.I., Babanly, D.M., Imamaliyeva, S.Z., Yusibov, Y.A., and Babanly, M.B., Experimental study of the phase relations and thermodynamic properties of Bi-Se system, J. Therm. Anal. Calorim., 2021, vol. 147, p. 6403. https://doi.org/10.1007/s10973-021-10975-0

  30. Imamaliyeva, S.Z., Mekhdiyeva, I.F., Jafarov, Y.I., and Babanly, M.B., Thermodynamic study of the thallium-thulium tellurides by EMF method, Bulletin of the Karaganda University. “Chemistry” series, 2021, vol. 21 (3), p. 43. https://doi.org/10.31489/2021Ch2/43-52

  31. Vassiliev, V.P. and Lysenko, V.A., A New Approach for the Study of Thermodynamic Properties of Lanthanide Compounds, Electrochim. Acta, 2016, vol. 222, p. 1770. https://doi.org/10.1016/j.electacta.2016.11.075

  32. Vassiliev, V.P., Lysenko, V., and Bros, J., Thermodynamic study of the Ag-In-Sn system by the EMF method, J. Alloys Compd., 2019, vol. 790, p. 370. https://doi.org/10.1016/J.JALLCOM.2019.03.016

  33. Машадиева, Л.Ф., Бабанлы, Д.М., Юсибов, Ю.А., Тагиев, Д.Б., Бабанлы, М.Б. Tермодинамическое исследование системы Ag-Sb-Se методом ЭДС с твердым электролитом Ag4RbI5. Электрохимия. 2021. Т. 57. С.162. [Mashadiyeva, L.F., Babanly, D.M., Yusibov, Yu.A., Tagiyev, D.B., and Babanly, M.B., Thermodynamic Study of the Ag–Sb–Se System by the EMF with solid electrolyte Ag4RbI5, Russ. J. Electrochem., 2021, vol. 57, p. 281.] https://doi.org/10.1134/S1023193521030083

  34. Алвердиев, И.Дж., Имамалиева, С.З., Бабанлы, Д.М., Юсибов, Ю.А., Тагиев, Д.Б., Бабанлы, М.Б. Термодинамическое исследование селенидов серебра–олова методом ЭДС с твердым электролитом Ag4RbI5. Электрохимия. 2019. Т. 55. С. 629. [Alverdiyev, I.J., Imamaliyeva, S.Z., Babanly, D.M., Yusibov, Yu.A., Tagiyev, D.B., and Babanly, M.B., Thermodynamic Study of Siver–Tin Selenides by the EMF Method with Ag4RbI5 Solid Electrolyte, Russ. J. Electrochem., 2019, vol. 55, p. 467.] https://doi.org/10.1134/S1023193519050021

  35. Moroz, M., Tesfaye, F., Demchenko, P., Mastronardo, E., and Mysina, O., Experimental Thermodynamic Characterization of the Chalcopyrite-Based Compounds in the Ag–In–Te System for a Potential Thermoelectric Application, Energies, 2022, vol. 15 (21), p. 8180. https://doi.org/10.3390/en15218180

  36. Мороз, Н.В., Прохоренко, М.В., Прохоренко, С.В., Яшков, М.В., Решетняк, О.В. Термодинамические свойства AgIn2Te3I и AgIn2Te3Br, определенные методом ЭДС. Журн. физич. химии. 2018. vol. 92(1). p. 25. [Moroz, M.V., Prokhorenko, M.V., Prokhorenko, S.V., Yatskov, M.V., and Reshetnyak, O.V., Thermodynamic Properties of AgIn2Te3I and AgIn2Te3Br, Determined by the EMF Method, Russ. J. Phys. Chem. A, 2018, vol. 92(1), p. 19.] https://doi.org/10.1134/S0036024418010168

  37. Мороз, Н.В., Прохоренко, М.В., Рудык, Б.П. Термодинамические свойства фаз в системе Ag–Ge–Te. Электрохимия. 2014. Т. 50. С. 1314. [Moroz, M.V., Prokhorenko, M.V., and Rudyk, B.P., Thermodynamic Properties of Phases of the Ag–Ge–Te System, Russ. J. Electrochem., 2014, vol. 50, p. 1177.] https://doi.org/10.1134/S1023193514120039

  38. Babanly, N.B., Orujlu, E.N., Imamalieva, S.Z., Yusibov, Yu.A., and Babanly, M.B., Thermodynamic investigation of silver-thallium tellurides by EMF method with solid electrolyte Ag4RbI5, J. Chem. Thermodyn., 2019, vol. 128, p. 78. https://doi.org/10.1016/j.jct.2018.08.012

  39. Алвердиев, И.Дж., Багхери, С.М., Имамалиева, С.З., Юсибов, Ю.А., Бабанлы, М.Б. Термодинамическое исследование соединения Ag8GeSe6 методом ЭДС с твердым электролитом Ag4RbI5. Электрохимия. 2017. Т. 53. С. 622. [Alverdiev, I.Dzh., Bagkheri, S.M., Imamalieva, S.Z., Yusibov, Yu.A., and Babanly, M.B., Thermodynamic Study of Ag8GeSe6 by EMF with an Ag4RbI5 Solid Electrolyte, Russ. J. Electrochem., 2017, vol. 53, p. 551.] https://doi.org/10.1134/S1023193517050032

  40. Бабанлы, М.Б., Машадиева, Л.Ф., Велиева, Г.М., Имамалиева, С.З. Термодинамическое исследование систем Ag–As–Se и Ag–S–I методом ЭДС с твердым электролитом. Электрохимия. 2009. Т. 45. С. 424. [Babanly, M.B., Mashadiyeva, L.F., Veliyeva, G.M., and Imamaliyeva, S.Z., Thermodynamic study of the Ag–As–Se and Ag–S–I systems using the EMF method with a sold Ag4RbI5 electrolyte, Russ. J. Electrochem., 2009, vol. 45, p. 399.] https://doi.org/10.1134/S1023193509040077

  41. Geller, S., Crystal Structure of the Solid Electrolyte, RbAg4I5, Science, 1967, vol. 157, p. 310.

  42. Шелимова, Л.Е., Томашик, В.Н., Грицыв, В.И. Диаграммы состояния в полупроводниковом материаловедении. М.: Наука, 1991. 369 с. [Shelimova L.E., Tomashyk, V.N., and Gricyv, V.I. Diagrammy sostoyaniya v poluprovodnikovom materialovedenii. M.: Nauka, 1991, 369 р. (In Russian).]

  43. Юсибов, Ю.А., Алвердиев, И.Дж., Ибрагимова, Ф.С., Мамедов, А.Г., Тагиев, Д.Б., Бабанлы, М.Б. Исследование и 3D моделирование фазовой диаграммы системы Ag–Ge–Se. Журн. неорган. химии. 2017. Т. 62. № 5. С. 1232. [Yusibov, Y.A., Alverdiev, I.D., Ibragimova, F.S., Mamedov, A.N., Tagiyev, D.B., and Babanly, M.B., Study and 3D modeling of the phase diagram of the Ag–Ge–Se system, Russ. J. Inorg. Chem., 2017, vol. 62, p.1223.] https://doi.org/10.1134/S0036023617090182

  44. Chizhevskaya, S.N. and Shelimova, L.E., Se–Te phase diagram and structures of amorphous and crystalline Se1 – xTex alloys: critical review, Russ. J. Inorg. Chem., 1997, vol. 42(5), p. 827.

  45. Amiraslanova, A.J., Mammadova, A.T., Alverdiyev, I.J., and Yusibov, Yu.A., Ag8GeS6(Se6)- Ag8GeTe6 systems: phase relations, synthesis and characterization of solid solutions, Azerb. Chem. J., 2023, no. 1, p. 22.

  46. База данных термические константы веществ. Электронная версия под ред. В.С. Иориша и В.С. Юнгмана. 2006 г. http://www.chem.msu.su/cgibin/ tkv [Database of thermal constants of substances Electronic version, Ed.: Iorish, V.S. and Yungman, V.S., 2006, http://www.chem.msu.su/cgi-bin/tkv.]

  47. Alakbarova, T.M., Thermodynamic properties of germanium telluride, New Mater., Compounds and Applications, 2021, vol. 5, no.1, p. 59.

  48. Hirayama, C., Thermodynamic Properties of Solid Monoxides, Monosulfides, Monoselenides, and Monotellurides of Ge, Sn, and Pb, J. Chem.l & Engin. Data, 1964, 9(1), p. 65.

  49. Sadikov, K.B. and Semenkovich, S.A., Study of the thermodynamic properties of germanium telluride, News of the Academy of Sciences of the Turkmen SSR series Physico-Technical, Chem. and Geol. Sci., 1966, vol. 3, p. 20.

  50. Kubaschewski, O., Alcock, C.B., and Spenser, P.J., Materials Thermochemistry, Pergamon Press, 1993, 350 p.

  51. Barin, I. Thermochemical Data of Pure Substances.Third Edition. VCH, 2008.

  52. Герасимов, Я.И., Крестовников, А.Н., Горбов, С.И. Химическая термодинамика в ветной металлургии, Справочник, т.6. М.: Металлургия, 1974. 312 с. [Gerasimov, Y.I., Krestovnikov, A.N., and Gorbov, S.I., Chemical thermodynamics in non-ferrous metallurgy (in Russian), Reference book. vol. 6, M.: Metallurgy, 1974, 312 p.]

  53. O’Hare, P.A.G., Susman, S., and Volin, K.J., The energy difference between the crystalline and vitreous forms of germanium diselenide as determined by combustion calorimetry in fluorine. The Ge–Se bond energy, J. Non. Cryst. Solids, 1987, vol. 89, no. 1–2, p. 24.

  54. Ghosh, G., Lukas, H. L., and Delaey, L., A thermodynamic assessment of the Se–Te system, CALPHAD, 1988, vol. 12, no. 3, p. 295. https://doi.org/10.1016/0364-5916(88)90010-7

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Электрохимия

Архивы выпусков Информация о журнале Отправить рукопись в журнал