Известия РАН. Физика атмосферы и океана, 2023, T. 59, № 6, стр. 686-706
Сравнение различных методов кластеризации для определения погодных режимов в Евро-Атлантическом секторе в зимний и летний сезоны
Б. А. Бабанов a, *, В. А. Семенов a, b, И. И. Мохов a, c
a Институт физики атмосферы им. А. М. Обухова РАН
119017 Москва, Пыжевский переулок, 3, Россия
b Институт географии РАН
119017 Москва, Старомонетный переулок, 29, Россия
c Московский государственный университет им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, Россия
* E-mail: babanov@ifaran.ru
Поступила в редакцию 03.06.2023
После доработки 25.07.2023
Принята к публикации 28.08.2023
- EDN: OSUIJZ
- DOI: 10.31857/S0002351523060020
Аннотация
Для выделения режимов крупномасштабной атмосферной циркуляции (погодных режимов) используются различные методы кластерного анализа. В статье приведено сравнение четырех, наиболее часто используемых методов – k-means (KM), иерархической кластеризации Уорда (HW), модели Гауссовой смеси (GM) и самоорганизующихся карт Кохонена (SOM) на примере выделения погодных режимов в Евро-Атлантическом секторе. Использовались данные реанализа ERA5 для высоты геопотенциала на уровне 500 гПа (z500) для периода 1940–2022 гг. Для зимних месяцев методом KM выделялись четыре классических для Евро-Атлантики погодных режима – два режима, ассоциированные с положительной и отрицательной фазами Североатлантического колебания (NAO+ и NAO–), режим Скандинавского блокинга (SB) и режим, характеризующийся повышенным давлением над Северной Атлантикой. Для летних месяцев методом KM выделены режимы, похожие по пространственной структуре на зимние. Методом SOM выделяются режимы, практически неотличимые от режимов, полученных методом KM. В отличие от KM и SOM, методами HW и GM выделены режимы, характерная пространственная структура которых не полностью совпадает с четырьмя классическими зимними режимами в Евро-Атлантике и их летними аналогами. Режимами, полученными методами HW и GM, объясняется меньшая доля дисперсии z500, для них отличаются особенности переходов, относительные повторяемости и характерные продолжительности, а летние режимы меньше похожи на зимние по сравнению с режимами, полученными методом KM. Средние коэффициенты пространственной корреляции между характерными полями аналогичных режимов, детектированных методами KM и HW, составили 0.76 для зимы и 0.83 для лета, методами KM и GM – 0.70 для зимы и 0.72 для лета, методами HW GM – 0.41 и 0.44 соответственно. При использовании некоторых методов кластеризации выявлены статистически значимые тренды сезонной повторяемости режимов – положительный тренд “NAO+” и отрицательный тренд “NAO–”.
1. ВВЕДЕНИЕ
Одним из способов описания крупномасштабной атмосферной циркуляции при изучении ее динамики и климатических изменений является подход [Barnston et al., 1987], при котором меняющаяся со временем структура атмосферных полей подразделяются на ограниченное число хорошо различимых между собою квазистационарных типов циркуляции, которые также называют погодными режимами или режимами атмосферной циркуляции [Corti et al., 1999]. При таком подходе атмосферная циркуляция, фактически непрерывно меняющая свое состояние, рассматривается в качестве системы, состоящей из ограниченного набора режимов, в каждом из которых она пребывает в течение определенного времени, а затем, постепенно или резко (в зависимости от способа выделения режимов), переходит в другой.
Первые крупные работы по выделению типов циркуляции известны с середины XX века, когда различными группами исследователей для территорий Центральной Европы и СССР были выделены несколько типов атмосферной циркуляции [Baur et al., 1944; Дзерзеевский и др., 1946]. Методы, применявшиеся тогда для выделения типов циркуляции, основанные на экспертной оценке погодных карт, впоследствии были названы субъективными [Huth et al., 2008], так как при выделении режимов исследователи во многом полагались на свое субъективное понимание погодных процессов. Методы субъективной классификации типов циркуляции продолжали использоваться и в последующие десятилетия XX века, например, можно отметить каталог Гесса-Брезовски [Hess et al., 1977] для Евро-Атлантики, типы циркуляции Лэмба для Британских островов [Lamb, 1972] или типизация Вангенгейма-Гирса для атлантико-евразийского сектора Северного полушария [Гирс, 1974].
В дальнейшем, внедрение компьютеров и последовательный рост их вычислительных мощностей позволили использовать машинные методы для обработки большого количества метеорологических данных, в том числе в задачах выделения погодных режимов, что позволило рутинно применять так называемые объективные методы [James, 2007], при использовании которых критерием для выделения типов циркуляции служит некоторое численное условие, например, минимизация (максимизация) внутригрупповой (межгрупповой) дисперсии [Kanungo et al., 2002] суточных полей давления на уровне моря [Santos et al., 2005] или высоты геопотенциальной поверхности на уровне 500 гПа (далее, поля циркуляции) [Cassou, 2008].
Самыми ранними и одновременно простыми объективными методами выделения режимов можно считать корреляционные методы [Lund, 1963]. При таком подходе центроидами режимов, то есть геометрическими центрами режимов в пространстве, в котором определены поля, объявляются суточные поля циркуляции с наибольшими средними попарными корреляциями с остальными полями [Willmott, 1987], а суточные поля циркуляции, имеющие попарную корреляцию с центроидами выше (или сумму квадратов расстояний – ниже) некоторого заданного порога, попадают в данный режим. Оставшиеся суточные поля объявляются переходными, то есть не принадлежащими к какому-либо из режимов.
В настоящее время наиболее распространенными подходами при выделении погодных режимов являются методы кластерного анализа, применяющиеся повсеместно в различных научных задачах. Благодаря своей простоте и низких вычислительных затратах наибольшее распространение в задачах выделения погодных режимов получил метод k-means [Hartigan, 1979]. Также относительно часто применяются метод иерархической кластеризации Уорда [Cheng et al., 1993], модель гауссовой смеси [Smyth et al., 1999] и алгоритм самоорганизующихся карт Кохонена [Liu et al., 2011], основанный на нейронных сетях. Подробное описание, а также сравнение результативности этих методов кластерного анализа на основе кластеризации погодных режимов в Евро-Атлантике, являющееся целью настоящей статьи, будет приведено в данной работе.
Как отмечено выше, одной из областей, для которых известны первые работы по выделению погодных режимов, является Европа. Ведущей модой низкочастотной изменчивости атмосферной циркуляции в зимние месяцы в Евро-Атлантике и Северном полушарии в целом является Северо-Атлантическое колебание (North-Atlantic Oscillation, NAO) [Hurrell et al., 2003; Vorobyeva et al., 2021], с которым ассоциированы аномалии осадков и температуры на территории Европы [Hurrell, 1995]. Из-за преобладающего для средних широт Северного полушария западного переноса, характер атмосферной циркуляции в Северной Атлантике, в том числе фаза и интенсивность NAO, имеют определяющее значение на погоду в густонаселенной Европе, в связи с чем в большинстве работ с использованием режимного подхода к изучению атмосферной циркуляции исследуется именно Евро-Атлантический сектор [Vautard et al., 1990]. В Евро-Атлантическом секторе (ЕАТ) различными исследователями обычно выделяется от 4 до 6 режимов [Falkena et al., 2020], двумя из которых неизменно являются режимы, характерные для положительной и отрицательной фаз NAO, и обозначаемые соответственно “NAO+” и “NAO–”.
Определение оптимального количества кластеров при кластеризации данных в некотором многомерном пространстве является отдельной задачей, для решения которой существует свои численные методы, которые кратко будут описаны в данной статье, однако, применительно к задачам выделения погодных режимов, вопрос их оптимального количества до сих пор остается открытым [Christiansen, 2007].
Несмотря на наличие большого числа работ по выделению погодных режимов в ЕАТ, в подавляющем большинстве из них режимы выделялись для зимних месяцев (часто включая ноябрь и март) [Matsueda et al., 2018], когда суточные аномалии полей давления или высоты избранной изобарической поверхности наиболее сильны, что позволяет выделять хорошо различимые (с относительно высоким межкластерным расстоянием) кластеры. Работ по определению погодных режимов в ЕАТ в летние месяцы относительно немного [Guemas et al., 2010], при этом основное внимание в них уделяется именно летним фазам Североатлантического колебания (SNAO) [Folland et al., 2009]. Целью настоящей работы, помимо сравнения результатов различных методов кластерного анализа при выделении погодных режимов в ЕАТ, является сравнение режимов атмосферной циркуляции в ЕАТ в различные сезоны и анализ долгопериодных изменений их характеристик.
2. МЕТОДЫ КЛАСТЕРНОГО АНАЛИЗА ДЛЯ ИДЕНТИФИКАЦИИ ПОГОДНЫХ РЕЖИМОВ
1) Метод k-means
Метод k-means (KM) в настоящее время является одним из самых распространенных и простых методов кластерного анализа, который позволяет разделять объекты кластеризации из набора данных на хорошо различимые группы (кластеры), выполняя задачу максимизации межкластерного и минимизации внутрикластерного расстояния лучше большинства других методов.
В случае выделения погодных режимов, объектами кластеризации являются суточные (или среднемесячные) поля атмосферной циркуляции, которые можно представить как точки, заданные в пространстве размерностью L. L будет определяться либо числом узлов сетки, на котором заданы поля, либо числом первых главных компонент разложения полей на эмпирические ортогональные функции, на которые предварительно, т.е. перед процессом кластеризации, были разложены поля, что, благодаря снижению размерности, позволяет получить более устойчивые результаты. Далее в тексте, представленные таким образом суточные поля циркуляции будут называться просто “точки”.
Перед началом работы алгоритма задается число K будущих кластеров и функция расстояния в пространстве набора данных, в качестве которой обычно используется Евклидово расстояние:
(1)
$\begin{array}{*{20}{c}} {d\left( {{{X}_{i}},{{X}_{j}}} \right) = \sqrt {\mathop \sum \limits_{l = 1}^L \begin{array}{*{20}{c}} {{{{\left( {{{x}_{{il}}} - {{x}_{{jl}}}} \right)}}^{2}}} \end{array}} } \end{array},$Алгоритм KM состоит из следующих шагов:
1) Некоторым случайным образом задаются K начальных положений центроидов будущих кластеров.
2) Точки набора данных присваиваются тем кластерам, к центроидам которых они ближе всего.
3) Положения центроидов кластеров пересчитываются как центры точек, присвоенных данному кластеру на предыдущем пункте.
4) Пункты 2 и 3 повторяются до тех пор, пока алгоритм не сойдется, то есть положения центроидов не перестанут меняться, а внутрикластерная дисперсия не перестанет убывать:
(2)
$\begin{gathered} \begin{array}{*{20}{c}} {{{V}_{{iter}}} = \mathop \sum \limits_{k = 1}^K \mathop \sum \limits_{i \in {{C}_{k}}} {{d}^{2}}\left( {{{C}_{k}},{{X}_{i}}} \right) = \mathop \sum \limits_{k = 1}^K \mathop \sum \limits_{i \in {{C}_{k}}} \mathop \sum \limits_{l = 1}^L {{{\left( {{{c}_{{kl}}} - {{x}_{{il}}}} \right)}}^{2}},} \end{array} \\ {{C}_{{k,iter}}} = \frac{1}{{{{N}_{k}}}}\mathop \sum \limits_{i \in {{C}_{k}}} {{X}_{i}}; \\ \end{gathered} $(3)
${{V}_{{{\text{iter}}\,{\text{max}}}}} = \min \left( {{{V}_{{{\text{iter}}}}}} \right);{{C}_{{k,{\text{iter}}\max + 1}}} = {{C}_{{k,{\text{iter}}\max }}},$Итоговое положение центроидов зависит исключительно от их начального положения, что, при их неоптимальной инициализации, приводит к возможному схождению алгоритма к локальному оптимуму, для которого итоговое V будет больше, чем могло быть. В связи с этим рекомендуется множественный прогон алгоритма по одному и тому же набору данных и последующий отбор решения с минимальным V [Bradley et al., 1998]. Для улучшения инициализации алгоритма KM существует оптимальный метод задания начальных положений центроидов – “k-means++” – при котором центроиды последовательно задаются с вероятностью, пропорциональной расстоянию до ближайшего из уже заданных центроидов. В работе [Arthur et al., 2007] показано, что такая инициализация центроидов позволяет алгоритму сходится с меньшими V за меньшее число итераций. Алгоритм инициализации “k-means++” состоит из следующих шагов:
1. Первый центроид C1 выбирается полностью случайно с координатами одной из точек кластеризуемого набора данных.
2. Второй центроид выбирается по координатам оставшихся точек с вероятностью, пропорциональной d2(Xi,C1) (формула 1). Вероятности нормируются так, чтобы в сумме по всем точкам вероятность равнялась 1.
3. Если K > 2, то все последующие k центроиды (k <= K) выбираются случайно по координатам точек с вероятностью, пропорциональной $\mathop {\min }\limits_{j = 1:k - 1} {{d}_{2}}({{X}_{i}},{{C}_{j}})$, т.е. пропорциональной расстоянию от точки до ближайшего из уже заданных центроидов.
Для устранения детерминированности метода KM, то есть зависимости итогового решения исключительно от инициализации центроидов, существует оптимизация “simulated annealing” (имитация отжига) [Selim et al., 1991]. Во время работы алгоритма на шаге присвоения точек кластерам точки могут быть отнесены не к кластеру ближайшего центроида, а к любому другому с вероятностью P, обратно пропорциональной удаленности от точки до центроида этого кластера:
(4)
$\begin{array}{*{20}{c}} {{{P}_{{k,{\text{iter}}}}} = \exp \left( {\frac{{d_{{{\text{old}}}}^{2} - d_{{k,~{\text{new}}}}^{2}}}{{{{T}_{{{\text{iter}}}}}}}} \right),} \end{array}$Коэффициент охлаждения C подбирается таким образом, чтобы в начале работы алгоритма точки часто приписывались к “неправильным”, т.е. не ближайшим, кластерам с целью обойти решения с локальными оптимумами V, но с ростом числа итераций сходились к итоговому решению, когда вероятности P будут настолько малы, что вероятности быть присвоенной к не ближайшему кластеру перестанут реализовываться, а алгоритм остановится по тому же критерию, что и оригинальный KM (формула 3). Стоит отметить, что при $d_{{{\text{old}}}}^{2}$ = $d_{{k,{\text{new}}}}^{2}$ вероятность P максимальна, то есть вероятность для точки остаться в ближайшем кластере выше (по формуле 4 она равна 1, но эти вероятности нормируются так, чтобы для каждой точки сумма вероятностей быть приписанной к любому из k кластеров равнялась 1), чем в более удаленном.
В работе по кластеризации суточных полей давления в Евро-Атлантике показано [Philipp et al., 2007], что использование оптимизации “simulated annealing” повышает воспроизводимость и лучше минимизирует V итоговых решений по сравнению с традиционным алгоритмом k-means.
2) Иерархическая кластеризация Уорда
Иерархическая кластеризация представляет собой подход, при котором данные разбиваются на систему вложенных кластеров, создавая “дерево” кластеров, которое можно визуализировать с помощью так называемой дендрограммы. Иерархическая кластеризация принципиально разделяется на два подвида – дивизивную (“сверху-вниз”) и агломеративную (“снизу-вверх”) [Roux, 2018].
При дивизивной кластеризации набор данных на начальном этап представляет собой единый кластер и последовательно разбивается на подкластеры, однако такой подход используется редко – для него не существует устоявшихся методов, например, на каждом этапе разбиения можно использовать k-means или другой метод [Lamrous et al., 2006], при этом на каждом этапе исследователю придется каким-то образом выбирать число кластеров K и заново прогонять алгоритм. Агломеративная кластеризация используется чаще [Murtagh et al., 2012], при этом подходе, наоборот, на начальном этапе каждая точка представляет собой отдельный кластер, далее кластеры попарно объединяются по одному из выбранных методов сцепки кластеров (linkage method), которых существует несколько [Murtagh et al., 2017].
На основе выбранного метода сцепки на каждой итерации ищется и объединяется такая пара кластеров, для которой будет минимален параметр, зависящий от выбранного метода сцепки [Govender et al., 2020]: 1) Single linkage, метод ближайшего соседа – расстояние двух ближайших точек из разных кластеров; 2) Complete linkage (метод дальнего соседа) – расстояние двух наиболее удаленных точек из разных кластеров; 3) Average linkage (метод средней связи) – среднее попарное расстояние между точками из разных кластеров; 4) Centroid linkage (центроидный метод) – расстояние между центроидами кластеров; 5) Ward’s linkage (метод Уорда) – расстояние считается как потенциальная прибавка к внутрикластерной дисперсии пары кластеров после их объединения, то есть ищется и объединяется такая пара кластеров (например, A и B), для которой ΔV будет минимально:
(5)
$\begin{gathered} \Delta {{V}_{{A \cup B}}} = \left( {\mathop \sum \limits_{i \in \left( {A \cup B} \right)} {{d}^{2}}\left( {{{C}_{{A \cup B}}},{{X}_{i}}} \right)} \right) - \\ - \left( {\mathop \sum \limits_{i \in A} {{d}^{2}}\left( {{{C}_{A}},{{X}_{i}}} \right) + \mathop \sum \limits_{i \in B} {{d}^{2}}\left( {{{C}_{B}},{{X}_{i}}} \right)} \right), \\ \end{gathered} $(6)
$\Delta {{V}_{{A \cup B}}} = \mathop {\min }\limits_{P,Q} \left( {\Delta {{V}_{{P \cup Q}}}} \right),$Применительно к задаче идентификации погодных режимов, при использовании иерархической кластеризации обычно применяется метод сцепки Уорда [Cheng et al., 1993], который похож на k-means тем, что основным минимизируемым параметром в процессе работы алгоритма здесь является внутрикластерная дисперсия. Преимуществом иерархической кластеризации Уорда (HW) является отсутствие зависимости от инициализации кластеров, которая в принципе отсутствует в HW. Конечный результат кластеризации методом HW зависит исключительно от кластеризуемых данных, при этом по итогу кластеризации исследователь получает возможность изучить дендрограмму кластеризации и остановиться на итерации с интересующим его числом кластеров K. В работе [Bao et al., 2015] кластеризация HW используется для выделения зимних режимов атмосферной циркуляции в Северном полушарии и сравнивается с результатами по методу SOM.
3) Модель гауссовой смеси
Одним из подходов при кластеризации многомерных данных является исследование их плотности распределения. Например, кластеры можно определять путем поиска локальных функций плотности распределения данных. При таком подходе в пространстве кластеризуемого набора данных ищутся локальные максимумы плотности распределения, представляющие из себя точки, имеющие максимальное число соседей (других точек) в некотором радиусе R многомерной сферы по сравнению с другими точками, который подбирается исследователем эмпирически. Такой метод, например, ранее использовался при выделении погодных режимов в Северном полушарии [Molteni et al., 1990]. Применительно к задачам выделения погодных режимов данный метод кластеризации последнее время применяется не так часто, этот метод похож на один из известных методов кластерного анализа под названием DBSCAN (Density-based spatial clustering of applications with noise) [Khan et al., 2014], преимущество которого состоит в способности отделять шум из набора данных, а также малом числе входных параметров перед кластеризацией, всего 2 параметра – радиус R и минимальное число соседей для формирования кластера. Одно из свойств данного метода, которое можно отметить как недостаток – формирование одного крупного, перенаселенного кластера, и большого числа небольших.
Частым предположением о природе кластеризуемых данных служит гипотеза, что данные распределены нормально. В случае кластеризации, когда исследователь полагает, что набор данных состоит из нескольких хорошо различимых групп, можно также предположить, что объекты внутри каждой из этих групп также распределены нормально [Banfield et al., 1993]. Кластеризация гауссовой смесью (GM), в отличие от KM и HW, относится к типу “мягких кластеризаций” (soft clustering) [Kearns et al., 1998], когда по результатам работы алгоритма каждый объект приписывается не к одному определенному кластеру, а к каждому из них с определенной вероятностью, однако исследователю не запрещается по результатам кластеризации присвоить каждый объект из набора данных исключительно тому кластеру, к которому он принадлежит с наибольшей вероятностью.
При кластеризации GM в пространстве набора данных инициализируется K многомерных нормальных распределений, то есть кластеров, для каждого из которых каким-либо способом задаются (угадываются) параметры – среднее и матрица ковариаций [Bilmes et al., 1998]. Среднее при этом можно считать аналогом центроида кластера. Также для каждого распределения задаются веса, которые можно трактовать как доля точек выборки, принадлежащих данному кластеру. Далее, в процессе так называемого EM-алгоритма (Expectation-maximization algorithm) [Yang et al., 2012], основанного на теореме Байеса, и который, вообще говоря, можно использовать и для смеси других распределений, средние, матрицы ковариаций и веса кластеров итеративно пересчитываются. Алгоритм можно представить в виде следующих этапов:
1. Инициализируются средние μk, матрицы ковариаций Σk и веса кластеров wk. Значения задаются, как правило, случайным образом, чтобы можно было прогнать алгоритм несколько раз и сравнить результаты. Для инициализации можно использовать, например, способ “k-means++” или найти K первых локальных максимумов плотности распределения точек набора данных по методу, кратко упомянутому в начале данного раздела и более подробнее описанного в [Molteni et al., 1990].
2. Для каждой точки Xi, i = (1…N) из набора данных пересчитывается вероятность ее принадлежности к одному из кластеров (многомерных нормальных распределений):
(7)
${{P}_{{{{X}_{i}}}}}\left( {{{B}_{k}}} \right) = \frac{{P\left( {{{B}_{k}}} \right){{P}_{{{{B}_{k}}}}}\left( {{{X}_{i}}} \right)}}{{P\left( {{{X}_{i}}} \right)}} = \frac{{{{w}_{k}}{{\rho }_{{{{B}_{k}}}}}\left( {{{X}_{i}}} \right)}}{{\sum\limits_{k = 1}^K {{{w}_{k}}} {{\rho }_{{{{B}_{k}}}}}\left( {{{X}_{i}}} \right)}},$(8)
$\begin{gathered} {{\rho }_{{{{B}_{k}}}}}\left( {{{X}_{i}}} \right) = \frac{1}{{{{{\left( {2\pi } \right)}}^{{\frac{L}{2}}}}{{{\left| {{{\Sigma }_{k}}} \right|}}^{{\frac{1}{2}}}}}} \times \\ \times \,\,\exp \left( {\frac{{ - 1}}{2}{{{\left( {{{X}_{i}} - {{\mu }_{k}}} \right)}}^{T}}\Sigma _{k}^{{ - 1}}\left( {{{X}_{i}} - {{\mu }_{k}}} \right)} \right), \\ \end{gathered} $3. По пересчитанным вероятностям принадлежностей точек пересчитываются параметры распределений wk, μk и Σk:
(9)
${{w}_{k}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N {{P}_{{{{X}_{i}}}}}\left( {{{B}_{k}}} \right);$(10)
${{\mu }_{k}} = \frac{{\sum\limits_{i = 1}^N {\left( {{{P}_{{{{X}_{i}}}}}\left( {{{B}_{k}}} \right){{X}_{i}}} \right)} }}{{\sum\limits_{i = 1}^N {{{P}_{{{{X}_{i}}}}}\left( {{{B}_{k}}} \right)} }};$(11)
${{\Sigma }_{k}} = ~\frac{{\sum\limits_{i = 1}^N {\left( {{{P}_{{{{X}_{i}}}}}\left( {{{B}_{k}}} \right)({{X}_{i}} - {{\mu }_{k}}){{{({{X}_{i}} - {{\mu }_{k}})}}^{T}}} \right)} }}{{\sum\limits_{i = 1}^N {{{P}_{{{{X}_{i}}}}}} \left( {{{B}_{k}}} \right)~~}}.$4. Пункты 2 и 3 алгоритма продолжаются до тех пор, пока алгоритм не сойдется, то есть параметры распределений не перестанут меняться.
Среди преимуществ метода GM можно отметить способность создания кластеров “эллиптической” формы, в отличие от методов KM и HW, в которых из-за минимизации внутрикластерного расстояния, при расчете которой дисперсии каждой из размерностей складываются в одно число (формула 2), кластеры получаются преимущественно “круглые”, т.е. кластеризация в них происходит по всем переменных независимо от их распределения.
В процессе EM-алгоритма происходит максимизация вероятности принадлежностей точек кластерам, а не минимизация V (формула 2), т.е. подбираются такие параметры K многомерных нормальных распределений, которые с наибольшей вероятностью описывают набор входных данных, что позволяет получать кластеры, имеющие вытянутую (“эллиптическую”) форму вдоль тех размерностей пространства набора данных, в которых выше дисперсия.
При режимном подходе к анализу атмосферной циркуляции метод кластеризации GM используется, например, в работах [Smyth et al., 1999; Hannachi, 1997], где с помощью него выделяются режимы низкочастотной изменчивости атмосферной циркуляции в тихоокеанском и атлантическом секторах Северного полушария.
4) Метод самоорганизующихся карт
Самоорганизующиеся карты Кохонена (Self-organizing maps, SOM) [Kohonen, 2012] представляют собой метод кластерного анализа, основанный на нейронных сетях. Данный метод позволяет получать кластеры из многомерного набора данных, которые удобно визуализировать на двумерной карте, кластеры в которой отсортированы друг относительно друга (отсюда “самоорганизующиеся”) на основе выбранной метрики расстояния (обычно Евклидовой).
Так как SOM входит в раздел методов машинного обучения на основе нейронных сетей, для него имеется своя сложившаяся терминология – кластеры называются “нейронами”. Перед запуском алгоритма кластеризации нейроны задаются в своем собственном двумерном пространстве, независимом от набора данных, т.е. на нейронной сети или карте. На нейронной сети определяются расстояния между нейронами или, иначе говоря, мера соседства нейронов, которая используется в процессе кластеризации для их взаимного “обучения”. Центроиды, т.е. координаты центров будущих кластеров, называются “векторами веса” или просто “весами” нейронов, итерации алгоритма называются “эпохами”.
Нейроны представляют из себя объекты, состоящие из двух векторов, заданных в разных пространствах – вектора веса, заданного в пространстве набора данных, и координат (как правило, двумерных), заданных в отдельном пространстве и определяющих положение нейрона на карте нейронной сети относительно других нейронов. В процессе работы алгоритма векторы веса нейронов как бы “натягиваются” на “облако” набора входных данных, при этом векторы веса нейронов, расположенных рядом друг с другом на карте нейронной сети, “притягиваются”, т.е. обновляют значения векторов веса относительно входных данных, к соседним областям в пространстве набора данных.
Алгоритм SOM состоит из следующих шагов:
1. Инициализация координат и весов нейронов. Координаты задаются на двумерной нейронной сети размера K = M × N, где M и N – размеры сети по горизонтали и вертикали. Нейроны могут взаимно располагаться в виде квадратной, шестиугольной или случайной сетки, от чего будет зависеть расстояние между соседствующими нейронами. Веса нейронов задаются (инициализируются) некоторым случайным образом в диапазоне значений набора входных данных, то есть в диапазоне координат, которые принимают точки в пространстве входных данных.
2. Из набора данных выбирается случайная точка. Среди кластеров (нейронов) ищется так называемый “нейрон-победитель”, вес которого на основе выбранной метрики, как правило, Евклидовой, будет ближе всего к данной точке:
(12)
$\forall k \in 1 \ldots K~\,d\left( {{{X}_{i}},{{W}_{c}}\left( t \right)} \right) \leqslant d\left( {{{X}_{i}},{{W}_{k}}\left( t \right)} \right),$3. Веса нейронов обновляются на основе расстояния от их весов до точки Xi и функции обучения, зависящей от эпохи и взаимного расстояния нейронов:
(13)
${{W}_{k}}\left( {t + 1} \right) = {{W}_{k}}\left( t \right) + {{h}_{{ck}}}\left( t \right)\left( {{{X}_{i}} - {{W}_{k}}\left( t \right)} \right);~~~$(14)
${{h}_{{ck}}}\left( t \right) = \alpha \left( t \right)\exp \left( {\frac{{ - {{{\left| {\left| {{{r}_{c}} - {{r}_{k}}} \right|} \right|}}^{2}}}}{{2{{\sigma }^{2}}\left( t \right)}}} \right),$4. Пункты 2 и 3 алгоритма продолжаются до достижения некоторого критерия – либо пока не будет достигнут заранее предзаданный номер эпохи tmax (наиболее частый критерий), либо пока “ошибка карты” не перестанет существенно убывать: ΔV = V(t + 1) – V(t) ≤ ε; V можно посчитать по формуле 2, где в качестве Ck используются веса нейронов Wk(t).
Примеры использования нейронных сетей для выделения режимов крупномасштабной атмосферной циркуляции можно найти в работах [Polo et al., 2011; Loikith et al., 2017]. В работе [Polo et al., 2011] утверждается, что KM и SOM показывают похожие результаты, что также является одним из выводов настоящей работой (см. главу “результаты”).
Одно из основных преимуществ SOM состоит в автоматической сортировке кластеров друг относительно друга, то есть близкие по Евклидовому расстоянию кластеры будут располагаться рядом на нейронной карте. Например, на двумерной нейронной карте M × N = 5 × 5 (итого, K = 25 нейронов, то есть кластеров), кластеры с координатами {1,1}, {1,2} и {2,1} будут похожи друг на друга и иметь схожие характеристики, а кластеры с координатами {1,1} и {5,5} будут наиболее различаться между собой (по метрике Евклидова расстояния). Для методов KM и HW такая взаимная сортировка кластеров потребовала бы отдельной процедуры, то есть при кластеризации с таким же K = 25 кластеры с номерами 1 и 2 могли бы располагаться где угодно (в пространстве набора данных) относительно друг друга. При использовании SOM обычно выбирают большие K, т.к. для небольших K, например <10, взаимная сортировка, как правило, не нужна.
3. ОПРЕДЕЛЕНИЕ ЧИСЛА КЛАСТЕРОВ
Вышеперечисленные методы, кроме HW, перед началом работы требуют от исследователя заранее выбрать количество кластеров K, и производят кластеризацию согласно выбранному числу. Метод HW в результате создания системы вложенных кластеров позволяет выбрать пользователю решение с любым заданным числом кластеров, однако так же не дает ответа, какое K является предпочтительным.
Для определения оптимального количества кластеров существует несколько простых (например, “метод локтя” или “силуэта” [Shi et al., 2021]) и более сложных методов (например, индексы классифицируемости и воспроизводимости [Michelangeli et al., 1995]). Применительно к задачам выделения погодных режимов через кластеризацию гладких суточных полей циркуляции атмосферы, простые методы, в которых оптимальное K определяется максимумом или точкой перегиба функции некоторого параметра от K, как правило, не дают четкого ответа [Christiansen, 2007]. Тем не менее, их стоит упомянуть, так как, при хорошей “кластеризуемости” набора данных, этих методов будет достаточно. Стоит отметить, что описанные ниже методы подходят прежде всего для кластеризации KM.
1) Метод локтя (Elbow method)
Данный метод является самым простым. Данные кластеризуются для каждого K в некотором интервале от 2 до Kmax. Строится график функции V(K) (формула 2), для которой ищется “локоть” – точка перегиба, такое K, после которого V(K) перестает заметно убывать, т.е. последующее добавление новых кластеров не приводит к заметному улучшению качества кластеризации. Стоит отметить, что V(K) это, в любом случае, монотонно убывающая функция, которая стремится к 0 при K стремящемся к N.
2) Метод Силуэта
Для каждого потенциального K проводится кластеризация данных. Для каждой точки i из набора данных считается величина S(i), называемая коэффициент силуэта:
(15)
$S\left( i \right) = \frac{{b\left( i \right) - a\left( i \right)}}{{\max \left\{ {a\left( i \right),b\left( i \right)} \right\}}},\,\,{\text{где}}$(16)
$\begin{gathered} a\left( i \right) = \frac{1}{{{{N}_{k}} - 1}}\mathop \sum \limits_{j \in {{C}_{k}},j \ne i} d\left( {{{X}_{i}},{{X}_{j}}} \right); \\ b\left( i \right) = \mathop {\min }\limits_{k{\kern 1pt} ' \ne k} \left\{ {\frac{1}{{{{N}_{{k{\kern 1pt} '}}}}}\mathop \sum \limits_{j \in {{C}_{{k{\kern 1pt} '}}}} d\left( {{{X}_{i}},{{X}_{j}}} \right)} \right\}, \\ \end{gathered} $3) Индекс классифицируемости
Индекс предложен в работе [Michelangeli et al., 1995] для выделения погодных режимов посредством кластеризации полей высоты геопотенциала на уровне 700 мбар. Идея состоит в том, что при оптимальном K различные решения при кластеризации методом KM, полученные путем разных инициализаций, более похожи друг на друга, чем при других K.
Допустим, что для данного K методом k-means по разным инициализациям посчитано M различных решений. Для каждой пары решений P, Q можно посчитать матрицу попарных корреляций центроидов кластеров:
(17)
${{A}_{{ij}}}\left( {P,Q} \right) = corr\left( {{{C}_{i}}\left( P \right),{{C}_{j}}\left( Q \right)} \right),$(18)
$c*\left( K \right) = \frac{1}{{M\left( {M - 1} \right)}}\mathop \sum \limits_{1 \leqslant m \ne m' \leqslant M} c\left( {{{P}_{m}}\left( K \right),{{P}_{{m'}}}\left( K \right)} \right).$Для оценки значимости, полученный индекс классифицируемости c * (K) сравнивают с таковым, полученным по случайным сгенерированным выборкам. Выборки генерируются как марковские процессы, имеющие такую же автокорреляцию 1-го порядка и ковариацию, что и оригинальные данные. Полученные Nген индексов сген * (K, N) сортируются по возрастанию. Долю сген * (K, N), которые оказались меньше с * (K), можно считать уровнем значимости индекса классифицируемости. Выбирается такое наименьшее K, для которого уровень значимости оказался выше уровня, заданного исследователем. При использовании данного индекса рекомендуется использовать как можно большие M и Nген (50 и 100 в оригинальной статье).
4) Индекс воспроизводимости
Идея данного индекса, также описанного в [Michelangeli et al., 1995], заключается в том, что если для определенного K набор данных хорошо кластеризуется, то и его случайные половинчатые подвыборки будут сходиться к решениям, аналогичным таковым у оригинальной выборки.
Методом KM создается M различных решений, полученных с помощью разных инициализаций. Среди них ищется эталонное решение – такое m решение, для которого будет максимально среднее ❬c(Pm, Pm')❭m' ≠m по всем остальным решениям m', т.е. решение, центроиды которого в среднем больше всего похожи на аналогичные центроиды остальных решений.
Далее, создаются R подвыборок, содержащих по 50% случайно выбранных точек оригинальной выборки данных. Для каждой из подвыборок, таким же образом, как для оригинальной выборки, проводится M кластеризаций и аналогичным образом выбирается эталонное решение. Методом попарных корреляций центроидов кластеров, аналогично индексу классифицируемости, для каждой пары эталонных решений оригинальной выборки Pm и одной из подвыборок Pmr считается $A_{i}^{'}({{P}_{m}},{{P}_{{mr}}})$ = $\mathop {\max }\limits_j {{A}_{{ij}}}({{P}_{m}},{{P}_{{mr}}})$ и осредняется по всем r = 1…R. Данная процедура проводится для каждого рассматриваемого K. Оптимальным можно считать такое K, для которого средняя по всем подвыборкам попарная корреляция центроидов эталонного решения оригинальной выборки и эталонных решений подвыборок – ${{\left\langle {A_{i}^{'}({{P}_{m}},{{P}_{{mr}}})} \right\rangle }_{r}}$ – будет выше некоторого заданного уровня значимости для каждого i = 1…K центроида эталонного решения оригинальной выборки.
Вопрос количества погодных режимов, остается одним из ключевых при режимном подходе в исследованиях крупномасштабной атмосферной циркуляции [Christiansen, 2007; Philipp et al., 2007]. Оптимальное K, если оно существует, зависит как от выбранного метода кластеризации, так и от свойств набора данных – исследуемой характеристики, определяющей циркуляцию (поле давления на уровне моря, высоты геопотенциальной поверхности или другой переменной), выбранной области, продолжительности временного ряда, процедуры предобработки данных и т.д. [Falkena et al., 2020].
4. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ РЕЖИМОВ
По результатам кластеризации каждое суточное поле, характеризующее атмосферную циркуляцию, присваивается одному из K режимов. Простейшей статистической характеристикой режима можно считать его населенность или относительную повторяемость, то есть долю суточных полей, отнесенных данному режиму. Другими статистическими характеристиками режимов являются их характерная продолжительность, наиболее вероятные и статистически значимые [Vautard et al., 1990] переходы между режимами, которые можно выявить, посчитав матрицу переходов.
В некоторых исследованиях используют переходные дни [Kondrashov et al., 2004], которые не относят к какому-либо из режимов. Их наличие меняет подход к изучению переходов между режимами, добавляя системе “переходное” состояние и позволяя рассматривать события, когда режимы переходят не только из одного в другой, но и возвращаются “сами в себя” через переходное состояние. В данной работе будет использоваться подход без использования переходных дней.
Как правило, наиболее населенные режимы являются в то же время самыми продолжительными и наиболее вероятными для переходов из других режимов, как бы стягивая переходы в свою сторону в виду большей населенности. Стоит отметить, что характерная (средняя или медианная) продолжительность режимов, описывающих низкочастотную изменчивость атмосферной циркуляции, существенно зависит от способа предобработки полей циркуляции, а именно применения (или неприменения) временной фильтрации данных для отсеивания синоптической изменчивости и соответствующего выбора периода отсечки фильтра (обычно выбирают период ~10 дней, от чего характерная продолжительность режимов устремляется к данному значению, но составляет ~5 дней без использования фильтрации).
При подсчете статистически значимых переходов, которые можно посчитать путем сравнения реальной матрицы перехода со случайно сгенерированными путем перемешивания режимных событий, происходит “нормировка” переходов режимов на их населенность. Таким образом переходы в малонаселенные режимы могут не быть наиболее вероятными, но в то же время статистически значимыми (т.е. происходить статистически значимо чаще, чем равновероятно), подробнее методика выявления статистически значимых переходов описана в [Vautard et al., 1990].
В различных исследованиях с выделением четырех погодных режимов в Евро-Атлантическом секторе – положительной и отрицательной фаз Североатлантического колебания (NAO+/NAO–), Скандинавского блокинга (SB) и Атлантического антициклона (AR) – их относительная населенность, как правило, различается, но при этом, независимо от выбранного способа предобработки для последних десятилетий прослеживается следующая картина – самым населенным (≈30% дней) и продолжительным является режим NAO+, средними по населенности оказываются режимы SB и AR (≈23–27% дней), наименее населенным NAO– (≈20% дней) [Cassou, 2008; Dawson et al., 2012; Charlton-Perez et al., 2018].
5. ПРЕДОБРАБОТКА ДАННЫХ И КЛАСТЕРИЗАЦИЯ
1) Данные и предобработка
Для идентификации режимов использовались поля высоты геопотенциала на уровне 500 гПа (z500) реанализа ERA5 [Hersbach et al., 2020] c 1940 по 2022 гг. Поля были осреднены до суточных и интерполированы на сетку с шагом в 1 градус для удобства. Для выделения режимов в Евро-Атлантике был выбран сектор 80 з.д.–40 в.д. по долготе и 30 с.ш.–80 с.ш. по широте, такая область чаще всего используется для выделения погодных режимов в ЕАТ [Fabiano et al., 2020].
Перед кластеризацией были получены поля аномалий путем вычитания из суточных полей сезонного хода, который считался осреднением суточных полей за одни и те же календарные даты разных лет за весь период (1940–2022 гг.), сглаженные скользящим средним в 5 суток. Для удаления высокочастотных синоптических волн к полям аномалий применялся фильтр Баттерворта низких частот [Selesnick et al., 1998] с периодом фильтрации 10 суток. Из фильтрованных суточных полей аномалий высоты геопотенциала выбирались зимние (декабрь, январь, февраль) и летние (июнь, июль, август) месяцы для кластеризации зимних и летних режимов соответственно. За исследуемый 83-летний период 1940–2022 гг. для зимних месяцев имеется 7491 суточных полей, для летних – 7636.
Для сглаживания пространственной дисперсии полей и уменьшения размерности данных фильтрованные суточные поля аномалий высоты геопотенциала (далее, поля аномалий) раскладывались на эмпирические ортогональные функции (ЭОФ). Перед разложением на ЭОФ поля аномалий были взвешены на корень из площади для уравнивания вклада в дисперсию узлов сетки полей на разных широтах. Для зимних полей было отобрано 13 первых ЭОФ, объясняющих 94.6% дисперсии, для летних полей 20 первых ЭОФ, объясняющих 94.8% дисперсии, такие числа ЭОФ выбраны, чтобы они объясняли примерно по 95% дисперсии в обоих случаях. Непосредственно кластеризации подвергались временные ряды главных компонент ЭОФ.
Отметим, что в разных работах с выделением режимов атмосферной циркуляции в ЕАТ перед кластеризацией используют разное число ЭОФ, например, 4 в работах [Dawson et al., 2012; Fabiano et al., 2020] или 14 в [Cassou, 2008; Charlton-Perez et al., 2018]. Как правило, авторы отмечают, что результаты кластеризации не сильно меняются при увеличении числа ЭОФ. В работе [Falkena et al., 2020] исследуются различия в погодных режимах, полученных методом KM, в зависимости от способа предобработки данных – использования (или неиспользования) временных фильтров и разложения на ЭОФ. Утверждается, что режимы, полученные при разложении данных на 10, 15 и 20 первых ЭОФ и без разложения (оригинальные данные), практически не отличаются и имеют схожие повторяемости и вероятности переходов.
2) Выбор количества режимов
Была проведена оценка оптимального количества режимов на интервале K от 2 до 10 для кластеризации методом KM. Как было отмечено выше, простые методы проверки оптимального числа кластеров (метод локтя и Силуэт) не дают четкого ответа. Графики V(K) и $\left\langle {{{S}_{i}}\left( t \right)} \right\rangle $ от K представляют собой убывающие функции, однако для зимних режимов наблюдается слабый перегиб V(K) и локальный максимум $\left\langle {{{S}_{i}}\left( t \right)} \right\rangle $ (при данном методе ищется глобальный максимум) при k = 4. Для летних режимов аналогичной картины не наблюдается, кривые V(K) и $\left\langle {{{S}_{i}}\left( t \right)} \right\rangle $ от K плавно убывают.
Для оценки оптимального числа режимов использовались в том числе индексы классифицируемости и воспроизводимости. Для подсчета индекса классифицируемости было сгенерировано 400 случайных выборок с одинаковыми дисперсиями и автокорреляцией 1-го порядка, как у оригинальных данных, и 400 случайных подвыборок для подсчета индекса воспроизводимости.
Для зимних режимов индексы показывают локальные пики для k = 4 и k = 6 (см. рис. 1), но ни для одного K индекс классифицируемости оригинальной выборки не оказался выше, чем у 95% сгенерированных выборок, т.е. никакое K не будет являться статистически значимым. Для летних режимов высокое значение индексов наблюдается при k = 3 (см. рис. 2).
Рис. 1.
Индексы классифицируемости (а) и воспроизводимости (б) для зимних режимов. а) пунктирными линиями обозначены 5% (20-ая выборка из 400) и 95% (380-ая выборка) уровни индекса сгенерированных выборок, сплошной линией с точками значение индекса для оригинальной выборки; б) сплошной линией среднее по всем режимам значение индекса воспроизводимости, точками обозначено значение индекса воспроизводимости для каждого из K режимов в отдельности.
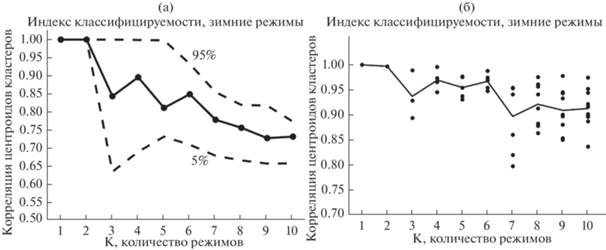
В целом, использованные методы не дали однозначного ответа об оптимальном количестве режимов. Так как в большинстве исследований для выделения зимних режимов в Евро-Атлантике используется K = 4 [Cassou, 2008; Michelangeli et al., 1995; Fabiano et al., 2020; Dawson et al., 2012; Charlton-Perez et al., 2018], было решено выбрать это число для возможности сопоставления с предыдущими результатами. Для летних режимов кластеризация так же проводилась с K = 4 для возможности сравнения полученных летних режимов с зимними. Стоит отметить, что существуют работы, в которых в ЕАТ зимой выделяется 6 режимов [Falkena et al., 2020], в таком случае режимы “NAO+”, “NAO–” остаются визуально неизменными (поля центроидов этих режимов), а у режимов “SB” и “AR” появляются “противоположные” – “SB-” и “AR-”.
Обработка данных и их последующая кластеризация выполнялись в программной среде MATLAB с использованием как встроенного функционала, так и дополнительных программ, разработанных в том числе авторами статьи. Предобработка данных (удаление сезонного хода, фильтрация по времени, разложение на ЭОФ) выполнялась как с использованием встроенных функций, так и функций из пакета “Climate Data Toolbox for MATLAB” [Greene et al., 2019] (“filt1”, “eof” и другие). Для кластеризации KM с использованием оптимизаций “kmeans++” и “simulated annealing”, а также для подсчета индексов классифицируемости и воспроизводимости использовались написанные авторами программы, для остальных методов кластеризации – GM, HW и SOM – использовались встроенные в MATLAB функции (“fitgmdist”, “cluster”, “linkage”, “nctool” и прочие).
6. РЕЗУЛЬТАТЫ
1) Поля зимних и летних погодных режимов
Средние характерные поля аномалий z500 режимов, полученные путем усреднения всех cуточных полей аномалий z500, попавших в соответствующие режимы, представлены на рис. 3. Режимы, полученные методом SOM, не приведены на рисунке. Результаты кластеризации методом SOM оказались практически идентичны результатам, полученным по методу KM – число суточных полей, попавших в другие, чем в методе KM, режимы, составило 12 и 10 полей из 7491 и 7636 для зимних и летних режимов соответственно, то есть менее 0.2% (также см. табл. 1), поэтому далее в данной главе результаты метода SOM не приведены, так как принимаются идентичными таковым по методу KM.
Рис. 3.
Средние поля аномалий z-500 зимних и летних режимов в ЕАТ секторе. Верхние три ряда – зимние режимы, нижние три ряда – летние, справа от полей соответствующие шкалы величины аномалий z500 в метрах для зимних и летних режимов.
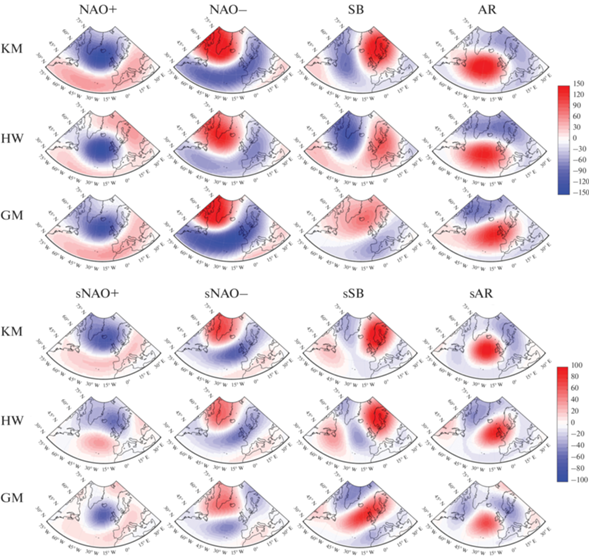
Таблица 1.
Сумма внутрикластерных расстояний зимних и летних погодных режимов, полученных разными методами кластеризации. Единица измерения – 104 м2
| Зимние погодные режимы | ||||||
|---|---|---|---|---|---|---|
| Метод кластеризации | sNAO+ | sNAO– | sSB | sAR | Суммарная внутрикластерная дисперсия | Доля объясненной дисперсии |
| KM | 1512 | 1374 | 1303 | 1323 | 5511 | 32.64% |
| SOM | 1514 | 1374 | 1304 | 1319 | 5511 | 32.64% |
| HW | 1267 | 2208 | 1248 | 1030 | 5753 | 29.68% |
| GM | 1537 | 676 | 2122 | 1561 | 5896 | 27.94% |
| Летние погодные режимы | ||||||
| KM | 462 | 603 | 494 | 476 | 2035 | 23.62% |
| SOM | 461 | 604 | 494 | 477 | 2035 | 23.62% |
| HW | 551 | 713 | 364 | 443 | 2070 | 22.29% |
| GM | 746 | 631 | 424 | 338 | 2139 | 19.72% |
Традиционные названия NAO+, NAO–, SB, AR даны для режимов, полученных методом KM, так как визуально они наиболее совпадают с традиционными зимними ЕАТ режимами, полученными этим методом в других исследованиях [Fabiano et al., 2020; Dawson et al., 2012; Charlton-Perez et al., 2018]. Не все режимы, полученные по методам HW и GM, воспроизводят вышеназванные режимы, однако они сопоставлены с режимами по методу KM таким образом, чтобы средняя пространственная корреляция режимов, названных аналогично, была максимальной. На рис. 3 и далее по тексту для летних режимов используются аналогичные зимним режимам (NAO+, NAO–, SB, AR) названия с припиской “s” (summer).
Из рис. 3 видно, что летние поля режимов являются менее выраженными (поля на рисунках более бледные даже с учетом использования уменьшенной шкалы) по сравнению с зимними, что является следствием более низкой изменчивости полей z500 в летние месяцы по сравнению с зимними.
В табл. 1 приведено сравнение внутрикластерных расстояний в зависимости от выбранного метода кластеризации. Видно, что KM и SOM произвели кластеры с близкими внутрикластерными расстояниями (разница в пользу k-means в 5-ом знаке после запятой, не приведено в таблице), при этом кластеризации HW и GM оказываются хуже в терминах суммарных внутрикластерных расстояний и доли объясненной дисперсии, то есть в среднем кластеры HW и GM менее плотные, несмотря на выраженность некоторых из них (например, NAO– в GM). Стоит отметить, что доля объясненной дисперсии (которая считается как 1 – Vk/V1) зависит от метода предобработки данных и выбранного числа ЭОФ разложения оригинальных полей, однако тенденция превосходства k-means при этом сохраняется.
В табл. 2 представлено сравнение пространственных корреляций средних полей режимов, полученных разными методами, а также сравнение пространственных корреляций зимних и летних полей для одного и того же метода. По приведенным значениям в таблице видно, что результаты кластеризации GM и HW плохо коррелируют между собой (<0.5 в среднем для обоих сезонов), но хорошо коррелируют с KM (>0.7 в среднем для обоих сезонов). Сравнение пространственных корреляций зимних и летних полей аналогичных режимов показывает, что наиболее похожие летние режимы по сравнению с зимними получаются при методе KM, хуже всего при методе HW, что так же свидетельствует о том, что KM является более предпочтительным методом при кластеризации полей циркуляции атмосферы.
Таблица 2.
Пространственные корреляции средних полей режимов, полученных разными методами для зимних и летних сезонов
| Корреляции режимов, полученных разными методами | |||||
|---|---|---|---|---|---|
| Методы кластеризации | sNAO+ | sNAO– | sSB | sAR | В среднем |
| Зимние погодные режимы | |||||
| KM и HW | 0.55 | 0.94 | 0.67 | 0.89 | 0.76 |
| KM и GM | 0.97 | 0.92 | 0.20 | 0.71 | 0.70 |
| HW и GM | 0.67 | 0.74 | –0.56 | 0.79 | 0.41 |
| Летние погодные режимы | |||||
| KM и HW | 0.79 | 0.99 | 0.92 | 0.63 | 0.83 |
| KM и GM | 0.66 | 0.84 | 0.65 | 0.73 | 0.72 |
| HW и GM | 0.19 | 0.84 | 0.37 | 0.37 | 0.44 |
| Корреляции аналогичных зимних и летних режимов, полученных одним методом | |||||
| Методы кластеризации | NAO+ и sNAO+ | NAO– и sNAO– | SB и sSB | AR и sAR | В среднем |
| KM | 0.90 | 0.81 | 0.85 | 0.81 | 0.84 |
| HW | –0.20 | 0.62 | 0.47 | 0.48 | 0.34 |
| GM | 0.83 | 0.83 | 0.25 | 0.51 | 0.60 |
2) Относительная и сезонная повторяемость режимов
Для полученных разными методами режимов анализировались и сравнивались относительная и сезонная повторяемости, средняя продолжительность и матрицы переходов. Относительная повторяемость режимов представлена в табл. 3, где также приведена повторяемость классических зимних погодных режимов, полученных другими авторами кластеризацией KM суточных полей z500 за разные временные периоды и с немного отличающимися способами предобработки данных.
Таблица 3.
Относительная повторяемость зимних и летних погодных режимов, полученных разными методами. Повторяемость традиционных зимних погодных режимов в ЕАТ-секторе, полученных в других работах методом KM, выделена курсивом. Режимы, для которых тренды сезонной повторяемости за 1940–2022 гг. значимы на уровне 95%, отмечены жирным шрифтом и соответствующим знаком тренда
| Метод кластеризации | sNAO+ | sNAO– | sSB | sAR |
|---|---|---|---|---|
| Зимние погодные режимы | ||||
| KM | 30.2% + | 21.4% – | 23.7% | 24.7% |
| Cassou, 2008 | 30% | 20% | 27% | 23% |
| Dawson et al., 2012 | 29.6% | 20.4% | 27.6% | 22.4% |
| Charlton-Perez et al., 2018 | 29.7% | 20.0% | 28.6% | 21.8% |
| HW | 23.6% | 31.5% – | 23.1% | 21.8% |
| GM | 30.0% + | 12.3% | 30.4% – | 27.4% |
| Летние погодные режимы | ||||
| KM | 25.5% | 28.1% | 23.4% | 23.0% |
| HW | 26.9% | 33.4% | 17.4% | 22.4% |
| GM | 37.8% | 25.4% + | 19.1% | 17.8% |
По табл. 3 видно, что полученная авторами повторяемость режимов NAO+/NAO– в пределах 1.5% согласуется с таковой в других работах [Cassou, 2008; Dawson et al., 2012; Charlton-Perez et al., 2018]. Полученные авторами повторяемости режимов SB и AR сильнее отличаются от их повторяемостей в других работах, что, скорее всего, является следствием большей чувствительности этих режимов к выбору временного интервала (1940–2022 гг. в настоящей работе) и способу предобработки данных (13 ЭОФ, 10-дневный фильтр). Прослеживается общая тенденция – самый частый режим – NAO+, средние по частоте SB и AR, NAO– – самый редкий. При кластеризации z500 другими методами данная тенденция не прослеживается – в HW режим NAO– оказался наиболее продолжительным с частотой в 33.38%, в GM NAO– – наименее продолжительный, но со слишком низкой относительной повторяемостью 12.25%.
Несмотря на хорошую пространственную корреляцию средних полей летних режимов по сравнению с зимними при методе KM (средняя корреляция 0.84, см. табл. 2), их относительная повторяемость отличается – самым частым оказался режим sNAO– с повторяемостью 28.06% против 21.39% зимой, а повторяемость sNAO+ уменьшилась с 30.20 до 25.51%. В целом, относительная населенность летних режимов получилась более равномерной по сравнению с зимними, что является одним из свойств метода KM при плохой кластеризуемости данных (доля объясненной кластеризацией дисперсии 23.62% летом против 32.64% зимой, см. табл. 1). Для методов HW и GM отмечается излишняя населенность некоторых режимов в летние месяцы – sNAO– для HW и sNAO+ для GM.
Помимо относительной повторяемости режимов, анализировались временные ряды сезонной повторяемости (количество суток за сезон, когда наблюдался данный режим) и их линейные тренды. Для сезонной повторяемости зимних режимов, полученных разными методами, получились разные по величине и значимости тренды, но наблюдается общая картина – положительный тренд повторяемости NAO+, который оказался значимым (на уровне 95%) для режимов, полученных по методам KM и GM, и отрицательный тренд повторяемости NAO–, который оказался значимым для режимов, полученных по методам KM и HW.
Временные ряды и линейные тренды режимов NAO+ и NAO–, полученных методом KM, представлены на рис. 4. Режимы NAO+ и NAO– ассоциированы с волнами тепла и холода соответственно над территориями Европы и Западной России [Cattiaux et al., 2010; Бардин и др., 2019], поэтому их многолетние тренды сезонной повторяемости могут частично объяснять общий тренд потепления в данных регионах в последние десятилетия.
Рис. 4.
Временные ряды (линии с точками), скользящие средние с окном осреднения в 10 лет (черные жирные кривые) и линейные аппроксимации (пунктирные линии) сезонной повторяемости режимов NAO+ и NAO-, полученных методов KM. Линейный тренд NAO+: +0.22 дней за сезон/год, p-value = 0.004; линейный тренд NAO–: –0.15 дней за сезон/год, p-value = 0.05.
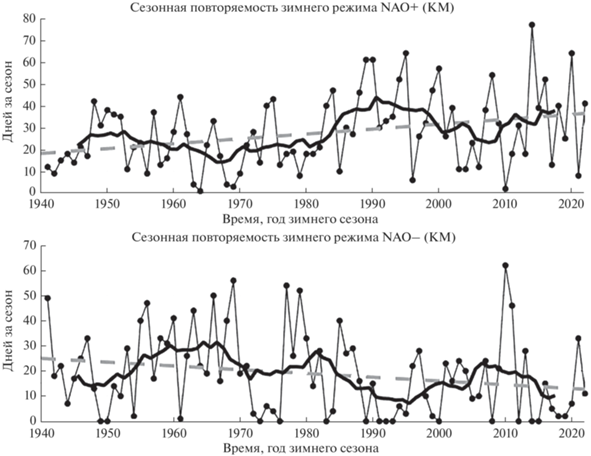
Зимние режимы SB и AR, полученные по различным методам, имеют незначимые разнонаправленные тренды сезонной повторяемости, кроме значимого отрицательного тренда SB при методе GM, который, однако, слабо похож на свои аналоги в методах HW и KM (см. рис. 3 и табл. 2), т.е., вообще говоря, не представляет собой скандинавский блокинг. Для летних месяцев значимые тренды сезонной повторяемости отсутствуют практически для всех режимов, полученных разными методами, кроме положительного тренда для режима sNAO–, полученного по методу GM.
3) Характерная продолжительность режимов
В табл. 4 представлены средние продолжительности режимов. Самым продолжительным оказался режим NAO–, причем как для зимних месяцев (>10 дней по методам KM и HW), так и для летних (sNAO–, >9 дней по методам KM и HW). Такая повышенная продолжительность отмечается на фоне самой низкой (по методу KM) среди четырех режимов относительной повторяемости в зимние месяцы. Наименее продолжительными оказались режимы SB в зимние месяцы и sAR в летние.
Таблица 4.
Статистические характеристики продолжительности режимов, полученных разными методами. Столбцы, обозначенные символом “w” – средние взвешенные (на относительную повторяемость) значения по всем четырем режимам
| Метод кластери-зации |
Зимние режимы | Летние режимы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NAO+ | NAO– | SB | AR | w | sNAO+ | sNAO– | sSB | sAR | w | |
| Средняя продолжительность, суток | ||||||||||
| KM | 9.5 | 10.4 | 7.8 | 8.2 | 9.0 | 7.2 | 9.1 | 7.3 | 6.7 | 7.6 |
| HW | 8.7 | 11.6 | 7.6 | 8.8 | 9.4 | 8.3 | 11.2 | 7.8 | 7.9 | 9.1 |
| GM | 8.6 | 8.6 | 7.4 | 8.5 | 8.2 | 8.5 | 7.1 | 7.0 | 5.9 | 7.4 |
| Медианная продолжительность, суток | ||||||||||
| KM | 7.0 | 8.0 | 6.0 | 6.0 | 6.7 | 6.0 | 7.0 | 6.0 | 5.0 | 6.1 |
| HW | 7.0 | 9.0 | 6.0 | 7.0 | 7.4 | 6.0 | 8.0 | 6.0 | 6.0 | 6.7 |
| GM | 7.0 | 7.5 | 6.0 | 6.0 | 6.5 | 6.0 | 5.0 | 5.0 | 4.0 | 5.2 |
| Среднеквадратичное отклонение, суток | ||||||||||
| KM | 8.6 | 8.2 | 6.0 | 7.4 | 7.6 | 5.9 | 7.4 | 6.0 | 5.2 | 6.2 |
| HW | 6.9 | 9.4 | 6.3 | 6.5 | 7.5 | 6.4 | 9.5 | 5.7 | 6.0 | 7.2 |
| GM | 7.3 | 7.1 | 5.9 | 7.8 | 7.0 | 7.8 | 5.9 | 6.5 | 4.7 | 6.5 |
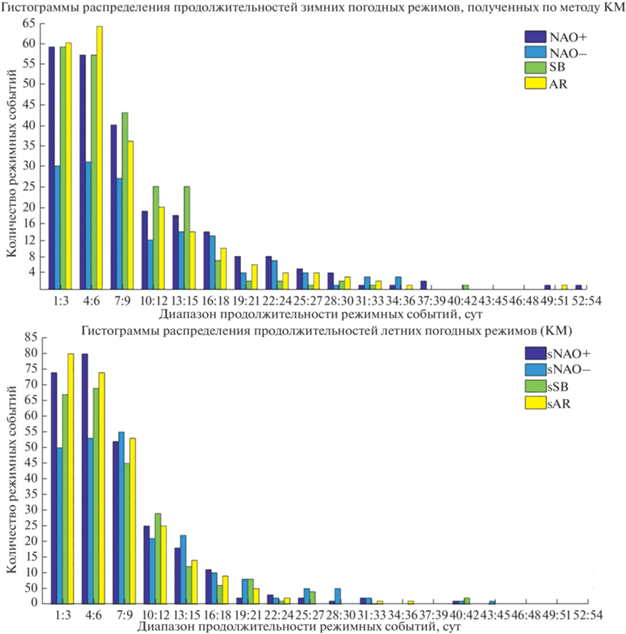
Сравнение средних и медианных значений продолжительности режимов, полученных разными методами, показывает, что наиболее продолжительные режимы получаются при кластеризации методом HW, а наименее продолжительные при кластеризации GM. Для всех режимов отмечается высокая величина стандартного отклонения их продолжительности, которая близка к средней продолжительности и превышает медианную, что говорит о том, что среди событий режимов часто встречаются как и очень короткие, продолжительностью не более трех суток, которые можно условно назвать переходными, так и довольно продолжительные, которые могут занимать до двух месяцев (средняя максимальная продолжительность по всем режимам и методам для зимних месяцев составляет 45 сут, для летних 40 сут). На рис. 5 представлены гистограммы распределения продолжительностей для режимов, полученных по методу KM. Из рисунка 5 и табл. 4 видно, что летние режимы оказываются менее продолжительными, чем зимние, также по рисунку заметно отличие в распределении продолжительностей режима NAO– и sNAO– относительно остальных.
Рис. 5.
Гистограммы распределения продолжительностей зимних и летних погодных режимов, полученных по методу KM.
Стоит упомянуть, что характерная продолжительность режимов сильно зависит от способа обработки данных, а именно от применения или неприменения фильтрации по времени и выбора периода отсечки. В данной работе применялся фильтр Баттерворта низких частот с периодом отсечки в 10 сут, из-за которого общая дисперсия суточных полей аномалий z500 снижается примерно в 1.5 раза, а характерная продолжительность режимов увеличивается.
4) Переходы между режимами
Были рассчитаны матрицы переходов между режимами, а также статистически значимые переходы (см. главу 4) с целью выяснить, какие переходы более или менее вероятны, что может иметь потенциальное применение в задачах предсказуемости. Вероятностные матрицы переходов режимов, в том числе статистически значимые из них, полученные для каждого из методов, представлены в табл. 5. Вероятностные матрицы получены путем деления числа переходов из данного режима в другие на суммарное число переходов из данного режима (т.е. сумма вдоль каждой строки в табл. 5 равна 1 без учета особенностей округления).
Таблица 5.
Матрицы вероятностей переходов зимних и летних режимов, полученных разными методами. Первый столбец – “Название режима” – указывает, из какого режима осуществляется переход (X → …), последние четыре столбца – в какой режим осуществляется переход (… → Y). Жирным (курсивным) шрифтом обозначены статистически значимо частые (редкие) переходы
| Название режима |
Метод кластеризации | Зимние режимы | |||
|---|---|---|---|---|---|
| NAO+ | NAO– | SB | AR | ||
| NAO+ | KM | – | 0.11 | 0.48 | 0.41 |
| HW | – | 0.36 | 0.48 | 0.16 | |
| GM | – | 0.12 | 0.39 | 0.49 | |
| NAO– | KM | 0.33 | – | 0.33 | 0.34 |
| HW | 0.35 | – | 0.28 | 0.37 | |
| GM | 0.52 | – | 0.48 | 0.00 | |
| SB | KM | 0.33 | 0.33 | – | 0.35 |
| HW | 0.42 | 0.23 | – | 0.35 | |
| GM | 0.37 | 0.25 | – | 0.37 | |
| AR | KM | 0.51 | 0.22 | 0.27 | – |
| HW | 0.20 | 0.36 | 0.44 | – | |
| GM | 0.41 | 0.00 | 0.59 | – | |
| Название режима |
Метод кластеризации | Летние режимы | |||
| sNAO+ | sNAO– | sSB | sAR | ||
| sNAO+ | KM | – | 0.21 | 0.45 | 0.34 |
| HW | – | 0.35 | 0.27 | 0.38 | |
| GM | – | 0.37 | 0.26 | 0.37 | |
| sNAO– | KM | 0.45 | – | 0.20 | 0.35 |
| HW | 0.52 | – | 0.23 | 0.26 | |
| GM | 0.58 | – | 0.21 | 0.21 | |
| sSB | KM | 0.25 | 0.35 | – | 0.40 |
| HW | 0.16 | 0.45 | – | 0.39 | |
| GM | 0.37 | 0.37 | – | 0.26 | |
| sAR | KM | 0.41 | 0.33 | 0.27 | – |
| HW | 0.47 | 0.27 | 0.26 | – | |
| GM | 0.49 | 0.25 | 0.27 | – | |
Статистические значимые переходы получены по методике, предложенной в [Vautard et al., 1990], т.е. это такие переходы, которые происходят в 95% случаев чаще или реже, чем в матрицах, случайно сгенерированных путем перемешивания режимных событий с сохранением общего числа событий каждого режима. Так как переходы рассматривались между режимными событиями, а не между отдельными суточными полями, то переходы режимов в самих себя (например, NAO+ → NAO+) при таком подходе отсутствуют.
Из табл. 5 видно, что вероятность перехода из режима NAO+ в “противоположный” режим NAO- довольно низкая – 0.11 для режимов по методу KM и 0.12 по GM, однако 0.36 по HW. При этом вероятность перехода из NAO– в NAO+ в 3–4 раза выше, чем из NAO+ в NAO–, что может объясняться как свойствами атмосферной циркуляции в Евро-Атлантике, так и разницей в повторяемости этих режимов, так как более населенные режимы “перетягивают” переходы в свою сторону, однако NAO+ является более населенным только по методам KM и GM, из-за чего, вероятно, такой разницы в вероятности переходов не наблюдается для этих режимов, полученных методом HW (0.36 для перехода из NAO+ в NAO– и 0.35 для перехода из NAO+ в NAO–), при этом режим NAO+ в HW заметно отличается от NAO+ по методам KM и GM (см. табл. 2).
Аналогичный, хоть и менее выраженный результат получился для летних режимов sNAO+ и sNAO– – вероятность перехода из sNAO– в sNAO+ 1.5–2 раза выше (для каждого из методов), чем из sNAO+ в sNAO–, что, при схожести летних и зимних режимов NAO разных фаз, может свидетельствовать о том, что разница в вероятности переходов между этими режимами объясняется не только разницей в их повторяемости, так как в летние месяцы повторяемость sNAO– выше, чем sNAO+ для всех методов, кроме GM, о чем так же свидетельствует тот факт, что для всех методов переход из sNAO– в sNAO+ оказался статистически значимо частым, а переход из sNAO+ в sNAO– статистически значимо редким.
Интересным результатом оказалась нулевая вероятность перехода между режимами NAO– и AR при кластеризации методом GM, т.е. за исследуемый период между полученными режимами такие переходы не наблюдались ни разу, однако стоит отметить, что режим AR для метода GM отличен от классического режима AR, полученного с помощью KM (см. рис. 3 и табл. 2). При других методах кластеризации между этими режимами наблюдаются либо незначимые, либо статистически значимо частые (NAO– → AR в HW) вероятности переходов. Также для метода GM, в отличие от остальных, наблюдаются “цепочки” значимых переходов, проходящие через каждый из режимов: NAO+ → AR → SB → NAO– → NAO+ → → … и, аналогично, sNAO+ → sAR → sSB → → sNAO– → sNAO+ → …, т.е. системы режимов, полученных методов GM для зимних и летних месяцев, со статистически значимо высокой вероятностью поочередно проходят через все свои состояния, несмотря на то, что летние режимы при методе GM относительно плохо воспроизвелись по сравнению с зимними (средняя корреляция полей аналогичных режимов 0.6). Такой результат может являться как простым совпадением, так и свойством метода GM.
Для других методов не наблюдается замкнутых цепочек статистически значимо частых переходов, проходящих через все режимы, так как не для каждого из режимов, полученных по методам KM и HW существуют значимо частые переходы, например, их нет для режимов NAO– и sAR по методу KM и режимов AR и sNAO+ по методу HW.
7. ЗАКЛЮЧЕНИЕ
В работе приведен краткий обзор четырех наиболее часто используемых методов кластеризации для выделения крупномасштабных режимов атмосферной циркуляции – k-means (KM), иерархической кластеризации со сцепкой Уорда (HW), модели Гауссовой смеси (GM) и Самоорганизующихся карт Кохонена (SOM), а также некоторых численных методов для определения оптимального количества режимов. По суточным данным реанализа ERA5 для высоты геопотенциальной поверхности на уровне 500 гПа (z500) с помощью вышеперечисленных методов выделены погодные режимы в зимние и летние месяцы, а также проведено сравнение их статистических характеристик.
Для Евро-Атлантического региона по данным z500 реанализа ERA5 для периода 1940–2022 гг. в зимние месяцы показано, что оптимальное число режимов K равно 4 или 6, для летних режимов оптимальное K = 3, при этом единственного, статистически значимого K, использованные авторами методы не дали. В целом, задача определения числа погодных режимов остается нерешенной по сей день [Christiansen, 2007]. В данной работе для обоих сезонов выделялись 4 погодных режима, как в большинстве работ по выделению зимних режимов в Евро-Атлантике [Cassou, 2008; Michelangeli et al., 1995; Fabiano et al., 2020; Dawson et al., 2012; Charlton-Perez et al., 2018] c помощью метода KM по данным о высоте геопотенциала. Летние режимы, выделенные методом KM, оказались визуально похожи на зимние, средний коэффициент пространственной корреляции характерных полей режимов оценен равным 0.84.
Режимы, полученные с помощью метода SOM, оказались практически неотличимы от режимов, выделенных методом KM. По результатам кластеризации из 7491 (7636) суточных полей z500 за зимний (летний) сезон для периода 1940–2022 гг. лишь 12 (10) суточных полей было отнесено к другим, чем при использовании метода KM, режимам. Это не повлияло на основные статистические характеристики режимов, в связи с чем результаты, полученные методом SOM, можно считать идентичными результатам, полученным методом KM.
Режимы, полученные с помощью методов HW и GM, в среднем менее выражены (имеют более низкую долю объясненной дисперсии аномалий z500), отличаются визуально и имеют другие статистические характеристики – относительную повторяемость, характерную продолжительность и вероятности переходов. Сопоставление структуры режимов, проведенное путем расчета коэффициентов пространственной корреляции их средних полей, показывает, что: а) режимы, полученные методами KM и HW и методами KM и GM более похожи, чем режимы, полученные методами HW и GM; б) летние режимы, полученные методом KM, меньше отличаются от зимних, чем при использовании других методов – средний коэффициент пространственной корреляции между полями зимних и их аналогичных летних режимов составил 0.84 для метода KM против 0.34 и 0.60 у методов HW и GM соответственно. Согласно полученным результатам, метод KM представляется более предпочтительным в задачах выделения погодных режимов, чем методы HW и GM. Метод SOM требует настройки большего числа параметров, чем KM, а его преимущество относительно других методов, состоящие во взаимной сортировке (самоорганизации) кластеров, при небольшом числе K не требуется.
Для некоторых из режимов проявляются многолетние значимые на уровне 95% тренды сезонной повторяемости – положительный тренд для режима NAO+ (выявленный методами KM и GM) и отрицательный тренд NAO– (выявленный методами KM и HW). Данные режимы в зимние месяцы связаны с волнами тепла и холода соответственно над территорией Европы и западной части России [Cattiaux et al., 2010; Бардин и др., 2019], поэтому долгосрочные изменения их сезонной повторяемости могут вносить вклад в локальные изменения климата. Следует отметить, что для более коротких временных интервалов (1979–2021 гг.) тренды ослабевают и перестают быть значимыми [Бабанов и др., 2023].
Для зимних и летних режимов, полученных разными методами, определены вероятностные матрицы переходов, различающиеся при использовании разных методов. Для всех методов отмечена пониженная в 1.5–3 раза вероятность перехода из (s)NAO+ в (s)NAO– по сравнению c обратным переходом из (s)NAO– в (s)NAO+. Для некоторых режимов отмечаются статистически значимо частые (редкие) переходы, то есть такие, которые, с учетом разницы в относительной повторяемости режимов, происходят со статистически значимо большей (меньшей) вероятностью, чем в другие режимы [Vautard et al., 1990]. Для метода GM выявлены замкнутые цепочки значимо частых переходов – NAO+ → AR → SB → NAO– → → NAO+ → … (sNAO+ → sAR → sSB → sNAO– → → sNAO+ => …). Этого не выявлено для режимов, полученных другими методами, для которых также отмечаются статистически значимо частые переходы, но не образующие замкнутых цепочек. Вопрос, является ли это результатом случайного совпадения или следствием особенностей режимов, получаемых при кластеризации методом GM, остается открытым и требует дальнейшего изучения.
Авторы благодарны М.В. Бардину за ценные замечания и конструктивные предложения. Сравнение методов идентификации погодных режимов выполнено при поддержке Минобрнауки РФ (соглашение № 075-15-2021-577), предобработка данных и анализ изменений характеристик режимов выполнены при поддержке грантов РНФ 19-17-00242 и РЦНИ 20-55-14003 АНФ_а.
Список литературы
Бабанов Б.А., Семенов В.А., Акперов М.Г., Мохов И.И., Keenlyside N.S. Повторяемость зимних режимов атмосферной циркуляции в Евро-Атлантическом регионе и связанные с ними экстремальные погодно-климатические аномалии в Северном полушарии // Оптика атмосферы и океана. 2023. Т. 36. № 4. С. 304–312.
Бардин М.Ю., Платова Т.В. Долгопериодные вариации показателей экстремальности температурного режима на территории России и их связь с изменениями крупномасштабной атмосферной циркуляции и глобальным потеплением // Метеорол. и гидрол. 2019. № 12. С. 5–19.
Гирс А.А. Макроциркуляционный метод долгосрочных метеорологических прогнозов. Л.: Гидрометеоиздат, 1974. 485 с.
Дзердзеевский Б.Л., Курганская В.М., Витвицкая З.М. Типизация циркуляционных механизмов в Северном полушарии и характеристика синоптических сезонов // Труды НИУ ГУГМС. Л.: Гидрометиздат. 1946. 80 с.
Arthur D., Vassilvitskii S. K-means++ the advantages of careful seeding // Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. 2007. P. 1027–1035.
Banfield J.D., Raftery A.E. Model-based Gaussian and non-Gaussian clustering // Biometrics. 1993. P. 803–821.
Bao M., Wallace J.M. Cluster analysis of Northern Hemisphere wintertime 500-hPa flow regimes during 1920–2014 // J. Atmospheric Sciences. 2015. V. 72. № 9. P. 3597–3608.
Barnston A.G., Livezey R.E. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns // Monthly weather review. 1987. V. 115. № 6. P. 1083–1126.
Baur F., Hess P., Nagel H. Kalender der grosswetterlagen Europas 1881–1939 // Bad Homburg. 1944. V. 35.
Bilmes J.A. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models // International computer science institute. 1998. V. 4. № 510. P. 126.
Bradley P.S., Fayyad U.M. Refining initial points for k-means clustering // ICML. 1998. V. 98. P. 91–99.
Cassou C. Intraseasonal interaction between the Madden–Julian oscillation and the North Atlantic Oscillation // Nature. 2008. V. 455. № 7212. P. 523–527.
Cattiaux J., Vautard R., Cassou C., Yiou P., Masson-Delmotte V., Codron F. Winter 2010 in Europe: A cold extreme in a warming climate // Geophysical Research Letters. 2010. V. 37. № 20.
Charlton-Perez A.J., Ferranti L., Lee R.W. The influence of the stratospheric state on North Atlantic weather regimes // Quarterly J. Royal Meteorological Society. 2018. V. 144. № 713. P. 1140–1151.
Cheng X., Wallace J.M. Cluster analysis of the Northern Hemisphere wintertime 500-hPa height field: Spatial patterns // J. atmospheric sciences. 1993. V. 50. № 16. P. 2674–2696.
Christiansen B. Atmospheric circulation regimes: Can cluster analysis provide the number? // J. Climate. 2007. V. 20. № 10. P. 2229–2250.
Corti S., Molteni F., Palmer T.N. Signature of recent climate change in frequencies of natural atmospheric circulation regimes // Nature. 1999. V. 398. № 6730. P. 799–802.
Dawson A., Palmer T.N., Corti S. Simulating regime structures in weather and climate prediction models // Geophysical Research Letters. 2012. V. 39. № 21.
Fabiano F., Christensen H.M., Strommen K., Athanasiadis P., Baker A., Schiemann R., Corti S. Euro-Atlantic weather Regimes in the PRIMAVERA coupled climate simulations: impact of resolution and mean state biases on model performance // Climate Dynamics. 2020. V. 54. P. 5031–5048.
Falkena S.K., de Wiljes J., Weisheimer A., Shepherd T.G. Revisiting the identification of wintertime atmospheric circulation regimes in the Euro-Atlantic sector // Quarterly J. Royal Meteorological Society. 2020. V. 146. № 731. P. 2801–2814.
Folland C.K., Knight J., Linderholm H.W., Fereday D., Ineson S., Hurrell J.W. The summer North Atlantic Oscillation: past, present, and future // J. Climate. 2009. V. 22. № 5. P. 1082–1103.
Govender P., Sivakumar V. Application of k-means and hierarchical clustering techniques for analysis of air pollution: A review (1980–2019) // Atmospheric pollution research. 2020. V. 11. № 1. P. 40–56.
Greene C.A. et al. The climate data toolbox for MATLAB // Geochemistry, Geophysics, Geosystems. 2019. V. 20. № 7. P. 3774–3781.
Guemas V., Salas-Mélia D., Kageyama M., Giordani H., Voldoire A., Sanchez-Gomez E. Summer interactions between weather regimes and surface ocean in the North-Atlantic region // Climate dynamics. 2010. V. 34. P. 527–546.
Hannachi A. Low-frequency variability in a GCM: Three-dimensional flow regimes and their dynamics // J. climate. 1997. V. 10. № 6. P. 1357–1379.
Hartigan J.A., Wong M.A. A k-means clustering algorithm // Applied statistics. 1979. V. 28. № 1. P. 100–108.
Hersbach H. et al. The ERA5 global reanalysis // Quarterly J. Royal Meteorological Society. 2020. V. 146. № 730. P. 1999–2049.
Hess P., Brezowsky H. Katalog der Grosswetterlagen Europas 1881–1976, 3. verbesserte und ergänzte Aufl // Berichte des Deutschen Wetterdienstes. 1977. V. 113. P. 1–140.
Hurrell J.W. Decadal trends in the North Atlantic Oscillation: Regional temperatures and precipitation // Science. 1995. V. 269. № 5224. P. 676–679.
Hurrell J.W., Kushnir Y., Ottersen G., Visbeck M. An overview of the North Atlantic oscillation // Geophysical Monograph-American Geophysical Union. 2003. V. 134. P. 1–36.
Huth R. et al. Classifications of atmospheric circulation patterns: recent advances and applications // Annals of the New York Academy of Sciences. 2008. V. 1146. № 1. P. 105–152.
James P.M. An objective classification method for Hess and Brezowsky Grosswetterlagen over Europe // Theoretical and Applied Climatology. 2007. V. 88. P. 17–42.
Kanungo T., Mount D.M., Netanyahu N.S., Piatko C.D., Silverman R., Wu A.Y. An efficient k-means clustering algorithm: Analysis and implementation // IEEE transactions on pattern analysis and machine intelligence. 2002. V. 24. № 7. P. 881–892.
Kearns M., Mansour Y., Ng A.Y. An information-theoretic analysis of hard and soft assignment methods for clustering // Learning in graphical models. 1998. P. 495–520.
Khan K., Rehman S.U., Aziz K., Fong S., Sarasvady S. DBSCAN: Past, present and future // The fifth international conference on the applications of digital information and web technologies (ICADIWT 2014). IEEE, 2014. P. 232–238.
Kohonen T. Self-organizing maps. Springer Science & Business Media. 2012. V. 30.
Kondrashov D., Ide K., Ghil M. Weather regimes and preferred transition paths in a three-level quasigeostrophic model // J. atmospheric sciences. 2004. V. 61. № 5. P. 568–587.
Lamb H.H. British Isles weather types and a register of the daily sequence of circulation patterns 1861–1971 // Geophysical Memoirs 116, HMSO, London. 1972. 85 p.
Lamrous S., Taileb M. Divisive hierarchical k-means // 2006 International Conference on Computational Intelligence for Modelling Control and Automation and International Conference on Intelligent Agents Web Technologies and International Commerce (CIMCA'06). IEEE. 2006. P. 18–18.
Liu Y., Weisberg R.H. A review of self-organizing map applications in meteorology and oceanography // Self-organizing maps: applications and novel algorithm design. 2011. V. 1. P. 253–272.
Loikith P.C., Lintner B.R., Sweeney A. Characterizing large-scale meteorological patterns and associated temperature and precipitation extremes over the northwestern United States using self-organizing maps // J. Climate. 2017. V. 30. № 8. P. 2829–2847.
Lund I.A. Map-pattern classification by statistical methods // J. Applied Meteorology and Climatology. 1963. V. 2. № 1. P. 56–65.
Matsueda M., Palmer T.N. Estimates of flow-dependent predictability of wintertime Euro-Atlantic weather regimes in medium-range forecasts // Quarterly J. Royal Meteorological Society. 2018. V. 144. № 713. P. 1012–1027.
Michelangeli P.A., Vautard R., Legras B. Weather regimes: Recurrence and quasi stationarity // J. atmospheric sciences. 1995. V. 52. № 8. P. 1237–1256.
Molteni F., Tibaldi S., Palmer T.N. Regimes in the wintertime circulation over northern extratropics. I: Observational evidence // Quarterly J. Royal Meteorological Society. 1990. V. 116. № 491. P. 31–67.
Murtagh F., Contreras P. Algorithms for hierarchical clustering: an overview // Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery. 2012. V. 2. № 1. P. 86–97.
Murtagh F., Contreras P. Algorithms for hierarchical clustering: an overview, II // Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery. 2017. V. 7. № 6. P. e1219.
Philipp A., Della-Marta P.M., Jacobeit J., Fereday D.R., Jones P.D., Moberg A., Wanner H. Long-term variability of daily North Atlantic–European pressure patterns since 1850 classified by simulated annealing clustering // J. Climate. 2007. V. 20. № 16. P. 4065–4095.
Polo I., Ullmann A., Roucou P., Fontaine B. Weather regimes in the Euro-Atlantic and Mediterranean sector, and relationship with West African rainfall over the 1989–2008 period from a self-organizing maps approach // J. Climate. 2011. V. 24. № 13. P. 3423–3432.
Roux M. A comparative study of divisive and agglomerative hierarchical clustering algorithms // J. Classification. 2018. V. 35. P. 345–366.
Santos J.A., Corte-Real J., Leite S.M. Weather regimes and their connection to the winter rainfall in Portugal // International J. Climatology: A J. Royal Meteorological Society. 2005. V. 25. № 1. P. 33–50.
Selesnick I.W., Burrus C.S. Generalized digital Butterworth filter design // IEEE Transactions on signal processing. 1998. V. 46. № 6. P. 1688–1694.
Selim S.Z., Alsultan K. A simulated annealing algorithm for the clustering problem // Pattern recognition. 1991. V. 24. № 10. P. 1003–1008.
Shi C., Wei B., Wei S. et al. A quantitative discriminant method of elbow point for the optimal number of clusters in clustering algorithm // EURASIP J. on Wireless Communications and Networking. 2021. V. 2021. № 1. P. 1–16.
Smyth P., Ide K., Ghil M. Multiple regimes in northern hemisphere height fields via mixturemodel clustering // J. Atmospheric Sciences. 1999. V. 56. № 21. P. 3704–3723.
Vautard R. Multiple weather regimes over the North Atlantic: Analysis of precursors and successors // Monthly weather review. 1990. V. 118. № 10. P. 2056–2081.
Vautard R., Mo K.C., Ghil M. Statistical significance test for transition matrices of atmospheric Markov chains // J. Atmospheric Sciences. 1990. V. 47. № 15. P. 1926–1931.
Vorobyeva V., Volodin E. Evaluation of the INM RAS climate model skill in climate indices and stratospheric anomalies on seasonal timescale // Tellus A: Dynamic Meteorology and Oceanography. 2021. V. 73. № 1. P. 1 t892 435.
Willmott C.J. Synoptic weather-map classification: correlation versus sums-of-squares // The Professional Geographer. 1987. V. 39:2. P. 205–207.
Yang M.S., Lai C.Y., Lin C.Y. A robust EM clustering algorithm for Gaussian mixture models // Pattern Recognition. 2012. V. 45. № 11. P. 3950–3961.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана



