1. На главную
  2. Электронные версии
  3. Физика и химия стекла
  4. T. 47, № 5, 2021

Физика и химия стекла, 2021, T. 47, № 5, стр. 582-589

Исследование механических свойств материалов с топологией ТППМЭ методом компьютерного моделирования

М. Ю. Арсентьев 1, *, Е. И. Сысоев 1, С. В. Балабанов 1

1 Институт химии силикатов им. И.В. Гребенщикова РАН
199034 Санкт-Петербург, наб. Макарова, 2, Россия

* E-mail: ars21031960@gmail.com

Поступила в редакцию 12.04.2021
После доработки 04.06.2021
Принята к публикации 07.06.2021

Полный текст (PDF)

Аннотация

В данной работе проведено исследование физико-механических свойств изделий с геометрией ТППМЭ методом компьютерного моделирования. Расчеты производились методом FEN (гиперупругого вязкопластического разрушения с конечной деформацией), для типичных образцов материала полиамида-12, полученного селективным лазерным спеканием (SLS, Selective Laser Sintering). В результате исследования с использованием программы Comsol Multiphysics получены распределения механических напряжений и внешний вид деформированных изделий при различных значениях прикладываемого механического напряжения, а также деформационные кривые. Показана сходимость расчетов от размера сетки исследуемой модели. Результаты моделирования хорошо согласуются с экспериментальными данными. В результате исследования обнаружены высокие физико-механические характеристики образцов с предложенной геометрией.

Ключевые слова: трижды периодическая поверхность минимальной энергии, ячеистые структуры, метод конечных элементов, механическое напряжение, полиамид-12

ВВЕДЕНИЕ

Еще с давних времен, на протяжении многих веков открывались и исследовались вдохновленные природой математические поверхности, основанные на тригонометрических выражениях [1–14]. Долгое время областью математики и моделирования ограничивалось практическое использование данных форм из-за ограничений, связанных с экономической эффективностью и практической реализуемости [15, 16]. В то же время, легкие и упорядоченные ячеистые структуры являются потенциальными кандидатами в качестве материалов с высочайшими удельными характеристиками, такими как превосходные энергопоглащающие характеристики, высокая жесткость и прочность, легкий вес и превосходные тепло- и звукоизоляционные свойства. Благодаря своим многочисленным свойствам, таким как способности изменять их удельную пористость, плотность, прочность и пластичность, на сегодняшний день ячеистые структуры находят широкое применение во многих областях, в частности как биомедицинские имплантаты [17], энергопоглощающие материалы [18].

Традиционные методы получения материалов с ячеистой структурой включают в себя метод инжекции газа [19], темплатный метод [20, 21], метод консолидации тканых проволочных сеток [22] и др. Однако данные методы ограничивают технологическое изготовление материалов, позволяя создавать только неоднородные стохастические пены или трехмерные проволочные каркасы. Недавние достижения в технологии аддитивного производства (additive manufacturing, АМ) способны устранить вышеупомянутые ограничения и позволяют получать сотовые материалы со сложной топологией [23, 24]. Среди процессов аддитивного производства можно выделить два ключевых процесса, основанных на плавлении и сплавлении/спекания порошков вместе: селективное лазерное плавление (Selective laser melting, SLM) и селективное лазерное спекание (Selective laser sintering, SLS). Такой подход позволяет изготавливать металлические, керамические компоненты с исключительно высокой плотностью и сложной геометрией [25–29].

МЕТОДЫ ИССЛЕДОВАНИЯ

В работе использовались метод конечных элементов (Comsol) совместно с программой (модулем) polyUmod, основанном на модели FEN. FEN – это универсальная конститутивная модель, которая, как было показано ранее, наилучшим образом позволяет описывать механические свойства термопластичного материала, используемого для 3D-печати [30–33]. Модель FEN считается наиболее сложной и совершенной и дает наиболее точное соответствие для материалов, используемых в 3D печати.

В модели FEN приложенный градиент деформации F действует на несколько (до 4) макромолекулярных сетей и раскладывается на упругую ${\mathbf{F}}_{i}^{e}$ вязкопластическую ${\mathbf{F}}_{i}^{{vp}}$ оставляющие:

(1)
${\mathbf{F}} = {\mathbf{F}}_{i}^{e}{\mathbf{F}}_{i}^{{vp}}.$

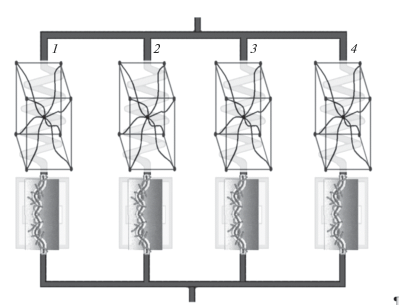
Структура модели FEN может быть представлена в виде четырех параллельных сетей, как показана на рис. 1.

Рис. 1.

Реологическое представление модели FEN.

Модель состоит из трех параметров: напряжения, текучести и разрушения. Функция плотности энергии деформации для i-ой сети имеет следующий вид:

(2)
${{{{\Psi }}}_{i}} = {{f}_{{i\mu }}}\left[ {{{f}_{{i\varepsilon P}}}{{f}_{{i{\text{M}}}}}{{{{\Psi }}}_{{yi}}} + \frac{k}{2}{{{\left( {J_{i}^{e} - 1} \right)}}^{2}}} \right],\,\,\,\,~i~\,\, \in \left[ {1,{\text{\;}}4} \right],$
(3)
$J_{i}^{e} = \det \left[ {{\mathbf{F}}_{i}^{e}} \right],$
(4)
$I_{{1i}}^{{e*}} = {\text{tr}}\left[ {{{{\left( {J_{i}^{e}} \right)}}^{{ - \frac{2}{3}}}}{\mathbf{F}}_{i}^{e}{\mathbf{F}}_{i}^{{eT}}} \right],$
(5)
$I_{{2i}}^{{e*}} = \frac{1}{2}\left( {{\text{tr}}{{{\left[ {{{{\left( {J_{i}^{e}} \right)}}^{{ - \frac{2}{3}}}}{\mathbf{F}}_{i}^{e}{\mathbf{F}}_{i}^{{eT}}} \right]}}^{2}} - {\text{tr}}{{{\left[ {{{{\left( {J_{i}^{e}} \right)}}^{{ - \frac{2}{3}}}}{\mathbf{F}}_{i}^{e}{\mathbf{F}}_{i}^{{eT}}} \right]}}^{2}}~} \right),$
где ${{f}_{{i\mu }}}$ – коэффициент модуля сдвига; ${{f}_{{i\varepsilon P}}}$ – коэффициент эволюции вязкопластического течения; ${{f}_{{i{\text{M}}}}}$ – коэффициент разрушения по Маллинзу. Если образец вначале деформируется, а затем освобождается от нагрузки, то для вторичной деформации требуется меньшее напряжение. Этот эффект (эффект Маллинза) количественно выражается гистерезисной энергией.

Далее, в формуле (5) k – модуль объемной упругости; ${{{{\Psi }}}_{{yi}}}$ – плотность энергии деформации, заданный моделью Йо с одним членом Муни–Ривлина $I_{{2i}}^{{e*}},$ таким, что

(6)
${{{{\Psi }}}_{{yi}}} = {{C}_{{10}}}\left( {I_{{1i}}^{{e*}} - 3} \right) + {{C}_{{20}}}\left( {I_{{1i}}^{{e*}} - 3} \right) + {{C}_{{30}}}\left( {I_{{1i}}^{{e*}} - 3} \right) + {{C}_{{01}}}\left( {I_{{2i}}^{{e*}} - 3} \right),$
где ${{C}_{{10}}},$ ${{C}_{{20}}},$ ${{C}_{{30}}}$ и ${{C}_{{01}}}$ параметры материала, МПа.

Модель гиперупругого материала Йо – это феноменологическая модель деформации почти несжимаемых нелинейно-упругих материалов, таких как резина. Модель основана на наблюдении Рональда Ривлина о том, что упругие свойства резины можно описать с помощью функции плотности энергии деформации.

Общее напряжение вычисляется по формуле:

(7)
$\sigma = \sum\limits_{i = 1}^4 {{{\sigma }_{i}}} = \sum\limits_{i = 1}^4 {{{{\left( {J_{i}^{e}} \right)}}^{{ - 1}}}} {{\left( {{\mathbf{F}}_{i}^{e}} \right)}^{{ - 1}}}\frac{{\partial {{\Psi }_{i}}}}{{\partial F_{i}^{e}}}{{\left( {{\mathbf{F}}_{i}^{e}} \right)}^{{ - T}}}.~$

Скорость вязкопластической части градиента деформации для i-ой сети определяется как:

(8)
${\mathbf{\dot {F}}}_{i}^{{vp}} = \dot {\gamma }_{i}^{{vp}}{{\left( {{\mathbf{F}}_{i}^{e}} \right)}^{{ - 1}}}\frac{{{{S}_{i}}}}{{{{\tau }_{i}}}}{\mathbf{F}},~$

где ${{S}_{i}} = {{\sigma }_{i}} - {{{\text{tr}}\left( {{{\sigma }_{i}}} \right)} \mathord{\left/ {\vphantom {{{\text{tr}}\left( {{{\sigma }_{i}}} \right)} 3}} \right. \kern-0em} 3}$ девиаторное напряжение, МПа; ${{\tau }_{i}} = \sqrt {3{{S}_{i}}:{{{{S}_{i}}} \mathord{\left/ {\vphantom {{{{S}_{i}}} 2}} \right. \kern-0em} 2}} $ напряжение по Мизесу, МПа; $\dot {\gamma }_{i}^{{vp}}$ скорость вязкопластической деформации, определяемая следующим законом:

(9)
$\dot {\gamma }_{i}^{{vp}} = {{\dot {\gamma }}_{0}}\left( {\bar {\lambda }_{i}^{{vp}} - 1} \right){{\left\langle {\left( {\frac{{{{\tau }_{i}}}}{{{{g}_{p}}{{g}_{{ei1}}}{{g}_{{ei2}}}\widehat {{{\tau }_{i}}}}} - {{\tau }_{0}}} \right)} \right\rangle }^{{{{m}_{i}}}}},~$

где $\dot {\gamma }_{0}^{~}$ – эталонная скорость деформации; $\bar {\lambda }_{i}^{{vp}} = \sqrt {{\text{tr}}{{\left[ {{\mathbf{b}}_{i}^{{vp}}} \right]} \mathord{\left/ {\vphantom {{\left[ {{\mathbf{b}}_{i}^{{vp}}} \right]} 3}} \right. \kern-0em} 3}} $ – вязкопластическое растяжение с ${\mathbf{b}}_{i}^{{vp}} = {\mathbf{F}}_{i}^{{vp}}{\mathbf{F}}_{i}^{{v{{p}^{T}}}}$; ${{\tau }_{0}}$ – начальный предел текучести; ${{g}_{p}} = \left\langle {1 + {{{\text{tr}}\left( \sigma \right)} \mathord{\left/ {\vphantom {{{\text{tr}}\left( \sigma \right)} {3{{p}_{0}}}}} \right. \kern-0em} {3{{p}_{0}}}}} \right\rangle $ – фактор зависимости от давления, где ${{p}_{0}}$ параметр материала; $~\left\langle {} \right\rangle $ – скобки Маколея; ${{g}_{{ei1}}}\,\,{\text{и}}\,\,~{{g}_{{ei2}}}$ – сопротивление вязкопластическому потоку, определяемое следующим уравнением:

(10)
${{\dot {g}}_{{ei1}}} = \frac{1}{{{{D}_{{e1}}}}}\left( {{{g}_{{ss1}}} - {{g}_{{ei1}}}} \right)\dot {\gamma }_{i}^{{{v}p}};~\,\,\,{{\dot {g}}_{{ei2}}} = \frac{1}{{{{D}_{{e2}}}}}\left( {{{g}_{{ss2}}} - {{g}_{{ei2}}}} \right)\dot {\gamma }_{i}^{{{v}p}},~$
где ${{g}_{{ei1}}} = {{g}_{{ei2}}} = 1$ при t = 0; ${{g}_{{ss1}}},$ ${{g}_{{ss2}}},$ ${{D}_{{e1}}}$ и ${{D}_{{e2}}}$ – параметры материала. Коэффициент эволюции вязкопластического течения в формуле (2) определяется как:
(11)
${{\dot {f}}_{{i\varepsilon P}}} = \frac{1}{{{{C}_{\varepsilon }}}}\left( {{{f}_{{ss}}} - {{f}_{{i\varepsilon vp}}}} \right)\dot {\gamma }_{i}^{{vp}},~$
где ${{f}_{{ss}}}$ и ${{C}_{\varepsilon }}$ параметры материала, при которых ${{f}_{{i\varepsilon vp}}} = 1$ при t = 0. Этот фактор полезен для некоторых полимеров, эффективная жесткость которых немного снижается из-за накопления вязкопластической деформации.

Повреждения, в виде снижения жесткости и прочности, учитываются в модели через фактор разрушения Маллинза ${{f}_{{i{\text{M}}}}}$ в формуле (2), описываемый как:

(12)
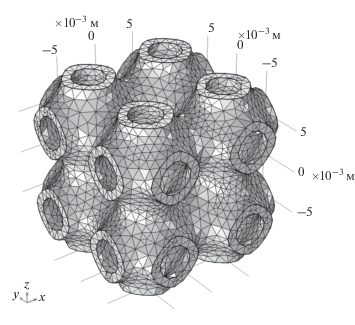
${{f}_{{i{\text{M}}}}} = 1 - \frac{1}{r}{\text{erf}}\left[ {\frac{{U_{{i.{\text{dev}}}}^{{{\text{max}}}} - {{U}_{{i.{\text{dev}}}}}}}{{\hat {U} + \beta U_{{i.{\text{dev}}}}^{{{\text{max}}}}}}} \right],~~$
где ${\text{erf}}$ – функция ошибок; ${{U}_{{i.{\text{dev}}}}}$ – девиаторная часть плотности энергии деформации; $U_{{i.{\text{dev}}}}^{{{\text{max}}}} = {\text{max}}\left[ {{{U}_{{i.{\text{dev}}}}},~~U_{{i.{\text{dev}}}}^{{{\text{max}}}}~} \right]$ при нагрузке, и ${{U_{{i.{\text{dev}}}}^{{{\text{max}}}}} \mathord{\left/ {\vphantom {{U_{{i.{\text{dev}}}}^{{{\text{max}}}}} {{{U}_{{i.{\text{dev}}}}}}}} \right. \kern-0em} {{{U}_{{i.{\text{dev}}}}}}} = - \alpha $ при нагрузке, где $r \geqslant 1$; $\hat {U}$, $\alpha $ и $\beta $ параметры материала.

В работе использовались образцы размером 2 × 2 × 2 ячейки (рис. 2). Используемый в расчетной модели материал – полиамид-12 (SLS 3D Печать). Коэффициент заполнения объема составлял 20%, скорость деформации – 0.004 с–1.

Рис. 2.

Внешний вид ТППМЭ решетки (Примитив-P) размером 2 × 2 × 2.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

На рис. 2 представлен вид ТППМЭ решетки размером 2 × 2 × 2, а на рис. 3 – соответствующий вид кривой деформация–напряжение, на котором виден максимум. В соответствии c ГОСТ 4651-2014 (ISO 604:2002, MOD), за прочность образцов принимали пик (максимум) на деформационной кривой, который соответствует переходу образца в область пластической деформации. Каждая кривая представляет собой график зависимости нагрузки от деформации. Кривые имеют ярко выраженные экстремумы (пики), каждый из которых соответствует разрушению одного из слоев ячеек, лежащих в плоскости, перпендикулярной оси нагружения. В таблице представлен расчетный предел прочности.

Рис. 3.

Зависимость рассчитанной кривой напряжение–деформация от числа элементов в полигональной сетке для модели ТППМЭ решетки (Примитив-P) размером 2 × 2 × 2 (материал – полиамид 12). Порядковый номер кривой соответствует числу элементов из таблицы 1.

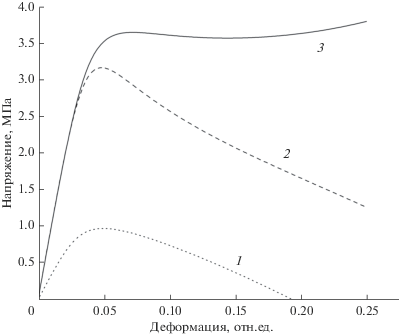
Таблица 1.  

Число элементов в полигональной сетке, использовавшихся для моделирования ТППМЭ решетки (Примитив-P).

Порядковый номер кривой Число элементов Расчетный предел прочности, МПа
1 6244 0.97
2 7996 3.16
3 10 414 3.64

Результаты расчета кривых напряжение–деформация (рис. 3) для модели ТППМЭ решетки (Примитив-P) с использованием полигональных сеток с различным числом элементов, в сравнении с экспериментальными данными, показывают, что модель, содержащая 10414 элементов, удовлетворительно описывает свойства изучаемого объекта.

При относительно высоком выбранном нами для исследований коэффициенте заполнения объема (20%), как правило, не наблюдается сложный характер деформации (вращения, изгибы, вызванные деформацией соседних ячеек), как показано в данном исследовании (рис. 4) и в работах [33, 34]. Кроме того, наблюдаются достаточно высокая концентрация напряжений на определенных участках образца, а также высокая неравномерность распределения напряжений. Наши исследования (рис. 4) и исследования авторов [33, 34] подтверждают данный факт. Как обнаружили авторы расчетными и экспериментальными методами Montazerian и др. [36 ] и Abou-Ali и др. [33] вращения и изгибы наблюдаются при более низких коэффициентах заполнения объема. Из рис. 4 видно, что верхний слой ячеек подвергается большей деформации, чем нижний, что также согласуется с наличием пика для кривой 3 на рис. 2.

Рис. 4.

Распределение напряжений для ТППМЭ решетки (Примитив-P) размером 2 × 2 × 2.

ЗАКЛЮЧЕНИЕ

Произведено компьютерное моделирование испытания на сжатие. В результате теоретического исследования были получены деформационные кривые для объектов с ТППМЭ геометрией, с различным числом элементов в полигональной сетке. Используемый в расчетной модели материал – полиамид-12 (SLS 3D Печать). Были проведены исследования распределения механических напряжений, особенности деформаций (проверка на наличие изгибов и вращений ячеек) на примере образца из полиамида-12. Выявлено, что при деформации образца напряжения распределяются неравномерно. В результате компьютерного моделирования обнаружены перспективные механические свойства для изделий с топологией ТППМЭ.

Исследование механических свойств конструкций и разработка топологий выполнены за счет гранта Российского научного фонда (проект № 20-73-10171). Разработка методики моделирования механических свойств выполнена в рамках Госзадания ИХС РАН (номер госрегистрации темы АААА-А19-119022290092-5).

Список литературы

  1. Bieri-Gross B., Nesper R. Topological modeling of reconstructive phase transitions through periodic surfaces: Tin dioxide I - A calcium chloride to palladium fluoride type transition // Zeitschrift Fur Anorganische Und Allgemeine Chemie. 2015. V. 641. P. 1503–1509.

  2. Makogon A.I., Shevchenko V.Ya., Sychov M.M. Modeling of reaction-diffusion processes of synthesis of materials with regular (periodic) microstructure // Open Ceramics. 2021. in press.

  3. Bieri-Gross B., Nesper R. Topological modeling of reconstructive phase periodic hyperbolic surfaces: The β-quartz to keatite type transition // Zeitschrift Fur Kristallographie. 2011. V. 226. P. 670–677.

  4. Шевченко В.Я. Топологические формы будущего структурной химии новых веществ и материалов // Труды Кольского научного центра РАН. 2018. Т. 9. № 2–1. С. 109–114.

  5. Zűrn A., Shnering H.G. Topological analysis of mesoporous solids and their ordered pore structures by periodic nodal surfaces, PNS // Zeitschrift Fur Anorganische Und Allgemeine Chemie. 2008. V. 634. P. 2761–2764.

  6. Leoni S., Nesper R. Elucidation of simple pathways for reconstructive phase transitions using periodic equi-surfaces (PES) descriptors. II. The strontium disilicide transition // Solid State Sciences. 2003. V. 5. P. 95–107.

  7. Nesper R, Leoni S. On tilings and patterns on hyperbolic surfaces and their relation to structural chemistry // Chemphyschem. 2001. V. 2. P. 413–422.

  8. Шевченко В.Я., Ковальчук М.В., Орыщенко А.С., Перевислов С.Н. Новые химические технологии на основе реакционно-диффузионных процессов тьюринга // Доклады Российской академии наук. Химия, науки о материалах. 2021. Т. 496. № 1. С. 25–29.

  9. Shevchenko V.Ya. What is a chemical substance and how it is formed? // Structural Chemistry. 2012. V. 23. № 4. P. 1089–1101.

  10. von Shnering H.G., Nesper R. How nature adapts chemical structures to curved surfaces // Angewandte Chemie International Edition. 1987. V. 26. № 11. P. 1059–1200.

  11. Andersson S., Hyde S.T., Larsson K., Lidin S. Minimal surfaces and structures: from inorganic and metal crys-tals to cell membranes and biopolymers // Chemical Reviews. 1988. v. 88. № 1. P. 221–242.

  12. Andersson S., Hyde S.T., von Schnering H.G. The intrinsic curvature of solids // Zeitschrift für Kristallographie. 1984. V. 168. № 1–4. P. 1–17.

  13. von Shnering H.G., Nesper R. Nodal surfaces of Fourier series: Fundamental invariants of structured matter // Zeitschrift für Physik B Condensed Matter. 1991. V. 83. P. 407–412.

  14. Mackay A.L. Crystallographic surfaces // Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences. 1993. v. 442. № 1914. P. 47–59.

  15. Schwarz H.A. Gesammelte Mathematische Abhandlungen, Springer, Berlin. 1933. P. 1843–1921.

  16. Han L., Che S. An Overview of Materials with Triply Periodic Minimal Surfaces and Related Geometry: From Biological Structures to Self-Assembled Systems // Adv. Mater. 2018. V. 30. № 17. P. 0935–9648.

  17. Thomsen P., Malmström J., Emanuelsson L., René M., Snis A. Electron beam-melted, free-form-fabricated titanium alloy implants: Material surface characterization and early bone response in rabbits // J. Biomed. Mater. Res. B Appl. Biomater. 2009. V. 90. № 1. P. 35–44.

  18. Tancogne-Dejean T., Spierings A.B., Mohr D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading // Acta Materialia. 2016. V. 116. P. 14–28.

  19. Leitlmeier D., Degischer H.P., Flankl H.J., Development of a foaming process for particulate reinforced aluminum melts // Advanced Engineering Materials. 2002. V. 4. № 10. P. 735–740.

  20. Wang Z., Jiao X., Feng P., Wang X., Liu Z., Akhtar F. Highly porous open cellular TiAl-based intermetallics fabricated by thermal explosion with space holder process // Intermetallics. 2016. V. 68. P. 95–100.

  21. Korner C., Singer R.F. Processing of metal foams—Challenges and opportunities // Advanced Engineering Materials. 2000. V. 2. № 4. P. 159–165.

  22. Ducheyne, P., Martens M. Orderly oriented wire meshes as porous coatings on orthopaedic implants I: Morphology // Clinical Materials. 1986. V. 1. № 1. P. 59–67.

  23. Tancogne-Dejean T., Spierings A.B., Mohr D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading // Acta Materialia. 2016. V. 116. P. 14–28.

  24. Yang L., Harrysson O., West H., Cormier D. Compressive properties of Ti–6Al–4V auxetic mesh structures made by electron beam melting // Acta Materialia. 2012. V. 60. № 8. P. 3370–3379.

  25. Van Bael S., Chai Y.C., Truscello S., Moesen M., Kerckhofs G., Van Oosterwyck H., Kruth J.-P., Schrooten J. The effect of pore geometry on the in vitro biological behavior of human periosteum-derived cells seeded on selective laser-melted Ti6Al4V bone scaffolds // Acta Biomaterialia. 2012. V. 8. № 7. P. 2824–2834.

  26. Bartolo P., Kruth J.-P., Silva J., Levy G., Malshe A., Rajurkar K., Mitsuishi M., Ciurana J., Leu M. Biomedical production of implants by additive electro-chemical and physical processes // Cirp Annals-Manufacturing Technology. 2012. V. 61. № 2. P. 635–655.

  27. McKown S., Shen Y., Brookes W.K., Sutcliffe C.J., Cantwell W.J., Langdon G.S., Nurick G.N., Theobald M.D. The quasi-static and blast loading response of lattice structures // International Journal of Impact Engineering. 2008. V. 35. № 8. P. 795–810.

  28. Yan C., Hao L., Hussein A., Wei Q., Shi Y. Microstructural and surface modifications and hydroxyapatite coating of Ti–6Al–4V triply periodic minimal surface lattices fabricated by selective laser melting // Materials Science and Engineering: C. 2017. V. 75. P. 1515–1524.

  29. Olakanmi E.O., Cochrane R.F., Dalgarno K.W. A review on selective laser sintering/melting (SLS/SLM) of aluminium alloy powders: Processing, microstructure, and properties // Progress in Materials Science. 2015. V. 74. P. 401–477.

  30. Bergstrom J.S. Mechanics of Solid Polymers: Theory and Computational Modeling. William Andrew. Elsevier. 2015. P. 520.

  31. Abueidda D.W., Bakir M., Abu Al-Rub R.K.B., Jörgen S., Sobh N.A., Jasiuk I. Mechanical properties of 3D printed polymeric cellular materials with triply periodic minimal surface architectures // Materials & Design. 2017. V. 122. P. 255–267.

  32. Bergström J. PolyUMod User’s Manual. Veryst Engineering. LLC. Needham. MA. 2009. P. 7.

  33. Abou-Ali A.M., Al-Ketan O., Lee D.-W., Rowshan R., Abu Al-Rub R.K. Mechanical behavior of polymeric selective laser sintered ligament and sheet based lattices of triply periodic minimal surface architectures // Materials & Design. 2020. V. 196. P. 109100.

  34. Montazerian H., Davoodi E., Asadi-Eydivand M., Kadkhodapour J., Solati-Hashjin M. Porous scaffold internal architecture design based on minimal surfaces: a compromise between permeability and elastic properties // Materials & Design. 2017. V. 126. P. 98–114.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика и химия стекла

Архивы выпусков Информация о журнале Отправить рукопись в журнал