Физика Земли, 2020, № 5, стр. 103-116

ВВЕДЕНИЕ

Искусственные или естественные системы трещин играют ключевую роль в добыче нефти и газа из низкопроницаемых коллекторов [Olson, 2004]. Методы разработки таких месторождений, как правило, включают те или иные модификации гидравлического разрыва пласта (например, многостадийный гидроразрыв на горизонтальной скважине с использованием воды с добавлением присадок, снижающих ее вязкость) [Warpinski, 2009; Barati, 2014], в результате которых в окрестности скважины создается проницаемая область (SRV – stimulated reservoir volume) [Warpinski, 2009; Wu, 2014]. В настоящей работе изучается принципиальная возможность формирования подобной области в низкопроницаемых коллекторах, связанная только с аномально высоким пластовым давлением, и влияние ее формирования на дебит скважины.

Давление в порах называется аномально высоким, если оно превышает гидростатический уровень. Аномально высокое пластовое давление (АВПД) является распространенным явлением в пластовых породах со сверхнизкой проницаемостью, таких как карбонаты, известняки и сланцы [Fertl, 1976; Magara, 1978; Мелик-Пашаев, 1983; Luo, 2002]. Выделяют несколько причин возникновения АВПД, связанных с историей формирования залежи, термическим состоянием пласта, физико-химическими процессами, движением флюидов в земной коре. В частности, основным механизмом формирования АВПД в нефтематеринских породах является генерация флюида в условиях сверхнизкой проницаемости. АВПД достигает значений до 0.95 от горного давления [Li, 2012], и может не только служить причиной разрушения стенок скважин [Мелик-Пашаев, 1983; Li, 2012], но и способно поддерживать дебит нефти в низкопроницаемых коллекторах в отсутствие возможности применения традиционных методов поддержания пластового давления [Sonnenberg, 2009]. Кроме того, АВПД может приводить к развитию вторичных трещин в породе с низкой проницаемостью. Это явление, называемое автофлюидоразрыв (NHF – natural hydraulic fracturing), хорошо известно и обсуждается в связи с проблемой миграции флюидов [Secor, 1965; Engelder, 1990; Luo, 2002].

Модель двойной пористости [Barenblatt, 1960] широко используется при моделировании движения флюидов в трещиновато-пористых пластах [Голф-Рахт, 1986; Wu, 2014]. Трещиновато-пористые пласты состоят из блоков насыщенной пористой низкопроницаемой породы (матрицы), разделенных магистральными трещинами, по которым может двигаться жидкость. При этом матрица осуществляет подпитку системы трещин. В основе семейства континуальных моделей среды с двойной пористостью, насыщенной одной жидкостью, лежит гипотеза суперпозиции трех континуумов (предполагается, что элементарный объем, по которому проводится усреднение, много больше характерного расстояния между магистральными трещинами). Первый континуум образован частью жидкости, насыщающей матрицу, которая характеризуется низкой проницаемостью, но достаточно большой пористостью. Второй континуум образован жидкостью, заполняющей систему магистральных трещин, объемная доля которых мала по сравнению с пористостью матрицы. При этом проницаемость системы трещин предполагается достаточно высокой, чтобы обеспечить подвижность второго континуума. Третьим континуумом является твердый скелет, который может быть жестким, пороупругим или проявлять вязкие и пластические свойства. Между первым и вторым континуумом возможен обмен массой за счет перетекания жидкости из матрицы в трещины и наоборот. Если блоки матрицы не изолированы и проницаемость матрицы сравнима с проницаемостью трещин, модель двойной пористости часто называют моделью двойной проницаемости.

Как правило, учет влияния АВПД на производство нефти или газа в сланцевых породах сводится к учету зависимости проницаемости системы трещин в среде с двойной пористостью от давления [Thompson, 2010] в связи с тем, что для движения флюидов в низкопроницаемых породах требуются значительные депрессии. В отличие от указанного подхода в данной работе развивается модель среды с двойной пористостью, матрица которой способна растрескиваться под действием АВПД. Первоначально концепция автофлюидоразрыва была развита в работе [Secor, 1965] на основе подходов к моделированию традиционного гидроразрыва. В работе [Secor, 1965] рассматривается набор произвольно ориентированных трещин с непроницаемыми стенками на достаточно большом расстоянии друг от друга, чтобы исключить их взаимное влияние. В качестве критерия распространения трещин используется вариант энергетической теории Гриффитса. В дальнейшем эта модель была обобщена на случай пороупругой среды в предположении, что давление в трещинах в каждый момент времени равно поровому давлению в пространстве между трещинами [Engelder, 1990]. Указанные модели изначально сформулированы для описания развития трещиноватости в горных породах на геологических масштабах времени. При этом указывается, что автофлюидоразрыв играет важную роль в миграции флюидов. Например, если в силу определенных причин поровое давление в низкопроницаемом пласте, постепенно повышаясь, достигает критерия страгивания трещин (initiation), трещины начинают расти (propagation), что приводит к увеличению их объема, падению давления и, в результате, прекращению роста трещин (arrest). Процесс повторяется циклически. В работе [Luo, 2002] показано, что в сланцевых пластах при наличии АВПД возможно установление равновесия в окрестности критерия разрушения, когда генерируемый в нефтематеринской породе флюид отводится по системе трещин автофлюидоразрыва (зона I на рис. 1).

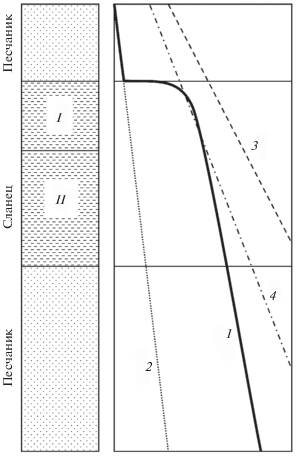
В задаче о производительности скважин характерные масштабы времени много меньше геологических, таким образом, возможной генерацией флюида в нефтематеринской породе можно пренебречь. В настоящей работе рассматривается ситуация, когда за длительный предшествующий период давление в матрице превысило гидростатический уровень, однако критерий разрушения еще не достигнут (например, зона II на рис. 1). Считается, что разрушение в матрице может произойти при участии АВПД в процессе технологических операций (например, бурение скважины, депрессия на забое скважины в процессе добычи и др.).

Развитие системы трещин, длина которых много меньше характерного размера элементарного объема, естественно моделировать методами теории повреждаемых сред (CDM – continuum damage mechanics) [Lemaitre, 1996; Murakami, 2012], в рамках которой коллектив микротрещин описывается осредненно с помощью специального параметра поврежденности. В настоящей работе для моделирования автофлюидоразрыва в матрице используется модель повреждаемости, аналогичная модели из работ [Kondaurov, 2009; Извеков, 2009; 2010]. Для простоты использован скалярный параметр поврежденности, что соответствует случайному распределению трещин по направлениям в пространстве. Критерий инициации начала развития повреждаемости в модели работ [Kondaurov, 2009; Извеков, 2009; 2010] является своеобразным обобщением энергетического критерия Гриффитса на случай рассеянного разрушения хрупких сред. Предполагается, что возникающие микротрещины в матрице в первую очередь усиливают массообмен между матрицей и магистральными трещинами.

ФОРМУЛИРОВКА МОДЕЛИ

Рассмотрим насыщенную пористую среду с упругим хрупким скелетом, включающим пористую матрицу и систему магистральных трещин. Матрица имеет низкую проницаемость и относительно высокую пористость. Система трещин характеризуется высокой проницаемостью и низкой пористостью (относительный объем пустот, содержащихся в трещинах). Матрица и трещины насыщены одной и той же слабосжимаемой жидкостью. Блоки матрицы изолированы друг от друга в том смысле, что непосредственное перемещение жидкости из блока в блок отсутствует и может осуществляться только через систему трещин.

Будем рассматривать среду с двойной пористостью как суперпозицию трех сплошных сред – двух флюидов и скелета. Первый континуум (флюид) соответствует жидкости, находящейся в матрице, второй – жидкости, заполняющей магистральные трещины. Жидкость взаимодействует со скелетом посредством массовых сил вязкого трения. В настоящей работе всюду используется изотермическое приближение (это предположение является традиционным при моделировании нетепловых методов добычи нефти). Предполагается наличие умеренного массообмена между матрицей и трещинами (это означает, что поток между матрицей и трещинами мал по сравнению с потоком в трещинах). Все движения предполагаются квазистатическими (что позволяет пренебречь кинетической энергией и влиянием массообмена на импульс), а деформации скелета малыми.

Далее используются индексы: “1”, “2”, “S” для обозначения величин, относящихся к флюиду, соответствующему жидкости в матрице, флюиду, соответствующему жидкости в трещинах, и к скелету соответственно. Также для обозначения величин, относящихся только к флюидам, используется индекс “α”, а к любому из континуумов индекс “A”. Определим величину ${{{\varphi }}_{{\alpha }}} = \frac{{dV_{{void}}^{{\alpha }}}}{{dV}}$ – объемную долю флюидов, где $dV_{{void}}^{{\alpha }}$ – объем, занимаемый жидкостью в подсистеме α (объем соответствующего пустотного пространства), $dV$ – элементарный объем. Определим плотности флюидов ${{r}_{{\alpha }}} = \frac{{d{{m}_{{\alpha }}}}}{{dV}}$ скелета ${{r}_{S}} = \frac{{d{{m}_{S}}}}{{dV}}$, где ${{m}_{{\alpha }}}$ ${{m}_{S}}$ – масса флюида в подсистеме α и масса скелета, содержащиеся в элементарном объеме $dV$, соответственно. Используя определение ${{\phi }_{{\alpha }}}$, получим, что ${{r}_{{\alpha }}} = {{\phi }_{{\alpha }}}{{{\rho }}_{f}}$ и ${{r}_{S}} = \left( {1 - {{\phi }_{1}} - {{\phi }_{2}}} \right){{{\rho }}_{S}}$, где ${{{\rho }}_{f}}$ – истинная плотность жидкости и ${{{\rho }}_{S}}$ – плотность материала скелета.

Выпишем основные уравнения в рамках сформулированных гипотез. Следствием закона сохранения массы являются три уравнения неразрывности, имеющие вид:

где ${{{\mathbf{v}}}_{A}}$ ‑ скорость континуумов, ${{\dot {m}}_{{12}}} = - {{\dot {m}}_{{21}}}$ – интенсивность массообмена между матрицей и трещинами.

Возьмем уравнения движения флюидов в форме закона Дарси

где: вектор фильтрации ${{{\mathbf{W}}}_{\alpha }} = {{\phi }_{\alpha }}{{{\mathbf{w}}}_{\alpha }} = {{\phi }_{\alpha }}\left( {{{{\mathbf{v}}}_{\alpha }} - {{{\mathbf{v}}}_{s}}} \right)$; ${{p}_{\alpha }}$ – поровое давление; ${{k}_{\alpha }}$ – проницаемость; ${{\mu }_{f}}$ – вязкость жидкости; ${\mathbf{g}}$ – ускорение свободного падения. Предположим, что проницаемость матрицы стремится к нулю, т.е. ${{k}_{1}} = 0$ (при этом ${{{\mathbf{v}}}_{1}} = {{{\mathbf{v}}}_{S}}$).

Запишем уравнение равновесия для скелета и флюидов как единое целое:

Определим тензор Коши полных напряжений в пористой среде:

где: ${{{\mathbf{T}}}_{s}}$ – тензор парциальных напряжений в скелете; ${{p}_{\alpha }}$ – поровое давление в подсистемах; величина $ - {{p}_{\alpha }}{{\phi }_{\alpha }}{\mathbf{I}}$ представляет собой тензор парциальных напряжений во флюидах ${{{\mathbf{T}}}_{\alpha }}$, ${{r}_{\Sigma }} = \sum\nolimits_A {{{r}_{A}}} $; ${\mathbf{I}} = {{\delta }_{{ij}}}{{{\mathbf{e}}}_{i}} \otimes {{{\mathbf{e}}}_{j}}$ – единичный тензор второго ранга; ${{\delta }_{{ij}}}$ – символ Кронекера, знаком “$ \otimes $” обозначено тензорное умножение.

Массовые силы взаимодействия между флюидами и скелетом, отнесенные к единице объема, имеют вид [Кондауров, 2007; Coussy, 2001]

где, в случае справедливости закона Дарси (4), диссипативная часть силы взаимодействия равна

Дифференциальный закон сохранения энергии для элементарного тела, состоящего из частиц трех континуумов, с учетом уравнений баланса массы (1)–(3) и уравнений (4), (5) имеет вид:

где: ${{{{d}_{A}}\left( {...} \right)} \mathord{\left/ {\vphantom {{{{d}_{A}}\left( {...} \right)} {dt}}} \right. \kern-0em} {dt}} = {{\partial \left( {...} \right)} \mathord{\left/ {\vphantom {{\partial \left( {...} \right)} {\partial t}}} \right. \kern-0em} {\partial t}} + {{{\mathbf{v}}}_{A}} \cdot \nabla (...)$ – материальная производная вдоль траектории частиц континуума A; ${{u}_{A}}$ – удельная внутренняя энергия; ${\mathbf{q}}$ – вектор суммарного теплового потока; ${{r}_{\Sigma }}Q$ – суммарная мощность внешних источников тепла; символом “:” обозначено двойное скалярное произведение, такое что ${\mathbf{A}}:{\mathbf{B}} = {{A}_{{ij}}}{{B}_{{ij}}}$.

Для того же элементарного тела второе начало термодинамики в форме неравенства Клаузиуса–Дюгема с учетом массообмена имеет вид:

где: ${{\eta }_{A}}$ – удельная энтропия; $\theta = {\text{const}}$ – температура континуумов.

Вводя удельную свободную энергию континуумов ${{\psi }_{A}} = {{u}_{A}} - {{\eta }_{A}}\theta $ и исключая из (9) поток приведенного тепла с помощью (8), а также используя (1)–(5), получим приведенное неравенство Клаузиуса–Дюгема в изотермическом приближении:

где: ${\mathbf{e}} = \frac{1}{2}\left( {\nabla \otimes {\mathbf{u}} + \nabla \otimes {{{\mathbf{u}}}^{T}}} \right)$ – тензор малой деформации скелета; ${\mathbf{u}}$ – вектор перемещения частиц скелета; ${{\delta }_{w}} = - \sum\nolimits_\alpha {{\mathbf{b}}_{\alpha }^{{dis}}} \cdot {{{\mathbf{w}}}_{\alpha }}$ $ = \sum\nolimits_\alpha {\frac{{{{\mu }_{\alpha }}}}{{{{\phi }_{\alpha }}{{k}_{\alpha }}}}{{{\left| {{{{\mathbf{W}}}_{\alpha }}} \right|}}^{2}}} \geqslant 0$ – диссипация, связанная с фильтрацией флюидов; ${{\delta }_{m}} = - \sum\nolimits_{\alpha \ne \beta } {{{\chi }_{\alpha }}{{{\dot {m}}}_{{\alpha \beta }}}} $ – диссипация, связанная с обменом массой между подсистемами; ${{\chi }_{\alpha }} = {{\psi }_{\alpha }} + {{{{p}_{\alpha }}} \mathord{\left/ {\vphantom {{{{p}_{\alpha }}} {{{\rho }_{\alpha }}}}} \right. \kern-0em} {{{\rho }_{\alpha }}}}$ – удельный потенциал Гиббса флюидов.

Для замыкания системы законов сохранения (1)–(5) сформулируем систему термодинамически согласованных определяющих соотношений. Согласно теории, развитой Колеманом, Ноллом и Трусделлом [Трусделл, 1975], определяющие соотношения должны удовлетворять ряду утверждений, среди которых принцип локального действия (изменение состояния в некоторой точке не может непосредственно повлиять на реакцию материала на конечном от нее расстоянии), принцип инвариантности от системы отсчета (вид определяющего соотношения должен быть одним и тем же в любых системах отсчета – инерциальных и неинерциальных), а также принцип термодинамической согласованности. Последний принцип утверждает, что второе начало термодинамики в форме неравенства Клаузиуса–Дюгема (9) или (10) накладывает ограничение на возможную реакцию среды в произвольном процессе.

Определим понятия “процесс” и “реакция” в рассматриваемом случае двойной пороупругой среды с хрупким склетом. Сначала определим состояние материальной частицы пористой среды как набор следующих параметров: тензор малой деформации скелета ${\mathbf{e}}$, истинные плотности жидкостей в матрице и трещинах ${{\rho }_{\alpha }}$, относительная скорость флюидов и скелета ${{{\mathbf{w}}}_{\alpha }}$, параметр поврежденности в матрице $\omega $. Параметр $\omega $ является внутренней переменной, для которой необходимо сформулировать кинетическое (эволюционное) уравнение. Будем считать, что $\omega $ накапливается необратимо, т.е. залечивания микротрещин не происходит. Под “процессом” будем понимать последовательность смены параметров состояния, а под “реакцией” – значения остальных неизвестных физических величин.

В общем виде, в рамках сделанных предположений, в качестве определяющих соотношений рассматриваемой среды примем набор функций, связывающих реакцию $\Upsilon $ с текущим состоянием пористой среды:

где $\Upsilon = \left\{ {{{\psi }_{\alpha }},{{{\mathbf{T}}}_{S}},{{p}_{\alpha }},{{\phi }_{\alpha }},{{{\dot {m}}}_{{12}}},b_{\alpha }^{{dis}}} \right\}.$ Соотношения (11) должны быть дополнены кинетическим уравнением для параметра поврежденности: где $\Omega $ – функция текущего состояния рассматриваемой среды.

Определяющие соотношения, необходимые и достаточные для выполнения (10), в произвольном процессе имеют следующий вид:

В выражениях (14) использован потенциал скелета $\Psi \left( {{{{\mathbf{e}}}_{s}},{{p}_{\alpha }},\omega } \right) = F - \sum\nolimits_\alpha {\frac{{{{p}_{\alpha }}}}{{{{r}_{s}}}}{{\phi }_{\alpha }}} $ [Кондауров, 2007], где $F\left( {{{{\mathbf{e}}}_{s}},{{\phi }_{\alpha }},\omega } \right)$ = ${{\psi }_{s}}\left( {{{{\mathbf{e}}}_{s}},{{\phi }_{\alpha }}\left( {{{{\mathbf{e}}}_{s}},{{\rho }_{\alpha }},\omega } \right),\omega } \right)$.

С учетом соотношений (13) и (14) неравенство (10) принимает вид:

где ${{\delta }_{\omega }} = - \left( {\frac{{\partial \Psi }}{{\partial \omega }}} \right)\frac{{{{d}_{s}}\omega }}{{dt}} = - \left( {\frac{{\partial \Psi }}{{\partial \omega }}} \right)\Omega $ – диссипация, связанная с растрескиванием матрицы.

Процедура доказательства соотношений (13)–(15) во многом аналогична используемой в работе [Кондауров, 2007] и здесь не приводится.

Далее примем гипотезу, что каждая диссипация в отдельности неотрицательна, что является достаточным условием для выполнения (15):

ЛИНЕЙНАЯ МОДЕЛЬ

Линеаризуем полученные определяющие соотношения в окрестности особого состояния $\left\{ {0,\,\rho _{\alpha }^{0},\,0,\,\omega } \right\}$, т.е. примем, что в этом состоянии скелет не деформирован, жидкости покоятся, давления флюидов $p_{1}^{0} = p_{2}^{0} = 0$. Давления во флюидах и напряжения в скелете в произвольных состояниях будем считать малыми по сравнению с характерными упругими модулями скелета ${{{{p}_{\alpha }}} \mathord{\left/ {\vphantom {{{{p}_{\alpha }}} K}} \right. \kern-0em} K} \ll 1$, ${{\left\| {{{{\mathbf{T}}}_{S}}} \right\|} \mathord{\left/ {\vphantom {{\left\| {{{{\mathbf{T}}}_{S}}} \right\|} K}} \right. \kern-0em} K} \ll 1$, где $K$ – модуль объемного сжатия скелета. Также рассмотрим частный случай, в котором начальные, полные напряжения в состоянии $\left\{ {0,\,\rho _{\alpha }^{0},\,0,\,0} \right\}$, равны нулю (в общем случае это не так (см. работу [Мухамедиев, 2018]).

Разложение свободной энергии в ряд по малому параметру ${{\delta {{\rho }_{\alpha }}} \mathord{\left/ {\vphantom {{\delta {{\rho }_{\alpha }}} {\rho _{\alpha }^{0}}}} \right. \kern-0em} {\rho _{\alpha }^{0}}} \ll 1$ до квадратичных членов в окрестности состояния $\left\{ {0,\,\rho _{\alpha }^{0},\,0,\,\omega } \right\}{\text{:}}$

где ${{K}_{f}}$ – модуль объемного сжатия жидкости, после подстановки в (13) дает линейное определяющее соотношение:

Вслед за авторами работ [Kondaurov, 2009; Извеков, 2009; 2010] положим, что влияние поврежденности на упругие модули пренебрежимо мало. При этом макроскопическим проявлением поврежденности становится остаточная деформация в поврежденном материале, что формально сближает данный вариант модели повреждаемости с теорией пластичности. Скелет будем считать изотропным. Представим разложение потенциала скелета до величин второго порядка малости, считая поврежденность одним из малых параметров, в следующем виде:

где: $\lambda $, $\mu $ – коэффициенты Ламе скелета; ${{I}_{1}} = {\mathbf{e}}:{\mathbf{I}}$, $J = \sqrt {{\mathbf{e}}{\kern 1pt} ':{\mathbf{e}}{\kern 1pt} '} $, ${\mathbf{e}}{\kern 1pt} '$ – девиатор тензора малых деформаций; ${{b}_{\alpha }}$ и ${{N}_{\alpha }}$ – аналоги коэффициентов Био и модуля Био для матрицы и трещин; ${{N}_{{12}}}$ – модуль, отвечающий за взаимное влияние поровых давлений в подсистемах; $\alpha \geqslant 0$, ${{\alpha }_{J}} \geqslant 0$, ${{\alpha }_{{p1}}} \geqslant 0$, ${{\alpha }_{{p2}}} \leqslant 0$ – коэффициенты, отвечающие за разгрузку упругой энергии при развитии поврежденности; $\gamma $, $\beta $ – положительные коэффициенты, задающие нелинейную зависимость от поврежденности нулевого члена разложения упругой энергии скелета, характеризующего затраты энергии на появление новых поверхностей.

Подстановка (19) в (14) дает линейные определяющие соотношения для скелета:

где $K = \lambda + \frac{2}{3}\mu $ – модуль объемного сжатия скелета.

Обсудим неравенства диссипации (16). Учтем, что, согласно сделанным предположениям относительно начального состояния флюидов, $\psi _{1}^{0} = \psi _{2}^{0} = 0,$ тогда справедлива оценка:

где введено обозначение $\dot {m} = {{\dot {m}}_{{21}}} = - {{\dot {m}}_{{12}}}$. Величина $\dot {m} > 0$, если матрица подпитывает трещины. Удовлетворим неравенству (23) с помощью простого уравнения, задающего закон обмена массой между флюидами: где $A\left( \omega \right) \geqslant 0$ – коэффициент, определяющий интенсивность массообмена. В результате растрескивания улучшается возможность транспорта жидкости внутри матрицы, что проявляется в усилении массообмена между флюидами. В случае неповрежденной матрицы (24) совпадает с классическим выражением [Баренблатт, 1960].

Поступая аналогично авторам [Kondaurov, 2009; Извеков, 2009; 2010], примем следующий закон эволюции поврежденности, достаточный для удовлетворения неравенству диссипации ${{\delta }_{\omega }} \geqslant 0$:

где: $\tau $ – характерное время запаздывания разрушения; $\beta $ – размерный параметр.

Физический смысл выражения (25) заключается в том, что поврежденность развивается только в том случае, когда упругая энергия, высвобождающаяся при появлении новых поверхностей, превышает энергозатраты на их появление. Чем сильнее эта разница, тем интенсивнее развивается поврежденность. Уравнение (25) является в некотором роде аналогом теории Гриффитса для изолированной трещины.

Подставляя в (25) представление потенциала скелета (19), получим линейное эволюционное уравнение:

Эволюция параметров однородного гидростатического напряженного состояния при отсутствии обмена между подсистемами описывается системой уравнений, следующих из (1), (2), (5) с учетом (20)–(22) и (26):

Решение данной системы имеет вид ${\mathbf{x}} = a{{e}^{{\Gamma t}}} + {\mathbf{b}}$, где ${\mathbf{x}} = {{({{I}_{1}},{{p}_{1}},{{p}_{2}},\omega )}^{T}}$, $a = {\text{const}},\;{\mathbf{b}} = {\text{const}}$.

Система неравенств:

является достаточным условием выполнения неравенства $\Gamma < 0$. В дальнейшем эти ограничения на коэффициенты модели, гарантирующие устойчивость однородного напряженного состояния, считаются выполненными.

Из ограниченности скорости ${{\partial \omega } \mathord{\left/ {\vphantom {{\partial \omega } {\partial t}}} \right. \kern-0em} {\partial t}}$ при $\tau \to 0$, из (26) следует выражение для параметра $\omega $:

Из выражения (26) следует критерий начала накопления поврежденности. Одновременное выполнение условий ${{\partial \omega } \mathord{\left/ {\vphantom {{\partial \omega } {\partial t}}} \right. \kern-0em} {\partial t}} \geqslant 0$ и $\omega = 0$ дает для границы зоны упругого поведения в пространстве инвариантов тензора малой деформации следующее уравнение:

Условие $\alpha {{I}_{1}} + {{\alpha }_{J}}J + {{\alpha }_{{p1}}}{{p}_{1}} + {{\alpha }_{{p2}}}{{p}_{2}} - \gamma < 0$ соответствует упругому поведению. При выполнении условия $\alpha {{I}_{1}} + {{\alpha }_{J}}J + {{\alpha }_{{p1}}}{{p}_{1}} + {{\alpha }_{{p2}}}{{p}_{2}} - \gamma > 0$ возможны активный процесс (${{\partial \omega } \mathord{\left/ {\vphantom {{\partial \omega } {\partial t}}} \right. \kern-0em} {\partial t}} > 0$) и упругая разгрузка (пассивный процесс). В пассивном процессе полагается $\omega = {\text{const}}$.

ОЦЕНКА ПОРОУПРУГИХ КОЭФФИЦИЕНТОВ

Выяснению физического смысла и способам лабораторного определения пороупругих констант для среды с двойной пористостью посвящен ряд работ [Bai et al., 1995; Berryman, Pride, 2002]. Существуют также обобщения пороупругой модели на случай мультипористости [Mehrabian, Abousleiman, 2015]. Приведем здесь простые оценки относительных значений коэффициентов ${{b}_{1}}$ и ${{b}_{2}}$, модулей ${{N}_{\alpha }}$ и ${{N}_{{12}}}$, подвергнув среду одноосному сжатию с нулевой поперечной деформацией. Соответствующая приближенная одномерная эквивалентная схема состоит из двух последовательно соединенных герметичных камер (элементов схемы). В ненапряженном состоянии продольные размеры камер равны $l_{1}^{0}$ и $l_{2}^{0}$, причем $l_{2}^{0} \ll l_{1}^{0}$, как показано на рис. 2. Торцевые стенки камер могут скользить без трения вдоль горизонтальной оси. Первая камера, играющая роль матрицы, заполнена пороупругой средой с пористостью ${{n}_{1}}$, упругим модулем ${{E}_{1}}$, коэффициентом Био ${{\alpha }_{1}}$ и модулем Био $\tilde {N}$. Внутри второй камеры, соответствующей магистральным трещинам, находится пружина жесткостью ${{E}_{2}}$ (считаем, что трещины не заполнены ничем, кроме жидкости). Обозначим ${{\xi }_{\alpha }} = {{l_{\alpha }^{{}}} \mathord{\left/ {\vphantom {{l_{\alpha }^{{}}} {\left( {l_{1}^{0} + l_{2}^{0}} \right)}}} \right. \kern-0em} {\left( {l_{1}^{0} + l_{2}^{0}} \right)}}$ объемные доли матрицы и трещин, так что ${{\xi }_{1}} + {{\xi }_{2}} = 1$. Объемные доли флюидов (“пористости”) будут равны ${{\phi }_{1}} = {{n}_{1}}{{\xi }_{1}}$, ${{\phi }_{2}} = {{\xi }_{2}}$. В камеры независимо нагнетаются давления ${{p}_{1}}$ и ${{p}_{2}}$.

Запишем условия равновесия:

где: $\sigma $ – внешнее сжимающее напряжение; ${{\varepsilon }_{1}} = {{\Delta {{l}_{1}}} \mathord{\left/ {\vphantom {{\Delta {{l}_{1}}} {l_{1}^{0}}}} \right. \kern-0em} {l_{1}^{0}}}$ и ${{\varepsilon }_{2}} = {{\Delta {{l}_{2}}} \mathord{\left/ {\vphantom {{\Delta {{l}_{2}}} {l_{2}^{0}}}} \right. \kern-0em} {l_{2}^{0}}}$ – относительные удлинения элементов схемы.

Запишем общую деформацию системы ${{\varepsilon }_{\Sigma }} = $ $ = {{\left( {\Delta {{l}_{1}} + \Delta {{l}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {\Delta {{l}_{1}} + \Delta {{l}_{2}}} \right)} {\left( {l_{1}^{0} + l_{2}^{0}} \right)}}} \right. \kern-0em} {\left( {l_{1}^{0} + l_{2}^{0}} \right)}}$ как комбинацию относительных удлинений камер:

Выражая относительные удлинения из (36), с помощью (35) получим аналог закона Гука:

где $E_{\Sigma }^{{}} = {{\left( {{{{{\xi }_{1}}} \mathord{\left/ {\vphantom {{{{\xi }_{1}}} {{{E}_{1}}}}} \right. \kern-0em} {{{E}_{1}}}} + {{{{\xi }_{2}}} \mathord{\left/ {\vphantom {{{{\xi }_{2}}} {{{E}_{2}}}}} \right. \kern-0em} {{{E}_{2}}}}} \right)}^{{ - 1}}}$ – суммарный упругий модуль системы.

Сравнивая (37) с (20) в отсутствие поврежденности, приходим к выводу, что коэффициенты при давлениях ${{p}_{1}}$ и ${{p}_{2}}$ играют роль коэффициентов ${{b}_{1}}$ и ${{b}_{2}}$. Таким образом,

При стремлении объемной доли ${{\xi }_{2}}$ к нулю, суммарный упругий модуль системы ${{E}_{\Sigma }}$ стремится к ${{E}_{1}}$, а коэффициент ${{b}_{1}}$ стремится к коэффициенту Био матрицы ${{\alpha }_{1}}$. Пусть ${{\xi }_{2}} \approx 0.01{{\xi }_{1}}$, тогда при соотношении модулей ${{{{E}_{2}}} \mathord{\left/ {\vphantom {{{{E}_{2}}} {{{E}_{1}}}}} \right. \kern-0em} {{{E}_{1}}}} \approx {{10}^{{ - 4}}} - 1$, отношение ${{{{b}_{1}}} \mathord{\left/ {\vphantom {{{{b}_{1}}} {{{b}_{2}}}}} \right. \kern-0em} {{{b}_{2}}}}$ будет лежать в диапазоне ${{10}^{{ - 2}}}{\kern 1pt} - {\kern 1pt} {{10}^{2}}$.

Модуль ${{E}_{2}}$ определяется как ${{E}_{2}} = {{S}_{n}}\Delta \lambda = {{S}_{n}}{{\xi }_{2}}L$, где: ${{S}_{n}}$ – нормальная жесткость одиночной трещины; $\Delta \lambda $ – ширина одиночной трещины; $L$ – характерный размер блока [Кочарян, 2016]. Возьмем ${{S}_{n}} \approx {{10}^{2}}$ ГПа/м, $L \approx 1$ м, ${{E}_{1}} = 10$ ГПа, согласующиеся с данными из табл. 1, получим, что отношение упругих модулей будет равно ${{{{E}_{2}}} \mathord{\left/ {\vphantom {{{{E}_{2}}} {{{E}_{1}}}}} \right. \kern-0em} {{{E}_{1}}}} \approx 0.1$, тогда согласно (38) отношение ${{{{b}_{1}}} \mathord{\left/ {\vphantom {{{{b}_{1}}} {{{b}_{2}}}}} \right. \kern-0em} {{{b}_{2}}}} \approx 10$, а из (37) следует ${{b}_{1}} = 0.9{{\alpha }_{1}}$, ${{b}_{2}} = 0.09{{\alpha }_{1}}$.

Оценим модули ${{N}_{\alpha }}$ и ${{N}_{{12}}}$ с помощью предложенной упрощенной схемы. Учитывая, что деформация трещин ${{\varepsilon }_{2}} = {{\Delta {{\phi }_{2}}} \mathord{\left/ {\vphantom {{\Delta {{\phi }_{2}}} {{{\phi }_{2}}}}} \right. \kern-0em} {{{\phi }_{2}}}}$, деформация матрицы ${{\varepsilon }_{1}} = {{\Delta {{\xi }_{1}}} \mathord{\left/ {\vphantom {{\Delta {{\xi }_{1}}} {{{\xi }_{1}}}}} \right. \kern-0em} {{{\xi }_{1}}}} = {{\Delta {{\phi }_{1}}} \mathord{\left/ {\vphantom {{\Delta {{\phi }_{1}}} {{{\phi }_{1}}}}} \right. \kern-0em} {{{\phi }_{1}}}} - {{\Delta {{n}_{1}}} \mathord{\left/ {\vphantom {{\Delta {{n}_{1}}} {{{n}_{1}}}}} \right. \kern-0em} {{{n}_{1}}}}$, при этом $\Delta {{n}_{1}} = {{\alpha }_{1}}{{\varepsilon }_{1}} + {{{{p}_{1}}} \mathord{\left/ {\vphantom {{{{p}_{1}}} {\tilde {N}}}} \right. \kern-0em} {\tilde {N}}}$ из уравнений (35) и (36) получим оценку:

Тогда для относительных величин справедливо:

При ${{{{b}_{1}}} \mathord{\left/ {\vphantom {{{{b}_{1}}} {{{b}_{2}}}}} \right. \kern-0em} {{{b}_{2}}}} \approx 10$ и ${{\alpha }_{1}} = 0.7$ из (43) получим оценку ${{{{N}_{2}}} \mathord{\left/ {\vphantom {{{{N}_{2}}} {{{N}_{{12}}}}}} \right. \kern-0em} {{{N}_{{12}}}}} \approx 0.68$. Если дополнительно положить ${{n}_{1}} = 0.1$ и ${{{{E}_{1}}} \mathord{\left/ {\vphantom {{{{E}_{1}}} {\left( {{{n}_{1}}\tilde {N}} \right)}}} \right. \kern-0em} {\left( {{{n}_{1}}\tilde {N}} \right)}} \approx 1$, тогда согласно соотношению (42) отношение ${{{{N}_{2}}} \mathord{\left/ {\vphantom {{{{N}_{2}}} {{{N}_{1}}}}} \right. \kern-0em} {{{N}_{1}}}} \approx 16.6$. Таким образом, абсолютные значения модулей ${{N}_{2}}$ и ${{N}_{{12}}}$ в рамках сделанных предположений имеют один порядок и более чем на порядок превышают модуль ${{N}_{1}}$. В последующих расчетах будем придерживаться полученных соотношений.

ОЦЕНКА ПАРАМЕТРОВ В МОДЕЛИ ПОВРЕЖДЕННОСТИ ДЛЯ МАТРИЦЫ

В предложенную линейную модель поврежденности входит ряд коэффициентов. Оценим их, задавшись гипотезой о частном механизме разрушения матрицы. Обозначим коэффициенты, отвечающие за уменьшение упругой энергии матрицы ${{\alpha }_{M}}$, ${{\alpha }_{{JM}}}$, ${{\alpha }_{{pM}}}$. В работах [Engelder, 1990; Luo, 2002] указывается, что трещины автофлюидоразрыва развиваются преимущественно за счет нормального раскрытия. Принимая указанный механизм разрушения, положим, что в матрице содержится некоторое количество плоских круглых трещин (penny shaped) диаметром $l$, ориентация которых имеет изотропное распределение. Пренебрежем взаимодействием этих трещин, таким образом, уравнение (34) при ${{p}_{2}} = 0$ соответствует условию начала развития одиночной трещины. В отличие от работы [Engelder, 1990] будем полагать, что стенки трещин непроницаемы для флюида, что правомерно в условиях сверхнизкой проницаемости.

В случае одноосного сжатия (рис. 3а) под действием внутреннего давления первой раскроется трещина, ориентированная перпендикулярно максимальному сжимающему напряжению ${{\sigma }_{V}} < 0$. Это произойдет при внутреннем давлении ${{p}_{{ini}}}$, равном [Engelder, 1990]:

где: $\nu $ – коэффициент Пуассона; ${{K}_{{IC}}}$ – критический коэффициент интенсивности напряжений при нормальном раскрытии одиночной трещины.

В случае всестороннего сжатия (рис. 3б) уравнение для критического давления будет иметь вид:

Сравнивая (28) с (47), получим оценки:

Аналогично рассматривая трещину в условиях одноосного сжатия (в этом случае $J = - \sqrt {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}} {{I}_{1}}$), получим:

В работе [Grytsenko, Galybin, 2010] с помощью численных расчетов методом сингулярных интегральных уравнений было показано, что в случае ансамбля из большого числа одинаковых трещин, находящихся на расстояниях больше либо порядка их длины, критический коэффициент интенсивности напряжений зависит от взаимного расположения трещин, однако отличается от ${{K}_{{IC}}}$ не более чем на 30% (в меньшую сторону).

Параметр $\beta $ в расчетах подбирался таким, чтобы выполнялось неравенство ${{\alpha _{M}^{2}} \mathord{\left/ {\vphantom {{\alpha _{M}^{2}} \beta }} \right. \kern-0em} \beta } < K.$

УСЛОВИЕ РАЗРУШЕНИЯ СРЕДЫ С ДВОЙНОЙ ПОРИСТОСТЬЮ

Обратимся теперь к среде с двойной пористостью. Воспользуемся одномерной моделью. Пусть условие начала поврежденности в матрице имеет вид:

Требуется переформулировать его в терминах полной деформации ${{\varepsilon }_{\Sigma }}$. Исключим ${{\varepsilon }_{1}}$ из условия (49) с помощью (35) и (36). В итоге получим:

где ${{a}_{1}} = \frac{{{{\xi }_{2}}}}{{{{\xi }_{1}}}}\frac{{{{b}_{1}}}}{{{{E}_{2}}}}$, ${{a}_{2}} = \frac{{{{b}_{2}}}}{{{{E}_{1}}}}$.

Сравнивая полученное выражение с (34), получим:

Используя ранее сделанные оценки ${{{{b}_{1}}} \mathord{\left/ {\vphantom {{{{b}_{1}}} {{{b}_{2}}}}} \right. \kern-0em} {{{b}_{2}}}} \approx 10$, ${{{{E}_{2}}} \mathord{\left/ {\vphantom {{{{E}_{2}}} {{{E}_{1}}}}} \right. \kern-0em} {{{E}_{1}}}} \approx 0.1$, ${{\xi }_{2}} \approx 0.01{{\xi }_{1}}$, получим ${{a}_{1}} \approx {{a}_{2}}$, $\alpha \approx {{\alpha }_{M}}$. Далее, используя оценку $\frac{{{{\alpha }_{M}}}}{{{{\alpha }_{p}}_{M}}} = {{E}_{1}}$ (одномерный аналог (46)), получим соотношение между коэффициентами ${{\alpha }_{{p1}}}$ и ${{\alpha }_{{p2}}}$:

ЗАДАЧА О ПРОИЗВОДИТЕЛЬНОСТИ СКВАЖИНЫ

Далее для определенности пренебрежем силой тяжести. Рассматривается однородный безграничный пласт. Начальные давления в трещинах и в матрице пласта одинаковы и равны ${{p}_{0}}$. На бесконечности задано сжимающее гидростатическое горное давление $\sigma _{0}^{{}} < 0$. В некоторый момент времени в пласте появляется длинная цилиндрическая скважина радиусом $a$, давление на забое которой устанавливается на заданном уровне ниже начального давления. В результате напряженное состояние среды изменяется, а флюиды из системы трещин начинают поступать в скважину. В процессе развития зоны депрессии в окрестности скважины под действием АВПД матрица растрескивается, что усиливает массообмен с трещинами.

Решим задачу численно в приближении радиальной симметрии, в котором перемещение частиц скелета происходит только в радиальном направлении и не зависит от полярного угла. Обозначим радиальную компоненту перемещения $u$. Тогда тензор напряжений в скелете принимает вид:

где: $r$ – расстояние от центра скважины; ${{{\mathbf{e}}}_{r}}$ и ${{{\mathbf{e}}}_{\theta }}$ – орты цилиндрической системы координат. Тогда след тензора ${\mathbf{e}}$ и инвариант девиатора будут равны:

Подставим определяющие соотношения (20)–(22), закон массобмена (24) и закон Дарси (4) в уравнение равновесия (5) и уравнения неразрывности (1), (2). Получим следующую систему уравнений:

где $M_{\alpha }^{{ - 1}} = N_{\alpha }^{{ - 1}} + \phi _{\alpha }^{{}}K_{f}^{{ - 1}}$.

Для постановки граничных условий заменим бесконечный пласт расчетной областью цилиндрической формы, так чтобы оси скважины и расчетной области совпадали. Пусть радиус расчетной области $R$ много больше радиуса скважины. Изначально недеформированную расчетную область (без скважины) подвергнем гидростатическому сжимающему напряжению $\sigma _{0}^{{}} < 0$ при условии постоянства давлений $p_{0}^{{}} > 0$ в матрице и трещинах. Перемещение границы на расстоянии $R \gg a$ от скважины будет равно:

В расчетах будем считать эту границу закрепленной, т.е. $u(R,\,t) = {{u}_{R}}$. Поставим следующие граничные условия на давление в трещинах:

Условие равенства полных радиальных напряжений на стенках скважины $\left( {r = a} \right)$ имеет вид:

В качестве начальных условий положим условие на начальное поле давлений

условие на начальное поле перемещений (перемещения в расчетной области до появления скважины) и равенство нулю параметра разрушения $\omega \left( {r,\,0} \right) = 0$ (при этом параметры и начальные условия на напряжения и на давление подобраны так, чтобы условие инициации разрушения в начальном состоянии не выполнялось).

СИСТЕМА УРАВНЕНИЙ В БЕЗРАЗМЕРНОМ ВИДЕ

Для представления системы (58)–(60) в безразмерном виде введем характерные масштабы для давления, напряжения и упругих модулей $\mu $, для координат и перемещений ${{r}_{0}}$, для времени ${{t}_{0}}$, для проницаемости системы трещин $k_{2}^{0}$. Увяжем масштабы ${{t}_{0}}$ и $k_{2}^{0}$ с помощью следующего соотношения:

Безразмерную функцию поврежденности, отвечающую за обмен между подсистемами трещины и матрицы, представим в виде $\overline {A(\omega )} = {{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} {k_{2}^{0}}}} \right. \kern-0em} {k_{2}^{0}}}A(\omega )$. Безразмерные коэффициенты в выражении для поврежденности $\bar {\alpha } = {\alpha \mathord{\left/ {\vphantom {\alpha \mu }} \right. \kern-0em} \mu },$ ${{\bar {\alpha }}_{p}} = {{\alpha }_{p}},$ $\bar {\beta } = {\beta \mathord{\left/ {\vphantom {\beta \mu }} \right. \kern-0em} \mu },$ $\bar {\gamma } = {\gamma \mathord{\left/ {\vphantom {\gamma \mu }} \right. \kern-0em} \mu }.$ Безразмерные коэффициенты Ламе $\bar {\lambda } = {\lambda \mathord{\left/ {\vphantom {\lambda \mu }} \right. \kern-0em} \mu }$, $\bar {\mu } = 1$.

После обезразмеривания система (58)–(60) принимает следующий вид (все переменные далее безразмерные, черточки над ними для удобства опущены):

где введены обозначения для безразмерных коэффициентов $\varepsilon = \frac{{{{M}_{2}}}}{\mu }$, ${{k}_{b}} = \frac{{{{b}_{2}}}}{{{{b}_{1}}}},$${{\varepsilon }_{M}} = \frac{{{{M}_{1}}}}{{{{M}_{2}}}}$, ${{\varepsilon }_{{12}}} = \frac{{{{M}_{2}}}}{{{{N}_{{12}}}}}$.

Принимая сделанные выше оценки пороупругих коэффициентов, получим, ${{\varepsilon }_{M}} \approx {{10}^{{ - 2}}}$, $\varepsilon \approx {{10}^{2}}$, ${{\varepsilon }_{{12}}} \approx - 1$, ${{k}_{b}} \approx {{10}^{{ - 1}}}$. В расчетах принималась степенная зависимость обменного члена от параметра поврежденности, $A\left( \omega \right) = A{{\omega }^{2}}$.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Система дифференциальных уравнений (68)–(71) решалась численно в области 1 < r < 10² на основе полностью неявной схемы. Графики на рис. 4–рис. 6 получены при следующих значениях параметров: ${{\sigma }_{0}} = - 0.0022$,${{p}_{0}} = 0.001$,${{p}_{a}} = 0.0001$, ${{\varepsilon }_{M}} = 0.013$, $\varepsilon = 50$, ${{\varepsilon }_{{12}}} = - 0.19$, ${{b}_{1}} = 0.6$, ${{b}_{2}} = 0.1$, $\lambda = 0.428$, $A = 3 \cdot {{10}^{9}}$, $\alpha = 0.5$, ${{\alpha }_{J}} = 0.5$, ${{\alpha }_{{p1}}} = 0.11$, ${{\alpha }_{{p2}}} = - 0.01$, $\beta = 0.5$, $\gamma = 8 \times {{10}^{{ - 5}}}$. На рис. 4 показана эволюция поврежденности и поровых давлений в матрице и системе трещин. На временах t ~ 1 наблюдается быстрый рост поврежденности в ближайшей (r < 2) окрестности скважины. В дальнейшем при t > 10 поврежденность в этой зоне не испытывает заметных изменений. Под влиянием волны депрессии, распространяющейся от границы скважины r = 1 вглубь пласта, происходит изменение параметров состояния (упругих напряжений и деформаций). Следствием этих факторов является волна разрушения, которая формирует область дренирования матрицы (граница области дренирования приближенно соответствует положению фронта разрушения, ограничивающего поврежденную область, см. рис. 4). Зависимость радиуса границы зоны разрушения d (области дренирования матрицы) от времени показана на рис. 5. Максимальная скорость границы области разрушения наблюдается при малых t. При 10² < t < 10³ закон движения границы d(r) аппроксимируется степенной зависимостью. Если принять следующие размерные параметры ${{\mu }_{f}} = {{10}^{3}}$ Па с, $\mu = 4 \times {{10}^{9}}$ Па, $k_{2}^{0} = {{10}^{{ - 12}}}$ м², получается оценка для характерного времени ${{t}_{0}} \approx 50$ с. Таким образом, согласно рис. 5, радиус границы зоны разрушения достигнет величины $3{{r}_{0}} = 30$ см за 10³ с.

Разрушение матрицы приводит к появлению ее проницаемости и перетеканию жидкости в трещины, что приводит к повышению дебита. Факторами, способствующими повышению дебита, являются рост зоны дренирования и увеличение поврежденности. Изменение дебита на единицу длины скважины (${{q(t)} \mathord{\left/ {\vphantom {{q(t)} {{{q}_{r}}}}} \right. \kern-0em} {{{q}_{r}}}}$, где ${{q}_{r}} = {{{{p}_{0}}k_{2}^{2}} \mathord{\left/ {\vphantom {{{{p}_{0}}k_{2}^{2}} {{{\mu }_{f}}}}} \right. \kern-0em} {{{\mu }_{f}}}}$) с течением времени показано на рис. 6 (кривая 1), на больших временах эта зависимость близка к степенной. Для сравнения показан дебит скважины при отсутствии обмена между трещинами и матрицей (кривая 2). В рамках проведенного расчета рост зоны дренирования матрицы не ограничен, однако следует иметь в виду, что максимальная достигаемая поврежденность в волне разрушения быстро падает с увеличением r (см. рис. 4). При достижении параметром поврежденности значений, при которых микротрещины не образуют связанную систему, дальнейший рост зоны дренирования матрицы неизбежно прекратится.

ВЫВОДЫ

В работе представлена модель двойной пористой среды с упругим трещиноватым скелетом с аномально высоким давлением в матрице в изотермическом приближении. Модель согласована с основными принципами механики сплошных сред и термодинамики. Модель включает в себя параметр разрушения, как внутреннюю переменную, характеризующую процесс разрушения в низкопроницаемой матрице вследствие комбинации изменения напряженного состояния и изменения порового давления. Закон образования разрушений сформулирован с учетом неотрицательности диссипации разрушений ${{\delta }_{\omega }}$ для любого механического процесса.

Показано, что аномально высокое давление может привести к развитию разрушений в низкопроницаемой матрице. Подобные условия возникают вследствие более быстрого уменьшения давления в трещинах по сравнению с поровым давлением в матрицах и вследствие изменения полного напряжения в скелете в окрестности скважины. При оценочных значениях параметров модели размер области дренирования первоначально непроницаемой матрицы в результате разрушения в волне депрессии существенно превысил радиус скважины.

Таким образом, продемонстрирована принципиальная возможность вовлечения в разработку низкопроницаемых трещиновато-пористых пластов с АВПД, с использованием только энергии АВПД.