Физика Земли, 2022, № 1, стр. 100-117
Сравнительный анализ методов оценки магнитуды представительной регистрации землетрясений
В. А. Павленко 1, *, А. Д. Завьялов 1, **
1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
* E-mail: pavlenko.vasily@gmail.com
** E-mail: zavyalov@ifz.ru
Поступила в редакцию 09.10.2020
После доработки 18.05.2021
Принята к публикации 11.06.2021
- EDN: RXQBFM
- DOI: 10.31857/S0002333722010069
Аннотация
Магнитуда представительной регистрации землетрясений ${{M}_{c}}$ – важный параметр, характеризующий полноту сейсмических данных. Известно, что пространственно-временные вариации ${{M}_{c}}$ необходимо учитывать для получения корректных оценок параметров сейсмического режима. В работе сравниваются шесть современных методов оценки ${{M}_{c}}$. Для сравнения методов использованы выборки из реальных инструментальных каталогов землетрясений, а также синтетические каталоги, сгенерированные на основе трех моделей распределения магнитуды. Проанализированы зависимости двух первых моментов распределений оценок ${{M}_{c}}$ от формы распределения магнитуды и объема выборки. Использованы три модели, отвечающие выборочным распределениям, встречающимся при анализе инструментальных каталогов землетрясений. На основе полученных результатов сформулированы рекомендации по выбору подходящего метода оценки ${{M}_{c}}$.
ВВЕДЕНИЕ
Одной из важнейших характеристик сейсмического процесса является частота возникновения землетрясений разной силы. Зависимость частоты землетрясений от магнитуды называют законом повторяемости землетрясений. В сейсмологии наиболее широко известен закон повторяемости Гутенберга–Рихтера [Gutenberg, Richter, 1944]:
где: $N$ – число землетрясений с магнитудой $m \geqslant M$; $a$ – параметр сейсмической активности; $b$ – наклон графика повторяемости землетрясений.Закон Гутенберга–Рихтера применим для описания сейсмичности различных тектонических режимов. Параметры $a$ и $b$ имеют принципиальное значение для анализа сейсмической опасности. Кроме того, временное снижение величины $b$ неоднократно наблюдалось перед возникновением сильных землетрясений [Gibowicz, 1973; Завьялов, 1984; 2006; Nuannin et al., 2005]. Временные снижения и нарастания сейсмической активности, известные как сейсмические затишья и форшоковые активизации, также рассматриваются в качестве возможных предвестников сильных землетрясений [Wyss et al., 1999; Zöller et al., 2002].
Определение значений a и b существенно осложняется тем, что обычно график повторяемости землетрясений соответствует теоретической зависимости (1) лишь на ограниченном интервале значений магнитуды (см. рис. 1). Выраженный излом кумулятивного графика повторяемости в области малых магнитуд обычно связывают с неполной регистрацией слабых землетрясений [Писаренко, 1989; Smirnov, 1998; Смирнов, Габсатарова, 2000; Wiemer, Wyss, 2000].
Рис. 1.
Метод MAXC. Дискретный и кумулятивный графики повторяемости для выборки из каталога NCSN (Northern California Seismic Network). Сплошной линией показана аппроксимация законом Гутенберга–Рихтера, вертикальная штриховая линия показывает оценку ${{M}_{c}}$, взятую в точке максимальной кривизны кумулятивного графика повторяемости. Полученные оценки параметров ${{M}_{c}} = 1.2$, $a = 5.25$, $b = 0.98$.

Магнитуда представительной регистрации ${{M}_{c}}$ – это минимальная магнитуда, для которой землетрясения в заданной области регистрируются в полном объеме. Значение ${{M}_{c}}$ соответствует началу линейной части графика повторяемости, поэтому знание ${{M}_{c}}$ становится критически важным для получения адекватных оценок параметров Гутенберга–Рихтера.
Из соотношения (1) следует, что магнитуда имеет экспоненциальное распределение с функцией плотности:
(2)
${{f}_{M}}\left( m \right) = {{\beta }}{{e}^{{ - \beta \left( {m\, - \,{{M}_{c}}} \right)}}},~\,\,\,\,m \geqslant {{M}_{c}},$Существующие методы оценки параметра $b$ включают метод наименьших квадратов [Guttorp, 1987; Nuannin et al., 2005], метод максимального правдоподобия [Aki, 1965; Гусев, 1974; Bender, 1983] и метод, основанный на минимизации статистики критерия согласия Колмогорова [Goldstein et al., 2004]. Прекрасный обзор наиболее распространенных на практике методов оценки $b$ представлен в работе [Marzocchi, Sandri, 2003].
В статье [Bengoubou-Valérius, Gibert, 2013] был выполнен сравнительный анализ этих методов. Авторы исследования пришли к выводу о том, что наиболее надежным является метод максимального правдоподобия. С учетом поправки за дискретизацию магнитуды [Utsu, 1966], оценка максимального правдоподобия $b$ будет иметь вид:
(3)
$\hat {b} = \frac{{{{{\lg }}_{{10}}}\left( e \right)}}{{\bar {M} - \left( {{{M}_{c}} - {{\Delta M} \mathord{\left/ {\vphantom {{\Delta M} 2}} \right. \kern-0em} 2}} \right)}},$Недооценка, т.е. занижение величины ${{M}_{c}}$ приводит к получению некорректных оценок параметров сейсмичности и ошибочной интерпретации данных. Так, включение событий с непредставительной регистрацией в оценку наклона графика повторяемости $b$ может привести к существенному занижению этой оценки (см. рис. 2б), что в свою очередь влечет недооценку частоты возникновения слабых землетрясений и переоценку частоты возникновения сильных землетрясений. Переоценка, т.е. завышение ${{M}_{c}}$ может быть не столь критична [Chen et al., 2011], но приводит к снижению объема анализируемой выборки, а значит повышает неопределенность всех дальнейших результатов анализа. Значение ${{M}_{c}}$ изменяется в пространстве и во времени и эти вариации необходимо учитывать при работе с каталогами землетрясений для оценки различных параметров сейсмического режима.
Рис. 2.
(a) – Метод GFT. График величины $100 - R$, построенный по выборке из каталога NCSN. Горизонтальные пунктирные линии показывают уровни величины критерия $R$, при достижении которых берется оценка ${{M}_{c}}$, вертикальная штриховая линия показывает оценку ${{M}_{c}}$; (б) – метод MBS. Графики текущих и усредненных значений $b$, построенные по выборке из каталога NCSN. Сплошной линией показан график значений $b$, пунктиром показаны границы одного стандартного отклонения $b$, линия с треугольными маркерами показывает график усредненных значений $b$, вертикальная штриховая линия показывает оценку ${{M}_{c}}$.

Таким образом, анализ пространственно-временных вариаций ${{M}_{c}}$ становится неотъемлемым элементом практически любого исследования, опирающегося на каталоги землетрясений.
Одна из первых методик оценки ${{M}_{c}}$ была предложена в работе [Stepp, 1972] и была основана на предположении о том, что последовательность основных землетрясений соответствует стационарному Пуассоновскому процессу. В таком случае средняя частота землетрясений $\lambda $ должна быть стабильна в представительной части каталога, а ее стандартное отклонение обратно пропорционально взятому для оценки $\lambda $ интервалу времени: ${{\sigma }_{\lambda }} = \sqrt {{\lambda \mathord{\left/ {\vphantom {\lambda T}} \right. \kern-0em} T}} $. По графику зависимости ${{\sigma }_{\lambda }}\left( T \right)$ для каждого значения магнитуды можно определить момент, когда график начинает отклоняться от степенной зависимости ${1 \mathord{\left/ {\vphantom {1 {\sqrt T }}} \right. \kern-0em} {\sqrt T }}$, что соответствует окончанию периода представительной регистрации.
Позднее был предложен метод оценки ${{M}_{c}}$, основанный на сравнении числа землетрясений, зарегистрированных в дневное и в ночное время [Rydelek, Sacks, 1989]. Этот метод предназначен для анализа локальных каталогов. Предполагается, что вероятность обнаружения землетрясений возрастает в ночное время вследствие снижения уровня индустриальных шумов. Таким образом, если преобладающее число землетрясений в заданном интервале значений магнитуды регистрируется ночью, каталог считается непредставительным в этом интервале.
В дальнейшем проблеме оценки ${{M}_{c}}$ уделялось существенное внимание и со временем число методов оценки ${{M}_{c}}$ значительно возросло. Подробный обзор современных методов оценки ${{M}_{c}}$ приводится в работе [Mignan, Woessner, 2012]. Большинство этих методов можно отнести к одной из двух категорий:
1. Методы, основанные на анализе каталогов землетрясений.
2. Методы, анализирующие возможности регистрации землетрясений станциями сейсмической сети заданной конфигурации [Ringdal, 1975; Gomberg, 1991].
Сопоставление результатов этих двух подходов выполнялось, в частности, в работе [Смирнов, Габсатарова, 2000], где по данным каталога землетрясений Северного Кавказа было показано, что оценки минимального представительного класса, полученные с помощью двух подходов, хорошо согласуются между собой и адекватно отражают изменения сейсмической сети.
Методы из первой категории менее трудоемкие, требуют меньшего объема информации и чаще применяются на практике. Кроме того, информация, необходимая для использования методов из второй категории, не всегда доступна для исследователей, вследствие чего эти методы не всегда применимы. Поэтому в данной работе рассматриваются только методы из первой категории. Существующее разнообразие приводит к тому, что сам по себе выбор предпочтительного метода оценки ${{M}_{c}}$ перестает быть тривиальным.
В настоящей работе рассмотрены шесть современных методов оценки ${{M}_{c}}$, проанализировано поведение оценок этих методов на синтетических каталогах землетрясений в зависимости от объема выборки и формы исходного распределения числа событий по магнитуде, использованного при создании синтетического каталога. Для анализа вариаций оценок ${{M}_{c}}$ использован метод бутстрап анализа.
МЕТОДЫ ОЦЕНКИ МАГНИТУДЫ ПРЕДСТАВИТЕЛЬНОЙ РЕГИСТРАЦИИ
Оценка ${{M}_{c}}$ в точке максимальной кривизны кумулятивного графика повторяемости землетрясений [Wiemer, Wyss, 2000]. Это самая простая и быстрая процедура оценки ${{M}_{c}}$. На практике точка максимальной кривизны кумулятивного графика повторяемости соответствует магнитуде, на которую приходится максимальное число событий в выборке. Несмотря на простоту и надежность, данная процедура имеет тенденцию занижать значение ${{M}_{c}}$, в особенности в тех случаях, когда дискретный график повторяемости не имеет выраженного максимума. Предположительно, такая форма дискретного графика повторяемости, а именно кривизна непредставительной его части, может указывать на неоднородность анализируемой выборки [Mignan, 2012]. Тем не менее, для однородных выборок такая оценка будет адекватной [Mignan et al., 2011]. Процедура будет обозначаться аббревиатурой MAXC (от Maximum curvature), а соответствующая оценка – $M_{c}^{{{\text{MAXC}}}}$. Пример такой оценки показан на рис. 1.
Оценка ${{M}_{c}}$ посредством расчета критерия согласия [Wiemer, Wyss, 2000]. Данный метод основан на сравнении анализируемой выборки значений магнитуды и созданной на ее основе синтетической выборки. На первом этапе выбирается значение магнитуды нижней отсечки ${{M}_{{co}}}$ (это значение не должно превышать $M_{c}^{{{\text{MAXC}}}}$), по части выборки с магнитудами $m \geqslant {{M}_{{co}}}$ методом максимального правдоподобия оцениваются параметры $a$, $b$ из (1). На основе полученных оценок $a$, $b$ создается синтетическая выборка из распределения Гутенберга–Рихтера. Далее сравниваются кумулятивные графики повторяемости для анализируемой и синтетической выборки и расчитывается критерий согласия:
(4)
$R\left( {a,b,{{M}_{{co}}}} \right) = 100 - \left( {\frac{{\sum\limits_{{{M}_{{co}}}}^{{{M}_{{{\text{max}}}}}} {\left| {{{B}_{i}} - {{S}_{i}}} \right|} }}{{\mathop \sum \nolimits_i {{B}_{i}}}} \times 100} \right),$Величина $R$ показывает, какой процент от объема анализируемой выборки можно описать соотношением (1) при данном значении ${{M}_{{co}}}$. Значение ${{M}_{{co}}}$ повышается на величину $\Delta M$, соответствующую точности определения магнитуды, и вычисления повторяются. В качестве оценки ${{M}_{c}}$ выбирается наименьшее значение ${{M}_{{co}}}$, для которого величина критерия согласия $R$ достигает заданного уровня (обычно это 90 или 95%). Процедура будет обозначаться аббревиатурой GFT (от Goodness-of-fit test), а соответствующая оценка – $M_{c}^{{{\text{GFT}}}}$. Пример применения данной процедуры показан на рис. 2a.
Оценка ${{M}_{c}}$ по стабилизации значений b-value. Данная процедура была предложена в работах [Арефьев и др, 1989; Cao, Gao, 2002], в ее основе лежит наблюдение, согласно которому величина $b$ возрастает при ${{M}_{{co}}} < {{M}_{c}}$ и при ${{M}_{{co}}} \gg {{M}_{c}}$, но остается практически неизменной при ${{M}_{{co}}} \geqslant {{M}_{c}}$. Соответственно, в качестве оценки ${{M}_{c}}$ можно взять магнитуду, для которой разность двух последовательных значений $b$ достаточно мала (например, меньше 0.03). В работе [Woessner, Wiemer, 2005] процедура была доработана и был предложен формализованный критерий стабилизации $b$. Модифицированная процедуры выполняется следующим образом: для некоторого диапазона значений ${{M}_{{co}}}$ по формуле (3) оцениваются значения $b$ и рассчитываются среднеквадратичные ошибки этих оценок ${{\sigma }_{b}}$ по формуле [Shi, Bolt, 1982]:
(5)
${{\sigma }_{b}} = \frac{{{{b}^{2}}}}{{{{{\lg }}_{{10}}}\left( e \right)}}\sqrt {\frac{{\sum\limits_{i = 1}^N {{{{\left( {{{M}_{i}} - \bar {M}} \right)}}^{2}}} }}{{N\left( {N - 1} \right)}}} ,$Затем в окне шириной $dM = 5\Delta M$ рассчитываются усредненные значения $b$:
(6)
$\bar {b} = \mathop \sum \limits_{{{M}_{{co}}}}^{{{M}_{{co}}} + 5\Delta M} b{{\left( {{{M}_{{co}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{M}_{{co}}}} \right)} 5}} \right. \kern-0em} 5}.$В качестве оценки ${{M}_{c}}$ выбирается наименьшее значение ${{M}_{{co}}}$, для которого разность между текущим и усредненным значениями $b$ не превосходит среднеквадратичную ошибку оценки этого параметра, т.е. выполняется условие $\Delta b = \left| {\bar {b} - b} \right| \leqslant {{\sigma }_{b}}$. Процедура обозначается аббревиатурой MBS (${{M}_{c}}$ by $b$-value stability), а соответствующая оценка – $M_{c}^{{{\text{MBS}}}}$. Пример применения метода показан на рис. 2б.
Оценка ${{M}_{c}}$ методом медианного анализа последовательности значений сдвигов дискретного графика повторяемости [Amorèse, 2007]. Метод основан на итерационной процедуре поиска точек, в которых происходит излом дискретного графика повторяемости. Для этого в каждой точке ${{M}_{i}}$, ($i > 1$) рассчитывается величина сдвига:
(7)
$s\left( {{{M}_{i}}} \right) = \frac{{{{{\lg }}_{{10}}}\left[ {N\left( {{{M}_{{i - 1}}}} \right)} \right] - {{{\lg }}_{{10}}}\left[ {N\left( {{{M}_{i}}} \right)} \right]}}{{{{M}_{{i - 1}}} - {{M}_{i}}}},$Сдвиги $s\left( {{{M}_{i}}} \right)$ характеризуют направленность и выраженность изменений дискретного графика повторяемости. Каждому значению $s\left( {{{M}_{i}}} \right)$ присваивается ранг ${{R}_{i}}$ так, что наименьшее значение получает минимальный ранг – 1. Затем ранги суммируются в каждой точке $S{{R}_{i}} = \sum\nolimits_{k = 1}^i {{{R}_{k}}} $ и рассчитывается модифицированная сумма рангов $S{{A}_{i}}$:
где $n$ – длина последовательности.Последовательность $S{{A}_{i}}$ достигает максимума в точке ${{n}_{1}}$, это наиболее вероятная точка излома дискретного графика повторяемости. В этой точке последовательность $s\left( {{{M}_{i}}} \right)$ делится на две части: ${{i}_{1}} = 2, \ldots ,{{n}_{1}}$ и ${{i}_{2}} = {{n}_{1}} + 1, \ldots ,n + 1$. Проверяется гипотеза о том, что в точке ${{n}_{1}}$ нет излома дискретного графика повторяемости, против альтернативной гипотезы о том, что излом есть. Решение принимается на основе непараметрического критерия суммы рангов Уилкоксона [Wilcoxon, 1945], также известного как U-критерий Манна–Уитни [Mann, Whitney, 1947]. Если основная гипотеза отвергается при заданном уровне значимости, точка ${{n}_{1}}$ заносится в список и итерации продолжаются. Процедура может обнаружить несколько значимых точек излома (рис. 3), магнитуде ${{M}_{c}}$ соответствует та точка, для которой вероятность ошибки первого рода при проверке гипотезы минимальна. Процедура обозначается аббревиатурой MBASS (Median-based analysis of the segment slope), а соответствующая оценка – $M_{c}^{{{\text{MBASS}}}}$.
Рис. 3.
Метод MBASS: (а) – дискретный и кумулятивный графики повторяемости для выборки из каталога NCSN. Стрелками показаны типичные точки излома графика повторяемости. Точка 2 соответствует магнитуде ${{M}_{c}}$. Бутстрап-распределения (б) основной точки излома (точка 2) и (в) второстепенной точки излома (точки 1 и 3).

Оценка ${{M}_{c}}$ методом моделирования полного диапазона значений магнитуды [Ogata, Katsura, 1993]. Согласно этому методу, для любого значения $m$ наблюдаемую интенсивность потока событий $\lambda \left( m \right)$ можно представить в виде:
где ${{\lambda }_{0}}\left( m \right) = {{e}^{{ - \beta m}}}$ – теоретическая интенсивность, $q\left( m \right)$ – вероятность обнаружения событий, которая задается нормальным распределением:(10)
$q\left( m \right) = \frac{1}{{\sqrt {2\pi } \sigma }}\mathop \smallint \limits_{ - \infty }^m {\text{exp}}\left( {\frac{{ - {{{\left( {x - \mu } \right)}}^{2}}}}{{2{{\sigma }^{2}}}}} \right)dx,$С учетом сделанных предположений в работе [Ogata, Katsura, 1993] была получена функция плотности распределения магнитуды на всем диапазоне ее значений:
(11)
${{f}_{M}}\left( m \right) = \beta {\text{exp}}\left( { - \beta \left( {m - \mu } \right) - {{\beta }^{2}}\frac{{{{\sigma }^{2}}}}{2}} \right)q\left( m \right).$Параметры этой модели оцениваются методом максимального правдоподобия. Магнитуда ${{M}_{c}}$ не входит в модель в явном виде и задается через параметры $\mu $ и $\sigma $: ${{M}_{c}}\left( n \right) = \mu + n\sigma $, $n$ – показатель уровня доверия. При $n = 0$ регистрируются лишь 50% событий с магнитудой $m \geqslant {{M}_{c}}$ при $n = \left( {1,\,\,2,\,\,3} \right)$ регистрируются 84, 98 и 99% событий, соответственно. Вопрос о том, как соотносятся уровни представительности ${{M}_{c}}\left( n \right)$ модели (11) с оценками ${{M}_{c}}$ остальных методов, рассматривался в статье [Mignan, Woessner, 2012], где на синтетических и реальных каталогах землетрясений было показано, что оценки ${{M}_{c}}$ преимущественно попадают в интервал $\left( {\mu ,\mu + \sigma } \right)$, в редких случаях могут достигать уровня $\mu + 2\sigma $, то есть 95%-ой вероятности обнаружения этой модели. Модель (11) обозначается аббревиатурой OK (от Ogata and Katsura), пример применения этой модели показан на рис. 4.
Рис. 4.
Модель OK: дискретный и кумулятивный графики повторяемости для выборки из каталога NCSN. Сплошной линией показана аппроксимация моделью OK, вертикальными штриховыми линиями показаны оценки ${{M}_{c}}\left( n \right)$ для $n = \left( {0,1,2,3} \right)$.

В дальнейшем метод был модифицирован для того, чтобы явно включить в модель ${{M}_{c}}$ [Woessner, Wiemer, 2005]. Была предложена составная модель, в которой нормальное распределение описывает вероятность обнаружения непредставительных событий:
(12)
$q\left( m \right) = \left\{ \begin{gathered} \frac{1}{{\sqrt {2\pi } \sigma }}\mathop \smallint \limits_{ - \infty }^m {\text{exp}}\left( {\frac{{ - {{{\left( {x - \mu } \right)}}^{2}}}}{{2{{\sigma }^{2}}}}} \right)dx\,\,\,\,m < {{M}_{c}} \hfill \\ 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m \geqslant {{M}_{c}} \hfill \\ \end{gathered} \right..$Важно отметить, что для этой модели уравнение (9) не выполняется, интенсивность потока событий задается следующей функцией:
(13)
$\lambda \left( m \right) = \left\{ \begin{gathered} \frac{1}{{\sqrt {2\pi } \sigma }}\mathop \smallint \limits_{ - \infty }^m {\text{exp}}\left( {\frac{{ - {{{\left( {x - \mu } \right)}}^{2}}}}{{2{{\sigma }^{2}}}}} \right)dx\,\,\,\,m < {{M}_{c}} \hfill \\ {\text{exp}}\left( { - \beta \left( {m - {{M}_{c}}} \right)} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m \geqslant {{M}_{c}} \hfill \\ \end{gathered} \right..$Эта модель будет обозначаться аббревиатурой WW (от Woessner and Wiemer), метод будет обозначаться аббревиатурой EMR (от Entire Magnitude Range), а соответствующая оценка – $M_{c}^{{{\text{EMR}}}}$. Параметры ${{\mu }}$ и ${{\sigma }}$ оцениваются методом нелинейной регрессии по данным выборки в диапазоне $m < {{M}_{c}}$, параметры $a$ и $b$ оцениваются методом максимального правдоподобия по данным в диапазоне $m \geqslant {{M}_{c}}$. На основе этих оценок и уравнения (13) рассчитывается теоретический дискретный график повторяемости на всем диапазоне значений магнитуды и оценивается правдоподобие получения такой выборки. Вычисления повторяются для некоторого диапазона значений ${{M}_{c}}$, итоговая оценка берется в максимуме функции правдоподобия. Такой подход дает наиболее всестороннее описание сейсмичности, но является наиболее затратным в плане времени вычислений. Применение метода показано на рис. 5.
Рис. 5.
Метод EMR: (а) – дискретный и кумулятивный графики повторяемости для выборки из каталога NCSN. Серыми кружками показана аппроксимация моделью WW, вертикальная штриховая линия показывает оценку ${{M}_{c}}$; (б) – график зависимости логарифма функции правдоподобия, взятого с минусом, от величины ${{M}_{c}}$, вертикальная штриховая линия показывает оценку ${{M}_{c}}$, взятую в максимуме функции правдоподобия.

Оценка ${{M}_{c}}$ в точке начала линейной части графика повторяемости [Писаренко, 1989; Смирнов, 2009]. Процедура основана на проверке гипотезы о прямолинейности графика повторяемости. На первом этапе выбирается начальное значение магнитуды нижней отсечки ${{M}_{{co}}}$ (это значение не должно превышать $M_{c}^{{{\text{MAXC}}}}$), по части выборки с магнитудами $m \geqslant {{M}_{{co}}}$ методом максимального правдоподобия оцениваются параметры закона повторяемости. Проверяется гипотеза ${{H}_{1}}$ о прямолинейности графика повторяемости в области $m \geqslant {{M}_{{co}}}$ против гипотезы ${{H}_{2}}$ о том, что график повторяемости в этой области нелинейный. Для этого рассчитываются наблюдаемые частоты попадания значений магнитуды в интервалы ${{M}_{i}} \pm {{\Delta M} \mathord{\left/ {\vphantom {{\Delta M} 2}} \right. \kern-0em} 2}$, где ${{M}_{i}} = {{M}_{{co}}} + i\Delta M,$ $i = 0, \ldots ,n$:
где ${{N}_{i}}$ – число событий в интервале ${{M}_{i}} \pm {{\Delta M} \mathord{\left/ {\vphantom {{\Delta M} 2}} \right. \kern-0em} 2}$, ${{Q}_{0}} = \sum\nolimits_{i = 0}^n {{{N}_{i}}} $.И теоретические частоты, соответствующие закону Гутенберга–Рихтера с параметром $\hat {b}$:
(15)
${{\pi }_{i}} = \frac{{{{{10}}^{{ - \hat {b}\left( {{{M}_{i}} - {{M}_{{co}}}} \right)}}}}}{{\sum\limits_{i = 0}^n {{{e}^{{ - \hat {b}\left( {{{M}_{i}} - {{M}_{{co}}}} \right)}}}} }}.$Рассчитывается выборочная статистика, характеризующая отклонение гипотезы ${{H}_{2}}$ от гипотезы ${{H}_{1}}$:
(16)
$\hat {I} = \mathop \sum \limits_{i = 0}^n {{p}_{i}}\ln \left( {\frac{{{{p}_{i}}}}{{{{\pi }_{i}}}}} \right).$Если верна гипотеза ${{H}_{1}}$, то величина $2{{Q}_{0}}\hat {I}$ имеет асимптотически при ${{Q}_{0}} \to \infty $ распределение ${{{{\chi }}}^{2}}$ с $\left( {n - 1} \right)$ степенью свободы. Для проверки гипотезы ${{H}_{1}}$ определяется уровень значимости $\mu $ величины $2{{Q}_{0}}\hat {I}$. Если $\mu $ меньше заданного уровня (например, 0.01 или 0.05), то гипотеза ${{H}_{1}}$ отвергается. В этом случае на следующем этапе решается вопрос о причинах нелинейности графика повторяемости. Если же гипотеза ${{H}_{1}}$ принимается, то ${{M}_{{co}}}$ – искомая оценка ${{M}_{c}}$ и процедура на этом завершается.
Вероятность регистрации землетрясений с $m = {{M}_{{co}}}$ обозначается как $p$, если $p = 1$ регистрация представительна, если $p < 1$ имеются пропуски землетрясений с $m = {{M}_{{co}}}$. Для решения вопроса о представительности регистрации землетрясений с $m = {{M}_{{co}}}$ строится оценка максимального правдоподобия $\hat {p}$ для $p$ и проверяется гипотеза об отличии этой оценки от 1. Оценка $\hat {p}$ определяется отношением наблюденной величины ${{N}_{0}}$ к оценке числа событий с $m = {{M}_{{co}}}$, построенной по старшим магнитудам с $m \geqslant {{M}_{{co}}} + \Delta M$. Пусть $\tilde {b}$ – оценка максимального правдоподобия, полученная по части выборки с $m \geqslant {{M}_{{co}}} + \Delta M$, ${{\tilde {x}}^{i}} = {{10}^{{ - \tilde {b}\left( {{{M}_{i}} - {{M}_{{co}}}} \right)}}}$. Тогда оценка $\hat {p}$ имеет вид:
а ее асимптотическая дисперсия оценивается как:(18)
$Var\left( {\hat {p}} \right) = \frac{{{{N}_{0}}\psi _{0}^{2}}}{{{{{\left( {{{Q}_{0}} - {{N}_{0}}} \right)}}^{2}}}} + \frac{{N_{0}^{2}\psi _{0}^{3}{{\psi }_{2}}}}{{{{{\left( {{{Q}_{0}} - {{N}_{0}}} \right)}}^{3}}{{{\left( {{{\psi }_{0}}{{\psi }_{2}} - \psi _{1}^{2}} \right)}}^{2}}}},$Для проверки гипотезы ${{H}_{0}}$ о представительной регистрации землетрясений с $m = {{M}_{{co}}}$ рассчитывается величина $t = \frac{{1 - \hat {p}}}{{{{{\left( {Var\left( {\hat {p}} \right)} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$, имеющая распределение Стьюдента, и определяется ее уровень значимости ${{{{\mu }}}_{0}}$. Гипотеза ${{H}_{0}}$ отвергается если ${{{{\mu }}}_{0}} \geqslant 1 - {{\varepsilon }}$, где ${{\varepsilon }}$ – некоторое малое число (например 0.05 или 0.1). В этом случае значение ${{M}_{{co}}}$ повышается на $\Delta M$ и вся процедура повторяется. Если гипотеза ${{H}_{0}}$ принимается, то ${{M}_{{co}}}$ – искомая оценка ${{M}_{c}}$. Метод будет обозначаться аббревиатурой LLS (от Lower end of linear segment), а соответствующая оценка – $M_{c}^{{{\text{LLS}}}}$. Пример применения метода показан на рис. 6.
Рис. 6.
Метод LLS. Треугольниками показаны уровни значимости статистики $2{{Q}_{0}}\hat {I}$, кружками показаны уровни значимости величины $t$, вертикальная штриховая линия показывает оценку ${{M}_{c}}$. При ${{M}_{{co}}} < 1.4$ гипотеза ${{H}_{1}}$ отвергается с высоким уровнем значимости. При ${{M}_{{co}}} < 1.2$ гипотеза ${{H}_{0}}$ также отвергается, но при ${{M}_{{co}}} = 1.2$ уже нет достаточных оснований считать, что регистрация событий непредставительная, это значение принимается в качестве оценки ${{M}_{c}}$.

Бутстрап [Efron, Tibshirani, 1993] – непараметрический метод исследования распределений искомых параметров, основанный на многократном извлечении методом Монте-Карло повторных выборок из имеющейся выборки. Метод позволяет быстро и просто оценивать разнообразные статистики (например, дисперсию, доверительные интервалы) для сложных моделей. Суть метода состоит в том, что из имеющейся выборки случайным выбором с повторением формируется некоторое множество ${{n}_{b}}$ повторных выборок заданного размера. На множестве повторных выборок оцениваются искомые параметры и по полученным эмпирическим распределениям определяются все необходимые статистики.
В частности, бутстрап применялся для анализа дисперсии оценок ${{M}_{c}}$ в работах [Woessner, Wiemer, 2005; Amorèse, 2007; Mignan et al., 2011; Mignan, Woessner, 2012]. В книге [Chernick, 1999] в качестве рекомендованного числа повторных выборок, достаточного для надежной оценки дисперсии, приводится цифра ${{n}_{b}} = 100$, однако при наличии достаточных вычислительных мощностей автор рекомендует использовать ${{n}_{b}} = 1000$. В работе [Woessner, Wiemer, 2005] авторы отмечают, что оценки дисперсии ${{M}_{c}}$ стабилизируются при ${{n}_{b}} \geqslant 200$. Эту рекомендацию использовали в работах [Mignan et al., 2011; Mignan, Woessner, 2012]. В работе [Amorèse, 2007] автор использовал ${{n}_{b}} = 1000$ повторных выборок. В настоящей работе бутстрап применяется с ${{n}_{b}} = 500$ повторных выборок.
АНАЛИЗ ПРЕДСТАВИТЕЛЬНОСТИ ВЫБОРОК ИЗ ИНСТРУМЕНТАЛЬНЫХ КАТАЛОГОВ ЗЕМЛЕТРЯСЕНИЙ
Все описанные процедуры были программно реализованы В.А. Павленко в MATLAB. В качестве проверки корректности работы процедур была предпринята попытка воспроизвести результаты, полученные в работах [Woessner, Wiemer, 2005; Amorèse, 2007]. Для этого были взяты те же выборки из каталогов землетрясений, которые использовали авторы этих работ в качестве демонстрационного материала:
1. Выборка из регионального каталога Швейцарской сейсмологической службы, the Earthquake Catalog of Switzerland (ECOS; http://ecos09.seismo.ethz.ch/query) за 1992–2002 гг.
2. Выборка из глобального каталога the Global Centroid Moment Tensor Catalog (CMT; https://www.globalcmt.org/CMTsearch) за 1983–2002 гг.
3. Выборка из регионального каталога землетрясений Северной Калифорнии, the Northern California Seismic Network (NCSN; https://www.ncedc.org/ncedc/catalog-search) за 1998–2000 гг.
4. Выборка из каталога землетрясений вулканической зоны сейсмичности Канто, the National Research Institute for Earth Science and Disaster Prevention Earthquake Catalog (NIED; http://evrrss.eri.u-tokyo.ac.jp/db/nied) за 1992–2002 гг.
Параметры получившихся выборок сведены в табл. 1, построенные по выборкам графики повторяемости показаны на рис. 7. Сравнение графиков повторяемости и объемов выборок с представленными в работах [Woessner, Wiemer, 2005; Amorèse, 2007], показывает, что ни одна из полученных выборок не совпадает в полной мере с теми выборками, которые использовали эти авторы. Вероятнее всего, причиной различий стали изменения, внесенные в каталоги со времени публикации этих работ.
Рис. 7.
Графики повторяемости, построенные по выборкам из каталогов: (a) – The Earthquake Catalog of Switzerland за 1992–2002 гг.; (б) – The Global Centroid Moment Tensor Catalog за 1983–2002 гг.; (в) – The Northern California Seismic Network за 1998–2000 гг.; (г) – The National Research Institute for Earth Science and Disaster Prevention Earthquake Catalog за 1992–2002 гг.

По каждой выборке с помощью описанных процедур и метода бутстрап оценивались средние значения и дисперсии оценок ${{M}_{c}}$. Полученные результаты представлены в табл. 1. Результаты для выборок из каталогов ECOS, NCSN и NIED хорошо согласуются с результатами, представленными в работах [Woessner, Wiemer, 2005; Amorèse, 2007]. Оценки ${{M}_{c}}$, полученные по выборке из каталога CMT, существенно отличаются от тех оценок, которые представлены в работе [Woessner, Wiemer, 2005], но это расхождение, по всей видимости, обусловлено различиями выборочных данных.
Таблица 1.
Параметры выборок из инструментальных каталогов землетрясений, оценки магнитуды ${{M}_{c}}$, оценки параметров и модели WW
| Каталог | ECOS | CMT | NCSN | NIED |
|---|---|---|---|---|
| Объем выборки | 988 | 16 472 | 19 833 | 31 372 |
| Диапазон значений магнитуды | 0.4–4.2 | 4.3–8.5 | 0.1–5.5 | 0.0-5.1 |
| Границы по долготе | 6.8°–8.4° в.д. | 120.5°–123° з.д. | 138.95°–139.35° в.д. | |
| Границы по широте | 45.9°–46.65° с.ш. | 36.0°–39.0° с.ш. | 34.8°–35.05° с.ш. | |
| Начало выборки | 01.01.1992 | 01.01.1983 | 01.01.1998 | 01.01.1992 |
| Окончание выборки | 31.12.2002 | 31.12.2002 | 31.12.2000 | 31.12.2002 |
| $M_{c}^{{{\text{MAXC}}}}$ | 1.37 ± 0.06 | 5.15 ± 0.06 | 1.20 ± 0.00 | 1.20 ± 0.01 |
| $M_{c}^{{{\text{GFT}}}}$ | 1.54 ± 0.16 | 5.20 ± 0.01 | 1.11 ± 0.03 | 1.35 ± 0.06 |
| $M_{c}^{{{\text{MBS}}}}$ | 1.66 ± 0.13 | 5.42 ± 0.06 | 1.46 ± 0.16 | 1.98 ± 0.10 |
| $M_{c}^{{{\text{MBASS}}}}$ | 1.39 ± 0.27 | 5.39 ± 0.07 | 1.20 ± 0.00 | 1.39 ± 0.10 |
| $M_{c}^{{{\text{EMR}}}}$ | 1.55 ± 0.14 | 5.31 ± 0.07 | 1.20 ± 0.03 | 1.27 ± 0.05 |
| $M_{c}^{{{\text{LLS}}}}$ | 1.55 ± 0.15 | 5.44 ± 0.05 | 1.20 ± 0.01 | 1.84 ± 0.15 |
| ${{\mu }}$ | 0.93 | 4.87 | 0.84 | 0.62 |
| ${{\sigma }}$ | 0.16 | 0.08 | 0.22 | 0.26 |
В этих результатах проявляются некоторые характерные особенности рассматриваемых методов: методы MAXC и GFT обычно дают самые низкие оценки ${{M}_{c}}$, оценки метода MBS обычно оказываются наиболее консервативными. Оценки остальных методов занимают промежуточные позиции.
Из табл. 1 видно, что для всех методов, кроме метода MBS, дисперсии оценок ${{M}_{c}}$, полученных по выборкам из каталогов NCSN и CMT, оказывались минимальными или близкими к минимальным. Форма распределения выборки из каталога NCSN близка к характерной угловой форме с выраженным максимумом, которая присуща выборкам с равномерным уровнем регистрации. Распределение выборки из каталога CMT имеет сглаженный максимум, для этой выборки разброс оценок ${{M}_{c}}$ заметно выше, чем для выборки из каталога NCSN.
Распределения выборок из каталогов ECOS и NIED имеют сглаженную форму с заметной кривизной непредставительной части дискретного графика повторяемости, которая может свидетельствовать о неоднородности выборочных данных. В целом это приводит и к возрастанию дисперсий оценок ${{M}_{c}}$ и к более значительным различиям в оценках ${{M}_{c}}$, полученных разными методами.
Полученные результаты демонстрируют чувствительность методов оценки ${{M}_{c}}$ к форме распределения анализируемой выборки. Этот эффект более детально рассмотрен на синтетических каталогах землетрясений в следующих секциях.
МОДЕЛИ РАСПРЕДЕЛЕНИЯ МАГНИТУДЫ
Создание синтетического каталога землетрясений требует применения модели распределения магнитуды, позволяющей описать как представительную, так и непредставительную часть каталога. Помимо уже упоминавшихся моделей OK и WW, существуют еще две модели распределения, подходящие для этих целей.
Модель, предложенная в работе [Mignan, 2012], описывает элементарный график повторяемости, построенный по выборке значений магнитуды, в которой пространственно-временные неоднородности ${{M}_{c}}$ сведены к минимуму. Вероятность обнаружения событий при $m < {{M}_{c}}$ изменяется по экспоненте:
(19)
$q\left( m \right) = \left\{ \begin{gathered} {\text{exp}}\left( {\kappa \left( {m - {{M}_{c}}} \right)} \right)\,\,\,\,m < {{M}_{c}} \hfill \\ 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m \geqslant {{M}_{c}} \hfill \\ \end{gathered} \right.,$В статье [García-Hernández et al., 2019] авторы предложили модель, в которой вероятность обнаружения событий задается полиномом второй степени (модель POL):
(20)
$q\left( m \right) = \left\{ \begin{gathered} 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m \leqslant {{M}_{i}} \hfill \\ 1 - {{\left( {\frac{{m - {{M}_{c}}}}{{{{M}_{c}} - {{M}_{i}}}}} \right)}^{2}}\,\,\,\,\,{{M}_{i}} < m < {{M}_{c}} \hfill \\ 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m \geqslant {{M}_{c}} \hfill \\ \end{gathered} \right.,$Такая форма распределения характерна для ранних периодов инструментальных наблюдений, когда ввиду сравнительно невысокой чувствительности приборов слабые события не регистрировались. Обе модели AN и POL подчиняются уравнению (9).
Авторы работы [García-Hernández et al., 2019] проанализировали формы выборочных распределений магнитуды в зависимости от объема выборки и радиуса области, из которой выбирались землетрясения. Для анализа были использованы данные Международного Сейсмологического Центра [ISC; www.isc.ac.uk/iscbulletin/search/catalogue/; Storchak et al., 2013], модели оценивались по критерию согласия Колмогорова и информационному критерию Акаике [Akaike, 1974]. Результаты этого исследования показали, что для всех моделей степень согласия с данными снижалась с возрастанием объема выборки, но практически не зависела от радиуса области выборки событий. Выраженное снижение согласия с данными наблюдалось для выборок, содержащих более 1000 событий. В целом модель OK чаще других оказывалась наилучшей в плане аппроксимации данных; модель AN показывала хорошие результаты для малых выборок объемом 100–300 событий; модель WW показывала хорошие результаты для более объемных выборок, включающих 1000–3000 событий; модель POL оказалась существенно хуже, показав относительно неплохой результат только для выборок объемом 100 событий.
Таким образом, для создания синтетических каталогов были выбраны модели WW, AN и POL. Модель WW описывает наиболее распространенную ситуацию, при которой выборка значений магнитуды неоднородна по ${{M}_{c}}$. Модель AN описывает выборку, в которой неоднородности ${{M}_{c}}$ сведены к минимуму. Модель POL описывает выборку, из которой удалены слабые землетрясения с магнитудами $m \leqslant {{M}_{i}}$. Различие этих трех моделей продемонстрировано на рис. 8.
Рис. 8.
Примеры случайных выборок объемом по 1000 событий из синтетических каталогов, демонстрирующие разницу формы графиков повторяемости, получаемых при использовании трех описанных в тексте моделей распределения магнитуды: (a) модель WW с параметрами ${{M}_{c}} = 1$, $b = 1$, $\mu = 0.5$, $\sigma = 0.2$; (б) модель AN с параметрами ${{M}_{c}} = 1$, $b = 1$, $k = 4$; (в) модель POL с параметрами ${{M}_{c}} = 1$, $b = 1$, ${{M}_{i}} = 0.7$.

ТЕСТИРОВАНИЕ МЕТОДОВ ОЦЕНКИ ${{M}_{c}}$ НА СИНТЕТИЧЕСКИХ КАТАЛОГАХ ЗЕМЛЕТРЯСЕНИЙ
При выборе значений параметров модели WW учитывались их оценки, полученные по выборкам из каталогов ECOS, CMT, NCSN и NIED (табл. 1). Из этих результатов видно, что магнитуда $\mu $ располагается примерно посередине между минимальной магнитудой в выборке и оценкой $~M_{c}^{{{\text{EMR}}}}$, а ${{\sigma }}$ имеет величину порядка 0.1–0.3.
Выборки из каталогов ECOS и NIED имеют типичную для модели WW форму распределения (рис. 7а, 7г). При фиксированном ${{\mu }}$, снижение ${{\sigma }}$ приводит к тому, что левый хвост распределения приобретает более крутой наклон, максимум распределения сглаживается, форма распределения приближается к форме выборки из каталога CMT (рис. 7б). При смещении ${{\mu }}$ ближе к ${{M}_{c}}$ при фиксированном ${{\sigma }}$ форма распределения становится близка к форме выборки из каталога NCSN (рис. 7в) с острым максимумом и крутым наклоном левого хвоста распределения.
На основе этих трех вариантов формы распределения WW были выбраны следующие комбинации значений параметров для создания синтетических каталогов: ${{{{\mu }}}_{1}} = 0.5,~\,\,{{{{\sigma }}}_{1}} = 0.25$ (такие значения параметров использовали для создания синтетического каталога авторы [Woessner, Wiemer, 2005]), ${{\mu }_{2}} = 0.5,\,\,~{{\sigma }_{2}} = 0.1$ и ${{\mu }_{3}} = 0.75,~\,\,{{\sigma }_{3}} = 0.25$.
В работе [Mignan, 2012] приводятся оценки параметра $k$ модели AN, полученные по данным каталогов землетрясений Невады и Южной Калифорнии. Для Невады оценки $k$ лежат в пределах от 1.4 до 5.4, максимум плотности распределения приходится на $\hat {k} = 3$, для Южной Калифорнии оценки лежат в пределах от 2 до 5 с максимумом плотности при $\hat {k} = 2.9$. По выборке из каталога NCSN была получена оценка максимального правдоподобия $\hat {k} = 2.95$. С повышением $k$ наклон левого хвоста распределения становится все более крутым, а число событий в непредставительной части распределения снижается. Для создания синтетических каталогов с распределением AN были использованы значения ${{k}_{1}} = 2$, ${{k}_{2}} = 3$, ${{k}_{3}} = 4$.
Значения параметра ${{M}_{i}}$ модели POL были заданы произвольно: ${{M}_{{i1}}} = 0.5$, ${{M}_{{i2}}} = 0.6$, ${{M}_{{i3}}} = 0.7$.
Для представительной части каталогов для всех трех моделей распределения магнитуды были заданы значения параметров ${{M}_{c}} = 1$, $b = 1$. Для каждой модели и для каждой комбинации значений параметров был сгенерирован синтетический каталог объемом 10 000 событий.
Далее по синтетическим каталогам с помощью метода бутстрап оценивались зависимости двух первых моментов распределений ${{M}_{c}}$ от объема выборки $N$. Объем выборки варьировался в диапазоне от ${{N}_{{{\text{min}}}}} = 20$ до ${{N}_{{{\text{max}}}}} = 2000$. Нижняя граница диапазона соответствует минимальному объему выборки, позволяющему применять описанные процедуры оценки ${{M}_{c}}$. Верхняя граница выбиралась как достаточно большое значение объема выборки, позволяющее оценить асимптотические свойства оценок ${{M}_{c}}$ при $N \to \infty $.
Как известно, состоятельной называется оценка, которая сходится по вероятности к оцениваемому параметру. Признаком состоятельной оценки служит асимптотическая несмещенность и убывание дисперсии с ростом объема выборки. Таким образом, от оценок ${{M}_{c}}$ ожидалось, что с ростом объема выборки средние значения будут приближаться к истинному значению ${{M}_{c}}$, а их дисперсии будут снижаться.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Результаты тестирования методов оценки ${{M}_{c}}$ на синтетических каталогах показаны на рис. 9–рис. 11. На этих рисунках слева направо по столбцам показаны результаты для каталогов с номерами 1, 2, 3. Сверху вниз по строкам показаны результаты для методов MAXC, GFT, MBS, MBASS, EMR и LLS. На графиках горизонтальной сплошной чертой показано истинное значение ${{M}_{c}}$, точками показаны средние значения оценок ${{M}_{c}}$, пунктирными линиями обозначены границы одного стандартного отклонения от среднего.
Рис. 9.
Результаты тестирования методов оценки ${{M}_{c}}$ на синтетических каталогах землетрясений, сгенерированных на основе модели WW. Слева направо по столбцам показаны результаты для каталогов с номерами 1, 2, 3. Сверху вниз по строкам показаны результаты для методов MAXC, GFT, MBS, MBASS, EMR и LLS. На графиках горизонтальной чертой показано истинное значение ${{M}_{c}}$, точками показаны средние значения оценок ${{M}_{c}}$, пунктирными линиями обозначены границы одного стандартного отклонения от среднего.

Рис. 10.
Результаты тестирования методов оценки ${{M}_{c}}$ на синтетических каталогах землетрясений, сгенерированных на основе модели AN.
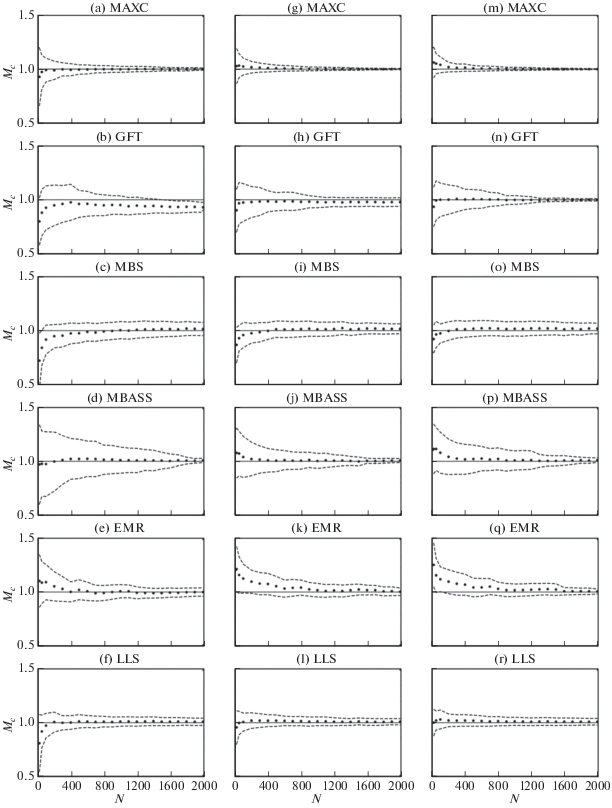
Рис. 11.
Результаты тестирования методов оценки ${{M}_{c}}$ на синтетических каталогах землетрясений, сгенерированных на основе модели POL.

Результаты для модели WW показаны на рис. 9. Оценка $M_{c}^{{{\text{MAXC}}}}$ для каталога WW1 медленно сходится к истинному значению ${{M}_{c}}$ и, следовательно, является состоятельной. Оценка $M_{c}^{{{\text{MAXC}}}}$ для каталога WW3 также является состоятельной. Оценка $M_{c}^{{{\text{MAXC}}}}$ для каталога WW2 недооценивает истинное значение ${{M}_{c}}$ на величину порядка 0.12 и имеет неубывающую дисперсию в силу особенностей формы распределения.
Оценка $M_{c}^{{{\text{GFT}}}}$ для всех трех каталогов WW имеет при $N \to \infty $ асимптотическое смещение размером порядка –0.1, –0.11 и –0.05 соответственно. Методы MBS и LLS дают схожие результаты, оба метода несколько недооценивают ${{M}_{c}}$ на малых выборках, но с ростом $N$ оценки постепенно сходятся к истинному значению ${{M}_{c}}$.
Результаты метода MBASS очень похожи на результаты метода MAXC, однако оценка $M_{c}^{{{\text{MBASS}}}}$ для каталога WW2 все же оказывается состоятельной. Метод EMR дает состоятельные оценки ${{M}_{c}}$ для каталогов WW1 и WW2. Оценка $M_{c}^{{{\text{EMR}}}}$ для каталога WW3 переоценивает ${{M}_{c}}$ на малых выборках, но с ростом $N$ постепенно сходится к истинному значению ${{M}_{c}}$.
Результаты для модели AN показаны на рис 10. Метод MAXC дает состоятельные оценки ${{M}_{c}}$ для всех трех каталогов AN. Метод GFT занижает значение ${{M}_{c}}$ для каталогов AN1 и AN2 на величину порядка 0.08 и 0.02 соответственно. Для каталога AN3 метод GFT дает состоятельную оценку ${{M}_{c}}$. Методы MBS и LLS вновь демонстрируют схожие результаты, однако оценка $M_{c}^{{{\text{MBS}}}}$ для всех трех каталогов AN имеет при $N \to \infty $ малое асимптотическое смещение размером порядка 0.02.
Оценки $M_{c}^{{{\text{MBASS}}}}$ в среднем соответствуют оценкам $M_{c}^{{{\text{MAXC}}}}$, но имеют более высокую дисперсию. Для всех трех каталогов AN метод EMR переоценивает ${{M}_{c}}$ на малых выборках, но с ростом $N$ оценка $M_{c}^{{{\text{EMR}}}}$ постепенно сходится к истинному значению ${{M}_{c}}$. Результаты слабо зависят от параметра $k$.
Результаты для модели POL показаны на рис. 11. Описанные методы оказываются не в состоянии корректно определить значение ${{M}_{c}}$ для модели POL. Особенно ярко это демонстрируют результаты метода MBASS, который катастрофически завышает значение ${{M}_{c}}$ для всех трех каталогов POL. Ни одна из оценок не является состоятельной. Результаты слабо зависят от параметра ${{M}_{i}}$.
Полученные результаты показывают, что все описанные методы хорошо справляются с задачей определения ${{M}_{c}}$ для модели AN, имеющей резкий переход между непредставительной и представительной частями выборки. Несколько хуже это получается в случае модели WW, со сглаженным максимумом распределения. Наконец, в случае модели POL, у которой этот переход практически никак не выражен, описанные методы оказываются не в состоянии корректно определить ${{M}_{c}}$.
С одной стороны, такой результат подсказывает, что следует с особым вниманием подходить к анализу представительности данных, относящихся к началу инструментальных каталогов. С другой стороны, наблюдения [García-Hernández et al., 2019], согласно которым модель POL в реальных каталогах встречается достаточно редко, дают надежду на то, что, возможно, на практике с таким распределением сталкиваться не придется.
Метод MAXC оказывается незаменимым при анализе представительности выборок из малых пространственно-временных объемов, для которых характерной является форма распределения AN. Это единственный метод, применимый для анализа представительности выборок экстремально малого объема $N \geqslant 4$ [Mignan et al., 2011]. Этот метод применялся для создания карт пространственных вариаций ${{M}_{c}}$ высокого разрешения на Тайване [Mignan et al., 2011]. Для более объемных выборок, включающих сотни и более событий, в которых максимум распределения магнитуды обычно сглажен, метод MAXC занижает ${{M}_{c}}$ и не рекомендуется к использованию.
Методы GFT и MBS – несложные методы, дающие реалистичные оценки ${{M}_{c}}$. Подходят для анализа представительности выборок среднего размера, содержащих от нескольких сотен до нескольких тысяч событий. Метод GFT применялся для картирования ${{M}_{c}}$ на Аляске, в Западных США и Японии [Wiemer, Wyss, 2000]. Учитывая, что метод GFT, как правило, дает более мягкую оценку ${{M}_{c}}$, а метод MBS – более консервативную, следует выбирать один из них, основываясь на тех требованиях к полноте каталога, которые предъявляет поставленная задача. Применять эти методы к более объемным выборкам следует с большой осторожностью.
Метод MBASS не обладает преимуществами перед более простым непараметрическим методом MAXC. В тех случаях, когда метод MBASS корректно определяет ${{M}_{c}}$, оценки оказываются близки к тем, что дает метод MAXC. При этом дисперсия оценок $M_{c}^{{{\text{MBASS}}}}$ как правило оказывается выше. По этой причине метод MBASS не рекомендуется к использованию.
Метод EMR долгое время позиционировался как лучший метод для анализа представительности каталогов землетрясений. В частности, он применялся для картирования значений ${{M}_{c}}$ по мировым каталогам ISC и CMT [Woessner, Wiemer, 2005], а также по каталогам землетрясений Южной Калифорнии [Hutton et al., 2010] и Японии [Nanjo et al., 2010]. Однако в итоге сами авторы метода EMR признали его неудачным [Mignan, Woessner, 2012] и призвали отказаться от его дальнейшего использования.
Метод LLS демонстрирует замечательные результаты: оценки $M_{c}^{{{\text{LLS}}}}$ достаточно быстро сходятся к истинному значению ${{M}_{c}}$ и имеют сравнительно невысокую дисперсию. Этот метод был внедрен в практику в организациях ЕГС РАН и применялся для картирования пространственно-временных неоднородностей ${{M}_{c}}$ по каталогам землетрясений Новой Зеландии, Греции, Камчатки, Кавказа, Киргизии и Северного Китая [Smirnov, 1998]. При этом, судя по публикациям, этот метод остается практически неизвестным за рубежом. Метод LLS можно использовать для анализа представительности выборок среднего и большого размера.
В заключение стоит отметить, что картирование ${{M}_{c}}$ в областях с высокими вариациями уровня регистрации, таких как Камчатка или Япония, должно опираться на анализ локальных распределений магнитуды, как было сделано, например, в работе [Mignan, 2012].
ВЫВОДЫ
В работе выполнен сравнительный анализ шести методов оценки магнитуды представительной регистрации землетрясений ${{M}_{c}}$. Для сравнения методов использовались как выборки из реальных инструментальных каталогов, так и синтетические каталоги землетрясений, сгенерированные на основе трех моделей распределения магнитуды. Для создания синтетических каталогов были использованы модели, соответствующие выборочным распределениям, встречающимся при анализе реальных данных инструментальных каталогов: модель неоднородной выборки, модель однородной выборки, модель выборки, из которой удалены слабые землетрясения. Показано, что результаты применения описанных методов оценки ${{M}_{c}}$ в значительной мере зависят от формы распределения и объема анализируемой выборки. По результатам анализа сформулированы рекомендации по выбору подходящих методов оценки ${{M}_{c}}$.
Список литературы
Гусев А.А. Прогноз землетрясений по статистике сейсмичности. Сейсмичность, сейсмический прогноз, свойства верхней мантии и их связь с вулканизмом на Камчатке. М.: Наука. 1974. С. 109–119.
Завьялов А.Д. Наклон графика повторяемости как предвестник сильных землетрясений на Камчатке. Прогноз землетрясений. 1984. С. 173–184.
Завьялов А.Д. Среднесрочный прогноз землетрясений: основы, методика, реализация. М.: Наука. 2006. 254 с.
Писаренко В.Ф. Дискретные свойства геофизической среды. О законе повторяемости землетрясений. М.: Наука. 1989. С. 47–60.
Смирнов В.Б., Габсатарова И.П. Представительность каталога землетрясений Северного Кавказа: расчетные данные и статистические оценки // Вестник ОГГГГН РАН. 2000. № 4. С. 83–99.
Смирнов В.Б. Прогностические аномалии сейсмического режима. Методические основы подготовки исходных данных // Геофизические исследования. 2006. № 2. С. 7–22.
Akaike H. A new look at the statistical model identification // IEEE Trans Autom Control. 1974. V. 19. № 6. P. 716–723. https://doi.org/10.1109/TAC.1974.1100705
Aki K. Maximum likelihood estimate of b in the formula logN = a – bM and its confidence limits // Bull. Earthq. Res. Inst. Univ. Tokyo. 1965. V. 43. P. 237–239.
Amorèse D. Applying a change-point detection method on frequency-magnitude distributions // Bull. Seismol. Soc. Am. 2007. V. 97. № 5. P. 1742–1749. https://doi.org/10.1785/0120060181
Bender B. Maximum likelihood estimation of b-values for magnitude grouped data // Bull. Seismol. Soc. Am. 1983. V. 73. № 3. P. 831–851.
Bengoubou-Valérius M., Gibert D. Bootstrap determination of the reliability of b-values: an assessment of statistical estimators with synthetic magnitude series // Nat. Hazards. 2013. V. 65. № 1. P. 443–459. https://doi.org/10.1007/s11069-012-0376-1
Cao A.M., Gao S.S. Temporal variation of seismic b-values beneath northeastern Japan island arc // Geophys. Res. Lett. 2002. V. 29. №9. P. 48–1–48–3. https://doi.org/10.1029/2001GL013775
Chen K.-P., Tsai Y.-B., Amorèse D., Chang W.-Y. Incorporating change-point detection updates of frequency-magnitude distributions within the Taiwan earthquake catalog // Terr. Atmos. Ocean. Sci. 2011. V. 22. № 3. P. 261–269. https://doi.org/10.3319/TAO.2010.09.17.01(T)
Chernick M.R. Bootstrap methods: a practitioner’s guide. Wiley and Sons. 1999. 288 p.
Efron B., Tibshirani R. An introduction to the bootstrap. Chapman and Hall. 1993. 436 p.
García-Hernández R., D’Auria L., Barrancos J., Padilla G.D. On the functional expression of frequency-magnitude distributions: a comprehensive statistical examination // Bull. Seismol. Soc. Am. 2019. V. 109. № 1. P. 482–486. https://doi.org/10.1785/0120180197
Gibowicz S.J. Variation of the frequency-magnitude relation during earthquake sequences in New Zealand // Bull. Seismol. Soc. Am. 1973. V. 63. № 2. P. 517–528.
Goldstein M.L., Morris S.A., Yena G.G. Problems with fitting to the power-law distribution // Eur. Phys. J. B. 2004. V. 41. № 2. P. 255–258. https://doi.org/10.1140/epjb/e2004-00316-5
Gomberg J. Seismicity and detection/location threshold in the Southern Great Basin seismic network // J. Geophys. Res. 1991. V. 96. № B10. P. 16401–16414. https://doi.org/10.1029/91JB01593
Gutenberg B. Richter C.F. Frequency of earthquakes in California // Bull. Seismol. Soc. Am. 1944. V. 34. № 4. P. 185–188.
Guttorp P. On least-squares estimation of b values // Bull. Seismol. Soc. Am. 1987. V. 77. № 6. P. 2115–2124.
Hutton K., Woessner J., Hauksson E. Earthquake monitoring in Southern California for seventy seven years (1932–2008) // Bull. Seismol. Soc. Am. 2010. V. 100. № 2. P. 423–446. https://doi.org/10.1785/0120090130
Mann H.B., Whitney D.R. On a test of whether one of two random variables is stochastically larger than the other // Ann. Math. Statist. 1947. № 18. P. 50–60.
Marzocchi W., Sandri L. A review and new insights on the estimation of the b-value and its uncertainty // Ann. Geophys. 2003. V. 46. № 6. P. 1271–1282. https://doi.org/10.4401/ag-3472
Mignan A., Woessner J. Estimating the magnitude of completeness for earthquake catalogs // Community Online Resource for Statistical Seismicity Analysis. 2012. https://doi.org/10.5078/corssa-00180805
Mignan A. Functional shape of the earthquake frequency-magnitude distribution and completeness magnitude // J. Geophys. Res. 2012. V. 117. № B08302. https://doi.org/10.1029/2012JB009347
Mignan A., Werner M. J., Wiemer S., Chen C.-C., Wu Y.-M. Bayesian estimation of the spatially varying completeness magnitude of earthquake catalogs // Bull. Seismol. Soc. Am. 2011. V. 101. № 3. P. 1371–1385. https://doi.org/10.1785/0120100223
Nanjo K. Z., Ishibe T., Tsuruoka H., Schorlemmer D., Ishigaki Y., Hirata N. Analysis of the completeness magnitude and seismic network coverage of Japan // Bull. Seismol. Soc. Am. 2010. V. 100. № 6. https://doi.org/10.1785/0120100077
Nuannin P., Kulhanek O., Persson L. Spatial and temporal b value anomalies preceding the devastating off coast of NW Sumatra earthquake of December 26, 2004 // Geophys. Res. Lett. 2005. V. 32. № L11307. https://doi.org/10.1029/2005GL022679
Ogata Y., Katsura K. Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogs. // Geophys. J. Int. 1993. V. 113. P. 727–738.
Ringdal F. On the estimation of seismic detection thresholds // Bull. Seismol. Soc. Am. 1975. V. 65. № 6. P. 1631–1642.
Rydelek P.A., Sacks I.S. Testing the completeness of earthquake catalogues and the hypothesis of self-similarity // Nature. 1989. 337. P. 251–253. https://doi.org/10.1038/337251a0
Shi Y., Bolt B.A. The standard error of the magnitude-frequency b-value // Bull. Seismol. Soc. Am. 1982. V. 72. № 5. P. 1677–1687.
Smirnov V.B. Earthquake catalogs: evaluation of data completeness // Volc. Seism. 1998. V. 19. P. 497–510.
Stepp J. C. Analysis of completeness of the earthquake sample in the Puget Sound area and its effects on statistical estimates of earthquake hazard. Proceedings of the International conference on microzonation for safer construction research and application. Seattle, USA. 1972. P. 897–909.
Storchak D.A., Giacomo D.D., Bondár I., Engdahl E.R., Harris J., Lee W.H.K., Villaseñor A., Bormann P. Public release of the ISC-GEM global instrumental earthquake catalog (1900–2009) // Seismol. Res. Lett. 2013. V. 84. № 5. P. 810–815. https://doi.org/10.1785/0220130034
Utsu T. A statistical significance test of the difference in b-value between two earthquake groups // J. Phys. Earth. 1966. V. 14. № 2. P. 37–40. https://doi.org/10.4294/jpe1952.14.37
Wiemer S., Wyss M. Minimum magnitude of completeness in earthquake catalogs: examples from Alaska, the Western United States, and Japan // Bull. Seismol. Soc. Am. 2000. V. 90. № 4. P. 859–869. https://doi.org/10.1785/0119990114
Wilcoxon F. Individual comparisons by ranking methods // Biometrics Bulletin. 1945. V. 1. № 6. P. 80–83.
Woessner J., Wiemer S. Assessing the quality of earthquake catalogues: estimating the magnitude of completeness and its uncertainty // Bull. Seismol. Soc. Am. 2005. V. 95. № 2. P. 684–698. https://doi.org/10.1785/0120040007
Wyss M., Hasegawa A., Wiemer S., Umino N. Quantitative mapping of precursory seismic quiescence before the 1989, M 7.1 off-Sanriku earthquake, Japan // Ann. Geofisc. 1999. V. 42. № 5. P. 851–869. https://doi.org/10.4401/ag-3765
Zoller G., Hainzl S., Kurths J., Zschau J. A systematic test on precursory seismic quiescence in Armenia // Nat. Hazards. 2002. V. 26. № 3. P. 245–263. https://doi.org/10.1023/a:1015685006180
Дополнительные материалы отсутствуют.


