Физика Земли, 2022, № 2, стр. 144-154
Обобщенная модель фильтрации в трещиновато-пористой среде с низкопроницаемыми включениями и ее возможные приложения
Л. И. Лобковский 1, *, М. М. Рамазанов 2, **
1 Институт океанологии им. П.П. Ширшова РАН
г. Москва, Россия
2 Институт проблем геотермии и возобновляемой энергетики (ОИВТ РАН)
г. Махачкала, Россия
* E-mail: llobkovsky@ocean.ru
** E-mail: mukamay-ipg@mail.ru
Поступила в редакцию 14.03.2021
После доработки 17.08.2021
Принята к публикации 01.10.2021
- EDN: MRUIGH
- DOI: 10.31857/S0002333722020053
Аннотация
Проведено обобщение классической математической модели фильтрации жидкости и газа в трещиновато-пористой среде. В результате получено обобщенное уравнение, учитывающее, в отличие от классической модели, эффекты непосредственной фильтрации энерго (или тепло)-носителя в малопроницаемых включениях (блоках). Обобщенная модель пригодна для описания фильтрации жидкости и газа также и в трещиновато-нанопористых средах, когда закон Дарси неприменим. Модель используется для исследования процесса деградации низкопроницаемых включений, насыщенных газом или нефтью (например, сланцевый газ или нефть), что позволяет одновременно улучшить понимание свойств решения предложенного уравнения. Получены кривые распределения давления во включениях и окружающей матрице в различные моменты времени, а также кривые расхода газа в зоне разгрузки; дан их сравнительный анализ по отношению к классическим моделям.
1. ВВЕДЕНИЕ
В связи с актуальной задачей создания и оптимизации технологий разработки нетрадиционных месторождений углеводородов (газогидраты, сланцевые газ и нефть и т.д.), возникает необходимость усовершенствования классических моделей механики подземных флюидов. В этой связи в работах [Баренблатт и др., 2016; Monteiro et al., 2012] предложена новая математическая модель, которая предполагает, что порода состоит из двух компонентов: матрицы, которая является обычной (подчиняющейся закону Дарси) пористой или деформированной пористой средой и специфических включений. Эти включения могут состоять, например, из агломерата лед–свободный газ–газогидрат [Баренблатт и др., 2016] или керогена в случае месторождения сланцевого газа [Monteiro et al., 2012]. Они могут иметь существенную пористость, но из-за наноразмеров пор, трубок и каналов, имеют чрезвычайно низкую проницаемость порядка нанодарси (~10–21 м2) или меньше. Существенной особенностью модели [Баренблатт и др., 2016; Monteiro et al., 2012] является то, что в ней эффективная проницаемость пропорциональна градиенту давления в некоторой степени $m \geqslant 0$.
Однако в цитированных работах рассматривается процесс фильтрации газа лишь во включениях, фильтрация же в матрице остается без внимания. В качестве естественного развития указанной модели представляется, что в этих и аналогичных случаях необходимо учитывать фильтрацию газа (жидкости) в матрице, т.е. для описания течения газа и жидкости в таких средах более адекватной является модель среды с двойной пористостью. С другой стороны, известная классическая модель фильтрации с двойной пористостью напротив – совсем не учитывает фильтрацию в малопроницаемых включениях и изменение давления во включениях происходит исключительно за счет их массообмена с матрицей [Баренблатт и др., 1960; 1972]. В работе [Лобковский, Рамазанов, 2019] кратко рассмотрена простейшая модель, которая обобщает и модель с включениями [Баренблатт и др., 2016; Monteiro et al., 2012], поскольку учитывает фильтрацию в матрице, и классическую модель с двойной пористостью [Баренблатт и др., 1960; 1972], поскольку непосредственно учитывает эффекты фильтрации во включениях.
Эта обобщенная модель содержит в себе как частный случай и обычное уравнение пьезопроводности, а также классическую модель Буссинеска–Лейбензона [Баренблатт и др., 1972]. В настоящей работе указанная модель сформулирована и описана более подробно с выводом основных соотношений и анализом ее отличий от классических моделей, а также кратким обсуждениям ее возможных геолого-геофизических приложений.
2. ПОСТАНОВКА ЗАДАЧИ
Предполагается, что горизонтальный пласт состоит из матрицы с нормальной проницаемостью, т.е. позволяющей использовать закон Дарси, (или трещиновато-пористой среды) и включений, насыщенных газом или нефтью (например, сланцевая нефть или газ). Включения имеют нормальную пористость (например, для сланца Барнетта сообщается о 30–40% пористости в керогене [Monteiro et al., 2012]), но очень малую проницаемость (вплоть до нанопроницаемости) в силу того, что поры имеют чрезвычайно малые размеры (порядка первых десятков нанометров). Модель в принципе может быть пригодна и в случае многолетнемерзлых пород, когда включения представляют собой агломераты из льда, метастабильных газогидратов и запертого в отдельных микропорах свободного газа (рис. 1а). Далее, для определенности, будем в основном говорить о включениях, насыщенных газом, хотя полученные уравнения применимы и в других перечисленных случаях.
Рис. 1.
(а) – Структура среды, состоящей из пористой минеральной матрицы с низкопроницаемыми включениями, насыщенными газом или нефтью, до начала движения, вызванного внешним воздействием: 1 – матрица; 2 – включение; (б) – истечение газа из включений в пористую среду под воздействием изменения внешнего давления.

В начальном состоянии давление газа во включениях предполагается такое же, как и в окружающей матрице. При снижении давления в матрице c проницаемостью ${{k}_{1}}$ ниже критического значения ${{p}_{c}}$, под действием большого градиента давления, во включениях образуется фронт разрушения структуры пор и микроканалов. За этим фронтом образуется связанная система пор и каналов, что приводит к резкому возрастанию проницаемости ${{k}_{2}}$, зависящей от градиента давления газа [Баренблатт и др., 2016].
Как матрицу, так и совокупность включений будем считать двумя разными сплошными средами, которые гидродинамически взаимодействуют. В общем случае в каждой точке пространства имеем два давления ${{p}_{1}},\,\,{{p}_{2}}$.
Предполагаем, что задача одномерна и матрица вместе с включениями имеет начальное давление газа ${{p}_{0}}$ и занимает полуплоскость $x \geqslant 0$ (ось $x$ направлена вниз). В случае газогидратов под термином давление понимается давление газа после диссоциации метастабильного газогидрата при отсутствии фильтрации в условиях его самоконсервации, т.е. предполагаются специальные термобарические условия [Якушев, 2009].
В некоторый момент времени давление на верхней границе $x = 0$ падает до значения ${{p}^{0}} < {{p}_{с}} < {{p}_{0}}$. Требуется описать процесс деградации включений, сопровождаемый дегазацией пласта. Для описания указанных процессов выведем и используем обобщенную, по сравнению с классической, модель с двойной пористостью.
3. ОБОБЩЕННАЯ МОДЕЛЬ ФИЛЬТРАЦИИ В СРЕДЕ С ДВОЙНОЙ ПОРИСТОСТЬЮ
Исходная система уравнений имеет вид:
(3.1)
$\frac{{\partial {{\phi }_{1}}{{\rho }_{1}}}}{{\partial t}} + {\text{div}}{{\rho }_{1}}{{{\mathbf{u}}}_{1}} = {{q}_{p}},$(3.4)
${{\rho }_{j}} = f({{p}_{j}},{{T}_{0}}){\text{,}}\,\,\,\,{{T}_{0}} = {\text{const,}}\,\,\,\,j = 1,\,2.$Здесь: индексами 1 и 2 обозначены величины, относящиеся к матрице и малопроницаемым включениям соответственно; ${{\phi }_{1}},\,\,{{\phi }_{2}}$ – эффективные пористости матрицы и включений (в расчете на полный объем среды); ${{\rho }_{1}},\,\,{{\rho }_{2}}$ – плотность газа в матрице и во включениях; ${{p}_{1}},{{p}_{2}},\,\,{{T}_{0}}$ – давление и температура в обеих средах; ${{k}_{1}}$ –эффективная проницаемость матрицы; $\mu $ – вязкость газа ; ${{p}_{0}}$ – начальное невозмущенные давление; ${{p}^{0}}$ – давление газа на границе разгрузки газа $x = 0$.
Уравнения (3.1)–(3.2) есть уравнения баланса газа в матрице и во включениях, соответственно. Далее следуют уравнения движения газа в матрице (3.3). Функция ${{q}_{p}}$ описывает массообмен между матрицей и включениями. Уравнение (3.4) есть уравнение состояния газа.
Для замыкания системы необходимо задать или вычислить выражение ${{q}_{p}}$ определяющее поток массы из включений в матрицу или обратно в зависимости от знака.
Далее будем рассматривать частный случай, когда газ подчиняется уравнению совершенного газа. Система уравнений (3.1)–(3.4) примет вид:
(3.5)
$\frac{{{{\phi }_{1}}}}{{R{{T}_{0}}}}\frac{{\partial {{p}_{1}}}}{{\partial t}} = \frac{{{{k}_{1}}}}{{R{{T}_{0}}\mu }}{\text{div}}\left( {{{p}_{1}}{\text{grad}}{{p}_{1}}} \right) + {{q}_{p}},$Отметим, что в (3.5) и, соответственно, в (3.6) для простоты эффективная пористость блоков ${{\phi }_{2}}$ как и пористость трещин (матрицы) полагается постоянной. Обычно ${{\phi }_{2}}$ считается линейной функцией давлений в обеих средах, однако это не приводит к изменению конечного вида уравнений, а лишь вносит поправки к постоянным коэффициентам [Баренблатт и др., 1960; 1972].
3.1. Вывод функции массобмена между матрицей и включениями
Вывод функции массообмена между средами ${{q}_{p}}({{p}_{1}},\,{{p}_{2}},t)$ основан на следующих шагах, по аналогии с дисперсными средами [Нигматулин, 1987]: на первом шаге рассматриваем уравнение фильтрации газа в отдельном взятом включении, т.е. “микроуравнение” и усредняем его по области, занимаемой включением с использованием теоремы Гаусса, для перехода от объемного к поверхностному интегралу; на втором шаге решая в одномерном приближении “микроуравнение”, находится плотность потока газа через границу включения. В итоге получим “макроуравнение” отнесенное к единице общего объема пласта имеющее вид (3.6); сравнивая полученное усредненное уравнение с (3.6) находится искомая функцию ${{q}_{p}}({{p}_{1}},\,{{p}_{2}},t)$.
Рассмотрим “микроуравнение” внутри отдельных включений, следуя работам [Monteiro et al., 2012; Баренблатт и др., 2016]. Толщина пограничного слоя (за фронтом разрушения микропор и микроканалов) мала, поэтому движение газа в пограничном слое можно считать одномерным, направленным по нормали к границе включения, которую мы принимаем за ось $x$.
С несколько более общими граничными условиями, задача запишется следующим образом:
(3.7)
$\begin{gathered} \frac{{{{\phi }_{{20}}}}}{{R{{T}_{0}}}}\frac{{\partial p}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {\frac{{{{k}_{2}}p}}{{\mu R{{T}_{0}}}}\frac{{\partial p}}{{\partial x}}} \right),\,\,\,\,{{k}_{2}} = A{{\left( {\frac{{\partial p}}{{\partial x}}} \right)}^{m}}, \\ A = {\text{const,}} \\ \end{gathered} $(3.8)
$\begin{gathered} {{\left. {p(0,x)} \right|}_{{x > 0}}} = {{p}_{2}},\,\,\,\,p(t,0) = {{p}_{1}},\,\,\,\,p(t,{{x}_{\xi }}) = {{p}_{c}}, \\ \left( {{{p}_{2}} - {{p}_{c}}} \right){{{\dot {x}}}_{\xi }} = {{\left. {\frac{{{{k}_{2}}{{p}_{c}}}}{\mu }\frac{{\partial p}}{{\partial x}}} \right|}_{{x = {{x}_{\xi }}}}}. \\ \end{gathered} $Здесь: ${{\phi }_{{20}}}$ – собственная пористость включений, в то время как ${{\phi }_{2}}$ – пористость в расчете на общий объем; ${{k}_{2}}$ – проницаемость включений; ${{x}_{\xi }}(t)$ – фронт разрушения структуры пор и микроканалов во включениях; последнее граничное условие есть условие баланса массы на фронте ${{x}_{\xi }}(t)$. При $x > {{x}_{\xi }}$ давление газа во включениях равно невозмущенному начальному значению ${{p}_{2}}$.
Подчеркнем, что в “макромодели” через ${{p}_{1}}$ и ${{p}_{2}}$ обозначены эффективные давления в обеих средах отнесенные к единице общего объема, а невозмущенное начальное давление обозначено через ${{p}_{0}}$.
Решая задачу (3.7)–(3.8), можно найти функцию массообмена ${{q}_{p}}({{p}_{1}},\,{{p}_{2}},{{p}_{c}},t)$. После этого, пренебрегая пористостью матрицы по сравнению с пористостью включений, одномерная “макрозадача” об истечении газа (нефти) из включений в среде с двойной пористостью запишется в виде:
(3.9)
$\frac{{{{k}_{1}}}}{{R{{T}_{0}}\mu }}\frac{\partial }{{\partial x}}\left( {{{p}_{1}}\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right) + {{q}_{p}} = 0,$(3.10)
$\frac{{{{\phi }_{2}}}}{{R{{T}_{0}}}}\frac{{\partial {{p}_{2}}}}{{\partial t}} = - {{q}_{p}},$(3.11)
$\begin{gathered} {{\left. {{{p}_{2}}(0,x)} \right|}_{{x > 0}}} = {{p}_{0}},\,\,\,\,{{p}_{1}}(t,0) = {{p}^{0}},\,\,\,\,{{p}_{1}}(t,{{x}_{*}}) = {{p}_{c}}, \\ \left( {{{p}_{0}} - {{p}_{c}}} \right){{{\dot {x}}}_{*}} = {{\left. {\frac{{{{k}_{1}}{{p}_{c}}}}{\mu }\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right|}_{{x = {{x}_{*}}}}}. \\ \end{gathered} $Здесь ${{x}_{*}}(t)$ – фронт фазового перехода (разрушения структуры пор включений) в среде с двойной пористостью.
Решение системы (3.9)–(3.11) при найденной из (3.7)–(3.8) функции ${{q}_{p}}({{p}_{1}},\,{{p}_{2}},{{p}_{c}},t)$ полностью решают поставленную задачу и позволяют найти как фронт деградации включений (в том числе и в случае газогидратов в изотермическом приближении) в пространстве с двойной пористостью ${{x}_{*}}(t)$, так и деградацию включений в объеме за этим фронтом с последующей дегазацией матрицы. Система (3.7)–(3.11) допускает естественное обобщение на неизотермический случай, если учесть зависимость критического давления ${{p}_{c}}$ от температуры, добавить уравнения переноса тепла в обеих средах, а так же условия для температуры и потока энергии с учетом теплоты фазового перехода.
Далее в данной работе для простоты ограничимся предельным случаем, когда ${{\left( {{{p}_{2}} - {{p}_{c}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{p}_{2}} - {{p}_{c}}} \right)} {{{p}_{2}} \ll 1}}} \right. \kern-0em} {{{p}_{2}} \ll 1}}$. При этом описанная выше схема решения задачи сохраняется.
Рассмотрим “микрозадачу” (3.7)–(3.8). В этом случае в последнем условии (3.8) левой частью в первом приближении можно пренебречь, и граничные условия запишутся в виде:
(3.12)
$\begin{gathered} {{\left. {p(0,x)} \right|}_{{x > 0}}} = {{p}_{2}},\,\,\,\,p(t,0) = {{p}_{1}},\,\,\,\,p(t,{{x}_{*}}) = {{p}_{2}}, \\ \frac{{\partial p}}{{\partial x}}\left| \begin{gathered} \hfill \\ x = {{x}_{*}} \hfill \\ \end{gathered} \right. = 0. \\ \end{gathered} $Заметим, что при $m > 0$ точное решение уравнения (3.7) на всей положительной оси обладает важным свойством – оно отлично от начального постоянного давления ${{p}_{2}}$ лишь на конечном интервале $\left( {0,\,\,{{x}_{\xi }}(t)} \right)$. Здесь ${{x}_{\xi }}(t)$ есть ничто иное как фронт разрушения структуры пор и микроканалов внутри включения. Этот фронт в данном приближении находится из условия ${{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial x}}} \right. \kern-0em} {\partial x}} = 0$. То есть решение “микрозадачи” на всей положительной полуоси автоматически содержит фронт разложения. Таким образом, можно задачу (3.7) рассматривать на всей положительной оси (как это сделано в работе [Баренблатт и др., 2016]) не вводя специально границу фазового перехода ${{x}_{\xi }}(t)$, т.е. решать уравнение (3.7) со следующими граничными условиями:
(3.13)
$\begin{gathered} p(t,0) = {{p}_{1}},\,\,\,\,p(t,\infty ) = {{p}_{2}}, \\ p(0,x) = {{p}_{2}},\,\,\,\,x > 0. \\ \end{gathered} $ .После чего фронт разложения газогидрата находится из последнего условия (3.12).
Уравнение (3.7) с граничными условиями (3.13), вводя безразмерное давление $f(\xi )$, можно записать в автомодельном виде [Баренблатт и др., 2016]:
(3.14)
$\begin{gathered} p = {{p}_{2}}f(\xi ),\,\,\,\,\xi = \frac{x}{{{{{\left( {{{\chi }_{2}}t} \right)}}^{{1/\left( {m + 2} \right)}}}p_{2}^{{\left( {m + 1} \right)/\left( {m + 2} \right)}}}}, \\ {{\chi }_{2}} = \frac{A}{{{{\phi }_{{20}}}\mu }},\,\,\,\frac{\xi }{{m + 2}}\frac{{df}}{{d\xi }} + \frac{d}{{d\xi }}\left[ {f(\xi ){{{\left( {\frac{{df}}{{d\xi }}} \right)}}^{{m + 1}}}} \right] = 0, \\ f(0) = \sigma ,\,\,\,\,f(\infty ) = 1,\,\,\,\,\sigma = \frac{{{{p}_{1}}}}{{{{p}_{2}}}}. \\ \end{gathered} $Представление (3.14) позволяет выразить формулу для оттока газа из включений в зависимости от параметров ${{p}_{1}},{{p}_{2}}$ и времени. Будем считать, что эта формула остается справедливой и в случае, когда ${{p}_{1}},{{p}_{2}}$ зависят от времени. Можно оценить, что ошибка при этом будет порядка величины ${{\left[ {{{\left( {{{p}_{2}} - {{p}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{p}_{2}} - {{p}_{1}}} \right)} {{{p}_{2}}}}} \right. \kern-0em} {{{p}_{2}}}}} \right]}^{2}}$, которая обычно мала.
Интегрируя (3.7) по всему объему включения и справа переходя к поверхностному интегралу, получим:
Здесь ${{V}_{0}},\,\,{{S}_{0}}$ – объем и площадь поверхности отдельного включения.
Отсюда, используя (3.8) имеем:
(3.15)
$\begin{gathered} {{\phi }_{2}}\frac{{\partial {{p}_{2}}}}{{\partial t}} \approx - \alpha \frac{{{{S}_{0}}{{\phi }_{2}}}}{{{{V}_{0}}}}\frac{{{{\chi }_{2}}p_{2}^{{m + 1}}{{p}_{1}}{{{\left( {f{\kern 1pt} '} \right)}}^{{m + 1}}}}}{{{{{\left( {p_{2}^{{m + 1}}{{\chi }_{2}}t} \right)}}^{{\left( {m + 1} \right)/\left( {m + 2} \right)}}}}} = \\ = - \alpha \frac{{{{S}_{0}}{{\phi }_{2}}}}{{{{V}_{0}}}}\frac{{{{\chi }_{2}}p_{2}^{{m + 2}}}}{{{{{\left( {p_{2}^{{m + 1}}{{\chi }_{2}}t} \right)}}^{{\left( {m + 1} \right)/\left( {m + 2} \right)}}}}}F(\sigma ,m), \\ \end{gathered} $Здесь $\alpha $ – безразмерный коэффициент порядка единицы, зависящий от геометрии включений.
Сравнивая (3.15) и (3.6), получим:
(3.17)
${{q}_{p}} \approx \alpha \frac{{{{S}_{0}}{{\phi }_{2}}}}{{{{V}_{0}}RT}}\frac{{{{\chi }_{2}}p_{2}^{{m + 2}}}}{{{{{\left( {p_{2}^{{m + 1}}{{\chi }_{2}}t} \right)}}^{{\left( {m + 1} \right)/\left( {m + 2} \right)}}}}}F(\sigma ,m),$здесь ${{{{S}_{0}}{{\phi }_{2}}} \mathord{\left/ {\vphantom {{{{S}_{0}}{{\phi }_{2}}} {\left( {{{V}_{0}}{{\phi }_{{20}}}} \right)}}} \right. \kern-0em} {\left( {{{V}_{0}}{{\phi }_{{20}}}} \right)}}$ – удельная поверхность включений (поверхность на единицу общего объема пород).
Из (3.17) следует, что для полного определения функции массообмена ${{q}_{p}}({{p}_{1}},\,{{p}_{2}},t)$осталось определить функцию $F(\sigma ,m)$ из (3.16).
3.2. Вывод функции $F(\sigma ,m)$
Для нахождения $F(\sigma ,m)$, как это следует из (3.16), необходимо решить задачу (3.14) и найти $f{\kern 1pt} '(0,\sigma )$. Однако эта задача не имеет точного аналитического решения. Это значит, что уравнение (3.14) необходимо решать совместно с системой уравнений (3.5)–(3.6), что составляет довольно сложную задачу. В этой связи, найдем приближенное аналитическое решение задачи (3.14), что существенно облегчит решение системы (3.5)–(3.6), следовательно, и всей задачи.
Заметим, что при малых $\xi $ первый член в уравнении (3.14) мал и в этой области решение определяется уравнением:
(3.18)
$\frac{d}{{d\xi }}\left[ {f(\xi ){{{\left( {\frac{{df}}{{d\xi }}} \right)}}^{{m + 1}}}} \right] = 0.$В исходных координатах это уравнение соответствует квазистационарному режиму. Указанное предположение означает, что в некоторой расширяющейся со временем области, примыкающей к границе разгрузки ($x = 0$), через малое время (по сравнению с характерным временем) задачи, устанавливается квазистационарный режим. Причем эффективная граница указанной области определяется из решения задачи. Эту границу в автомодельных координатах обозначим l = const. Вдали же от границы $x = 0$ решение должно быть близко к невозмущенному распределению. Простейшее решение задачи (3.14) можно получить, если сшить указанные два решения. Таким образом, имеем следующее приближенное решение:
(3.19)
$f(\xi ) = \left\{ \begin{gathered} {{\left[ {{{\sigma }^{{\frac{{m + 2}}{{m + 1}}}}} + \frac{1}{l}\left( {1 - {{\sigma }^{{\frac{{m + 2}}{{m + 1}}}}}} \right)\xi } \right]}^{{\frac{{m + 1}}{{m + 2}}}}},\,\,\,\,0 \leqslant \xi \leqslant l \hfill \\ 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\xi > l, \hfill \\ \end{gathered} \right.$Для нахождения l проинтегрируем уравнение (3.14) по всей положительной полуоси:
(3.20)
$\frac{1}{{m + 2}}\int\limits_0^\infty {\xi \frac{{df}}{{d\xi }}d\xi - } f(0)\left( {\frac{{df}}{{d\xi }}} \right)_{{\xi = 0}}^{{m + 1}} = 0.$Потребуем, что бы уравнение (3.20) выполнялось для решения (3.19), тогда получим уравнение:
(3.21)
$\begin{gathered} \frac{1}{{m + 2}}\int\limits_0^l {\xi \frac{{df}}{{d\xi }}d\xi } - f(0)\left( {\frac{{df}}{{d\xi }}} \right)_{{\xi = 0}}^{{m + 1}} = 0, \\ f(\xi ) = {{\left[ {{{\sigma }^{{\frac{{m + 2}}{{m + 1}}}}} + \frac{1}{l}(1 - {{\sigma }^{{\frac{{m + 2}}{{m + 1}}}}})\xi } \right]}^{{\frac{{m + 1}}{{m + 2}}}}}. \\ \end{gathered} $Решая это уравнение получим:
(3.22)
$\begin{gathered} l = \frac{{{{{\left( {m + 1} \right)}}^{{\frac{{m + 1}}{{m + 2}}}}}}}{{{{{\left( {m + 2} \right)}}^{{\frac{m}{{m + 2}}}}}}}(1 - {{\sigma }^{{\frac{{m + 2}}{{m + 1}}}}}) \times \\ \times \,\,{{\left[ {\frac{{m + 1}}{{2m + 3}}(1 - {{\sigma }^{{\frac{{2m + 3}}{{m + 1}}}}}) - {{\sigma }^{{\frac{{m + 2}}{{m + 1}}}}}\left( {1 - \sigma } \right)} \right]}^{{ - \frac{1}{{m + 2}}}}}. \\ \end{gathered} $А для $f{\kern 1pt} '(0)$ получим выражение:
Отсюда имеем искомую функцию:
(3.23)
$\begin{gathered} F(\sigma ,m) = \sigma {{\left[ {f{\kern 1pt} '(0,\sigma )} \right]}^{{m + 1}}} = \frac{{{{{\left( {m + 1} \right)}}^{{\frac{{m + 1}}{{m + 2}}}}}}}{{{{{\left( {m + 2} \right)}}^{{\frac{{2\left( {m + 1} \right)}}{{m + 2}}}}}}} \times \\ \times \,\,{{\left[ {\frac{{m + 1}}{{2m + 3}}(1 - {{\sigma }^{{\frac{{2m + 3}}{{m + 1}}}}}) - {{\sigma }^{{\frac{{m + 2}}{{m + 1}}}}}\left( {1 - \sigma } \right)} \right]}^{{\frac{{m + 1}}{{m + 2}}}}}. \\ \end{gathered} $Отсюда, в частности, при $m = 0$ получим:
4. ФОРМУЛИРОВКА ОБОБЩЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Сформулируем предлагаемую математическую модель в окончательном виде в предельном случае ${{\left( {{{p}_{0}} - {{p}_{c}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{p}_{0}} - {{p}_{c}}} \right)} {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}} \ll 1$. В системе (3.5)–(3.6), следуя работе [Баренблатт и др., 1960; 1972], для трещиновато-пористой среды, пренебрегаем пористостью матрицы по сравнению с пористостью включений, а газ считаем термодинамически идеальным. Тогда, учитывая (3.17) и (3.23) получим следующую систему уравнений:
(4.1)
$\frac{{{{k}_{1}}}}{{R{{T}_{0}}\mu }}\frac{\partial }{{\partial x}}\left( {{{p}_{1}}\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right) + {{q}_{p}} = 0,$(4.3)
$\begin{gathered} {{q}_{p}} = \alpha \frac{{{{S}_{0}}{{\phi }_{2}}}}{{{{V}_{0}}R{{T}_{0}}}}\frac{{{{\chi }_{2}}p_{2}^{{m + 2}}}}{{{{{\left( {p_{2}^{{m + 1}}{{\chi }_{2}}t} \right)}}^{{\left( {m + 1} \right)/\left( {m + 2} \right)}}}}}F(\sigma ,m), \\ \sigma = \frac{{{{p}_{1}}}}{{{{p}_{2}}}}, \\ \end{gathered} $(4.4)
$\begin{gathered} F(\sigma ,m) = \frac{{{{{\left( {m + 1} \right)}}^{{\frac{{m + 1}}{{m + 2}}}}}}}{{{{{\left( {m + 2} \right)}}^{{\frac{{2\left( {m + 1} \right)}}{{m + 2}}}}}}} \times \\ \times \,\,{{\left[ {\frac{{m + 1}}{{2m + 3}}(1 - {{\sigma }^{{\frac{{2m + 3}}{{m + 1}}}}}) - {{\sigma }^{{\frac{{m + 2}}{{m + 1}}}}}\left( {1 - \sigma } \right)} \right]}^{{\frac{{m + 1}}{{m + 2}}}}}. \\ \end{gathered} $Граничные и начальные условия:
(4.5)
$\begin{gathered} {{p}_{1}}(t,0) = {{p}^{0}},\,\,\,\,{{p}_{1}}(t,\infty ) = {{p}_{0}}, \\ {{p}_{2}}(0,x) = {{p}_{0}},\,\,\,\,x > 0. \\ \end{gathered} $Во многих случаях удобно решать задачу в безразмерном виде. Запишем (4.1)–(4.5) в безразмерном виде, используя следующие масштабы величин:
(4.6)
$t = \frac{{{{L}^{2}}}}{{{{\chi }_{1}}{{p}_{0}}}}t{\kern 1pt} ',\,\,\,\,x = Lx{\kern 1pt} ',\,\,\,\,{{p}_{i}} = {{p}_{0}}p_{i}^{'},\,\,\,{{\chi }_{1}} = \frac{{{{k}_{1}}}}{{\mu {{\phi }_{2}}}}.$Здесь $L$ – некоторый характерный размер длины, который будет определен ниже.
Опуская штрихи, имеем:
(4.7)
$\begin{gathered} \frac{\partial }{{\partial x}}\left[ {{{p}_{1}}\left( {\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right)} \right] + B(t)p_{2}^{{\left( {2m + 3} \right)/\left( {m + 2} \right)}}F(\sigma ,m) = 0, \\ \frac{{\partial {{p}_{2}}}}{{\partial t}} = - B(t)p_{2}^{{\left( {2m + 3} \right)/\left( {m + 2} \right)}}F(\sigma ,m) = 0, \\ F(\sigma ,m) = \frac{{{{{\left( {m + 1} \right)}}^{{\frac{{m + 1}}{{m + 2}}}}}}}{{{{{\left( {m + 2} \right)}}^{{\frac{{2\left( {m + 1} \right)}}{{m + 2}}}}}}} \times \\ \times \,\,{{\left[ {\frac{{m + 1}}{{2m + 3}}(1 - {{\sigma }^{{\frac{{2m + 3}}{{m + 1}}}}}) - {{\sigma }^{{\frac{{m + 2}}{{m + 1}}}}}\left( {1 - \sigma } \right)} \right]}^{{\frac{{m + 1}}{{m + 2}}}}}, \\ B(t) = \frac{{{{B}_{0}}}}{{{{t}^{{\left( {m + 1} \right)/\left( {m + 2} \right)}}}}}, \\ {{B}_{0}} = \frac{{\alpha {{S}_{0}}}}{{{{V}_{0}}}}p_{0}^{{m/\left( {m + 2} \right)}}{{\left( {\frac{{{{\phi }_{2}}A}}{{{{\phi }_{{20}}}{{k}_{1}}}}} \right)}^{{1/\left( {m + 2} \right)}}}{{L}^{{2/\left( {m + 2} \right)}}}. \\ \end{gathered} $Параметр $A$ в общем случае имеет дробную размерность, поэтому ее удобно выразить через другую постоянную. Используя равенство:
Отсюда следует, что ${{k}_{{20}}}$ есть проницаемость среды при $m = 0$. Далее будем полагать, что ${{k}_{{20}}}$ является константой, характеризующей фильтрационные свойства данного пористого материала и не зависящей ни от $m$, ни от граничных условий. Она имеет размерность проницаемости. В результате справедливы также формулы:
При условии ${{({{p}_{2}} - {{p}_{1}})} \mathord{\left/ {\vphantom {{({{p}_{2}} - {{p}_{1}})} {{{p}_{2}}}}} \right. \kern-0em} {{{p}_{2}}}} = 1 - \sigma \ll 1$, которое обычно выполняется, можно записать:
Учитывая это выражение, из (4.7) имеем:
(4.8)
$\begin{gathered} \frac{\partial }{{\partial x}}\left[ {{{p}_{1}}\left( {\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right)} \right] + {{B}_{1}}(t)\left( {{{p}_{2}} - {{p}_{1}}} \right) = 0, \\ \frac{{\partial {{p}_{2}}}}{{\partial t}} = - {{B}_{1}}(t)\left( {{{p}_{2}} - {{p}_{1}}} \right), \\ {{B}_{1}}(t) = 2{{\left[ {2\left( {m + 2} \right)} \right]}^{{ - \frac{{\left( {m + 1} \right)}}{{m + 2}}}}}\frac{{\alpha {{S}_{0}}}}{{2{{V}_{0}}}} \times \\ \times \,\,{{\left( {\frac{{{{\phi }_{2}}{{k}_{{20}}}}}{{{{\phi }_{{20}}}{{k}_{1}}}}} \right)}^{{1/\left( {m + 2} \right)}}}L_{v}^{{m/\left( {m + 2} \right)}}{{L}^{{2/\left( {m + 2} \right)}}}{{t}^{{ - \left( {m + 1} \right)/\left( {m + 2} \right)}}}. \\ \end{gathered} $Эту систему можно переписать в виде одного уравнения:
(4.9)
$\frac{{\partial {{p}_{1}}}}{{\partial t}} = \frac{\partial }{{\partial t}}\left( {\frac{1}{{{{B}_{1}}}}D{{p}_{1}}} \right) + D{{p}_{1}},\,\,\,\,D{{p}_{1}} = \frac{\partial }{{\partial x}}\left[ {{{p}_{1}}\left( {\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right)} \right].$Выберем $L = {{L}_{0}}$ так, что
Тогда
(4.10)
$\begin{gathered} \frac{{\partial {{p}_{1}}}}{{\partial t}} = \frac{\partial }{{\partial t}}\left( {\frac{1}{{{{B}_{2}}}}D{{p}_{1}}} \right) + D{{p}_{1}}, \\ D{{p}_{1}} = \frac{\partial }{{\partial x}}\left[ {{{p}_{1}}\left( {\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right)} \right], \\ {{B}_{2}}(t) = 2{{\left[ {2\left( {m + 2} \right)} \right]}^{{ - \frac{{\left( {m + 1} \right)}}{{m + 2}}}}} \times \\ \times \,\,{{\left( {\frac{{\alpha {{S}_{0}}{{L}_{v}}}}{{2{{V}_{0}}}}} \right)}^{{m/\left( {m + 2} \right)}}}{{t}^{{ - \left( {m + 1} \right)/\left( {m + 2} \right)}}}. \\ \end{gathered} $В большинстве случаев уравнение (4.10) можно рассматривать как исходное. Если вместо уравнения совершенного газа использовать линейную зависимость плотности от давления, которая характерна для сжимаемой жидкости, то в (4.10) получим $D{{p}_{1}} = {{{{\partial }^{2}}{{p}_{1}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{p}_{1}}} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}}$. Если, кроме того, положить ${{B}_{2}} = {\text{const}}$ и $m = 0$, получим хорошо известное уравнение для модели фильтрации жидкости в среде с двойной пористостью [Баренблатт и др., 1972], которую будем называть классической.
Систему (4.10) можно записать и относительно ${{p}_{2}}$:
Отмеченная выше классическая модель с двойной пористостью в безразмерном виде запишется следующим образом [Баренблатт и др, 1960; 1972]:
(4.11)
$\begin{gathered} \frac{{\partial {{p}_{1}}}}{{\partial t}} = \frac{1}{B}\frac{\partial }{{\partial t}}D{{p}_{1}} + D{{p}_{1}},\,\,\,\,B = {\text{const,}} \\ D{{p}_{1}} = \frac{\partial }{{\partial x}}\left[ {{{p}_{1}}\left( {\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right)} \right]. \\ \end{gathered} $Ниже при сравнении различных моделей рассматривается также уравнение Буссинеска–Лейбензона в безразмерном виде:
(4.12)
$\frac{{\partial {{p}_{1}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left[ {{{p}_{1}}\left( {\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right)} \right].$Это уравнение описывает изотермическую фильтрацию совершенного газа в однородной пористой среде без включений.
Полученные выводы справедливы не только для трещиновато-пористых сред, но и для любой матрицы, обладающей значительно большей проницаемостью по сравнению с проницаемостью включений. Действительно, если, например, для простоты предположить, что фильтрация во включениях также подчиняется закону Дарси, то для того, чтобы можно было пренебречь производной по времени в уравнении (3.1), должно выполняться неравенство:
В случае трещиновато-пористых сред это неравенство выполняется за счет малости отношения эффективных пористостей трещин и блоков, а в случае малопроницаемых включений, расположенных в матрице с нормальной проницаемостью – за счет отношения эффективных проницаемостей.
5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Предложенная общая модель с двойной пористостью (3.7)–(3.11) при заданном критическом давлении ${{p}_{c}}$ позволяет решить задачу о деградации включений, содержащих газ или нефть (в том числе и задачу о разложении скоплений газогидратов в криолитозоне), в изотермическом приближении. Эта модель на “макроуровне” учитывает одновременно и поверхностное разрушение (разложение) структуры включений на фронте фазового перехода ${{x}_{*}}(t)$ и их объемную деградацию в области за фронтом. Модель легко обобщить на неизотермический случай, если учесть зависимость ${{p}_{c}}$ от температуры и добавить уравнение переноса тепла в обеих средах с соответствующими граничными условиями.
Однако в данной работе для простоты использован предельный случай модели (3.7)–(3.11), когда выполняются условия ${{\left( {{{p}_{0}} - {{p}_{c}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{p}_{0}} - {{p}_{c}}} \right)} {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}} \ll 1$. Рассмотрим полученные результаты в этом предельном случае.
Прежде всего, приведем обоснование полученного выражения (3.23) для $F(\sigma ,m)$, которое определяет интенсивность массообмена между включениями и окружающей матрицей. На рис. 2 сравнивается численные решение уравнения (3.7) с его аналитическим квазистационарным решением для двух разных значений $m = 0;2$. Как показывает рисунок, максимальная погрешность достигается в переходной области кусочно-дифференцируемого квазистационарного решения и не превосходит нескольких процентов. Что касается искомой величины – производной давления в начале координат, определяющей величину $F(\sigma ,m)$, то ее погрешность составляет 11%, что представляется вполне приемлемой величиной. При желании уточнить результат полученное решение можно рассматривать как первое приближение.
Рис. 2.
Распределение давления при $m = 0;2$: 1, 3 – численные решения; 2, 4 – соответствующие аналитические решения; 5, 6 – погрешности аналитических решений.

Полученная система уравнений (4.8) (или уравнение (4.10)) обобщает аналогичную систему уравнений в классической модели с двойной пористостью (КМ) (4.11) [Баренблатт и др., 1960; 1972]. Классическая модель из данной получится, если положить $m = 0$ и $B = {\text{const}}$. Таким образом, в данном случае величина $B$ зависит от времени даже при $m = 0$ (когда проницаемость постоянна и не зависит от градиента давления), что является следствием, того, что в настоящей модели учитывается эффект, связанный с фильтрацией газа во включениях, которым в КМ пренебрегается.
Коротко обсудим, как изменились свойства решений полученных уравнений по сравнению с КМ. Тем же способом, как это сделано в работе [Баренблатт и др., 1972] можно показать, что и в обобщенной модели для получения непрерывного решения по времени произвольно можно задавать лишь начальное распределение в блоках (включениях) ${{p}_{2}}$. Что касается начального распределения ${{p}_{1}}$ в окружающей матрице, то его необходимо найти из уравнения:
(5.1)
$\begin{gathered} \frac{\partial }{{\partial x}}\left[ {{{p}_{1}}\left( {\frac{{\partial {{p}_{1}}}}{{\partial x}}} \right)} \right] + {{\left( {m + 2} \right)}^{{ - \frac{{2\left( {m + 1} \right)}}{{m + 2}}}}} \times \\ \times \,\,{{B}_{2}}({{t}_{0}})\left[ {{{p}_{2}}(x,0) - {{p}_{1}}} \right] = 0. \\ \end{gathered} $Это означает, что если ${{p}_{1}}$ задать иным, то оно скачком перейдет в распределение (5.1). Данный вывод является следствием пренебрежения пористостью матрицы (трещин). Если указанной малой величиной не пренебречь, то решение не скачком, но достаточно быстро (тем быстрее, чем меньше пористость матрицы) перейдет от начального распределения к распределению (5.1).
Другим свойством решения системы (4.8), как и в КМ является то, что ${{p}_{2}}$ может терпеть разрывы в пространстве, и эти скачки не исчезают мгновенно, как при упругом режиме (уравнение пъезопроводности), а затухают по некоторому закону. В классической модели с двойной пористостью они затухают по экспоненциальному закону ${{e}^{{ - At}}}$. В данном случае этот закон несколько иной и имеет вид $\exp \left( { - A{{t}^{{1/\left( {m + 2} \right)}}}} \right)$, что связано с зависимостью $B(t)$от времени и, следовательно, с эффектом фильтрации газа (жидкости) в блоках. Видно, что указанный эффект замедляет затухание скачка.
На рис. 3–рис. 5 показаны результаты расчетов истечения газа из включений (например, керогена) в матрицу с последующей дегазацией пласта. Уравнение (4.9) решалось в безразмерном виде. После этого распределение ${{p}_{2}}$ находилось из второго уравнения системы (4.8). Начальное условие ${{p}_{2}}$ полагалось равным единице, а начальное распределение ${{p}_{1}}$ вычислялось из уравнения (5.1). Задача решалась конечно-разностным методом.
Рис. 3.
Распределение давления в матрице${{p}_{1}}$ для $m = 1.1$ в различные моменты безразмерного времени t = 0.015; 0.15; 0.5; 2; 5; 12.5 (1–6). Пунктиром показаны кривые для модели Буссинеска–Лейбензона в соответствующие моменты времени.

На рис. 3 показаны распределения давления в матрице в различные возрастающие моменты времени. Пунктиром показаны кривые, рассчитанные для модели Буссинеска–Лейбензона (4.12) в соответствующие моменты времени. Следует отметить, что в данном случае уравнение Буссинеска–Лейбензона описывает пространственно-временное распределение давление в однородной (без включений), но в некотором смысле “усредненной” среде, у которой пористость равна пористости включений, а проницаемость равна проницаемости матрицы. Это следует из введенного в разделе 4 масштаба времени (4.6).
Рис. 4 иллюстрирует характер эволюции распределений давления во включениях (блоках). При наибольшем из рассмотренных моментов времени для сравнения приведено также распределение в матрице ${{p}_{1}}$ – кривая 7. Расчеты показывают, что с одной стороны распределения в обеих средах асимптотически приближаются друг к другу и в тоже время они приближаются к классическому распределению.
Рис. 4.
Распределение давления во включениях${{p}_{2}}$ для $m = 1.1$ в различные моменты безразмерного времени t = 0.015; 0.15; 0.5; 2; 5; 12.5 (1–6); Пунктиром 7 для сравнения показано распределение давления в матрице ${{p}_{1}}$ при $t = 12.5$.

Рис. 5 показывает зависимость безразмерного расхода газа на границе разгрузки $x = 0$ от безразмерного времени для различных случаев. Кривые 1 и 2 на рис. 5 построены на основе текущей модели при $m = 0;1.1$. Видно, что бо́льшим $m$ на начальном отрезке времени соответствуют бо́льшие расходы, затем при существенно меньших потоках происходит инверсия. Кривая 3 соответствует классической модели с двойной пористостью. Расход в этой модели меньше, чем в текущей на начальном интервале времени и затем происходит инверсия. Наконец, кривая 4 соответствует классической модели Буссинеска–Лейбензона для отмеченной выше в некотором смысле “усредненной” однородной среды, т.е. среды с проницаемостью матрицы и пористостью включений. Как видно из рис. 5, в этой модели расход выше других на всем, рассмотренном на верхнем рисунке, отрезке времени.
Рис. 5.
Зависимость безразмерного расхода от времени на границе разгрузки $x = 0$: 1 – $m = 0;$ 2 – $m = 1.1$; 3 – $m = 0,\,\,B \equiv 1$, т.е. классическая модель с двойной пористостью; 4 – модель Буссинеска–Лейбензона.
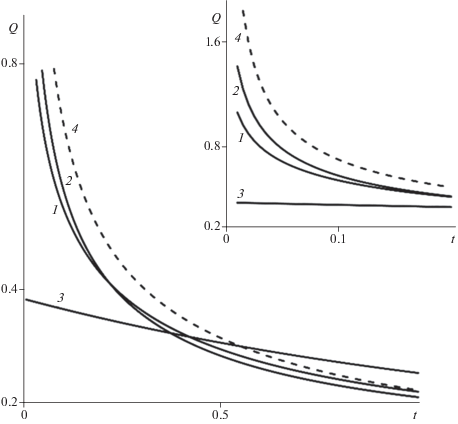
Отметим, что рис. 2 работы [Лобковский, Рамазанов, 2019] несколько отличается от своего аналога рис. 5 данной работы. Это связано с тем, что в работе [Лобковский, Рамазанов, 2019] рассмотрен масштаб времени зависящий от $m$, что не удобно для сравнения кривых, в то время как на рис. 5 данной работы для всех кривых масштаб времени одинаковый и не зависит от $m$.
Оценим выбранный в (4.6) масштаб времени, который можно записать в виде:
(5.2)
${{t}_{0}} = \frac{{\mu {{\phi }_{{20}}}}}{{{{k}_{{20}}}{{p}_{0}}}}{{\left( {\frac{{2{{V}_{0}}}}{{\alpha {{S}_{0}}}}} \right)}^{2}}.$Положим:
Если условно считать, что включения имеют сферическую форму, то для радиуса 1 и 5 метра соответственно, поучим следующие масштабы времени:
При этом существенное увеличение теплового потока в обобщенной модели по сравнению с классической, как следует из рис. 5, будет длиться порядка одного года и десять лет соответственно. Если проницаемость включений на порядок меньше, то соответственно масштабы (5.3) увеличатся на порядок. Из (5.2) следует, что масштаб времени обратно пропорционален проницаемости включений и прямо пропорционален квадрату характерного размера включений (отношение объема включений к его площади).
В завершение данного раздела оценим, как зависит от показателя $m$ скорость деградации включений и соответственно поток газа через границу разгрузки. Скорость разгрузки согласно (4.10) пропорциональна величине:
(5.4)
$\begin{gathered} {{B}_{2}}(m,t) = 2{{\left[ {2\left( {m + 2} \right)} \right]}^{{ - \frac{{\left( {m + 1} \right)}}{{m + 2}}}}} \times \\ \times \,\,{{\left( {\frac{{\alpha {{S}_{0}}{{L}_{v}}}}{{2{{V}_{0}}}}} \right)}^{{m/\left( {m + 2} \right)}}}{{t}^{{ - \left( {m + 1} \right)/\left( {m + 2} \right)}}},\,\,\,\,\alpha \sim 1. \\ \end{gathered} $Если в качестве включения взять шар (${{L}_{v}} = 2{{R}_{0}}$), то для разных значений безразмерного времени $t$ и параметра m получим следующие оценки:
Здесь первый результат соответствует кривым 1 и 2 на рис. 5.
Из (5.4) следует, что для вытянутых областей, например, для вытянутых эллиптических цилиндров, результат еще сильнее зависит от показателя $m$. В этом случае будем иметь ${{B}_{2}}$ пропорционально ${{a}^{{m/\left( {m + 2} \right)}}}$, где $a \gg 1$ отношение большой и малой полуосей эллипса.
6. ЗАКЛЮЧЕНИЕ
Выведена обобщенная модель фильтрации жидкости и газа в среде с двойной пористостью. А именно, в отличие от классической модели [Баренблатт и др., 1960; 1972], учитывается эффект фильтрации в малопроницаемых блоках. Для этого используется современное представление о законе фильтрации в малопористой, в частности, нанопористой среде. Этот закон отличается от закона Дарси тем, что проницаемость пропорциональна градиенту давления в некоторой степени $m > 0$. Показано, что свойства решения полученного обобщенного уравнения сходны со свойствами классической модели с двойной пористостью. Однако имеются и отличия. Как известно в классической модели скачки давления в блоках затухают по закону ${{e}^{{ - At}}}$. В обобщенной модели указанные скачки затухают несколько медленнее, по закону $\exp ( - A{{t}^{{1/\left( {m + 2} \right)}}})$.
Полученная модель может быть использована для исследования истечения газа из малопроницаемых включений в пласте (например, керогена в сланцах или включений агломератов насыщенного газом льда с частично диссоциированными метастабильными газогидратами [Якушев, 2009]). Отметим, что данная модель отличается от классической модели с двойной пористостью даже в простейшем случае $m = 0$, когда выполняется закон Дарси, поскольку учитывает эффект фильтрации в малопроницаемых включениях.
Показан характер эволюции полей давления во включениях и в окружающей матрице. Приводится сравнение законов изменения расхода газа на границе разгрузки для различных параметров, для классической модели с двойной пористостью и для модели Буссинеска–Лейбензона. Показана закономерность зависимости темпов деградации скоплений от показателя проницаемости $m$.
Список литературы
Баренблатт Г.И., Лобковский Л.И., Нигматулин Р.И. Математическая модель истечения газа из газонасыщенного льда и газогидратов // Докл. РАН. 2016. Т. 470. № 4. С. 458-461.
Баренблатт Г.И., Желтов Ю.П., Кочина И.Н. Об основных представлениях теории фильтрации однородных жидкостей в трещиноватых породах // ПММ. Т. 24. 1960. Вып. 5. С. 852–864.
Баренблатт Г.И., Ентов В.М., Рыжик В.М. Теория нестационарной фильтрации жидкости и газа. М.: Недра. 1972. 288 с.
Лобковский Л.И., Рамазанов М.М. К теории фильтрации в среде с двойной пористостью // Докл. РАН. 2019. Т. 484. № 3. С. 348–351.
Нигматулин Р.И. Динамика многофазных сред. Ч. I, II. М.: Наука. Гл. ред. физ.-мат. лит. 1987. 464с. 360 с.
Якушев В.С. Природный газ и газовые гидраты в криолитозоне. М.: ВНИИГАЗ. 2009. 190 с.
Monteiro P.M., Rycroft C.H., Barenblatt G.I. A Mathematical Model of Fluid and Gas Flow in Nanoporous Media // Proc. Nat. Acad. Sci. 2012. V. 109. № 50. P. 20309–20313.
Дополнительные материалы отсутствуют.


