Физика Земли, 2022, № 3, стр. 92-107
Прямая и обратная задача геоэлектрики бианизотропных сред на основе объемных интегральных уравнений
П. Н. Александров 1, *, В. Н. Кризский 2, **
1 Институт физики Земли им. О.Ю. Шмидта РАН
г. Москва, Россия
2 Санкт-Петербургский горный университет
г. Санкт-Петербург, Россия
* E-mail: alexandr@igemi.troitsk.ru
** E-mail: Krizskiy_VN@pers.spmi.ru
Поступила в редакцию 22.11.2021
После доработки 06.12.2021
Принята к публикации 24.12.2021
- EDN: PZBGMR
- DOI: 10.31857/S0002333722030012
Аннотация
Изучение бианизотропных сред началось более века назад. Одним из фундаментальных исследований является работа В.Р. Бурсиана – известного автора первого учебника по электроразведке. Целью настоящей работы является поиск решения обратных задач для бианизотропных сред. В статье предложено решение обратной задачи геоэлектрики бианизотропных сред на основе интегральных уравнений электродинамики, сводящихся к системе линейных алгебраических уравнений относительно искомых электромагнитных параметров среды. Приведены результаты математического моделирования по решению прямых и обратных задач для бианизотропных моделей геоэлектрической среды.
ВВЕДЕНИЕ
Решение прямых и обратных трехмерных задач геоэлектрики бианизотропных сред представляет актуальную проблему современной электроразведки, поскольку такие среды позволяют максимально полно описать линейные электромагнитные свойства горной породы [Туров, 1983; Александров, 2000]. Сложность решения таких задач связана с большим количеством электромагнитных параметров (максимально 36), которыми характеризуются линейные среды и сложностью решения уравнений относительно компонент электромагнитного поля для таких сред. Одним из способов решения прямых задач для бианизотропных сред является способ сведения системы уравнений Максвелла к системе обыкновенных дифференциальных уравнений первого порядка. Однако такой подход эффективен только для одномерных сред. Для трехмерных сред наиболее перспективным способом является способ, основанный на решении объемных интегральных уравнений. Вследствие этого, прежде получим объемные интегральные уравнения относительно компонент электромагнитного поля для случая трехмерной бианизотропной неоднородности, находящейся в однородном бианизотропном пространстве.
ВЫВОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Для решения прямой трехмерной задачи геоэлектрики бианизотропных сред воспользуемся методом интегральных уравнений на основе леммы Лоренца [Марков и др., 1979].
Рассмотри две системы уравнений Максвелла:
(1)
${\text{rot}}{\mathbf{H}} = \sigma {\mathbf{E}} + \alpha {\mathbf{H}} + {{{\mathbf{J}}}^{{ext}}},$(2)
${\text{rot}}{\mathbf{E}} = - i\omega (\mu {\mathbf{H}} + \beta {\mathbf{E}}) + {{{\mathbf{B}}}^{{ext}}},$(3)
${\text{rot}}{\mathbf{G}}_{x}^{e} = {{\sigma }_{0}}{\mathbf{Q}}_{x}^{e} + {{\alpha }_{0}}{\mathbf{G}}_{x}^{e} + \delta {\mathbf{i}},$(4)
${\text{rot}}{\mathbf{Q}}_{x}^{e} = - i\omega ({{\mu }_{0}}{\mathbf{G}}_{x}^{e} + {{\beta }_{0}}{\mathbf{Q}}_{x}^{e}),$Магнитная проницаемость $\mu $ и удельная электропроводность $\sigma $ – известные параметры в геоэлектрике, $\alpha $, $\beta $ – бианизотропные параметры, физическая размерность которых, соответственно, равны (${1 \mathord{\left/ {\vphantom {1 {\text{м}}}} \right. \kern-0em} {\text{м}}}$) и (${1 \mathord{\left/ {\vphantom {1 {\text{м}}}} \right. \kern-0em} {\text{м}}} \cdot {\text{c}}$). Все эти параметры описывают наиболее общие линейные электромагнитные свойства среды и являются матрицами размерностью 3 × 3 и, следовательно, общее количество электромагнитных параметров равно 36. Как показано в работе [Александров, 2000], бианизотропные параметры $\alpha $, $\beta $ связаны с извилистостью токопроводящих путей. Они являются комплексными функциями частоты и равны нулю при $\omega = 0$, т.е. при постоянном токе они исчезают.
Отметим, что исследованиями бианизотропных сред занимался один из основоположников теории геоэлектрики В.Р. Бурсиан [Bursian, Timorew, 1926; Бурсиан, 1972], получивший фундаментальные научные результаты, имеющие огромное значение и в настоящее время. Рассмотрение уравнений Максвелла в наиболее общей линейной постановке связано с объектом геофизических исследований, для которого заранее нельзя определить конкретный вид материальных уравнений.
Умножим уравнение (1) на транспонированный вектор электрического поля ${\mathbf{Q}}{{_{x}^{e}}^{T}}$, уравнение (4) на транспонированный вектор магнитного поля ${{{\mathbf{H}}}^{T}}$, и результаты умножения вычтем:
Далее, умножим уравнение (3) на ${{{\mathbf{E}}}^{T}}$, уравнение (2) на транспонированный вектор электрического поля ${\mathbf{G}}_{x}^{T}$ и результаты умножения вычтем:
Вычитая результаты этих операций, получим:
Для остальных компонент электрического поля (меняя ориентацию источников в уравнении (3) на $y$-компоненту с ортом ${\mathbf{j}}$ и $z$-компоненту с ортом ${\mathbf{k}}$), действуя аналогично, получим:
Отсюда, после интегрирования по всему пространству, получим:
Аналогичные интегральные уравнения получим, введя точечный источник сторонней магнитной индукции:
Тогда:
Вводя вектор ${\mathbf{X}} = \left( {\begin{array}{*{20}{c}} {\mathbf{E}} \\ {\mathbf{H}} \end{array}} \right)$, получим векторные объемные интегральные уравнения в случае бианизотропных сред:
(5)
${\mathbf{X}} = \int\limits_V {\left( {\begin{array}{*{20}{c}} {{{{\hat {Q}}}_{e}}(\sigma - \sigma _{0}^{T}) - i\omega {{{\hat {G}}}_{e}}(\beta - \beta _{0}^{T})}&{ - i\omega {{{\hat {G}}}_{e}}(\mu - \mu _{0}^{T}) + {{{\hat {Q}}}_{e}}(\alpha - \alpha _{0}^{T})} \\ {{{{\hat {Q}}}_{h}}(\sigma - \sigma _{0}^{T}) - i\omega {{{\hat {G}}}_{h}}(\beta - \beta _{0}^{T})}&{ - i\omega {{{\hat {G}}}_{h}}(\mu - \mu _{0}^{T}) + {{{\hat {Q}}}_{h}}(\alpha - \alpha _{0}^{T})} \end{array}} \right){\mathbf{X}}dv} + {{{\mathbf{X}}}^{f}},$Здесь интегрирование производится по области источников и носителей неоднородностей во вмещающей среде с параметрами ${{\sigma }_{0}}$, ${{\mu }_{0}}$, ${{\alpha }_{0}}$, ${{\beta }_{0}}$.
РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Для практических вычислений в качестве вмещающей среды использовалось однородное изотропное пространство. Найдем выражения для тензорной функции Грина электрического ${{\hat {Q}}_{e}} = \left( {\begin{array}{*{20}{c}} {{\mathbf{Q}}{{{_{x}^{e}}}^{T}}} \\ {{\mathbf{Q}}{{{_{y}^{e}}}^{T}}} \\ {{\mathbf{Q}}{{{_{z}^{e}}}^{T}}} \end{array}} \right)$ и магнитного ${{\hat {G}}_{e}} = \left( {\begin{array}{*{20}{c}} {{\mathbf{G}}_{x}^{{eT}}} \\ {{\mathbf{G}}_{y}^{{eT}}} \\ {{\mathbf{G}}_{z}^{{eT}}} \end{array}} \right)$ типов. Ротируя систему уравнений (3) и (4) и учитывая ${\text{div}}{\mathbf{G}}_{x}^{e} = 0$ и ${\text{div}}{\mathbf{Q}}_{x}^{e} = - \frac{1}{{{{\sigma }_{0}}}}{\text{div}}\delta {\mathbf{i}}$, получим:
Тогда:
Учитывая, что ${{\hat {Q}}_{h}} = {{\hat {G}}_{e}}$, ${{\hat {G}}_{h}} = - \frac{{{{\sigma }_{0}}}}{{i\omega {{\mu }_{0}}}}{{\hat {Q}}_{e}}$, получим:
Последнее уравнение можно привести к виду:
$Q = \left( {\begin{array}{*{20}{c}} {{{{\hat {Q}}}_{e}}}&{{{{\hat {G}}}_{e}}} \\ {{{{\hat {G}}}_{e}}}&{ - \frac{{{{\sigma }_{0}}}}{{i\omega {{\mu }_{0}}}}{{{\hat {Q}}}_{e}}} \end{array}} \right);$ $G = \left( {\begin{array}{*{20}{c}} {{{{\hat {Q}}}_{e}}}&{{{{\hat {G}}}_{e}}} \\ {{{{\hat {G}}}_{e}}}&{ - \frac{{{{\sigma }_{0}}}}{{i\omega {{\mu }_{0}}}}{{{\hat {Q}}}_{e}}} \end{array}} \right)$ – тензорные функции Грина электродинамической задачи. Теория функций Грина хорошо разработана (см., например, [Дмитриев, 2012]), поэтому в настоящей работе явный вид этих величин выписываться не будет.
Полагая, что в области элементарного объема $dV = \Delta x\Delta y\Delta z$ поле и электромагнитные параметры среды постоянны, переход к системе линейных алгебраических уравнений будет связан с вычислением интегралов по элементарному объему от тензорных функций Грина. Для тензорной функции Грина электрического типа получим:
Для тензорной функции Грина магнитного типа получим:
РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ ГЕОЭЛЕКТРИКИ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Решения прямых задач для большинства физических полей, используемых при изучении геологической среды, могут быть сведены к решению интегральных уравнений вида (5), где ${\mathbf{X}}$ – вектор напряженностей электромагнитного поля; ${{{\mathbf{X}}}^{f}}(x,y,z,\omega )$ – вектор первичного поля – решение прямой задачи для среды, для которой имеется функция Грина $G(x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} ',x,y,z,\omega )$; $\Delta S(x,y,z) = $ $S(x,y,z) - {{S}^{0}}$ – избыточные значения физической величины неоднородностей, которые являются искомыми, где ${{S}^{0}}$ – электромагнитные параметры вмещающей среды, $S(x,y,z)$ – электромагнитные параметры неоднородностей.
В дискретном виде, разбивая интеграл на сумму в выражении (5), получим:
где индексы означают: $p$ – точку наблюдения; $s$ – точку источника; $\nu $ – точку в неоднородности; $\Delta S$ – квадратная матрица электромагнитных параметров, имеющая квазидиагональный (принципиально для дальнейших вычислений) вид:(6)
$\Delta S = \left( {\begin{array}{*{20}{c}} {\Delta {{S}_{1}}}&{[0]}& \vdots &{[0]} \\ {[0]}&{\Delta {{S}_{2}}}& \vdots &{[0]} \\ \cdots & \cdots & \vdots & \cdots \\ {[0]}&{[0]}& \vdots &{\Delta {{S}_{N}}} \end{array}} \right),$Найдем поле в неоднородностях ${{{\mathbf{X}}}_{v}} = $ $ = G_{v}^{v}\Delta S{{{\mathbf{X}}}_{v}} + {\mathbf{X}}_{v}^{s}$, тогда ${{{\mathbf{X}}}_{v}} = {{([1] - G_{v}^{v}\Delta S)}^{{ - 1}}}{\mathbf{X}}_{v}^{s}$.
Отсюда ${{{\mathbf{X}}}^{p}} = G_{v}^{p}\Delta S{{{\mathbf{X}}}_{v}} + {\mathbf{X}}_{p}^{s} = $ $G_{v}^{p}\Delta S([1] - $ $ - \,\,G_{v}^{v}\Delta S{{)}^{{ - 1}}}{\mathbf{X}}_{v}^{s} + {\mathbf{X}}_{p}^{s}$.
Здесь ${\mathbf{X}}_{v}^{s}$ – поле от источника в неоднородность, вычисляется через функцию Грина вмещающей среды, ${\mathbf{X}}_{p}^{s}$ – первичное поле в точке наблюдения, вычисляется через функцию Грина вмещающей среды.
Или для конкретного источника
Используя дополнительные источники, введем составные матрицы:
(7)
$\begin{gathered} X = [{\mathbf{X}}_{1}^{p},{\mathbf{X}}_{2}^{p},{\mathbf{X}}_{3}^{p},...,{\mathbf{X}}_{M}^{p}], \\ Y = [{\mathbf{X}}_{v}^{{{{s}_{1}}}},{\mathbf{X}}_{v}^{{{{s}_{2}}}},{\mathbf{X}}_{v}^{{{{s}_{3}}}},...,{\mathbf{X}}_{v}^{{{{s}_{M}}}}], \\ Z = [{\mathbf{X}}_{p}^{{{{s}_{1}}}},{\mathbf{X}}_{p}^{{{{s}_{2}}}},{\mathbf{X}}_{p}^{{{{s}_{3}}}},...,{\mathbf{X}}_{p}^{{{{s}_{M}}}}], \\ \end{gathered} $Перейдем от векторной системы уравнений к матричной:
Для переопределенной и нормально определенной системы из цепочки уравнений:
(8)
$\begin{gathered} \Delta {{S}^{{ - 1}}}{{(G{{_{v}^{p}}^{T}}G_{v}^{p})}^{{ - 1}}}G{{_{v}^{p}}^{T}}(X - Z) = \\ = Y + G_{v}^{v}{{(G{{_{v}^{p}}^{T}}G_{v}^{p})}^{{ - 1}}}G{{_{v}^{p}}^{T}}(X - Z). \\ \end{gathered} $Перепишем последнее уравнение в виде $\Delta {{S}^{{ - 1}}}A = B,$ где $A = {{(G{{_{v}^{p}}^{T}}G_{v}^{p})}^{{ - 1}}}G{{_{v}^{p}}^{T}}(X - Z) = \{ {{a}_{{ij}}}\} $, $B = Y + $ $ + \,\,G_{v}^{v}{{(G{{_{v}^{p}}^{T}}G_{v}^{p})}^{{ - 1}}}G{{_{v}^{p}}^{T}}(X - Z) = \{ {{b}_{{ij}}}\} $.
Последнее уравнение с учетом представления (6) разбивается на отдельные уравнения по следующе схеме:
Отсюда нахождение искомых параметров разбивается на решение отдельных систем матричных уравнений
(9)
$\begin{gathered} \Delta {{S}_{1}}^{{ - 1}}\left( {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}& \cdots &{{{a}_{{1M}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{b}_{{11}}}}&{{{b}_{{12}}}}& \cdots &{{{b}_{{1M}}}} \end{array}} \right), \\ \Delta {{S}_{2}}^{{ - 1}}\left( {\begin{array}{*{20}{c}} {{{a}_{{21}}}}&{{{a}_{{22}}}}& \cdots &{{{a}_{{2M}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{b}_{{21}}}}&{{{b}_{{22}}}}& \cdots &{{{b}_{{2M}}}} \end{array}} \right), \\ ............................................................. \\ \Delta {{S}_{N}}^{{ - 1}}\left( {\begin{array}{*{20}{c}} {{{a}_{{N1}}}}&{{{a}_{{N2}}}}& \cdots &{{{a}_{{NM}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{b}_{{N1}}}}&{{{b}_{{N2}}}}& \cdots &{{{b}_{{NM}}}} \end{array}} \right). \\ \end{gathered} $Подматрицы ${{a}_{{ij}}}$ имеют размеры 6 × 1 (вектор-столбец). Для разрешимости каждого из этих уравнений необходимо минимум 6 источников. В случае 6 источников система уравнений является нормально определенной, в случае большего количества источников система уравнений становиться переопределенной, в случае менее 6 источников система уравнений становится недоопределенной и в дальнейшем последний случай рассматриваться не будет.
Отметим, что параметры среды вычисляются для каждой частоты, что позволяет восстанавливать частотную зависимость электромагнитных параметров горной породы.
ПРИМЕР РЕШЕНИЯ ПРЯМОЙ И ОБРАТНОЙ ЗАДАЧИ НА ОСНОВЕ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
В настоящее время активно развивается георадарный метод изучения гоэлектрической среды. Особенностью этого метода является использование высокочастотного источника и основным изучаемым электромагнитным параметром является диэлектрическая проницаемость среды. Однако нельзя исключать и другие электромагнитные параметры (бианизотропные), которые могут влиять на взаимодействие высокочастотного электромагнитного поля и сплошной среды. В связи с этим рассмотрим решения прямых и обратных задач на примере георадарного метода.
С использованием изложенного подхода был разработан алгоритм и создано программное обеспечение математического моделирования электромагнитных полей в линейных трехмерных неоднородных средах, при этом, в целях упрощения изложения, функция Грина вмещающей среды взята для однородного пространства. Программа позволяет вычислять все компоненты электромагнитного поля ${{E}_{x}}$, ${{E}_{y}}$, ${{E}_{z}}$, ${{H}_{x}}$, ${{H}_{y}}$, ${{H}_{z}}$ от всех возможных видов источников – ${{J}_{x}}^{{ext}}$, ${{J}_{y}}^{{ext}}$, ${{J}_{z}}^{{ext}}$, ${{B}_{x}}^{{ext}}$, ${{B}_{y}}^{{ext}}$, ${{B}_{z}}^{{ext}}$. Количество сторонних источников электрического типа (${{J}_{x}}^{{ext}}$, ${{J}_{y}}^{{ext}}$, ${{J}_{z}}^{{ext}}$), и сторонних источников магнитного типа (${{B}_{x}}^{{ext}}$, ${{B}_{y}}^{{ext}}$, ${{B}_{z}}^{{ext}}$), сосредоточенных в одной точке равно шести ($k = 6$). Этого достаточно, чтобы сформировать составные матрицы в выражении (7) и разрешить системы линейных алгебраических уравнений (9) относительно искомых электромагнитных параметров неоднородностей.
Рассмотрим изотропную вмещающую среду с параметрами воздуха: ${{\sigma }_{0}} = {{10}^{{ - 14}}} + i\omega \varepsilon ,$ $\varepsilon = \frac{1}{{36\pi }}{{10}^{{ - 9}}}\,\,{{\text{Ф}} \mathord{\left/ {\vphantom {{\text{Ф}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$, ${{\mu }_{0}} = 4\pi {{10}^{{ - 7}}}\,\,{{{\text{Гн}}} \mathord{\left/ {\vphantom {{{\text{Гн}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$, ${{\alpha }_{0}} = {{\beta }_{0}} = [0]$, где $[0]$ – нулевая матрица размерностью 3 × 3.
Рассмотрим объемный источник, частотой $\omega = 2\pi {{10}^{6}}\,{\text{Гц}}$, в виде куба со сторонами $\Delta x = 0.01\,{\text{м}}$, $\Delta y = 0.01\,{\text{м}}$, $\Delta z = 0.01\,{\text{м}}$, параллельными осям координат, центр которого находится в точке с координатами (0,0, ${{Z}_{s}} = 0.1\,{\text{м}}$). На рис. 1 его местоположение отмечено окружностью черного цвета на соответствующей глубине. Местоположение приемников в плоскости $Z = 0$ обозначены красными точками, неоднородность – звездочкой синего цвета, которая имеет размер $0.1\,{\text{м}} \times 0.1\,{\text{м}} \times 0.1\,{\text{м}}$ и находится на глубине $2\,{\text{м}}$ (рис.1).
Рис. 1.
Система наблюдения и модель среды, используемая при численном решении прямых и обратных задач георадарного метода.

Пример 1. Решение прямой задачи для изотропной неоднородности.
Неоднородность – проводящий объект с параметрами
На рис. 2 приведены только действительная и мнимая часть $x$ – компоненты напряженности электрического поля ${{E}_{x}}$ от источника $J_{x}^{{ext}}$.
Рис. 2.
Действительная и мнимая часть $x$ – компоненты напряженности электрического поля ${{E}_{x}}$ от источника $J_{x}^{{ext}}$.

Пример 2. Решение прямой задачи для бианизотропной неоднородности.
Неоднородность – проводящий объект с параметрами
На рис. 3 приведены действительные и мнимые части всех компонент электромагнитного поля от всех источников.
Рис. 3.
Действительная и мнимая части компонент электромагнитного поля от точечного источника $J_{x}^{{ext}}$.
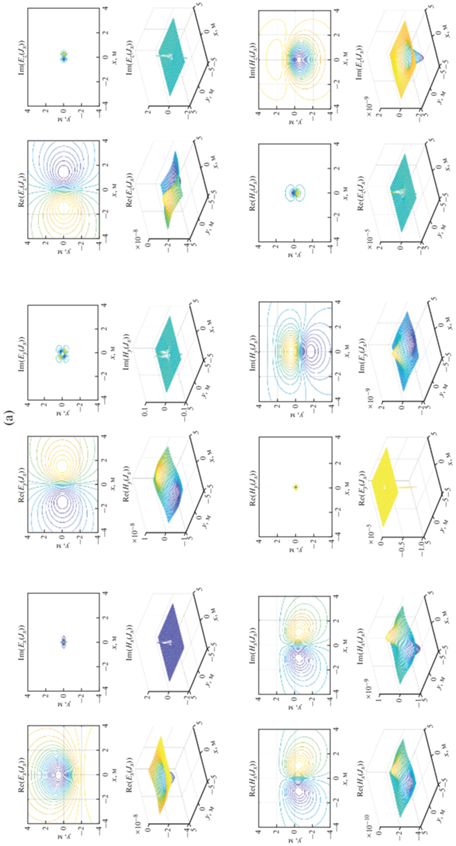
Рис. 3.
Продолжение.

Рис. 3.
Продолжение.

Рис. 3.
Продолжение.
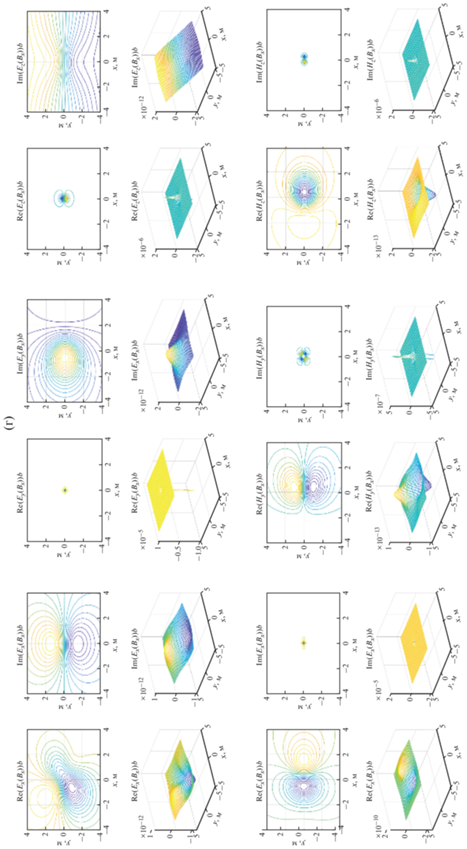
Рис. 3.
Продолжение.
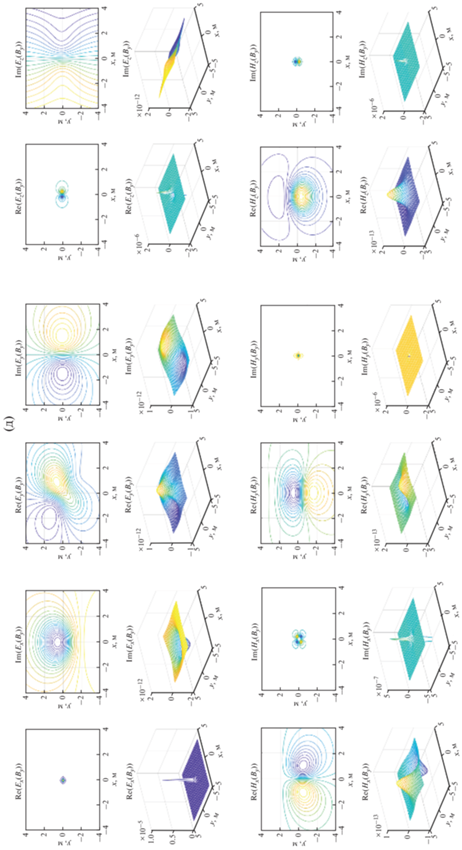
Рис. 3.
Окончание.

Пример 3. Решение обратной задачи на основе примера 2.
Ниже приведены результаты решения обратной задачи на основе изложенного выше алгоритма. Индекс “исх” означает исходный тензор, “найд” – найденные значения тензора на основе алгоритма решения обратной задачи. В таблицах приведено покомпонентное сравнение величин.
Тензор удельной электропроводности:
| $\begin{array}{*{20}{c}} {\sigma _{{ij}}^{{{\text{исх}}}}} \\ {\sigma _{{ij}}^{{{\text{найд}}}}} \end{array}$ | j = 1 | j= 2 | j = 3 |
|---|---|---|---|
| i = 1 | $1.0000e - 02{\text{ }} + {\text{ }}5.5556e - 04i$ $9.9992e - 03{\text{ }} + {\text{ }}5.0129e - 04i$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$$ - 1.2060e - 10{\text{ }} + {\text{ }}1.0243e - 12i$ | $0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $7.0693e - 07{\text{ }} + {\text{ }}2.1142e - 08i$ |
| i = 2 | $0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $ - 1.2060e - 10{\text{ }} + {\text{ }}1.0243e - 12i$ |
$1.0000e - 02{\text{ }} + {\text{ }}5.5556e - 04i$ $9.9992e - 03{\text{ }} + {\text{ }}5.0129e - 04i$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $ - 7.0693e - 07{\text{ }} - {\text{ }}2.1142e - 08i$ |
| i = 3 | $0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $ - 4.9504e - 09{\text{ }} + {\text{ }}8.6426e - 09i$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ |
$1.0000e - 02{\text{ }} + {\text{ }}5.5556e - 04i$$1.0000e - 02{\text{ }} + {\text{ }}4.9767e - 04i$ |
Относительная погрешность ${{\left\| {\sigma _{{}}^{{{\text{исх}}}} - \sigma _{{}}^{{{\text{найд}}}}} \right\|} \mathord{\left/ {\vphantom {{\left\| {\sigma _{{}}^{{{\text{исх}}}} - \sigma _{{}}^{{{\text{найд}}}}} \right\|} {\left\| {\sigma _{{}}^{{{\text{исх}}}}} \right\|}}} \right. \kern-0em} {\left\| {\sigma _{{}}^{{{\text{исх}}}}} \right\|}} \times 100\% = 0.0263\% .$
Тензор магнитной проницаемости:
| $\begin{array}{*{20}{c}} {\mu _{{ij}}^{{{\text{исх}}}}} \\ {\mu _{{ij}}^{{{\text{найд}}}}} \end{array}$ | j =1 | j = 2 | j = 3 |
|---|---|---|---|
| i = 1 | $2.5133e - 06$ $1.2569e - 06{\text{ }} + {\text{ }}6.6473e - 11i~$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $2.7070e - 14{\text{ }} + {\text{ }}1.4564e - 10i$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $ - 2.7549e - 14{\text{ }} + {\text{ }}7.9235e - 11i$ |
| i = 2 | $0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $2.7070e - 14{\text{ }} + {\text{ }}1.4564e - 10i~$ |
$2.5133e - 06$ $1.2569e - 06{\text{ }} + {\text{ }}6.6473e - 11i$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $2.7549e - 14{\text{ }} - {\text{ }}7.9235e - 11i$ |
| i = 3 | $0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $ - 2.3788e - 10{\text{ }} + {\text{ }}8.2058e - 11i$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$$2.3788e - 10{\text{ }} - {\text{ }}8.2058e - 11i$ | $2.5133e - 06$ $1.2566e - 06{\text{ }} - {\text{ }}1.6425e - 10i$ |
Относительная погрешность ${{\left\| {\mu _{{}}^{{{\text{исх}}}} - \mu _{{}}^{{{\text{найд}}}}} \right\|} \mathord{\left/ {\vphantom {{\left\| {\mu _{{}}^{{{\text{исх}}}} - \mu _{{}}^{{{\text{найд}}}}} \right\|} {\left\| {\mu _{{}}^{{{\text{исх}}}}} \right\|}}} \right. \kern-0em} {\left\| {\mu _{{}}^{{{\text{исх}}}}} \right\|}} \times 100\% = 0.0378\% .$
Бианизотропный параметр $\alpha $:
| $\begin{array}{*{20}{c}} {\alpha _{{ij}}^{{{\text{исх}}}}} \\ {\alpha _{{ij}}^{{{\text{найд}}}}} \end{array}$ | j = 1 | j = 2 | j = 3 |
|---|---|---|---|
| i = 1 | $0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $1.3044e - 11{\text{ }} + {\text{ }}1.4309e - 13i$ |
$0.0000e + 00{\text{ }} - {\text{ }}7.8957e - 04i$ $9.4320e - 08{\text{ }} - {\text{ }}7.8927e - 04i$ |
$0.0000e + 00{\text{ }} - {\text{ }}7.8957e - 04i$ $1.0333e - 07{\text{ }} - {\text{ }}7.8957e - 04i$ |
| i = 2 | $0.0000e + 00{\text{ }} + {\text{ }}7.8957e - 04i$ $ - 9.4320e - 08{\text{ }} + {\text{ }}7.8927e - 04i~$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $ - 1.3044e - 11{\text{ }} - {\text{ }}1.4310e - 13i$ |
$0.0000e + 00{\text{ }} - {\text{ }}7.8957e - 04i$ $1.0333e - 07{\text{ }} - {\text{ }}7.8957e - 04i$ |
| i = 3 | $0.0000e + 00{\text{ }} + {\text{ }}7.8957e - 04i$ $1.8515e - 07{\text{ }} + {\text{ }}7.8958e - 04i$ |
$0.0000e + 00{\text{ }} + {\text{ }}7.8957e - 04i$ $1.8515e - 07{\text{ }} + {\text{ }}7.8958e - 04i$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $4.6420e - 18{\text{ }} + {\text{ }}1.5556e - 18i$ |
Относительная погрешность решения обратной задачи относительно бианизотропного параметра $\alpha $ ${{\left\| {\alpha _{{}}^{{{\text{исх}}}} - \alpha _{{}}^{{{\text{найд}}}}} \right\|} \mathord{\left/ {\vphantom {{\left\| {\alpha _{{}}^{{{\text{исх}}}} - \alpha _{{}}^{{{\text{найд}}}}} \right\|} {\left\| {\alpha _{{}}^{{{\text{исх}}}}} \right\|}}} \right. \kern-0em} {\left\| {\alpha _{{}}^{{{\text{исх}}}}} \right\|}} \times 100\% = 0.0301\% .$
Бианизотропный параметр $\beta $:
| $\begin{array}{*{20}{c}} {\beta _{{ij}}^{{{\text{исх}}}}} \\ {\beta _{{ij}}^{{{\text{найд}}}}} \end{array}$ | j = 1 | j = 2 | j = 3 |
|---|---|---|---|
| i = 1 | $0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i$ $ - 1.8980e - 15{\text{ }} + {\text{ }}1.1368e - 15i$ |
$0.0000e + 00{\text{ }} + {\text{ }}7.8957e - 06i~$ $ - 1.0034e - 09{\text{ }} + {\text{ }}7.8951e - 06i$ |
$0.0000e + 00{\text{ }} + {\text{ }}7.8957e - 06i$ $1.8447e - 09{\text{ }} + {\text{ }}7.8952e - 06i$ |
| i = 2 | $0.0000e + 00{\text{ }} - {\text{ }}7.8957e - 06i~$ $1.0034e - 09{\text{ }} - {\text{ }}7.8951e - 06i~$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i~$ $1.8979e - 15{\text{ }} - {\text{ }}1.1366e - 15i$ |
$0.0000e + 00{\text{ }} + {\text{ }}7.8957e - 06i$ $1.8447e - 09{\text{ }} + {\text{ }}7.8952e - 06i$ |
| i = 3 | $0.0000e + 00{\text{ }} - {\text{ }}7.8957e - 06i~$ $1.0399e - 09{\text{ }} - {\text{ }}7.8951e - 06i$ |
$0.0000e + 00{\text{ }} - {\text{ }}7.8957e - 06i$ $1.0399e - 09{\text{ }} - {\text{ }}7.8951e - 06i$ |
$0.0000e + 00{\text{ }} + {\text{ }}0.0000e + 00i~$ $ - 2.8947e - 19{\text{ }} - {\text{ }}5.2818e - 18i$ |
Относительная погрешность решения обратной задачи относительно бианизотропного параметра $\beta $ составляет ${{\left\| {\beta _{{}}^{{{\text{исх}}}} - \beta _{{}}^{{{\text{найд}}}}} \right\|} \mathord{\left/ {\vphantom {{\left\| {\beta _{{}}^{{{\text{исх}}}} - \beta _{{}}^{{{\text{найд}}}}} \right\|} {\left\| {\beta _{{}}^{{{\text{исх}}}}} \right\|}}} \right. \kern-0em} {\left\| {\beta _{{}}^{{{\text{исх}}}}} \right\|}} \times 100\% = 0.0215\% .$
Таким образом, проведенный вычислительный эксперимент демонстрирует возможность решения обратных задач геоэлектрики бианизотропных сред – восстановление всех электромагнитных параметров линейных сред, с достаточной точностью.
ВЫВОДЫ
1. Рассмотренный подход к решению обратных задач геоэлектрики приводит к решению системы линейных алгебраических уравнений, что упрощает анализ устойчивости, точности и разрешающей способности геофизических методов по решению геологических задач.
2. Единственным требованием к данной постановке обратных задач является требование линейности материальных уравнений. При этом электромагнитные параметры могут зависеть от частоты и, следовательно, решение обратной задачи на основе изложенного подхода позволяет восстанавливать их частотную зависимость.
3. Новизной данного подхода является использование таких типов источников и такого их количества, которые позволяет сформулировать линейную постановку обратных задач геофизики. Это накладывает определенные требования к аппаратуре и системам полевых наблюдений.
Список литературы
Александров П.Н. Эффективные электромагнитные параметры капиллярной системы электропроводности горной породы // Физика Земли. 2000. № 2. С. 87–94.
Александров П.Н. Теоретические основы георадарного метода. М.: ФИЗМАТЛИТ. 2017. 120 с. ISBN 978-5-9221-1701-2.
Бурсиан В.Р. Теория электромагнитных полей, применяемых в электроразведке. Л.: Недра. 1972. 368с.
Дмитриев В.И. Обратные задачи геофизики. М.: МАКС Пресс. 2012. 340с.
Туров Е.А. Материальные уравнения электродинамики. М.: Наука. 1983. 158 с.
Bursian V., Timorew A. Zur Theorie der optisch aktiven isotropen Medien. Zeitschrift fur Physik. Bd. XXXVIII. 1926. P. 475–484.
Дополнительные материалы отсутствуют.


