Известия РАН. Энергетика, 2020, № 5, стр. 32-39

Электродинамические силы, действующие на линию с током, проложенную вдоль протяженных металлических конструкций

Г. Н. Цицикян^1, *, А. И. Сенченко^1, **

¹ Филиал “ЦНИИ СЭТ”ФГУП “Крыловский государственный научный центр”
Санкт-Петербург, Россия

^* E-mail: george.20021940@mail.ru
^** E-mail: spb-1205@mail.ru

Поступила в редакцию 09.06.2020
После доработки 27.07.2020
Принята к публикации 30.07.2020

DOI: 10.31857/S0002331020050106

Аннотация

Выражения для электродинамических сил в системе прямолинейных линий с током, проложенных вдоль протяженных сплошных металлических конструкций, получены двумя методами с использованием вносимых коэффициентов самоиндукции, в пределе, когда либо удельная проводимость материала, либо его магнитная проницаемость весьма велики и с помощью векторов магнитной индукции. Выражения для электродинамических сил между трехпроводной линией и сплошной металлической конструкцией получены для важного в практическом отношении случая трехфазной системы токов.

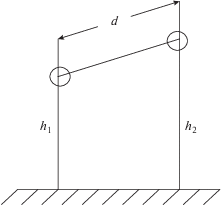
Ключевые слова: линия с током, металлическая обшивка, электродинамические силы, сопоставление методов определения

Электродинамические силы, действующие на линию с током, проложенную вдоль металлических конструкций, могут быть определены, если известна ее индуктивность с учетом хорошо проводящих и ферромагнитных оболочек, характерных для транспортных средств с металлической обшивкой, например, в судостроении и авиации. Существуют две возможности для нахождения электродинамических сил, действующих на провода линии с расстоянием d друг от друга, одна из которых предполагает использование соответствующих связей между силой взаимодействия ${{f}_{d}}$ в направлении d (рис. 1) и выражениями для индуктивности линии, если они известны в тех или иных конкретных ситуациях, а именно:

(1)

${{f}_{d}} = \frac{1}{2}{{i}^{2}}\frac{{\partial L}}{{\partial d}}.$

Рис. 1.

К вопросу о вносимой индуктивности в линию $(\mu \to \infty ,\,\,\gamma \to \infty ).$

Другая возможность определения электродинамических сил состоит в нахождении векторов магнитной индукции с применением векторного произведения для элементарной силы

(2)

$id\vec {l} \times \vec {B}$

с последующим суммированием вдоль линии. В случае плоскопараллельного магнитного поля это достигается наиболее просто.

Можно заимствовать выражения для коэффициентов самоиндукции с учетом влияния металлических оболочек, как правило, листовых конструкций, в свою очередь, в двух основных случаях когда $\mu = {{\mu }_{0}},$ но удельная проводимость достаточно велика $(\gamma \to \infty ),$ и когда удельная проводимость относительно мала, но магнитная проницаемость достаточно велика $(\mu \to \infty )$ [1]. Второй путь предполагает нахождение магнитной индукции в соответствии с указанными предпосылками. Решение для двухпроводной линии при конечном $\gamma $ и $\mu = {{\mu }_{0}}$ будет приведено для синусоидального изменения тока во времени.

В справочном руководстве [1] в разделе плоский магнитный экран приведены выражения для вносимых индуктивностей $\Delta L$ в линию при $(\mu \to \infty ).$ Для случая $(\gamma \to \infty )$ те же выражения следует брать со знаком минус, что и отмечено на примере формулы (11–5) в [1].

Вносимая индуктивность в [1] для линии (рис. 1) записана в виде:

(3)

$\Delta L = \frac{{{{\mu }_{0}}}}{{2\pi }}\ln \left( {1 + \frac{{{{d}^{2}}}}{{4{{h}_{1}}{{h}_{2}}}}} \right),$

а собственная индуктивность линии в виде:

(4)

$L{\kern 1pt} ' = \frac{{{{\mu }_{0}}}}{\pi }\left( {\ln \frac{d}{r} + \frac{1}{4}} \right),$

где r – радиус провода.

Тогда будем иметь: $L = L{\kern 1pt} '\, \pm \Delta L,$ где знак плюс следует брать при $(\mu \to \infty ),$ а знак минус при $(\gamma \to \infty ).$ Для электродинамической силы взаимодействия в линии с учетом (3) и (4) находим:

(5)

${{\left. {{{f}_{d}}} \right|}_{{{{h}_{1}} \ne {{h}_{2}}}}} = \frac{1}{2}{{i}^{2}}\frac{{\partial L}}{{\partial d}} = \frac{1}{2}{{i}^{2}}\frac{{\partial \left( {L{\kern 1pt} '\, \pm \Delta L} \right)}}{{\partial d}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\left( {1 \pm \frac{{{{d}^{2}}}}{{4{{h}_{1}}{{h}_{2}} + {{d}^{2}}}}} \right).$

Для верхнего знака $(\mu \to \infty )$ будем иметь:

(6)

${{\left. {{{f}_{d}}} \right|}_{{{{h}_{1}} \ne {{h}_{2}},\,\,{\mu } \to \infty }}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\frac{{4{{h}_{1}}{{h}_{2}} + 2{{d}^{2}}}}{{4{{h}_{1}}{{h}_{2}} + {{d}^{2}}}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{\pi d}}\frac{{2{{h}_{1}}{{h}_{2}} + {{d}^{2}}}}{{4{{h}_{1}}{{h}_{2}} + {{d}^{2}}}},$

а для $(\gamma \to \infty ),$ т.е. для нижнего знака:

(7)

${{\left. {{{f}_{d}}} \right|}_{{{{h}_{1}} \ne {{h}_{2}},\,\,{\gamma } \to \infty }}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{\pi d}}\frac{{2{{h}_{1}}{{h}_{2}}}}{{4{{h}_{1}}{{h}_{2}} + {{d}^{2}}}}.$

При ${{h}_{1}} = {{h}_{2}} = h$

(8)

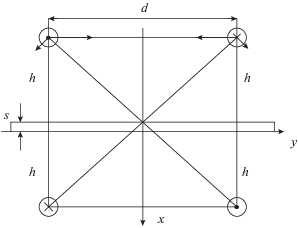
${{\left. {{{f}_{d}}} \right|}_{{{{h}_{1}} = {{h}_{2}} = h}}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\left( {1 \pm \frac{{{{d}^{2}}}}{{4{{h}^{2}} + {{d}^{2}}}}} \right).$

Остановимся на вопросе, связанном с оценкой взаимодействия собственно двухпроводной линии над хорошо проводящей плоской листовой оболочкой толщиной s, показанной на (рис. 2) с векторами магнитной индукции, которые и обуславливают электродинамические силы в направлении оси x.

Рис. 2.

Двухпроводная линия над плоской листовой оболочкой.

Тогда:

(9)

${{B}_{y}} = \frac{{{{\mu }_{0}}i}}{{2\pi 2h}} - \frac{{{{\mu }_{0}}i}}{{2\pi }}\frac{{2h}}{{\left( {{{d}^{2}} + 4{{h}^{2}}} \right)}} = \frac{{{{\mu }_{0}}i}}{{2\pi 2h}}\left( {1 - \frac{{4{{h}^{2}}}}{{{{d}^{2}} + 4{{h}^{2}}}}} \right) = \frac{{{{\mu }_{0}}i}}{{4\pi h}}{{\left[ {1 + {{{\left( {\frac{{2h}}{d}} \right)}}^{2}}} \right]}^{{ - 1}}}.$

С учетом второго проводника линии с током противоположного направления, имеем в совокупности величину силы в направлении координаты х в виде

(10)

${{f}_{x}} = - \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi h}}\frac{1}{{1 + {{{\left( {\frac{{2h}}{d}} \right)}}^{2}}}}.$

В [3] этот результат записан для средней во времени силы при синусоидальном процессе в следующем виде:

(11)

${{\left. {{{F}_{x}}} \right|}_{{({\gamma } \to \infty )}}} = - \frac{{{{\mu }_{0}}{{I}^{2}}}}{{2\pi h}}\frac{1}{{1 + {{{\left( {\frac{{2h}}{d}} \right)}}^{2}}}},$

где I – действующее значение тока. В [3] приведено также выражение для средней во времени силы, но с учетом конечной проводимости $\gamma $ листовой оболочки, которую можно записать с учетом принятых здесь обозначений в следующем виде.

(12)

$\begin{gathered} {{F}_{x}} = - \frac{{{{\mu }_{0}}{{I}^{2}}}}{{4\pi h}}\operatorname{Re} \left\{ {j\,2\beta h\left[ {2{{e}^{{j2{\beta }h}}}{{E}_{1}}\left( {j\,2\beta h} \right) - {{e}^{{{\beta }d + j2{\beta }h}}}{{E}_{1}}\left( {\beta d + j\,2\beta h} \right) - } \right.} \right. \\ \left. {\left. { - \,\,{{e}^{{ - {\beta }d + j2{\beta }h}}}{{E}_{1}}\left( { - \beta d + j\,2\beta h} \right)} \right]} \right\}, \\ \end{gathered} $

где $\beta h = 0.5\omega {{\mu }_{0}}\gamma hs,$ $\omega $ – круговая частота, $s$ – толщина листа (рис. 2), а ${{E}_{1}}(z)$ – интегральная показательная функция от комплексного аргумента. Пользуясь ее асимптотическим разложением и ограничиваясь первым членом этого же разложения [4, 51.51] ${{E}_{1}}(z) \approx \frac{{{{e}^{{ - z}}}}}{z}$, где $z$ достаточно велико, получим:

${{F}_{x}} = - \frac{{{{\mu }_{0}}{{I}^{2}}}}{{2\pi h}}\frac{1}{{1 + {{{\left( {\frac{{2h}}{d}} \right)}}^{2}}}},$

т.е. выражение (11). Здесь следует отметить, что в оригинале [3.(П-24б)] по сравнению с (12) допущена опечатка: вместо $\frac{{{{\mu }_{0}}{{I}^{2}}}}{{2\pi h}}$ должно быть $\frac{{{{\mu }_{0}}{{I}^{2}}}}{{4\pi h}}.$

Рассмотрим линию с прямым и обратным током, расположенную вблизи проводящего массива с плоской границей (рис. 3), предполагая $(\gamma \to \infty ).$ Введем обозначения ${{r}_{1}} = 2{{h}_{1}},$ ${{r}_{2}} = 2{{h}_{2}},$ $r_{1}^{'} = r_{2}^{'} = r$ и остановимся на z – составляющей векторного потенциала прямолинейных токов в предположении плоскопараллельности магнитного поля (ось z направлена от плоскости рисунка к наблюдателю).

Рис. 3.

Линия с прямым и обратным током: d – расстояние между осями, h₁ и h₂ – высота проложения прямолинейных проводов с током.

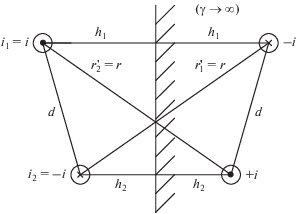
Тогда с точностью до постоянной z – составляющая векторного потенциала от тока (–i) и от тока (i) зеркальных отображений (рис. 3) на оси тока ${{i}_{1}} = i$ равна:

$\frac{{{{\mu }_{0}}i}}{{2\pi }}\ln 2{{h}_{1}} - \frac{{{{\mu }_{0}}i}}{{2\pi }}r_{2}^{'},$

а z – составляющая векторного потенциала от тех же зеркально отображенных токов, но на оси тока (–i) равна:

$ - \frac{{{{\mu }_{0}}i}}{{2\pi }}\ln 2{{h}_{2}} + \frac{{{{\mu }_{0}}i}}{{2\pi }}\ln r_{1}^{'}.$

Разность этих составляющих определяет собой вносимый поток на единицу длины рассматриваемой линии, равный:

$\frac{{{{\mu }_{0}}i}}{{2\pi }}\ln 2{{h}_{1}} + \ln 2{{h}_{2}} - \frac{{{{\mu }_{0}}i}}{{2\pi }}\ln r.$

Разделив записанное выражение на i, получим вносимую индуктивность от проводящего полупространства при $(\gamma \to \infty ).$ При $(\mu \to \infty )$ вносимой индуктивности следует приписать обратный знак. Таким образом, для вносимой индуктивности имеем:

(13)

$\begin{gathered} \Delta L = \frac{{{{\mu }_{0}}}}{{2\pi }}\left[ {\ln \left( {4{{h}_{1}}{{h}_{2}}} \right) - \ln {{r}^{2}}} \right] = \frac{{{{\mu }_{0}}}}{{2\pi }}\left\{ {\ln \left( {4{{h}_{1}}{{h}_{2}}} \right) - \ln \left[ {{{{\left( {{{h}_{1}} + {{h}_{2}}} \right)}}^{2}} + {{d}^{2}} - {{{\left( {{{h}_{1}} - {{h}_{2}}} \right)}}^{2}}} \right]} \right\} = \\ = - \frac{{{{\mu }_{0}}}}{{2\pi }}\ln \left( {\frac{{{{d}^{2}} + 4{{h}_{1}}{{h}_{2}}}}{{4{{h}_{1}}{{h}_{2}}}}} \right) = - \frac{{{{\mu }_{0}}}}{{2\pi }}\ln \left( {1 + \frac{{{{d}^{2}}}}{{4{{h}_{1}}{{h}_{2}}}}} \right) \\ \end{gathered} $

в полном соответствии с выражениями (11–5) и (11–29) [1]. Для $(\mu \to \infty )$ в формуле (13) следует изменить знак на противоположный. При ${{h}_{1}} = {{h}_{2}} = h$ вносимая индуктивность равна:

(14)

$\Delta L = \mp \frac{{{{\mu }_{0}}}}{{2\pi }}\ln \left( {1 + \frac{{{{d}^{2}}}}{{4{{h}^{2}}}}} \right).$

Теперь можно записать и вносимую электродинамическую силу, обусловленную близостью проводящего массива в предположении $(\gamma \to \infty ),$ $(\mu \to \infty ){\text{:}}$

(15)

${{\left. {\Delta {{f}_{d}}} \right|}_{{{\gamma } \to \infty ,\,\,{\mu } \to \infty }}} = \frac{{{{i}^{2}}}}{2}\frac{{\partial \left( {\Delta L} \right)}}{{\partial d}} = \mp \frac{{{{\mu }_{0}}{{i}^{2}}}}{{4\pi }}\frac{{2d}}{{4{{h}_{1}}{{h}_{2}} + {{d}^{2}}}} = \mp \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\frac{{{{d}^{2}}}}{{4{{h}_{1}}{{h}_{2}} + {{d}^{2}}}}.$

Соответственно, результирующая сила равна:

(16)

${{\left. {{{f}_{d}}} \right|}_{{{\gamma } \to \infty }}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\left[ {1 - \frac{{{{d}^{2}}}}{{4{{h}_{1}}{{h}_{2}} + {{d}^{2}}}}} \right] = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{\pi d}}\frac{{2{{h}_{1}}{{h}_{2}}}}{{4{{h}_{1}}{{h}_{2}} + {{d}^{2}}}},$

а для ${{\left. {{{f}_{d}}} \right|}_{{{\mu } \to \infty }}}$ будем иметь:

(17)

${{\left. {{{f}_{d}}} \right|}_{{{\mu } \to \infty }}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\left[ {1 + \frac{{{{d}^{2}}}}{{{{d}^{2}} + 4{{h}_{1}}{{h}_{2}}}}} \right] = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{\pi d}}\frac{{2{{h}_{1}}{{h}_{2}} + {{d}^{2}}}}{{4{{h}_{1}}{{h}_{2}} + {{d}^{2}}}}.$

В полном соответствии с (7) и (6)

При ${{h}_{1}} = {{h}_{2}} = h$

(18)

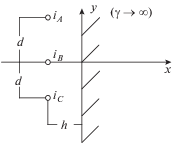
${{\left. {{{f}_{d}}} \right|}_{{{\gamma } \to \infty ,\,\,{\mu } \to \infty }}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\left[ {1 \mp \frac{{{{d}^{2}}}}{{{{d}^{2}} + 4{{h}^{2}}}}} \right].$

Перейдем к вопросу о средней во времени силы взаимодействия между трехфазной трехпроводной линией и массивом $(\gamma \to \infty )$ с плоской границей (рис. 4) в направлении оси х, когда ${{i}_{A}} + {{i}_{B}} + {{i}_{C}} = 0.$ Общее выражение для электродинамической силы ${{\left. {{{f}_{x}}} \right|}_{{{\gamma } \to \infty }}}$ может быть записано в виде.

(19)

$\begin{gathered} {{\left. {{{f}_{x}}} \right|}_{{{\gamma } \to \infty }}} = - \frac{{{{\mu }_{0}}}}{{2\pi \times 2h}}\left[ {i_{A}^{2} + i_{B}^{2} + i_{C}^{2} + 2\left( {{{i}_{A}}{{i}_{B}} + {{i}_{B}}{{i}_{C}} + {{i}_{A}}{{i}_{C}}} \right)} \right] + \\ + \,\,\frac{{{{\mu }_{0}}\left( {2{{i}_{A}}{{i}_{B}} + 2{{i}_{B}}{{i}_{C}}} \right)}}{{2\pi \times 2h}}\frac{1}{{1 + {{{\left( {\frac{{2h}}{d}} \right)}}^{2}}}} + \frac{{{{\mu }_{0}} \times 2{{i}_{A}}{{i}_{C}}}}{{2\pi \times 2h}}\frac{1}{{1 + {{{\left( {\frac{h}{d}} \right)}}^{2}}}}. \\ \end{gathered} $

Рис. 4.

Трехфазная линия вблизи плоской граничной поверхности.

Можно убедиться в том, что при выполнении условия, когда ${{i}_{C}} = - {{i}_{A}} - {{i}_{B}},$ квадратная скобка обращается в нуль, и остаются два последних члена

(20)

$\begin{gathered} - \frac{{{{\mu }_{0}} \times 2i_{B}^{2}}}{{2\pi \times 2h}}\frac{1}{{1 + {{{\left( {\frac{{2h}}{d}} \right)}}^{2}}}} - \frac{{{{\mu }_{0}} \times 2\left( {i_{A}^{2} + {{i}_{A}}{{i}_{B}}} \right)}}{{2\pi \times 2h}}\frac{1}{{1 + {{{\left( {\frac{h}{d}} \right)}}^{2}}}} = \\ = - \frac{{{{\mu }_{0}} \times 2i_{B}^{2}}}{{2\pi \times 2h}}\frac{1}{{1 + {{{\left( {\frac{{2h}}{d}} \right)}}^{2}}}} + \frac{{{{\mu }_{0}} \times 2{{i}_{A}}{{i}_{C}}}}{{2\pi \times 2h}}\frac{1}{{1 + {{{\left( {\frac{h}{d}} \right)}}^{2}}}}. \\ \end{gathered} $

Полагая теперь, что токи изменяются по синусоидальному закону и ${{i}_{A}} = {{I}_{m}}\sin \omega t,$ ${{i}_{B}} = {{I}_{m}}\sin \left( {\omega t - \frac{{2\pi }}{3}} \right),$ ${{i}_{C}} = {{I}_{m}}\sin \left( {\omega t + \frac{{2\pi }}{3}} \right),$ записываем выражения для $i_{B}^{2}$ и ${{i}_{A}}{{i}_{C}}{\text{:}}$

$\begin{gathered} i_{B}^{2} = {{I}^{2}}\left[ {1 - \cos \left( {2\omega t - \frac{{4\pi }}{3}} \right)} \right], \\ {{i}_{A}}{{i}_{C}} = I_{m}^{2}\sin \omega t\sin \left( {\omega t - \frac{{2\pi }}{3}} \right) = {{I}^{2}}\left[ {\cos \frac{{2\pi }}{3} - \cos \left( {2\omega t + \frac{{2\pi }}{3}} \right)} \right]. \\ \end{gathered} $

Тогда в среднем за период будем иметь следующее выражение для электродинамической силы

(21)

${{\left. {{{F}_{x}}} \right|}_{{{\gamma } \to \infty }}} = - \frac{{{{\mu }_{0}}{{I}^{2}}}}{{2\pi 2h}}\left[ {\frac{2}{{1 + {{{\left( {\frac{{2h}}{d}} \right)}}^{2}}}} + \frac{1}{{2 + \frac{1}{2}{{{\left( {\frac{{2h}}{d}} \right)}}^{2}}}}} \right].$

При этом обнаруживается расхождение во втором члене выражения (П-25) в [3], которое следует исправить путем замены в числителе второго члена (П-25) 2 на 1, а в знаменателе 1/8 на 1/2.

Рассмотрим теперь случай, когда двухпроводная линия проложена вдоль магнитных стенок с плоскими границами в соответствии с рис. 5.

Рис. 5.

Двухпроводная линия вдоль магнитной обшивки с расстоянием по x равным d.

Индуктивность линии на единицу длины равна:

$L = \frac{{{{\mu }_{0}}}}{\pi }\ln \left( {{d \mathord{\left/ {\vphantom {d r}} \right. \kern-0em} r} + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right),$

где r – радиус проводника, а вносимая индуктивность определяется выражением (11.31) в [1]

(22)

$\Delta L = \frac{{{{\mu }_{0}}}}{\pi }\ln \left( {\frac{h}{{\pi x}}{\text{sh}}\frac{{\pi x}}{h}} \right),$

где $x = \frac{d}{2}.$

Тогда сила электродинамического взаимодействия равна:

(23)

$\begin{gathered} f = \frac{1}{2}{{i}^{2}}\frac{{\partial \left( {L + \Delta L} \right)}}{{\partial d}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}} + \frac{1}{2}{{i}^{2}}\frac{{{{\mu }_{0}}}}{\pi }\frac{\partial }{{\partial d}}\ln \left( {\frac{{2h}}{{\pi d}}{\text{sh}}\frac{{\pi d}}{{2h}}} \right) = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}} + \frac{1}{2}\frac{{{{\mu }_{0}}{{i}^{2}}}}{\pi }\frac{\partial }{{\partial d}} \times \\ \times \,\,\left[ {\ln \frac{{2h}}{{\pi d}} + \ln \left( {{\text{sh}}\frac{{\pi d}}{{2h}}} \right)} \right] = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}} - \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}} + \frac{1}{2}\frac{{{{\mu }_{0}}{{i}^{2}}}}{\pi }\frac{{{\text{ch}}\left( {\frac{{\pi d}}{{2h}}} \right)\left( {\frac{\pi }{{2h}}} \right)}}{{{\text{sh}}\left( {\frac{{\pi d}}{{2h}}} \right)}} = \frac{1}{2}\frac{{{{\mu }_{0}}{{i}^{2}}}}{{\pi d}}\frac{{\pi d}}{{2h}}{\text{cth}}\left( {\frac{{\pi d}}{{2h}}} \right). \\ \end{gathered} $

Полагая теперь ${{\left( {\frac{{\pi d}}{{2h}}} \right)}^{2}} < {{\pi }^{2}}$ или ${{\left( {\frac{d}{{2h}}} \right)}^{2}} < 1.0$, будем иметь для этого случая

(24)

$f \cong \frac{1}{2}\frac{{{{\mu }_{0}}{{i}^{2}}}}{{\pi d}}\frac{{\pi d}}{{2h}}\left( {\frac{{2h}}{{\pi d}} + \frac{{\pi d}}{{2h \times 3}}} \right) = \frac{1}{2}\frac{{{{\mu }_{0}}{{i}^{2}}}}{{\pi d}}\left( {1 + \frac{{{{\pi }^{2}}{{d}^{2}}}}{{4{{h}^{2}} \times 3}}} \right).$

При ${{h}^{2}} \gg {{d}^{2}}$ результат сводится к силе взаимодействия двухпроводной линии без учета влияния плоского магнитного экрана, что и следовало ожидать.

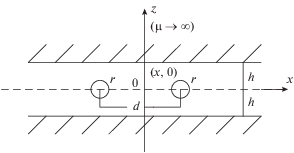
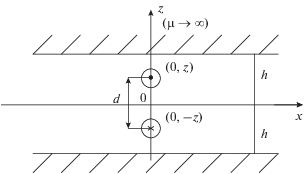
Под конец рассмотрим еще одну ситуацию, когда двухпроводная линия проложена вдоль оси z внутри металлической обшивки с плоскими границами и с высокой магнитной проницаемостью материала $(\mu \to \infty )$ (рис. 6).

Рис. 6.

Двухпроводная линия вдоль магнитной обшивки с z = d/2.

В соответствие с формулой (11–32) [1] индуктивность такой линии может быть записана в виде:

$L = {{L}_{\Lambda }} + \Delta L = \frac{{{{\mu }_{0}}}}{\pi }\ln \left( {\frac{d}{r} + \frac{1}{4}} \right) + \frac{{{{\mu }_{0}}}}{\pi }\ln \left( {\frac{{4h}}{{\pi d}}{\text{tg}}\frac{{\pi d}}{{4h}}} \right) = \frac{{{{\mu }_{0}}}}{\pi }\left[ {\ln \left( {\frac{d}{r} + \frac{1}{4}} \right) + \ln \frac{{4h}}{{\pi d}} + \ln {\text{tg}}\frac{{\pi d}}{{4h}}} \right].$

Тогда

(26)

${{f}_{z}} = \frac{1}{2}{{i}^{2}}\frac{{\partial L}}{{\partial d}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}} - \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}} + \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\frac{\partial }{{\partial d}}\ln \left( {{\text{tg}}\frac{{\pi d}}{{4h}}} \right).$

Производная по d приводит к выражению

(27)

${{f}_{d}} = \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\frac{{\frac{{\pi d}}{{2h}}}}{{\sin \left( {\frac{{\pi d}}{{2h}}} \right)}} \cong \frac{{{{\mu }_{0}}{{i}^{2}}}}{{2\pi d}}\frac{1}{{1 - {{{\left( {\frac{{\pi d}}{h}} \right)}}^{2}}\frac{1}{{3!}}}}.$

При $\frac{d}{h} \ll 1.0$ результат для ${{f}_{d}}$ вполне предсказуем.

Т.о., рассмотрены два подхода к вопросу о силах, действующих на двухпроводную и трехпроводную линию, проложенную вдоль протяженной листовой конструкции. Проведены необходимые сопоставления и отмечены некоторые расхождения с указанием по их исправлению. Получены выражения для силы взаимодействия в линии, проложенной вдоль магнитных стенок с плоскими границами.

Список литературы

Калантаров П.Л., Цейтлин Л.А. Расчет индуктивностей. Л. Энергоатомиздат. Ленингр. отд-ние. 1986. 488 с.
Цицикян Г.Н. Электродинамические силы в токоведущих частях электротехнических комплексов. Издание ФГУП “Крыловский государственный научный центр”. 2016. 93 с.
Кузнецов И.Ф., Цицикян Г.Н. Электродинамические усилия в токоведущих частях электрических аппаратов и токопровода. Л.: Энергоатомиздат. Ленингр. отд-ние, 1989. 176 с.
Справочник по специальным функциям с формулами, графиками и математическими таблицами. Под ред. Абрамовица М. и Стиган Н. М. Изд. “Наука”, 1979. 832 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал