Космические исследования, 2020, T. 58, № 4, стр. 291-304
Исследование эволюции вращательного движения спутника Фотон М-2
Д. М. Буланов 1, В. В. Сазонов 2, *
1 Московский государственный университет им. М.В. Ломоносова
г. Москва, Россия
2 Институт прикладной математики им. М.В. Келдыша РАН
г. Москва, Россия
* E-mail: sazonov@keldysh.ru
Поступила в редакцию 24.09.2019
После доработки 24.09.2019
Принята к публикации 23.10.2019
Аннотация
Описаны результаты повторной обработки магнитных измерений, выполненных на спутнике Фотон М-2 (находился на орбите 31.V–16.VI.2005). Обработка проводилась с целью реконструкции неуправляемого вращательного движения этого спутника. При повторной обработке использовалась более простая математическая модель вращательного движения, чем при обработке, выполненной вскоре после полета. Упрощения сделаны таким образом, чтобы новая модель соответствовала моделям, использованным В.В. Белецким в его теоретическом анализе эволюции неуправляемого вращательного движения спутника в случае, когда это движение близко к регулярной прецессии Эйлера осесимметричного твердого тела. Результаты обработки измерений на 14 непродолжительных (4.5–5 ч) интервалах времени напрямую сопоставлены с эволюционными уравнениями, возникающими в теории В.В. Белецкого. Это позволило интерпретировать эволюцию вращательного движения Фотона М-2 и объяснить возникновение режима движения, установившегося к концу полета.
1. ВВЕДЕНИЕ
Вскоре после полета Фотона М-2 его вращательное движение было реконструировано с помощью достаточно детальных математических моделей [1, 2]. Наиболее детальная реконструкция была выполнена по данным бортовых измерений напряженности магнитного поля Земли (МПЗ). Из этих данных, охватывающих первые две трети полета, выбирались отрезки длиной несколько часов. На каждом таком отрезке данные обрабатывались совместно методом наименьших квадратов с помощью интегрирования уравнений движения спутника относительно центра масс. При обработке оценивались начальные условия движения и параметры используемой математической модели. Полученные результаты дали полное представление о движении спутника. Это движение, начавшееся с малой угловой скоростью, постепенно становилось быстрее и через двое суток стало близко к регулярной прецессии Эйлера осесимметричного твердого тела. В последний день измерений 9.VI.2005 угловая скорость спутника относительно его продольной оси составляла примерно 1.1 град/с, проекция угловой скорости на плоскость, перпендикулярную этой оси, имела модуль около 0.11 град/с.
Ниже описаны результаты повторной обработки отрезков магнитных измерений, использованных в [1]. Обработка проведена с помощью более простой, чем в [1, 2], математической модели вращательного движения спутника. Упрощения сделаны таким образом, чтобы новая модель соответствовала моделям, использованным В.В. Белецким в его теоретическом анализе эволюции неуправляемого вращательного движения спутника в случае, когда это движение близко регулярной прецессии Эйлера осесимметричного твердого тела [3]. В результате за счет некоторого огрубления реконструкции удалось напрямую сопоставить полученные экспериментальные результаты с теорией и провести их детальный анализ.
2. УПРОЩЕННЫЕ УРАВНЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ СПУТНИКА
Спутник считаем осесимметричным твердым телом, центр масс которого движется по неизменной круговой орбите. Для записи уравнений движения спутника введем три правых декартовых системы координат.
Система $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ образована главными центральными осями инерции спутника. Точка $O$ – центр масс спутника, ось $O{{x}_{1}}$ совпадает с продольной осью спутника и направлена от спускаемого аппарата к приборному отсеку. В этой системе интерпретируются данные измерений бортовых датчиков. Моменты инерции спутника относительно оси $O{{x}_{1}}$ обозначим ${{I}_{1}}$, одинаковые моменты инерции относительно осей $O{{x}_{2}}$ и $O{{x}_{3}}$ обозначим ${{I}_{2}}$.
Вспомогательная система координат $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ служит для записи уравнений вращательного движения спутника. Ось $O{{y}_{1}}$ совпадает с осью $O{{x}_{1}}$; оси $O{{x}_{2}}$, $O{{x}_{3}}$ получаются из осей $O{{y}_{2}}$, $O{{y}_{3}}$ поворотом системы $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ на угол φ вокруг оси $O{{y}_{1}}$. Кинематическая связь между системами $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ и $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ задается условием, что проекция абсолютной угловой скорости второй из них на ось $O{{y}_{1}}$ равна нулю. Проекции этой угловой скорости на оси $O{{y}_{2}}$, $O{{y}_{3}}$ обозначим ${{w}_{2}}$, ${{w}_{3}}$. Пусть абсолютная угловая скорость спутника ${\mathbf{\omega }}$ имеет в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ компоненты $({{\omega }_{1}},\;{{\omega }_{2}},\;{{\omega }_{3}})$. Тогда $\dot {\varphi } = {{\omega }_{1}}$
(1)
$\begin{gathered} {{\omega }_{2}} = {{w}_{2}}\cos \varphi + {{w}_{3}}\sin \varphi , \\ {{\omega }_{3}} = - {{w}_{2}}\sin \varphi + {{w}_{3}}\cos \varphi . \\ \end{gathered} $Здесь и ниже точкой обозначается дифференцирование по времени $t$.
Вращательное движение спутника изучается относительно орбитальной системы координат $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$. Ее оси $O{{X}_{1}}$ и $O{{X}_{3}}$ направлены по геоцентрическим скорости и радиусу-вектору точки $O$.
Матрицу перехода от системы $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ к орбитальной системе обозначим $\left\| {{{a}_{{ij}}}} \right\|_{{i,j}}^{3}$, ${{a}_{{ij}}}$ – косинус угла между осями $O{{X}_{i}}$ и $O{{y}_{j}}$. Элементы этой матрицы будем выражать в функции углов $\gamma $, $\delta $ и $\beta $, которые введем так, чтобы систему $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ можно было перевести в систему $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ тремя последовательными поворотами: 1) на угол $\delta + {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ вокруг оси $O{{X}_{2}}$, 2) на угол $\beta $ вокруг новой оси $O{{X}_{3}}$, 3) на угол $\gamma $ вокруг новой оси $O{{X}_{1}}$, совпадающей с осью $O{{y}_{1}}$.
Направление оси $O{{y}_{1}}$ в системе $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ будем задавать углами $\theta $ и $\psi $: $\theta $ – угол между этой осью и плоскостью $O{{X}_{1}}{{X}_{2}}$, $\psi $ – угол между проекцией оси $O{{y}_{1}}$ на плоскость $O{{X}_{1}}{{X}_{2}}$ и осью $O{{X}_{1}}$. Направления отсчета углов $\theta $ и $\psi $ согласованы с направлениями осей $O{{y}_{2}}$ и $O{{X}_{3}}$ соответственно. Орт оси $O{{y}_{1}}$ имеет в системе $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ компоненты $(\cos \theta \cos \psi ,\;\cos \theta \sin \psi ,\; - \sin \theta )$. Будем использовать также угол $\Lambda = \arccos (\cos \theta \sin \psi )$ между осями $O{{y}_{1}}$ и $O{{X}_{2}}$.
Система уравнений вращательного движения спутника образована динамическими уравнениями Эйлера для угловых скоростей ${{w}_{2}}$, ${{w}_{3}}$ и кинематическими уравнениями Пуассона для первой и третьей строк матрицы $\left\| {{{a}_{{ij}}}} \right\|$. В уравнениях Эйлера учитываются гравитационный и восстанавливающий аэродинамический моменты, а также постоянный момент вдоль оси $O{{x}_{1}}$. При вычислении аэродинамического момента атмосфера считается неподвижной в абсолютном пространстве, внешняя оболочка спутника принимается сферой с центром на оси $O{{x}_{1}}$. Система уравнений вращательного движения имеет вид [4, 5]
(2)
$\begin{gathered} {{{\dot {w}}}_{2}} + \lambda {{\omega }_{1}}{{w}_{3}} = - 3\omega _{0}^{2}(1 - \lambda ){{a}_{{31}}}{{a}_{{33}}} + p{{a}_{{13}}}, \\ {{{\dot {w}}}_{3}} - \lambda {{\omega }_{1}}{{w}_{2}} = 3\omega _{0}^{2}(1 - \lambda ){{a}_{{31}}}{{a}_{{32}}} - p{{a}_{{12}}}, \\ {{{\dot {a}}}_{{11}}} + {{w}_{2}}{{a}_{{13}}} - {{w}_{3}}{{a}_{{12}}} = - {{\omega }_{0}}{{a}_{{31}}}, \\ {{{\dot {a}}}_{{12}}} + {{w}_{3}}{{a}_{{11}}} = - {{\omega }_{0}}{{a}_{{32}}}, \\ {{{\dot {a}}}_{{13}}} - {{w}_{2}}{{a}_{{11}}} = - {{\omega }_{0}}{{a}_{{33}}}, \\ {{{\dot {a}}}_{{31}}} + {{w}_{2}}{{a}_{{33}}} - {{w}_{3}}{{a}_{{32}}} = {{\omega }_{0}}{{a}_{{11}}}, \\ {{{\dot {a}}}_{{32}}} + {{w}_{3}}{{a}_{{31}}} = {{\omega }_{0}}{{a}_{{12}}}, \\ {{{\dot {a}}}_{{33}}} - {{w}_{2}}{{a}_{{31}}} = {{\omega }_{0}}{{a}_{{13}}}, \\ {{\omega }_{1}} = \Omega + \varepsilon (t - {{t}_{0}}),\,\,\lambda = \frac{{{{I}_{1}}}}{{{{I}_{2}}}}. \\ \end{gathered} $Здесь ${{\omega }_{0}}$ – орбитальная частота, $p$ – аэродинамический параметр, $\Omega $ и $\varepsilon $ – постоянные величины. В (1) использован явный вид решения одного из уравнений Эйлера ${{\dot {\omega }}_{1}} = \varepsilon $ с начальным условием ${{\omega }_{1}}({{t}_{0}}) = \Omega $. Выбор ${{t}_{0}}$ будет указан ниже.
При численном интегрировании уравнений (2) единицей измерения времени служит ${{10}^{3}}\,\,{\text{c}}$, единицы измерения других величин: $[{{\omega }_{i}}] = [{{w}_{i}}] = {{10}^{{ - 3}}}\,\,{{{\text{c}}}^{{ - 1}}}$, $[\varepsilon ] = [p] = {{10}^{{ - 6}}}\,\,{{{\text{c}}}^{{ - 2}}}$. Элементы второй строки матрицы $\left\| {{{a}_{{ij}}}} \right\|$ вычисляются как векторное произведение ее третьей и первой строк. Формулы (1) и соотношение $\varphi = \Omega (t - {{t}_{0}}) + {{\varepsilon {{{(t - {{t}_{0}})}}^{2}}} \mathord{\left/ {\vphantom {{\varepsilon {{{(t - {{t}_{0}})}}^{2}}} 2}} \right. \kern-0em} 2}$ позволяют найти функции ${{\omega }_{2}}(t)$, ${{\omega }_{3}}(t)$ и движение системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, решая уравнения (2).
Переменные ${{a}_{{1i}}}$ и ${{a}_{{3i}}}$ зависимы, они связаны условиями ортогональности матрицы $\left\| {{{a}_{{ij}}}} \right\|$. По этой причине начальные условия ${{a}_{{1i}}}({{t}_{0}})$ и ${{a}_{{3i}}}({{t}_{0}})$ выражаются через углы $\gamma $, $\delta $ и $\beta $.
Параметр $\lambda $ известен: $\lambda \approx 0.27$. Тем не менее, он и параметры $p$ и $\varepsilon $ определяются из обработки данных измерений наряду с неизвестными начальными условиями движения спутника, т.е. служат параметрами согласования.
Уравнения (2) и некоторые другие принятые ниже математические модели проще, чем уравнения движения и модели [1]. Это сделано, чтобы уменьшить число уточняемых параметров и избежать использования априорной информации и методов регуляризации в статистических процедурах. Для компенсации сделанных упрощений ограничимся реконструкцией сравнительно простых движений спутника, в которых компонента угловой скорости ${{\omega }_{1}}$ достаточно велика. Уравнения (2) – упрощенный вариант аналогичных уравнений вращательного движения [6], записанных для реальной орбиты спутника. Переход к круговой орбите не изменил основных результатов [6], где исследование выполнено по той же схеме, что и в данной работе.
3. РЕКОНСТРУКЦИИ ДВИЖЕНИЯ СПУТНИКА ПО МАГНИТНЫМ ИЗМЕРЕНИЯМ
На борту Фотона М-2 находилась аппаратура “Мираж”, с несколькими трехкомпонентными магнитометрами. Поскольку движение спутника было неуправляемым, полученные данные и уравнения (2) можно использовать для определения фактического вращательного движения спутника по обычным статистическим методикам. Методика, использованная ниже, состоит в следующем [1, 6]. По измерениям, выполненным на некотором отрезке времени ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T$, строились функции ${{\hat {h}}_{i}}(t)$, которые задавали на этом отрезке компоненты вектора местной напряженности магнитного поля в системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$. Среднеквадратичные ошибки аппроксимации не превышали 200$\gamma $ ($1\,\gamma = {{10}^{{ - 5}}}$ Э). Затем вычислялись псевдоизмерения $h_{i}^{{(n)}} = {{\hat {h}}_{i}}({{t}_{n}})$, ${{t}_{n}} = {{t}_{0}} + {{nT} \mathord{\left/ {\vphantom {{nT} N}} \right. \kern-0em} N}$, где $n = 0,\;1,\;2,\;...\;N$. Обычно было $T = 100{\kern 1pt} - {\kern 1pt} 300$ мин, ${T \mathord{\left/ {\vphantom {T N}} \right. \kern-0em} N} \approx 1$ мин. Псевдоизмерения служили исходной информацией для отыскания решений уравнений (2), описывающих фактическое движение спутника.
В соответствии с методом наименьших квадратов реконструкцией фактического движения спутника считалось решение уравнений (2), доставляющее минимум функционалу
(3)
$\begin{gathered} \Phi = \sum\limits_{i = 1}^3 {\left\{ {\sum\limits_{n = 0}^N {{{{[h_{i}^{{(n)}} - {{h}_{i}}({{t}_{n}})]}}^{2}} - (N + 1)\Delta _{i}^{2}} } \right\}} , \\ {{\Delta }_{i}} = \frac{1}{{N + 1}}\sum\limits_{n = 0}^N {[h_{i}^{{(n)}} - {{h}_{i}}({{t}_{n}})]} . \\ \end{gathered} $Здесь ${{\Delta }_{i}}$ – оценки постоянных смещений в псевдоизмерениях, ${{h}_{i}}(t)$ – компоненты напряженности МПЗ в точке $O$ в системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, рассчитываемые с помощью модели IGRF2005.
Расчет функционала выполнялся следующим образом. Предварительно фактическая орбита спутника на отрезке ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T$ аппроксимировалась круговой орбитой. Аппроксимация строилась методом наименьших квадратом по достаточно точным значениям реального фазового вектора центра масс спутника, заданным на равномерной сетке с шагом 3 мин. По этой аппроксимации определялась орбитальная частота ${{\omega }_{0}}$. Вдоль круговой орбиты вычислялись компоненты напряженности МПЗ в системе координат $O{{X}_{1}}{{X}_{2}}{{X}_{3}}$ на моменты ${{t}_{n}}$. Эти компоненты использовались при многократном вычислении функционала (3) в процессе его минимизации. С помощью решения уравнений (2) они пересчитывались в систему $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ и затем в систему $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ – в компоненты ${{h}_{i}}({{t}_{n}})$. В качестве ${{t}_{0}}$ в уравнениях (2) всегда использовалась начальная точка обрабатываемого отрезка данных.
Функционал (3) минимизировался по 9 величинам: начальным условиям решения системы (2) $\gamma ({{t}_{0}})$, $\delta ({{t}_{0}})$, $\beta ({{t}_{0}})$, ${{w}_{2}}({{t}_{0}})$, ${{w}_{3}}({{t}_{0}})$ и ее параметрам $\Omega $, $\lambda $, $p$, $\varepsilon $. Заключительный этап минимизации выполнялся методом Гаусса–Ньютона. Точность аппроксимации псевдоизмерений и разброс в оцениваемых величинах характеризовались соответствующими стандартными отклонениями. Стандартные отклонения рассчитывались в предположении, что ошибки в псевдоизмерениях $h_{i}^{{(n)}}$ некоррелированы и имеют одинаковые дисперсии, средние значения ошибок в псевдоизмерениях с одинаковым нижним индексом $i$ одинаковы (величины ${{\Delta }_{i}}$ в (3) – оценки этих средних значений). Стандартные отклонения вычислялись так. Пусть ${{\Phi }_{{\min }}}$ – значение функционала (3) в точке минимума, $C$ – матрица системы нормальных уравнений метода Гаусса–Ньютона в этой точке (матрица $2C$ приблизительно равна матрице квадратичной формы ${{d}^{2}}\Phi $ в точке минимума $\Phi $). Тогда дисперсия ошибок в псевдоизмерениях оценивается величиной
Стандартные отклонения оцениваемых величин равны квадратным корням из соответствующих диагональных элементов матрицы $\sigma _{H}^{2}{{C}^{{ - 1}}}$. Стандартные отклонения величин $\gamma ({{t}_{0}})$, $\delta ({{t}_{0}})$, $\beta ({{t}_{0}})$, ${{w}_{2}}({{t}_{0}})$, ${{w}_{3}}({{t}_{0}})$, $\Omega $, $\lambda $, $p$, $\varepsilon $ обозначим соответственно ${{\sigma }_{\gamma }}$, ${{\sigma }_{\delta }}$, ${{\sigma }_{\beta }}$, ${{\sigma }_{{w2}}}$, ${{\sigma }_{{w3}}}$, ${{\sigma }_{\Omega }}$, ${{\sigma }_{\lambda }}$, ${{\sigma }_{p}}$, ${{\sigma }_{\varepsilon }}$.
Примеры реконструкции фактического движения спутника Фотон М-2, полученные описанным способом, приведены на рис. 1, 2 и в табл. 1–3. В подписях к рисункам и в таблице использовано Московское время. Движение реконструировано на 14 временных интервалах. Их длины и начальный момент времени указаны в табл. 1. Длины интервалов выбраны таким образом, чтобы значения ${{\sigma }_{H}}$ для них были не слишком велики, т.е. принятая модель движения была достаточно адекватна. Рисунки иллюстрируют качество аппроксимации псевдоизмерений с помощью найденных решений уравнений (2) и описываемое этими решениями движение спутника относительно орбитальной системы координат. Рис. 1, 2 естественным образом разбиваются на три части – левую, среднюю и правую. В правой части сплошные кривые суть графики функций ${{h}_{i}}(t)$ на отрезке ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T$ (${{t}_{0}}$ служит началом отсчета времени), маркеры указывают точки $({{t}_{n}},\;h_{i}^{{(n)}} - {{\Delta }_{i}})$, $n = 0,\;1,\;2,\;...\;N$. Количественно аппроксимация псевдоизмерений характеризуется стандартным отклонением ${{\sigma }_{H}}$, значения которого приведены в табл. 1 и в подписях к рисункам. Приведенные примеры демонстрируют менее точную чем в [1] аппроксимацию псевдоизмерений. Значения ${{\sigma }_{H}}$ в табл. 1 несколько выше, чем в [1]. Тем не менее, достигнутая точность достаточна для целей данной работы.
Рис. 1.
Интервал 5. Момент $t = 0$ соответствует 16:15:06 (московское время) 4.VI.2005, ${{\sigma }_{H}} = 1208\gamma $.
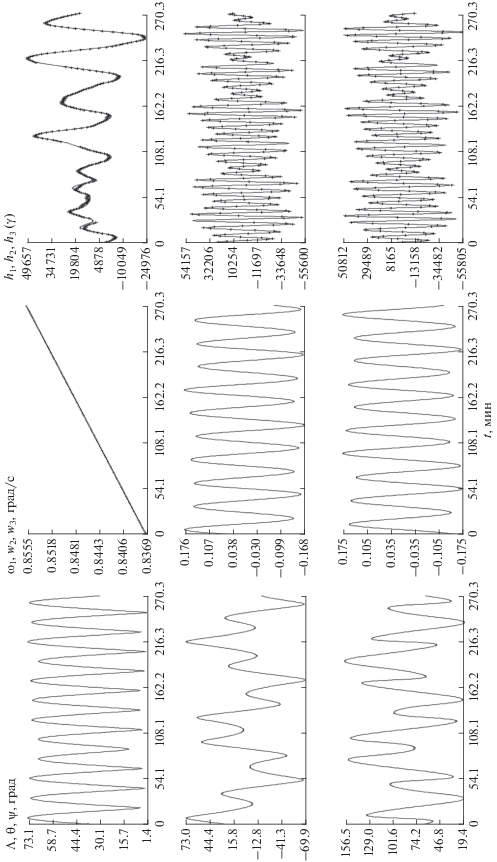
Рис. 2.
Интервал 14. Момент $t = 0$ соответствует 12:42:04 (московское время) 9.VI.2005, ${{\sigma }_{H}} = 1146\gamma $.

Таблица 1.
Результаты обработки измерений МПЗ, выполненных на спутнике Фотон М-2
| № инт. |
Дата VI.05 |
${{t}_{0}}$ | T, мин |
${{\sigma }_{H}}$, $\gamma $ |
${{\bar {\omega }}_{1}}$, град/с |
$\delta {{\omega }_{1}}$, град/с |
${{\bar {\omega }}_{ \bot }}$, град/с |
$\delta {{\omega }_{ \bot }},$ град/с |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 14:12:25 | 270.3 | 1218 | 0.521 | 0.0090 | 0.0675 | 0.0289 |
| 2 | 3 | 03:13:07 | 270.2 | 1068 | 0.6454 | 0.0164 | 0.0719 | 0.0230 |
| 3 | 3 | 14:13:43 | 270.2 | 942 | 0.7458 | 0.0058 | 0.0547 | 0.0173 |
| 4 | 4 | 03:14:24 | 270.2 | 1094 | 0.7888 | 0.0062 | 0.0942 | 0.0288 |
| 5 | 4 | 16:15:06 | 270.3 | 1208 | 0.8462 | 0.0054 | 0.1524 | 0.013 |
| 6 | 5 | 13:36:15 | 270.3 | 1264 | 0.9322 | 0.0012 | 0.1467 | 0.011 |
| 7 | 6 | 14:17:34 | 270.2 | 995 | 1.0062 | 0.0071 | 0.1516 | 0.011 |
| 8 | 7 | 12:18:45 | 270.2 | 1220 | 1.0671 | 0.0006 | 0.1298 | 0.010 |
| 9 | 8 | 09:29:43 | 300.3 | 1163 | 1.1121 | 0.0002 | 0.1131 | 0.010 |
| 10 | 8 | 04:19:58 | 300.6 | 1145 | 1.1183 | 0.0048 | 0.1150 | 0.011 |
| 11 | 8 | 19:10:34 | 300.3 | 1418 | 1.1256 | 0.0011 | 0.1064 | 0.010 |
| 12 | 9 | 03:00:49 | 300.3 | 1267 | 1.1336 | 0.0005 | 0.1126 | 0.010 |
| 13 | 9 | 07:51:05 | 301.0 | 1315 | 1.1346 | 0.0051 | 0.1179 | 0.011 |
| 14 | 9 | 09:42:04 | 327.9 | 1146 | 1.1505 | 0.0007 | 0.1098 | 0.011 |
Таблица 2.
Стандартные отклонения оценок начальных условий вращательного движения
| № инт. | ${{\sigma }_{\gamma }}$ | ${{\sigma }_{\delta }}$ | ${{\sigma }_{\beta }}$ | ${{\sigma }_{\Omega }}$ | ${{\sigma }_{{w2}}}$ | ${{\sigma }_{{w3}}}$ |
|---|---|---|---|---|---|---|
| 1 | 0.021 | 0.019 | 0.0075 | 0.0029 | 0.017 | 0.013 |
| 2 | 0.0084 | 0.0069 | 0.0039 | 0.0036 | 0.013 | 0.016 |
| 3 | 0.0065 | 0.0029 | 0.0015 | 0.0025 | 0.012 | 0.013 |
| 4 | 0.0097 | 0.0065 | 0.0041 | 0.0035 | 0.013 | 0.013 |
| 5 | 0.0091 | 0.0074 | 0.0067 | 0.0053 | 0.026 | 0.012 |
| 6 | 0.0079 | 0.0072 | 0.0057 | 0.0050 | 0.028 | 0.0098 |
| 7 | 0.012 | 0.0097 | 0.0056 | 0.0049 | 0.0086 | 0.024 |
| 8 | 0.016 | 0.013 | 0.0058 | 0.0053 | 0.012 | 0.032 |
| 9 | 0.0047 | 0.026 | 0.018 | 0.0090 | 0.0084 | 0.0058 |
| 10 | 0.0034 | 0.025 | 0.0096 | 0.0083 | 0.0057 | 0.0026 |
| 11 | 0.0038 | 0.016 | 0.029 | 0.014 | 0.013 | 0.0069 |
| 12 | 0.0037 | 0.014 | 0.023 | 0.014 | 0.012 | 0.0058 |
| 13 | 0.0048 | 0.013 | 0.028 | 0.0097 | 0.0083 | 0.0052 |
| 14 | 0.0037 | 0.020 | 0.023 | 0.0084 | 0.0069 | 0.0030 |
Таблица 3.
Оценки и стандартные отклонения параметров системы (2)
| № инт. | $p$ | ${{\sigma }_{p}}$ | $\lambda $ | ${{\sigma }_{\lambda }}$ | $\varepsilon $ | ${{\sigma }_{\varepsilon }}$ |
|---|---|---|---|---|---|---|
| 1 | –0.145 | 0.0088 | 0.2739 | 0.00030 | 0.0335 | 0.00029 |
| 2 | –0.389 | 0.0052 | 0.2700 | 0.00018 | 0.0613 | 0.00033 |
| 3 | –0.292 | 0.011 | 0.2677 | 0.00020 | 0.0214 | 0.00027 |
| 4 | –0.164 | 0.00095 | 0.2658 | 0.000086 | 0.0232 | 0.00032 |
| 5 | –0.220 | 0.014 | 0.2643 | 0.00023 | 0.0199 | 0.00027 |
| 6 | –0.142 | 0.018 | 0.2641 | 0.00021 | 0.0441 | 0.00025 |
| 7 | –0.215 | 0.014 | 0.2604 | 0.00019 | 0.0265 | 0.00023 |
| 8 | –0.137 | 0.022 | 0.2610 | 0.00021 | 0.0242 | 0.00028 |
| 9 | – 0.126 | 0.020 | 0.2619 | 0.00018 | 0.00055 | 0.00019 |
| 10 | – 0.209 | 0.0015 | 0.2608 | 0.00012 | 0.0161 | 0.00016 |
| 11 | – 0.195 | 0.021 | 0.2621 | 0.00015 | 0.0036 | 0.00019 |
| 12 | – 0.209 | 0.022 | 0.2608 | 0.00014 | 0.0018 | 0.00017 |
| 13 | – 0.231 | 0.019 | 0.2601 | 0.00018 | 0.0171 | 0.00021 |
| 14 | – 0.158 | 0.018 | 0.2616 | 0.00014 | – 0.0023 | 0.00015 |
В средней части рисунков помещены графики компонент угловой скорости ${{\omega }_{1}}$, ${{w}_{2}}$ и ${{w}_{3}}$ в найденных решениях уравнений (2). Похожий режим вращательного движения был у Фотонов-11 и -12 [7, 8]. По мере увеличения угловой скорости спутника его движение становилось все больше похоже на регулярную прецессию Эйлера осесимметричного твердого тела. Формирование регулярной прецессии с медленно возрастающей угловой скоростью ${{\omega }_{1}}$ и мало меняющимся значением ${{\omega }_{ \bot }} = \sqrt {w_{2}^{2} + w_{3}^{2}} $ завершилось после полутора–двух суток полета.
Точная регулярная прецессия Эйлера может иметь место лишь в случае, когда спутник осесимметричен и главный момент приложенных к нему внешних сил равен нулю. Тогда величины ${{\omega }_{1}}$ и $\omega {}_{ \bot }$ остаются неизменными во время движения. Для используемой модели первое условие выполнено, а второе – нет. По этой причине можно говорить лишь о движениях, близких к регулярной прецессии. Такие движения удобно характеризовать величинами
Вернемся к рисункам. В левой части рис. 1, 2 находятся графики зависимости от времени углов $\Lambda $, $\psi $ и $\theta $, задающих положение оси $O{{x}_{1}}$ относительно орбитальной системы координат. Анализ рисунков, не вошедших в статью, показал, что движение спутника по углам установилось только к пятому интервалу (ср. [6]).
Приведем еще несколько рисунков, служащих дополнительной иллюстрацией уже сформировавшегося режима вращательного движения с большой угловой скоростью. На рис. 3 изображены фрагменты проекции годографа орта оси $O{{x}_{1}}$ на плоскость орбиты. Проекции изображены в (квази) инерциальной системе координат $O{{Z}_{1}}{{Z}_{2}}{{Z}_{3}}$, получающейся из орбитальной системы преобразованием
Рис. 3.
Проекция орта оси $O{{x}_{1}}$ на плоскость $C{{Z}_{1}}{{Z}_{3}}$ (точка $O$ перенесена в точку $C$) (а) в движении на интервале 5, (б) в движении на интервале 14.

Оси этой системы сохраняют неизменное направление в абсолютном пространстве. Если бы движение спутника было точной регулярной прецессией Эйлера и его орбита была неизменной в абсолютном пространстве, то кривые на этих рисунках представляли бы собой эллипсы. Вследствие действия на спутник внешних моментов и регрессии узла орбиты направление оси прецессии медленно менялось [3], поэтому кривые выглядят как проекции на плоскость кусков изогнутой спирали.
Во второй половине полета собственный (относительно центра масс) кинетический момент спутника ${\mathbf{L}}$ был достаточно велик по модулю, а пределы его изменения сравнительно медленно менялись во времени. Рис. 4 иллюстрирует поведение кинетического момента на интервалах 5, 7, 14. Здесь
Рис. 4.
Характеристики изменения кинетического момента спутника: (a) в движении на интервале 5, (б) в движении на интервале 7, (в) в движении на интервале 14.

Иными словами, $\vartheta $ и $\rho $ – углы вектора ${\mathbf{L}}$ с осями $O{{x}_{1}}$ и $O{{Z}_{2}}$, $\alpha $ – угол между осью $O{{Z}_{3}}$ и проекцией ${\mathbf{L}}$ на плоскость $O{{Z}_{1}}{{Z}_{3}}$.
Регулярная прецессия Эйлера осесимметричного твердого тела (${\mathbf{L}} \ne 0$) обычно описывается углом нутации $\vartheta $, углом прецессии ${{\phi }_{1}}$ и углом собственного вращения ${{\phi }_{2}}$, причем эти углы определяются по отношению к системе координат, связанной с вектором ${\mathbf{L}}$. В этом движении $\vartheta = {\text{const}}$,
Адаптируя эти формулы к движению Фотона М-2, имеем
В функциях ${{w}_{2}}$ и ${{w}_{3}}$ (см. рис. 1, 2) доминирует частота $\lambda {{\bar {\omega }}_{1}}$, в соответствующих функциях (1) – частота $(1 - \lambda ){{\bar {\omega }}_{1}}$. В движении на интервале 14 имеем $\vartheta = 20.04^\circ $, ${{\dot {\phi }}_{2}} = 0.85$ град/с, ${{\dot {\phi }}_{1}} = 0.32$ град/с.
Рассмотрим эволюцию вектора ${\mathbf{L}}$. Угол $\rho $ на интервалах 5–10 меняется в довольно узких пределах, следовательно, действие на спутник гравитационного момента преобладало [3]. В такой ситуации $\dot {\alpha } \approx {\text{const}}$. Для этой угловой скорости существует приближенная формула (см. [3] и ниже), но в данном месте проще оценить ее из графика функции $\alpha (t)$. Например, на интервалe $\dot {\alpha } \approx 0.012$ град/с.
Дополнительные сведения о точности построенных реконструкций можно получить из табл. 2, 3. В табл. 2 приведены стандартные отклонения оценок параметров, задающих начальные условия найденных решений системы (2), в табл. 3 приведены оценки параметров $p$, $\lambda $, $\varepsilon $ и их стандартные отклонения. Как показывает сопоставление значений ${{\bar {\omega }}_{1}}$ и $\varepsilon $ в табл. 1 и 3, с ростом ${{\bar {\omega }}_{1}}$ значения $\varepsilon $ имеют тенденцию к уменьшению. По-видимому, вместе с ${{\omega }_{1}}$ возрастает не учитываемый в уравнениях (2) момент сопротивления. Значения $p$ в табл. 3 меняются более чем в 2 раза, хотя сохраняют знак. Для всех приведенных интервалов ${{\sigma }_{p}} \ll \left| p \right|$. Это не удивительно, поскольку принятая модель действующего на спутник аэродинамического момента весьма упрощенная. По сравнению с параметром $p$ оценки параметра $\lambda $ намного более стабильны, хотя в них заметна зависимость от ${{\bar {\omega }}_{1}}$.
На интервалах 9, 11, 12 и 14 достаточно точная аппроксимация магнитных измерений достигается и в случае $\varepsilon = 0$. При этом ${{\sigma }_{H}}$ увеличивается примерно на 15%. Аналогичное упрощение модели интервале 13 увеличивает ${{\sigma }_{H}}$ более чем в 2 раза.
4. УВЕЛИЧЕНИЕ УГЛОВОЙ СКОРОСТИ СПУТНИКА
Согласно высказанной выше гипотезе раскрутка спутника происходила под действием механического момента, компоненты которого были неизменны в системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$. Раскрутка происходила вокруг оси $O{{x}_{1}}$ и согласно принятой модели вызывалась компонентой ${{I}_{1}}\varepsilon $ указанного постоянного момента.
На спутник действовали и другие моменты, не учтенные в уравнениях (2) и аналогичных уравнениях работ [1, 2, 4–7], в частности, диссипативный аэродинамический момент и диссипативный момент от вихревых токов, наведенных МПЗ в корпусе спутника. Оба эти момента линейно зависят от угловой скорости спутника и очень малы. Их невозможно отделить от постоянного момента на интервалах времени длиной 270 мин, но именно эти диссипативные моменты препятствовали неограниченному возрастанию угловой скорости ${{\omega }_{1}}$. Наличие этих моментов проявляется как уменьшение оценок величины $\varepsilon $ с ростом ${{\bar {\omega }}_{1}}$ (см. табл. 1, 3 и аналогичные таблицы в [1, 2]). В действительности оценка $\varepsilon $ представляет собой некоторое среднее значение деленной на ${{I}_{1}}$ суммы постоянного момента и ряда других малых внешних моментов, в том числе, диссипативных. Принимая во внимание характер движения спутника, влияние перечисленных выше малых моментов на эволюцию ${{\omega }_{1}}$ во время неуправляемого полета можно приближенно описать уравнением
Здесь $a$ и $\varepsilon $ – постоянные параметры, причем ${{I}_{1}}\varepsilon $ и $ - {{I}_{1}}a{{\omega }_{1}}$ – компоненты постоянного момента и диссипативного момента вдоль оси $O{{x}_{1}}$. Общее решение уравнения (4) имеет вид
(5)
${{\omega }_{1}} = \omega _{1}^{ * } + c\exp ( - at),\,\,\,\,\omega _{1}^{ * } = \frac{\varepsilon }{a},$Описанным способом были получены следующие значения параметров формулы (5)
Среднеквадратичная ошибка аппроксимации величин ${{\bar {\omega }}_{1}}$ составила ${{\sigma }_{{{{{\bar {\omega }}}_{1}}}}} = 0.0125$ град/с, стандартные отклонения уточняемых параметров равны ${{\sigma }_{a}} = {\text{0}}{\text{.021}}$ сут–1, ${{\sigma }_{{\omega _{1}^{ * }}}} = 0.019$ град/с, ${{\sigma }_{c}} = 0.039$ град/с. В этом случае $\varepsilon = a\omega _{1}^{ * } = $ $ = 0.0722 \cdot {{10}^{{ - 6}}}\,\,{{{\text{c}}}^{{ - {\text{2}}}}}$. Оценки $\omega _{1}^{ * }$ и $\varepsilon $ наиболее интересны из полученных оценок. В частности, $\omega _{1}^{ * }$ является предельным значением компоненты угловой скорости ${{\omega }_{1}}$ при $t \to + \infty $. Судя по найденному значению $\omega _{1}^{ * }$ и приведенному в [2] значению ${{\bar {\omega }}_{1}} = 1.303$ град/с для сеанса измерений угловой скорости спутника 13.VI.2005, к концу полета процесс раскрутки практически завершился.
5. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ СПУТНИКА С БОЛЬШОЙ УГЛОВОЙ СКОРОСТЬЮ
Как следует из рис. 4, через несколько суток после начала полета угловая скорость спутника увеличилась настолько, что для исследования его вращательного движения стало возможным воспользоваться приближенной аналитической теорией, развитой в [3]. Приведем основные соотношения этой теории применительно к рассматриваемой модели движения Фотона М-2. Орбиту спутника примем круговой.
Кинетический момент ${\mathbf{L}}$ спутника в его движении относительно центра масс и угловая скорость спутника ω связаны соотношением
(6)
${\mathbf{\omega }} = \frac{{\mathbf{L}}}{{{{I}_{2}}}} + \left( {\frac{1}{{{{I}_{1}}}} - \frac{1}{{{{I}_{2}}}}} \right)({\mathbf{L}} \cdot {{{\mathbf{e}}}_{1}}){{{\mathbf{e}}}_{1}},$(7)
${\mathbf{\dot {L}}} = {\mathbf{M}},\,\,\,\,{{{\mathbf{\dot {e}}}}_{1}} = \frac{{{\mathbf{L}} \times {{{\mathbf{e}}}_{1}}}}{{{{I}_{2}}}}.$Здесь M – вычисленный относительно точки O главный момент внешних сил, приложенных к спутнику. Первое уравнение (7) выражает общую теорему динамики об изменении кинетического момента ${\mathbf{L}}$, второе уравнение – следствие формулы (6) и кинематического уравнения Пуассона ${{{\mathbf{\dot {e}}}}_{1}} = {\mathbf{\omega }} \times {{{\mathbf{e}}}_{1}}$.
Уравнения (7) не дают полного описания вращательного движения спутника. Они описывают только изменение его собственного кинетического момента и движение оси $O{{x}_{1}}$. Однако для описания эволюции движения спутника с большой угловой скоростью эти уравнения достаточны.
В уравнениях (7) будем учитывать: 1) гравитационный момент, 2) восстанавливающий аэродинамический момент, 3) диссипативный момент, направленный вдоль оси $O{{x}_{1}}$, 4) момент с постоянными компонентами в системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$. Это, по-видимому, минимальный состав моментов, позволяющий объяснить эволюцию вращательного движения спутника. Обозначим ${\mathbf{\alpha }}$, ${\mathbf{\beta }}$, ${\mathbf{\gamma }}$ орты осей $O{{X}_{1}}$, $O{{X}_{2}},$ $O{{X}_{3}}$. Гравитационный момент зададим формулой, принятой в уравнениях (2):
Восстанавливающий аэродинамический момент возьмем в виде
Здесь $p^\circ = {\text{const}}$, ${{t}_{\pi }}$ – время прохождения спутника через перигей, $\exp (2\eta )$ – отношение плотностей атмосферы в апогее и перигее, $\eta < 0$, $\left| \eta \right| \ll 1$. Множитель $\chi (t)$ грубо учитывает изменение плотности атмосферы вдоль слабо эллиптической орбиты. При $\chi \equiv \;1$ эта формула использована (2).
Диссипативный момент вдоль оси $O{{x}_{1}}$ зададим выражением
Момент с постоянными компонентами в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ представим в этой системе в виде ${{{\mathbf{M}}}_{0}} = ({{I}_{1}}\varepsilon ,\;{{M}_{{02}}},\;{{M}_{{03}}})$. Такой момент использован в (2) при ${{M}_{{02}}} = {{M}_{{03}}} = 0$.
Согласно сказанному выше в уравнениях (7)
Эти уравнения допускают интегральное соотношение ${{{\mathbf{e}}}_{1}} \cdot {{{\mathbf{e}}}_{1}} = 1$. Приведем еще одно следствие этих уравнений, которое будет использовано в дальнейшем. Умножим скалярно первое уравнение (7) на ${{{\mathbf{e}}}_{1}}$, второе – на ${\mathbf{L}}$. Получим после некоторых преобразований с учетом (6)
(8)
$\frac{{d({\mathbf{L}} \cdot {{{\mathbf{e}}}_{1}})}}{{dt}} = {{I}_{1}}\varepsilon - \kappa ({\mathbf{\omega }} \cdot {{{\mathbf{e}}}_{1}}).$Движение спутника с большим значением $L = \left| {\mathbf{L}} \right|$ близко к регулярной прецессии Эйлера осесимметричного твердого тела. При изучении такого движения внешние моменты можно рассматривать как малые возмущения. Приближенное интегрирование системы (7) в такой ситуации выполняется методом усреднения. Правые части первого уравнения этой системы и уравнения (8) усредняются по регулярной прецессии Эйлера в предположении, что параметры прецессии и положение спутника на орбите остаются неизменными. Замена точных уравнений усредненными допустима, если за период прецессии указанные параметры и положение меняются мало [3].
Прежде чем приступить к усреднению, приведем основные соотношения, описывающие регулярную прецессию Эйлера. В этом движении ${\mathbf{L}} = {\text{const}}$, изменение орта ${{{\mathbf{e}}}_{1}}$ описывается вторым уравнением (6), и в силу этих двух соотношений ${\mathbf{L}} \cdot {{{\mathbf{e}}}_{1}} = {\text{const}}$. Для описания регулярной прецессии введем новый ортонормированный базис
Орт ${{{\mathbf{E}}}_{1}}$ сохраняет неизменное направление в абсолютном пространстве и образует постоянный угол с ортом ${{{\mathbf{e}}}_{1}}$, орты ${{{\mathbf{E}}}_{2}}$ и ${{{\mathbf{E}}}_{3}}$ вращаются вокруг ${{{\mathbf{E}}}_{1}}$ с постоянной угловой скоростью ${{\omega }_{p}} = {L \mathord{\left/ {\vphantom {L {{{I}_{2}}}}} \right. \kern-0em} {{{I}_{2}}}}$. Последнее утверждение следует из соотношений
Перейдем к усреднению правой части первого уравнения (7). Начнем с гравитационного момента. Операцию усреднения некоторой функции по регулярной прецессии Эйлера будем обозначать угловыми скобками с индексом 1: ${{\langle \; \cdot \;\rangle }_{1}}$. Поскольку при усреднении орт ${\mathbf{\gamma }}$ считается неизменным, имеет место соотношение
Дальнейшие вычисления основаны на равенствах
Первое из них имеет место, поскольку базис ${{{\mathbf{E}}}_{1}}$, ${{{\mathbf{E}}}_{2}}$ и ${{{\mathbf{E}}}_{3}}$ ортонормирован; при выводе второго учитывалось, что здесь ${\mathbf{\gamma }} = {\text{const}}$, и использовались приведенные выше выражения для производных ${{{\mathbf{\dot {E}}}}_{2}}$ и ${{{\mathbf{\dot {E}}}}_{3}}$. Из выписанных равенств получаем
Усредним эти равенства по регулярной прецессии Эйлера и учтем, что среднее значение полной производной по времени ограниченной функции равно нулю. Получим
Так как ${{{\mathbf{e}}}_{1}} = {{c}_{1}}{{{\mathbf{E}}}_{1}} + {{c}_{2}}{{{\mathbf{E}}}_{2}}$, ${{c}_{1}} = {{{\mathbf{e}}}_{1}} \cdot {{{\mathbf{E}}}_{1}}$, ${{c}_{2}} = \sqrt {1 - c_{1}^{2}} $, то
Имеем также ${{\langle {{{\mathbf{E}}}_{2}}\rangle }_{1}} = - \omega _{p}^{{ - 1}}{{\langle {{{\mathbf{\dot {E}}}}_{3}}\rangle }_{1}} = 0$, поэтому
Окончательно получаем
Усреднение аэродинамического момента приводит к формуле
Здесь использовано соотношение ${{\langle {{{\mathbf{e}}}_{1}}\rangle }_{1}} = {{c}_{1}}{{{\mathbf{E}}}_{1}}$.
Усредняем диссипативный момент. Так как в регулярной прецессии Эйлера ${\mathbf{\omega }} \cdot {{{\mathbf{e}}}_{1}} = {{({\mathbf{L}} \cdot {{{\mathbf{e}}}_{1}})} \mathord{\left/ {\vphantom {{({\mathbf{L}} \cdot {{{\mathbf{e}}}_{1}})} {{{I}_{1}}}}} \right. \kern-0em} {{{I}_{1}}}} = {{L{{c}_{1}}} \mathord{\left/ {\vphantom {{L{{c}_{1}}} {{{I}_{1}}}}} \right. \kern-0em} {{{I}_{1}}}}$, имеем
Усреднение моментов ${{{\mathbf{M}}}_{0}}$ проведем при условии
которое далее полагаем выполненным. Сначала установим несколько вспомогательных соотношений. Рассмотрим уравнения Пуассона для ортов ${{{\mathbf{e}}}_{2}}$, ${{{\mathbf{e}}}_{3}}$ осей $O{{x}_{2}}$, $O{{x}_{3}}$. Подставим в уравнение ${{{\mathbf{\dot {e}}}}_{2}} = {\mathbf{\omega }} \times {{{\mathbf{e}}}_{2}}$ выражение (6), предварительно преобразоваего к видуС учетом соотношения ${{{\mathbf{e}}}_{1}} \times {{{\mathbf{e}}}_{2}} = {{{\mathbf{e}}}_{3}}$ рассматриваемое уравнение Пуассона можно записать следующим образом
Аналогичным образом уравнение ${{{\mathbf{\dot {e}}}}_{3}} = {\mathbf{\omega }} \times {{{\mathbf{e}}}_{3}}$ следует уравнение
Усреднение полученных уравнений по регулярной прецессии Эйлера дает
Умножив последние уравнения скалярно на ${{{\mathbf{E}}}_{1}}$ и полагая ${{\omega }_{n}} \ne 0$, будем иметь ${{{\mathbf{E}}}_{1}} \cdot {{\langle {{{\mathbf{e}}}_{2}}\rangle }_{1}} = {{{\mathbf{E}}}_{1}} \cdot {{\langle {{{\mathbf{e}}}_{3}}\rangle }_{1}} = 0$. Умножив те же уравнения векторно на ${{\omega }_{p}}{{{\mathbf{E}}}_{1}}$, получим после несложных преобразований
При выполнении условия (9) $\omega _{p}^{2} \ne \omega _{n}^{2}$ (${{\omega }_{p}} = {{\dot {\phi }}_{1}}$, ${{\omega }_{n}} = {{\dot {\phi }}_{2}}$, см. раздел 3), поэтому ${{\langle {{{\mathbf{e}}}_{2}}\rangle }_{1}} = {{\langle {{{\mathbf{e}}}_{3}}\rangle }_{1}} = 0$. В силу последних соотношений
Полученные соотношения позволяют выписать первое уравнение (7) и уравнение (8), усредненные по регулярной прецессии Эйлера (вместо переменной ${\mathbf{L}} \cdot {{{\mathbf{e}}}_{1}}$ используем переменную ${{c}_{1}} = {{({\mathbf{L}} \cdot {{{\mathbf{e}}}_{1}})} \mathord{\left/ {\vphantom {{({\mathbf{L}} \cdot {{{\mathbf{e}}}_{1}})} L}} \right. \kern-0em} L}$):
(10)
$\begin{gathered} {\mathbf{\dot {L}}} = \frac{3}{2}\omega _{0}^{2}({{I}_{1}} - {{I}_{2}})(3c_{1}^{2} - 1)({\mathbf{\gamma }} \cdot {{{\mathbf{E}}}_{1}})({\mathbf{\gamma }} \times {{{\mathbf{E}}}_{1}}) + \\ + \,\,{{I}_{2}}{{c}_{1}}\chi (t)p^\circ ({\mathbf{\alpha }} \times {{{\mathbf{E}}}_{1}}) - \frac{{\kappa c_{1}^{2}}}{{{{I}_{1}}}}{\mathbf{L}} + {{I}_{1}}{{c}_{1}}{{{\mathbf{E}}}_{1}}, \\ \end{gathered} $(11)
${{\dot {c}}_{1}} = c_{2}^{2}\left( {\frac{{{{I}_{1}}\varepsilon }}{L} - \frac{{\kappa {{c}_{1}}}}{{{{I}_{1}}}}} \right).$Выписанные уравнения образуют замкнутую систему относительно переменных ${\mathbf{L}}$ и ${{c}_{1}}$. Входящие в их правые части величины ${{{\mathbf{E}}}_{1}}$ и ${{c}_{2}}$ должны быть выражены через указанные переменные по формулам, приведенным выше. Входящие в эти уравнения орты ${\mathbf{\alpha }}$ и γ определяются уравнениями ${\mathbf{\dot {\alpha }}} = - {{\omega }_{0}}{\mathbf{\gamma }}$, ${\mathbf{\dot {\gamma }}} = {{\omega }_{0}}{\mathbf{\alpha }}$. В рамках схемы усреднения В.М. Волосова [8] (см. также [3]) полученные усредненные уравнения с малой погрешностью описывает эволюцию переменных ${\mathbf{L}}$ и ${{c}_{1}}$ на достаточно продолжительном отрезке времени. Параметры ${{M}_{{02}}}$, ${{M}_{{03}}}$ не входят в усредненные уравнения. Они слабо влияют на движение спутника с достаточно большой угловой скоростью и поэтому не учитывались в уравнениях (2).
Полученные усредненные уравнения допускает дальнейшее упрощение. А именно, если за время одного оборота спутника по орбите его собственный кинетический момент почти не меняется, то это уравнение можно усреднить по орбитальному движению [3]. Операцию усреднения по орбитальному движению будем обозначать угловыми скобками с индексом 2, двойное усреднение – по прецессии Эйлера и по орбитальному движению – угловыми скобками без индексов. Проведем усреднение отдельных моментов.
Уравнение (11) и моменты ${{\langle {{{\mathbf{M}}}_{d}}\rangle }_{1}}$, ${{\langle {{{\mathbf{M}}}_{0}}\rangle }_{1}}$ дополнительного усреднения не требуют. Усреднение гравитационного момента выполняется по схеме, использованной при усреднении по регулярной прецессии Эйлера, с заменой ${\mathbf{\gamma }} \to {{{\mathbf{E}}}_{1}}$, ${{{\mathbf{E}}}_{1}} \to {\mathbf{\beta }}$, ${{{\mathbf{E}}}_{2}} \to {\mathbf{\gamma }}$, ${{{\mathbf{E}}}_{3}} \to {\mathbf{\alpha }}$. Оно основано на формулах
Имеем
Усреднение восстанавливающего аэродинамического момента основано на формуле ${{\langle \chi (t){\kern 1pt} {\kern 1pt} {\mathbf{\alpha }}\rangle }_{2}} = \bar {\chi }(\eta ){{{\mathbf{\alpha }}}_{\pi }},$ где ${{{\mathbf{\alpha }}}_{\pi }} = {\mathbf{\alpha }}({{t}_{\pi }})$,
Имеем $\langle {{{\mathbf{M}}}_{a}}\rangle = {{I}_{2}}{{c}_{1}}\bar {\chi }p^\circ ({{{\mathbf{\alpha }}}_{\pi }} \times {{{\mathbf{E}}}_{1}})$.
Выписанные формулы позволяют получить двукратно усредненное уравнение для ${\mathbf{L}}$. Это уравнение представим в виде двух уравнений – для переменных $l = {L \mathord{\left/ {\vphantom {L {{{I}_{2}}}}} \right. \kern-0em} {{{I}_{2}}}}$ и ${{{\mathbf{E}}}_{1}}$:
(12)
$\begin{gathered} \dot {l} = \varepsilon \lambda {{c}_{1}} - {{\kappa }_{d}}lc_{1}^{2},\,\,\,\,{{{{\mathbf{\dot {E}}}}}_{1}} = {\mathbf{\Omega }} \times {{{\mathbf{E}}}_{1}}, \\ {\mathbf{\Omega }} = \frac{1}{l}[{{\kappa }_{g}}(3c_{1}^{2} - 1)({\mathbf{\beta }} \cdot {{{\mathbf{E}}}_{1}}){\mathbf{\beta }} + {{\kappa }_{a}}{{c}_{1}}{{{\mathbf{\alpha }}}_{\pi }}], \\ {{\kappa }_{g}} = \frac{3}{4}\omega _{0}^{2}(1 - \lambda ),\,\,\,\,{{\kappa }_{a}} = \bar {\chi }p^\circ ,\,\,\,\,{{\kappa }_{d}} = \frac{\kappa }{{{{I}_{1}}}}. \\ \end{gathered} $Оценим параметры, входящие в систему (11), (12). Для оценки коэффициента ${{\kappa }_{g}}$ примем ${{\omega }_{0}} = 0.00116$ с–1, $\lambda = 0.262$. Получим ${{\kappa }_{g}} = 7.45 \cdot {{10}^{{ - 7}}}$ с–2. Со-гласно оценкам раздела 4 $\varepsilon = 7.22 \cdot {{10}^{{ - 8}}}\,\,{{{\text{c}}}^{{ - {\text{2}}}}}$, поэтому $\varepsilon \lambda = 1.89 \cdot {{10}^{{ - 8}}}$ с$^{{ - 2}}$. Оценивая ${{\kappa }_{a}}$, возьмем $\bar {\chi } = 0.040$ ($\eta = - 0.088$), $p^\circ = - 1.5 \cdot {{10}^{{ - 7}}}$ с$^{{ - 2}}$. (ср. табл. 3). Получим ${{\kappa }_{a}} = - 6.00 \cdot {{10}^{{ - 9}}}$ с–2.
Чтобы оценить ${{\kappa }_{d}}$, рассмотрим уравнение (11), переписав его в виде
и первое уравнение (12). Они образуют замкнутую систему, которую можно проинтегрировать. Эта система допускает первый интеграл $l{{c}_{2}} = {\text{const}}$, а произведение $z = l{{c}_{1}}$ удовлетворяет уравнению $\dot {z} + {{\kappa }_{d}}z = \lambda \varepsilon $ (напомним, $c_{1}^{2} + c_{2}^{2} = 1$). В терминах предыдущих разделов $z = \lambda {{\bar {\omega }}_{1}}$, $l{{c}_{2}} = {{\bar {\omega }}_{ \bot }}$, ${{c}_{1}} = \cos \vartheta $, ${{c}_{2}} = \sin \vartheta $. Отсюда следует равенство ${{\kappa }_{d}} = a$. По табл. 1 можно проверить постоянство величины ${{\omega }_{ \bot }}$. Она менялась со временем, хотя в последние двое суток магнитных измерений ее изменение было малым. Из уравнения относительно $z$ следует, что предельное при $t \to + \infty $ значение ${{l}_{\infty }}$ величины $l$ оценивается неравенством ${{l}_{\infty }} \leqslant {{\lambda \varepsilon } \mathord{\left/ {\vphantom {{\lambda \varepsilon } {{{\kappa }_{d}}}}} \right. \kern-0em} {{{\kappa }_{d}}}}$, и если $l{{c}_{2}} > 0$, то предельное значения величин ${{c}_{2}}$ и $\vartheta = {{\vartheta }_{\infty }}$ положительны. Величины ${{l}_{\infty }}$ и ${{\vartheta }_{\infty }}$ выражаются через предельные значения величин ${{\bar {\omega }}_{1}}$ и ${{\bar {\omega }}_{ \bot }}$ по формулам (см. раздел 3)
Приняв предельные значения ${{\bar {\omega }}_{1}} = \omega _{1}^{ * } = {\text{1}}{\text{.236}}$ град/с, ${{\bar {\omega }}_{ \bot }} = 0.11$ град/с и взяв $\lambda = 0.262$, получим ${{\vartheta }_{\infty }} = 18.8^\circ $, ${{l}_{\infty }} = 0.32$ град/с. Использованная здесь величина $\omega _{1}^{ * }$ найдена в разделе 4.
Движение орта ${{{\mathbf{E}}}_{1}}$ описывается вторым уравнением (12), причем в выражении для ${\mathbf{\Omega }}$ согласно приведенным выше оценкам ${{\kappa }_{a}} \ll {{\kappa }_{g}}$. В этом выражении доминирует слагаемое, обусловленное гравитационным моментом. Движение орта ${{{\mathbf{E}}}_{1}}$ близко движению с постоянной угловой скоростью по конусу с осью параллельной орту ${\mathbf{\beta }}$ (нормаль к плоскости орбиты). Угол между ортами ${\mathbf{\beta }}$ и ${{{\mathbf{E}}}_{1}}$ меняется в узких пределах. Это согласуется с теорией [3] и подтверждается графиками на рис. 4. В случае рассматриваемого спутника такое описание адекватно на интервале времени около суток. На более продолжительных интервалах оно нарушается из-за прецессии орбиты и влияния аэродинамического момента. В частности, в силу второго уравнения (12)
Как видим, полученные в рамках теории В.В. Белецкого усредненные уравнения (11), (12) оказались достаточно точными, несмотря на не очень большую угловую скорость Фотона М-2. Они позволили из результатов обработки магнитных измерений на 14 непродолжительных интервалах времени (4.5–5 часов) составить единую картину эволюции вращательного движения этого спутника в течение недели и объяснить возникновение режима движения, установившегося к концу полета.
Данная работа выполнена при поддержке РФФИ (проект 17-01-00143).
Список литературы
Абрашкин В.И., Богоявленский Н.Л., Воронов К.Е. и др. Неуправляемое движение спутника Фотон М-2 и квазистатические микроускорения на его борту // Космич. исслед. 2007. Т. 45. № 5. С. 450–470. (Cosmic Research. P. 424).
Абрашкин В.И., Казакова А.Е., Сазонов В.В., Чебуков С.Ю. Определение вращательного движения спутника Фотон М-2 по данным бортовых измерений угловой скорости // Космич. исслед. 2008. Т. 46. № 2. С. 148–167. (Cosmic Research. P. 146).
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965.
Бойзелинк Т., Ван Бавинхов К., Сазонов В.В., Чебуков С.Ю. Определение вращательного движения спутника Фотон М-2 по данным измерений микроускорения // Космич. исслед. 2009. Т. 47. № 6. С. 537–549. (Cosmic Research. P. 500).
Сазонов В.В. Обработка данных измерений угловой скорости и микроускорения, полученных на спутнике Фотон-12 // Космич. исслед. 2011. Т. 49. № 5. С. 419–435. (Cosmic Research. P. 407).
Буланов Д.М., Сазонов В.В. Исследование эволюции вращательного движения спутника Фотон М-2 // Препринты ИПМ им. М.В. Келдыша. 2016. № 116.
Абрашкин В.И., Балакин В.Л., Белоконов И.В. и др. Неуправляемое вращательное движение спутника Фотон-12 и квазистатические микроускорения на его борту // Космич. исслед. 2003. Т. 41. № 1. С. 45–56. (Cosmic Research. P. 39).
Сазонов В.В., Чебуков С.Ю., Абрашкин В.И. и др. Низкочастотные микроускорения на борту ИСЗ Фотон-11 // Космич. исслед. 2004. Т. 42. № 2. С. 185–200. (Cosmic Research. P. 178).
Волосов В.М. Усредненеие в системах обыкновенных дифференциальных уравнений // Успехи математических наук. 1962. Т. 27. № 6(108). С. 3–126.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования


