Неорганические материалы, 2023, T. 59, № 11, стр. 1234-1244
Атомная структура и правила роста моноанионных кремний-танталовых кластеров TaSi$_{n}^{ - }$ (n = 12–17)
Н. А. Борщ 1, *, Н. С. Переславцева 1, С. И. Курганский 2
1 Воронежский государственный технический университет
394006 Воронеж, ул. 20-летия Октября, 84, Россия
2 Воронежский государственный университет
394018 Воронеж, Университетская пл., 1, Россия
* E-mail: n.a.borshch@ya.ru
Поступила в редакцию 10.07.2023
После доработки 02.10.2023
Принята к публикации 03.10.2023
- EDN: CWZQHO
- DOI: 10.31857/S0002337X23110027
Аннотация
Представлены результаты расчета атомной структуры и электронного спектра кластеров ${\text{TaSi}}_{n}^{ - }$ (n = 12–17) в рамках теории функционала плотности с использованием трех различных функционалов. Рассматривается влияние выбора функционала на результаты оптимизации структуры кластеров. Приводится сравнение рассчитанных электронных спектров наиболее стабильных изомеров кластеров с экспериментальными фотоэлектронными спектрами, что позволяет определить адекватность метода расчета и установить структуры кластеров.
ВВЕДЕНИЕ
Для современных технологий необходимы качественно новые функциональные материалы. Эти материалы должны быть доступны технически и экономически и обладать легко варьируемыми свойствами. Кремний – это материал, который используется в электронной промышленности на протяжении десятилетий, поэтому очевидно, что многие экспериментальные и теоретические исследования по поиску новых материалов посвящены поиску неизвестных форм кремния. Одно из направлений такого поиска – получение и исследование нольмерных кремниевых структур, в т.ч. атомных кластеров на основе кремния. Особый интерес представляют кремниевые кластеры с замкнутой структурой, допированные атомами различных металлов. Свойства таких кластеров зависят как от числа атомов в них, так и от сорта атома металла [1–5]. Это позволяет рассматривать их как строительные блоки для формирования более крупных наноструктур: одномерных, двумерных или трехмерных [6].
Очевидно, что для этого необходимо знать структуры кремний-металлических кластеров и понимать основные закономерности их формирования. Экспериментальное исследование геометрии кластеров в настоящее время ограничено техническими возможностями, поэтому особое значение приобретают методы компьютерного моделирования. Известно множество работ, в которых представлены результаты расчетов оптимальной структуры атомных кластеров [1–5], однако подтвердить адекватность этих результатов удается далеко не всегда. Практически существует единственный способ оценить, насколько вероятны рассчитанные структуры, – расчет их электронных спектров и сравнение с экспериментальными фотоэлектронными спектрами [7–9]. Это позволяет не только подтвердить адекватность того или иного расчета, но и сравнить результаты, полученные различными методами, и выбрать оптимальный.
В данной работе представлены результаты расчета атомной структуры и электронного спектра кластеров ${\text{TaSi}}_{n}^{ - }$ (n = 12–17) в рамках теории функционала плотности с использованием трех функционалов – B3LYP [10–13], B3PW91 [14, 15] и PBE [16, 17] – с комбинированным базисом 6-311 + + g(2d) для Si [18–20] и Jorge-TZP [21–24] для Ta. Рассматривается влияние выбора функционала на результаты оптимизации структуры кластеров. Приводится сравнение рассчитанных электронных спектров наиболее стабильных изомеров кластеров с экспериментальными фотоэлектронными спектрами [25], что позволяет определить адекватность метода расчета.
ДЕТАЛИ РАСЧЕТА
Расчеты проводились с использованием пакета программ Gaussian 09 [26]. Для каждой оптимизированной структуры в результате расчета электронного спектра получались собственные значения энергии каждой молекулярной орбитали, т.е. энергетический спектр, в котором каждую молекулярную орбиталь можно представить в виде уровня. Для построения электронных спектров кластеров каждый энергетический уровень заменялся гауссовым распределением с полушириной 0.12 эВ и интенсивности всех распределений при каждом значении энергии складывались.
Средняя энергия связи ${{E}_{b}}$ вычислялась по формуле
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Закономерности формирования стабильных изомеров кластеров мы рассматривали в рамках 4n-модификации правила Уэйда–Мингоса [27, 28]. Моноанионные кластеры ${\text{TaSi}}_{n}^{ - }$ имеют 4n + 6 валентных электронов, структуры их изомеров могут относиться к т.н. arachno-структурам, которые получаются удалением двух вершин из closo-многогранников [27, 28], являющихся стабильными изомерами кластеров с 4n + 2 электронами, т.е. ${\text{TaSi}}_{{n\, + \,2}}^{{3 + }}.$ Расчеты по оптимизации пространственной структуры трикатионных кластеров показали, что стабильными изомерами являются не только структуры, аналогичные closo-структурам, описанным для боранов и карборанов [27, 28], но и другие типы структур, причем не всегда эндоэдральных. Далее они обозначены как closo-изомеры, однако это условное обозначение.
На рис. 1–6 показаны атомные структуры наиболее стабильных изомеров кластеров ${\text{TaSi}}_{n}^{ - }$ (n = 12–17), схемы их формирования и сопоставление рассчитанных плотностей электронных состояний в каждом изомере с экспериментальным фотоэлектронным спектром [25]. Поскольку оказалось, что профиль плотности электронных состояний практически не зависит от метода расчета, то на рисунках приведены рассчитанные электронные спектры изомеров, полученные только методом B3PW91/6-311 + g(2d)-TZP. В табл. 1 приведены разницы средних энергий связи между основным изомером кластера и его остальными структурами.
Рис. 1.
Пространственные структуры и схема формирования стабильных изомеров кластера ${\text{TaSi}}_{{{\text{12}}}}^{ - },$ сопоставление рассчитанных электронных спектров кластера с экспериментальным фотоэлектронным спектром [25]: серым цветом показаны атомы кремния, синим – атом тантала; связи Ta–Si в замкнутых структурах не показаны для упрощения рисунка.
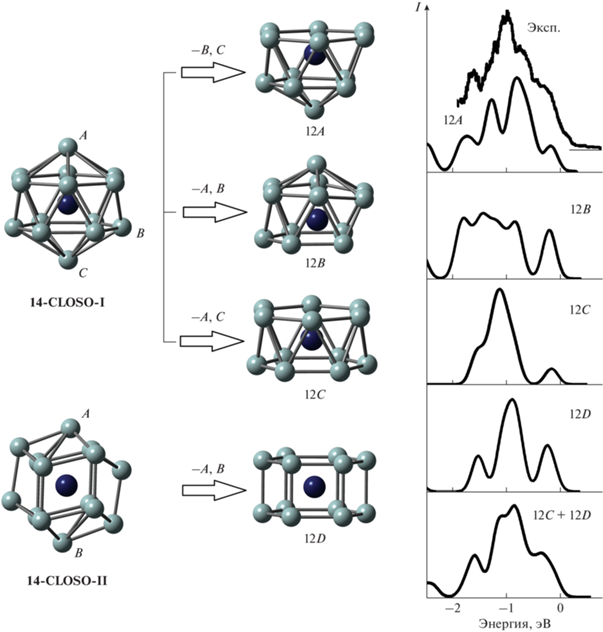
Таблица 1.
Разницы в средних энергиях связи между основным изомером и остальными в расчетах с использованием трех различных функционалов
| n | Изомер | Есв, эВ/атом | ||
|---|---|---|---|---|
| B3LYP | B3PW91 | PBE | ||
| 12 | A | 0.0000 | 0.0000 | 0.0000 |
| B | 0.0248 | 0.0222 | 0.0187 | |
| C | – | 0.0669 | 0.0688 | |
| D | 0.0060 | 0.0314 | 0.0480 | |
| 13 | A | 0.0005 | 0.0002 | 0.0062 |
| B | 0.0000 | 0.0000 | 0.0020 | |
| C | 0.0230 | 0.0058 | 0.0000 | |
| D | 0.0179 | 0.0253 | 0.0352 | |
| 14 | A | 0.0000 | 0.0000 | 0.0000 |
| B | 0.0398 | 0.0450 | 0.0472 | |
| C | 0.0155 | 0.0496 | 0.0697 | |
| 15 | A | 0.0000 | 0.0000 | 0.0000 |
| B | 0.0069 | 0.0113 | 0.0112 | |
| C | 0.0030 | 0.0042 | 0.0056 | |
| D | 0.0239 | 0.0570 | – | |
| E | 0.0523 | 0.1091 | 0.1361 | |
| F | 0.0505 | – | – | |
| 16 | A | 0.0608 | 0.0124 | 0.0000 |
| B | 0.0000 | 0.0000 | 0.0236 | |
| 17 | A | 0.0503 | 0.0026 | 0.0000 |
| B | 0.0000 | 0.0000 | 0.0326 | |
${\mathbf{TaSi}}_{{{\mathbf{14}}}}^{ - }$. Для кластера ${\text{TaSi}}_{{{\text{12}}}}^{ - }$ получено четыре наиболее стабильных изомера. Изомеры 12A, 12B и 12C получаются удалением двух атомов кремния из вершин closo-многогранника 14-CLOSO-I (см. рис. 1), а изомер 12D – удалением двух атомов кремния из вершин многогранника 14-CLOSO-II. При этом изомер 12С имеет структуру правильной шестиугольной антипризмы, а изомер 12D – структуру правильной шестиугольной призмы с атомом тантала в центре. Изомер 12С стабилен только в случае оптимизации c использованием функционалов B3PW91 и PBE. При оптимизации с использованием B3LYP-функционала стартовая структура антипризмы трансформируется в призматический изомер 12D. Изомер 12A является основным по результатам всех расчетов, причем в B3PW91- и PBE-расчетах – с существенным энергетическим отрывом от остальных. В B3LYP-расчете средние энергии связи в изомере 12А и в призматическом изомере 12D близки.
Рассчитанный электронный спектр 12A-изомера достаточно хорошо совпадает с экспериментальным фотоэлектронным [25] (см. рис. 1). Кроме того, рассчитанный спектр призматического изомера 12D и суммарный спектр изомеров 12А и 12D тоже хорошо согласуются с экспериментальным. Это позволяет утверждать, что в эксперименте возможно наблюдение кластеров ${\text{TaSi}}_{{{\text{12}}}}^{ - }$ со структурой как 12А, так и 12D.
${\mathbf{TaSi}}_{{{\mathbf{13}}}}^{ - }$. Кластер ${\text{TaSi}}_{{{\text{13}}}}^{ - }$ имеет три стабильных изомера: 13A, 13В и 13C, которые получены удалением двух атомов кремния из closo-многогранника 15-CLOSO-I. Изомер 13С при этом имеет структуру искаженной шестиугольной антипризмы с дополнительным атомом кремния над одним из оснований. Еще один изомер, 13D, имеет структуру шестиугольной призмы с дополнительным атомом кремния над центром одного из оснований. Этот изомер был получен удалением двух вершин из closo-многогранника 15-CLOSO-II.
По результатам B3PW91- и PBE-расчетов наиболее стабильны изомеры 13A, 13В и 13C. Средние энергии связи в них имеют близкие значения. B3LYP-расчет показал, что основными можно считать изомеры 13В и 13C, а изомер со структурой антипризмы имеет значительно меньшую среднюю энергию связи. Как видно из рис. 2, наилучшее согласие с экспериментом [25] показывает рассчитанный спектр изомера 13С, а также суммарные спектры трех изомеров: 13A, 13В и 13C или 13В и 13C.
${\mathbf{TaSi}}_{{{\mathbf{14}}}}^{ - }$. Изомеры 14A и 14B получаются удалением двух вершин из closo-многогранника 16‑CLOSO-I. При формировании изомера 14A удалены две противолежащие вершины на боковой поверхности многогранника, а при формировании изомера 14B – две противолежащие вершины в одном из оснований. Изомер 14С можно назвать фуллереноподобным. Он формируется при удалении двух противолежащих вершин из фуллереноподобного closo-многогранника 16-CLOSO-II.
По результатам всех расчетов основным является изомер 14A. Во всех расчетах, кроме расчета с использованием B3LYP-функционала, энергетический отрыв изомера 14A от остальных радикально велик, что снижает вероятность наблюдения других структур в эксперименте до незначительной. B3LYP-расчет показал, что средняя энергия связи в фуллереноподобном изомере 14С немного меньше, чем в основном, что не исключает его наблюдения в эксперименте.
На рис. 3 показано сопоставление рассчитанных электронных спектров различных изомеров кластера ${\text{TaSi}}_{{{\text{14}}}}^{ - }$ с экспериментальным фотоэлектронным спектром [25]. Наилучшее согласие с экспериментальным наблюдается у рассчитанных спектров изомеров 14A и 14В, однако наблюдение изомера 14В в эксперименте все же следует считать маловероятным, поскольку средняя энергия связи в нем существенно меньше, чем в изомере 14А. Суммарный спектр изомеров 14А и 14С плохо согласуется с экспериментальным, поэтому результаты B3LYP-расчета оказываются наименее адекватными.
${\mathbf{TaSi}}_{{{\mathbf{15}}}}^{ - }$. Для кластера ${\text{TaSi}}_{{15}}^{ - }$ получены шесть стабильных изомеров. Изомеры 15A, 15B и 15C получаются удалением двух атомов кремния из вершин closo-многогранника 17-CLOSO-I. Эти изомеры можно отнести к дельтаэдрическим структурам, поскольку большинство граней в многогранниках 15A, 15B и 15C являются треугольными. Большинство атомов кремния в такой структуре образует по пять связей Si–Si. Изомеры 15D и 15E формируются путем удаления двух атомов кремния из структуры 17-CLOSO-II. Изомер 15F имеет фуллереноподобную структуру, которая получена удалением двух атомов кремния из структуры 17-CLOSO-III. Изомеры 15D, 15E и 15F имеют трехсвязную структуру – большинство атомов кремния в них формируют по три связи Si–Si.
Согласно расчетам с использованием любого из трех потенциалов, основными можно считать изомеры 15A, 15B и 15C, поскольку средние энергии связи в них практически равны. Фуллереноподобная структура 15F оказалась стабильна только по результатам B3LYP-расчета, а при оптимизации с использованием других функционалов она трансформировалась в структуру 15В.
Поскольку качественно структуры 15A, 15B и 15C схожи, то и их рассчитанные электронные спектры имеют схожие профили, которые хорошо согласуются с экспериментальным фотоэлектронным спектром [25]. Кроме того, их суммарный спектр также совпадает с экспериментальным (рис. 4). Рассчитанные спектры трехсвязных структур 15D, 15E и 15F показывают значительно худшее согласие с экспериментальным спектром. Учитывая, что по результатам всех трех расчетов средние энергии связи в них значительно меньше, чем в изомерах 15A, 15B и 15C, можно утверждать, что формирование в эксперименте этих трехсвязных структур маловероятно.
${\mathbf{TaSi}}_{{{\mathbf{16}}}}^{ - }$. Изомер 16A получен добавлением дополнительного атома кремния к структуре, аналогичной структуре изомера 15A, а изомер 16B – к структуре, аналогичной структуре 15F (рис. 5). Таким образом, при n = 16 происходит переход от эндоэдральных структур к структурам, которые можно назвать квазиэндоэдральными. Они построены добавлением дополнительного атома кремния к замкнутой эндоструктуре одного из изомеров кластера ${\text{TaSi}}_{{15}}^{ - }.$
В расчете с использованием B3LYP-функционала основным изомером является фуллереноподобный изомер 16B, причем энергия связи в нем значительно выше, чем в изомере 16А. По результатам PBE-расчета, напротив, основным является изомер 16А, и его энергия связи намного выше, чем в изомере 16В. По результатам B3PW91-расчета изомеры 16А и 16В имеют близкие энергии связи, что приводит к выводу об их равновозможном наблюдении в эксперименте.
Сопоставление рассчитанных электронных спектров с экспериментальным [25] показывает, что спектры изомеров 16А и 16В по отдельности плохо согласуются с фотоэлектронным спектром, тогда как их суммарный спектр показывает значительно лучшее соответствие экспериментальному. Таким образом, использование B3PW91-функционала для оптимизационного расчета позволяет получить более адекватные результаты.
${\mathbf{TaSi}}_{{{\mathbf{17}}}}^{ - }$. Изомер 17A получается добавлением двух атомов кремния к многограннику, подобному изомеру 15B. Изомер 17B можно назвать фуллереноподобным, поскольку он получается добавлением двух атомов кремния к фуллереноподобному изомеру 15Н.
В B3LYP-расчете основным изомером является фуллереноподобный изомер 17B, причем с радикально большим энергетическим отрывом от изомера 17А. В PBE-расчете основным является изомер 17A, также с существенной разницей в энергиях связи с остальными изомерами. Таким образом, по результатам этих расчетов можно сделать вывод об однозначном преобладании в эксперименте одного из изомеров. Результаты расчета с использованием B3PW91-функционала показали, что средние энергии связи в изомерах 17A и 17B практически одинаковы, т.е. они оба могут с примерно равными вероятностями наблюдаться экспериментально.
Профили рассчитанной плотности электронных состояний как в изомере 17A, так и в изомере 17В плохо согласуются с экспериментальным фотоэлектронным спектром [25], поэтому вероятность того, что экспериментально был детектирован только один из этих изомеров, невысока. Наилучшее соответствие профилю экспериментального фотоэлектронного спектра показывает суммарный электронный спектр изомеров 17A и 17B. Это может означать, что экспериментально были детектированы оба этих изомера, т.е. наилучшее согласие с экспериментальными данными показывают результаты расчета с использованием B3PW91-функционала.
Представленные результаты расчета структуры основных изомеров кластеров ${\text{TaSi}}_{n}^{ - }$ значительно отличаются от опубликованных в [29]. Принципиальным отличием можно считать то, что основные изомеры в [29] имеют преимущественно трехсвязные структуры. Так, основной изомер кластера ${\text{TaSi}}_{{{\text{12}}}}^{ - }$ имеет структуру шестиугольной призмы, а основные изомеры кластеров с n = 13–15 получаются добавлением дополнительных атомов к ней. Дельтаэдрические изомеры кластеров ${\text{TaSi}}_{n}^{ - }$ с n = 12–15, согласно результатам [29], либо не представлены в числе стабильных изомеров, либо являются значительно менее стабильными, чем трехсвязные. Авторы [29] также приводят сопоставление рассчитанных электронных спектров стабильных изомеров с экспериментальными, но полученные в [29] фотоэлектронные спектры измерены в очень узком энергетическом интервале (шириной около 1.2 эВ) и не содержит каких-либо характерных особенностей, тогда как спектры, представленные в [25], измерены в значительно более широком энергетическом интервале и содержат специфические особенности тонкой структуры. Идентификация реальных структур и оценка адекватности метода расчета путем сравнения с такими малоинформативными спектрами [29] представляются затруднительными и неубедительными. Для оптимизации геометрии кластеров в [29] используется B3LYP-функционал, который, как было показано выше, может давать результаты с завышенными средними энергиями связи трехсвязных структур относительно дельтаэдрических. Очевидно, именно это и привело к превалированию среди наиболее стабильных изомеров призматических структур.
ЗАКЛЮЧЕНИЕ
Формирование стабильных изомеров кластеров ${\text{TaSi}}_{n}^{ - }$ (n = 12–17) может быть описано в рамках модификации правила Уэйда–Мингоса. Кластеры ${\text{TaSi}}_{n}^{{3 + }}$ с числом валентных электронов 4n + 2 являются аналогом closo-многогранников в правиле Уэйда–Мингоса и могут иметь несколько стабильных изомеров, в т.ч. со структурами, идентичными closo-многогранникам Уэйда–Мингоса. Моноанионные кластеры ${\text{TaSi}}_{n}^{ - }$ (n = 12–15) с числом валентных электронов 4n + 6 имеют по несколько стабильных изомеров, структуры которых формируются удалением двух атомов кремния из изомеров кластеров ${\text{TaSi}}_{{n{\text{ + 2}}}}^{{3 + }}.$ Все наиболее стабильные изомеры этих кластеров имеют эндоэдральную структуру. Стабильные изомеры кластеров ${\text{TaSi}}_{n}^{ - }$ (n = 16, 17) получаются добавлением одного или двух дополнительных атомов кремния к стабильным изомерам кластера ${\text{TaSi}}_{{{\text{15}}}}^{ - }.$ Эти изомеры имеют квазиэндоэдральную структуру, в которой один или два атома кремния слабо связаны с атомом тантала.
Результаты расчетов по оптимизации пространственной структуры кластеров могут радикальным образом зависеть от выбора функционала. Так, использование B3LYP-функционала для оптимизации геометрии может приводить к завышению средней энергии связи в трехсвязных структурах относительно дельтаэдрических, т.е. тех, в которых атомы кремния имеют большее число ближайших соседей. В свою очередь, использование PBE-функционала может приводить к завышению средней энергии связи в дельтаэдрических структурах. Сопоставление рассчитанных электронных спектров стабильных изомеров с экспериментальными фотоэлектронными спектрами показывает, что оптимальным выбором потенциала является B3PW91-функционал, однако для уточнения данных оптимизации следует проводить ее несколькими методами.
Список литературы
Dong C., Yang J., Lu J. Structural and Electronic Properties of Nanosize Semiconductor ${\text{HfSi}}_{n}^{{0/ - /2 - }}$ (n = 6–16) Material: a Double-Hybrid Density Functional Theory Investigation // J. Mol. Model. 2020. V. 26. P. 85-1–85-9. https://doi.org/10.1007/s00894-020-04352-110.1007/s00894-020-04352-1
Yang J., Wang J., Hao Y. Europium-Doped Silicon Clusters EuSin (n = 3–11) and Their Anions: Structures, Thermochemistry, Electron Affinities, and Magnetic Moments // Theor. Chem. Acc. 2015. V. 134. P. 81-1–81-11. https://doi.org/10.1007/s00214-015-1684-9
Liu Y., Yang J., Cheng L. Structural Stability and Evolution of Scandium-Doped Silicon Clusters: Evolution of Linked to Encapsulated Structures and Its Influence on the Prediction of Electron Affinities for ScSin (n = 4–16) Clusters // Inorg. Chem. 2018. V. 57. № 20. P. 12934–12940. https://doi.org/10.1021/acs.inorgchem.8b02159
Xie X., Hao D., Yang J. Ytterbium Doped Silicon Clusters YbSin (n = 4–10) and Their Anions: Structures, Thermochemistry, and Electron Affinities // Chem. Phys. 2015. V. 461. P. 11–19. https://doi.org/10.1016/j.chemphys.2015.08.024
Dong X., Yang Z., Yang J. Study on the Growth Behavior and Photoelectron Spectroscopy of Neodymium-Doped Silicon Nanoclusters NdSi$_{n}^{{0/ - }}$ (n = 8–20) with a Double-Hybrid Density Functional Theory // J. Mol. Model. 2021. V. 27. P. 27-1–27-11. https://doi.org/10.1007/s00894-020-04637-510.1007/s00894-020-04637-5
Jena P., Sun Q. Super Atomic Clusters: Design Rules and Potential for Building Blocks of Materials // Chem. Rev. 2018. V. 118. № 11. P. 5755–5870. https://doi.org/10.1021/acs.chemrev.7b00524
Borshch N., Kurganskii S. Geometric Structure, Electron-energy Spectrum, and Growth of Anionic Scandium-Silicon Clusters ScSi$_{n}^{ - }$ (n = 6–20) // J. Appl. Phys. 2014. V. 116. № 12 P. 124302. https://doi.org/10.1063/1.489652810.1063/1.4896528
Борщ Н.А., Курганский С.И. Анионные германий-ниобиевые кластеры: атомная структура, механизмы кластерообразования, электронные спектры // Журн. физ. химии. 2018. Т. 92. № 9. С. 1431–1438. https://doi.org/10.1134/S0044453718090078
Борщ Н.А., Курганский С.И. Пространственная структура, электронно-энергетический спектр и рост кластеров HfSi$_{n}^{ - }$ (n = 6–20) // Журн. неорган. химии. 2018. Т. 63. № 8. С. 1028–1035. https://doi.org/10.1134/S0044457X1808003210.1134/S0044457X18080032
Becke A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange // J. Chem. Phys. 1993. V. 98. P. 5648–5652. https://doi.org/10.1063/1.464913
Lee C., Yang W., Parr R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density // Phys. Rev. B. 1988. V. 37. P. 785–789. https://doi.org/10.1103/PhysRevB.37.785
Vosko S.H., Wilk L., Nusair M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: a Critical Analysis // Can. J. Phys. 1980. V. 58. P. 1200–1211. https://doi.org/10.1139/p80-159
Stephens P.J., Devlin F.J., Chabalowski C.F., Frisch M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields // J. Phys. Chem. 1994. V. 98. P. 11623–11627. https://doi.org/10.1021/j100096a001
Becke A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange // J. Chem. Phys. 1993. V. 98. P. 5648–5652. https://doi.org/10.1063/1.464913
Perdew J.P., Wang Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy // Phys. Rev. B. 1992. V. 45. P. 13244–13249. https://doi.org/10.1103/PhysRevB.45.13244
Perdew J.P., Ernzenhof M., Burke K. Rationale for Mixing Exact Exchange with Density Functional Approximations // J. Chem. Phys. 1996. V. 105. P. 9982–9985. https://doi.org/10.1063/1.472933
Adamo C., Barone V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model // J. Chem. Phys. 1996. V. 110. P. 6158–6170. https://doi.org/10.1063/1.478522
Dobbs K.D., Hehre W.J. Molecular Orbital Theory of the Properties of Inorganic and Organometallic Compounds 5. Extended Basis Sets for First-Row Transition Metals // J. Comput. Chem. 1987. V. 8. P. 861–879. https://doi.org/10.1002/jcc.540080614
Gordon M.S., Binkley J.S., Pople J.A., Pietro W.J., Hehre W.J. Self-Consistent Molecular-Orbital Methods. 22. Small Split-Valence Basis Sets for Second-Row Elements // J. Am. Chem. Soc. 1982. V. 104. P. 2797–2803. https://doi.org/10.1021/ja00374a017
Rassolov V.A., Pople J.A., Ratner M.A., Windus T.L. 6-31G* Basis Set for Atoms K Through Zn // J. Chem. Phys. 1998. V. 109. P. 1223–1229. https://doi.org/10.1063/1.476673
Martins L.S.C., Jorge F.E., Machado S.F. All-Electron Segmented Contraction Basis Sets of Triple Zeta Valence Quality for the Fifth-Row Elements // Mol. Phys. 2015. V. 113. P. 3578–3586. https://doi.org/10.1080/00268976.2015.1040095
Pritchard B.P., Altarawy D., Didier B., Gibson T.D., Windus T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community // J. Chem. Inf. Model. 2019. V. 59. P. 4814–4820. https://doi.org/10.1021/acs.jcim.9b00725
Feller D. The Role of Databases in Support of Computational Chemistry Calculations // J. Comput. Chem. 1996. V. 17. P. 1571–1586. https://doi.org/10.1002/(SICI)1096-987X(199610)17: 13%3C1571::AID-JCC9%3E3.0.CO;2-P
Schuchardt K.L., Didier B.T., Elsethagen T., Sun L., Gurumoorthi V., Chase J., Li J., Windus T.L. Basis Set Exchange: a Community Database for Computational Sciences // J. Chem. Inf. Model. 2007. V. 47. P. 1045–1052. https://doi.org/10.1021/ci600510j
Koyasu K., Atobe J., Furuse S., Nakajima A. Anion Photoelectron Spectroscopy of Transition Metal- and Lanthanide Metal-Silicon Clusters: MSi$_{n}^{ - }$ (n = 6–20) // J. Chem. Phys. 2008. V. 129. P. 214301-1–214301-7. https://doi.org/10.1063/1.302308010.1063/1.3023080
Frisch M.J. et al. Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
Wade K. The Structural Significance of the Number of Skeletal Bonding Electron-Pairs in Carboranes, the Higher Boranes and Borane Anions, and Various Transition-Metal Carbonyl Cluster Compounds // J. Chem. Soc. D. 1971. P. 792–793. https://doi.org/10.1039/C29710000792
Mingos D.A. A General Theory for Cluster and Ring Compounds of the Main Group and Transition Elements // Nature Phys. Sci. 1972. V. 236. P. 99–102. https://doi.org/10.1038/physci236099a0
Lu S.-J., Xu H.-G., Xu X.-L., Zheng W.-J. Structural Evolution and Electronic Properties of TaSi$_{n}^{{^{{--/0}}}}$ (n = 2–15) Clusters: Size-Selected Anion Photoelectron Spectroscopy and Theoretical Calculations // J. Chem. Phys. A. 2020. V. 124. № 47. P. 9818–9831. https://doi.org/10.1021/acs.jpca.0c0920910.1021/acs.jpca.0c09209
Дополнительные материалы отсутствуют.
Инструменты
Неорганические материалы







