Проблемы машиностроения и надежности машин, 2020, № 1, стр. 21-30

При создании новых типов высокопроизводительного инновационного оборудования для различных применений (механической обработки, резки, сварки, сборки, окраски) возникают проблемы разработки новых схемно-технических решений, их компоновок, обеспечивающих сложные виды движений выходного звена в пространстве и высокую точность позиционирования. Одним из вариантов решения этих проблем является использование механизмов параллельной структуры для относительного манипулирования. В последнее время произошел значительный скачок в исследованиях механизмов параллельной структуры [1–7].

Одной из важных проблем при создании роботизированных комплексов на основе механизмов параллельной структуры является обеспечение требуемой точности механической обработки. В работах [8, 9], проведены экспериментальные исследования точности позиционирования, точности воспроизведения “эталонной” траектории, статической и динамической жесткости станка-гексапода “Гексамех-1”.

Для определения точности механизмов параллельной структуры-необходимо определить жесткость конструкции. Жесткость механизма во многом определяет его качество: производительность, надежность, долговечность и точность. Возрастающее значение высокой точности и динамических характеристик роботизированных систем параллельной структуры увеличило использование высокопрочных материалов и легких конструкций за счет значительного сокращения поперечных сечений звеньев и их массы. Но такие решения увеличивают структурные деформации и могут привести к интенсивным резонансным и самовозбуждающимся колебаниям высокой частоты. Поэтому исследование жесткости приобретает первостепенное значение при проектировании робототехнических систем параллельной структуры с целью правильного выбора материалов, геометрии, формы и размеров элементов конструкции, а также взаимодействия каждого элемента с другими.

Общая жесткость манипулятора зависит от нескольких факторов, включая размеры и материал звеньев. Для реализации механизма высокой жесткости многие элементы конструкции должны быть большими и тяжелыми. Однако для достижения высокоскоростного движения необходимо, чтобы они были небольшими и легкими.

Для получения модели жесткости механизмов параллельной структуры используются четыре основных метода, основанных: 1) на вычислении матрицы Якоби [10–13]; 2) на анализе конечных элементов [14]; 3) на матричном структурном анализе [15, 16], 4) на использовании набора виртуальных соединений, которые описывают упругие свойства звеньев, соединений и пружин [17, 18].

Однако работы, посвященные исследованию жесткости, не учитывают технологический процесс обработки, силу резания, оказывающую влияние на смещение выходного звена.

Рассмотрим использование метода на основе матрицы Якоби для нахождения жесткости и смещения выходного звена робота-трипода, входящего в состав роботизированного комплекса с модулями относительного манипулирования. Такой комплекс с шестью степенями свободы выполнен в виде соединения двух механизмов параллельной структуры с тремя степенями свободы каждый. На рис. 1 представлен макет манипулятора относительного манипулирования по патенту РФ [19], имеющегося в распоряжении Лаборатории мехатроники и робототехники БГТУ им. В.Г. Шухова.

На рис. 2 приведена 3D-модель роботизированного комплекса с модулями относительного манипулирования.

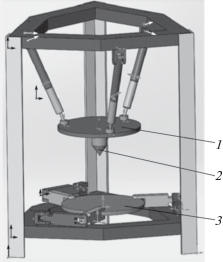
Механизм содержит модуль для установки инструмента и модуль для установки обрабатываемой детали на базе триподов. Использование таких механизмов позволит повысить техническую и эксплуатационную эффективность устройств манипулирования в пространстве по шести координатам. Важным преимуществом данного комплекса является отсутствие динамической связанности приводов, которая усложняет задачу моделирования и управления.

Верхний модуль для установки инструмента представляет собой трипод, который состоит из трех штанг переменной длины, соединенных вращательными шарнирами с основанием и рабочей платформой. Модуль может совершать вращение вокруг горизонтальных осей х и у, а также поступательное движение вдоль вертикальной оси z.

Нижний модуль для установки детали выполнен в виде плоского механизма параллельной структуры. Каждая кинематическая цепь имеет одну вращательную кинематическую пару, сопряженную с основанием, одну вращательную кинематическую пару, сопряженную с выходной платформой, и одну промежуточную вращательную кинематическую пару. Модуль имеет перемещения вдоль горизонтальных осей х и у, а также вращение вокруг вертикальной оси z.

Рассмотрим верхний модуль, выполненный в виде трипода. Основание и рабочая платформа верхнего модуля (рис. 3) представляют собой равносторонние треугольники, точки A_i, i = 1, 2, 3 и точек B_i, i = 1, 2, 3, соответственно расположены на вершинах равностороннего треугольника, минимальная и максимальная длины каждой штанги одинаковы. Поэтому механизм полностью симметричен.

Воспользуемся принципом виртуальной работы. В общем виде для трипода, представленного на рис. 2, работы, совершаемые силой резания и тремя силами, возникающими в штангах, можно выразить уравнением

где ${\mathbf{F}}_{{\text{p}}}^{T} = {{[{{F}_{z}},{{M}_{{\varphi }}},{{M}_{\vartheta }}]}^{T}}$ – вектор силы резания; $\Delta {\mathbf{P}} = {{[\Delta z,\Delta {\varphi },\Delta \vartheta ]}^{T}}$ – вектор бесконечно малого перемещения выходного звена, возникающего под действием силы резания; ${{{\mathbf{f}}}^{T}} = {{[{{f}_{1}},{{f}_{2}},{{f}_{3}}]}^{T}}$ – вектор сил в штангах; $\Delta {\mathbf{q}} = {{[\Delta {{q}_{1}},\Delta {{q}_{2}},\Delta {{q}_{3}}]}^{T}}$ – вектор бесконечно малых деформаций, возникающих под действием сил в штангах, $\Delta {{q}_{1}}$, $\Delta {{q}_{2}}$, $\Delta {{q}_{3}}$ – обобщенные координаты. В данном случае за обобщенные координаты принимаем изменение длин штанг.

Длины штанг трипода определим на основе соотношений

где φ и ϑ – углы поворота вокруг осей x и y соответственно, r – радиус окружности, описанной около треугольника A_i, i = 1, 2, 3, R – радиус окружности, описанной около треугольника B_i, i = 1, 2, 3, z – расстояние между точками O и O', x, y, ψ – дополнительные смещения выходного звена при его поворотах относительно горизонтальных осей, налагаемых кинематическими цепями трипода [4, 20].

Из [21] эти смещения равны

Для преобразования уравнения (1) применим методику расчета, основанную на использование матрицы Якоби. Учитывая, что погрешность позиционирования центра подвижной платформы можно найти из уравнения

где J – прямая матрица Якоби, подставим выражение (2) в уравнение (1)

После преобразований выразим силу резания через усилия, возникающие в штангах

Для данного механизма силы, возникающие в штангах под действием силы резания, являются осевыми. Согласно закону Гука, справедливо выражение

где ε – относительная деформация, Δq_i – изменение длины штанги под действием силы резания, q_i – длина штанги, E – модуль упругости при растяжении и сжатии, A – площадь поперечного сечения штанги,  f_i – сила в штанге, $\left( {\frac{{A \cdot E}}{{{{q}_{i}}}}} \right)~$ – жесткость штанги на растяжение–сжатие.

Выразим из уравнения (4) силу, возникающую в штанге

Запишем уравнение (5) с учетом жесткости трипода

где K_s – пространственная матрица жесткости трипода.

После преобразований получим

где ${{{\mathbf{K}}}_{{\mathbf{c}}}} = {{{\mathbf{J}}}^{{ - T}}} \cdot {{{\mathbf{K}}}_{{\text{s}}}} \cdot {{{\mathbf{J}}}^{{ - 1}}}$ – пространственная матрица жесткости механизма в декартовой системе координат основания.

J^–1 – обратный Якобиан

Выразим из уравнения (6) смещения центра платформы под действием силы резания

где ${\mathbf{K}}_{{\text{c}}}^{{ - 1}}$ – матрица статической жесткости параллельного робота; F_р – сила резания.

Механизм может не соответствовать требуемой жесткости в некоторых точках и областях рабочего пространства. Поэтому для механизма параллельной структуры полезно иметь атлас матриц жесткости в зависимости от положения. Из такого атласа можно выбрать рабочую конфигурацию, матрица жесткости в которой наиболее полно соответствует требованиям поставленной задачи. Механизм можно спроектировать таким образом, чтобы его матрица жесткости была близка к желаемой, по крайней мере, в некоторых положениях. В этом случае может потребоваться изменение геометрии и/или топологии структуры механизма. Карты позволяют выявить наличие зон, где жесткость неприемлема, а также помогают проектировщику, обеспечивая более точное представление о свойствах данного механизма.

Построим карты жесткости для роботизированного комплекса (рис. 3) с геометрическими размерами: z = 200 мм, R = 200 мм, r  = 100 мм, q₁, q₂, q₃ ∈ [170 мм, 250 мм], модуль упругости для стержней из стали E = 2 × 10⁵ МПа.

На рис. 4 приведены карты жесткости по оси z при изменении углов ϑ и φ как множество кривых жесткости для различных значений z в программной среде Matlab. В ходе вычислений производился циклический перебор значений углов поворота ϑ и φ от –45° до 45° с шагом 5°. Сетка строится по области рабочего пространства, а матрица жесткости вычисляется на каждом узле сетки. Карты показывают минимальную и максимальную жесткость в рабочем пространстве робота. Из таких графиков можно определить, какие области рабочего пространства удовлетворяют заданным критериям жесткости. Из рис. 4 видно, что жесткость по z выше вблизи центра рабочего пространства, что является наилучшим положением для поддержания вертикальных нагрузок (например, инструмента на рабочей платформе). Чем меньше z, тем выше жесткость, т.е. жесткость в верхней части механизма выше, т.к. рабочая платформа находится ближе к основанию.

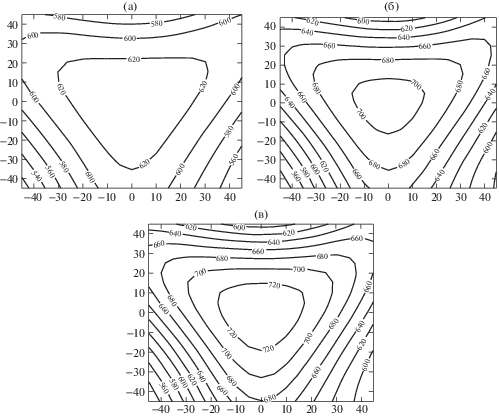
Такая оценка жесткости может использоваться как инструмент для проектировщика с целью выбора между различными вариантами конструкции механизма или для оценки существующей структуры.

На рис. 5 представлен алгоритм расчета погрешности (7), вызываемой смещением выходного звена под действием силы резания для трипода (рис. 3). Среди полученных значений координат рабочего органа исключены значения, не удовлетворяющие условиям

где q_i – длина i-й штанги; q_min – минимальное значение длины штанги; q_max – максимальное значение длины штанги.

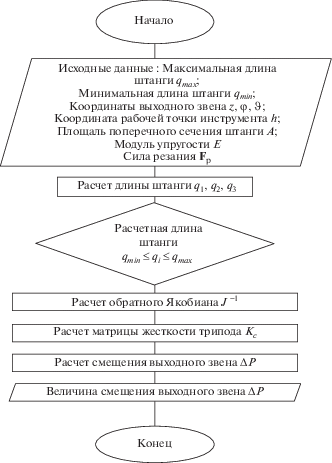
На основании предложенного алгоритма составлена программа в среде Matlab для нахождения жесткости и погрешности, вызываемой смещением выходного звена под действием силы резания для трипода (рис. 2).

По полученной программе в среде Matlab были построены зависимости смещения выходного звена по оси z от главной составляющей силы резания при чистовом фрезеровании Fz (рис. 6), которая изменялась в пределах от 10 до 150 Н, при трех различных конфигурациях механизма z = 180 мм, z = 200 мм, z = 250 мм и при, φ = 30°, ϑ = 0°. На рис. 6а приведены зависимости для случая, когда стержни переменной длины изготовлены из стали, на рис. 6б – из алюминия.

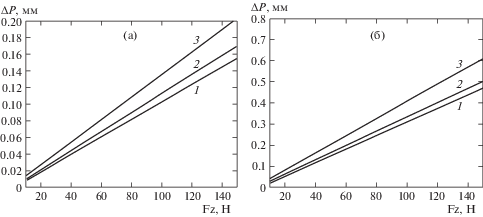
Из графиков видно, что с увеличением расстояния между платформой и основанием механизма, увеличивается смещение выходного звена под действием силы резания. Например, при силе Fz =70 Н, смещение выходного звена ΔP составляет 0.07 мм для z = 180 мм; ΔP = 0.076 мм для z = 200 мм; ΔP = 0.09 мм для z = 250 мм (рис. 6а). Из рис. 6б видно, что смещение выходного звена в случае использования штанг робота-трипода из алюминия выше, чем при использовании штанг из стали. При силе Fz = 70Н смещение выходного звена при z = 200 мм составляет ΔP = 0.076 мм (рис. 6а) против ΔP = 0.2 мм (рис. 6б). Целесообразно использовать данный механизм при небольших динамических нагрузках: для чистовой механической обработки, сварки, 3D-печати, покраски.

Предложенные алгоритмы позволяют на стадии проектирования выбрать геометрические параметры механизма параллельной структуры, материал штанг для обеспечения требуемой жесткости и точности обработки. Пользователь может задавать любые исходные параметры моделирования. Используемая методология может применяться для анализа жесткости и точности параллельных механизмов других кинематических структур.