Прикладная математика и механика, 2022, T. 86, № 3, стр. 404-423

1. Введение. При контактном взаимодействии твердых тел область фактического контакта, как правило, дискретна. Размеры и положение пятен фактического контакта зависят от условий контактного взаимодействия, механических характеристик тел и их поверхностной микроструктуры. Для описания дискретного (множественного) контакта твердых тел предложены различные математические модели, учитывающие параметры макро- и микрогеометрии реальных поверхностей и условия их контактного взаимодействия [1–4]. Большинство этих моделей основано на классической теории контактного взаимодействия деформируемых тел [5, 6]. Подробный обзор современного состояния исследований в области механики дискретного контакта, включая основные подходы к постановке задач, методы аналитического и численного решения, конкретные результаты и области их практического использования, приведен в статье [7].

В настоящей работе рассматриваются задачи дискретного контакта упругой полосы и жесткого штампа конечных размеров. На части границы полосы, по которой возможен контакт со штампом, задаются условия одностороннего контакта, трение на площадках контакта отсутствует. Такие задачи не являются периодическими вследствие неравномерного распределения нагрузки между отдельными пятнами контакта.

При решении краевых задач для упругой полосы преимущественно применяется интегральное преобразование Фурье [8]. В ряде случаев удается получить аналитические выражения для трансформант Фурье искомых функций, однако выполнить аналитически обратное преобразование Фурье этих трансформант весьма затруднительно, поэтому используют приближенные методы. Асимптотические методы представлены в монографиях [9, 10]. Численные методы, как правило, основаны на дискретном преобразовании Фурье (ДПФ), при реализации которого применяются алгоритмы быстрого преобразования Фурье (БПФ) [11, 12]. Подробный обзор современного состояния исследований и анализ различных аспектов применения ДПФ и БПФ в контактных задачах приведен в [13, 14].

Задачи дискретного контакта с односторонними связями являются нелинейными вследствие наличия в постановке граничных условий в виде неравенств. Для их численного решения требуется применение итерационных алгоритмов. Наиболее распространенный подход к построению вычислительных алгоритмов решения контактных задач с односторонними связями состоит в применении вариационных методов [15–17]. Отметим, что вариационные формулировки также используются для исследования проблемы существования, единственности и регулярности решения контактных задач [18–20]. Вариационные формулировки смешанных задач для упругой полосы приведены в [9].

В результате аппроксимации вариационных формулировок контактных задач с односторонними связями методами конечных или граничных элементов получают задачи квадратичного программирования, для решения которых в настоящее время наиболее эффективными считаются алгоритмы, разработанные на основе метода сопряженных градиентов (МСГ).

Впервые алгоритм решения задач квадратичного программирования на основе МСГ был предложен в [21]. Идея алгоритма состояла в использовании стратегии рабочего списка активных ограничений-неравенств (активного набора) и применении МСГ для нахождения минимума на текущем рабочем подпространстве. Была доказана теоретическая сходимость алгоритма за конечное число шагов. При практическом использовании алгоритма оказалось, что скорость сходимости итерационного процесса существенно зависит от количества и вида ограничений. Поэтому впоследствии были предложены различные модификации базового алгоритма, адаптированные для решения конкретных классов прикладных задач. Приведено [22, 23] описание и анализ алгоритмов на основе МСГ для решения контактных задач с односторонними связями.

Один из наиболее известных алгоритмов [24], отличается от базового алгоритма [21] учетом специфики множества ограничений решаемой задачи квадратичного программирования. При аппроксимации граничной вариационной формулировки контактной задачи количество ограничений в виде неравенств (условий неположительности нормальных напряжений при одностороннем контакте) совпадает с количеством неизвестных. Поэтому в алгоритме [24] при нарушении неактивных ограничений применяется метод проекции точки на допустимое множество, позволяющий включать в рабочий список сразу несколько ограничений, что существенно снижает количество рестартов по сравнению с алгоритмом [21]. Для сокращения вычислительных затрат также допускается, в отличие от алгоритма [21], исключение ограничений из рабочего списка до нахождения минимума на текущем рабочем подпространстве.

Следует отметить, что алгоритм [24] имеет существенное ограничение. В нем учитывается только одно уравнение равновесия штампа (для сил) и, следовательно, только поступательное движение штампа. Это не позволяет использовать алгоритм для решения контактных задач при внецентренном нагружении штампа, когда необходимо учитывать его повороты. Кроме того, на каждом шаге итерационного процесса дважды выполняется операция умножения матрицы Гессе минимизируемой функции на вектор, тогда как в алгоритме [21] эта операция выполняется лишь один раз. При изменении размерности рабочего подпространства рестарт алгоритма [24], как и алгоритма [21], производится с направления антиградиента, что замедляет их сходимость.

Автором предложен [25] новый алгоритм решения задач дискретного контакта для упругой полуплоскости, разработанный на основе МСГ. Основная идея этого алгоритма состоит в применении линейного преобразования переменных, позволяющего свести ограничения в виде равенств, которые аппроксимируют уравнения равновесия штампа и содержат все переменные задачи, к простым ограничениям, содержащим только одну переменную. Такие ограничения несложно учесть в алгоритме МСГ. Этот прием позволяет рассматривать оба уравнения равновесия штампа и задавать значение момента внешних сил. Кроме того, в качестве направления рестарта в алгоритме [25] используется редукция направления поиска с предыдущего шага на новое рабочее подпространство, при этом после рестарта для сохранения сопряженности направления поиска вычисляются по трехчленной формуле. Отметим также, что в алгоритме [25] операция умножения матрицы Гессе на вектор дважды выполняется только в случае уменьшения размерности рабочего подпространства.

В настоящей работе для решения задачи квадратичного программирования используется алгоритм МСГ [25], позволяющий рассматривать случаи внецентренного нагружения жесткого штампа.

2. Постановка задачи. Пусть аналогично [9] невесомая однородная изотропная упругая полоса в прямоугольной системе координат $O{{x}_{1}}{{x}_{2}}$ занимает область $\Omega = \{ x$ = = $({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}}$ : $\left| {{{x}_{1}}} \right| \leqslant \infty $, $0 \leqslant {{x}_{2}} \leqslant h\} $. Границу полосы ${{x}_{2}} \equiv 0$ обозначим ${{\Gamma }_{0}}$, а границу ${{x}_{2}} \equiv h$ – через ${{\Gamma }_{1}}$. Далее под $u(x),\varepsilon (x)$, $\sigma (x)$ будем понимать соответственно вектор перемещений и тензоры деформаций и напряжений в точке $x \in \Omega $. Предполагается, что полоса находится в условиях плоской деформации, деформации малы, а массовые силы и напряжения в недеформированном состоянии отсутствуют. Напряженно-деформированное состояние полосы описывается системой уравнений:

где $def \equiv 1{\text{/}}2(grad + gra{{d}^{T}})$, $S$ – тензор модулей упругости.

По границе ${{\Gamma }_{0}}$ полоса соединена с недеформируемым основанием. В случае идеального контакта граничные условия имеют вид

В полосу вдавливается гладкий жесткий штамп. Часть границы ${{\Gamma }_{1}}$, по которой возможен контакт полосы со штампом, обозначается ${{\Gamma }_{p}}$. Положение и предельные размеры ${{\Gamma }_{p}}$, т.е. номинальная область контакта, задаются априори, исходя из геометрических соображений. Предполагается, что часть границы ${{\Gamma }_{p}}$ является односвязной и конечной.

Форма основания штампа описывается функцией $\Phi {\kern 1pt} ({{x}_{1}})$, значение которой в точке $x \in {{\Gamma }_{p}}$ равно расстоянию от этой точки до поверхности штампа, измеренному вдоль направления внешней нормали к границе ${{\Gamma }_{p}}$. Расстояние $\Phi {\kern 1pt} ({{x}_{1}})$ отсчитывается по отношению к недеформированному состоянию полосы. Для определенности будем полагать $\mathop {min}\limits_{x \in {{\Gamma }_{p}}} \Phi ({{x}_{1}})$ = 0. В задачах дискретного контакта функция $\Phi {\kern 1pt} ({{x}_{1}})$ является мультимодальной (многоэкстремальной). Положение штампа определяется вектором перемещений $\delta = ({{\delta }_{1}},{{\delta }_{2}})$ и углом поворота ${{\varphi }_{3}}$. Главный вектор $F = ({{F}_{1}},{{F}_{2}})$ и главный момент ${{M}_{3}}$ внешних сил, приложенных к штампу, считаются заданными. В качестве центра приведения выбирается точка ${{x}^{c}} = (x_{1}^{c},x_{2}^{c})$. Далее рассматривается задача нормального контакта полосы со штампом, поэтому будем полагать ${{F}_{1}} = 0$ и ${{\delta }_{1}} = 0$.

Контактное взаимодействие упругой полосы с жестким штампом описывается условиями одностороннего гладкого контакта:

Остальная часть границы ${{\Gamma }_{1}}$ полосы свободна от внешних нагрузок:

Уравнения равновесия жесткого штампа имеют вид:

Отметим, что соотношения (2.5), по существу, представляют собой нелокальные граничные условия.

Для существования решения рассматриваемой контактной задачи далее будем предполагать, что внешние силы и моменты, приложенные к жесткому штампу, удовлетворяют следующим условиям:

– компонента ${{F}_{2}}$ ограничена по абсолютной величине и ${{F}_{2}} < 0$;

– значения ${{F}_{2}}$ и ${{M}_{3}}$ согласованы между собой таким образом, что существует распределение нормальных напряжений ${{\sigma }_{{22}}} \leqslant 0$ на ${{\Gamma }_{p}}$, удовлетворяющее уравнениям равновесия штампа (2.5).

Для замыкания постановки контактной задачи необходимо задать условия на бесконечности. Обычно в качестве таковых используются условия, характеризующие определенный порядок изменения перемещений и напряжений на бесконечности. Как правило, эти условия носят чисто математический характер. Более естественным является условие конечности потенциальной энергии деформации полосы

которое вполне замыкает постановку задачи и определяет поведение решения на бесконечности [9].

Задача (в дифференциальной постановке) состоит в определении полей перемещений $u(x)$, деформаций $\varepsilon (x)$ и напряжений $\sigma (x)$, удовлетворяющих уравнениям (2.1), граничным условиям (2.2)–(2.4), уравнениям равновесия штампа (2.5) и условию (2.6). Также необходимо найти смещение ${{\delta }_{2}}$ и поворот ${{\varphi }_{3}}$ штампа. Подчеркнем, что фактические зоны контакта полосы со штампом заранее неизвестны и подлежат определению.

3. Функциональные пространства. Решение $u(x)$ задачи (2.1)–(2.6), принадлежащее классу функций ${{[{{C}^{2}}(\Omega )]}^{2}} \cap {{[{{C}^{1}}(\bar {\Omega })]}^{2}}$, является классическим решением. Переход к вариационной формулировке задачи позволяет определить обобщенное решение. Введем необходимые для этого функциональные пространства [27, 28]. Обозначим

где ${{H}^{1}}(\Omega ) = {{[{{H}^{1}}(\Omega )]}^{2}}$, ${{L}_{2}}(\Omega ) = {{[{{L}_{2}}(\Omega )]}^{2}}$ – прямые произведения пространств Соболева. Пространство ${{H}^{1}}(div;\Omega )$ является гильбертовым со скалярным произведением

Для однородной изотропной полосы несложно получить неравенство

с положительной постоянной ${{c}_{1}}$, не зависящей от $v$. Следовательно, элементы пространства ${{H}^{1}}(div;\Omega )$ удовлетворяют условию конечности потенциальной энергии деформации полосы (2.6).

Выделим в ${{H}^{1}}(div;\Omega )$ подпространство

Можно увидеть, что

Из результатов [18] с учетом (3.5) следует, что существует постоянная ${{c}_{2}} > 0$, зависящая лишь от $\Omega $, такая, что

Неравенство (3.6) представляет собой первое неравенство Корна.

Используя далее результаты [9, 29], можно показать, что существуют линейные непрерывные операторы следа

определяющие для полей перемещений $v \in V$ векторные функции перемещений ${{\gamma }_{u}}v = ({{{v}}_{1}},{{{v}}_{2}})$ и напряжений ${{\gamma }_{t}}v = ({{\sigma }_{{12}}},{{\sigma }_{{22}}})$ на ${{\Gamma }_{1}}$ такие, что где ${{c}_{3}},{{c}_{4}}$ – положительные постоянные, не зависящие от $v$.

Обратно, существует линейный непрерывный оператор

такой, что для заданного $t \in {{[{{H}^{{ - 1/2}}}({{\Gamma }_{1}})]}^{2}}$ можно построить функцию $v \in V$, обладающую свойством ${{\gamma }_{t}}{\kern 1pt} v = t$.

Введем пространство сужений на ${{\Gamma }_{p}}$ функций из ${{H}^{{1/2}}}({{\Gamma }_{1}})$

и оснастим его нормой

Имеет место вложение пространств ${{H}^{{1/2}}}({{\Gamma }_{p}}) \subset {{L}_{2}}({{\Gamma }_{p}})$ [30]. Двойственным к пространству ${{H}^{{1/2}}}({{\Gamma }_{p}})$ является пространство ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ – пополнение ${{L}_{2}}({{\Gamma }_{p}})$ по норме

т.е. отношение двойственности ${}_{{{{{\tilde {H}}}^{{ - 1/2}}}({{\Gamma }_{p}})}}{{\langle \cdot , \cdot \rangle }_{{{{H}^{{1/2}}}({{\Gamma }_{p}})}}}$ порождается продолжением стандартного скалярного произведения в ${{L}_{2}}({{\Gamma }_{p}})$ и имеет место плотное вложение пространств [30]

Для упрощения обозначений указанное отношение двойственности далее будем обозначать как $\langle \cdot , \cdot \rangle $.

Заметим, что тривиальное продолжение функции $p \in {{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ на ${{\Gamma }_{1}}$ принадлежит пространству ${{H}^{{ - 1/2}}}({{\Gamma }_{1}})$, т.е. существует функция $p* \in {{H}^{{ - 1/2}}}({{\Gamma }_{1}})$ такая, что $\operatorname{supp} p* \subset {{\bar {\Gamma }}_{p}}$, $p$ является сужением $p{\kern 1pt} *$ на ${{\Gamma }_{p}}$ и выполняется равенство [29]

Поэтому с учетом (3.9) существует линейный непрерывный оператор

такой, что для заданного $p \in {{[{{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})]}^{2}}$ можно построить функцию $v \in V$, обладающую свойством ${{\left. {{{\gamma }_{t}}{\kern 1pt} v} \right|}_{{{{\Gamma }_{p}}}}} = p$.

4. Интегральное представление решения. Рассмотрим вспомогательную краевую задачу для упругой полосы: найти поле перемещений $u$, удовлетворяющее уравнениям (2.1), граничным условиям (2.2) и (2.4), а также условиям

Показано [9], что для любого $q \in {{L}_{2}}({{\Gamma }_{p}})$ данная задача имеет единственное решение $u$ и выполняется интегральное тождество (обобщенная формула Грина)

Из (4.2) с учетом (3.6) следует оценка

с положительной постоянной ${{c}_{5}}$, не зависящей от $q$. Следовательно, с помощью решения вспомогательной краевой задачи можно определить линейный непрерывный оператор ${{G}_{s}}:q \mapsto u$ из ${{L}_{2}}({{\Gamma }_{p}})$ в $V$.

Решение вспомогательной краевой задачи для $q \in {{L}_{2}}({{\Gamma }_{p}})$ имеет вид

Выражение для ядра $U({{x}_{2}},\alpha )$ приведено, например, в [31]. Учитывая плотность вложения (3.13), оператор ${{G}_{s}}$ можно продолжить по непрерывности на ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ и с учетом (3.15) рассматривать как оператор, действующий из ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ в $V$.

Таким образом, использование интегрального представления (4.4)–(4.5) в предположении, что $\Phi \in {{H}^{{1/2}}}({{\Gamma }_{p}})$, позволяет свести решение контактной задачи (2.1)–(2.6) к нахождению нормальных напряжений ${{\sigma }_{{22}}}$ = $q \in {{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$, удовлетворяющих следующей системе уравнений и неравенств:

Перемещения $u = {{G}_{s}}q$, соответствующие решению $q \in {{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ системы (4.6)–(4.9), будем называть обобщенным решением контактной задачи (2.1)–(2.6).

5. Оператор Пуанкаре–Стеклова. Введем оператор Пуанкаре–Стеклова ${{G}_{{ps}}}:q \mapsto w$, отображающий посредством решения (4.4)–(4.5) нормальные напряжения $q({{x}_{1}}) \equiv {{\sigma }_{{22}}}({{x}_{1}},h)$ на части ${{\Gamma }_{p}}$ границы упругой полосы в нормальные перемещения $w({{x}_{1}}) \equiv {{u}_{2}}({{x}_{1}},h)$ на ${{\Gamma }_{p}}$.

Соответствующее решению (4.4)–(4.5) выражение для оператора Пуанкаре–Стеклова ${{G}_{{ps}}}:q \mapsto w$ для $p \in {{L}_{2}}({{\Gamma }_{p}})$ имеет вид:

Отметим, что ядро ${{K}_{s}}( \cdot )$ интегрального представления (5.1) является разностным [31]. Учитывая плотность вложения (3.13), оператор ${{G}_{{ps}}}$ можно продолжить по непрерывности на ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ и с учетом (3.7), (3.10), (3.15) рассматривать как оператор, действующий из ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ в ${{H}^{{1/2}}}({{\Gamma }_{p}})$.

Введем на ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}}) \times {{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ непрерывную билинейную форму

Учитывая плотность вложения (3.13), из (4.2) получим, что

где $u = {{G}_{s}}q$, $v = {{G}_{s}}p$.

Для изотропной упругой полосы билинейная форма ${{g}_{{ps}}}(p,q)$ является симметричной. Используя (3.6), далее получим неравенство

из которого с учетом (3.8) и (3.14) следует оценка с положительной постоянной ${{c}_{6}}$, не зависящей от $q$. Следовательно, билинейная форма ${{g}_{{ps}}}(p,q)$ и оператор Пуанкаре–Стеклова ${{G}_{{ps}}}$ являются положительно определенными на ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$.

6. Вариационная формулировка задачи. Для решения системы (4.6)–(4.9), содержащей уравнения и неравенства, используется вариационный подход [15–20]. Образуем множество статически допустимых нормальных напряжений на ${{\Gamma }_{p}}$

Можно показать, что множество $\Sigma $ является замкнутым выпуклым множеством в ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$. Кроме того, в соответствии со сделанными при постановке задачи предположениями это множество является непустым.

Пусть $q \in \Sigma $ – решение системы (4.6)–(4.9). Тогда для произвольного $p \in \Sigma $ получим следующую оценку

Из (6.2) следует, что искомые нормальные напряжения $q \in \Sigma $ удовлетворяют граничному вариационному неравенству

где $\phi ( \cdot )$ – определенная на ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ линейная форма

Отметим, что неравенство (6.3) не содержит неизвестных смещения ${{\delta }_{2}}$ и поворота ${{\varphi }_{3}}$ жесткого штампа. Как нетрудно видеть из преобразований (6.2), это является следствием того, что элементы множества статически допустимых нормальных напряжений $\Sigma $ удовлетворяют уравнениям равновесия штампа (4.9).

Используя известные приемы [15, 32], можно доказать обратное утверждение: решение $q$ вариационного неравенства (6.3) удовлетворяет системе уравнений и неравенств (4.6)–(4.9).

Учитывая, что билинейная форма ${{g}_{{ps}}}(p,q)$ является положительно определенной, а множество $\Sigma $ – непустым замкнутым выпуклым множеством в ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$, вариационное неравенство (6.3) эквивалентно задаче минимизации граничного функционала: найти $q \in \Sigma $ такой, что

Кроме того, решение вариационного неравенства (6.3) и задачи минимизации (6.5) существует и единственно [15, 19, 20].

Отыскав нормальные напряжения $q \equiv {{\sigma }_{{22}}}$ на ${{\Gamma }_{p}}$ как решение задачи (6.5), можно определить напряженно-деформированное состояние всей полосы, используя (4.4)–(4.5).

7. Аппроксимация задачи. Выбор метода аппроксимации задачи минимизации (6.5) определяется, в первую очередь, возможностью построения эффективной с вычислительной точки зрения аппроксимации оператора Пуанкаре–Стеклова ${{G}_{{ps}}}$, ядро интегрального представления (5.1) которого имеет вид [31]

Аналитическое выражение для интеграла (7.1) неизвестно. Применение квадратурных формул для вычисления этого несобственного интеграла представляет собой трудоемкую вычислительную задачу. Альтернативный подход состоит в следующем. Нетрудно видеть, что ${{\tilde {K}}_{s}}(\alpha h)$ является косинус-трансформантой Фурье функции ${{K}_{s}}(z)$. Подвергнем (5.1) преобразованию Фурье и в соответствии с теоремой о свертке [11] получим

где $\tilde {w}(\alpha )$, $\tilde {q}(\alpha )$ – трансформанты Фурье соответственно нормальных перемещений $w({{x}_{1}})$ на ${{\Gamma }_{1}}$ и тривиального продолжения на ${{\Gamma }_{1}}$ нормальных напряжений $q({{x}_{1}})$. Следовательно, вычисление оператора Пуанкаре–Стеклова ${{G}_{{ps}}}$ сводится к выполнению пары (прямого и обратного) преобразований Фурье и перемножению спектров (7.3).

В численном анализе использование преобразования Фурье наиболее эффективно в случае периодических функций благодаря дискретности их спектра и, как следствие, переходе от непрерывного преобразования к дискретному [11, 12]. Поэтому основная идея используемого ниже подхода состоит в аппроксимации искомых нормальных напряжений на ${{\Gamma }_{p}}$ сеточными функциями, периодическими на всей границе ${{\Gamma }_{1}}$, и применении алгоритмов БПФ. Для уменьшения возникающей при этом ошибки периодичности вводится расширенная вычислительная область ${{\Gamma }_{c}}$ [13, 14].

Выберем односвязную конечную вычислительную область ${{\Gamma }_{c}} \subset {{\Gamma }_{1}}$ так, чтобы выполнялись условия

где $\chi $ – коэффициент расширения вычислительной области. Далее аналогично (3.10)–(3.12) введем пространство ${{H}^{{1/2}}}({{\Gamma }_{c}})$ и двойственное ему пространство ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{c}})$. Используя результаты [30], можно показать, что сужения функций из ${{H}^{{1/2}}}({{\Gamma }_{c}})$ на ${{\Gamma }_{p}}$ принадлежат пространству ${{H}^{{1/2}}}({{\Gamma }_{p}})$, а тривиальное продолжение ${{q}_{0}}$ функции $q \in {{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ на ${{\Gamma }_{c}}$ принадлежит пространству ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{c}})$. Обозначим через ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }^{{ - 1/2}}}({{\Gamma }_{c}})$ подпространство функций из ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{c}})$, имеющих носитель на ${{\bar {\Gamma }}_{p}}$. Учитывая (7.4), аналогично [33] продолжим периодически функции из ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }^{{ - 1/2}}}({{\Gamma }_{c}})$ на всю границу ${{\Gamma }_{1}}$ с периодом $L$ и образуем пространство $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} _{\sharp }^{{ - 1/2}}({{\Gamma }_{1}})$ $L$-периодических функций. Далее функции из ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }^{{ - 1/2}}}({{\Gamma }_{c}})$ будем отождествлять с их периодическими продолжениями на ${{\Gamma }_{1}}$. Тем самым определим оператор $\Pi :{{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ → $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} _{\sharp }^{{ - 1/2}}({{\Gamma }_{1}})$, ставящий в соответствие функции из $q \in {{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ периодическое продолжение ${{q}_{{{\text{per}}}}} \in \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} _{\sharp }^{{ - 1/2}}({{\Gamma }_{1}})$ на ${{\Gamma }_{1}}$ ее тривиального продолжения ${{q}_{0}} \in {{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{c}})$ на ${{\Gamma }_{c}}$.

Обозначим через ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} }_{2}}({{\Gamma }_{c}})$ подпространство функций из ${{L}_{2}}({{\Gamma }_{c}})$, имеющих носитель на ${{\bar {\Gamma }}_{p}}$. Используя (3.13), можно показать, что имеет место плотное вложение пространств ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} }_{2}}({{\Gamma }_{c}}) \subset {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }^{{ - 1/2}}}({{\Gamma }_{c}})$. Функции из ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} }_{2}}({{\Gamma }_{c}})$ можно рассматривать как $L$-периодические, следовательно система функций $\exp \left( {i2\pi k{{x}_{1}}{\text{/}}L} \right)$, $k = 0, \pm 1, \pm 2$, …, является плотной в ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} }_{2}}({{\Gamma }_{c}})$ [34]. Поэтому $q \in {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }^{{ - 1/2}}}({{\Gamma }_{c}})$ можно аппроксимировать с заданной точностью конечным отрезком ряда Фурье

Для вычисления коэффициентов Фурье $c_{k}^{q}$ с помощью ДПФ введем сеточные функции. Построим на ${{\Gamma }_{c}}$ регулярную (равномерную) сетку ${{T}_{c}}$, состоящую из $M$ одноузловых граничных элементов нулевого порядка размером ${{\delta }_{e}} = L{\text{/}}M$. Узлы ${{T}_{c}}$ обозначим ${{s}_{m}}$, $m = \overline {1,M} $. Часть ${{T}_{c}}$, расположенную на ${{\Gamma }_{p}}$ и содержащую $N$ элементов, обозначим ${{T}_{p}}$. Из (7.4) следует, что $N = M{\text{/}}\chi $.

Далее векторы и матрицы будем обозначать большими латинскими буквами, а их элементы – соответствующими малыми латинскими буквами.

Введем на ${{T}_{c}}$ сеточные функции нормальных напряжений и перемещений

а также редукции этих функций на ${{T}_{p}}$где ${{R}_{{pc}}}$ – прямоугольная матрица размеров $N \times M$, в каждой строке которой имеется ровно один ненулевой элемент, равный 1.

Обратные операции тривиального продолжения (дополнения нулевыми элементами) ${{Q}_{p}}$ и ${{W}_{p}}$ на ${{T}_{c}}$ могут быть выполнены с помощью транспонированной матрицы $R_{{pc}}^{T}$

Известно [11, 12], что спектр сеточной функции является периодическим и представляет собой бесконечный ряд сдвинутых копий спектра аппроксимируемой функции. Расстояние в частотной области между соседними копиями спектра равно частоте дискретизации ${{\omega }_{0}} = 2\pi {\text{/}}{{\delta }_{e}}$. Для исключения эффекта наложения частот, а также возможности восстановления периодической функции по ее сеточной аппроксимации будем полагать, что число гармоник ${{K}_{f}}$ в (7.5) и количество узлов $M$ сетки ${{T}_{c}}$ удовлетворяют условию

вытекающему из теоремы Котельникова–Шеннона [11, 12].

Введем матрицу Фурье порядка $M$

Матрица Фурье обратима и при этом обратная матрица имеет вид

где $F_{c}^{*}$ – эрмитово сопряженная матрица.

Используя матрицу ${{F}_{c}}$, вычислим образы Фурье ${{\tilde {Q}}_{c}}$ и ${{\tilde {W}}_{c}}$ соответственно сеточных функций нормальных напряжений и перемещений

Сеточные функции ${{Q}_{c}}$ и ${{W}_{c}}$ являются вещественными, поэтому из свойств ДПФ следует, что компоненты ${{\tilde {Q}}_{c}}$ и ${{\tilde {W}}_{c}}$ удовлетворяют условиям

Для сеточных функций соотношение (7.3) примет вид

где с учетом (7.14)

Можно показать, что ${{\tilde {k}}_{0}}$ представляет собой коэффициент податливости рассматриваемой упругой полосы для случая приложения равномерной нормальной нагрузки по всей границе ${{\Gamma }_{1}}$.

Из (7.12)–(7.13) и (7.15) следует, что сеточная аппроксимация ${{G}_{{ps}}}:{{Q}_{p}} \mapsto {{W}_{p}}$ оператора Пуанкаре–Стеклова ${{G}_{{ps}}}$ имеет вид

Учитывая, что все диагональные элементы матрицы ${{\tilde {K}}_{s}}$ положительны, можно показать, что ${{G}_{{ps}}}$ является симметричной положительно-определенной квадратной матрицей порядка $N$. При численной реализации формировать матрицу ${{G}_{{ps}}}$ в явном виде не требуется, достаточно программно реализовать вычисление произведений каждой из матриц в правой части (7.18) на векторы. Учитывая, что матрицы ${{R}_{{pc}}}$ и $R_{{pc}}^{T}$ содержат только $N$ ненулевых элементов равных 1, вычисление произведений этих матриц на векторы сводится к выполнению $N$ операций присваивания. Умножение диагональной матрицы ${{\tilde {K}}_{s}}$ на вектор требует выполнения $M$ операций умножения. Для вычисления произведений матриц ${{F}_{c}}$ и $F_{c}^{*}$ на векторы целесообразно использовать алгоритмы БПФ. Поэтому далее будем полагать $M = {{2}^{m}}$, $m \in \mathbb{N}$. В этом случае число операций для выполнения одного преобразования имеет порядок $O(M{\kern 1pt} m)$ = $O(M{{\log }_{2}}M)$ [11, 12].

Далее для аппроксимации задачи (6.5) применим гранично-элементный подход [35–37]. Для вычисления билинейной ${{g}_{{ps}}}( \cdot , \cdot )$ и линейной $\phi ( \cdot )$ форм используем квадратурную формулу прямоугольников, узлы которой совпадают с узлами сетки ${{T}_{p}}$. Тем самым определяются аппроксимирующие билинейная $g_{{ps}}^{h}( \cdot , \cdot )$ и линейная ${{\phi }^{h}}( \cdot )$ формы в пространстве ${{\mathbb{R}}^{N}}$

где $\Phi \in {{\mathbb{R}}^{N}}$ – сеточная аппроксимация на ${{T}_{p}}$ функции $\Phi {\kern 1pt} ({{x}_{1}})$, описывающей форму основания штампа.

При аппроксимации множества статически допустимых нормальных напряжений $\Sigma $, определенного формулой (6.1), применяется комбинированный подход. Для аппроксимации ограничений в виде неравенств используется коллокационный метод, а при аппроксимации ограничений в виде равенств – квадратурная формула прямоугольников, узлы которой совпадают с узлами сетки ${{T}_{p}}$. В результате получается замкнутое выпуклое множество статически допустимых узловых нормальных напряжений

Коэффициенты ${{\lambda }_{i}}$ и ${{\vartheta }_{i}}$ вычисляются по формулам

где $x_{1}^{i}$ – координата $i$-го узла сетки ${{T}_{p}}$.

В результате для задачи минимизации (6.5) получим сеточную аппроксимацию – задачу квадратичного программирования: найти сеточную функцию нормальных напряжений ${{Q}_{p}} \in {{\mathbb{R}}^{N}}$ такую, что

Отметим, что размерность задачи (7.22) равна $N$ – количеству узлов сетки на ${{\Gamma }_{p}}$ и не зависит от размера вычислительной области ${{\Gamma }_{c}}$, т.е. от выбора коэффициента расширения вычислительной области $\chi $.

8. Решение задачи квадратичного программирования. Одна из сложностей, возникающих при численном решении задачи (7.22), состоит в наличии ограничений в виде равенств, содержащих все переменные задачи. В [25] для упрощения вида ограничений предложено линейное преобразование переменных позволяющее свести эти ограничения к простым ограничениям, содержащим только одну переменную. Для численного решения полученной в результате преобразования задачи квадратичного программирования с простыми ограничениям в настоящей работе используется вариант МСГ, подробно рассмотренный в [25] при решении задач дискретного контакта для упругой полуплоскости.

9. Численные результаты. Разработанный алгоритм реализован на языке FORTRAN с применением NVIDIA HPC SDK. Для выполнения БПФ использовалась библиотека cuFFT, позволяющая с помощью технологии CUDA производить вычисления на графических процессорах.

Для верификации алгоритма и разработанного программного обеспечения проведено сравнение численных решений ряда задач дискретного контакта, в частности, рассмотренных ниже задач для штампов с регулярным поверхностным рельефом с решениями, полученными с помощью известного алгоритма [24]. Учитывая возможности последнего, при постановке контактных задач использовалось лишь первое из уравнений равновесия штампа (2.5) и полагалось ${{\varphi }_{3}} = 0$. Проведенные расчеты показали, что среднеквадратичные относительные расхождения решений (сеточных функций нормальных напряжений) не превышают $2 \times 1{{0}^{{ - 5}}}$.

Кроме того, получены численные решения задач о вдавливании в упругую полосу штампа, форма основания которого описывается функцией

где $a$ – размер области контакта ${{\Gamma }_{p}}$, $\vartheta > 0$ – безразмерный параметр.

Несложно показать аналитически, что в случае нагружения такого штампа с эксцентриситетом $ea$ относительно точки начального контакта ${{x}_{1}} = 0$ распределение нормальных напряжений будет соответствовать распределению при отсутствии эксцентриситета, смещенному на величину $ea$, осадка штампа ${{\delta }_{2}}$ уменьшится на $\vartheta a{{e}^{2}}$, а сам штамп повернется на угол ${{\varphi }_{3}} = 2\vartheta e$. Проведенные расчеты подтвердили эти выводы.

Далее приведен анализ результатов решения задач дискретного контакта, в которых область фактического контакта состояла из совокупности отдельных пятен контакта. Рассматривались задачи для гладких штампов с регулярным поверхностным рельефом, состоящим из $K$ микровыступов. Номинальная область контакта полагалась равной ${{\Gamma }_{p}}$ = $\{ 0 \leqslant {{x}_{1}} \leqslant a$, ${{x}_{2}} = h\} $. Форма основания штампов задавалась функцией

где ${{\Phi }_{1}}({{x}_{1}})$ – выпуклая функция, определяющая макроформу штампа; ${{\Phi }_{2}}({{\xi }_{1}})$ – строго выпуклая функция, характеризующая форму микровыступов; ${{\xi }_{1}} = \left\{ {K{{x}_{1}}{\text{/}}a} \right\}$ – “ быстрая” координата, $\left\{ \cdot \right\}$ – дробная часть числа.

Для заданной пары функций ${{\Phi }_{1}}({{x}_{1}})$ и ${{\Phi }_{2}}({{\xi }_{1}})$ формула (9.2) определяет однопараметрическое семейство штампов $\Xi (K)$, в качестве параметра которого выступает число микровыступов $K$. Штампы, принадлежащие к одному семейству, имеют одинаковую макроформу, а их микровыступы являются подобными.

Расчеты выполнялись для следующего класса жестких штампов:

где ${{\alpha }_{1}} \geqslant 0$, ${{\alpha }_{2}} > 0$, ${{m}_{1}} > 1$, ${{m}_{2}} > 1$ – безразмерные параметры.

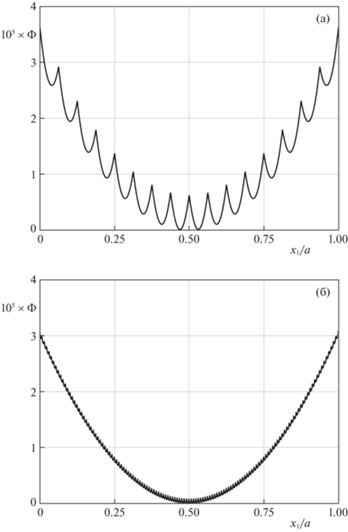
Из формул (9.2)–(9.3) следует, что однопараметрическое семейство штампов $\Xi (K)$ определяется заданным набором параметров ${{\alpha }_{1}}$, ${{\alpha }_{2}}$, ${{m}_{1}}$, ${{m}_{2}}$. Рассмотрим в качестве примера семейство штампов $\Xi (K)$ при ${{\alpha }_{1}} = 3 \times 1{{0}^{{ - 5}}}$, ${{\alpha }_{2}} = 1{{0}^{{ - 4}}}$, ${{m}_{1}} = {{m}_{2}} = 2$. На рис. 1, а–б изображены профили штампов соответственно с 16 и 128 микровыступами. Следует отметить, что на обоих рисунках масштабы изображения по вертикальной и горизонтальной осям отличаются на пять порядков.

Нормальная компонента главного вектора (погонная сила) и главный момент внешних сил, приложенных к штампу, задавались в виде:

где $E{\kern 1pt} * = E{\text{/}}(1 - {{\nu }^{2}})$ – приведенный модуль упругости; $f > 0$ – безразмерный параметр; $e$ – безразмерный параметр, характеризующий эксцентриситет равнодействующей внешней нагрузки относительно центра приведения ${{x}^{c}} = (0.5a,h)$. При проведении расчетов значения параметров внешней нагрузки $f$ и $e$ выбирались таким образом, чтобы решение контактной задачи существовало и пятна контакта для отдельных микровыступов оставались изолированными друг от друга.

Введем на множестве микровыступов сеточную координату $i = \overline {1,K} ,$ и обозначим через ${{\Gamma }_{i}}$ часть ${{\Gamma }_{p}}$, соответствующую микровыступу с сеточной координатой $i$. Далее для каждого штампа введем пары сеточных функций:

– значений $P = [{{p}_{i}}]$ и координат ${{X}_{p}} = [{{({{x}_{1}})}_{i}}]$ максимумов контактного давления на микровыступах

– нормализованных контактных усилий $R = [{{r}_{i}}]$ и координат ${{X}_{r}} = [{{({{x}_{1}})}_{i}}]$ точек их приложения на микровыступах

– относительных величин площадей $S = [{{s}_{i}}]$ и координат ${{X}_{s}} = [{{({{x}_{1}})}_{i}}]$ центров тяжести пятен фактического контакта на микровыступах

где $[\, \cdot \,]$ – скобка Айверсона (функция равная 1 для истинного аргумента и равная 0 в противном случае).

Для каждой пары функций $\{ P,{{X}_{p}}\} $, $\{ R,{{X}_{r}}\} $ и $\{ S,{{X}_{s}}\} $ путем интерполяции построим на ${{\Gamma }_{p}}$ непрерывные функции $p({{x}_{1}})$, $r({{x}_{1}})$ и $s({{x}_{1}})$, называемые далее соответственно огибающей контактного давления, огибающей нормализованных контактных усилий и огибающей относительных величин фактических площадей контакта микровыступов.

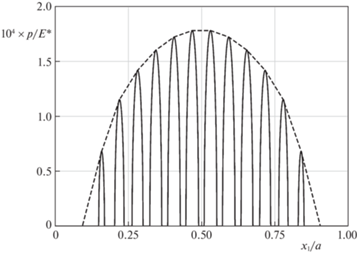
На рис. 2 в качестве примера приведено распределение контактного давления $p \equiv - {{\sigma }_{{22}}}$ на ${{\Gamma }_{p}}$ для штампа, изображенного на рис. 1, а. Толщина полосы принималась равной $h = a{\text{/}}5$. Параметры внешней нагрузки в (9.4) полагались следующими: $f = 2 \times 1{{0}^{{ - 5}}}$ и $e = 0$. Сплошная кривая соответствует контактному давлению, а пунктирная – огибающей контактного давления.

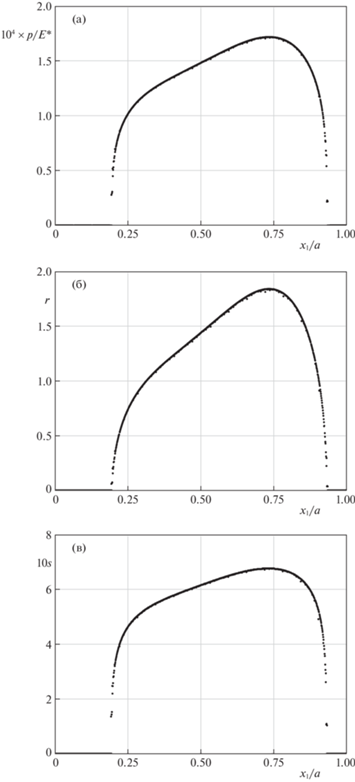
В результате обработки результатов расчетов установлена следующая закономерность: если условия нагружения штампов таковы, что пятна контакта отдельных микровыступов остаются изолированными друг от друга, то для однопараметрического семейства штампов $\Xi ({\rm K})$ существуют единая огибающая контактного давления $\tilde {p}({{x}_{1}})$, единая огибающая нормализованных контактных усилий $\tilde {r}({{x}_{1}})$ и единая огибающая относительных величин фактических площадей контакта $\tilde {s}({{x}_{1}})$ микровыступов, форма и положение которых зависят от параметров $f$ и $e$ внешней нагрузки, а также отношения размера $a$ номинальной области контакта к толщине полосы $h$.

Для подтверждения этой закономерности на рис. 3, а–в приведены множества точек, соответствующих парам сеточных функций $\{ P,{{X}_{p}}\} $, $\{ R,{{X}_{r}}\} $ и $\{ S,{{X}_{s}}\} $ сразу для шести штампов, имеющих 16, 32, 64, 128, 256 и 512 микровыступов. Значения параметров принимались следующими: ${{\alpha }_{1}} = 3 \times 1{{0}^{{ - 5}}}$, ${{\alpha }_{2}} = 1{{0}^{{ - 4}}}$, ${{m}_{1}} = 4$, ${{m}_{2}} = 2$, $f = 2 \times 1{{0}^{{ - 5}}}$, $e = 0.1$ и $h = a{\text{/}}5$.

При проведении расчетов необходимое количество $N$ граничных элементов определялось путем сравнения решений, полученных на вложенных сетках при их двукратном последовательном измельчении. При решении рассмотренных выше задач для штампов с регулярным поверхностным рельефом каждый микровыступ ${{\Gamma }_{i}}$ аппроксимировался сеткой из 1024 граничных элементов. Наибольшее количество элементов сетки для штампа с 512 микровыступами составляло 2¹⁹ = 524288 элементов.

Заключение. Для решения задач дискретного контакта упругой полосы и жесткого штампа с заранее неизвестными площадками фактического контакта в настоящей работе применяется вариационный подход. Построено граничное вариационное неравенство с использованием оператора Пуанкаре–Стеклова, отображающего на части границы упругой полосы нормальные напряжения в нормальные перемещения. Получена эквивалентная задача минимизации граничного функционала на множестве статически допустимых нормальных напряжений.

Оператор Стеклова–Пуанкаре для упругой полосы строится с помощью интегрального преобразования Фурье, поэтому при аппроксимации этого оператора используется ДПФ. Для численной реализации прямого и обратного ДПФ применяются алгоритмы БПФ.

В результате аппроксимации вариационной формулировки с использованием гранично-элементного подхода получена задача квадратичного программирования с ограничениями в виде равенств и неравенств. Для численного решения этой задачи использован алгоритм на основе МСГ [25], учитывающий специфику множества ограничений и позволяющий получать решения контактных задач при внецентренном нагружении штампа, когда необходимо учитывать его повороты.

Построены однопараметрические семейства штампов с поверхностным рельефом, в качестве параметра которых выступает число микровыступов. Штампы, принадлежащие к одному семейству, имеют одинаковую макроформу, а их микровыступы являются подобными. В результате вычислительных экспериментов установлено существование для каждого семейства штампов единой огибающей контактного давления, единой огибающей нормализованных контактных усилий и единой огибающей относительных величин фактических площадей контакта микровыступов. Форма и положение этих огибающих для семейства штампов зависят от параметров внешней нагрузки и отношения размера номинальной области контакта к толщине полосы.