Программирование, 2023, № 2, стр. 36-45

1. ВВЕДЕНИЕ

Понятие амебы [2], [3, глава 1] многочлена Лорана нескольких комплексных переменных прочно вошло в современную математику и широко используется в многочисленных приложениях. В частности, оно возникает в задачах математической физики [4, 5] и при построении решений разностных уравнений и их систем [1]. Известно, что фазовая диаграмма мер Гиббса для димеров на графе может быть представлена в виде амебы ассоциированной спектральной кривой [6, Теорема 4.1]. Изучение распределения энергии в квантовых термодинамических ансамблях естественным образом приводит к рассмотрению понятия амебы и ее т.н. контура [7]. Двойственность Лежандра между энтропией и свободной энергией позволяет вычислять последнюю в рамках теории колчанов как площадь амебы, заданной многочленом Ньютона для модели димеров [8]. С понятием амебы связан ряд важных открытых вопросов, в частности, остающаяся недоказанной на протяжении длительного времени гипотеза М. Пассаре о сплошном свойстве амебы произвольного максимально разреженного многочлена. Эти и многие другие приложения теории амеб в математической физике [9] и вещественной алгебраической геометрии [10] обуславливают давно назревшую необходимость в разработке алгоритмов и общедоступного программного обеспечения для вычисления амеб многочленов Лорана нескольких комплексных переменных.

Попытки создания таких алгоритмов и их программной реализации предпринимались многими исследователями на протяжении трех последних десятилетий. В их основе лежали численное решение алгебраического уравнения относительно выделенного переменного или группы переменных [11–15], аппроксимация амеб с помощью сумм квадратов [16], полиэдральная аппроксимация фиксированной компоненты дополнения к амебе [17], подход с использованием циклических результантов [18] и другие методы [19]. Существенную роль в работах [16, 18] играют методы современной компьютерной алгебры. Сетевой ресурс http://dvbogdanov.ru/amoeba позволяет генерировать программный код на языке среды MATLAB для расчета аффинных и компактифицированных амеб многочленов двух переменных [20, 21]. Текущие границы применимости данного подхода иллюстрируются набором данных www.researchgate.net/publication/338341129_Giant_amoeba_zoo.

Однако, несмотря на значительный прогресс по сравнению с первоначальным представлением авторов определения амебы о виде амеб многочленов нескольких комплексных переменных (см. [2], стр. 194, рис. 16 ), задача вычисления и визуализации амебы многочлена нескольких комплексных переменных (особенно в размерности 3 и выше) в настоящий момент не может считаться удовлетворительно разрешенной. Причин этому несколько: общедоступный программный код для генерации амеб дает приемлемые результаты лишь для многочленов невысокой степени и, как правило, в размерности 2; при этом некоторые из имеющихся решений существенно опираются на функционал коммерческих программных продуктов с закрытым кодом; отсутствует общедоступный сетевой сервис для интерактивной генерации амеб достаточно сложных многочленов двух и трех переменных; не существует инструментария для визуализации деформации амебы многочлена, зависящего от параметров. Настоящая работа призвана восполнить этот пробел.

Высокая вычислительная трудность задачи расчета и визуализации амебы многочлена нескольких переменных обусловлена, в первую очередь, следующими обстоятельствами:

1. За исключением тривиального одномерного случая, амеба многочлена является неограниченным подмножеством вещественного линейного пространства.

2. Амеба ${{\mathcal{A}}_{f}}$ многочлена f двух переменных имеет конечную площадь. В размерности три и выше отношение меры пересечения ${{\mathcal{A}}_{f}} \cap B(a,r)$ амебы многочлена  f с шаром радиуса $r$ и центром в точке $a$ к объему этого шара стремится к нулю при $r \to \infty $ для любого многочлена  f и любой точки $a \in {{\mathbb{R}}^{n}}$. Таким образом, определение местоположения амебы многочлена в пространстве ${\kern 1pt} {{\mathbb{R}}^{n}}$ само по себе является, как правило, нетривиальной задачей.

3. Ограниченные связные компоненты дополнения к амебе могут быть сколь угодно малы, а получение оценок снизу на их размеры является весьма трудоемкой задачей.

4. Количество связных компонент дополнения к амебе многочлена f с фиксированным многогранником Ньютона $\mathcal{N}$ может принимать (в зависимости от выбора коэффициентов  f  ) произвольные значения в диапазоне от числа вершин многогранника $\mathcal{N}$ до числа целых точек в нем [13].

5. Численный расчет достаточно сложной амебы многочлена высокой степени возможен лишь при весьма высокой точности вычислений. Например, при расчете амебы многочлена десятой степени от двух переменных с целыми коэффициентами в квадрате $[ - 20,20] \times [ - 20,20]$ необходимо оперировать величинами порядка ${{e}^{{10 \cdot 20}}} \simeq 7.22597$ × 10⁸⁶, поддерживая точность вычислений, сравнимую с ${{e}^{{ - 10 \cdot 20}}} \simeq 1.38389 \times {{10}^{{ - 87}}}.$ Многочисленные компьютерные эксперименты показывают, что уменьшение точности расчета приводит, как правило, к быстрому накоплению вычислительной погрешности и потере связи результата расчета с подлинной геометрией амебы.

В настоящей работе представлен новый метод вычисления и визуализации амебы многочлена нескольких комплексных переменных, применимый в произвольной размерности. Разработанные алгоритмы вычисления амеб многочленов нескольких переменных реализованы в виде общедоступного сетевого сервиса http://amoebas.ru/. Данный ресурс позволяет в интерактивном режиме выполнять расчет и визуализацию амеб многочленов двух переменных, а также содержит заранее рассчитанные облака точек, аппроксимирующие амебы некоторых оптимальных гипергеометрических многочленов [22] трех и четырех переменных. Для визуализации четырехмерных амеб на сайте выполняется отрисовка их сечений трехмерными гиперплоскостями.

2. ОСНОВНЫЕ ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯ

Всюду в дальнейшем n ≥ 2 обозначает размерность пространства комплексных переменных, $f \in \mathbb{C}[x_{1}^{{ \pm 1}}, \ldots ,x_{n}^{{ \pm 1}}]$ – многочлен Лорана от переменных $({{x}_{1}}, \ldots ,{{x}_{n}})\, \in \,{{\mathbb{C}}^{n}}$. Обозначим через $\mathbb{C}{\kern 1pt} *$ := ${\kern 1pt} \mathbb{C}{{\backslash }}\{ 0\} $ проколотую комплексную плоскость и рассмотрим отображение ${\text{Log}}:(\mathbb{C}{\kern 1pt} *{{)}^{n}} \to {{\mathbb{R}}^{n}}$, определенное формулой

Амебой (см. [2, глава 6, определение 1.4]) алгебраического множества $V \subset {{(\mathbb{C}{\kern 1pt} *)}^{n}}$ называется образ ${\text{Log}}{\kern 1pt} V$, который обозначается ${{\mathcal{A}}_{V}}$. Данное название связано с характерной формой множества ${{\mathcal{A}}_{V}}$ в случае, когда множество V является комплексной алгебраической кривой $\{ (x,y) \in {{\mathbb{C}}^{2}}:f(x,y)$ = 0}. Соответствующая такому множеству амеба, как правило, ограничивает шарообразные “вакуоли” и содержит тонкие “щупальца”, уходящие в бесконечность (см. примеры амеб в работах [14, 20, 21] и на сайте http://amoebas.ru/).

Амеба подмножества комплексного пространства лишь логарифмической шкалой отличается от его диаграммы Рейнхардта. Помимо амебы, были предложены и исследованы другие проекции комплексного пространства ${{\mathbb{C}}^{n}}$ на вещественное пространство той же размерности, на следующие ключевые аналитические и топологические свойства дополнения к алгебраической гиперповерхности. К их числу относятся, в частности, компактифицированная амеба (см. [2], глава 6, теорема 1.12 и рис. 19 ) и “амебоподобный” полиэдральный комплекс, конструкция которого предложена в работе [21]. Следующий результат [2], глава 6, следствие 1.6 устанавливает простую связь между амебой многочлена Лорана f  и разложениями рациональной функции 1/f в ряды Лорана с центром в нуле.

Теорема 1 (см. [2], глава 6). Дополнение $^{c}{{\mathcal{A}}_{f}}: = {{\mathbb{R}}^{n}}{{\backslash }}{{\mathcal{A}}_{f}}$ к амебе многочлена f есть объединение конечного числа непересекающихся связных компонент. Эти компоненты выпуклы и находятся во взаимно-однозначном соответствии с разложениями рациональной функции $1{\text{/}}f$ в ряды Лорана с центром в начале координат.

Выпуклость связных компонент дополнения к амебе алгебраической гиперповерхности выгодно отличает ее от всех конкурирующих проекций комплексного пространства в вещественное и, как будет показано далее, играет существенную роль в построении алгоритмов для вычисления амеб.

Напомним, что носителем многочлена Лорана f называется конечное множество целых точек $\alpha \in {{\mathbb{Z}}^{n}},$ таких, что моном $x_{1}^{{{{\alpha }_{1}}}} \ldots x_{n}^{{{{\alpha }_{n}}}}$ входит в многочлен f с ненулевым коэффициентом. Многогранником Ньютона ${{\mathcal{N}}_{f}}$ многочлена Лорана f называется выпуклая оболочка (в пространстве ${\kern 1pt} {{\mathbb{R}}^{n}}$) носителя многочлена f. Следующий результат показывает, что многогранник Ньютона ${{\mathcal{N}}_{f}}$ несет в себе информацию о геометрии амебы ${{\mathcal{A}}_{f}}$ [23, теорема 2.8 и предложение 2.6].

Теорема 2 (см. [23]). Пусть f – многочлен Лорана. Обозначим через $\{ M\} $ семейство связных компонент дополнения к амебе $^{c}{{\mathcal{A}}_{f}}.$ Существует инъективное отображение

такое, что конус, двойственный к ${{\mathcal{N}}_{f}}$ в точке ${{\nu }_{f}}(M),$ совпадает с конусом рецессии множества $M.$

Целочисленный вектор ${{\nu }_{f}}(M)$ называется порядком компоненты M дополнения к амебе многочлена f. Из приведенных теорем следует, что число связных компонент дополнения к амебе ${{\mathcal{A}}_{f}}$ ограничено снизу числом вершин многогранника ${{\mathcal{N}}_{f}}$ и сверху – числом целых точек в данном многограннике. Нижняя граница была получена в [2]. Варьируя коэффициенты многочлена Лорана f с заданным многогранником Ньютона, можно добиться достижения как верхней [10], так и нижней [13] границы для числа связных компонент множества $^{c}{{\mathcal{A}}_{f}}.$ Более того, вершины многогранника Ньютона всегда лежат в образе отображения ${{\nu }_{f}}.$ Из теоремы 2 следует, что конусы тех связных компонент множества $^{c}{{\mathcal{A}}_{f}},$ которые соответствуют вершинам многогранника ${{\mathcal{N}}_{f}},$ заведомо имеют непустую внутренность. В то же время связные компоненты дополнения амебы, соответствующие внутренним точкам многогранника Ньютона, являются ограниченными.

Пусть $f(\zeta )\, = \,{{a}_{0}}\, + \,{{a}_{1}}\zeta \, + \,{{a}_{2}}{{\zeta }^{2}}\, + \ldots + \,{{a}_{{m - 1}}}{{\zeta }^{{m - 1}}}\, + \,{{\zeta }^{m}}$ – многочлен одного переменного $\zeta \in \mathbb{C}{\kern 1pt} $ с корнями ${{\zeta }_{1}}, \ldots ,{{\zeta }_{m}}.$ Будем без ограничения общности предполагать, что ${\text{|}}{{\zeta }_{1}}{\text{|}}\; \leqslant \;{\text{|}}{{\zeta }_{2}}{\text{|}}\; \leqslant \; \ldots \; \leqslant \;{\text{|}}{{\zeta }_{m}}{\text{|}}$. Амеба многочлена $f$ есть конечное множество точек ln|ζ₁|, ..., $\ln {\text{|}}{{\zeta }_{m}}{\text{|}},$ из которого исключены повторяющиеся элементы. Типичная компонента дополнения $^{c}{{\mathcal{A}}_{f}}$ к амебе данного многочлена есть (непустой) интервал $(\ln {\text{|}}{{\zeta }_{k}}{\text{|}},\ln {\text{|}}{{\zeta }_{{k + 1}}}{\text{|}})$ для некоторого k = $1, \ldots ,m - 1,$ порядок данной компоненты равен $k.$ Таких компонент может, однако, не быть вовсе, в случае, если все корни многочлена $f(\zeta )$ лежат на некоторой окружности $\{ {\text{|}}\zeta {\text{|}} = r\} \subset \mathbb{C}$ с центром в точке $\zeta = 0.$ Кроме того, всегда присутствуют две неограниченные компоненты дополнения $( - \infty ,\ln {\text{|}}{{\zeta }_{1}}{\text{|}})$ и $(\ln {\text{|}}{{\zeta }_{m}}{\text{|}},\infty ),$ чьи порядки равны $0$ и $m,$ соответственно. Таким образом, в одномерном случае вычисление амебы многочлена сводится к нахождению его корней. Для решения данной задачи существует широкий спектр точных и приближенных методов и в настоящей работе мы не рассматриваем этот частный случай, предполагая всюду в дальнейшем, что n ≥ 2.

Задача вычисления амебы многочлена двух или более переменных может, конечно, рассматриваться как задача разрешения алгебраического уравнения относительно одного из входящих в него переменных. Ключевое отличие от одномерного случая состоит в том, что при n ≥ 2 алгебраическое уравнение необходимо решать для всевозможных значений прочих присутствующих в нем переменных. В общем случае осуществить это не представляется возможным, что заставляет обращаться к другим методам вычисления амеб многочленов нескольких переменных.

В некоторых простейших случаях амеба многочлена может быть вычислена точно, а ее граница явно задана трансцендентными уравнениями. Например, амеба многочлена двух переменных $f(x,y) = 1 + x + y$ имеет вид

Аналогичное описание допускает амеба любой комплексной гиперплоскости в произвольной размерности. Амеба многочлена $f(x,y) = a + x$ + + y + xy с произвольным комплексным параметром $a$ есть множество решений неравенства (см. [13, стр. 57])

Сложность вычисления границы амебы многочлена быстро растет с увеличением его степени и числа переменных. Несмотря на это, контуры амеб произвольных классических и обобщенных дискриминантов [2] допускают бирациональную параметризацию Горна–Капранова [24]. Однако амеба многочлена достаточно высокой степени, чьи коэффициенты не обладают многочисленными свойствами симметрии, допускает, вообще говоря, лишь приближенное описание. Построение множества, аппроксимирующего амебу с заданной точностью, является задачей высокой вычислительной сложности.

Под вычислением амебы многочлена Лорана f мы будем всюду в дальнейшем понимать построение достаточно плотного облака точек, лежащих в пересечении амебы с заданной областью $D \subset {{\mathbb{R}}^{n}},$ такой, что $D$ содержит точки любой связной компоненты дополнения $^{c}{{\mathcal{A}}_{f}}.$

3. АЛГОРИТМ ВЫЧИСЛЕНИЯ АМЕБЫ МНОГОЧЛЕНА НА ОСНОВЕ ПОРЯДКА КОМПОНЕНТЫ ЕЕ ДОПОЛНЕНИЯ

В работе [23] показано, что каждой точке дополнения к амебе ${{\mathcal{A}}_{f}}$ многочлена f можно сопоставить целую точку из многогранника Ньютона ${{\mathcal{N}}_{f}}$ с помощью отображения порядка ${{\nu }_{f}}$:

где для всех $j = 1, \ldots ,n$ и $i = \sqrt { - 1} .$ Всюду в дальнейшем вектор ${{\nu }_{f}}({\mathbf{s}})$ называется порядком точки ${\mathbf{s}}{{ \in }^{c}}{{\mathcal{A}}_{f}}$. Любые две точки, лежащие в одной связной компоненте дополнения к амебе многочлена f, имеют одинаковый порядок, называемый порядком этой компоненты (см. формулу (2.1) в Теореме 2); более того, порядки точек из разных компонент дополнения к амебе различны. Таким образом, порядок ${{\nu }_{f}}({\mathbf{s}})$ является классификатором точек дополнения к амебе многочлена  f, позволяющим устанавливать их принадлежность к компоненте заданного порядка.

В работе [23] показано, что для $s \in {{\,}^{c}}{{\mathcal{A}}_{f}}$ интеграл (3.1) допускает представление в следующем существенно более простом виде:

причем значение данного интеграла не зависит от $\arg {{x}_{k}}$ при $k \ne j.$ Поведение интеграла (3.2) в случае, когда точка $s$ лежит внутри или на границе амебы ${{\mathcal{A}}_{f}},$ является, вообще говоря, весьма сложным. В этом случае интеграл (3.2) может оказаться расходящимся, однако в большинстве случаев он сходится, а его значение существенным образом зависит от $\arg {{x}_{k}}$ для всех $k = 1, \ldots ,n.$ Скачок интеграла (3.2) может быть выявлен с помощью символьно-численных алгоритмов контурного интегрирования и использован в качестве критерия принадлежности точки s амебе многочлена $f.$ Данное наблюдение является основой алгоритма вычисления амеб, представленного в настоящей работе и реализованного в виде сетевого сервиса http://amoebas.ru/.

Входные данные алгоритма: размерность пространства переменных $n \geqslant 2$; многочлен $f({\mathbf{x}})$ от $n$ комплексных переменных ${{x}_{1}}, \ldots ,{{x}_{n}};$ множество вершин ${\text{vert}}(\Pi )$ прямоугольного параллелепипеда $\Pi \subset {{\mathbb{R}}^{n}};$ малое число $\varepsilon > 0,$ равное линейному размеру наименьшего элемента объема в ${\kern 1pt} {{\mathbb{R}}^{n}}$, подлежащего проверке на предмет принадлежности амебе многочлена $f({\mathbf{x}})$. Предполагается, что объем параллелепипеда $\Pi $ не равен нулю, а длина по крайней мере одного из его ребер больше $\varepsilon .$

Результатом работы алгоритма является облако точек, аппроксимирующее множество $^{c}{{\mathcal{A}}_{f}} \cap \Pi $ с точностью $\varepsilon .$

Схема работы алгоритма состоит в следующем. Будем обозначать через $S(\Pi )$ конечное множество прямоугольных параллелепипедов в пространстве ${\kern 1pt} {{\mathbb{R}}^{n}}$ и положим на первом шаге работы алгоритма $S(\Pi ): = \{ \Pi \} .$

Пусть ${{\Pi }_{\alpha }}$ – некоторый элемент множества $S(\Pi ).$ Если длина всех его ребер меньше $\varepsilon ,$ то ${{\Pi }_{\alpha }}$ исключается из множества $S(\Pi )$ и осуществляется переход к следующему его элементу. В противном случае каждая из точек множества ${\text{vert}}({{\Pi }_{\alpha }})$ проверяется на принадлежность амебе многочлена $f(x)$ путем выявления скачка интеграла (3.2) по его параметрам $\arg {{x}_{k}},$ $k \ne j.$

Если все точки множества ${\text{vert}}({{\Pi }_{\alpha }})$ лежат в одной и той же связной компоненте дополнения к амебе ${{\mathcal{A}}_{f}},$ то, в силу выпуклости и открытости любой такой компоненты, делается вывод об отсутствии точек амебы ${{\mathcal{A}}_{f}}$ в ${{\Pi }_{\alpha }}.$ Координаты точек ${\text{vert}}({{\Pi }_{\alpha }})$ и порядок содержащей их компоненты дополнения к амебе сохраняются, и выполняется переход к следующему элементу множества $S(\Pi ).$ Если рассмотрены все элементы данного множества, то алгоритм завершает работу.

Если же множество ${\text{vert}}({{\Pi }_{\alpha }})$ содержит точки амебы ${{\mathcal{A}}_{f}}$ или точки, лежащие в разных компонентах ее дополнения, то параллелепипед ${{\Pi }_{\alpha }}$ разбивается на 2ⁿ равных параллелепипедов своими $n$ плоскостями симметрии, параллельными координатным плоскостям в ${\kern 1pt} {{\mathbb{R}}^{n}}$. Эти параллелепипеды добавляются к множеству $S(\Pi )$ и описанный выше процесс повторяется, пока не будут рассмотрены все элементы данного множества. В двумерном случае результатом выполнения данного дихотомического (по каждой размерности) процесса является аппроксимирующее амебу квадродерево, см. рис. 1.

По завершении перебора элементов множества $S(\Pi )$ для каждого возможного значения порядка компоненты дополнения к амебе ${{\mathcal{A}}_{f}}$ сформирован список точек (вершин рассмотренных параллелепипедов), лежащих в компоненте с данным порядком. Для отрисовки этой компоненты берется выпуклая оболочка всех точек из данного списка.

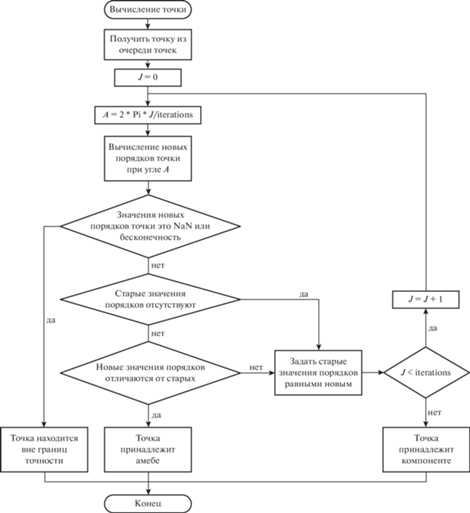
Блок-схема изложенного выше алгоритма представлена на рис. 2. Данный алгоритм реализован на языке программирования C$\# $ и лежит в основе вычислительного функционала сетевого сервиса http://amoebas.ru/. Объем связной компоненты дополнения к амебе может быть сколь угодно мал, а число таких компонент, вообще говоря, весьма сложным образом зависит от коэффициентов многочлена. Эта зависимость не является непрерывной. Например, дополнение к амебе многочлена $x + y + \lambda xy + {{x}^{2}}y + x{{y}^{2}}$ при $\lambda > 0$ содержит компоненту порядка $(1,1)$ в том и только том случае, когда $\lambda > 4$ (см. [22]). При этом площадь данной компоненты стремится к нулю при $\lambda \to 4 + .$ В силу этих причин предложенный алгоритм не может, вообще говоря, гарантировать обнаружение связной компоненты, чей диаметр меньше величины $\varepsilon .$ Более того, мера подмножества в пространстве аргументов комплексных переменных, на котором наблюдается скачок интеграла (3.2), может быть сколь угодно мала, если степень многочлена достаточно высока, а его коэффициенты велики. Однако в некоторых классах частных случаев скорость работы предложенного алгоритма допускает оценку снизу. Например, в случае, когда f – оптимальный гипергеометрический многочлен $n$ комплексных переменных, алгоритм позволяет не более чем за $n{\kern 1pt} {{2}^{{n - 1}}}{\text{Vol}}(\Pi )(1 + 1{\text{/}}\varepsilon {{)}^{n}}$ шагов, представленных на блок-схеме 2, выявить все связные компоненты дополнения к амебе ${{\mathcal{A}}_{f}}$, лежащие в параллелепипеде $\Pi ,$ и такие, что все их линейные размеры не меньше $\varepsilon $. Данное обстоятельство является следствием строгой логарифмической выпуклости функции, определяющей коэффициенты такого многочлена, благодаря которой проверку скачка интеграла (3.2) достаточно осуществлять в двух точках в пространстве аргументов комплексных переменных многочлена  f.

4. СЕТЕВОЙ СЕРВИС ДЛЯ ВЫЧИСЛЕНИЯ И ИЗОБРАЖЕНИЯ АМЕБ МНОГОЧЛЕНОВ ДВУХ И ТРЕХ ПЕРЕМЕННЫХ

Визуализация амебы многочлена трех переменных достаточно высокой степени, вычисленной в виде облака точек, является в большинстве случаев концептуально и технически нетривиальной задачей ввиду сложной геометрической структуры амебы: наличия в “теле” амебы “полостей” и уходящих на бесконечность параллельных слоев, а также возможности присутствия на границе амебы подмножеств негладкости границы с труднопредсказуемой структурой. В силу этих причин в сетевом сервисе http://amoebas.ru/amoeba_3d.html визуализация амебы многочлена f трех переменных осуществляется путем отрисовки пересечений всех компонент дополнения $^{c}{{\mathcal{A}}_{f}}$ с кубом $[ - a,a] \times [ - a,a] \times [ - a,a]$ для некоторого значения $a > 0.$ По умолчанию все эти компоненты отрисованы полупрозрачными, при этом каждая из них может быть сделана непрозрачной путем ее выбора с помощью левой кнопки мыши. Сама же амеба ${{\mathcal{A}}_{f}}$ представлена как пустое пространство между компонентами своего дополнения. Визуализация амеб осуществляется с помощью пакета интерактивной трехмерной графики plotly (см. https://plotly.com/), обеспечивающего возможность приближения, удаления и вращения амебы, а также движения “наблюдателя” внутри нее.

Различные компоненты дополнения к амебе окрашены в различные цвета. Длина волны, соответствующая цвету связной компоненты дополнения к амебе многочлена f двух переменных, пропорциональна евклидову расстоянию от порядка компоненты до центра тяжести многоугольника ${{\mathcal{N}}_{f}}$ (см. рис. 3).

Тестирование алгоритмов вычисления амеб и оценку скорости их работы целесообразно проводить на многочленах, чьи амебы имеют предсказуемую, но при этом достаточно сложную структуру. Для этой цели хорошо подходят т.н. оптимальные гипергеометрические многочлены нескольких переменных [22]: число связных компонент дополнения к амебе такого многочлена является максимально возможным, то есть, совпадает с числом целых точек в его многограннике Ньютона. Для генерации оптимальных гипергеометрических многочленов от трех переменных, амебы которых представлены на общедоступном сетевом ресурсе http://amoebas.ru/amoeba_3d.html, был использован, в частности, следующий программный код в системе компьютерной алгебры Mathematica 11.3:

OptimalPolynomialSimplex[dimension_,

 degree_,power_]:=

Block[{variables,coefficient,exponents},

variables=Table[${{x}_{j}}$,{$j$,1,dimension}];

coefficient[vector_]:=

(Gamma[1+degree-Total[vector]]

(Times @@ Gamma[vector + 1]))^–power;

exponents=Flatten[Outer @@

(Join[List, Table[Range[0, degree],

dimension]]), dimension-1];

Factor[(coefficient /@ exponents).

(Times @@@ (variables^# & /@ exponents))]]

Результатом работы функции OptimalPolynomialSimplex является оптимальный [22] многочлен степени degree с заданным числом переменных, равным dimension. Коэффициенты данного многочлена заданы сужением строго логарифмически вогнутой функцией на множество целых точек симплекса с вершинами $(0,0, \ldots ,0),$ (degree, $0, \ldots ,0), \ldots ,(0, \ldots ,0$, degree). Технический параметр power позволяет управлять “степенью логарифмической вогнутости” коэффициентов генерируемого многочлена, отвечающей за геометрию его амебы. Непрерывная деформация амеб, соответствующая изменению данного параметра в пределах некоторых интервалов, представлена на сайте http://amoebas.ru/. Примерами многочленов, генерируемых функцией OptimalPolynomialSimplex, являются многочлены, чьи амебы представлены на рис. 4 и 5.

Обширный класс выпуклых многогранников, важных в многочисленных приложениях алгебраической и вычислительной геометрии, образуют зонотопы. Напомним, что под зонотопом понимается сумма Минковского конечного числа отрезков в вещественном пространстве. Следующий фрагмент программного кода на языке системы компьютерной алгебры Mathematica 11.3 предназначен для генерации оптимального гипергеометрического многочлена с носителем в произвольном зонотопе с вершинами в узлах целочисленной решетки, заданном как сумма Минковского векторов из списка vectors.

OptimalPolyZonotope[vectors_,power_]:=

Block[{dimension,variables,crossProducts,

normals,sumsOfVectors,massCenter,

constants,coefficient,maxDegree,exponents},

dimension=Length[First[vectors]]; variables=Table[${{x}_{j}}$,{$j$,1,dimension}];

crossProducts=Cross @@@ Subsets[vectors,

 {dimension-1}];

normals=Join[crossProducts,-crossProducts];

sumsOfVectors=

 Join[Table[0,dimension],Union[Total /@

 Drop[Subsets[vectors],1]]];

massCenter=

 Total[sumsOfVectors]/Length[sumsOfVectors];

distanceFromSideToMassCenter[sideNormal_]:=

 Max[Norm /@ ((#.sideNormal)

sideNormal/Norm[sideNormal]$^{2}$ & /@

(# - massCenter & /@ sumsOfVectors))];

constants=

distanceFromSideToMassCenter[#]Norm[#] & /@ normals;

coefficient[vec_]:=

  Simplify[(Times @@ Gamma /@

  (1+constants +((vec+massCenter).# & /@

  normals)))^-power];

maxDegree=Abs[Max[Max /@ (Total /@

   Subsets[vectors])]];

exponents=

   Flatten[Outer@@(Join[List,

    Table[Range[-maxDegree,maxDegree],

     dimension]]),dimension-1];

Numerator[

  Factor[

    (coefficient /@ exponents).

  (Times @@@ (variables$^{\# }$ & /@ exponents))

  ]]]

Результаты расчета и визуализации амеб оптимальных гипергеометрических многочленов с носителями в зонотопах представлены на сайте http://amoebas.ru/. Таблица 1 содержит данные о скорости расчета амеб многочленов двух, трех и четырех переменных, генерируемых с помощью приведенного выше программного кода, для различных значений размерности (dimension), степени многочлена (degree), cтепени логарифмической вогнутости его коэффициента (power) и числа уровней квадродерева, с помощью которого аппроксимируется амеба. Расчеты выполнялись на компьютере с центральным процессором Intel Xeon Gold 6146 с тактовой частотой 3.20 ГГц и 128 Гб оперативной памяти.