Теплофизика высоких температур, 2021, T. 59, № 2, стр. 242-247
Обоснование технологии выращивания монокристаллов лейкосапфира из корунда технической чистоты
Е. И. Школьников, П. П. Иванов *
Объединенный институт высоких температур РАН
Москва, Россия
* E-mail: peter-p-ivanov@yandex.ru
Поступила в редакцию 03.07.2020
После доработки 14.08.2020
Принята к публикации 14.10.2020
Аннотация
Рассматривается процесс высокотемпературной вакуумной очистки пористого гранулированного корунда в качестве этапа подготовки перед использованием в установке промышленного производства монокристаллов сапфира (типа НИКА-М60). Характеристики процесса очистки оцениваются с помощью математических моделей на основе твердотельной диффузии и кнудсеновской диффузии из пористых частиц и через слой пористых частиц. Твердотельная диффузия атомов примеси и кнудсеновское течение паров примеси по порам гранул описываются аналитическими выражениями с подгоночными коэффициентами, идентифицированными с помощью численных решений. Модель кнудсеновского течения через слой гранулированного порошка содержит возможность учета продувки нейтральным газом (аргоном) в целях интенсификации процесса. Получены значения времени очистки порядка нескольких часов при наличии продувки аргоном с расходом на уровне 10–5 кг/(м2 с). В расчете на установку НИКА-М60 расход составляет 7 × 10–7 кг/с или 2.5 г/ч.
ВВЕДЕНИЕ
Мировой рынок лейкосапфира и изделий из него является развивающимся с темпом роста 10–15% в год [1]. Разработка технологии получения монокристаллов лейкосапфира и изделий из них во многом определяет успехи развития важнейших направлений квантовой электроники, микроэлектроники, атомной энергетики. Весьма широк диапазон потребительских свойств монокристаллического лейкосапфира: от генерации, усиления и преобразования электромагнитных колебаний до использования в качестве конструкционного материала. Такое широкое применение монокристаллов лейкосапфира связано с тем, что они обладают набором уникальных качеств: высокая оптическая однородность и прозрачность в широком диапазоне длин волн, радиационная стойкость, хорошие механические, термические и диэлектрические свойства.
В настоящее время широкое распространение для промышленного производства монокристаллов сапфира оптоэлектронного качества получил метод Киропулоса. В работах [2, 3] описана реализация этого метода в установке НИКА-М60: тигель для загрузки сырья (корунда) диаметром 300 мм и высотой 450 мм, рабочая температура выше температуры плавления корунда (2317 К), предельный вакуум – 1.5 × 10–5 Тор.
Сырьем для промышленного производства монокристаллов сапфира может быть побочный продукт установки алюмоводородной технологии, описанной в [4]. Эта установка при расходе алюминия 28 г/с производит 260 кВт тепла, 110 нм3/ч водорода и 56.39 г/с бемита. Последний в результате формовки экструзионным методом гранул в виде цилиндров и прогрева в муфельной печи при температуре 1100°С на воздухе для удаления из него кристаллизационной воды и перевода в α-оксид алюминия приобретает товарный вид технического корунда, состоящего из пористых гранул с характерным диаметром 2–3 мм и длиной 7–14 мм.
Технический корунд, произведенный на алюмоводородной установке, содержит целый букет примесей, среди которых на первом месте стоит железо (до 500 ppm). Для выращивания монокристаллов хорошего качества требуется корунд с чистотой на два порядка выше. В связи с этим ранее была разработана лабораторная технология высокотемпературной вакуумной очистки корунда [5, 6], подкрепленная моделированием и экспериментом при малой толщине слоя пористых гранул. При большей толщине слоя для хорошей очистки за приемлемое время требуется интенсификация процесса путем продувки нейтральным газом [7].
В настоящей работе предлагается в качестве сырья использовать в установке промышленного производства монокристаллов сапфира (типа НИКА-М60) корунд технической чистоты. А процесс высокотемпературной вакуумной очистки корунда рассматривать в качестве этапа подготовки сырья без его перезагрузки и, возможно, разгерметизации установки. При этом некоторые параметры модели процесса отличаются от рассмотренных в [5–7]. Расчет ведется на толщину слоя корунда около 0.4 м, доступны повышенные температуры, ограниченные только температурой плавления, есть ограничение по минимальному давлению вакуума – 1.5 × 10–5 Тор.
МОДЕЛИРОВАНИЕ ВЫСОКОТЕМПЕРАТУРНОЙ ВАКУУМНОЙ ОЧИСТКИ КОРУНДА
В работах [5–7] процесс очистки рассмотрен как выход примеси железа из слоя гранулированного оксида алюминия, состоящий из трех этапов:
– движение атома примеси по радиусу монокристаллической микрочастицы и последующая сублимация примеси с поверхности микрочастицы;
– движение примеси в газовой фазе по радиусу пористой сферической гранулы, сложенной из сплошных микрочастиц;
– движение примеси в газовой фазе сквозь слой сферических гранул по промежуткам между ними.
Каждый этап может быть смоделирован в одномерном приближении.
Выход примеси из сплошной микрочастицы в вакуум. Диффузия примеси к поверхности частиц является первым этапом сложного процесса очистки порошка оксида алюминия. В [6] задача об испарении примеси из сплошной сферической микрочастицы решается по аналогии с задачей охлаждения шара с пространственным краевым условием второго рода, когда на границе задается тепловой поток, характерный для конвективной теплоотдачи [8].
Диффузионная задача выглядит следующим образом:
(1)
$\frac{{\partial {{\rho }_{{{\text{Fe}}}}}}}{{\partial t}} = D\frac{{\partial \left( {{{r}^{2}}\frac{{\partial {{\rho }_{{{\text{Fe}}}}}}}{{\partial r}}} \right)}}{{{{r}^{2}}\partial r}},$(2)
$\begin{gathered} r = 0,\,\,\,\,\frac{{\partial {{\rho }_{{{\text{Fe}}}}}}}{{\partial r}} = 0,\,\,\,\,r = R, \\ {{J}_{X}} = - D\frac{{\partial {{\rho }_{{{\text{Fe}}}}}}}{{\partial r}} = \frac{{J{\kern 1pt} {\text{*}}}}{{\rho _{{{\text{Fe}}}}^{{\text{0}}}}}\left( {{{\rho }_{{{\text{Fe}}}}} - {{p}_{Y}}\frac{{\rho _{{{\text{Fe}}}}^{0}}}{{{{{v}}_{T}}J{\kern 1pt} {\text{*}}}}} \right). \\ \end{gathered} $Для того чтобы воспользоваться приведенным в [8] решением, предположим, что уравнения (1) и (2) используются в некотором интервале времени, в течение которого величина ${{p}_{Y}}$ постоянна и равна какому-то среднему для интервала значению. В этом случае граничное условие (2) можно написать в виде
(4)
$r = 0,\,\,\,\,U(0,t) = 0,\,\,\,\,r = R,\,\,\,\,\frac{{dU}}{{dr}} + \left( {\frac{{{{k}_{1}}}}{D} - \frac{1}{R}} \right)U = 0.$Согласно [8], решение уравнения (3) при граничных условиях (4) выглядит следующим образом:
(5)
$\begin{gathered} {{\rho }_{{{\text{Fe}}}}}(r,t) = \\ = \frac{2}{r}{\kern 1pt} \sum\limits_{m{\kern 1pt} = {\kern 1pt} 1}^\infty {{{{\text{e}}}^{{ - {\kern 1pt} D\beta _{m}^{2}t}}}{\kern 1pt} \frac{{\beta _{m}^{2} + {{{\left( {\frac{{{{k}_{1}}}}{D} - \frac{1}{R}} \right)}}^{2}}}}{{R{\kern 1pt} \left( {\beta _{m}^{2} + {{{\left( {\frac{{{{k}_{1}}}}{D} - \frac{1}{R}} \right)}}^{2}}} \right) + \left( {\frac{{{{k}_{1}}}}{D} - \frac{1}{R}} \right)}}} {\kern 1pt} \,{\kern 1pt} {\kern 1pt} \times \\ \times \,\,\sin {\kern 1pt} ({{\beta }_{m}}r)\int\limits_{r{\kern 1pt} '{\kern 1pt} = {\kern 1pt} 0}^R {r{\kern 1pt} 'F(r{\kern 1pt} ')\sin ({{\beta }_{m}}r{\kern 1pt} ')dr{\kern 1pt} '} + {{k}_{0}}, \\ \end{gathered} $(6)
$\frac{{ppm}}{{pp{{m}_{0}}}} = {{\varepsilon }_{1}}{{e}^{{ - \frac{t}{\chi }}}},\,\,\,\,\chi = \frac{R}{3}\left( {\frac{{\rho _{{{\text{Fe}}}}^{0}}}{{J{\kern 1pt} *}} + \frac{R}{{2D{{\varepsilon }_{0}}}}} \right)$(7)
$\begin{gathered} {{J}_{X}} = {{c}_{1}}{{\rho }_{{{\text{AV}}}}} - {{c}_{2}}{{p}_{Y}},\,\,\,\,{{c}_{1}} = \frac{R}{{3\chi }},\,\,\,\,{{c}_{2}} = {{c}_{1}}\frac{{\rho _{{{\text{Fe}}}}^{0}}}{{{{{v}}_{T}}J{\kern 1pt} {\text{*}}}}, \\ \frac{{\partial {{\rho }_{{{\text{AV}}}}}}}{{\partial t}} = - \frac{3}{R}{{J}_{X}}. \\ \end{gathered} $Диффузия примеси по порам сферической гранулы, сложенной из сплошных микрочастиц. Одномерное уравнение сохранения импульса для кнудсеновского течения по оси y – по радиусу пористой частицы – имеет вид [11]
Поток паров железа ${{J}_{Y}}$ складывается из потоков с поверхности микрочастиц в соответствии с уравнением
где ${{N}_{S}}$ – удельная поверхность микрочастиц (м2/м3); ${{J}_{X}}$ – поток пара через поверхность микрочастиц, представляющий собой функцию ${{J}_{X}} = f({{p}_{Y}}),$ за которой стоит решение задачи об испарении примеси из сплошной микрочастицы (формула (2)). Таким образом, фактическое давление паров в глубине пористой среды вблизи поверхности частиц ${{p}_{Y}}$ определяется как решение двух взаимосвязанных задач.Уравнения (8), (9) составляют пространственную краевую задачу с граничными условиями
Численное решение этой задачи достаточно трудоемко, поэтому имеет смысл построить аналитическую модель с подгоночным параметром, используя одношаговое представление уравнений (8) и (9):
(10)
$\begin{gathered} {{p}_{0}} = {{p}_{1}} + {{c}_{3}}{{J}_{Y}},\,\,\,\,{{c}_{3}} = \frac{{3{{{v}}_{T}}{{R}_{y}}}}{{16R_{Y}^{p}}}, \\ {{J}_{Y}} = {{c}_{4}}{{J}_{X}},\,\,\,\,{{c}_{4}} = \frac{1}{3}{{N}_{S}}{{R}_{y}}, \\ \beta = 1 - \varepsilon {{(1 - \alpha )}^{3}}, \\ \end{gathered} $Решение системы уравнений (10)–(14) быстро сходится после нескольких итераций при задании начального значения $\alpha $ = 0.5. Здесь $\varepsilon $ является заданным подгоночным параметром.
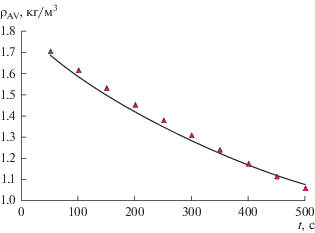
На рис. 1 представлено сравнение процесса снижения средней плотности примеси ${{\rho }_{{{\text{AV}}}}}$ в грануле радиусом 1 мм, сложенной из сплошных микрочастиц радиусом 0.8 мкм, при температуре 1750°С и давлении вакуума 10–5 Тор в численном и аналитическом расчетах. Здесь значение подгоночного параметра $\varepsilon $ = 3.
Рис. 1.
Сравнение аналитического по уравнениям (10)–(14) (сплошная кривая) и численного решения (треугольные маркеры) по (8), (9).
Течение примеси через слой сферических гранул по промежуткам между гранулами. Кнудсеновское течение пара примеси через слой пористых частиц описывается уравнениями, аналогичными (8) и (9). Испарившееся вещество движется вдоль оси z, направленной от дна к поверхности слоя:
Здесь ${{N}_{S}}$ – удельная поверхность гранул (м2/м3), ${{J}_{Y}}$ – поток пара через поверхность гранул.Граничные условия для системы (15), (16):
Предположим, что в случае, когда поток ${{J}_{Z}}$ представляет собой поток смеси аргона и паров железа $\left( {{{J}_{Z}} = J_{Z}^{{{\text{Fe}}}} + J_{Z}^{{{\text{Ar}}}}} \right),$ как это рассматривается в [7] в рамках интенсификации процесса, уравнение сохранения импульса в виде (15) применимо, если под давлением понимать суммарное давление ${{p}^{\Sigma }} = {{p}_{{{\text{Fe}}}}} + {{p}_{{{\text{Ar}}}}}{\text{:}}$(17)
$\frac{{d{{p}^{\Sigma }}}}{{dz}} = - \frac{{3{{{v}}_{T}}}}{{8R_{Z}^{p}}}({{J}_{Z}} + {{J}_{{{\text{Ar}}}}}).$Система обыкновенных дифференциальных уравнений (16), (17) относительно фазовых координат ${{J}_{Z}}$ и ${{p}^{\Sigma }}$ описывает процесс выхода паров железа, поступающих через поверхность гранул в пространство между ними (поток ${{J}_{Y}}$) из толщи слоя гранул на поверхность в вакуумируемое пространство. Это последний этап трехэтапного процесса. В правую часть уравнения (16) входит поток ${{J}_{Y}},$ который вычисляется с помощью модели второго этапа по уравнениям (10)–(14), среди которых уравнение (11) для вычисления ${{J}_{X}}$ использует модель первого этапа – уравнение (7).
ПОИСКОВЫЕ РАСЧЕТЫ
Эффективность процесса высокотемпературной вакуумной очистки микропористого оксида алюминия от примеси железа в настоящем разделе характеризуется относительной остаточной концентрацией примеси. Эта величина равна плотности примеси ρ, осредненной по глубине слоя и по частицам гранулы, отнесенной к начальной плотности примеси ${{\rho }_{0}}.$ На рис. 2 и 3 приведены зависимости относительной остаточной концентрации примеси от продолжительности процесса для различных значений температуры и расхода аргона. Прочие параметры задачи приняты на основе предыдущего экспериментального опыта и с ориентировкой на параметры установки промышленного производства монокристаллов сапфира [3]:
Рис. 2.
Зависимость относительной остаточной концентрации примеси от продолжительности процесса для расхода аргона 10–5 кг/(м2 с) и трех значений температуры: 1 – 1700, 2 – 1750, 3 – 1800°С.
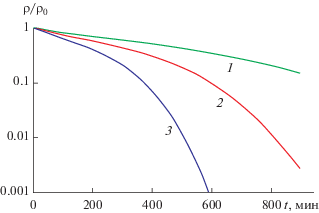
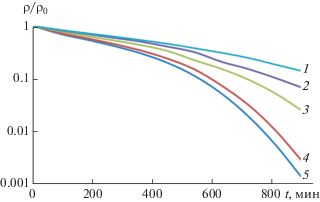
Рис. 3.
Зависимость относительной остаточной концентрации примеси от продолжительности процесса для температуры 1750°C при вариации расхода аргона: 1 – 10–8, 2 – 10–7, 3 – 10–6, 4 – 10–5, 5 – 10–4 кг/(м2 с).
– радиус сплошной микрочастицы R = 0.8 мкм;
– радиус пористой гранулы Ry = 1 мм;
– толщина слоя гранул L = 0.4 м;
– давление вакуума – 1.5 × 10–5 Тор;
– начальная концентрация примеси – 450 ppm;
– базовая температура процесса – 1750°C.
Подгоночные параметры аналитических моделей второго и первого этапа (по осям y и r) приняты по результатам проведенного выше сравнения с численными моделями: $\varepsilon $ = 3 в (10) и ${{\varepsilon }_{0}}$ = 1.68 в (6).
Рис. 2 показывает, что характерное время очистки сильно зависит от температуры. При снижении температуры с 1800°C на 50 градусов время снижения концентрации примеси в 100 раз увеличивается с 500 до 800 мин. Согласно рис. 3, при одних и тех же значениях температуры и длительности процесса с помощью продувки аргоном можно добиться гораздо большей степени очистки. При экспериментально проверенной температуре 1750°C приемлемое время очистки (15 ч) может обеспечить расход аргона 10–5 кг/(м2 с). Данную величину расхода можно считать оптимальной для данных условий проведения процесса. Увеличение расхода аргона не дает ощутимого результата по сокращению времени очистки. Напротив, уменьшение существенно увеличивает время очистки (рис. 3).
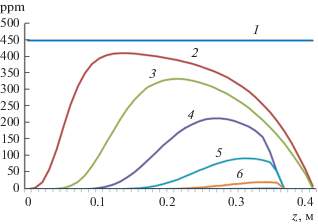
Для практических целей важна максимальная остаточная концентрация примеси в гранулах корунда. На рис. 4 представлена история очистки при температуре 1800°C. Показаны кривые распределения концентрации примеси в ppm по глубине слоя порошка в различные моменты времени процесса (в минутах). Начиная с 450 мин максимальное значение концентрации примеси локализуется при z = 0.35 м (5 см от поверхности). Дальнейшее снижение максимума концентрации примеси показано в таблице.
ЗАКЛЮЧЕНИЕ
Сырьем для промышленного производства монокристаллов сапфира является оксид алюминия (корунд) высокой чистоты. Таким сырьем может стать побочный продукт алюмоводородной технологии – пористый гранулированный корунд, если очистить его от примесей, прежде всего от железа до парциальной концентрации около 5 ppm. В данной работе предложена концепция использования корунда технической чистоты. Существо концепции заключается в добавлении к основному технологическому процессу выращивания монокристалла предварительной стадии высокотемпературной вакуумной очистки корунда, время которой составляет незначительную долю общего времени процесса.
Концепция основана на показанной в работе возможности интенсификации процесса высокотемпературной вакуумной очистки слоя гранулированного корунда до заметного разрушения его пористой структуры. Твердотельная диффузия атомов примеси и кнудсеновское течение паров примеси по порам гранул описываются аналитическими выражениями с подгоночными коэффициентами, идентифицированными с помощью численных решений. Модель кнудсеновского течения через слой гранулированного оксида алюминия включает в себя возможность продувки нейтральным газом (аргоном) в целях интенсификации процесса.
При использовании для высокотемпературной вакуумной очистки температур (до 1750°C) и давлений вакуума (1.5 × 10–5 Тор), доступных на установке выращивания кристаллов сапфира типа НИКА-М60, время снижения на два порядка концентрации примеси железа в техническом корунде не превышает 15 ч. Это время на порядок меньше периода выращивания кристалла, что позволяет рассматривать очистку как некоторую предварительную операцию процесса выращивания кристалла. Такие значения времени очистки реализуются при наличии продувки аргоном с расходом на уровне 10–5 кг/м2с. В расчете на тигель установки НИКА-М60 диаметром 300 мм (площадь – 0.07 м2) необходимый расход равен 7 × 10–7 кг/с или 2.5 г/час.
Список литературы
Кожина Т.Д., Юдин А.В., Ерошков В.Ю. Исследование процессов, разработка технологий и обучение специалистов в области выращивания монокристаллов лейкосапфира для оптики и наноэлектроники // Инновация и экспертиза. 2013. Вып. 1(10).
Бородин А.В., Бородин В.А., Смирнов К.Н., Ширяев Д.Б., Францев Д.Н., Юдин М.В.Установка для выращивания монокристаллов сапфира методом Киропулоса с устройством динамического взвешивания кристалла и автоматическим управлением c обратной связью // Научное приборостроение. 2014. Т. 24. № 3. С. 92.
http://www.ezan.ac.ru/products/crystalgrowth/nikam70/
Grigorenko A.V., Shkolnikov E.I., Zhuk A.Z., Vlaskin M.S. Experience in Creation and Exploitation of Energetic and Energy-Technological Plants Based on Hydrothermal Oxidation of Aluminum // IOP Conf. Series: Materials Science and Engineering. 2018. V. 381. P. 012049.
Иванов П.П., Жук А.З., Власкин М.С. Высокотемпературная вакуумная очистка микропористого оксида алюминия от примеси железа // Вестник ОИВТ РАН. 2018. Т. 1. С. 61.
Жук А.З., Иванов П.П. Моделирование испарения примеси железа из микропористого оксида алюминия в вакуум // ТВТ. 2019. Т. 57. № 5. С. 786.
Школьников Е.И., Иванов П.П. Интенсификация процесса очистки микропористого оксида алюминия от примеси железа с помощью продувки аргоном // ТВТ. 2020. Т. 58. № 1. С. 123.
Ernesto G.M. Heat Conduction in Cylindrical and Spherical Coordinates. 2006. https://ru.scribd.com/ document/52509959/Heat-Conduction
Белов Г.В., Иориш В.С., Юнгман В.С. Моделирование равновесных состояний термодинамических систем с использованием ИВТАНТЕРМО для Windows // ТВТ. 2000. Т. 38. № 2. С. 209.
Doremus R.H. Diffusion in Alumina // J. Appl. Phys. 2006. V. 100. № 10. P. 101301.
Welty J.R., Wicks C.E., Wilson R.E., Rorrer G.L. Fundamentals of Momentum, Heat and Mass Transfer. 5th ed. Hoboken: John Wiley and Sons, 2008.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур