Теплофизика высоких температур, 2022, T. 60, № 1, стр. 108-114

ВВЕДЕНИЕ

Одним из перспективных направлений аддитивных технологий является технология селективного лазерного сплавления (СЛС) – технология послойного выращивания металлических изделий сложной формы, которая представляет собой сплавление частиц металлического порошка с использованием лазерного излучения в качестве источника тепла [1].

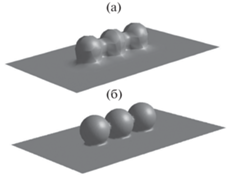
В настоящее время технология СЛС открывает широкие возможности по созданию металлических метаматериалов, обладающих уникальными свойствами, зависящими от их микро- и наногеометрии. Проведены исследования по выращиванию образцов гироидной структуры с характерными масштабами от 0.5 до 5 мм на СЛС-машине М250 [2] из стали AISI-316 и применению этих структур для лопаток соплового аппарата (рис. 1).

Одной из проблем технологии СЛС является проблема контроля микроструктуры и свойств готового изделия. Если параметры процесса выбраны неправильно, могут возникать дефекты, такие как поры несплавления и поры кипения, трещины и т.п. Стабильность процесса СЛС определяется физическими процессами, протекающими во время наращивания изделия. Выявление и понимание этих процессов и их взаимодействия имеет важное значение для получения качественного изделия. Основные процессы: кондуктивная теплопроводность, конвекция в газовой и металлической фазах, излучение, термодинамика фазовых переходов, силы тяжести и плавучести, силы поверхностного натяжения, сила реакции паров металла, эффект Марангони.

В технологии СЛС удовлетворительные по качеству слои для каждого конкретного металла или сплава формируются только в узком диапазоне режимов обработки лазерным излучением. Экспериментальный поиск таких режимов крайне трудоемкий. Численное моделирование СЛС-процессов снижает трудозатраты на подбор режимов для удовлетворительного по качеству и времени сплавления порошков [3].

Анализ работ по численному моделированию процесса СЛС [1, 4–6] показал, что для решения задачи моделирования используется подход расщепления сложной задачи на задачи различных уровней, решения которых согласуются по специально установленной процедуре. Можно выделить три уровня численного моделирования процесса СЛС: микромасштабный, мезомасштабный и макромасштабный. В рамках представленной работы рассматривается первый из них – микроуровень.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Обобщенная математическая модель микроуровня, которая сложилась в литературе к настоящему времени [7–9], представляет собой систему уравнений механики сплошной среды с переменными свойствами и состоит из уравнений состояния, неразрывности, движения и энергии.

Перечисленные уравнения для несжимаемой жидкости имеют следующий вид:

Здесь $\rho $ – плотность, кг/м³; $\bar {\rho }$ – средняя плотность смеси, кг/м³; ${{\rho }_{1}}$ – плотность металла, кг/м³; ${{\rho }_{2}}$ — плотность газа, кг/м³; ${\mathbf{u}}$ – скорость потока, м/с; P – давление, Н/м; τ – скорость деформации, Н/м; g – ускорение свободного падения, Н/кг; β – коэффициент теплового расширения, К^–1; $T$ – текущая температура вещества, К; T_ref – исходная температура вещества, К; ${{k}_{c}}$ – коэффициент сдерживающей силы; ${{f}_{L}}$ – доля жидкой фазы; ${{C}_{K}}$ – константа; σ – коэффициент поверхностного натяжения, Н/м; $k \equiv 1{\text{/}}R$ – кривизна поверхности, м^–1; ${\mathbf{n}}$ – вектор нормали к свободной поверхности; ${{\alpha }_{1}}$ – доля металлической фазы; $t$ ‒ время, с; ${{\bar {C}}_{P}}$ – средняя удельная теплоемкость смеси, Дж/(кг К); $\Delta {{H}_{f}}$ – теплота фазового перехода; $\bar {k}$ – средний коэффициент теплопроводности смеси, Вт/(м К); ${{h}_{c}}$ – коэффициент теплоотдачи, Вт/(м² К); $\varepsilon $ – степень черноты; ${{\sigma }_{s}}$ – постоянная Стефана–Больцмана, Вт/(м² К⁴).

В уравнениях движения и энергии учитываются следующие силы и процессы:

– выталкивающая сила (сила Архимеда) $\bar {\rho }\beta \left( {T - {{T}_{{{\text{ref}}}}}} \right){\mathbf{g}}$;

– сдерживающая сила (аналог закона Дарси) $ - {{k}_{c}}\left( {\frac{{{{{\left( {1 - {{f}_{L}}} \right)}}^{2}}}}{{f_{L}^{3} + {{C}_{K}}}}} \right){\mathbf{u}}$, обеспечивающая неподвижность твердой фазы;

– сила поверхностного натяжения $\sigma kn$, действующая в окрестности “размазанной” свободной поверхности;

– сила Марангони $\frac{{d\sigma }}{{dT}}\left( {\nabla T - {\mathbf{n}}\left( {{\mathbf{n}} \cdot \nabla T} \right)} \right)$, также действующая в окрестности свободной поверхности и возникающая из-за пространственной неравномерности поверхностного натяжения;

– $\left| {\nabla {{\alpha }_{1}}} \right|$ – модуль градиента доли металлической фазы, использование которого позволяет локализовать в пространстве эффекты, связанные со свободной поверхностью металла и “конвертировать” поверхностную силу в объемную;

– поправочный коэффициент $\frac{{2\bar {\rho }}}{{{{\rho }_{1}} + {{\rho }_{2}}}}$;

– испарение металла: ${{Q}_{V}} \approx {{m}_{V}}\Delta {{H}_{V}}$, где ${{m}_{V}}$ – массовый расход, кг/с; $\Delta {{H}_{V}}$ – удельная теплота парообразования, Дж/кг;

– лазерный источник тепла ${{Q}_{T}}$.

Поверхность раздела фаз можно определить по параметру доли металлической фазы ${{\alpha }_{1}}$ (сплошная линия на рис. 2). Объемная доля металла при переходе через границу раздела двух фаз меняется скачкообразно (штриховая вертикальная линия на рис. 2), но поскольку дифференциальные уравнения оперируют непрерывными дифференцируемыми функциями, необходимо бесконечно тонкую поверхность заменить на зону конечной толщины. Граница двух фаз как бы размывается, вводятся приграничные области как в жидкой, так и в газообразной фазе (пунктирные вертикальные линии на рис. 2). Таким образом, происходит переход от сил, сосредоточенных на поверхности, к силам, распределенным по конечному объему. Функция ${{\alpha }_{1}}$ становится гладкой (штриховая линия на рис. 2). Градиент ${{\alpha }_{1}}$ обладает свойствами δ-функции и является ее аналогом (штрихпунктирная линия на рис. 2). Отличие состоит в том, что δ-функция позволяет описать эффекты, сосредоточенные на поверхности, в то время как использование градиента ${{\alpha }_{1}}$ позволяет распределить эти поверхностные эффекты по зоне конечного объема, прилегающей к свободной поверхности.

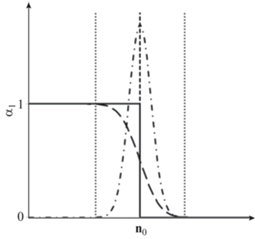
Переход от фазы металла ${{\alpha }_{1}} = 1$ к газовой фазе ${{\alpha }_{1}} = 0$ задается функцией

где $r$ – расстояние от центра частицы до ячейки, в которую записывается значение, м; ${{r}_{0}}$ – радиус частицы порошка, м.

Введенный множитель $\left| {\nabla {{\alpha }_{1}}} \right|$ оказывает симметричное влияние поверхностных сил на приграничные области относительно границы раздела двух фаз. Поэтому необходимо ввести поправку $2{{\bar {\rho }/}}\left( {{{{{\rho }}}_{1}} + {{{{\rho }}}_{2}}} \right)$, которая сместит влияние поверхностных сил в область частиц, находящихся в жидкой фазе.

Поскольку ${{\rho }_{1}} \gg {{\rho }_{2}}$, при $\bar {\rho } = {{\rho }_{1}}$ поправочный коэффициент стремится к 2, при $\bar {\rho } = {{\rho }_{2}}$ ‒ к нулю.

Следует рассмотреть также эффективную “сдерживающую” силу, описывающую разницу в подвижности твердой и жидкой фаз. Вычислительная модель построена таким образом, что частицы металла, находящиеся в твердом состоянии, заданы как жидкость со свойствами металла в твердом состоянии и малыми скоростями движения. В уравнения движения [10–12] входит слагаемое – аналог закона Дарси:

Введем обозначение

Доля жидкой фазы изменяется в диапазоне от нуля до единицы. Пусть ${{f}_{L}} = 0$, а скорость положительна, тогда выражение $ - {{k}_{c}}\left( {\frac{{{{{\left( {1 - {{f}_{L}}} \right)}}^{2}}}}{{f_{L}^{3} + {{C}_{K}}}}} \right){\mathbf{u}} \to - \frac{{{{k}_{c}}}}{{{{C}_{K}}}}{\mathbf{u}}$, сила действует против скорости. Пусть ${{f}_{L}} = 1$, тогда $ - {{k}_{c}}\left( {\frac{{{{{\left( {1 - {{f}_{L}}} \right)}}^{2}}}}{{f_{L}^{3} + {{C}_{K}}}}} \right){\mathbf{u}} \to 0$, т.е. данный член уравнения не оказывает влияния на элемент среды.

Если следовать логике работ [10–12] и выбрать величину коэффициента C_K малой, величина сдерживающей силы будет в сотни раз больше. Таким образом, сдерживающая сила будет быстро меняться в узком интервале значений доли фазы, вследствие чего решение может быть неустойчивым. Чтобы использовать такую функцию, потребуется чрезвычайно мелкая вычислительная сетка в окрестности свободной поверхности и малый шаг по времени, в результате чего сильно растет объем вычислений. В настоящей работе коэффициент $A$ для описания сдерживающей силы принимается в следующем виде (рис. 3):

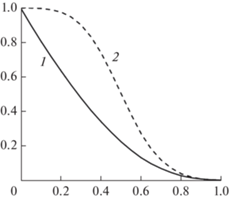
Предлагаемая новая формулировка этого члена не содержит произвольных постоянных, в отличие от общепринятой, она более гладкая и имеет нулевую производную в нуле. Это снижает требования к дискретизации по времени и дает возможность тем самым избавиться от численной неустойчивости и повысить эффективность вычислений. Хотя использование коэффициента $A$ позволяет более точно описать процесс фазового перехода, с использованием коэффициента $A'$ можно достичь большей надежности вычислительной модели.

ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ

Микроуровневая математическая модель процесса СЛС может быть реализована в рамках пакетов, предназначенных для моделирования гидродинамики, с дополнениями, описывающими переменные свойства среды.

Для уравнений, включенных в математическую модель процесса СЛС на микроуровне, применяются следующие схемы пространственной дискретизации:

− противопоточная схема второго порядка – для уравнения энергии. При таком подходе точность более высокого порядка на границе ячейки достигается расширением ряда Тейлора для решения в центре ячейки;

− монотонная гибридная схема третьего порядка, в которой конвективный член описывается с помощью противопоточной схемы второго порядка и центральной разностной схемы (MUSCL [13]) – для уравнения импульсов. Обладает потенциалом для повышения пространственной точности для всех типов сеток за счет уменьшения численной диффузии;

− неявная cхема взвешенных объемных сил – для градиента давления. Данная схема вычисляет давление на грани ячейки, в предположении, что разница нормированных градиентов давления и объемных сил постоянна. Используется, поскольку все действующие силы реализованы как объемные источники.

В многофазной модели для описания границы раздела двух фаз применяется метод объема жидкости (VOF [14]). В модели обе среды – и жидкая (твердая), и газовая – совместно описываются одной системой уравнений, а объемная доля каждой из сред в каждой вычислительной ячейке изменяется и отслеживается по всей расчетной области. В многофазной модели применяется комбинация противопоточных и прямопоточных схем – модифицированная версия схемы c высокой разрешающей способностью определения границы двух сред (HRIC [15]).

Для связи давления и скорости с целью получения дополнительного условия для давления применяется алгоритм предиктор-корректор (PISO [16]), обладающий более высокой степенью приближенной зависимости между поправками на давление и скорость.

Для вычисления градиента с целью получения значений на границах ячейки, вычисления вторичных диффузионных членов и производных по скорости применяется метод наименьших квадратов. Этот метод требует меньше вычислительных ресурсов, а точность вычислений сравнима с точностью других методов.

Одной из важных настроек модели является критерий остановки применения алгебраического многосеточного метода. В задаче микроуровнего масштаба для остановки используется значение 10^–9 (обычно 10^–3), что позволяет получить решение за меньшее количество итераций (на одном временном шаге).

При моделировании процессов СЛС применяется неравномерная сетка, поскольку при использовании мелкой сетки потребуются большие вычислительные ресурсы для всей расчетной области, т.е. продукт будет не рассчитан на массовую вычислительную платформу. Следовательно, можно применить композитный подход к построению сеток для задач данного класса, сократив общее количество ячеек, но сгустив сетку локально в тех подобластях, где это необходимо (пограничные слои частиц порошка).

Для построения сетки с адаптивным сгущением проводится декомпозиция расчетной области на подобласти, в каждой из которых построение и сгущение сетки определяется несколькими управляющими параметрами (рис. 4). Для построения вычислительной сетки вводятся два условия: 1) условие сгущения – амплитуда градиента от максимума $\nabla {{\alpha }_{1}} > 25\% $; 2) условие загрубления – амплитуда градиента от максимума $\nabla {{\alpha }_{1}} < 5\% $.

Поскольку положение поверхности раздела фаз с течением времени трансформируется, сетка должна трансформироваться вслед за ней.

ЧИСЛЕННЫЙ ПРИМЕР

Рассматривается задача расчета двойного прохода лазерного пятна по слою частиц металлического порошка во время процесса СЛС на основе реализованной численной модели микроуровня.

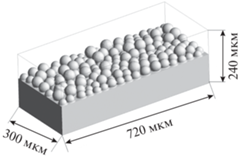
На первом этапе необходимо построить геометрическую модель микроструктуры плотного слоя частиц порошка. Для сферических и эллипсоидальных частиц с произвольной функцией распределения по размерам и для произвольной сплюснутости или вытянутости такой метод разработан в работе [17]. На рис. 5 показано использование метода механической аналогии для построения микрогеометрии слоя сферических микрочастиц порошка на плоской подложке. Смоделирована полидисперсная засыпка частицами с размерами 33–57 мкм, получены координаты центров сфер, их радиусы. Размеры расчетной области выбраны таким образом, что после адаптации вычислительной сетки размер ячейки приблизительно равен 0.1 части диаметра самой маленькой частицы.

Следующим этапом является задание параметров лазерного излучения и материала металлического порошка. Вычислительная модель является универсальной с точки зрения выбора материала порошка. Для демонстрации работоспособности модели и ее результатов выбрана аустенитная нержавеющая сталь AISI 316 [18, 19], хотя большое распространение получили и другие сплавы, например 17-4РН [20].

Основные параметры лазерной обработки порошка выбраны следующими: мощность излучения – 130 Вт, скорость сканирования – 600 мм/с, диаметр лазерного пятна – 70 мкм.

Важную роль при печати изделий технологией СЛС играет стратегия сканирования, влияющая на величину остаточной пористости и напряжений. В данном примере рассматривается зигзагообразная траектория (рис. 6).

Моделирование двойного прохода лазерного излучения реализовано в рамках CFD-пакета ANSYS Fluent.

Частицы порошка вблизи лазерного луча нагреваются и полностью расплавляются. Сила поверхностного натяжения вызывает слияние расплавленных частиц [21]. Подложка под слоем порошка также расплавляется (рис. 7). Поле соответствует безразмерным параметрам: число Пекле Pe = ud/a = 9.2, время $\bar {t} = tu{\text{/}}d = 5.1 \times {{10}^{{ - 6}}}$, где $u$ – скорость сканирования, $d$ – диаметр пятна, $a$ – температуропроводность металла.

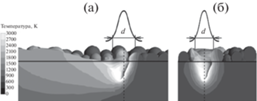
Под воздействием поверхностного натяжения соседние расплавленные частицы стекаются к подложке и смачивают ее, в результате чего расплавленный металл равномерно распределяется по поверхности подложки, что приводит к хорошему сцеплению между верхним слоем и подложкой.

Большая часть энергии лазерного излучения поглощается в центре лазерного пятна. Плотность энергии лазерного излучения достаточно велика для испарения металла. При этом возникает мощная циркуляция жидкого металла, управляемая силами поверхностного натяжения, эффектом Марангони, силой Архимеда, силой тяжести и реактивной силой отдачи испаряющегося металла. Тепловая энергия передается порошку и подложке, окружающим лазерное пятно.

Поскольку в центре лазерного пятна металл испаряется, возникает давление отдачи, которое толкает центральную область металла, находящуюся в лазерном пятне, вниз. Испарение может привести к быстрому охлаждению поверхности ванны расплава и появлению теплового градиента, а впоследствии к развитию эффекта Марангони.

Вследствие возникновения эффекта Марангони высокотемпературный расплавленный металл вытекает из области лазерного пятна вперед или назад, относительно центра пятна. Тепловой поток той части металла, которая выталкивается в хвостовую часть ванны расплава, легко может отводиться в жидкий металл, из-за чего температура вблизи центра лазерного пятна уменьшается. Тепловой поток, который идет от части металла, выталкиваемой вперед, как бы задерживается нерасплавленными частицами. Высокотемпературная жидкость накапливается в передней области лазерного пучка, поэтому большая часть испарения происходит именно в этой области и в центре лазерного пятна. Описанные факты являются причиной утолщения хвостовой части ванны расплава и наличия более высоких температур передней части ванны расплава по сравнению с хвостовой.

И давление отдачи, и сила Марангони способствуют углублению ванны расплава. Давление отдачи углубляет ванну расплава, толкая поверхность металла в центральной области пятна вниз. В дополнение к этому, из-за температурной зависимости поверхностного натяжения жидкость с более высокой температурой в центральной области будет выталкиваться наружу из ванны расплава силой Марангони, таким образом углубляя ванну расплава. Давление отдачи является экспоненциальной функцией температуры, тогда как сила Марангони является линейной функцией температуры. Когда плотность энергии высока, давление отдачи увеличивается намного быстрее, чем сила Марангони. Однако, когда плотность энергии низкая, преобладание давления отдачи уменьшается, поэтому глубина ванны расплава меньше. Таким образом, глубина ванны расплава является нелинейной функцией интенсивности в лазерном пятне.

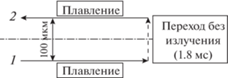
После получения первого прохода установлены два краевых эффекта (рис. 8):

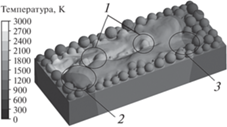
− в начале прохода образуется утолщение;

− в конце прохода, где находится лазерный пучок, образуется углубление, вызванное действием реактивной силы отдачи паров металла.

Во время второго прохода частицы, находящиеся между треками, постепенно расплавляются, на некоторых участках наблюдается недоплав (рис. 8). Возникший дефект может быть устранен уменьшением расстояния между проходами лазерного излучения или увеличением мощности и/или диаметра лазерного пятна.

ЗАКЛЮЧЕНИЕ

Численное моделирование является эффективным инструментом для определения технологических режимов процесса СЛС. Анализ публикаций позволяет сделать вывод о переходе к методологии многоуровневого моделирования, включающей микро-, мезо- и макроуровни. В представленной работе рассмотрена модель микроуровня (масштаб порядка размера частиц), модифицированная для увеличения производительности вычислений: в уравнении импульсов предложена новая формулировка источникового члена, соответствующего сдерживающей силе. Проведен численный эксперимент по моделированию двойного прохода лазерного излучения, в результате которого обнаружены краевые эффекты: углубление в конце прохода и утолщение в начале прохода. Показано, что микроуровневое моделирование является полезным инструментом, позволяющим исследовать влияние режимов обработки на качество получаемого материала, определять оптимальные параметры и оценивать границы области допустимых режимов.