Теоретические основы химической технологии, 2022, T. 56, № 4, стр. 474-495
Теоретический анализ реагентного фильтрования водных суспензий при нерегулируемой скорости фильтрации
В. Л. Поляков *
Институт гидромеханики НАНУ
Киев, Украина
* E-mail: polyakov_igm@list.ru
Поступила в редакцию 31.12.2021
После доработки 16.01.2022
Принята к публикации 15.02.2022
- EDN: OZAAHZ
- DOI: 10.31857/S0040357122030101
Аннотация
Сформулированы три математические задачи осветления водных суспензий на скорых фильтрах с накопителем при нерегулируемой скорости фильтрования с учетом гидравлики отводящих коммуникаций. Фактически они составляют единый цикл, описывающий работу фильтра вплоть до исчерпания его защитного ресурса или снижения производительности до экономически обоснованного минимума. Полученные преимущественно аналитическими методами их решения благодаря своей строгости обеспечивают надежный прогноз изменения характеристик фильтрования (концентрации, скорость, уровень, напор) при разных способах подачи суспензии на фильтр и могут служить эталоном при оценке точности приближенных подходов к аналогичным задачам. На основе указанных решений разработан и проиллюстрирован на типичных примерах метод технологического моделирования реагентного фильтрования, который способствует рациональному выбору технологических (длительность фильтроцикла) и конструктивных (высота загрузки) параметров. Предложен прием упрощения исходной модели (динамическое осреднение), который позволяет получать близкие к точным решения подобных задач для более сложных условий фильтрования. Показано, что вследствие неудачного выбора фильтрующего материала и размеров загрузки возможно существенное снижение эффективности работы фильтра.
ВВЕДЕНИЕ
Эффективность работы водоочистных высокоскоростных фильтров в первую очередь определяется качеством фильтрата и их производительностью [1–3]. При этом ключевую роль играет гидродинамический фактор и особенно скорость движения водной суспензии в слое фильтрующего материала (загрузке), а также в транспортной системе фильтровального сооружения, обеспечивающей его устойчивое функционирование. Скоростная характеристика однозначно связана с производительностью фильтра, но вместе с тем активно влияет на обменные процессы в загрузке, гидравлическое сопротивление ее и отводящих, подводящих коммуникаций. Сложным образом подвижность суспензии отражается на осаждении дисперсной примеси в пористом пространстве загрузки. Обычно с увеличением фильтрационного расхода сорбционная способность материала здесь улучшается, а значит, усиливается прилипание взвешенных (включая и коллоидных) частиц к элементам загрузки (зернам, волокнам и пр.). С другой стороны, таким образом, сокращается динамическая грязеемкость [4, 5], которую следует отличать от истинной постоянной. Впрочем, иногда случается, что больший расход суспензии обусловливает ослабление иммобилизации примеси. Объяснение подобным разноречивым фактам удалось получить благодаря теоретическому анализу динамики отдельных подвижных частиц в пористой среде, то есть на микроуровне. В процессе их осаждения были выделены две характерные стадии [6, 7]. Выявлены прежде всего механизмы доставки взвешенных частиц к частицам-коллекторам (первая стадия), а затем особенности закрепления первых на поверхности вторых и его последствия (вторая стадия) [8–10]. В итоге связь коэффициента скорости прилипания взвеси $\alpha $, который непосредственно контролирует удаление примеси из суспензии, со скоростью фильтрования $V$ была сначала формализована для отдельных механизмов, а затем применительно к реальным случаям, когда в доставке частиц загрязнения принимают участие одновременно, но в разной степени три основных механизма [11–14]. Однако, практическое применение даже обобщенных теоретических формул крайне затруднительно ввиду многообразия условий фильтрования, в частности, полидисперсности примесей, разнородности элементов загрузки, нестабильности расходной характеристики и других причин. Поэтому в настоящее время при математическом моделировании осветления суспензий фильтрованием и тем более в инженерных расчетах, по-прежнему, предпочтение отдается макроподходу, который базируется на концепции сплошной среды. При этом обменные коэффициенты приходится конкретизировать исключительно экспериментальным путем, что увеличивает затраты на научное обоснование конструкции фильтра, технологии фильтрования, но зато серьезно повышается достоверность результатов моделирования и расчетов. Обработка на основе принятой математической модели многочисленных опытных данных по концентрациям взвеси и осадка внутри загрузки и на выходе из нее позволила установить ряд зависимостей $\alpha \left( V \right)$, имевших одночленную степенную форму [1, 15, 16]. При этом возможные значения показателя степени находятся в весьма узком диапазоне, изменяясь от малых отрицательных значений до 1. Последнее значение с одной стороны является предельно большим, поскольку ограничивает указанный диапазон сверху. С другой стороны подобный случай не является надуманным или одним из многих. В действительности он нашел и экспериментальное, и теоретическое подтверждение, а главное, широкое распространение в практике фильтрования. Так, в случае доминирования сил Ван-дер-Ваальса $\alpha \,{{\sim }}{{V}^{{0.875}}}$ [17]. При проведении в Киевском национальном университете строительства и архитектуры (КНУБА) в течение ряда лет на лабораторной установке скорого фильтра с накопителем комплексных исследований был установлен практически линейный характер связи между $\alpha $ и $V$ [18]. Кроме того, ранее выдвинута и обоснована гипотеза о пропорциональности скорости осаждения примеси ее потоку, а не просто концентрации взвеси [19–21].
Экспериментально доказано, что взаимодействие между элементами загрузки и частицами суспензии существенно зависит от их размеров. Особо мелкие частицы (коллоиды) удаляются хуже. Поэтому для интенсификации осветления фильтрованием водной суспензии с относительно высоким содержанием коллоидных частиц широко применяются специальные реагенты (коагулянты, флоккулянты). Благодаря им, физико-химическая обстановка в жидкой фазе рабочего слоя дестабилизируется и указанные частицы активно слипаются, образуя намного более крупные, агрегированные частицы. Подобные частицы не только лучше поглощаются фильтрующим материалом, но вместе с тем при осаждении демонстрируют повышенную чувствительность к гидродинамическому фактору. Отмеченная их особенность также формально выражается в почти линейном характере зависимости ключевого массообменного коэффициента $\left( \alpha \right)$ от скорости $V$. В то же время влияние $V$ на осаждение мелких частиц явно слабее.
Вместе с тем случай линейности $\alpha \left( V \right)$ представляет серьезный методологический интерес, так как для него удалось получить фактически строгие решения ряда задач отрывного фильтрования сложных нестационарных задач в частных производных с переменными коэффициентами, которые ввиду их зависимости от неизвестной величины $V$ изначально являются неопределенными. Также нахождению точных решений способствовало принятие допущения о пропорциональности скорости отрыва прилипших частиц (осадка) фильтрационному расходу. Правомочность такого допущения также подтверждается результатами вышеупомянутых лабораторных исследований. Вообще взаимодействие частиц примеси с зернами-коллекторами носит физико-химический характер и механическое состояние первых обусловлено действием четырех сил, две из которых имеют гидродинамическую природу [22–24]. Линейная зависимость фильтрационной силы от скорости $V$, которая справедлива при ламинарном течении в скорых фильтрах, дает основание связывать коэффициент скорости отрыва осажденных частиц с ней аналогичным образом. Тогда в данной разработке применительно к реагентному отрывному фильтрованию водных суспензий (природных или предварительно очищенных сточных вод) оправдано для обоих массообменных коэффициентов принимать линейную форму зависимости от $V$, так что
где $\alpha ,\,\,\,\beta $ – функциональные коэффициенты скоростей прилипания взвешенных частиц суспензии и отрыва прилипших частиц; ${{\alpha }_{V}},\,\,\,{{\beta }_{V}}$ – аналогичные приведенные коэффициенты, которые в отличие от $\alpha ,\,\,\,\beta $ не меняются со временем.Следует подчеркнуть, что исследования именно отрывного фильтрования в настоящее время являются важнейшим и перспективным направлением в теории фильтрования и им посвящено множество работ, например [25–28]. Однако, аналитические методы здесь при переменной гидравлической нагрузке за исключением отмеченного случая оказываются малоэффективными.
Даже столь краткий обзор достижений при изучении экспериментальными и теоретическими методами значимости скорости фильтрования для осветлительного процесса позволяет заключить о необходимости тщательного учета гидродинамического фактора при решении практических вопросов фильтрования. И прежде всего актуальным остается вопрос о выборе скоростного режима.
Ранее главным образом использовался и поэтому всесторонне изучен режим фильтрования с постоянной скоростью [29–32]. Однако, усиление отрыва осадка по мере заиления загрузки, ненадежность регуляторов скорости, связь поглотительной способности фильтрующего материала со скоростью послужили основанием для реализации режимов с нерегулируемой скоростью. На практике они все чаще применяются на скорых фильтрах с фиксированным перепадом между входным и выходным напорами [33–35], а также при наличии накопителя над загрузкой (стакана фильтра) и подаче на них суспензии постоянным расходом (split filter flow) [36–39]. Ниже детально анализируется аналитическими методами вторая разновидность второго режима. Также заслуживает внимания комбинированный режим, при котором на протяжении одного рабочего периода (фильтроцикла) последовательно задействованы оба упомянутых режима [39, 40]. Сначала фильтрационный процесс сопровождается аккумуляцией суспензии в накопителе и ростом входного напора, а скорость $V$ при этом стабилизируется. Затем уровень в накопителе устанавливается на высоте его кромки и указанная скорость быстро снижается.
Прогрессирующее заиление пористой загрузки обусловливает увеличение ее гидравлического сопротивления. При реализации первого скоростного режима рост потерь напора в ней служит индикатором работоспособности фильтра. При нерегулируемой скорости фильтрования стабильность указанных потерь, в конце концов, должна приводить к значительному снижению производительности фильтра. Ключом к установлению и потерь напора, и переменной скорости являются эмпирические зависимости между концентрацией осадка и градиентом напора или коэффициентом фильтрации (проницаемостью) [41–44]. Поскольку в первую очередь моделируется осаждение частиц суспензии, которые составляют малую часть осадка, то решающее значение для достоверного нахождения гидродинамических характеристик приобретает изучение закономерностей формирования и состава осадка. Экспериментальные исследования меняющегося со временем состава проведены в работах [18, 45–48].
Часто информация об экономических показателях работы фильтра в полном объеме отсутствует и тогда в качестве меры его эффективности приходится использовать время непрерывной работы (длительность фильтроцикла ${{t}_{f}}$). Величина ${{t}_{f}}$ определяется путем технологического [49–51] или математического моделирования с привлечением системы ограничений на осветлительный и фильтрационный процессы [52, 53]. Наиболее жестким является требование к качеству фильтрата. При переменной скорости фильтрования также не допускается ее чрезмерное убывание. Если фильтр оборудован накопителем, то осветление суспензии нередко прекращается при подъеме уровня в нем до отметки кромки. Промежутки времени, в течение которых указанные требования выполняются, ограничены соответственно временем защитного действия загрузки ${{t}_{p}}$, временем допустимого снижения скорости $V$ ${{t}_{V}}$, временем заполнения накопителя ${{t}_{H}}$. Ключевой технологический параметр ${{t}_{f}}$ отождествляется с наименьшим из значений ${{t}_{p}}$, ${{t}_{V}}$, ${{t}_{H}}$ [38, 54, 55].
При проектировании фильтра и заранее известных условиях фильтрования после его ввода в эксплуатацию имеется возможность заблаговременно интенсифицировать технологический процесс, подбирая при его моделировании рациональные конструктивные параметры. Основными среди них являются высота слоя загрузки $L$ и размеры элементов загрузки, в частности эквивалентный диаметр зерна ${{d}_{g}}$. Устройство загрузки со строго определенным (оптимальным) размером зерен в действительности трудно осуществимо. В то же время вполне реально конструирование и эксплуатация загрузок с произвольной высотой $L$. Поэтому изучение разностороннего влияния $L$ на технологический процесс и поиск его оптимальной величины имеют очевидный практический смысл. Некоторые оценки последствий изменения высоты $L$ для характеристик фильтрования при его постоянной скорости экспериментальными и теоретическими методами сделаны, например в работах [37, 56–59].
Итак, целью данной статьи является проведение аналитическими методами анализа осветлительного действия скорых фильтров при линейной зависимости массообменных коэффициентов от скорости фильтрации (реагентное фильтрование) в отсутствии ее регулирования. В его основу положены фактически строгие решения трех математических задач фильтрования при переменном и постоянном уровне суспензии в накопителе над загрузкой. Разработанный при этом инженерный метод позволяет надежно прогнозировать развитие физико-химической обстановки в загрузке с учетом гидравлики транспортной системы фильтровального сооружения. Также он служит теоретической базой для технологического анализа. Как раз на технологических аспектах при разработке рационального алгоритма управления скорым фильтром, совершенствовании его конструкции и акцентируется в статье внимание.
ПОСТАНОВКА И РЕШЕНИЕ МАТЕМАТИЧЕСКИХ ЗАДАЧ
Последовательно рассмотрены аналитическими методами три задачи осветления малоконцентрированной суспензии на скором фильтре с переменной (убывающей) скоростью фильтрования $V$ (рис. 1). Они принципиально различаются характером подачи суспензии на фильтр, исходной загрязненностью его загрузки, ее первичным запасом в стакане. В принятых математических моделях отмеченные особенности находят отражение в уравнении баланса для необработанной суспензии, начальном условии для осадка, граничном условии на входе в загрузку $\left( {z = 0} \right)$. Указанные задачи представляют самостоятельный интерес для эксплуатационных служб, но вместе с тем могут cоставлять единый цикл и привлекаться для теоретического анализа комплексных технологических процессов, описывая их отдельные стадии и в целом. Общим для них являются динамичность фильтрационного расхода и в случае отрывного фильтрования линейная связь между исходными массообменными коэффициентами $\alpha ,\,\,\,\beta $ и скоростью $V$ (1). Следует подчеркнуть, что строгость в математическом отношении представленных ниже аналитических решений не только гарантирует надежность прогнозов развития осветлительного процесса, выбора технологических и конструктивных параметров в надлежащих условиях, но и позволяет их использовать в качестве эталонных при оценке точности приближенных решений более общих задач фильтрования. В первую очередь приводятся уравнения и условия, которые являются общими для трех исходных математических моделей, включающих три взаимосвязанных блока.
Рис. 1.
Схема фильтровальной установки с нерегулируемой скоростью фильтрования: 1 – подводящий трубопровод, 2 – накопитель (стакан), 3 – кромка накопителя, 4 – загрузка фильтра, 5 – сборный трубопровод, 6 – отводящий трубопровод, 7 – задвижка, 8 – коллектор фильтрата.

Осветлительный блок описывает пространственно-временные изменения объемных концентраций загрязнения, состоящего из скоагулированной тонкодисперсной и грубодисперсной примесей, во взвешенном (С) и осажденном (S) состояниях в пределах слоя загрузки $\left( {L \geqslant z \geqslant 0} \right)$. Содержит он, прежде всего, уравнения массопереноса и кинетики массообмена
(3)
$\frac{{\partial S}}{{\partial t}} = {{\alpha }_{V}}V\left( t \right)C - {{\beta }_{V}}V\left( t \right)S,$а также условие постоянства входной концентрации взвеси
где $L$ – высота загрузки, ${{C}_{0}}$ – исходная концентрация примеси в суспензии.Фильтрационный блок образуют уравнения движения суспензии в слое загрузки (линейная фильтрация), его гидравлического сопротивления и состояния осадка
(6)
$k\left( {{{S}_{S}}} \right) = {{k}_{0}}{{f}_{k}}\left( {{{S}_{S}}} \right) = {{k}_{0}}{{\left[ {1 - {{{\left( {\frac{{{{S}_{S}}}}{{{{n}_{0}}}}} \right)}}^{{{{m}_{1}}}}}} \right]}^{{{{m}_{2}}}}},$Здесь $k,{{k}_{0}}$ – коэффициенты фильтрации заиленного и чистого фильтрующего материала; ${{S}_{S}}$ – объемная концентрация осадка; $h$ – пьезометрический напор; ${{n}_{0}}$ – пористость чистой загрузки; ${{m}_{1}},{{m}_{2}}$ – эмпирические коэффициенты (часто принимаются значения ${{m}_{1}} = 1,\,\,{{m}_{2}} = 3$); $\gamma $ – отношение объемных концентраций осадка и твердых частиц в нем (в расчетной части статьи принимается его среднее значение ${{\gamma }_{c}}$).
Гидравлический блок характеризует динамику уровня суспензии в стакане фильтра, его начальное положение, а также потери механической энергии в отводящих коммуникациях
Здесь $H,\,\,\,H{}^{0}$ – текущий и начальный уровни суспензии над загрузкой; $\omega $ – площадь поверхности загрузки; ${{Q}_{{{\text{in}}}}}$ – расход подаваемой на фильтр суспензии; ${{H}_{{{\text{out}}}}}$ – напор в коллекторе фильтрата, $R$ – гидравлическое сопротивление отводящих коммуникаций.
Принятие линейной кинетики межфазного массообмена и математической модели (2)–(10) в качестве базовой оправдано, поскольку проведенные теоретические и экспериментальные [18] исследования ориентированы на технологические аспекты работы скорых фильтров с нерегулируемой скоростью. И естественно, что внимание в них акцентировалось на заключительной стадии фильтрования. Тогда появляется возможность учитывать в указанной модели и автокатализ (ripening), и ограниченность поглотительного ресурса путем соответствующей коррекции массообменных коэффициентов.
Серьезные с технологической точки зрения отличия в рассматриваемых условиях фильтрования, которые приводят к разным расчетным формализмам на его трех этапах, отражены в недостающих граничных и начальных условиях. Так, в первой задаче, отвечающей первому этапу, принимается, что изначально загрузка была чистой, а на входе в нее напор контролируется растущей высотой поверхностного слоя суспензии. Таким образом
Во второй задаче полагается, что уровень суспензии в стакане фильтра стабильно поддерживается на максимальной отметке, а именно, высоте его кромки ${{H}_{e}}$. При этом за время подъема уровня до указанной отметки загрузка успела заметно заилиться, так что
а при отсчете времени с момента заполнения стакана
Очевидно, что суспензия ввиду постоянства ${{H}_{e}}$ фактически будет поступать на фильтр с убывающим расходом ${{Q}_{{{\text{in}}}}}\left( t \right)$, который формально находится из (8) при ${{dH} \mathord{\left/ {\vphantom {{dH} {dt}}} \right. \kern-0em} {dt}} = 0.$
Наконец, третья задача характеризует осветление новым фильтром порции суспензии объемом $\omega {{H}^{0}}$ (или $\omega {{H}_{e}}$), первоначально находившейся в стакане. Поэтому базовая система уравнений и условий (2)–(10) дополняется неоднородным начальным условием (14) и граничным условием (12). Однако, ввиду отсутствия подачи суспензии в фильтр $\left( {{{Q}_{{{\text{in}}}}} = 0} \right)$ здесь в отличие от первой задачи уровень суспензии над загрузкой постепенно срабатывается и удается построить строгое решение.
Для обобщения результатов теоретических исследований вводятся следующие безразмерные переменные и параметры: $\bar {C} = {C \mathord{\left/ {\vphantom {C {{{C}_{0}}}}} \right. \kern-0em} {{{C}_{0}}}},$ $\bar {S}$ = = ${S \mathord{\left/ {\vphantom {S {\left( {{{n}_{0}}{{C}_{0}}} \right)}}} \right. \kern-0em} {\left( {{{n}_{0}}{{C}_{0}}} \right)}},$ $\bar {z} = {z \mathord{\left/ {\vphantom {z L}} \right. \kern-0em} L},$ $\bar {t} = {{{{k}_{0}}t} \mathord{\left/ {\vphantom {{{{k}_{0}}t} {\left( {{{n}_{0}}L} \right)}}} \right. \kern-0em} {\left( {{{n}_{0}}L} \right)}},$ $\bar {V} = {V \mathord{\left/ {\vphantom {V {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}},$ $\bar {h} = {{\left( {h - {{H}_{{{\text{out}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {h - {{H}_{{{\text{out}}}}}} \right)} L}} \right. \kern-0em} L},$ $\bar {H} = {{\left( {H - {{H}_{{{\text{out}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {H - {{H}_{{{\text{out}}}}}} \right)} L}} \right. \kern-0em} L},$ ${{\bar {\alpha }}_{V}} = L{{\alpha }_{V}},$ ${{\bar {\beta }}_{V}} = {{n}_{0}}L{{\beta }_{V}},$ $\bar {k} = {k \mathord{\left/ {\vphantom {k {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}},$ $\bar {\gamma } = \gamma {{C}_{0}},$ $\bar {R} = {{{{\omega }^{2}}k_{0}^{2}R} \mathord{\left/ {\vphantom {{{{\omega }^{2}}k_{0}^{2}R} L}} \right. \kern-0em} L},$ ${{\bar {Q}}_{{{\text{in}}}}} = {{{{Q}_{{{\text{in}}}}}} \mathord{\left/ {\vphantom {{{{Q}_{{{\text{in}}}}}} {\left( {\omega {{k}_{0}}} \right)}}} \right. \kern-0em} {\left( {\omega {{k}_{0}}} \right)}}$.
Итак, базовая система после введения новой независимой переменой $\tau = \int\limits_0^{\bar {t}} {\bar {V}\left( \xi \right)d\xi } $ и замены размерных величин безразмерными аналогами преобразуется к такому виду
(15)
$\frac{{\partial{ \bar {C}}}}{{\partial{ \bar {z}}}} + \frac{{\partial{ \bar {S}}}}{{\partial \tau }} = 0;$(16)
$\frac{{\partial{ \bar {S}}}}{{\partial \tau }} = {{\bar {\alpha }}_{V}}\bar {C} - {{\bar {\beta }}_{V}}\bar {S};$(18)
$\bar {V}\left( {\bar {t}} \right) = - \bar {k}\left( {\bar {S}} \right)\frac{{\partial{ \bar {h}}}}{{\partial{ \bar {z}}}};$(19)
$\bar {k}\left( {\bar {S}} \right) = {{\left[ {1 - {{{\left( {\bar {\gamma }\bar {S}} \right)}}^{{{{m}_{1}}}}}} \right]}^{{{{m}_{2}}}}};$(21)
$\frac{{d\bar {H}}}{{d\bar {t}}} = {{n}_{0}}\left[ {{{{\bar {Q}}}_{{{\text{in}}}}} - \bar {V}\left( {\bar {t}} \right)} \right];$(22)
$\bar {t} = 0,\,\,\,\,\bar {H} = \bar {H}{}^{0};\,\,\left( {{\text{или}}} \right)\bar {H} = {{\bar {H}}_{e}}.$К системе (15)–(22) присоединяются условия (11)–(14) также в безразмерной форме
Решение осветлительного блока первой задачи выражается известными зависимостями [60]
(27)
$\bar {S}\left( {\bar {z},\tau } \right) = {{\bar {\alpha }}_{V}}{{e}^{{ - {{{\bar {\alpha }}}_{V}}\bar {z}}}}\int\limits_0^\tau {{{e}^{{ - {{{\bar {\beta }}}_{V}}\varsigma }}}{{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}\bar {z}\varsigma } } \right)\,d\varsigma ,} $(28)
$\begin{gathered} \bar {C}\left( {\bar {z},\tau } \right) = {{e}^{{ - {{{\bar {\alpha }}}_{V}}\bar {z}}}} \times \\ \times \,\,\left[ {{{e}^{{ - {{{\bar {\beta }}}_{V}}\tau }}}{{I}_{0}}{\kern 1pt} \left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}\bar {z}\tau } } \right) + {{{\bar {\beta }}}_{V}}\int\limits_0^\tau {{{e}^{{ - {{{\bar {\beta }}}_{V}}\varsigma }}}{{I}_{0}}{\kern 1pt} \left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}\bar {z}\varsigma } } \right){\kern 1pt} d\varsigma } } \right]. \\ \end{gathered} $В результате решения фильтрационного блока первой задачи получено квадратное уравнение относительно скорости $\bar {V}$, которая формально зависит от $\bar {t}$и $\tau $
где $\Psi (\tau ) = \int\limits_0^1 {\frac{{d\bar {z}}}{{\bar {k}\left( {\bar {S}\left( {\bar {z},\tau } \right)} \right)}}} $. Отсюда следует, что(30)
$\bar {V}\left( {\bar {t},\tau } \right) = \frac{1}{{2\bar {R}}}\left\{ {\sqrt {{{\Psi }^{2}}(\tau ) + 4\bar {R}\bar {H}\left( {\bar {t},\tau } \right)} - \Psi (\tau )} \right\}.$Интегрирование уравнения (20) при втором условии (21) дает
(31)
$\bar {H}\left( {\bar {t},\tau } \right) = {{\bar {H}}^{0}} + {{n}_{0}}\left( {{{{\bar {Q}}}_{{{\text{in}}}}}\bar {t} - \tau } \right).$Из (30) с учетом (31) следует задача Коши относительно функции $\tau \left( {\bar {t}} \right)$
(32)
$\begin{gathered} \frac{{d\tau }}{{d\bar {t}}} = \frac{1}{{2\bar {R}}} \times \\ \times \,\,\left\{ {\sqrt {{{\Psi }^{2}}(\tau ) + 4\bar {R}\left[ {{{{\bar {H}}}^{0}} + {{n}_{0}}\left( {{{{\bar {Q}}}_{{{\text{in}}}}}\bar {t} - \tau } \right)} \right]} - \Psi (\tau )} \right\}; \\ \end{gathered} $Численно решить задачу (32), (33) с любыми точностью и дискретом не составляет труда, если привлечь стандартные пакеты программ математического анализа, например, Mathcad, Matlab и пр. Точное решение задачи (32), (33) удалось получить только в частном случае ничтожно малого сопротивления отводящих коммуникаций $(\bar {R} \approx 0)$. Здесь оно не приводится ввиду большого объема статьи. После установления однозначной зависимости между $\tau $ и $\bar {t}$ легко увязываются с реальным временем изменения $\bar {S}$ по (27), $\bar {C}$ по (28), $\bar {V}$ по (30) и $\bar {H}$по (31).
Формально третья задача может рассматриваться как частный случай первой. Тогда ввиду ${{Q}_{{in}}} = 0$ будет
и можно не прибегать к численному решению задачи (32), (33). Действительно связь между $\tau $ и $\bar {t}$ принимает форму обратной интегральной функции
(35)
$\bar {t}\left( \tau \right) = 2\bar {R}\int\limits_0^\tau {\frac{{d\varsigma }}{{\sqrt {{{\Psi }^{2}}(\zeta ) + 4\bar {R}\left( {{{{\bar {H}}}^{0}} - {{n}_{0}}\tau } \right)} - \Psi (\zeta )}}} .$Искомые же характеристики $\left( {\bar {S},\,\,\bar {C},\,\,\bar {V},\,\,\bar {H}} \right)$ также определяются соответственно по формулам (27), (28), (30), (34). При этом концентрация $\bar {S}$ во входном сечении загрузки будет
(36)
${{\bar {S}}_{0}}\left( \tau \right) = \bar {S}\left( {0,\tau } \right) = \frac{{{{{\bar {\alpha }}}_{V}}}}{{{{{\bar {\beta }}}_{V}}}}\left( {1 - {{e}^{{ - {{{\bar {\beta }}}_{V}}\tau }}}} \right) + {{\bar {S}}^{0}}(0){{e}^{{ - {{{\bar {\beta }}}_{V}}\tau }}}.$При достижении уровнем суспензии в стакане его кромки $\left( {\bar {z} = {{{\bar {H}}}_{e}}} \right)$ на практике фильтрование обычно прекращается и начинается промывка фильтра. Однако, нередко он к этому моменту не исчерпывает свой осветлительный ресурс и может еще некоторое время продуктивно работать. Теоретически обосновать продление фильтроцикла позволяет решение второй задачи. В такой ситуации, во-первых, необходимо учесть степень загрязненности загрузки к моменту наполнения стакана (в дальнейших расчетах $t = 0$) согласно условию (26), во-вторых, уравнение (20) вырождается и теперь лишь отражает факт синхронного изменения со временем ${{Q}_{{{\text{in}}}}}$ и $V$.
Итак, из решения соответствующего осветлительного блока, включающего условие (26), найдены следующие выражения для обеих концентраций [61]
(37)
$\begin{gathered} \bar {S}\left( {\bar {z},\tau } \right) = {{{\bar {S}}}^{0}}\left( {\bar {z}} \right){{e}^{{ - {{{\bar {\beta }}}_{V}}\tau }}} + \\ + \,\,{{{\bar {\alpha }}}_{V}}{{e}^{{ - {{{\bar {\alpha }}}_{V}}\bar {z}}}}\int\limits_0^\tau {{{e}^{{ - {{{\bar {\beta }}}_{V}}\varsigma }}}{{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}\bar {z}\varsigma } } \right)d\varsigma + } \\ + \,\,{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}{{e}^{{ - {{{\bar {\beta }}}_{V}}\tau }}}\int\limits_0^{\bar {z}} {{{{\bar {S}}}^{0}}\left( \eta \right){{e}^{{ - {{{\bar {\alpha }}}_{V}}\left( {\bar {z} - \eta } \right)}}}} \times \\ \times \,\,\int\limits_0^\tau {{{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}\left( {\bar {z} - \eta } \right)\varsigma } } \right)d\varsigma d\eta {\kern 1pt} ,} \\ \end{gathered} $(38)
$\begin{gathered} \bar {C}\left( {\bar {z},\tau } \right) = {{e}^{{ - {{{\bar {\alpha }}}_{V}}\bar {z}}}}\left[ {{{e}^{{ - {{{\bar {\beta }}}_{V}}\tau }}}{{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}\bar {z}\tau } } \right) + \frac{{^{{^{{}}}}}}{{_{{}}}}} \right. \hfill \\ \left. { + \,\,{{{\bar {\beta }}}_{V}}\int\limits_0^\tau {{{e}^{{ - {{{\bar {\beta }}}_{V}}\varsigma }}}{{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}\bar {z}\varsigma } } \right)d\varsigma } } \right] + {{{\bar {\beta }}}_{V}}{{e}^{{ - {{{\bar {\beta }}}_{V}}\tau }}} \times \hfill \\ \times \,\,\int\limits_0^{\bar {z}} {{{{\bar {S}}}^{0}}\left( \eta \right){{e}^{{ - {{{\bar {\alpha }}}_{V}}\left( {\bar {z} - \eta } \right)}}}{{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}\tau \left( {\bar {z} - \eta } \right)} } \right)d\eta {\kern 1pt} {\kern 1pt} .} \hfill \\ \end{gathered} $Точное аналитическое решение фильтрационного блока представляется в параметрической форме
(39)
$\bar {h}\left( {\bar {z},\tau } \right) = {{\bar {H}}_{e}} - \bar {V}\left( \tau \right)\int\limits_0^{\bar {z}} {\frac{{d\eta }}{{\bar {k}\left( {\bar {S}\left( {\eta ,\tau } \right)} \right)}},} $(40)
$\bar {V}\left( \tau \right) = \frac{1}{{2\bar {R}}}\left\{ {\sqrt {{{\Psi }^{2}}(\tau ) + 4\bar {R}{{{\bar {H}}}_{e}}} - \Psi (\tau } \right\}.$При этом время $\bar {t}$ связано с $\tau $ следующим образом
(41)
$\bar {t}\left( \tau \right) = 2\bar {R}\int\limits_0^\tau {\frac{{d\varsigma }}{{\sqrt {{{\Psi }^{2}}(\zeta ) + 4\bar {R}{{{\bar {H}}}_{e}}} - \Psi (\zeta )}}} .$В случае гидравлически совершенных отводящих коммуникаций
(42)
$\bar {t}\left( \tau \right) = \frac{1}{{{{{\bar {H}}}_{e}}}}\int\limits_0^\tau {\int\limits_0^1 {\frac{{d\bar {z}d\varsigma }}{{\bar {k}\left( {\bar {S}\left( {\bar {z},\varsigma } \right)} \right)}}} } {\kern 1pt} .$Представленные выше расчетные зависимости и уравнения в основном являются строгими, и таким образом обеспечивают высокую достоверность результатов моделирования осветления суспензии на скорых фильтрах с переменной скоростью при адекватности исходной математической модели и ее информационного обеспечения фактическим условиям фильтрования. Однако, практическое применение (27), (28), (30), (31) для условий первой задачи фильтрования и $R$ > $0$ затрудняется ввиду неэффективности аналитических методов при установлении здесь связи между $\bar {t}$ и $\tau $. Поэтому приходится прибегать за исключением частного случая $R = 0$ к численному решению обыкновенного нелинейного уравнения первого порядка с интегральными коэффициентами (32) при однородном условии (33)
Для более общих условий фильтрования, например, при нелинейной связи между $\alpha ,\,\,\beta $ и $V$ (безреагентное фильтрование суспензии с тонкодисперсной примесью), аналитические решения соответствующих математических задач фильтрования реально получать только приближенными методами. И здесь действенным может оказаться динамическое осреднение скорости $V$ в пределах расчетного периода (от 0 до $T$). По существу, вводится новый параметр следующим образом
При этом длительность периода $T$ может быть любой и поэтому параметр ${{V}_{c}}$ является фактически функциональным, но в операциях дифференцирования и интегрирования считается постоянным. Ниже приводятся зависимости и уравнение, вытекающие из аналитического решения первой задачи с использованием указанного приема. В итоге получено
(44)
$F\left( {\bar {t},{{{\bar {V}}}_{c}}} \right) = 2\bar {R}{{\bar {V}}_{c}}\bar {t} - \int\limits_0^{\bar {t}} {\left\{ {\sqrt {{{{\left[ {\int\limits_0^1 {\frac{{d\bar {z}}}{{\bar {k}\left( {\bar {S}\left( {\bar {z},\xi ;{{{\bar {V}}}_{c}}} \right)} \right)}}} } \right]}}^{2}} + 4\bar {R}\left[ {{{{\bar {H}}}^{0}} + \left( {{{{\bar {Q}}}_{{in}}} - {{{\bar {V}}}_{c}}} \right){{n}_{0}}\bar {t}} \right]} - \int\limits_0^1 {\frac{{d\bar {z}}}{{\bar {k}\left( {\bar {S}\left( {\bar {z},\xi ;{{{\bar {V}}}_{c}}} \right)} \right)}}} } \right\}d\xi = 0} ,$(45)
$\bar {S}\left( {\bar {z},\bar {t};{{{\bar {V}}}_{c}}} \right) = {{\bar {\alpha }}_{V}}{{\bar {V}}_{c}}{{e}^{{ - {{{\bar {\alpha }}}_{V}}\bar {z}}}}\int\limits_0^{\bar {t}} {{{e}^{{ - {{{\bar {\beta }}}_{V}}{{{\bar {V}}}_{c}}\varsigma }}}{{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}{{{\bar {V}}}_{c}}\bar {z}\varsigma } } \right)d\varsigma ,} $(46)
$\bar {V}\left( {\bar {t},{{{\bar {V}}}_{c}}} \right) = \frac{1}{{2\bar {R}}}\left\{ {\sqrt {{{{\left[ {\int\limits_0^1 {\frac{{d\bar {z}}}{{\bar {k}\left( {\bar {S}\left( {\bar {z},\bar {t};{{{\bar {V}}}_{c}}} \right)} \right)}}} } \right]}}^{2}} + 4\bar {R}\left[ {{{{\bar {H}}}^{0}} + \left( {{{{\bar {Q}}}_{{in}}} - {{{\bar {V}}}_{c}}} \right){{n}_{0}}\bar {t}} \right]} - \int\limits_0^1 {\frac{{d\bar {z}}}{{\bar {k}\left( {\bar {S}\left( {\bar {z},\bar {t};{{{\bar {V}}}_{c}}} \right)} \right)}}} } \right\},$(47)
$\bar {H}\left( {\bar {t};{{{\bar {V}}}_{c}}} \right) = {{\bar {H}}^{0}} + \left( {{{{\bar {Q}}}_{{in}}} - {{{\bar {V}}}_{c}}} \right){{n}_{0}}\bar {t},$(48)
$\begin{gathered} {{{\bar {C}}}_{e}}\left( {\bar {t},{{{\bar {V}}}_{c}}} \right) = {{e}^{{ - {{{\bar {\alpha }}}_{V}}}}}\left[ {{{e}^{{ - {{{\bar {\beta }}}_{V}}{{{\bar {V}}}_{c}}\bar {t}}}}{{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}{{{\bar {V}}}_{c}}\bar {t}} } \right) + \frac{{^{{^{{}}}}}}{{}}} \right. \hfill \\ \left. { + \,\,\,{{{\bar {\beta }}}_{V}}{{{\bar {V}}}_{c}}\int\limits_0^{\bar {t}} {{{e}^{{ - {{{\bar {\beta }}}_{V}}{{{\bar {V}}}_{c}}\xi }}}{{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}{{{\bar {V}}}_{c}}\xi } } \right)d\xi } } \right], \hfill \\ \end{gathered} $Показательным при нерегулируемом и интенсивном фильтрационном процессе в водоочистных фильтрах является теоретический анализ скорости фильтрования. Ее изменения со временем обусловлены двумя разнонаправленными факторами. С одной стороны, накапливаемая над загрузкой фильтра суспензия способствует росту напора на ее входе и тем самым указанный процесс интенсифицируется. С другой стороны, прогрессирующее заиление фильтрующего материала ведет к постепенному ухудшению его водно-физических свойств, а значит к снижению производительности фильтра. Влияние отмеченных факторов существенно отличается как по степени, так и во времени. Поэтому представляет интерес изучение значимости каждого фактора отдельно. Сравнительно легко провести подобное исследование в отношении первого фактора. Пусть на фильтр постоянно подается чистая вода расходом ${{Q}_{{{\text{in}}}}}$. С учетом сопротивления отводящих коммуникаций скорость фильтрации составит
или в безразмерной форме
(49)
$\bar {V}\left( {\bar {t}} \right) = \frac{1}{{2\bar {R}}}\left[ {\sqrt {1 + 4\bar {R}\bar {H}\left( {\bar {t}} \right)} - 1} \right].$Тогда уравнение относительно искомого уровня $\bar {H}$ принимает следующий вид
(50)
$\frac{{d\bar {H}}}{{d\bar {t}}} = \frac{{{{n}_{0}}}}{{2\bar {R}}}\left[ {2\bar {R}{{{\bar {Q}}}_{{{\text{in}}}}} + 1 - \sqrt {1 + 4\bar {R}\bar {H}\left( {\bar {t}} \right)} } \right].$Решение уравнения (50) при начальном условии
выражается такой обратной функцией
(52)
$\begin{gathered} \bar {t} = \frac{{2\bar {R}}}{{{{n}_{0}}}}\int\limits_{{{{\bar {H}}}^{0}}}^{\bar {H}} {\frac{{d\varsigma }}{{2\bar {R}{{{\bar {Q}}}_{{{\text{in}}}}} + 1 - \sqrt {1 + 4\bar {R}\varsigma } }} = \frac{1}{{2{{n}_{0}}}}\left[ {2\sqrt {1 + 4\bar {R}{{{\bar {H}}}^{0}}} - 2\sqrt {1 + 4\bar {R}\bar {H}} + } \right.} \\ + \,\,\left. {\left( {2\bar {R}{{{\bar {Q}}}_{{{\text{in}}}}} + 1} \right)\ln \frac{{\left( {\sqrt {1 + 4\bar {R}\bar {H}} + 2\bar {R}{{{\bar {Q}}}_{{{\text{in}}}}} + 1} \right)\left( {\sqrt {1 + 4\bar {R}{{{\bar {H}}}^{0}}} - 2\bar {R}{{{\bar {Q}}}_{{{\text{in}}}}} - 1} \right)\left( {{{{\bar {H}}}^{0}} - \bar {R}\bar {Q}_{{{\text{in}}}}^{2} - {{{\bar {Q}}}_{{{\text{in}}}}}} \right)}}{{\left( {\sqrt {1 + 4\bar {R}{{{\bar {H}}}^{0}}} - 2\bar {R}{{{\bar {Q}}}_{{{\text{in}}}}} - 1} \right)\left( {\sqrt {1 + 4\bar {R}{{{\bar {H}}}^{0}}} + 2\bar {R}{{{\bar {Q}}}_{{{\text{in}}}}} + 1} \right)\left( {\bar {H} - \bar {R}\bar {Q}_{{{\text{in}}}}^{2} - {{{\bar {Q}}}_{{{\text{in}}}}}} \right)}}} \right]. \\ \end{gathered} $По мере увеличения $\bar {H}$ скорость $\bar {V}$ неограниченно долго стремится к своему предельному значению ${{\bar {Q}}_{{in}}}$. Ему отвечает стационарное значение ${{\bar {H}}_{\infty }}$, которое, как следует из (52) , равно
Очевидно, что в случае гидравлически совершенных коммуникаций фильтра
Поведение функции $\bar {H}\left( {\bar {t}} \right)$ применительно к идеализированным условиям фильтрования чистой воды или к начальному этапу разделения суспензии иллюстрируется результатами ее расчетов на трех примерах с различными комбинациями значений параметров ${{\bar {Q}}_{{{\text{in}}}}}$ (0.5, 1) и $\bar {R}$ (0, 1). Соответствующие кривые определялись в диапазоне $0 \leqslant \bar {t} \leqslant 10$ на основе (52) и представлены на рис. 2. Следует отметить, что искомая величина в конце расчетного периода приближается к своему стационарному значению, отличаясь от него всего на 2.76% в первом примере $\left( {{{{\bar {Q}}}_{{{\text{in}}}}} = \bar {R} = 1} \right)$, на 2.67% – во втором $\left( {{{{\bar {Q}}}_{{{\text{in}}}}} = 0.5,\,\,\bar {R} = 1} \right)$ и практически совпадает с ним в третьем примере $\left( {{{{\bar {Q}}}_{{{\text{in}}}}} = 1,\,\,\bar {R} = 0} \right)$. Увеличение $\bar {R}$ ведет к более резкому подъему уровня жидкости со временем (кривые 3, 4). В целом из рисунка очевидна выраженная неравномерность формирования поверхностного слоя жидкости, причем слабее она проявляется при минимальных потерях напора в отводящих коммуникациях (пример 3, кривая 5). В дальнейшем уровень суспензии в стакане фильтра будет расти все более замедляясь, поскольку характерное время осветлительного процесса намного превосходит аналогичное время заполнения его емкости. При этом отметка $\bar {H}$ в принципе может, в конце концов, значительно превысить характерное для установившихся условий значение ${{\bar {H}}_{\infty }}$. Однако, установление динамики уровенного режима в течение длительного времени требует уже привлечения намного более сложного инструментария, который отражает специфику и последствия прогрессирующего осаждения взвешенного вещества в порах загрузки и описан в теоретической части данной работы. Полученный с его помощью массив данных вычислений и выявленные при этом закономерности обсуждаются в заключительной, расчетной части работы. Кривые 1, 2 будут прокомментированы ниже при оценивании влияния высоты $L$ на осветлительный эффект.
Рис. 2.
Подъем относительного уровня воды в стакане фильтра над незаиляемой загрузкой: 1–4 – ${{\bar {Q}}_{{{\text{in}}}}} = 1$; 5 – ${{\bar {Q}}_{{{\text{in}}}}} = 0.5$; 1–3, 5 – $\bar {R} = 1$; 4 – $\bar {R} = 0$; 3–5 – $\bar {L} = {L \mathord{\left/ {\vphantom {L {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}} = 1$; 1 – $\bar {L} = 2\,\,\left( {W{{\sim }}L} \right)$; 2 – $\bar {L} = 2\,\,\left( {W = {\text{const}}} \right)$ $\left( {{{L}_{0}}} \right.$– масштаб высоты).

ПРОГНОЗ ИЗМЕНЕНИЯ ХАРАКТЕРИСТИК ФИЛЬТРОВАНИЯ В КОНКРЕТНЫХ УСЛОВИЯХ
Большие возможности предложенной выше совокупности обобщенных расчетных формализмов, которые в комплексе можно трактовать и как инженерный метод расчета реагентного фильтрования водных суспензий на скорых фильтрах с накопителем при нерегулируемой скорости, демонстрируют результаты разностороннего количественного анализа совместно протекающих осветлительного, фильтрационного и гидродинамического процессов. Предметом такого анализа, который проведен на множестве примеров с характерными исходными данными, стал, прежде всего, прогноз поведения важнейших относительных характеристик фильтрования, а именно, объемной концентрации взвеси на выходе из фильтра ${{\bar {C}}_{e}}$, глубины слоя суспензии на поверхности загрузки $\bar {H}$, скорости фильтрования $\bar {V}$, (удельного) объема осветленной суспензии $\tau $.
При подборе исходной информации ориентиром служили данные уже упоминавшихся лабораторных исследований безреагентного и реагентного фильтрования с переменной скоростью [18]. Ввиду большого количества параметров, задействованных в принятых математических моделях, и большого объема статьи только часть из них непрерывно или дискретно варьировались. Значения же других параметров фиксировались. Тем самым удалось углубить понимание особенностей функционирования скорых фильтров с накопителями суспензии, получивших в последнее время широкое распространение в Украине и за рубежом. Так, была выявлена важная роль сорбционной составляющей в массообмене между твердой и жидкой фазами, физико-химического взаимодействия между ними в кольматаже загрузки фильтра, гидравлики основных и вспомогательных конструктивных элементов в общей гидродинамике фильтровальной установки.
В первой серии тестовых примеров прогнозировались изменения вышеупомянутых характеристик со временем в течении минимум 1000 условных единиц (примерно соответствует 80 ч) при заданных ${{\bar {\beta }}_{V}} = 0.01,$ ${{\bar {\gamma }}_{c}} = 0.0005,$ ${{n}_{0}} = 0.47,$ ${{\bar {H}}^{0}} = 0,$ $\bar {R} = 1$ (только в одном примере принято $\bar {R} = 0$). При этом менялись ${{\bar {\alpha }}_{V}}\left( {5,\;7\;,9} \right)$ и ${{\bar {Q}}_{{in}}}\left( {0.2,\;1} \right)$. Здесь значение ${{\bar {\alpha }}_{V}} = 5$ означает, что фильтрующий материал является умеренно сорбирующим; ${{\bar {\alpha }}_{V}} = 7$ – хорошо сорбирующий материал; ${{\bar {\alpha }}_{V}} = 9$ – сильно сорбирующий. Подобранная же и неоднократно используемая пара значений ${{\bar {Q}}_{{{\text{in}}}}}$ отвечает как низкой интенсивности подачи воды и реальным условиям малопродуктивного фильтрования на скорых фильтрах с замедленным подъемом уровня над загрузкой $\left( {{{{\bar {Q}}}_{{{\text{in}}}}} = 0.2} \right)$, так и высокой интенсивности $\left( {{{{\bar {Q}}}_{{{\text{in}}}}} = 1} \right)$ и экстремальным условиям, когда удается обрабатывать значительные объемы воды, но при этом уже изначально имеют место значительные потери напора в фильтре, а также существует серьезная опасность ускоренных заиления загрузки (верхнего участка при нисходящем фильтровании) и наполнения стакана фильтра.
Первостепенное значение для контроля работы фильтра имеет оперативная информация о качестве осветления суспензии, которую сравнительно просто получить теоретическим путем. Содержание взвешенного вещества в фильтрате определялось надежно по формуле (28) и с привлечением (32), (33), а также параллельно по приближенной формуле (48) с учетом (44). Необходимо подчеркнуть, что полученное выше аналитико-численное решение (строгое при $\bar {R} = 0)$ первой задачи в состоянии обеспечить любую точность вычислений искомых характеристик. Поэтому его можно считать эталонным и задействовать для оценок погрешностей вследствие применения приближенных приемов и, в частности, динамического осреднения скорости фильтрования, благодаря которому и удалось вывести расчетные выражения (44)–(48).
Два семейства кривых роста ${{\bar {C}}_{e}}$, отвечающие ${{\bar {Q}}_{{{\text{in}}}}} = 0.2$ и 1, показаны соответственно на рис. 3 и 4. Расхождение между эталонными и приближенными кривыми оказалось настолько малым что на указанных рисунках они попарно слились, причем вплоть до момента полной выработки защитного ресурса загрузки, когда ${{\bar {C}}_{e}}$ приближается к 1. Естественно, что увеличение ${{\bar {Q}}_{{{\text{in}}}}}$ способствовало пропуску через фильтр большего количества суспензии и, как следствие, его ускоренному кольматажу. Действительно, концентрация примеси на выходе из фильтра сокращается на порядок при ${{\bar {\alpha }}_{V}} = 5,\;\,7,\;\,9$ и ${{\bar {Q}}_{{{\text{in}}}}} = 1$ через соответственно время 142.75, 267.5, 402.9, а при ${{\bar {Q}}_{{in}}} = 0.2$ снизится в первом случае на порядок примерно через 700 единиц. Следует заметить, что совершенствование коммуникаций фильтра и таким образом минимизация их гидравлического сопротивления (в идеале $\bar {R} = 0$) практически не отразились на качестве фильтрата.
Рис. 3.
Рост относительной объемной концентрации взвешенного вещества в фильтрате со временем $\left( {{{Q}_{{{\text{in}}}}}} \right. = 0.2$ и $\left. 1 \right)$: 1, 3, 5 – приближенный расчет; 2, 4, 6 – точный; 1, 2 – ${{\bar {\alpha }}_{V}} = 5$; 3, 4 – ${{\bar {\alpha }}_{V}} = 7$; 5, 6 – ${{\bar {\alpha }}_{V}} = 9$.

Рис. 4.
Рост относительной объемной концентрации взвешенного вещества в фильтрате со временем $\left( {{{Q}_{{{\text{in}}}}}} \right. = 0.2$ и $\left. 1 \right)$: 1, 3, 5 – приближенный расчет; 2, 4, 6 – точный; 1, 2 – ${{\bar {\alpha }}_{V}} = 5$; 3, 4 – ${{\bar {\alpha }}_{V}} = 7$; 5, 6 – ${{\bar {\alpha }}_{V}} = 9$.

Также анализировалась пригодность приближенного решения для инженерных расчетов путем сопоставления данных вычислений динамики поверхностного слоя суспензии, найденных с использованием эталонного аналитико-численного решения на основе (31)–(33) и приближенного на базе (44), (47). Результаты в форме графиков зависимости $\bar {H}\left( {\bar {t}} \right)$ изображены при ${{\bar {Q}}_{{{\text{in}}}}} = 1$ на рис. 5, а при ${{\bar {Q}}_{{{\text{in}}}}} = 1.5$ на рис. 6. Значительные различия между соответствующими значениями $\bar {H}$ имеют место только на начальном этапе осветления $\left( {\bar {t} < 10} \right)$, то есть в течение максимум первого часа работы фильтра, а в дальнейшем не превышают 4% при ${{\bar {\alpha }}_{V}} = 9$ и 8% при ${{\bar {\alpha }}_{V}} = 5$. Здесь в приближенных расчетах величина ${{\bar {H}}^{0}}$ отождествлялась с ${{\bar {H}}_{\infty }}$, а в эталонных ранний подъем уровня накопителя определялся в соответствии с зависимостью $\bar {t}(\bar {H})$ (52). Итак, можно утверждать, что отмеченное приближенное решение непригодно на начальной стадии, которая не представляет практического интереса, но в целом правильно отражает последствия прогрессирующего заиления загрузки и интенсивной подачи суспензии на фильтр. Также определялась величина $\bar {H}$ и при $\bar {R} = 0$. Соответствующие значениям $\bar {R}$ (0 и 1) при ${{\bar {\alpha }}_{V}} = 9$ кривые 1 и 3 существенно различаются на протяжении всего расчетного периода, так что, например, уменьшение $\bar {R}$ может ощутимо замедлить подъем уровня суспензии и тем самым продлить работу фильтра. Важное значение сорбционных свойств загрузки для формирования поверхностного слоя подтверждается рис. 6.
Рис. 5.
Подъем относительного уровня суспензии над заиляемой загрузкой со временем $\left( {{{{\bar {Q}}}_{{in}}} = 0.2} \right)$: 1, 3 – точный расчет; 2, 4 – приближенный; 1, 2 – ${{\bar {\alpha }}_{V}} = 9$; 3, 4 – ${{\bar {\alpha }}_{V}} = 5$.
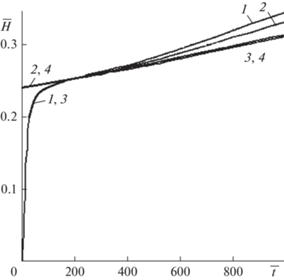
Рис. 6.
Подъем относительного уровня суспензии над заиляемой загрузкой со временем $\left( {{{{\bar {Q}}}_{{{\text{in}}}}} = 1} \right)$: 1, 3, 5, 6 – точный расчет; 2, 4 – приближенный; 1–3 – ${{\bar {\alpha }}_{V}} = 9$; 4–6 – ${{\bar {\alpha }}_{V}} = 5$; 1, 2, 4, 5 – $\bar {R} = 1$; 3, 6 – $\bar {R} = 0$.

Объем осветленной суспензии при постоянной гидравлической нагрузке определяется временем работы фильтра в течение одного фильтроцикла и его производительностью, которая прямо пропорциональна скорости фильтрования. В отсутствии регуляторов скорости фильтрационный расход в пористой загрузке меняется со временем вследствие и осаждения внутри нее взвеси, и роста входного напора. Поведение искомой функции $V\left( t \right)$ диктуется технологией фильтрования. На рис. 7 изображены кривые, описывающие изменения относительной скорости $\bar {V}$ под влиянием указанных факторов применительно к условиям первой (кривые 4–6) и второй (кривые 1–3) задач. В первом случае вычисления проводились при ${{\bar {Q}}_{{in}}} = 0.5$ и 1, а также разных значениях ${{\bar {\alpha }}_{V}}$ по (30)–(34) и свидетельствуют о сбалансированности факторов на протяжении всего расчетного периода, причем варьирование ${{\bar {\alpha }}_{V}}$ практически не сказывалось на величине $\bar {V}$. Как следствие, участки кривых, отвечающие ${{\bar {\alpha }}_{V}} = 5,\;\,7,\,\;9$ и времени продуктивной работы фильтра, практически слились. Если же над изначально чистой загрузкой поддерживать постоянный уровень (например, на высоте кромки стакана), то динамическая картина, рассчитанная по (40), (41), существенно меняется. Сразу фильтрационный процесс протекает с высокой интенсивностью, которая неуклонно снижается. И закономерно, что темп такого снижения диктуется коэффициентом, характеризующим сорбционную способность материала загрузки. Вообще в подобных ситуациях при выполнении технологического анализа особого внимания заслуживает величина $\bar {V}$, поскольку ее быстрое убывание может стать причиной ранней промывки фильтра. Вычислительные ошибки, вносимые вышеупомянутым приемом при ${{\bar {Q}}_{{{\text{in}}}}} = 1$, были в пределах нескольких процентов.
Рис. 7.
Изменение относительной скорости фильтрования со временем: 1–3 – $H = {\text{const}}$; 4–6 – ${{\bar {Q}}_{{{\text{in}}}}} = 1$; 7–9 – ${{\bar {Q}}_{{{\text{in}}}}} = 0.5$; 1, 4, 7 – ${{\bar {\alpha }}_{V}} = 5$; 2, 5, 8 – ${{\bar {\alpha }}_{V}} = 7$; 3, 6, 9 – ${{\bar {\alpha }}_{V}} = 9$.

Непосредственно судить о результативности работы фильтра дает возможность объем осветленной с начала фильтроцикла суспензии за вычетом затрат на промывку. Приведенная величина такого объема в эталонных решениях выражается новой переменной $\tau $, а в приближенном величиной ${{\bar {V}}_{c}}$. На рис. 8 даны кривые нарастания со временем $\tau $, во-первых, для трех значений ${{\bar {Q}}_{{{\text{in}}}}}\left( {0.2,1,1.5} \right)$ и двух значений ${{\bar {H}}_{e}}$ (2, 4). Отсюда очевидно, что равномернее увеличивается $\tau $ при скомпенсированности влияния заиления загрузки и подъема уровня над ней на фильтрационный процесс $\left( {{{{\bar {Q}}}_{{{\text{in}}}}} = {\text{const}}} \right)$. Вместе с тем величины ${{\bar {Q}}_{{{\text{in}}}}},{{\bar {H}}_{e}}$ существенно отражаются на скорости и результатах обработки суспензии.
ТЕХНОЛОГИЧЕСКИЙ АНАЛИЗ С ПРИМЕРАМИ
При выработке алгоритма управления технологическим процессом фильтрования с нерегулируемой скоростью определяющее значение приобретает учет лимитирования работы фильтра вследствие неудовлетворительного качества и высокой стоимости осветления, а также из-за конструктивных особенностей. Очевидно, что в течение всего срока эксплуатации очистной фильтр обязан гарантировать снижение концентрации дисперсной примеси в воде как минимум до установленного нормативными документами предельно допустимого значения ${{C}_{ * }}$. Формально это жесткое требование удобно представить в виде следующего соотношения
(54)
${{\bar {C}}_{e}}\left( {\bar {t}} \right) = \bar {C}\left( {1,\bar {t}} \right) \leqslant {{\bar {C}}_{ * }}.$Период, на протяжении которого такое снижение постоянно обеспечивается, или, другими словами, время защитного действия загрузки ${{\bar {t}}_{p}}$ предлагается рассчитывать, привлекая полученные выше решения двух задач фильтрования. Тогда общее выражение для относительного значения ${{\tau }_{p}}$, с которым однозначно связано искомое ${{\bar {t}}_{p}}$, согласно (28) принимает вид
(55)
$\begin{gathered} {{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}{{\tau }_{p}}} } \right) + {{{\bar {\beta }}}_{V}}\int\limits_0^{{{\tau }_{p}}} {{{e}^{{ - {{{\bar {\beta }}}_{V}}\left( {\varsigma - \tau } \right)}}}} {{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}\varsigma } } \right)d\varsigma + \\ + \,\,{{{\bar {\beta }}}_{V}}\int\limits_0^{\bar {z}} {{{{\bar {S}}}^{0}}\left( \eta \right){{e}^{{ - {{{\bar {\alpha }}}_{V}}\left( {\bar {z} - 1 - \eta } \right)}}}} {{I}_{0}}\left( {2\sqrt {{{{\bar {\alpha }}}_{V}}{{{\bar {\beta }}}_{V}}{{\tau }_{p}}\left( {\bar {z} - \eta } \right)} } \right) \times \\ \times \,\,d\eta = {{{\bar {C}}}_{ * }}{{e}^{{\left( {{{{\bar {\alpha }}}_{V}} + {{{\bar {\beta }}}_{V}}{{\tau }_{p}}} \right)}}}. \\ \end{gathered} $Определяется же ${{\bar {t}}_{p}}$ при известном ${{\tau }_{p}}$ в случае ${{Q}_{{{\text{in}}}}} > 0$ из решения задачи (32), (33), а в случае $H = {\text{const}}$ по формуле (35). Итак, критерий (54) выполняется, если расчетные значения $\bar {t}$ и $\tau $ находятся в таких интервалах
Вместе с тем на работу фильтра приходится накладывать и другие ограничения, диктуемые режимом фильтрования и способом, средствами его реализации. Так, при фильтровании с постоянной скоростью важно контролировать потери механической энергии. Если же фильтрование осуществляется с убывающей скоростью, то особое значение для оценки эффективности фильтра имеет анализ его производительности. Из экономических соображений оправдано снижение скорости фильтрования только до некоторого порогового значения ${{V}_{ * }}$, которое целесообразно устанавливать предварительно на базе специальных технико-экономических расчетов. Тогда второе серьезное ограничение имеет следующий формальный вид
и будет справедливо, если $\bar {t}$ и $\tau $ изменяются в таких пределах
Расчеты времени ${{t}_{V}}$ достижения скоростью $V$ минимально допустимой величины ${{V}_{ * }}$ осложняются, когда ${{Q}_{{{\text{in}}}}} = {\text{const}}$ и, кроме того, $V$ существенно убывает. Тогда сначала из (30) находится связь между ${{\bar {t}}_{V}}$ и ${{\tau }_{V}}$
(57)
${{\bar {t}}_{V}} = \frac{1}{{{{{\bar {Q}}}_{{{\text{in}}}}}}}\left[ {{{\tau }_{V}} + \frac{1}{{{{n}_{0}}}}\left( {\bar {R}\bar {V}_{ * }^{2} + {{{\bar {V}}}_{ * }}} \right)\Psi ({{\tau }_{V}}) - {{{\bar {H}}}^{0}}} \right],$которая затем используется после численного или аналитического (при $\bar {R} = 0$) решения задачи (32), (33). Найденная таким путем зависимость $\tau = F\left( {\bar {t}} \right)$ с учетом (57) позволяет получить уравнение относительно одной неизвестной
Однако, вычисление ${{\tau }_{V}}$ из (58) оказывается весьма трудоемким. На практике обычно или скорость $V$ меняется незначительно, оставаясь при этом больше ${{V}_{ * }}$, или же суспензия фильтруется при частично заполненном стакане. В первом случае экономический критерий вообще может не приниматься во внимание, поскольку ограничения по скорости не актуальны. Во втором же искомое технологическое время легко находится в два этапа. В первую очередь определяется значение ${{\tau }_{V}}$ подбором из уравнения
(59)
$\sqrt {{{\Psi }^{2}}({{\tau }_{V}}) + 4\bar {R}{{{\bar {H}}}_{e}}} - \Psi ({{\tau }_{V}}) = 2\bar {R}{{\bar {V}}_{ * }},$а после этого время ${{\bar {t}}_{V}}$ при уже известном ${{\tau }_{V}}$ сразу вычисляется из (41).
В настоящее время фильтрование с нерегулируемой скоростью часто прекращают как только уровень суспензии в стакане достигнет его кромки. Тогда важным становится третий критерий, а именно,
а время работы фильтра также ограничивается моментом ${{\bar {t}}_{H}}$ (первый этап), так что
Вычисляется относительное время наполнения стакана ${{\bar {t}}_{H}}$ также пошагово при ${{\bar {Q}}_{{{\text{in}}}}} = {\text{const}}$. Прежде всего из (31) ${{\bar {t}}_{H}}$ выражается через ${{\tau }_{H}}$
(61)
${{\bar {t}}_{H}} = \frac{1}{{{{{\bar {Q}}}_{{{\text{in}}}}}}}\left( {{{\tau }_{H}} + \frac{{{{{\bar {H}}}_{e}} - {{{\bar {H}}}^{0}}}}{{{{n}_{0}}}}} \right),$а затем из численного или аналитического решения задачи (32), (33) подбирается такая пара значений ${{\bar {t}}_{H}}$, ${{\tau }_{H}}$, которая связана соотношением (61). Очевидно, что при $H = {\text{const}}$ третий критерий оказывается невостребованным. С практической точки зрения третий критерий более удобен, так как для контроля за его выполнением не требуется измерительная аппаратура, как в случае первого и второго критериев. Но в принципе переполнение стакана не может быть достаточным основанием для выключения фильтра. Действительно, нередко фильтр в таком состоянии способен продолжать работать продуктивно и с высоким качеством. С другой стороны, нередко случается, что концентрация примеси в фильтрате достигает предельного значения при еще незаполненном стакане. Тем не менее, ниже при технологическом моделировании фильтрования полагаются равнозначными и задействованы все три описанных критерия. Решение об остановке фильтра будет обоснованным только после установления длительности фильтроцикла, которая приравнивается наименьшему из технологических времен, то есть формально
(62)
${{\bar {t}}_{f}} = \min \left( {{{{\bar {t}}}_{p}},{{{\bar {t}}}_{V}},{{{\bar {t}}}_{H}}} \right).$Вообще очистные фильтры работают с максимальной отдачей, если обеспечивают осветление необходимых объемов воды с минимальными затратами. Показателем эффективности фильтра при фильтровании в обоих режимах (с постоянной и убывающей скоростью) может служить длительность фильтроцикла, поскольку значение ${{t}_{f}}$ учитывает и санитарно-экологические аспекты (посредством первого критерия), и экономические аспекты (посредством второго критерия), и продуктивность (без или с учетом потерь на промывку) фильтра. Поэтому весь последующий теоретический анализ, направленный на поиск рациональных технологических и конструктивных параметров, опирается на данные многочисленных расчетов прежде всего технологических времен, но в конечном итоге длительности ${{\bar {t}}_{f}}$.
Уместно заметить, что при рассмотрении последовательного ряда фильтроциклов возможны две характерные ситуации. В первой фильтр работает стабильно, поскольку количество осадка от цикла к циклу не увеличивается. Во второй ситуации имеет место прогрессирующее накопление осадка, как например, при физико-химическом обезжелезивании подземных вод. Далее в центре внимания будет именно первая ситуация. Тогда срок службы загрузки определяется не растущим количеством невымываемого осадка, а другими причинами. Как следствие, достаточно выполнить технологические расчеты для одного, произвольного фильтроцикла и затем распространить полученные таким образом результаты на весь срок службы загрузки с возможными поправками на истираемость зерен и другие подобные факторы, сокращающие его.
Целью многочисленных технологических расчетов было установление относительных временных параметров, регламентирующих работу фильтра, исходя из текущих загрязненности фильтрата, производительности фильтровальной установки, запаса суспензии в накопителе фильтра (${{\bar {t}}_{p}},\;{{\bar {t}}_{V}},\;{{\bar {t}}_{H}}$), а в конечном итоге длительности фильтроцикла ${{\bar {t}}_{f}}$, прежде всего, в зависимости от непосредственно контролирующих межфазный массообмен коэффициентов ${{\bar {\alpha }}_{V}},{{\bar {\beta }}_{V}}$. Вместе с тем анализировалась значимость высоты слоя загрузки, как основного конструктивного параметра, для осветления суспензии, реальность ее рационального выбора с целью интенсификации работы фильтра при заданном технологическом алгоритме.
Базовыми для указанных расчетов стали три примера, различающиеся комбинациями двух значений ${{\bar {\gamma }}_{c}}$ (0.0005 и 0.001) и $\bar {R}$ (1, 0). Таким образом, благодаря принятым для примера 1 ${{\bar {\gamma }}_{c}} = 0.0005,$ $\bar {R} = 1$; для примера 2 – ${{\bar {\gamma }}_{c}} = 0.001,\;\bar {R} = 1$; для примера 3 – ${{\bar {\gamma }}_{c}} = 0.0005,\;\bar {R} = 0$ удалось оценить влияние на технологический процесс двух факторов (состав осадка, сопротивление отводящих коммуникаций), сократив до минимума вычисления.
Во второй серии примеров варьировались сорбционные свойства фильтрующего материала, так что коэффициент ${{\bar {\alpha }}_{V}}$ непрерывно менялся в пределах от 4 до 10. При этом были задействованы единственные значения модельных $({{\bar {\beta }}_{V}} = 0.01,$ ${{n}_{0}} = 0.47,{{\bar {H}}^{0}} = 0)$ и критериальных (${{\bar {C}}_{ * }} = 0.1,$ ${{\bar {V}}_{ * }} = 0.75{{\bar {V}}^{0}},$ ${{\bar {H}}_{ * }} = 4$) параметров. Расчеты выполнялись последовательно для условий первой (${{Q}_{{{\text{in}}}}} = {\text{const}}$) и второй ($H = {\text{const}}$) задач. Так, здесь и в дальнейшем для ${{\bar {Q}}_{{{\text{in}}}}}$ принимались два значения (0.5 и 1), отвечающие интенсивной и очень интенсивной подаче суспензии на фильтр. Тогда ввиду однозначной связи между начальной скоростью ${{\bar {V}}^{0}}$ и ${{\bar {Q}}_{{{\text{in}}}}}$ окончательные значения ${{\bar {V}}_{ * }}$ составили соответственно 0.375 и 0.5. Расчетный период во всех рассмотренных случаях ограничивался значением $\bar {t} = 1000$, которое можно условно приравнять примерно трем суткам реального времени. Семейства кривых зависимостей ${{\bar {t}}_{{p,H,V}}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ для ${{\bar {Q}}_{{{\text{in}}}}}$ = 0.5 и 1 даны соответственно на рис. 9, 10. Поведение однотипных кривых для разных ${{\bar {Q}}_{{{\text{in}}}}}$ во многом сходное, но вместе с тем существуют и некоторые важные различия. В поле рис. 9 вообще не попали кривые ${{\bar {t}}_{H}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ из примеров 1, 3. Следовательно, если суспензия подается на фильтр небольшим расходом, то подъем уровня в стакане будет происходить замедленно, а значит лимитироваться работа фильтра должна только содержанием дисперсной примеси в фильтрате. Важно отметить, что при ${{\bar {\gamma }}_{c}}$ = 0.0005 (примеры 1 и 3) производительность фильтра была стабильной независимо от сорбционных свойств загрузки. Но при более активном связывании осажденным веществом воды (${{\bar {\gamma }}_{c}}$ = 0.001, пример 2) имело место, во-первых, резкое уменьшение значений ${{\bar {t}}_{H}}$ (кривые 4 на рис. 9 и низко расположенная 7 на рис. 10), во-вторых, наглядно проявилось ограничение на производительность за счет второго критерия в виде кривых ${{\bar {t}}_{V}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ (5 на рис. 9 и 6 на рис. 10). При еще бóльших значениях ${{\bar {\alpha }}_{V}}$ указанное ограничение вообще может стать решающим и определить длительность ${{\bar {t}}_{f}}$. В свою очередь параметр $\bar {R}$ практически не влияет на защитную способность загрузки, а поэтому кривые фактически сливаются. Однако, с увеличением доли связанной воды в осадке (пример 2) и к тому же при больших значениях ${{\bar {\alpha }}_{V}}$ наблюдается ощутимое приращение параметра ${{\bar {t}}_{p}}$. Таким образом, вопрос о качестве фильтрата при обосновании ${{t}_{f}}$ утрачивает актуальность и на первый план выходят второй и особенно третий критерии.
Рис. 9.
Зависимости ${{\bar {t}}_{p}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$, ${{\bar {t}}_{H}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$, ${{\bar {t}}_{V}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$, ${{\bar {t}}_{f}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ при ${{\bar {Q}}_{{{\text{in}}}}} = 0.5$: 1–3 – ${{t}_{p}}$; 4 – ${{t}_{H}}$; 5 – ${{t}_{V}}$; 1, 4, 5 – пример 2; 2 – пример 1; 3 – пример 3; ${{\bar {t}}_{f}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ – сплошные линии.

Рис. 10.
Зависимости ${{\bar {t}}_{p}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$, ${{\bar {t}}_{H}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$, ${{\bar {t}}_{V}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$; ${{\bar {t}}_{f}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ при ${{\bar {Q}}_{{{\text{in}}}}} = 1$: 1, 2, 7 – ${{\bar {t}}_{H}}$; 3–5 – ${{\bar {t}}_{p}}$; 6 – ${{\bar {t}}_{V}}$; 1, 5 – пример 3; 2, 4 – пример 1; 3, 6, 7 – пример 2; ${{\bar {t}}_{f}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ – сплошные.

Также нелинейным образом влияет на технологические параметры приведенный коэффициент скорости отрыва осажденных частиц, о чем свидетельствует рис. 11. Действительно, при значительном усилении одновременно и устойчивости осадка по отношению к гидродинамическим воздействиям $\left( {{{{\bar {\beta }}}_{V}} < 0.0075} \right)$, и связывания воды (${{\bar {\gamma }}_{c}}$ = 0.001) наблюдается с уменьшением ${{\bar {\beta }}_{V}}$ практически скачкообразный рост времени ${{\bar {t}}_{p}}$ даже при умеренной сорбционной способности (${{\bar {\alpha }}_{V}}$ = 7) фильтрующего материала (кривая 3). Отмеченный факт также объясняется интенсивным заилением входного участка загрузки и, следовательно, серьезным повышением гидравлического сопротивления фильтровальной установки. В итоге скорость $\bar {V}$ стремительно снижается даже несмотря на сопутствующее этому незначительное сокращение сопротивления ее транспортной системы. В случае примера 3 кривая ${{\bar {t}}_{f}}\left( {{{{\bar {\beta }}}_{V}}} \right)$ идентифицируется как кривая ${{\bar {t}}_{p}}\left( {{{{\bar {\beta }}}_{V}}} \right)$, поскольку последняя полностью расположена ниже кривой ${{\bar {t}}_{H}}\left( {{{{\bar {\beta }}}_{V}}} \right)$. В двух остальных примерах искомая ${{\bar {t}}_{f}}\left( {{{{\bar {\beta }}}_{V}}} \right)$ представляет собой непрерывную ломанную линию, состоящую как и ранее из двух фрагментов. Скорость фильтрования и в этой серии расчетов не лимитировала работу фильтра.
Рис. 11.
Зависимости ${{\bar {t}}_{p}}\left( {{{{\bar {\beta }}}_{V}}} \right)$, ${{\bar {t}}_{H}}\left( {{{{\bar {\beta }}}_{V}}} \right)$; ${{\bar {t}}_{f}}\left( {{{{\bar {\beta }}}_{V}}} \right)$: 1, 2, 6 – ${{\bar {t}}_{H}}$; 3–5 – ${{\bar {t}}_{p}}$; 1, 5 – пример 3; 2, 4 – пример 1; 3, 6 – пример 2; ${{\bar {t}}_{f}}\left( {{{{\bar {\beta }}}_{V}}} \right)$ – сплошные линии.

Очевидно, что стабилизация уровня в стакане (обычно на отметке кромки стакана) обусловливает кардинальные изменения и в поведении гидравлической нагрузки, и в подходе к технологическим расчетам. Действительно, в отсутствии подъема уровня и роста входного напора величина $V$ будет неуклонно уменьшаться со временем. Естественно, что по мере улучшения сорбционных свойств загрузки время ${{t}_{p}}$ должно расти, а время ${{\bar {t}}_{V}}$ наоборот снижаться, причем ускоренно. А поскольку для всех выбранных примеров при определении времени продуктивной работы фильтра первый и второй критерии оказываются равными по значению, то и соответствующие им кривые ${{\bar {t}}_{f}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ опять будут ломаными, составленными из подходящих участков кривых ${{\bar {t}}_{p}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ и ${{\bar {t}}_{V}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$, которые изображены на рис. 12 сплошными линиями.
Рис. 12.
Зависимости ${{\bar {t}}_{p}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$, ${{\bar {t}}_{V}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$; ${{\bar {t}}_{f}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ при $\bar {H} = {\text{const}}$: 1, 4, 5 – ${{\bar {t}}_{p}}$; 2, 3, 6 –${{\bar {t}}_{V}}$; 1, 6 – пример 2; 2, 5 – пример 3; 3, 4 – пример 1; ${{\bar {t}}_{f}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$ – сплошные линии.

Полученные выше фактически строгие решения последовательности из трех задач разделения суспензии фильтрованием также полезны и при проектировании фильтра с накопителем, если заранее известны условия его эксплуатации, а именно, гидравлическая нагрузка на фильтр, физико-химические и фильтрационные свойства фильтрующего материала и дисперсной примеси, исходное содержание последней. Тогда разработанные расчетные формализмы после их адаптации к технологическим требованиям могут способствовать проведению конструктивного анализа с целью рационального выбора конструктивных параметров и прежде всего обоснованию высоты слоя загрузки, а при наличии необходимой информации также и размеров (эквивалентного диаметра) зерен материала. Что касается высоты стакана, то ввиду усиления фильтрации за счет накопления в нем суспензии, ее приходится ограничивать сверху исходя из технических, а не технологических возможностей. Оценивать же значимость диаметра элементов-коллекторов теперь реально, если известна связь с ним массообменных коэффициентов ${{\alpha }_{V}},{{\beta }_{V}}$. Известны теоретические формулы для функционального параметра $\alpha $ в зависимости от скорости фильтрования, размеров зерен и частиц примеси [11–14]. Однако, с одной стороны они не получили надежного экспериментального подтверждения, а с другой стороны их сложно применять на практике в случае неоднородных примесей. Аналогичные эмпирические зависимости автору неизвестны и поэтому ниже внимание акцентируется на высоте $L$.
Последовательно рассмотрены две характерные ситуации с фильтрующим материалом, которые существенно отличаются по экономическим показателям. В первой указанный материал из отходов местного производства является дешевым и доступен в практически неограниченных количествах. Тогда величина $L$ при оборудовании фильтровального сооружения почти не отражается на капитальных затратах и логично полагать, что оптимальной и с экономической, и с технологической точек зрения будет такая высота, при которой длительность фильтроцикла окажется максимальной. Поскольку в конструктивном анализе параметр $L$ становится независимой переменной, а в ранее введенных безразмерных переменных и параметрах он присутствовал в качестве масштаба длины, то приходится вводить новые и масштаб ${{L}_{0}}$, и переменную $\bar {L} = {L \mathord{\left/ {\vphantom {L {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}$, так что $\tilde {z} = {z \mathord{\left/ {\vphantom {z {{{L}_{0}},}}} \right. \kern-0em} {{{L}_{0}},}}$ $\tilde {t} = {{{{k}_{0}}t} \mathord{\left/ {\vphantom {{{{k}_{0}}t} {\left( {{{n}_{0}}{{L}_{0}}} \right)}}} \right. \kern-0em} {\left( {{{n}_{0}}{{L}_{0}}} \right)}},$ $\tilde {h},\tilde {H} = {{h,H} \mathord{\left/ {\vphantom {{h,H} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}},$ ${{\tilde {\alpha }}_{V}} = {{L}_{0}}{{\alpha }_{V}},$ ${{\tilde {\beta }}_{V}} = {{n}_{0}}{{L}_{0}}{{\beta }_{V}},$ $\tilde {R} = {{{{\omega }^{2}}k_{0}^{2}R} \mathord{\left/ {\vphantom {{{{\omega }^{2}}k_{0}^{2}R} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}},$
Тогда после перемасштабирования зависимости (27), (28), (30), (31) и уравнение (32) преобразовываются к следующему виду
(63)
$\begin{gathered} {{{\bar {C}}}_{e}}\left( {\tilde {\tau };\bar {L}} \right) = {{e}^{{ - {{{\tilde {\alpha }}}_{V}}\bar {L}}}} \times \\ \times \,\,\left[ {{{e}^{{ - {{{\tilde {\beta }}}_{V}}\tilde {\tau }}}}{{I}_{0}}\left( {2\sqrt {{{{\tilde {\alpha }}}_{V}}{{{\tilde {\beta }}}_{V}}\tilde {\tau }\bar {L}} } \right) + {{{\tilde {\beta }}}_{V}}\int\limits_0^{\tilde {\tau }} {{{e}^{{ - {{{\tilde {\beta }}}_{V}}\varsigma }}}{{I}_{0}}\left( {2\sqrt {{{{\tilde {\alpha }}}_{V}}{{{\tilde {\beta }}}_{V}}\bar {L}\varsigma } } \right)d\varsigma } } \right], \\ \end{gathered} $(64)
$\bar {S}\left( {\tilde {z},\tilde {\tau }} \right) = {{\tilde {\alpha }}_{V}}{{e}^{{ - {{{\tilde {\alpha }}}_{V}}\tilde {z}}}}\int\limits_0^{\tilde {\tau }} {{{e}^{{ - {{{\tilde {\beta }}}_{V}}\varsigma }}}{{I}_{0}}\left( {2\sqrt {{{{\tilde {\alpha }}}_{V}}{{{\tilde {\beta }}}_{V}}\tilde {z}\varsigma } } \right)d\varsigma } ,$(65)
$\begin{gathered} \bar {V}\left( {\tilde {t},\tilde {\tau };\bar {L}} \right) = \frac{1}{{2\tilde {R}}} \times \\ \times \,\,\left\{ {\sqrt {{{\Psi }^{2}}(\tilde {\tau },\bar {L}) + 4\tilde {R}\left[ {{{{\tilde {H}}}^{0}} + {{n}_{0}}\left( {{{{\bar {Q}}}_{{in}}}\tilde {t} - \tilde {\tau }} \right)} \right]} - \Psi (\tilde {\tau },\bar {L})} \right\}, \\ \end{gathered} $(66)
$\tilde {H}\left( {\tilde {t},\tilde {\tau }} \right) = {{\tilde {H}}^{0}} + {{n}_{0}}\left( {{{{\bar {Q}}}_{{{\text{in}}}}}\tilde {t} - \tilde {\tau }} \right),$(67)
$\begin{gathered} \frac{{d\tilde {\tau }}}{{d\tilde {t}}} = \frac{1}{{2\tilde {R}}} \times \\ \times \,\,\left\{ {\sqrt {{{\Psi }^{2}}(\tilde {\tau },\bar {L}) + 4\tilde {R}\left[ {{{{\tilde {H}}}^{0}} + {{n}_{0}}\left( {{{{\bar {Q}}}_{{{\text{in}}}}}\tilde {t} - \tilde {\tau }} \right)} \right]} - \Psi (\tilde {\tau },\bar {L})} \right\}, \\ \end{gathered} $Во второй ситуации теперь уже кондиционный фильтрующий материал имеет высокую стоимость из-за значительных затрат на добычу, производство, транспортировку, подготовку (сортировка, модификация и пр.) и обычно его количество строго ограничено. Тогда необходимо расходовать такой материал предельно экономно, добиваясь от каждого его объема (загрузки) $W$ максимальной отдачи. В этом случае высоту $L$ и площадь $\omega $ следует варьировать так, чтобы объем $W = \omega L$ оставался неизменным. Естественно, что уменьшение $L$ в данном случае означает соразмерное увеличение площади поверхности загрузки $\omega $ и уменьшение удельного расхода ${{{{Q}_{{{\text{in}}}}}} \mathord{\left/ {\vphantom {{{{Q}_{{{\text{in}}}}}} \omega }} \right. \kern-0em} \omega }$. И опять ввиду переменности теперь площади $\omega $ приходится трансформировать содержавшие ее выражения для ${{\bar {Q}}_{{{\text{in}}}}},\bar {R}$. Тогда вводятся
(68)
${{\tilde {Q}}_{{{\text{in}}}}} = \frac{{{{L}_{0}}{{Q}_{{{\text{in}}}}}}}{{W{{k}_{0}}}} = \frac{{{{{\bar {Q}}}_{{{\text{in}}}}}}}{{\bar {L}}},\,\,\,\,\tilde {\tilde {R}} = \frac{{{{W}^{2}}k_{0}^{2}}}{{L_{0}^{3}}}R = {{\bar {L}}^{3}}\tilde {R}$и с учетом (32) расчетные формализмы будут
(69)
$\begin{gathered} \bar {V}\left( {\tilde {t},\tilde {\tau };\bar {L}} \right) = \frac{{{{{\bar {L}}}^{2}}}}{{2\tilde {\tilde {R}}}} \times \\ \times \,\,\left\{ {\sqrt {{{\Psi }^{2}}(\tilde {\tau },\bar {L}) + 4\frac{{\tilde {\tilde {R}}}}{{{{{\bar {L}}}^{2}}}}\left[ {{{{\tilde {H}}}^{0}} + {{n}_{0}}\left( {{{{\tilde {Q}}}_{{{\text{in}}}}}\bar {L}\tilde {t} - \tilde {\tau }} \right)} \right]} - \Psi (\tilde {\tau },\bar {L})} \right\}, \\ \end{gathered} $(70)
$\tilde {H}\left( {\tilde {t},\tilde {\tau };\bar {L}} \right) = {{\tilde {H}}^{0}} + {{n}_{0}}\left( {{{{\tilde {Q}}}_{{{\text{in}}}}}\bar {L}\tilde {t} - \tilde {\tau }} \right),$(71)
$\begin{gathered} \frac{{d\tilde {\tau }}}{{d\tilde {t}}} = \frac{{{{{\bar {L}}}^{2}}}}{{2\tilde {\tilde {R}}}} \times \\ \times \,\,\left\{ {\sqrt {{{\Psi }^{2}}(\tilde {\tau },\bar {L})\, + \,4\frac{{\tilde {\tilde {R}}}}{{{{{\bar {L}}}^{2}}}}\left[ {{{{\tilde {H}}}^{0}}\, + \,{{n}_{0}}\left( {{{{\tilde {Q}}}_{{{\text{in}}}}}\bar {L}\tilde {t}\, - \,\tilde {\tau }} \right)} \right]} \, - \,\Psi (\tilde {\tau },\bar {L})} \right\}. \\ \end{gathered} $Выражения для концентраций $\bar {C},\,\,\bar {S}$ (63), (64) остаются без изменений.
Прежде всего, возвращаясь к рис. 2, оценивается влияние $L$ на формирование слоя суспензии над чистой загрузкой. Ее формальное удвоение при аналогичном увеличении объема $W$ (кривая 2) или неизменном $W$ (кривая 1) ведет в первом случае к несущественному, а во втором – к значительному ускорению подъема уровня суспензии в стакане вследствие соразмерного сокращения площади поверхности загрузки.
При изучении закономерных изменений технологических времен из-за увеличения (или сокращения) высоты рабочего слоя привлекались первый и третий критерии, если суспензия поступала на фильтр с постоянным расходом, и первый, второй критерии, если поступала с переменным расходом (при $H = {\text{const}}$). В случае ${{Q}_{{{\text{in}}}}} = {\text{const}}$ предварительно рассчитывалась скорость $\bar {V}$ в течение длительного времени (несколько тысяч единиц) для данных трех базовых примеров, а также ${{\tilde {\alpha }}_{V}} = 3,\;{{\tilde {\beta }}_{V}} = 0.005$. При этом выяснилось, что отклонения от ${{\bar {V}}^{0}}$ не превышали нескольких процентов. В первой ситуации (дешевый материал загрузки) для ${{\bar {Q}}_{{in}}}$, как и ранее, принимались значения 0.2, 0.5 и 1. Соответствующие семейства графиков зависимостей ${{\bar {t}}_{p}}\left( {\bar {L}} \right)$, ${{\bar {t}}_{H}}\left( {\bar {L}} \right)$ и итоговой ${{\bar {t}}_{f}}\left( {\bar {L}} \right)$ вычислялись по (63), (66) с учетом (67) и изображены на рис. 13, 14. При малой подаче суспензии $\left( {{{{\bar {Q}}}_{{in}}} = 0.2} \right)$ даже минимальное приращение $\bar {L}$ (на несколько десятков процентов) приводило к многократному увеличению времени ${{\bar {t}}_{p}}$. Намного слабее ${{\bar {t}}_{p}}$ реагирует на наращивание $L$ при большой подаче $\left( {{{{\bar {Q}}}_{{{\text{in}}}}} = 1} \right)$. При этом параметры ${{\bar {\gamma }}_{c}},\bar {R}$ практически не влияли на защитную способность загрузки (кривые 24 на рис. 14 почти сливаются), но существенно отражались на положении и наклоне кривых ${{\bar {t}}_{H}}\left( {\bar {L}} \right)$ (1, 5, 6 на рис. 14). Естественно, что удлинение фильтрационного пути и соразмерное увеличение гидравлического сопротивления слабо заиленной загрузки, как и увеличение ${{\bar {Q}}_{{{\text{in}}}}}$, обусловливает сокращение ${{\bar {t}}_{H}}$, которое было особенно большим при ${{\bar {Q}}_{{{\text{in}}}}} = 1$ и $\bar {L} > 3$. Высокую чувствительность параметр ${{\bar {t}}_{H}}$ продемонстрировал по отношению к $\bar {L}$ при благоприятных для фильтрационного процесса условиях (пример 1, ${{\bar {Q}}_{{{\text{in}}}}} = 1$). Кривые зависимости ${{\bar {t}}_{f}}\left( {\bar {L}} \right)$, как и подобные им ${{\bar {t}}_{f}}\left( {{{{\bar {\alpha }}}_{V}}} \right)$, часто являются непрерывными ломаными линиями с одним изломом. В реже встречающихся случаях, когда решающее значение для ограничения работы фильтра имеют только один или все три критерия, аналогичные кривые соответственно или вообще являются гладкими, или же имеют два излома, оставаясь непрерывными. Для практики проектирования особый интерес представляет абсцисса точек излома ${{\bar {L}}_{m}}$, поскольку здесь указанные кривые достигают максимума. Следовательно, в новом фильтре целесообразно использовать слой из дешевого материала именно высотой ${{\bar {L}}_{m}}$. Уместно отметить, что максимальные значения ${{\bar {t}}_{f}}$ в базовых примерах, как и соответствующие им значения ${{\bar {L}}_{m}}$, существенно различались. Это еще раз подтверждает серьезность влияния параметров $\bar {\gamma },\;\;\bar {R}$ на осветлительный ресурс фильтра и важность обоснованного выбора $L$.
Рис. 13.
Зависимости ${{\tilde {t}}_{p}}\left( {\bar {L}} \right)$, ${{\tilde {t}}_{H}}\left( {\bar {L}} \right)$ $\left( {W{{\sim }}L} \right)$: 2–5 – ${{\bar {Q}}_{{{\text{in}}}}} = 0.5$; 1 – ${{\bar {Q}}_{{{\text{in}}}}} = 0.2$; 5 – ${{\tilde {t}}_{H}}$; 1–4 – ${{\tilde {t}}_{p}}$; 1, 3 – пример 1; 2, 5 – пример 2; 4 – пример 3.

Рис. 14.
Зависимости ${{\tilde {t}}_{p}}\left( {\bar {L}} \right)$, ${{\tilde {t}}_{H}}\left( {\bar {L}} \right)$, ${{\tilde {t}}_{f}}\left( {\bar {L}} \right)$ $\left( {{{{\bar {Q}}}_{{{\text{in}}}}} = 1,\,\,W{{\sim }}L} \right)$: 1, 5, 6 – ${{\tilde {t}}_{H}}$; 2–4 – ${{\tilde {t}}_{p}}$; 1, 4 – пример 3; 2, 6 – пример 2; 3, 5 – пример 1; ${{\bar {t}}_{f}}\left( {\bar {L}} \right)$ – сплошные линии.

Иная картина наблюдается при постоянном уровне суспензии над загрузкой (рис. 15). Здесь ломаные кривые, составленные из фрагментов кривых 1, 6; 2, 5, и гладкая кривая 3 ограничивают область эффективного применения такого режима фильтрования (множество подходящих пар значений ${{\bar {t}}_{f}}$ и $\bar {L}$). Максимальное значение ${{\bar {t}}_{f}}$ в примерах оказывается примерно одинаковым, но опять отвечающие экстремумам значения ${{\bar {L}}_{m}}$ существенно разнятся. Чрезмерное увеличение толщины загрузки опасно тем, что сразу после прохождения через нее первой порции суспензии скорость $\bar {V}$ упадет до критического значения ${{\bar {V}}_{ * }}$ и фильтр, как, впрочем, и при слишком малой толщине, окажется изначально недееспособным. Во всех примерах критическое значение $\bar {L}\;\left( {{{{\bar {t}}}_{V}} = 0} \right)$ было примерно одинаковым и равнялось 2.245. Отмеченные особенности поведения технологических времен при варьировании высоты рабочего слоя четко указывают на важность теоретического обоснования данного конструктивного параметра.
Рис. 15.
Зависимости ${{\tilde {t}}_{p}}\left( {\bar {L}} \right)$, ${{\tilde {t}}_{V}}\left( {\bar {L}} \right)$, ${{\tilde {t}}_{f}}\left( {\bar {L}} \right)$ $\left( {\bar {H} = {\text{const}},\,\,W{{\sim }}L} \right)$: 1–3 – ${{\tilde {t}}_{V}}$; 4–6 – ${{\tilde {t}}_{p}}$; 1, 6 – ${{\tilde {\alpha }}_{V}} = 5$; 2, 5 – ${{\tilde {\alpha }}_{V}} = 7$; 3, 4 – ${{\tilde {\alpha }}_{V}} = 9$; ${{\bar {t}}_{f}}\left( {\bar {L}} \right)$ – сплошные линии.

И наконец, в ситуации с дефицитным фильтрующим материалом анализируются на базовых примерах последствия одновременного уменьшения гидравлической нагрузки на фильтр и сопротивления загрузки. На рис. 16 показаны кривые изменения времен ${{\bar {t}}_{p}}$ (1–3) и ${{\bar {t}}_{H}}$ (4–6) при гипотетическом постепенном и непрерывном истончении загрузки максимум в 2.5 раза. Рассчитывались указанные кривые с учетом (71) и принятых выше значений ${{\bar {C}}_{ * }},{{\bar {H}}_{ * }}$ по формулам (63), (70). При усиленном осадкообразовании (пример 2) технологический процесс для всего выбранного диапазона значений $\bar {L}$ лимитировался ранним переполнением стакана фильтра и в результате кривая ${{\bar {t}}_{f}}\left( {\bar {L}} \right)$ совпала с кривой 6. В двух других случаях искомая кривая имеет привычный вид ломаной с одним изломом. Гидравлика отводящих коммуникаций слабо влияет на максимальную длительность фильтроцикла и соответствующее ей значение ${{\bar {L}}_{m}}$, которые, однако, существенно уменьшаются с увеличением ${{\bar {\gamma }}_{c}}$. Сокращение толщины загрузки с одновременным увеличением площади ее поверхности чаще всего будет способствовать продлению работы фильтра. Вместе с тем, при значительном уменьшении $\bar {L}$ возможна и обратная картина, когда более тонкие загрузки быстрее исчерпают свой осветлительный ресурс (кривые 1, 3 при $\bar {L} < 0.55$).
Рис. 16.
Зависимости ${{\tilde {t}}_{p}}\left( {\bar {L}} \right)$, ${{\tilde {t}}_{H}}\left( {\bar {L}} \right)$, ${{\tilde {t}}_{f}}\left( {\bar {L}} \right)$ $\left( {W = {\text{const}}} \right)$: 1–3 – ${{\tilde {t}}_{p}}$; 4–6 – ${{\tilde {t}}_{H}}$; 1, 5 – пример 1; 2, 6 – пример 2; 3, 4 – пример 3; ${{\tilde {t}}_{f}}\left( {\bar {L}} \right)$ – сплошные линии.

ЗАКЛЮЧЕНИЕ
Сформулированы три математические задачи осветления водной суспензии на скорых фильтрах с накопителем при нерегулируемой скорости фильтрования с учетом гидравлики отводящих коммуникаций. Серьезные различия между постановками задач обусловлены способом подачи суспензии на фильтр, а именно, с постоянным расходом, переменным при фиксированном уровне в накопителе, в отсутствии подачи с понижающимся уровнем. В совокупности они фактически составляют единый цикл, поскольку способны детально и полно описать работу указанных фильтров в течение произвольного фильтроцикла (без учета времени промывки) с момента включения до окончания осветления суспензии из накопителя. Принципиально, что массообмен между фазами загрузки, как правило, существенно зависит от скорости фильтрационного процесса. Здесь обстоятельно и преимущественно аналитическими методами исследован случай усиленного влияния указанного процесса и на осаждение, и на отрыв частиц суспензии, что характерно для реагентного фильтрования. Для второй и третьей задач получены строгие решения. При решении же первой задачи были задействованы и аналитические, и численные методы. В итоге для искомых характеристик фильтрования выведены аналитические выражения в параметрической форме. Связь введенного параметра со временем устанавливается благодаря численному решению обыкновенного дифференциального уравнения с коэффициентами в интегральной форме, которое просто и с любой точностью получить, привлекая широкоизвестные пакеты программ математического анализа. Таким образом, все найденные выше решения могут рассматриваться как эталонные и применяться для оценки погрешностей вследствие реализации приближенных подходов. Вместе с тем в условиях, сходных с принятыми при постановке вышеупомянутых задач, указанные решения являются надежным инструментом для прогноза изменения искомых характеристик (концентрации взвеси и осадка, скорость фильтрования, напор, уровень в стакане, общий объем осветленной суспензии) со временем и по высоте загрузки. Для более общих условий предлагается выполнять динамическое осреднение скорости фильтрования, что позволяет получить близкие к точным решения.
Опираясь на разработанные расчетные формализмы, детально проанализированы технологические аспекты работы фильтров с накопителем и без регуляторов скорости. Сформулирована система накладываемых на нее ограничений, полный учет которой позволяет своевременно выключить фильтр и начать его промывку. В технологических расчетах водоочистного фильтра указанная система ограничений служит основой при установлении ряда временных параметров (технологических времен). Каждый из них обозначает интервал времени, в пределах которого осветлительный процесс еще не лимитируется соответствующим фактором. Максимальная отдача фильтра гарантируется при равной значимости трех накладываемых на технологический процесс ограничений, а именно, по качеству фильтрата, производительности фильтра, наполнению его стакана. Очевидно, что время эффективной работы фильтра (длительность фильтроцикла) ${{t}_{f}}$ следует отождествлять с наименьшим из вычисленных технологических времен. Соответствующая зависимость длительности ${{t}_{f}}$ от некоторого показателя $F$, в роли которого при моделировании работы фильтра с нерегулируемой скоростью могут быть модельные $\left( {{{\alpha }_{V}},{{\beta }_{V}}} \right)$, конструктивный $\left( L \right)$ и другие задействованные в исходной модели параметры, обязательно является непрерывной функцией, которая описывается или гладкой линией (решающее значение имеет только один критерий) или ломаной с одним изломом (определяющими являются два критерия) или с двумя изломами (все три ограничения существенные). Во втором случае максимальная величина ${{t}_{f}}$, как правило, достигается при строго определенных промежуточных значениях показателя $F$ и может оказаться намного больше реальной длительности при организации технологического процесса без должного научного обоснования.
ОБОЗНАЧЕНИЯ
| $C$ | объемная концентрация взвешенных частиц, м3/м3 |
| ${{C}_{e}}$ | объемная концентрация взвешенных частиц в фильтрате, м3/м3 |
| ${{f}_{k}}$ | безразмерный текущий коэффициент фильтрации фильтрующего материала |
| $H$ | текущий уровень суспензии в накопителе, м |
| ${{H}_{e}}$ | высота кромки накопителя, м |
| $h$ | пьезометрический напор, м |
| ${{I}_{0}}$ | символ функции Бесселя мнимого аргумента первого рода нулевого порядка |
| $L$ | высота загрузки, м |
| ${{L}_{0}}$ | исходное значение высоты загрузки при ее варьировании, м |
| $k$ | текущий коэффициент фильтрации фильтрующего материала м/ч |
| ${{k}_{0}}$ | коэффициент фильтрации чистой загрузки, м/ч |
| ${{n}_{0}}$ | пористость чистой загрузки, м3/м3 |
| ${{Q}_{{{\text{in}}}}}$ | объемный расход подаваемой на фильтр суспензии, м3/ч |
| $R$ | гидравлическое сопротивление отводящих коммуникаций, ч2/м5 |
| $S$ | объемная концентрация осажденных частиц суспензии м3/м3 |
| $t$ | время, ч |
| ${{t}_{f}}$ | длительность фильтроцикла, ч |
| ${{t}_{H}}$ | время наполнения накопителя, ч |
| ${{t}_{p}}$ | время защитного действия загрузки, ч |
| ${{t}_{V}}$ | время достижения минимально допустимой скорости фильтрования, ч |
| $W$ | объем загрузки, м3 |
| $\alpha $ | коэффициент скорости прилипания взвешенных частиц, ч–1 |
| $\beta $ | коэффициент скорости отрыва прилипших частиц, ч–1 |
| $\gamma $ | характеристика состава осадка |
| $\tau $ | относительный объем осветленной за расчетное время суспензии |
| $\omega $ | площадь входной поверхности загрузки, м2 |
ИНДЕКСЫ
Список литературы
Минц Д.М. Теоретические основы технологии очистки воды. М.: Стройиздат, 1964.
Pin Gao, Gang Xue, Xin-shan Song, Zhen-hong Liu. Depth filtration using novel fiber-ball filter media for the treatment of high-turbidity surface water // Sep. Purif. Technol. 2012. 95. № 1. P. 32.
Williams G.J., Sheikh B., Holden R.B. Kouretas T.J., Nelson K.L. The impact of increased loading rate on granular media, rapid depth filtration of wastewater // Water Res. 2007. 41. № 19. P. 4535.
Ярошевская Н.В., Сотскова Г.З. Расчет параметров блока фильтров с дренажом большого сопротивления, работающих с убывающей скоростью // Химия и технология воды. 1996. 18. № 4. С. 356.
Kau S.M., Lawler D.F. Dynamics of deep-bed filtration: velocity, depth and media // J. Environ. Eng. 1995. 121. № 12. P. 850.
Резников Г.Д. О поглощении частиц в фильтрах водопроводных очистных сооружений // Инженерно-физический журнал. 1999. 72. № 1. С. 38.
Elimelech M., O’Melia C.R. Kinetics of deposition of colloidal particles in porous media // Environ. Sci. Technol. 1990. 24. № 10. P. 1528.
Веницианов Е.В., Рубинштейн Р.Н. Динамика сорбции из жидких сред. М.: Наука, 1983.
Ison C.R., Ives K.J. Removal mechanism in deep bed filtration // Chem. Engng. Sci. 1969. 24. № 4. P. 717.
Tung K.L., Chang Y.L., Lai J.Y., Chang C.H., Chuang C.J. A CFD study of the deep bed filtration mechanism for submicron/nano-particle suspension // Water Sci. Technol. 2004. 50. № 12. P. 255.
Ren J, Packman A.I., Welty C. Correlation of colloid efficiency with hydraulic conductivity of silica sands // Water Resour. Res. 2000. 36. № 9. P. 2493.
Tobiason J.E., Vigneswaran B. Evaluation of a modified model for deep bed filtration // Water Res. 1994. 28. № 2. P. 335.
Tufenkji N., Elimelech M. Correlation equation for predicting single-collector efficiency in physicochemical filtration in saturated porous media // Environ. Sci. Technol. 2004. 38. № 2. P. 529.
Veerapaneni S., Wiesner M.R. Role of suspension polydispersivity in granular media filtration // J. Environ. Eng. 1991. 119. № 1. P. 172.
Сенявин М.М., Веницианов Е.В., Аюкаев Р.И. О математических моделях и инженерных методах расчета процесса очистки природных вод фильтрованием // Водные ресурсы. 1977. № 2. С. 157.
Kretzsehmar R., Barmettler K., Grolimund D., Yao-de Y, Barkovec M., Sticher H. Experimental determination of colloid deposition rates and collision efficiencies in natural porous media // Water Resour. Res. 1997. 33. № 5. P. 1129.
Rajagopalan R., Tien C. Trajectory analysis of deep bed filtration with sphere in cell porous media model // AIChE J. 1976. 22. № 3. P. 523.
Poliakov V., Kravchuk A., Kochetov G., Kravchuk O. Clarification of aqueous suspensions with a high content of suspended solids in rapid sand filters // Eureka: Physics and Engineering. 2019. № 1. P. 28.
Adin A., Rebhun M. Deep-bed filtration: accumulation – detachment model parameters // Chem. Eng. Sci. 1987. 42. № 5. P. 1213.
Akgiray O., Saatci A.M. An algorithm for bank operation of declining rate filters // Water Res. 1998. 32. № 7. P.2095.
Bai R., Tien C. Effect of deposition in deep-bed filtration: determination and search of rate parameters // J. Colloid. Interface Sci. 2000. 231. № 2. P. 299.
Bai R., Tien C. Particle detachment in deep bed filtration // J. Colloid. Interface Sci. 1997. 186. № 2. P. 307.
Bergendahi J.A., Grasso D. Mechanistic basis for particle detachment from granular media // Environ. Sci. Technol. 2003. 37. № 10. P. 2317.
Sharma M.M., Chauman H., Sarma D.S., Schechter R.S. Factors controlling the hydrodynamic detachment of particles from surfaces // J. Colloid Interface Sci. 1992. 149. № 1. P. 121.
Polyakov J.S., Kazenin D.A., Maksimov E.D., Polyakov S.V. Kinetic model of depth filtration with reversible adsorption // Theor. Found. Chem. Eng. 2003. 37. № 5. P. 439. [Поляков Ю.С., Казенин Д.А., Максимов Е.Д., Поляков С.В. Кинетическая модель объемной фильтрации с обратимой адсорбцией // Теор. основы хим. технологии. 2003. 37. № 5. С. 471.]
Corapciooglu M.Y., Jiang S. Colloid-facilitated groundwater contaminant transport // Water Resour. Res. 1993. 29. № 7. P. 2215.
Moran M.C., Moran D.C., Cushing R.S., Lawler D.F. Particle behavior in deep bed filtration: Part 2 – Particle detachment // J. Am. Water Works Assoc. 1993. 85. № 12. P. 82.
Saiers J.E., Hornberger G.M. The role of colloidal kaolinite in the transport of cezium through laboratory sand columns // Water Resour. Res. 1996. 32. № 1. P. 33.
Шевчук Е.А., Мамченко А.В., Гончарук В.В. Технология прямоточного фильтрования природных и сточных вод через зернистые загрузки // Химия и технология воды. 2005. 27. № 4. С. 369.
Hornberger G.M., Mills A.L., Herman J.S. Bacterial transport in porous media: Evaluation of a model using laboratory observations // Water Resour. Res. 1992. 28. № 3. P. 915.
Kim J., Lawler D.F. The influence of hydraulic loads on depth filtration // Water Res. 2012. 46. № 2. P. 433.
Mays D.S., Hunt J.R. Hydrodynamic aspects of particle clogging in porous media // Environ. Sci. Technol. 2005. 39. № 2. P. 577.
Поляков В.Л. Осветление суспензии фильтрованием с убывающим расходом // Доп.НАН України. 2010. № 5. С. 57.
Lozada P.T., Cruz-Velez C.H. Influence of the flow control (declining – constant rate) on the filtration process in drinking water treatment // Inginieria y Universidad. 2014. 18. № 2. P. 217.
Reddy L.N., Xiao M., Hajra M.C., Lee J.M. Physical clogging of soil filters under constant flow rate versus constant head // Can. Geotechnical J. 2005. 42. № 3. P. 804.
Грабовский П.А. Фильтрование воды через зернистый слой с убывающей скоростью // Доп.НАН України. 2016. № 8. С. 40.
Chaundry F.H. Theory of declining rate filtration. I. Continuous operation // J. Environ. Eng. Div. ASCE. 1987. 113. № 4. P. 834.
Cleasby J.L. Status of declining rate filtration design // Water Sci. Technol. 1993. 27. № 10. P. 151.
Saatci A.M. Application of the declining rate filtration theory – Continuous operation // J. Environ. Eng. Div. ASCE. 1990. 116. № 1. P. 87.
Дзюбо В.В., Алферова Л.И. Фильтрование природных вод в режиме неравномерных скоростей // Вестник ТГАСУ. 2007. № 2. С. 180.
Минц Д.М., Мельцер В.З. Гидравлическое сопротивление зернистой пористой среды в процессе кольматации // Доклады Академии наук СССР. 1970. 192. № 2. С. 304.
Jegatheesan V., Vigneswaran S. Deep bed filtration: mathematical models and observations // Crit. Rev. Environ. Sci. Technol. 2005. 35. № 6. P. 515.
Khilar K., C., Fogler H.S. Migration of fines in porous media. Dordrecht: Kluwer Academic Publishers, 1998.
McDowell L.M., Hunt J.R., Sitar N. Particle transport through porous media // Water Resour. Res. 1986. 22. № 3. P. 1901.
Бугай Н.Г., Кривоног А.И., Кривоног В.В. Безреагентная очистка воды фильтрами из волокнисто-пористого полиэтилена // Прикладна гідромеханіка. 2004. 6(78). № 2. С. 27.
Носков М.Д., Зайцева М.С., Истомин А.Д., Лукашевич О.Д. Математическое моделирование работы скорых фильтров // Вестник ТГАСУ. 2008. № 2. С. 126.
Boller M.A., Kavanauch M.C. Particle characteristics and headloss increase in granular media filtration // Water Res. 1995. 29. № 4. P. 1139.
Ojha C.S.P., Graham N.J.D. Appropriate use of deep-bed filtration models // J. Environ. Engineering. 1992. 118. № 6. P. 964.
Аюкаев Р.И., Мельцер В.З. Производство и применение фильтрующих материалов для очистки воды. Справочное пособие. Ленинград: Стройиздат, 1985.
Журба М. Водоочистные фильтры с плавающей загрузкой. Научное издание. – М.: РИО ВоГТУ, 2011.
Ярошевская Н.В., Кульский Л.А. Метод расчета фильтровальных сооружений, работающих с убывающей скоростью // Химия и технология воды. 1985. 7. № 2. С. 3.
Гуринчик Н.А. Определение продолжительности работы фильтров для разных режимов фильтрования // Вісник ОДАБА. 2010. Вип. 42. С. 56.
Poliakov V.L. The theoretical analysis of the filter run time // J. Water Chem. Technol. 2009. V. 31. № 6. P. 345. [Поляков В.Л. Теоретический анализ длительности фильтроцикла // Химия и технология воды. 2009. Т. 31. № 6. С. 605.]
Басс Г.М., Грабовский П.А., Ларкина Г.М. Оптимальная продолжительность фильтроцикла скорых фильтров, работающих с падающей скоростью // Наука и техника в гор.хоз-ве. 1978. Вып. 38. С. 37.
Журба М.Г. Применение теории фильтрования в инженерных расчетах // ВСТ. Водоснабжение и санитарная техника. 1993. № 7. С. 2.
Демчин И.И., Орлов В.О., Веницианов Е.В. Расчет технологических параметров фильтров с плавающими загрузками // Химия и технология воды. 1994. 16. № 2. С. 115.
Минц Д.М., Мельцер В.З. Упрощенный метод технологического моделирования процесса фильтрования // Научные труды АКХ. М.: ОНТИ AKX. 1973. Вып. 98. С. 57.
Поляков В.Л. О влиянии высоты загрузки и скорости фильтрования на осветление суспензии // Проблеми водопостачання, водовідведення та гідравліки. 2007. Вип. 9. С. 131.
Kim J., Tobiasson J.E. Particles in filter effluent: the Roles of deposition and detachment // Environ. Sci. Tech. 2004. 38. № 22. P. 6132.
Poliakov V.L. Filtration of suspension at the descending rate at linear kinetics of mass exchange // J. Water Chem. Technol. 2012. V.34. № 2. P. 65. [Поляков В.Л. Фильтрование суспензий с убывающей скоростью при линейной кинетике массообмена // Химия и технология воды. 2012. Т. 34. № 2. С. 107.]
Поляков В.Л. О фильтровании суспензии при начальном загрязнении загрузки (линейная кинетика массообмена) // Доп. НАН України. 2006. № 10. С. 65.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии



