Журнал вычислительной математики и математической физики, 2019, T. 59, № 6, стр. 1047-1062

ВВЕДЕНИЕ

Задача о распространении тепловой волны по холодному фону с конечной скоростью для нелинейного уравнения теплопроводности (задача о тепловой волне) начала изучаться в послевоенные годы в связи с необходимостью математического описания процессов, происходящих после ядерного взрыва. По-видимому, впервые в научной литературе она была поставлена в работе [1]. Несколько позднее близкие задачи рассматривались при моделировании фильтрации газа в пористой среде [2]. В дальнейшем задача о тепловой волне активно изучалась ведущими российскими (советскими) математиками, механиками и физиками, при этом в связи с настоящим исследованием особого упоминания заслуживают результаты, полученные в научной школе А.А. Самарского [3], свердловской (екатеринбургской) школе по математике и механике под руководством А.Ф. Сидорова [4] и в МФТИ [5].

Настоящая статья посвящена построению приближенных решений, имеющих вид тепловой волны, для нелинейного параболического уравнения второго порядка

которое описывает процесс распространения тепла в случае степенной зависимости коэффициента теплопроводности от температуры. Здесь $T$ – температура, зависящая от времени $t$ и пространственных координат, $div$ и $\nabla $ – операторы дивергенции и градиента по пространственным переменным. В отечественной литературе подобное уравнение называют “нелинейным уравнением теплопроводности со степенной нелинейностью” [3] и “уравнением нелинейной фильтрации” [4]; в зарубежной литературе закрепился термин “the porous medium equation”, т.е. “уравнение пористой среды” [6].

Стандартная замена $u = {{T}^{\sigma }}$, $t{\kern 1pt} {\text{'}} = \alpha t$ сводит уравнение (0.1) к виду

где $\Delta $ – оператор Лапласа.

Поскольку на фронте тепловой волны искомая функция, очевидно, обращается в нуль, т.е. множитель перед старшими производными зануляется, то в этом случае параболический тип уравнения (0.2) вырождается. Указанное обстоятельство заметно усложняет изучение задачи о тепловой волне. Эффективным способом преодоления указанных сложностей в данной ситуации оказывается применение различных приближенных аналитических и численно-аналитических методов. Так, приближенные решения одномерной задачи на полубесконечной прямой при заданной температуре на границе в виде степенной и экспоненциальной зависимостей, которые могут рассматриваться как точные, были предложены Н.А. Кудряшовым [7] (см. также [8]); одним из авторов статьи найдены точные решения одномерной задачи о тепловой волне с логарифмическим, степенным и экспоненциальным фронтом [9].

Еще одним возможным способом построения решения задачи о тепловой волне является применение метода граничных элементов в сочетании с методом двойственной взаимности [10], позволяющим при решении краевых задач математической физики свести все вычисления на границу исследуемой области, что дает возможность понизить размерность решаемой задачи.

Кроме того, А.Ф. Сидоровым и его учениками для построения решений нелинейных задач математической физики с вырождением развит метод “специальных рядов”, позволяющий раскрыть особенность за счет эффективного выбора базисных функций [4], [11].

Настоящая статья продолжает аналитические исследования задачи о тепловой волне для уравнения (0.2), выполненные авторами ранее в одномерной [11] и неодномерной [12], [13] постановках, в части построения решений в виде специальных степенных рядов. Тем не менее основным содержанием представленной работы являются разработка и реализация новых алгоритмов построения приближенных решений задачи о тепловой волне с использованием метода граничных элементов (МГЭ).

Ранее авторами уже строились алгоритмы численного решения уравнения (0.2) при различных краевых условиях на основе МГЭ. Были рассмотрены случаи одной [14], [15] и двух пространственных переменных [16]. В основе алгоритмов на каждом шаге по времени лежит итерационное решение методом граничных элементов уравнения Пуассона в области ненулевых значений искомой функции. Вид краевого условия при этом существенно влияет на сходимость итерационных процедур и разрешимость задачи в целом. В случае, когда область ненулевых значений в каждый момент времени не задана краевым условием, для одномерных задач сходимость итерационных процедур менее стабильна, а в двумерном случае предложенный в работе [16] подход реализовать, по-видимому, вообще невозможно. Примером таких задач является известная задача об инициировании тепловой волны [3], [4], [7]. Для ее решения в данной работе предложены новые алгоритмы, позволяющие повысить точность приближенных решений, которые основаны на замене ролями искомой функции и пространственной переменной.

1. ПОСТАНОВКА ОДНОМЕРНОЙ ЗАДАЧИ И ТЕОРЕМА СУЩЕСТВОВАНИЯ

Рассмотрим случай, когда искомая функция зависит от одной пространственной переменной в соответствующей системе координат. Уравнение (0.2) при этом можно представить в следующем виде:

Здесь $\rho $ – пространственная координата; константа $\gamma $ принимает значения 0, 1, 2 для задач теплопроводности на прямой, на плоскости (задачи с круговой симметрией) и в пространстве (задачи со сферической симметрией) соответственно. В работе [14] разработан общий подход к решению рассматриваемых задач методом граничных элементов, а также алгоритмы решения для $\gamma = 0$. В работе [15] подход распространен на случаи центральной симметрии задачи ($\gamma = 1,\;2$). Во всех упомянутых работах уравнение (1.1) решалось, в частности, при следующих видах краевых условий: Предполагается, что $a{\text{'}}\left( 0 \right) > 0$, $f\left( 0 \right) = 0$, $f{\kern 1pt} {\text{'}}\left( 0 \right) > 0$; при $\gamma = 0$ имеем $a(0) = 0$, $R = 0$, а при $\gamma = 1,2$ имеем $a(0) > 0$, $R > 0$. Построенные в [14], [15] алгоритмы позволяют строить на заданном конечном промежутке времени непрерывные по пространственной переменной решения с достаточной точностью.

Для задачи (1.1), (1.2а) с заданным нулевым фронтом $\rho = a(t)$ наблюдается устойчивая хорошая сходимость итерационных процессов, входящих в алгоритм на каждом шаге по времени. Она объясняется тем, что на каждом шаге $t = {{t}_{k}}$ задача решается в известной области $\rho \in \left[ {a\left( 0 \right),a\left( {{{t}_{k}}} \right)} \right]$.

Для задачи (1.1), (1.2б), которая является задачей об инициировании тепловой волны, при построении решения на каждом шаге область решения задачи (область ненулевых значений искомой функции) неизвестна и определяется в ходе итерационного процесса. Это приводит к отсутствию стабильной сходимости итерационных процессов, а для некоторых функций $f(t)$ к невозможности корректного решения на достаточно продолжительном промежутке времени. В связи с этим для решения задачи (1.1), (1.2б), поменяем местами искомую функцию и пространственную переменную. Подобная замена в уравнении (1.1) ранее неоднократно использовалась в работах А.Ф. Сидорова (см. [4, с. 231, 235, 269]).

В случае монотонной функции $f(t)$ в каждый момент времени функция $u\left( {t,\rho } \right)$ является обратимой. Рассмотрим обратную к ней функцию $\rho = \rho \left( {t,u} \right)$, $u \in \left[ {0,L} \right]$, где $L = f(t)$. Уравнение (1.1) для этой функции можно записать в виде

В каждый момент времени $t$ задача (1.1), (1.2б) может быть теперь представлена в известной области $u \in \left[ {0,L} \right]$ в следующем виде: Неизвестный нулевой фронт для исходной задачи (1.1), (1.2б) будет соответствовать значениям искомой функции $\rho \left( {t,u} \right)$ при $u = 0$: Можно показать [14], что для этой функции справедливо равенство Здесь ${{q}^{{\left( \rho \right)}}}$ – поток для функции $\rho \left( {t,u} \right)$, ${\mathbf{n}}$ – внешняя нормаль в граничных точках, ${\mathbf{n}}\left( 0 \right) = - 1$, ${\mathbf{n}}\left( L \right) = 1$.

Замечание 1. Условие (1.6) можно обобщить следующим образом:

при этом случай $f(t) \equiv 0$ соответствует заданию фронта движения тепловой волны (см. условие (1.2а)).

Для задачи (1.3), (1.8) справедлива следующая теорема существования и единственности аналитического решения (под аналитической здесь и далее понимается функция вещественной переменной, совпадающая в некоторой области со своим тейлоровским разложением).

Теорема 1. Пусть функции $a(t)$, $f(t)$ являются аналитическими в некоторой окрестности начального момента времени $t = 0$ и обладают следующими свойствами: $a{\kern 1pt} \left( 0 \right) = R$, $f{\kern 1pt} \left( 0 \right) = 0$, $f{\kern 1pt} {\text{'}}{\kern 1pt} \left( 0 \right) \geqslant 0$, $\left[ {f{\kern 1pt} {\text{'}}{\kern 1pt} \left( 0 \right)} \right]{{{\text{ }}}^{2}} + \left[ {a{\kern 1pt} {\text{'}}{\kern 1pt} \left( 0 \right)} \right]{{{\text{ }}}^{2}} > 0$. Тогда задача (1.3), (1.8) имеет единственное (с точностью до выбора направления движения тепловой волны) аналитическое решение, представимое в виде кратного ряда по степеням переменных $t$ и $u - f(t)$ с рекуррентно определяемыми коэффициентами.

Доказательство. Будем строить решение в виде ряда

Подобные конструкции в работах А.Ф. Сидорова [4] и его учеников, как уже отмечалось, обычно именуются “специальными рядами”.

Коэффициенты (1.9) определяются по следующей индуктивной процедуре.

Вначале создадим базу индукции. Пусть ${{a}^{{\left( k \right)}}}{\kern 1pt} \left( 0 \right) = {{a}_{k}}$, ${{f}^{{\left( k \right)}}}{\kern 1pt} \left( 0 \right) = {{f}_{k}}$. Из (1.8) и условия теоремы 1 имеем, что ${{x}_{{k,0}}} = {{a}_{k}}$. В частности, ${{x}_{{0,0}}} = R$, ${{x}_{{1,0}}} = {{a}_{1}}$. Для нахождения ${{x}_{{0,1}}}$ положим $t = 0$, $u = 0$ в уравнении (1.3). С учетом того, что ${{\left. {{{\rho }_{t}}} \right|}_{{t = 0,{\text{ }}u = 0}}} = {{x}_{{1,0}}} - f{\kern 1pt} \left( 0 \right){{x}_{{0,1}}} = {{a}_{1}} - {{f}_{1}}{{x}_{{0,1}}}$, ${{\left. {{{\rho }_{u}}} \right|}_{{t = 0,{\text{ }}u = 0}}} = {{x}_{{0,1}}}$, получим следующее нелинейное (кубическое) алгебраическое уравнение:

которое имеет нулевой корень ${{x}_{{0,1}}} = 0$, и в общем случае два ненулевых корня в особом случае ${{f}_{1}} = 0$ ненулевой корень один: ${{x}_{{0,1}}} = - \frac{1}{{\sigma {{a}_{1}}}}$.

Отметим, что выбор знака перед корнем соответствует упомянутому в условии теоремы выбору направления движения тепловой волны.

Итак, база индукции установлена.

Случай ${{x}_{{0,1}}} = 0$, как легко убедиться, приводит к решению $\rho \equiv R$.

Далее полагаем, что ${{x}_{{0,1}}} \ne 0$. Сделаем предположение индукции. Пусть найдены все ${{x}_{{m,l}}}$ при $m + l \leqslant n$. Докажем, что все ${{x}_{{m,l}}}$, $m + l = n + 1$ тогда определяются однозначно. Дифференцируя уравнение (1.3) $k$ раз по $t$, $n - k$ раз по $u$ ($k = 0,1,\; \ldots ,\;n$) и полагая $t = 0$, $u = 0$, с учетом условий (1.8) и предположения индукции, получим для нахождения ${{x}_{{m,l}}}$, $m + l = n + 1$, следующую систему линейных алгебраических уравнений (СЛАУ):

Здесь $k = 0,\; \ldots ,\;n$, значения ${{p}_{{k,n - k}}}$ известны в силу предположения индукции, соответствующие выражения здесь не приводятся из-за громоздкости.

Рассмотрим более подробно матрицу СЛАУ (1.11) и убедимся в том, что она невырожденна при всех возможных ненулевых значениях ${{x}_{{0,1}}}$. В самом деле, с учетом того, что ${{x}_{{n + 1,0}}} = {{a}_{{n + 1}}}$, она может быть представлена в виде

где $a = x_{{0,1}}^{2}$, ${{b}_{k}} = 3{{f}_{1}}x_{{0,1}}^{2} - 2{{a}_{1}}{{x}_{{0,1}}} - {1 \mathord{\left/ {\vphantom {1 \sigma }} \right. \kern-0em} \sigma } + k$, ${{c}_{k}} = k{{f}_{1}}$, $k = 0,\; \ldots ,\;n$. Можно видеть, что матрица (1.12) квадратная, в общем случае является трехдиагональной, а в особом случае ${{f}_{1}} = 0$ – двухдиагональной.

Докажем, что при выполнении условий теоремы система (1.11) однозначно разрешима при всех $n \in N$.

Рассмотрим сначала общий случай. Легко убедиться, что условие диагонального преобладания в данном случае, вообще говоря, не выполнено. Для того, чтобы доказать однозначную разрешимость (1.11) и построить решение, следуя [15], введем вспомогательные числовые последовательности по следующим формулам:

Из леммы 1 [15] следует, что $\det {{X}_{n}} = {{\lambda }_{{n,n + 1}}} = {{\eta }_{{n,n + 1}}}$. Можно показать, что ${{b}_{0}} > 0$ (в случае ${{a}_{1}} \leqslant 0$ это очевидно, в случае ${{a}_{1}} > 0$ требует проведения довольно громоздких, но тривиальных выкладок), а значит, ${{b}_{k}} > 0$ при всех $k \in N$. Отсюда следует, что все элементы вспомогательных последовательностей (1.13) положительны, т.е. и $\det {{X}_{n}} > 0.$

В особом случае дело упрощается – положительность определителя СЛАУ (1.11) прямо следует из того, что ${{b}_{0}} = - 2{{a}_{1}}{{x}_{{0,1}}} - 1{\text{/}}\sigma = 1{\text{/}}\sigma > 0$.

Таким образом, установлено, что система (1.11) во всех рассмотренных случаях является крамеровской, т.е. доказана однозначная определимость коэффициентов ${{x}_{{m,l}}}$, $m + l = n + 1$. Формулы для вычисления коэффициентов ряда (1.9) имеют следующий вид (см. [15], лемма 2):

где $k = 0,\; \ldots ,\;n$. Если верхний предел суммирования оказывается меньше нижнего, то соответствующее слагаемое принимается равным нулю. Соотношения (1.14) справедливы как при ${{f}_{1}} > 0$, так и при ${{f}_{1}} = 0$, но в последнем случае часть слагаемых в правой части обращается в нуль.

Таким образом, ряд (1.9) построен. Сходимость его следует из ранее доказанной авторами теоремы (см. [13]).

Замечание 2. Теорема 1 не только обеспечивает разрешимость задачи (1.3), (1.8) в классе аналитических функций, но и доставляет конструктивную процедуру построения коэффициентов рядов (1.9), что позволяет получить последние в явном виде и использовать отрезки рядов, наряду с известными точными решениями, для верификации результатов расчетов.

2. АЛГОРИТМ ЧИСЛЕННОГО РЕШЕНИЯ ОДНОМЕРНОЙ ЗАДАЧИ

Аналогично работам [14], [15], решение задачи (1.4), (1.5) будем строить по шагам по времени: ${{t}_{k}} = kh$, $k = 0,1,2,\; \ldots $, $h = {{t}_{k}} - {{t}_{{k - 1}}}$ – величина шага по времени. На каждом шаге будем искать непрерывное по пространственной координате решение.

Используя соотношение (1.7) и квадратичную аппроксимацию граничного значения $\rho \left( {t,0} \right) = a\left( t \right)$ на отрезке $t \in \left[ {{{t}_{{k - 1}}},{{t}_{k}}} \right]$ для каждого шага по времени, построим приближенное соотношение, связывающее следующие граничные значения искомой функции и ее потока в моменты времени ${{t}_{{k - 1}}}$ и ${{t}_{k}}$: ${{\rho }_{{1(k - 1)}}} = \rho \left( {{{t}_{{k - 1}}},0} \right)$, ${{\rho }_{{1k}}} = \rho \left( {{{t}_{k}},0} \right)$, $q_{{1k}}^{{(\rho )}} = {{q}^{{(\rho )}}}\left( {{{t}_{k}},0} \right)$, $q_{{1\left( {k - 1} \right)}}^{{\left( \rho \right)}} = {{q}^{{\left( \rho \right)}}}\left( {{{t}_{{k - 1}}},0} \right)$. Квадратичная интерполяция функции $\rho \left( {t,0} \right)$ на отрезке $\left[ {{{t}_{{k - 1}}},{{t}_{k}}} \right]$ имеет вид

Запишем для функции (2.1) соотношение (1.7) при $t = {{t}_{{k - 1}}}$ и $t = {{t}_{k}}$ в следующем виде: Складывая два уравнения (2.2), получаем Если для момента $t = {{t}_{{k - 1}}}$, $k > 1$ задача решена, то значения ${{\rho }_{{1\left( {k - 1} \right)}}}$ и $q_{{1\left( {k - 1} \right)}}^{{\left( \rho \right)}}$ известны, и в момент $t = {{t}_{k}}$ уравнение (2.3) связывает неизвестные величины ${{\rho }_{{1k}}}$ и $q_{{1k}}^{{\left( \rho \right)}}$.

Рассмотрим теперь уравнение (2.3) на первом шаге по времени, при $k = 1$, ${{t}_{0}} = 0$, ${{t}_{1}} = h$. Из граничного условия (1.5) и условия $f\left( 0 \right) = 0$ следует, что в момент ${{t}_{0}} = 0$ справедливо равенство ${{\rho }_{{10}}} = \rho \left( {{\text{0,}}0} \right) = R$. Возьмем полную производную по времени в граничном условии (1.5):

Отсюда получаем, что при $u = f(t) = L$ для любого $t$ справедливо Подставим последнее соотношение в уравнение (1.3) при $u = f(t)$При $t = 0$ получаем Напомним, что $f{\text{'}}\left( 0 \right) > 0$. Примем для определенности, что тепловая волна движется в направлении от начала координат. В этом случае $\rho \left( {t,u} \right)$ – строго убывающая функция переменной $u$ при любом значении $t$. В силу непрерывности ее производная ${{\rho }_{u}}\left( {0,0} \right) < 0$. Следовательно, и Таким образом, при $k = 1$ значения ${{\rho }_{{1\left( {k - 1} \right)}}}$ и $q_{{1\left( {k - 1} \right)}}^{{\left( \rho \right)}}$ также известны. Следовательно, на каждом шаге по времени $t = {{t}_{k}}$ соотношение (2.3) содержит две неизвестные: ${{\rho }_{{1k}}}$ и $q_{{1k}}^{{\left( \rho \right)}}$. Отметим, что в случае движения тепловой волны в направлении начала координат рассуждения абсолютно аналогичны.

Перейдем непосредственно к решению задачи (1.4), (1.5). В момент $t = {{t}_{k}}$ в области $u \in \left[ {0,L} \right]$, $L = f{\kern 1pt} \left( {{{t}_{k}}} \right)$, решение этой задачи методом граничных элементов имеет следующий вид [17]:

Здесь $q_{{2k}}^{{\left( \rho \right)}} = {{q}^{{\left( \rho \right)}}}\left( {{{t}_{k}},L} \right)$, $u{\text{*}}\left( {\text{v},u} \right)$ – фундаментальное решение стационарной задачи теории потенциала для одномерных задач, Значения ${{\rho }_{{1k}}}$, $q_{{1k}}^{{\left( \rho \right)}}$ и $q_{{2k}}^{{\left( \rho \right)}}$ не заданы граничными условиями и должны быть определены.

Перейдя в уравнении (2.4) к пределам при $u \to 0$ и $u \to L$, получим граничные интегральные уравнения

Уравнения (2.5) и соотношение (2.3) образуют систему трех уравнений относительно ${{\rho }_{{1k}}}$, $q_{{1k}}^{{\left( \rho \right)}}$ и $q_{{2k}}^{{\left( \rho \right)}}$: Далее задача решается итерационно. В качестве начального приближения принимается решение ${{\rho }^{{\left( 0 \right)}}} \equiv R$. На $n$-й итерации, где $n = 1,2,\; \ldots $, в подынтегральные выражения в (2.6) входит $(n - 1)$-я итерация решения ${{\rho }^{{\left( {n - 1} \right)}}}$: Решением системы (2.7) являются $n$-я итерация граничных значений искомой функции и потока: $\rho _{{1k}}^{{\left( n \right)}}$, $q_{{1k}}^{{\left( \rho \right)\left( n \right)}}$, $q_{{2k}}^{{\left( \rho \right)\left( n \right)}}$. Эти значения определяют $n$-ю итерацию решения Интегралы в уравнениях (2.7), (2.8) вычисляются через разложения по радиальным базисным функциям, с помощью метода двойственной взаимности [10]. Итерационный процесс заканчивается при достаточной близости значений $\rho _{{1k}}^{{\left( n \right)}}$ и $\rho _{{1k}}^{{\left( {n - 1} \right)}}$. В качестве решения задачи (1.4), (1.5) в момент $t = {{t}_{k}}$ при этом принимается $n$-я итерация (2.8): $\rho \left( {{{t}_{k}},u} \right) = {{\rho }^{{\left( n \right)}}}\left( u \right)$.

Функция $\rho \left( {{{t}_{k}},u} \right)$ является в момент времени $t = {{t}_{k}}$ обратной к решению $u\left( {{{t}_{k}},\rho } \right)$ исходного уравнения (1.1) функцией при краевом режиме (1.2б). Непрерывный вид решения (2.8) позволяет восстановить решение исходной задачи без потери точности.

3. ПОСТАНОВКА ДВУМЕРНОЙ ЗАДАЧИ И СУЩЕСТВОВАНИЕ ЕЕ РЕШЕНИЯ

Решение задачи об инициировании тепловой волны в случае двух пространственных переменных заметно сложнее, чем в одномерном случае. Алгоритм решения методом граничных элементов двумерной краевой задачи при заданном нулевом фронте тепловой волны представлен в работе [16]. Распространение этого алгоритма на решение задачи об инициировании тепловой волны невозможно, поскольку в каждый момент времени область решения задачи неизвестна, нулевой фронт также неизвестен. В одномерном случае неизвестный нулевой фронт может быть определен в процессе решения задачи [14], [15]. Однако в случае двух пространственных переменных нулевой фронт представляет собой уже не точку, а замкнутую линию, интегрирование по которой входит в алгоритм решения на каждом шаге по времени. В связи с этим применим для решения двумерной задачи об инициировании тепловой волны подход, предложенный в предыдущем разделе.

В двумерном случае уравнение (0.2) имеет следующий вид в полярной системе координат:

Зададим краевое условие в виде где уравнение $\rho = R\left( \varphi \right)$ задает замкнутую гладкую линию, содержащую начало координат, $f{\kern 1pt} \left( {0,\varphi } \right) = 0$, ${{f}_{t}}\left( {0,\varphi } \right) > 0$. В каждый момент времени область решения задачи (область ненулевых значений искомой функции $u\left( {t,\rho ,\varphi } \right)$) ограничена линией $\rho = R\left( \varphi \right)$ и нулевым фронтом – линией $\rho = a\left( {t,\varphi } \right)$, такой что Отметим, что $a\left( {0,\varphi } \right) = R\left( \varphi \right)$. В случае, когда задано граничное условие (3.3), область решения задачи известна в каждый момент времени, что, как уже отмечено, дает возможность применить алгоритмы, предложенные в [14]–[16]. В нашем случае функция $a\left( {t,\varphi } \right)$ неизвестна и должна определяться в процессе решения.

Поменяем местами в рассматриваемой задаче (3.1), (3.2) искомую функцию $u$ и координату $\rho $ и сделаем замену новой независимой переменной $\text{v} = u + 1$, которая необходима для корректности дальнейших рассуждений. Уравнение (3.1) примет вид

Будем рассматривать далее переменные $\text{v}$, $\varphi $ как полярные координаты в плоскости декартовых координат $\xi $, $\eta $: $\xi = \text{v}\cos \varphi $, $\eta = \text{v}\sin \varphi $.

Краевое условие (3.2) в новых обозначениях примет вид

Условие $\text{v} = 1 + f\left( {t,\varphi } \right)$ задает в плоскости координат $\xi $, $\eta $ в каждый момент времени замкнутую линию ${{C}^{{\left( t \right)}}}$, ограничивающую область ${{U}^{{\left( t \right)}}}$, содержащую начало координат, при этом ${{C}^{{\left( 0 \right)}}}$ – окружность единичного радиуса с центром в начале координат.

Решению исходной задачи (3.1), (3.2) в новых переменных соответствует задача (3.4), (3.5), состоящая в определении функции $\rho = \rho \left( {t,\text{v},\varphi } \right)$ в области $t \in [0,{{t}_{*}}]$, $\left( {\text{v},\varphi } \right) \in {{W}^{{\left( t \right)}}}$, где ${{W}^{{\left( t \right)}}}$ – известная в каждый момент область, ограниченная линиями ${{C}^{{\left( 0 \right)}}}$ и ${{C}^{{\left( t \right)}}}$.

Замечание 3. Для задачи (3.4), (3.5) справедлива теорема существования и единственности аналитического решения, являющаяся аналогом доказанной выше теоремы 1. При этом процедура построения решения очень близка: решение строится в виде ряда вида (1.9) с той разницей, что коэффициенты ${{x}_{{m,l}}}$ уже, вообще говоря, не являются константами, а зависят от полярного угла $\varphi $:

${{x}_{{0,1}}} = \left( \varphi \right)$ определяется из уравнения (1.10) (с тем отличием, что ${{a}_{1}} \equiv 0$, а ${{f}_{1}}$ является уже не константой, а функцией переменной $\varphi $). Коэффициенты ряда (1.9) более высокого порядка определяются последовательно при решении СЛАУ вида (1.11), параметры которых зависят от $\varphi $, и т.п. Сходимость построенных рядов следует из того же доказанного ранее авторами утверждения (см. [13]), которое использовалось при доказательстве теоремы 1.

4. АЛГОРИТМ ЧИСЛЕННОГО РЕШЕНИЯ ДВУМЕРНОЙ ЗАДАЧИ

Представим уравнение (3.4) в виде уравнения Пуассона. Для этого выразим $\Delta \rho $, добавив соответствующие слагаемые $\left( {\Delta \rho = {{\rho }_{{\text{vv}}}} + {{{{\rho }_{\text{v}}}} \mathord{\left/ {\vphantom {{{{\rho }_{\text{v}}}} \text{v}}} \right. \kern-0em} \text{v}} + {{{{\rho }_{{\varphi \varphi }}}} \mathord{\left/ {\vphantom {{{{\rho }_{{\varphi \varphi }}}} {{{\text{v}}^{2}}}}} \right. \kern-0em} {{{\text{v}}^{2}}}}} \right),$

Таким образом, задача (3.4), (3.5) преобразована в краевую задачу для уравнения Пуассона (4.1), которое сокращенно запишем в виде с краевым условием (3.5).

Вдоль границы ${{C}^{{\left( 0 \right)}}}$ области ${{W}^{{\left( t \right)}}}$ имеем $\text{v} = 1$. Из уравнения (3.4) получаем

С учетом того, что ${{C}^{{\left( 0 \right)}}}$ – окружность, получаем выражение для потока вдоль этой границы: Здесь ${\mathbf{n}}$ – вектор внешней нормали к границе области ${{W}^{{\left( t \right)}}}$.

В граничном условии (3.5) возьмем полную производную по времени

Отсюда ${{\rho }_{t}} = - {{\rho }_{\text{v}}}{{f}_{t}}$ при $\text{v} = 1 + f{\kern 1pt} \left( {t,\varphi } \right)$. Подставляя полученное в (3.4) и рассматривая момент $t = 0$, когда $\text{v} = 1$, получаем

Примем вновь направление движения тепловой волны от начала координат, тогда производная ${{\rho }_{\text{v}}}$ должна быть отрицательной. Отсюда, учитывая, что $\rho = R$, ${{\rho }_{\varphi }} = R{\text{'}}\left( \varphi \right)$ при $t = 0$, $\text{v} = 1$, получаем откуда

Перейдем непосредственно к решению задачи (4.2), (3.5). Для решения в момент времени $t = {{t}_{k}}$ аппроксимируем границу области ${{W}^{{\left( {{{t}_{k}}} \right)}}}$ ломаными из $2N$ прямолинейных граничных элементов: ${{e}_{{1k}}},\;{{e}_{{2k}}},\; \ldots ,\;{{e}_{{Nk}}}$ – на границе ${{C}^{{\left( 0 \right)}}}$, ${{e}_{{(N + 1)k}}},\;{{e}_{{(N + 2)k}}},\; \ldots ,\;{{e}_{{(2N)k}}}$ – на границе ${{C}^{{\left( {{{t}_{k}}} \right)}}}$. Будем использовать постоянную аппроксимацию искомой функции и потока на элементе. Тогда решение задачи методом граничных элементов имеет следующий вид [18]:

где $\zeta \left( {\text{v},\varphi } \right)$ – внутренняя точка области ${{W}^{{\left( {{{t}_{k}}} \right)}}}$, ${{\rho }_{{ik}}}$ и $q_{{ik}}^{{\left( \rho \right)}}$ – значения искомой функции и потока в момент ${{t}_{k}}$ на элементе ${{e}_{{ik}}}$, $u{\kern 1pt} {\text{*}}{\kern 1pt} \left( {\zeta ,z} \right)$ – фундаментальное решение для двумерной задачи теории потенциала, $q{\kern 1pt} {\text{*}}{\kern 1pt} \left( {\zeta ,z} \right) = \frac{{\partial u{\kern 1pt} {\text{*}}{\kern 1pt} \left( {\zeta ,z} \right)}}{{\partial {\mathbf{n}}}}$. В узлах граничных элементов ${{z}_{{ik}}}$, расположенных в средних точках элементов, справедливо

В соотношениях (4.5) и (4.6) значения ${{\rho }_{{ik}}}$, $i = N + 1,\; \ldots ,\;2N$, заданы граничным условием (3.5). Значения ${{\rho }_{{ik}}}$, $i = 1,\; \ldots ,\;N$, и $q_{{ik}}^{{\left( \rho \right)}}$, $i = 1,\; \ldots ,\;2N$, составляют $3N$ неизвестных, которые должны быть определены при решении задачи. Для этого к $2N$ граничным интегральным уравнениям (4.6) добавим $N$ уравнений, полученных с помощью разностного представления производных в уравнении (4.3)

Здесь ${{h}_{\varphi }} = \frac{{2\pi }}{N}$ – шаг по переменной $\varphi $.

Таким образом, уравнения (4.6), (4.7) образуют систему $3N$ уравнений для $3N$ неизвестных.

Решение задачи, как и в одномерном случае, проводится итерационно. В качестве начального приближения принимается решение ${{\rho }^{{\left( 0 \right)}}} = R\left( \varphi \right)$. На $n$-й итерации, $n = 1,2,\; \ldots $, решается система (4.6), (4.7). При этом в подынтегральные выражения интегралов по области ${{W}^{{\left( {{{t}_{k}}} \right)}}}$ в уравнениях (4.6) входит правая часть уравнения (4.2), определяемая $(n - 1)$-й итерацией решения ${{\rho }^{{\left( {n - 1} \right)}}}$: $P(\text{v},{{\rho }^{{(n - 1)}}},\rho _{t}^{{(n - 1)}},\rho _{\text{v}}^{{(n - 1)}},\rho _{\varphi }^{{(n - 1)}},\rho _{{\varphi \varphi }}^{{(n - 1)}},\rho _{{\text{v}\varphi }}^{{(n - 1)}})$. Решением такой системы являются $n$-е итерации узловых значений искомой функции и потока: $\rho _{{ik}}^{{\left( n \right)}}$, $i = 1,\; \ldots ,\;N$, и $q_{{ik}}^{{\left( \rho \right)\left( n \right)}}$, $i = 1,\; \ldots ,\;2N$. Эти значения определяют $n$-ю итерацию решения

Нелинейная система уравнений (4.6), (4.7) решается методом Ньютона. В качестве начальных приближений (на нулевой итерации) при $k > 1$ принимаются значения на предыдущем шаге по времени, а при $k = 1$ – начальные значения искомой функции и значения потока, соответствующие соотношению (4.4). Интегралы по области ${{W}^{{\left( {{{t}_{k}}} \right)}}}$ в соотношениях (4.6), (4.8) вычисляются с помощью метода двойственной взаимности [10]. Интегралы по граничным элементам от функций $u{\kern 1pt} {\text{*}}{\kern 1pt} \left( {\zeta ,z} \right)$ и $q{\kern 1pt} {\text{*}}{\kern 1pt} \left( {\zeta ,z} \right)$ вычисляются точно с помощью аналитических формул [19]. Итерационный процесс заканчивается при достаточной близости значений $\rho _{{ik}}^{{\left( n \right)}}$ и $\rho _{{ik}}^{{(n - 1)}}$. В качестве решения задачи (4.2), (3.5) в момент $t = {{t}_{k}}$ при этом принимается $n$-я итерация (4.8): $\rho \left( {{{t}_{k}},\text{v},\varphi } \right) = {{\rho }^{{\left( n \right)}}}\left( {\text{v},\varphi } \right)$.

Решение исходной задачи (3.1), (3.2) в момент $t = {{t}_{k}}$ $u\left( {{{t}_{k}},\rho ,\varphi } \right)$ получается из непрерывного по пространственным координатам решения $\rho \left( {{{t}_{k}},\text{v},\varphi } \right)$ без потери точности.

5. ПРИМЕРЫ

Разработанные алгоритмы были протестированы с помощью сравнения результатов их применения с известными точными решениями. В примерах 1 и 2 рассмотрены одномерные задачи, в примерах 3 и 4 – двумерные.

Пример 1. Одномерная задача, $\gamma = 0$.

Предложенный алгоритм был применен для решения уравнения (1.1) при краевом условии

соответствующем известному точному решению [6] Здесь $\lambda = 2 + 4{\text{/}}\sigma $, ${{C}_{1}}$ и ${{C}_{2}}$ – положительные константы. Отметим, что результаты численного решения по предложенному алгоритму при различных значениях параметров оказались достаточно близки к точному решению. Также отметим стабильную сходимость итерационных процедур. Для иллюстрации на фиг. 1 приведено сравнение решений уравнения (1.1) при краевом условии (5.1) в различные моменты времени для следующих значений параметров: $\sigma = 3$, ${{C}_{1}} = 10$, ${{C}_{2}} = 1$, $h = 0.25$. Для оценки точности решений результаты расчетов сведены в таблицы. В табл. 1 сравниваются относительные погрешности полученного численного решения и решения, полученного ранее [14]. В табл. 2 представлены относительные погрешности нулевого фронта, найденного в результате решения, по сравнению с нулевым фронтом соответствующим точному решению (5.2), а также нулевого фронта, найденного в [14]. Сравнение показывает более высокую точность решения по новому алгоритму по сравнению с предложенным ранее.

Пример 2. Одномерные задачи, $\gamma = 1,2$.

Сравнение решений уравнения (1.1) по различным алгоритмам было также проведено для задач с круговой и сферической симметрией. Были решены задачи при краевом условии

соответствующем точному решению [15] Здесь $\mu = 2 + 2\gamma + 4{\text{/}}\sigma $, $k = 2\left( {1 + \gamma } \right){\text{/}}\mu $, $C$ и $R$ – положительные константы.

Вновь результаты решения по предложенному алгоритму сравнивались с полученными ранее численными решениями [15]. В табл. 3 сравниваются относительные погрешности решений при следующих значениях параметров: $\gamma = 1$, $\sigma = 3$, $C = 10$, $R = 1$, $h = 0.1$. В табл. 4 представлены относительные погрешности найденного при численном решении нулевого фронта по сравнению с нулевым фронтом

соответствующим точному решению (5.4). Здесь $\alpha = 1{\text{/}}\left( {\left( {1 + \gamma } \right)\sigma + 2} \right)$. Аналогичные результаты при $\gamma = 2$ показаны в табл. 5, 6. Следует отметить стабильную сходимость итерационных процедур, а также более высокую точность новых численных решений по сравнению с полученными ранее.

Пример 3. Для верификации алгоритма численного решения двумерной задачи об инициировании тепловой волны в двумерной постановке была решена задача с симметричным краевым условием вида (3.2), соответствующим условию (5.3) при $\gamma = 1$:

Отличие двумерной задачи от рассмотренной в примере 2 состоит в том, что краевое условие задано не в точке, а на окружности с радиусом $R$, и решение строится на плоскости. В результате численного решения методом граничных элементов было получено симметричное относительно начала координат решение. Граница области решения на каждом шаге по времени разбивалась на 500 граничных элементов. В табл. 7 решение при значениях параметров $\sigma = 3$, $С = 10$, $R = 1$, $h = 0.1$ сравнивается с точным решением (5.4). В табл. 8 сравниваются соответствующие нулевые фронты. Сравнение показывает хорошую точность решения.

Отметим, что алгоритм решения двумерных задач тестировался на симметричной задаче, поскольку точные решения двумерной задачи, не обладающие центральной симметрией, авторам неизвестны.

Пример 4. В качестве примера двумерной задачи, не обладающей симметрией, была решена задача (3.1), (3.2) при $R\left( \varphi \right) = R$, $f\left( {t,\varphi } \right) = 0.1t\left( {1 + 0.3\cos \left( \varphi \right)} \right)$. Численное решение МГЭ сравнивалось с решением, соответствующим аналитическому решению задачи (3.4), (3.5) в виде ряда

Результаты расчетов сравнивались с решениями, соответствующими отрезкам рядов

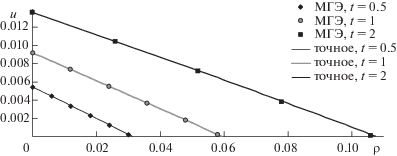
На фиг. 2 показано сравнение численного решения $u\left( {t,\rho ,\varphi } \right)$ с аналитическим решением, соответствующим (5.6) при $n = 3$, в различные моменты времени вдоль лучей $\varphi = 0$, $\varphi = \pi {\text{/}}4$, $\varphi = \pi {\text{/}}2$. Приведенные графики демонстрируют близость численного и аналитического решений.

Количественный анализ решений приведен в табл. 9, где численное решение сравнивается с аналитическими при различных порядках отрезков ряда. Сравниваются найденные в процессе решения точки нулевого фронта $\rho = a\left( {t,\varphi } \right)$ (см. (3.3)). Количественный анализ показывает “машинную” сходимость аналитических решений с увеличением $n$, причем аналитические решения приближаются к численному. Такое соответствие свидетельствует о корректности численного решения.

ЗАКЛЮЧЕНИЕ И ВЫВОДЫ

Главным результатом проведенного исследования, по мнению авторов, является то, что в ходе работы удалось преодолеть значительные аналитические и вычислительные трудности и создать на основе граничноэлементного подхода эффективный алгоритм решения двумерных задач об инициировании тепловой волны для нелинейного уравнения теплопроводности в случае степенной зависимости коэффициента теплопроводности от температуры.

Результаты значительного количества проведенных вычислительных экспериментов показали как устойчивую сходимость результатов расчетов к известным точным решениям, так и хороший уровень совпадения результатов расчетов с частичными суммами степенных рядов, в виде которых представлены решения при различных краевых условиях.

Также новый подход показал высокую эффективность при решении одномерных задач, для которых наблюдались более устойчивая сходимость итерационных процессов по сравнению с разработанными ранее алгоритмами и более высокая точность расчетов.

Наконец, была доказана новая теорема существования и единственности решения задачи об инициировании тепловой волны, которая дополняет ранее полученные аналитические результаты авторов.

Дальнейшие направления исследований могут быть связаны, во-первых, с рассмотрением задач с источником и/или стоком; во-вторых, с изучением других разновидностей нелинейного уравнения теплопроводности. Логичным развитием выполненных работ также стало бы рассмотрение трехмерных задач, однако, ввиду большой сложности подобного рода постановок, по-видимому, придется ограничиться частными случаями.