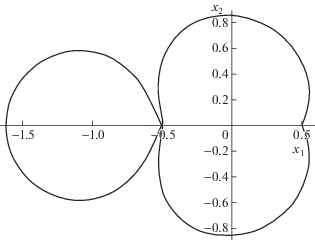Журнал вычислительной математики и математической физики, 2019, T. 59, № 7, стр. 1158-1173
Интегрирование обыкновенных дифференциальных уравнений на римановых поверхностях с неограниченной точностью
В. П. Варин *
ИПМ
125047 Москва, Миусская пл., 4, Россия
* E-mail: varin@keldysh.ru
Поступила в редакцию 11.02.2019
После доработки 11.02.2019
Принята к публикации 11.03.2019
Аннотация
Рассматриваются аналитические системы обыкновенных дифференциальных уравнений (ОДУ) с вещественным и комплексным временем. Интегрирование таких ОДУ эквивалентно аналитическому продолжению решения вдоль некоторого пути, который обычно расположен на вещественной оси. Возникающие на этом пути препятствия часто обусловлены особенностями решения, которые расположены вне вещественной оси. Оказывается, возможно обойти проблемные участки (включая сингулярности), просто выходя на риманову поверхность решения (т.е. в комплексную область). Естественным способом реализации такой программы является метод тейлоровских разложений, который не требует формальной комплексификации системы (т.е. замен переменных). На примере двух классических задач: ограниченной задачи трех тел и уравнения Ван дер Поля – мы покажем, как метод Тейлора применяется для интегрирования ОДУ с неограниченной точностью. В этих задачах нами получены новые результаты. Библ. 15. Фиг. 13. Табл. 3.
1. ВВЕДЕНИЕ
Численное интегрирование ОДУ является одной из основных задач численного анализа, что видно уже по тому объему, который этот раздел занимает в учебниках по данному предмету.
Существует множество различных алгоритмов численного интегрирования ОДУ, предназначенных для различных задач. При этом традиционно одним из основных критериев эффективности численного алгоритма является та быстрота, с которой данный алгоритм может проинтегрировать типовую задачу с заданной точностью.
В этой связи методы Рунге–Кутты имеют плохую репутацию (см., например, [1, с. 706]), так как требуют большего количества обращений к правой части системы, чем другие более популярные методы.
Наряду с этим большинство авторов отмечают большую надежность методов Рунге–Кутты, имея в виду, как правило, классический метод четвертого порядка точности (см., например, [2, с. 253]).
Однако экономия машинного времени уже далеко не всегда является приоритетом. Особенно когда мы имеем дело со сложными или уникальными задачами, где надежность и точность результата стоят на первом месте. В этой связи методы Рунге–Кутты вновь привлекли к себе заслуженное внимание.
В настоящее время существуют методы Рунге–Кутты 4, 5, 8, 10, 12 и 14-го порядков точности. Однако помимо классического метода Рунге–Кутты 4-го порядка, в виде программных продуктов реализованы только метод 5-го порядка (Cash-Karp) и метод 8-го порядка (Dormand-Prince).
Напомним, что порядок точности $N$ – это априорная оценка локальной погрешности $O({{h}^{{N + 1}}})$ на каждом шаге $t \to t + h$.
Таким образом, методы Рунге–Кутты по построению предполагают дифференцируемость решения и правой части системы ОДУ до нужного порядка. Мы же в дальнейшем будем предполагать аналитичность и того и другого (т.е. требуется выполнение условий теоремы Коши).
В данной ситуации методы Рунге–Кутты полностью эквивалентны классическому методу тейлоровских разложений (МТР).
Однако в то время как построение метода Рунге–Кутты высокого порядка является черезвычайно сложной алгебраической задачей, МТР не имеет подобных ограничений, и его сложность или простота целиком определяются конкретной системой ОДУ, которую требуется проинтегрировать.
В настоящее время МТР не только не получил широкого распространения, но, напротив, многие авторы ссылаются на него лишь в историческом контексте наряду с методом Эйлера.
Основное заблуждение относительно МТР, которое встречается даже в современных учебниках (см., например, [3, с. 411]), – это представление о том, что правую часть системы ОДУ придется символьно дифференцировать (вручную или в системе компьютерной алгебры) до высокого порядка, что технически сложно и очень громоздко.
Отметим, что именно такой подход реализован в системе Maple, где отмечается высокая эффективность МТР для интегрирования ОДУ с высокой точностью.
Между тем еще в начале 60-х годов прошлого века была предложена техника вычисления тейлоровских разложений правых частей ОДУ до произвольного порядка без символьного дифференцирования. Было показано (см., например, [4, с. 26]), что при весьма общих предположениях относительно правой части системы всегда можно предъявить простые рекуррентные формулы, по которым можно вычислить наперед заданное количество тейлоровских коэффициентов решения. Иными словами, порядок численного интегрирования МТР неограничен и может меняться на каждом шаге без изменений в программе.
Эта техника позволяет конструировать МТР не только для алгебраических ОДУ, но и для любых уравнений, выраженных в элементарных и большинстве специальных функций (которые удовлетворяют алгебраическим ОДУ). При этом вычисление тейлоровских коэффициентов решения может быть представлено в виде серии простых операций не сложнее свертки (с весами) двух числовых массивов.
Приведем пример (известный уже Эйлеру, см. [5]) возведения ряда в произвольную степень, который понадобится нам в дальнейшем. Пусть
Весьма нетривиальный пример применения МТР для интегрирования задачи $N$ тел приведен в [6]. Отметим также, что знаменитый отчет Брука о лунных орбитах (см. [7]) был выполнен с использованием этого метода.
Помимо неограниченного порядка точности, МТР имеет еще ряд неоспоримых преимуществ, которыми мы воспользуемся.
Любой продвинутый метод численного интегрирования ОДУ использует автоматический выбор шага интегрирования, что необходимо как для контроля точности вычислений, так и для эффективности алгоритма.
Современные методы Рунге–Кутты (embedded methods) решают эту проблему посредством построения одновременно двух сплайнов, приближающих решение. Сравнение двух приближенных решений позволяет контролировать шаг интегрирования.
Другие методы интегрирования ОДУ решают эту проблему похожим образом.
Однако подобный контроль точности является априорным, и он не может полностью учитывать свойства решения, которые заранее неизвестны.
Напротив, МТР обладает внутренним контролем точности, который следует прямо из свойств решения, т.е. его тейлоровских коэффициентов. Это позволяет менять порядок метода и/или величину шага динамически в зависимости от локальных свойств решения.
Заметим, что ряды Тейлора решений суммируются по правилу Хорнера. Данная операция весьма экономна с вычислительной точки зрения и устойчива по отношению к малым погрешностям.
С учетом сказанного, МТР является прямым аналогом методов без насыщения (см. [8]), которые применяются к краевым задачам.
Другим преимуществом МТР, которое не описано в литературе (насколько нам известно), является возможность произвольно менять путь интегрирования, т.е. выходить на риманову поверхность решения по мере необходимости, не производя никаких изменений в программе (кроме клонирования и изменения типов данных).
МТР в его комплексной реализации позволяет численно и с неограниченной точностью исследовать римановы поверхности решений ОДУ. При этом под неограниченной точностью понимается не только неограниченный порядок метода, но и возможность увеличивать длину разрядной сетки по мере надобности (что, конечно, относится к возможностям современных компьютеров).
Интегрирование ОДУ по комплексному пути теоретически не является ограничением при наличии стандартных программ, которые интегрируют только по вещественному пути. Однако практическая реализация такого подхода потребует параметризации пути, комплексификации системы и последующих замен переменных. И так при каждом изменении пути.
Возможность менять путь интегрирования может быть необходима для исходно стандартной задачи интегрирования по вещественному пути (см. разд. 2). Это связано с тем, что любые, в принципе, трудности или препятствия на вещественном пути интегрирования являются проявлением особенностей решения, лежащих достаточно близко к вещественной оси.
Это наблюдение является очевидным, если сравнить риманову поверхность решения с рельефом пересеченной местности, а вещественный путь интегрирования – с прямой дорогой из пункта А в пункт Б.
Приведем пример задачи Коши, которая, согласно [9, с. 196], не может быть численно проинтегрирована на заданном интервале:
Этот пример является весьма популярным (см. также [10, с. 333]).Поскольку решением (1) является функция $y(x) = 1{\text{/}}(1 - x)$, имеющая полюс в середине интервала интегрирования, авторы полагают, что численно такая задача не может быть решена. Однако с помощью МТР интегрируем без проблем, например, по пути
используя одну и ту же программу для всех отрезков пути.Заметим также, что МТР с автоматическим выбором шага остановит работу, подойдя достаточно близко к особенности. Иными словами, имеется возможность локализовывать особенности решения автоматически (см. разд. 3).
В данной работе мы применим МТР для двух хорошо известных задач: ограниченной (круговой) задачи трех тел (ОЗТТ) и уравнения Ван дер Поля.
Насколько нам известно, в этих задачах интегрирование по комплексному пути никогда ранее не применялось.
В разд. 2 мы покажем, как МТР применяется для вычисления периодических орбит в ОЗТТ, близких к столкновительным. Такие орбиты (fly-by orbits) весьма важны для целей космической навигации и гравитационного ускорения космических аппаратов.
До настоящего времени интегрирование ОЗТТ для подобных орбит проводилось с помощью регуляризации, что технически весьма сложно (см. [11, с. 83]).
Уравнение Ван дер Поля
(с различными модификациями) используется и в настоящее время для моделирования различных колебательных процессов в динамических системах. В частности, уравнение (2) с периодической вынуждающей силой демонстрирует переход к хаотическому режиму через разрушение инвариантных торов.Само уравнение Ван дер Поля, будучи эквивалентно автономной системе на плоскости, в принципе не может иметь хаотических режимов, а имеет только предельные циклы.
Однако эта прописная истина справедлива только для вещественного времени. Введение комплексного времени эквивалентно, в некотором смысле, удвоению размерности динамической системы, поэтому можно ожидать существенного усложнения решений.
В разд. 3 мы покажем, что хорошо известные релаксационные колебания решений уравнения (2) связаны, как мы и предсказывали, с (подвижными) особенностями уравнения (2), расположенными вне (но достаточно близко) к вещественной оси.
Как оказалось, уравнение (2) имеет счетное множество таких особенностей, и попытка их обойти по комплексному пути (окружности) приводит к появлению все более длинно-периодических решений.
Эти решения претерпевают перестройку и увеличение периода каждый раз, когда внутрь окружности обхода попадают новые особенности решения, что, в конечном счете, приводит к появлению хаотического режима.
Нам удалось детально проследить этот механизм перехода к хаосу.
2. ОСОБЕННОСТИ РЕШЕНИЙ ОЗТТ
ОЗТТ и ее модификации весьма важны как в небесной механике, так и для целей космической навигации (см. [11]). Например, модель Земля–Луна–спутник использовалась при расчете лунных орбит (см. [7]); а модель Солнце–Юпитер–астероид применялась для объяснения структуры распределения астероидов (см. [12], [13]).
Напомним, что (круговая) ОЗТТ в безразмерной синодической (комплексной) системе координат имеет вид
(3)
$\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}z(t) + 2i\frac{d}{{dt}}z(t) = z(t) + h - \mu - \frac{{\left( {1 - \mu } \right)\left( {z(t) + h} \right)}}{{\mathop {\left| {z(t) + h} \right|}\nolimits^3 }} - \frac{{\mu \left( {z(t) - h} \right)}}{{\mathop {\left| {z(t) - h} \right|}\nolimits^3 }},$Как правило, интерес представляют не столько индивидуальные периодические орбиты, т.е. решения уравнения (3), сколько (однопараметрические) семейства орбит.
Продолжение семейства периодических решений по внутреннему параметру возможно до тех пор, пока мы не встретим особенность на семействе. Как показано в [11], такая особенность может быть вызвана только особенностями уравнения (3), т.е. столкновительными орбитами.
Орбиты, близкие к столкновительным, имеют большое значение для гравитационного разгона космических аппаратов.
На фиг. 1 показаны фрагменты орбит на семействе (симметричных) периодических решений ОЗТТ до, в момент и после столкновения с Солнцем или Юпитером.
Любой алгоритм, предназначенный для расчета регулярных решений уравнения (3), даст отказ не только на сингулярном решении, но и достаточно близко к нему.
Проблема продолжения семейства, на котором имеются столкновительные орбиты (либо близко к нему расположенные), до сих пор решалась с помощью различного рода регуляризаций (см. [11, с. 83]).
Опишем вкратце наиболее простую регуляризацию Леви-Чевита для столкновительных орбит с Юпитером.
Сначала в уравнении (3) делается замена переменной
которая по сути локально выпрямляет траекторию столкновения. Однако теперь астероид пролетает сквозь Юпитер с бесконечной скоростью. Поэтому делается замена времени которая полностью устраняет особенность решения.Однако проделанных манипуляций еще недостаточно, так как полученное в результате уравнение плохо обусловлено. Поэтому замены (4), (5) делают также в интеграле Якоби, а затем исключают квадрат скорости $w{\text{'}}(s)$ из полученных уравнений.
Мы не приводим регуляризованное уравнение, которое весьма громоздко.
Аналогичные манипуляции требуются для регуляризации орбит столкновения с Солнцем.
Заметим также, что одному периоду решения уравнения (3) соответствует только полпериода решения регуляризованного уравнения (этот факт не отмечен в [11]).
В случае орбит, где происходит близкий пролет как к Солнцу, так и к Юпитеру, регуляризация Леви-Чевита неприменима. В этих случаях применяются более сложные регуляризации Биркгофа или Тиле-Барро (см. [11]).
В общей задаче $N$ тел, насколько нам известно, не существует регуляризаций периодических орбит, близких к столкновительным с многими телами.
Вышесказанного должно быть достаточно, чтобы сделать перспективу расчета любых орбит ОЗТТ (или задачи $N$ тел) по одному и тому же алгоритму весьма привлекательной. Описанный во введении МТР как раз и дает такую возможность.
Ниже мы покажем, как МТР работает вблизи сингулярных решений ОЗТТ.
Напомним, что МТР для задачи $N$ тел приведен в [6]. Аналогичный алгоритм для ОЗТТ получается в результате очевидных модификаций алгоритма в [6].
На фиг. 2 приведен пример орбиты с близким пролетом как вблизи Солнца, так и Юпитера. Ранее данную орбиту удавалось посчитать только с использованием регуляризации Тиле-Барро. Параметры орбиты в исходных координатах:
(6)
$\begin{array}{*{20}{c}} {\mu = 0.000953880,\quad P = 3.154687648517,} \\ {{{x}_{1}}(0) = - 1.617285336966,\quad {{{\dot {x}}}_{2}}(0) = 1.083230074442,\quad {{{\dot {x}}}_{1}}(0) = 0,\quad {{x}_{2}}(0) = 0,} \\ {{{x}_{1}}(P) = 0.498876827368,\quad {{{\dot {x}}}_{2}}(P) = - 1.681789734519,\quad {{{\dot {x}}}_{1}}(P) = 0,\quad {{x}_{2}}(P) = 0,} \end{array}$На фиг. 3 показаны фрагменты орбиты вблизи Солнца и Юпитера. Небольшая скорость пролета вблизи Юпитера (${{\dot {x}}_{2}}(P)$) не должна вводить в заблуждение. Без регуляризации такой близкий пролет астероида вычисляется (ежели вообще) с большими затратами. Это связано с тем, что решение проходит близко к особенности $z(t) = 1{\text{/}}2$, которая в данном случае расположена в области комплексного времени. Это, в свою очередь, означает, что ряд Тейлора решения $z(t)$ будет иметь малый радиус сходимости вблизи особенности, что так или иначе проявляется при любом численном методе интегрирования, так как порядок точности метода выражается в терминах тейлоровских разложений.
Для вычисления симметричной орбиты достаточно отследить ее на полупериоде. Покажем, как обойти близкий пролет астероида к Солнцу с помощью выхода на риманову поверхность решения.
К сожалению, комплексная форма уравнения (3) (необходимая для регуляризации Тиле-Барро) не удовлетворяет теореме Коши. Однако вещественная форма уравнений, которая и используется обычно для расчетов, удовлетворяет теореме Коши. Иными словами, функции ${{x}_{1}}(t)$ и ${{x}_{2}}(t)$ являются аналитическими, т.е. использование комплексного времени допустимо.
Ближайшая точка к Солнцу (на посчитанной сетке), расположенная на вещественной орбите, имеет координаты
Поскольку рассматриваемая орбита вещественна, то по принципу симметрии Шварца существуют две комплексно-сопряженные особенности решения, т.е. $z(t) = - 1{\text{/}}2$, при некотором комплексном времени $t = {{t}_{ * }}$ и $t = {{\bar {t}}_{*}}$. Ясно, что $\left| {{{t}_{S}} - {{t}_{ * }}} \right|$ достаточно мало, хотя ${{t}_{ * }}$ заранее неизвестно.
Подчеркнем, что две указанные подвижные особенности уравнения (3) принадлежат решению (6), но расположены в комплексной области.
Выберем следующий комплексный путь, который обходит особенности $t = {{t}_{ * }}$ и $t = {{\bar {t}}_{ * }}$ с некоторым запасом. А именно,
Таким образом, сложный участок орбиты с близким проходом к Солнцу окажется обойден. Однако указанные выше особенности являются алгебраическими полюсами с ветвлением кратности 2. Поэтому потребуется 3 оборота, чтобы из точки $t = 1.2$ прийти в нее же, или 3/2 оборота, чтобы попасть в $t = 1.4$.
В табл. 1 приведены координаты решения для значений времени
Таблица 1.
Обход Солнца по комплексному пути
| ${{x}_{1}}(t)$ | ${{\dot {x}}_{1}}(t)$ | ${{x}_{2}}(t)$ | ${{\dot {x}}_{2}}(t)$ |
|---|---|---|---|
| −0.65488 | 1.06300 | 0.32453 | −1.64053 |
| −0.55849 + i0.10104 | 0.81674 − i0.10782 | 0.20711 − i0.25124 | −1.67358 − i1.32606 |
| −0.49424 + i0.07641 | −0.08687 + i0.22465 | −0.15562 − i0.28593 | −1.12524 − i0.28593 |
| −0.39069 + i0.06428 | −0.81780 + i0.75559 | −0.37110 + i0.05707 | −0.13048 − i2.65667 |
| −0.41103 − i0.10293 | −0.62617 + i1.07788 | −0.16265 + i0.34614 | 0.79480 − i2.01576 |
| −0.54652 − i0.05530 | −0.18257 + i0.76697 | 0.15819 + i0.30344 | 1.75589 − i1.32986 |
| −0.52589 | −0.01461 | 0.30061 | 2.20192 |
Из табл. 1 видно, что решение по сути регуляризовано. Ясно, что для чисто столкновительной орбиты (см. фиг. 1) обход совершается аналогичным образом.
Однако необходимо отметить, что данный метод регуляризации нельзя признать универсальным, так как мы априори ничего не знаем об особенностях решений ОЗТТ в комплексной области.
Например, описанный выше обход Солнца по комплексному пути работает также и при обходе Юпитера. Однако оказалось, что вблизи Юпитера имеются по крайней мере еще две комплексно-сопряженные особенности.
Это привело к тому, что при обходе Юпитера потребовалось совершить 5/2 оборотов, подобных описанному выше.
Причина, по которой алгебраические полюса внутри пути обхода добавляют новые листы римановой поверхности решения, довольно очевидна. Однако заранее предсказать поведение решения, не зная, где расположены его особенности, по-видимому, невозможно.
Мы вернемся к данному вопросу в следующем разделе.
В завершение данного раздела отметим один технический момент, без которого описанный выше алгоритм не работает.
Общий алгоритм интегрирования задачи $N$ тел описан в [6], однако он применим только в вещественном случае, как и модифицированный алгоритм, предназначенный для ОЗТТ. Это связано с тем, что система ОДУ (3) не является алгебраической.
Описанный во введении алгоритм возведения ряда в степень применяется в этих задачах для случая $s = - 3{\text{/}}2$, т.е.
При этом функция ${\text{arg}}(x)$ определена при $ - \pi < x \leqslant \pi $. Поэтому при отслеживании решения на его римановой поверхности будет происходить скачок каждый раз, когда точка пересекает ось $( - \infty ,0)$. Чтобы этого избежать, при вычислении коэффициента $Y(0) = {{X}^{s}}(0)$ необходимо использовать функцию ${\text{Arg}}(x)$, которая не является стандартной (и зависит от своей предыстории).3. УРАВНЕНИЕ ВАН ДЕР ПОЛЯ
Применение МТР к уравнению Ван дер Поля (2) дает еще один пример “регуляризации” (за неимением лучшего термина) особенностей ОДУ на оси $\mathbb{R}$ путем выхода на риманову поверхность решения.
Как известно, по мере увеличения $\mu $ период релаксационных колебаний, которые устанавливаются при $t \to \infty $, увеличивается неограниченно, а сама “релаксация”, т.е. срыв решения к минимальному или максимальному значению, происходит все более резким образом. Иными словами, градиент ${\text{max}}\left| {\dot {x}(t)} \right|$ неограничен при $\mu \to \infty $.
Ясно, что $\dot {x}(t)$ как аналитическая функция $t$ имеет особенности достаточно близко к оси $\mathbb{R}$, причем тем ближе, чем больше параметр $\mu $.
Возьмем начальные данные $\mu = 16$, $x(0) = 2$, $\dot {x}(0) = 0$ и проинтегрируем уравнение (2) по вещественному времени достаточно далеко (к примеру, $t > 100$) так, что предельный цикл можно считать установившимся. График решения имеет вид, представленный на фиг. 4.
Ясно, что численное интегрирование данной задачи будет представлять все большие трудности по мере увеличения $\mu $.
Данная модельная задача первоначально использовалась нами как пример применения МТР для обхода сложного участка решения по комплексному пути, где градиент $\left| {\dot {x}(t)} \right|$ уже не является неограниченным при любом параметре $\mu $. Эта техника, разумеется, работает и в данном случае.
Однако акцент наших исследований изменился, и теперь мы рассмотрим задачу локализации подвижных особенностей ОДУ (уравнения (2)); и как они (особенности) влияют на структуру римановой поверхности решения.
Как известно, уравнение Ван дер Поля не интегрируемо (хотя нам не удалось найти ссылку на доказательство этого факта). Интегрируемость ОДУ подразумевает в некотором интуитивном смысле относительную простоту римановых поверхностей его решений.
Напротив, очень сложная структура римановой поверхности решения ОДУ указывает с большой вероятностью на неинтегрируемость уравнения.
Как оказалось, структура римановых поверхностей решений уравнения Ван дер Поля является фрактально сложной. Мы продемонстрируем этот экспериментальный факт на примере решения на фиг. 4.
Рассмотрим вначале, какие особенности может иметь решение уравнения (2).
Подставим пробную функцию $x(t) = {{t}^{r}}$ в каждый моном уравнения (2) и измерим степень $s$ получившихся мономов. Получим
Полагая, что $r$ – это минимальная степень в разложении решения $x(t)$ в степенной ряд, получаем, что единственная возможность привести подобные члены, это $r - 2 = 3r - 1$, т.е. $r = - 1{\text{/}}2$.Задача вычисления степенного разложения решения ОДУ является по сути алгебраической, а данный выше способ найти первый член разложения аналогичен методу диаграмм Ньютона. Все последующие члены разложений, как и их коэффициенты, находятся методом неопределенных коэффициентов. В результате получаем
(7)
$\begin{gathered} \pm x(t) = \frac{1}{2}\frac{{\sqrt 6 }}{{\sqrt {\mu t} }} + \frac{1}{4}\sqrt {6\mu t} + At + \frac{1}{{48}}\frac{{\sqrt 6 ({{\mu }^{2}} - 16){{t}^{{3/2}}}}}{{\sqrt \mu }} - \frac{1}{7}A\mu {{t}^{2}} - \\ - \;\frac{1}{{96}}\sqrt {6\mu } (12{{A}^{2}} + {{\mu }^{2}}){{t}^{{5/2}}} - \frac{1}{{21}}A(2{{\mu }^{2}} - 7){{t}^{3}} + \ldots , \\ \end{gathered} $На самом деле, разложение (7) представляет собой два различных семейства разложений, соответствующих двум ветвям функции $\sqrt t $.
Разложение (7) сходится в некоторой окрестности нуля, хотя доказать данный факт не просто. Однако мы будем численно локализовывать особые точки, поэтому сходимость будет установлена экспериментально.
Отметим также, что $t$ является локальным временем, так как уравнение (2) автономно. Иными словами, локализовав особенность решения $t = {{t}_{0}} \in \mathbb{C}$, получим локальную параметризацию решения в окрестности ${{t}_{0}}$, подставив $t \to t - {{t}_{0}}$ в одно из разложений (7).
Опишем алгоритм, позволивший нам локализовать алгебраические полюса уравнения (2) (далее просто: полюса) с большой точностью (более 20 десятичных разрядов).
Напомним, что $\mu = 16$ фиксировано в данных расчетах.
Выберем точку, ближайшую к локальному минимуму решения на фиг. 4, и поместим ее в начало отсчета ${{t}_{0}} = 0$
(8)
$\begin{gathered} {{P}_{0}} = \left\{ {x(0) = - 2.0096031185320952154535856749935} \right., \\ \dot {x}(0) = \left. { - 0.0076566170015969985933383406195} \right\}. \\ \end{gathered} $Зададим сперва небольшое значение радиуса $R$ обхода точки ${{P}_{0}}$. Затем интегрируем по вещественному времени до точки ${{P}_{1}} = \left\{ {t = R,x(R),\dot {x}(R)} \right\}$. Затем интегрируем по комплексному времени $t = Rexp(is)$, $s \in [0,2k\pi ]$, где $k$ – число оборотов вокруг точки ${{P}_{0}}$.
Ясно, что при достаточно малом $R$ потребуется 1 оборот, т.е. $k = 1$, чтобы вновь попасть в точку ${{P}_{1}}$, что следует из теоремы Коши. Иными словами, решение на фиг. 4 голоморфно в некоторой полосе вдоль оси $\mathbb{R}$.
Ясно также, что голоморфность пропадет, как только внутрь круга обхода попадет хоть одна особая точка (7). Однако для выбранного пути обхода полюса (7) будут попадать внутрь круга обхода только парами по принципу симметрии Шварца.
Таким образом, при первом попадании двух полюсов внутрь круга обхода период функции $x(s)$, заданной на выбранной окружности, скачком изменится с $k = 1$ до $k = 3$. Это связано с тем, что решение $x(t)$ с комплексным временем $t$ имеет ветвление кратности два в окрестности особенности (7). Поэтому каждый из полюсов, попавших внутрь круга обхода, добавляет по одному листу к их общей римановой поверхности.
Эта закономерность сохраняется, как мы увидим, при попадании новых особых точек внутрь круга обхода.
Будем называть такие решения $k$-периодическими в зависимости от числа $k$ оборотов, необходимых, чтобы вернуться в точку ${{P}_{1}}$.
На фиг. 5 показаны графики вещественной части решений $\operatorname{Re} x(s)$ при $R = 0.1$ и $R = 0.155$, когда решения являются 1-периодическими. Можно наблюдать, что два локальных минимума решения становятся неограниченными при увеличении $R$. Ясно, что эти две особенности на решении вызваны полюсами (7), которые пока не попали внутрь круга обхода.
Полагая, что окружность при $R = 0.155$ подходит уже достаточно близко к особенностям (7), выберем на решении некоторую точку $t = {{t}_{1}}$, $\operatorname{Re} {{t}_{1}} > 0$ с наибольшими по модулю значениями начальных данных $x({{t}_{1}})$, $\dot {x}({{t}_{1}})$.
Значение $t = {{t}_{1}}$ является первым приближением к полюсу $t = t_{1}^{ * }$.
Теперь вычислим начальные данные $x({{t}_{1}})$, $\dot {x}({{t}_{1}})$ по разложению (7).
Подставим $t \to t - t_{1}^{ * }$ в одну из формул (7). Как оказалось, в данном случае нужен знак минус в левой части (7). Таким образом, получаем систему двух комплексных уравнений относительно двух комплексных неизвестных $t = t_{1}^{ * }$ и константы $A$, входящей в (7). Второе уравнение получается дифференцированием (7).
Заметим, что ввиду (как оказалось) малого радиуса сходимости рядов (7) нам потребовалось около 40 членов разложения.
Полученная система решается методом Ньютона, хотя никакой гарантии сходимости к решению в данном случае нет, так как начальное приближение для константы $A$ неизвестно. Тем не менее нам удалось решить эту систему, как и все последующие (см. табл. 2, 3). Найденные закономерности в распределении особых точек весьма облегчили эту задачу.
Таблица 2.
Полюса решения на фиг. 4 в верхней полуплоскости
| m | $t_{m}^{ * }$ |
|---|---|
| 1 | −0.143635096586858774576 + i0.064101173248089007412 |
| 2 | −0.144524946094801725948 + i0.192293492052137572817 |
| 3 | −0.146303872904806513723 + i0.320455748871354480046 |
| 4 | −0.148970335584450943889 + i0.448567972558227459393 |
| 5 | −0.152522029406850820546 + i0.576610296777213311347 |
| 6 | 0.156955895182703329996 + i0.704563001032015368052 |
| 7 | −0.162268130914189986860 + i0.832406550808482140203 |
| 8 | −0.168454206168543420101 + i0.960121636598907336894 |
| 9 | −0.175508879046594844814 + i1.087689211586842545839 |
Таблица 3.
Константы Am полюсов решения на фиг. 4 в верхней полуплоскости
| m | Am |
|---|---|
| 1 | 4.595717511093524351499 − i0.051665157429471040414 |
| 2 | 4.596163848580922561123 − i0.154990800529872752765 |
| 3 | 4.597056175462809521155 − i0.258302437677033262102 |
| 4 | 4.598393796852653348217 − i0.361590762587487369923 |
| 5 | 4.600175673657477809793 − i0.464846515310824276113 |
| 6 | 4.602400426430320360832 − i0.568060500375348543911 |
| 7 | 4.605066340454501277531 − i0.671223604551770801884 |
| 8 | 4.608171372015902031908 − i0.774326814133654155209 |
| 9 | 4.611713155809797417399 − i0.877361231639020907791 |
Для того чтобы удостовериться, что полюс $t = t_{m}^{ * }$, $m = 1,2,\; \ldots $, найден правильно, вычислим начальные значения решения по его разложению (7) в некоторой достаточно близкой регулярной точке. Затем интегрируем до точки (8) и сравниваем полученные значения. Наши вычисления давали совпадение значений с абсолютной погрешностью менее 10–25 при расчетах в DD-арифметике, т.е. с 32 десятичными разрядами.
Описанный выше алгоритм вычисления особых точек, соответствующих решению (8), работает, однако, только до полюса с номером $m = 4$.
Дело в том, что, как упоминалось ранее, при попадании очередной пары полюсов внутрь круга обхода период обхода точки ${{P}_{0}}$ увеличивается на 2 единицы. Иными словами, $m = 1,2,\; \ldots $ соответствует $k$-периодическим решениям, где $k = 3,5,7,9,\; \ldots $, т.е. $k = 2m + 1$.
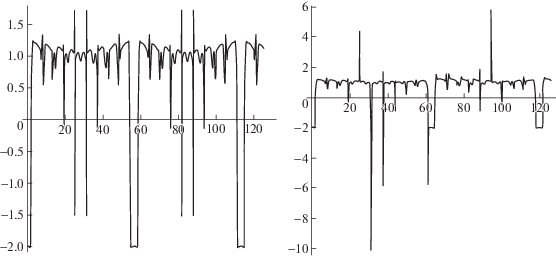
На фиг. 8, 9 показаны графики 5-, 7- и 9-периодических решений ${\text{Re}}x(s)$ при $R = 0.35$ и $R = 0.37$; и при $R = 0.47$ и $R = 0.48$.
На фиг. 10 мы видим, что после 9-периодического решения по какой-то причине получается хаотическое решение (далее мы уточним этот термин). Таким образом, двигаясь по окружностям, как описано выше, мы никогда не локализуем полюса с номерами $m > 4$.
Причина появления хаотического решения связана с попаданием еще одного полюса (7) внутрь круга обхода. Но на этот раз полюс принадлежит другому семейству и не попадает в табл. 2, 3.
Напомним, что полюса в табл. 2, 3 соответствуют семейству со знаком минус в левой части (7). Как оказалось, на римановой поверхности решения имеются также полюса, соответствующие семейству со знаком плюс в (7). Один из таких полюсов попадает внутрь круга обхода при $R > 0.54$
(9)
$\begin{gathered} t{\kern 1pt} * = 0.534289605458396884193 + i0.031299142576563586648, \\ A = - 4.880881662382845745931 - i0.011455835832935449935. \\ \end{gathered} $Из фиг. 10 видно, что потребовалось несколько оборотов, чтобы подойти достаточно близко к точке (9), которая, таким образом, не имеет комплексно-сопряженной пары на этом листе римановой поверхности решения (8).
Разумеется, принцип симметрии Шварца никто не отменял, так что комплексно-сопряженная особенность (9) принадлежит решению (8). Однако она расположена на другом листе римановой поверхности, и чтобы к ней приблизиться, нужно описывать круги по часовой стрелке, т.е. двигаться в направлении $s \to - \infty $.
Таким образом, появление еще одной особой точки, не входящей в регулярную и предсказуемую структуру табл. 2, 3 (см. ниже), “путает все карты”, т.е. листы римановой поверхности решения. Так что при $R > \left| {t_{4}^{ * }} \right| \approx 0.53520558557149$ более не существует периодических решений.
Данный факт, разумеется, является экспериментальным, но воспроизводимым с большой точностью.
На фиг. 11 показано хаотическое решение при $R = 1$.
Полюса (7) могут быть расположены только дискретно на римановой поверхности любого решения. Поэтому вероятность встретить полюс на окружности радиуса $R$ при обходе точки ${{P}_{0}}$ равна нулю.
В частности, решение на фиг. 11 может быть продолжено неограниченно по параметру $s$, оставаясь ограниченным на любом конечном интервале, т.е. при любом фиксированном числе $N$ оборотов вокруг точки ${{P}_{0}}$. Это означает, что некоторое ограниченное пространство заключает в себе неограниченное число листов римановой поверхности решения.
Таким образом, весьма вероятно, что риманова поверхность решения на фиг. 4 устроена фрактально.
Прежде чем вернуться к обсуждению хаотичного поведения комплексных решений уравнения Ван дер Поля, покажем, как находить полюса в табл. 2, 3 при $m > 4$.
Поскольку, двигаясь по окружностям, невозможно приблизиться к полюсам с номерами $m > 4$, то единственная возможность получить первое приближение для метода Ньютона – это найти закономерности в их распределении.
Как оказалось, структура распределения полюсов решения весьма проста.
Рассмотрим последовательности
Структура вещественных частей этих констант устроена не намного сложнее.
Введем две вещественные константы:
Тогда для $n = 1,2,\; \ldots $ имеемОтметим также, что $\tau {\text{/}}a = - 1.99367966268073 \approx - 2$, что вряд ли является случайным совпадением.
На фиг. 12 показаны посчитанные полюса решения на фиг. 4.
Все полюса в левой полуплоскости лежат на одном листе римановой поверхности, т.е. к ним можно подойти по отрезку прямой от начала координат.
Напротив, чтобы приблизиться к точке (9), требуется сделать несколько оборотов, что видно из фиг. 10.
Заметим, что обход точки ${{P}_{0}}$ по кругам различного радиуса на римановой поверхности одного и того же решения может быть представлен в рамках обычного формализма вещественных динамических систем.
Сделаем замену времени $t = Rexp(is)$, $R > 0$, в уравнении (2), а затем подстановку
Отделив вещественную и мнимую части уравнения, получим вещественную динамическую систему с периодическими коэффициентами и вещественным параметром $R$ с поведением решений, полностью совпадающим с описанным выше.На фиг. 13 представлены спектры решений на фиг. 10 при $R = 0.53$ и $R = 0.54$. Видно, что спектр 9-периодического решения образует характерную гребенку с равноотстоящими зубцами. В то время как увеличение $R$ на $0.01$ приводит к появлению непрерывного спектра.
Заметим, что последовательность $3,5,7,9,\; \ldots $, которая проявляется то здесь то там при исследовании комплексных решений уравнения Ван дер Поля, является также первой последовательностью в порядке Шарковского (см. [14]). Возможно, данное обстоятельство является случайным совпадением, но также возможно, что здесь есть скрытый (пока) смысл.
Напомним, что в настоящее время существуют три сценария возникновения хаоса в динамических системах (см. [15]). Это
а) перемежаемость (Pomeau-Manneville);
б) каскад удвоений периода (Feigenbaum);
в) разрушение инвариантных торов (Ruelle-Takens-Newhouse).
Несмотря на то что работа [15] опубликована около 40 лет назад, в настоящее время общепризнанными являются именно эти три сценария перехода к хаосу.
Таким образом, представленный нами механизм возникновения хаоса имеет шанс пополнить этот короткий список.
Список литературы
Press W.H. et al. Numerical Recipes: The Art of Scientific Computing. Cambridge University Press, 1986.
Калиткин Н.Н. Численные методы. М.: Наука, 1978.
Atkinson K., Han W. Elementary Numerical Analysis. John Wiley & Sons, 2004.
Moore R.E. Methods and applications of interval analysis. Philadelphia: SIAM, 1979.
Euler L. Introduction to the analysis of the infinite (Blanton J.D., tr.). New York: Springer, 1988, 1990.
Broucke R. Solution of the n-body problem with recurrent power series // Cel. Mech. 1971. № 4. P. 110–115.
Broucke M.R. Periodic orbits in the restricted three-body problem with Earth–Moon masses // NASA Techn. Rep. 32–1168. Pasadena, 1968.
Бабенко К.И. Основы численного анализа. М.: Наука, 1986.
Aberth O. Introduction to precise numerical methods. Elsevier, 2007.
Dahlquist G., Bjorck A. Numerical Methods. Dover, 1974.
Себехей В. Теория орбит: Ограниченная задача трех тел. М.: Наука, 1982.
Варин В.П. Замкнутые семейства периодических решений ограниченной задачи трех тел // Препринт ИПМ им. М.В. Келдыша РАН. № 16. 2008.
Брюно А.Д., Варин В.П. Замкнутые семейства периодических решений ограниченной задачи трех тел // Астрон. вестн. 2009. Т. 43. № 3. С. 265–288.
Шарковский А.Н. Сосуществование циклов непрерывного преобразования прямой в себя // Укр. матем. ж. 1964. Т. 16. № 1. С. 61–71.
Eckmann J.-P. Roads to turbulence in dissipative dynamical systems // Reviews of Modern Physics. 1981. V. 53. № 4. Part I.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики