Журнал вычислительной математики и математической физики, 2019, T. 59, № 8, стр. 1448-1456

ВВЕДЕНИЕ

Работа основана на результатах из [1], [2] и является дальнейшим развитием построений в [3], [4]. Классическая модель “нападение–оборона” Ю.Б. Гермейера была определена и изучена в работе [5]. Она является модификацией модели О. Гросса [6]. В военных моделях пункты интерпретируются обычно как направления и характеризуют пространственное распределение ресурсов защиты по ширине. Однако реально имеет место также пространственное распределение ресурсов обороны по глубине, характеризующейся количеством уровней рубежей на данном направлении.

Простейшая модель, учитывающая рубежность обороны, состоит в модификации классической модели [5], в которой функция выигрыша нападения имеет вид (см. [1])

а векторы $x$, $y$ принадлежат множествам где ${{T}_{i}}$ – количество рубежей обороны на $i$-м направлении $i = 1,\; \ldots ,\;n$, ${{r}_{i}}$ – максимальное количество воздействий, которое может произвести одна единица обороны, ${{p}_{i}}$ – вероятность поражения одного средства нападения противника одним воздействием на $i$-м направлении, которая предполагается не зависящей от номера $t = 1,\; \ldots ,\;{{T}_{i}}$ рубежа обороны, ${{q}_{i}} = 1 - {{p}_{i}}$ – соответствующая вероятность непоражения, $M$ и $N$ – общее количество средств нападения и обороны, которые считаются однородными и бесконечно-делимыми, ${{x}_{i}}$ и ${{y}_{i}}$ – количество средств нападения и обороны на $i$-м направлении. В частности, формально при ${{p}_{i}} = 1$ получается классическая модель Гермейера [5]. Далее будем считать, что ${{r}_{i}} = 1$, поскольку величины ${{r}_{i}}$ формально можно включить в ${{p}_{i}}$, положив $p_{i}^{'} = {{p}_{i}}{{r}_{i}}$.

В работе [7] исследована игровая модель, обобщающая модели Гросса и Гермейера, в которой получено конструктивное описание множества всех оптимальных смешанных стратегий нападения. В работе [8] изучалась модель Гросса с непротивоположными интересами сторон, в работах [9], [10] – динамические расширения модели. В работе [11] было предложено прямое обобщение игры нападение–оборона на сетях, описывающих топологию путей, ведущих к обороняемым объектам.

Дальнейшее обобщение классической игры нападение–оборона может состоять в учете рубежности обороны, имеющей сетевую структуру, что приводит в общем случае к выпуклым минимаксным задачам, которые могут быть решены методом субградиентного спуска. В частном случае параллельной сетевой структуры, когда пути из источника $s$ в сток $t$ не пересекаются и могут быть отождествлены с направлениями, а ребра однорубежны, предложенная модель формально обобщает игру нападение–оборона Ю.Б. Гермейера на многорубежный случай без упрощающих предположений, использованных в [11].

1. СЕТЕВОЕ ОБОБЩЕНИЕ МОДЕЛИ

Обобщая модель, предложенную в [11], определим игру нападение–оборона на ориентированном графе $G$, состоящем из множества вершин $N = \left\{ i \right\}$ и множества $L = \left\{ {(i,j)} \right\}$ ориентированных ребер ($i$, $j$), ведущих из $i$ в $j$, без контуров с одним источником $s$ и стоком $t$. Далее – орграфе $G$. Пусть

Каждое ориентированное ребро характеризуется величинами: ${{p}_{{ij}}}$, означающими вероятность поражения одного средства нападения одним средством обороны, которые считаются однородными, величинами ${{q}_{{ij}}} = 1 - {{p}_{{ij}}}$ соответственно – не поражения, и количеством ${{T}_{{ij}}}$ рубежей на оперативном направлении, задаваемом ребром ($i$, $j$).

Стратегии $\rho $ нападения и обороны $u$ принадлежат множествам

Используя известный алгоритм (см. [12, с. 252]), разобьем все вершины на ранги

так, что

Определим поток $x = x(\rho ,u)$ в сети из источника $s$ в сток $t$ при помощи рекуррентного соотношения последовательно по мере увеличения ранга $k = 0,\; \ldots ,\;K$. Положим

Пусть для вершин $j$-го ранга $j < k$ определены величины узловых потоков ${{X}_{i}}$, $i \in \bigcup\nolimits_{j < k}^{} {{{N}_{j}}} $.

Определим

и положим и т.д. Положим $I(\rho ,u) = {{X}_{t}}$.

Таким образом, стратегия нападения (${{\rho }^{i}}$, $i \in N{\backslash }t$), определяющая поток однородных средств нападения (${{x}_{{ij}}}$, $(i,j) \in L$) с потерями, из источника $s$ в сток $t$, представляет собой набор векторов ${{\rho }^{i}} = (\rho _{j}^{i},j \in \pi (i))$ целераспределения узлового потока ${{X}_{i}}$, по вытекающим из него инцидентным дугам, обеспечивающим баланс входящего и выходящего из узла потоков. Величина

представляет собой математическое ожидание количества средств нападения, преодолевших эшелонированную оборону на оперативном направлении, задаваемом ребром ($i$, $j$), и определяет потери потока на текущем ребре. Эта формула была установлена в [1], при упрощающем предположении, что вероятности поражения ${{p}_{{ij}}}$ не зависят от рубежа $s = 1,\; \ldots ,\;T_{{ij}}^{{}}$. Критерий нападения состоит в максимизации величины $I(\rho ,u) = {{X}_{t}}$, представляющей математическое количество средств нападения, достигших стока $t$. Критерий обороны прямо противоположен. Источников и стоков может быть несколько, но эту ситуацию всегда можно свести к одному источнику и одному стоку, введя искусственно один сток, соединенный со всеми стоками и один источник, соединенный со всеми стоками ребрами с нулевыми вероятностями ${{p}_{{ij}}}$ поражения. Предполагается, что эта процедура уже проделана и ориентированная сеть содержит единственный источник и сток. Заметим, что мы не накладываем априорно никаких ограничений на пропускную способность дуг.

Содержательно модель интерпретируется следующим образом: нападению нужно проникнуть из источника базирования к объекту обороны, представляющему сток, преодолев оборону в виде сети, которая задает возможные пути подлета к объекту. Каждая дуга сети интерпретируется как одно операционное направление, на котором нужно преодолеть локальную эшелонированную оборону противника. Результат боевого столкновения на одном рубеже обороны дается функцией

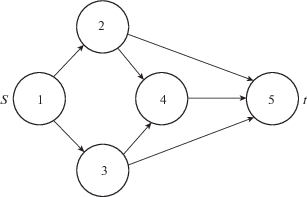
которая представляет собой результат дискретной одношаговой модели динамики средних Осипова–Ланчестера. Она получается следующим образом: количество средств нападения, получивших воздействие на данном рубеже, равно ${{n}_{{ij}}} = \min [{{x}_{{ij}}};{{u}_{{ij}}}]$ при условии, что на одно средство нападения назначается ровно одно средство обороны. Математическое количество потерь нападения составит ${{m}_{{ij}}} = {{p}_{{ij}}}{{n}_{{ij}}}$. В результате математическое ожидание числа прорвавшихся средств составит Итоговая формула для математического ожидания средств нападения, преодолевших все ${{T}_{{ij}}}$ рубежей, составит с учетом оптимизации для обороны распределения своих ${{u}_{{ij}}}$ средств по рубежам и выведена в [1]. Заметим, что в [11] был рассмотрен частный случай, когда который можно считать предельным при ${{T}_{{ij}}} \to \infty $, если ${{q}_{{ij}}} < 1$.

Пример 1. Рассмотрим орграф $G$ из [11], состоящей из множества вершин $N = \left\{ {1,2,3,4,5} \right\}$, $s = 1$, $t = 5$ и множества ориентированных ребер $L = \left\{ {(1,2),\left( {1,3} \right),\left( {2,4} \right),\left( {3,4} \right),\left( {2,5} \right),\left( {3,5} \right),\left( {4,5} \right)} \right\}$, представленный на фигуре. Требуется ранжировать его вершины.

Решение. Используя указанный алгоритм ранжирования вершин из (см. [12, с. 252]), получаем разбиение $N = \bigcup\nolimits_k^{} {{{N}_{k}}} $, где ${{N}_{0}} = \left\{ 1 \right\}$, ${{N}_{1}} = \left\{ {2,3} \right\}$, ${{N}_{2}} = \left\{ 4 \right\}$, ${{N}_{3}} = \left\{ 5 \right\}$.

2. МИНИМАКСНАЯ СТРАТЕГИЯ ОБОРОНЫ

Из выпуклости критерия по $u$ следует, что определенная на сети игра допускает исследование полученной игры в чистых и смешанных стратегиях по схеме [13]. Наилучший гарантированный результат (НГР) обороны, совпадающий со значением игры, равен

Все угловые точки множества $R$ описываются как множество точек вида

С учетом выпуклости функции $I(\rho ,u) = {{X}_{t}}$ по ${{\rho }^{i}} = (\rho _{j}^{i},j \in \pi (i))$ величину $\bar {v}$ можно записать в виде

Множество ${{R}_{0}}$ отображается на множество $\Omega $ путей $l$ из $s$ в $t$, т.е. последовательности дуг, примыкающих друг к другу с учетом их ориентации. Это отображение осуществляется следующим образом. Каждому элементу

соответствует однозначно направление движения из каждого узла, что приводит при выходе из источника к одному единственному пути из источника в сток. Соответствующий этой стратегии нападения поток (${{x}_{{ij}}}$, $(i,j) \in L$) будет отличен от нуля только на дугах, входящих в построенный путь. Обозначим через ${{\rho }^{{(l)}}}$ любой элемент ${{R}_{0}}$, переходящий в $l \in \Omega $ при указанном отображении. Тогда величину $\bar {v}$ можно записать в виде где

Таким образом, задача нахождения чистой оптимальной стратегии обороны состоит в нахождении такого $u$, принадлежащего множеству $V$, определенному в (2.2), которые реализуют минимум в (2.1). Такую стратегию обороны, следуя [5], назовем минимаксной, а задачу ее определения для краткости будем называть в дальнейшем задачей (2.1), (2.2).

3. СМЕШАННАЯ СТРАТЕГИЯ НАПАДЕНИЯ

Рассмотрим смешанную стратегию вида

где ${{I}_{{{{\rho }^{{(l)}}}}}}$ – вероятностная мера, сосредоточенная в точке ${{\rho }^{{(l)}}}$. Это означает содержательно, что нападение всеми силами действует по $l$-му пути с вероятностью $p_{l}^{0}$. Повторяя почти дословно доказательство леммы 2, из [4] получаем, что справедлива

Теорема 1. Для того чтобы стратегия ${{\varphi }_{0}}$ была оптимальной смешанной стратегией нападения, достаточно, чтобы

где

Таким образом, задача нахождения смешанной оптимальной стратегии нападения состоит в нахождении таких ${{p}^{0}}$, принадлежащих множеству $\Lambda $, определенному (3.2), которые реализуют максимум в (3.1). Эту задачу для краткости будем в дальнейшем обозначать (3.1), (3.2).

4. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НАХОЖДЕНИЯ ОПТИМАЛЬНЫХ СТРАТЕГИЙ СТОРОН

В силу выпуклости функций $I({{\rho }^{{(l)}}},u)$ по $u \in Y$ и линейности функций

по $p_{{}}^{0} \in \Lambda $ задачи (2.1), (2.2) и (3.1), (3.2) представляют собой задачи выпукло-вогнутого программирования и могут быть решены субградиентным методом. При этом нахождение субградиентов $g \in \partial I({{\rho }^{{(l)}}},u)$ функций $I({{\rho }^{{(l)}}},u)$ может быть сведено к решению двойственных задач линейного программирования по схеме, предложенной в [3].

Рассмотрим произвольный путь $l \in \Omega $ из $s$ в $t$

Тогда величину $I\left( {{{\rho }^{{(l)}}},u} \right) = {{x}_{T}}$ можно определить по рекуррентной формуле

Задачу определения $I({{\rho }^{{(l)}}},u) = {{x}_{L}}$ можно свести к вспомогательной задаче линейного программирования

Формально будем считать, что на переменные ${{x}_{k}}$ дополнительно наложены условия не отрицательности ${{x}_{k}} \geqslant 0$, которые очевидно выполняются автоматически. Матрица $A$ этой системы имеет вид представленной в следующей таблице.

Здесь через $(y,z)$, $y = ({{y}_{{ - 1}}},{{y}_{0}},\; \ldots ,\;{{y}_{{L - 1}}}) \in {{E}^{{L + 1}}}$, $z = ({{z}_{0}},\; \ldots ,\;{{z}_{{L - 1}}}) \in {{E}^{L}}$, обозначен вектор двойственных переменных.

Теперь можно записать двойственную задачу в виде

Здесь ${{A}_{1}}$, ${{A}_{2}}$ – подматрицы $A = (A_{1}^{*},A_{2}^{*}){\text{*}}$, $\{ {{p}_{k}}{{u}_{k}}\} \in {{E}^{L}}$ – вектор с координатами ${{p}_{k}}{{u}_{k}}$, $k = 0,\; \ldots ,\;L - 1$. Согласно формуле субградиента функции максимума в [14] имеет место формула где $\tilde {W} \subseteq W$ – подмножество решений множества $W$ допустимых решений двойственной задачи, ${{u}^{l}} = ({{u}_{0}},\; \ldots ,\;{{u}_{{L - 1}}})$. Заметим, что условие $(y,z) \in \tilde {W}(u)$ равносильно $z \in {{P}_{z}}(\tilde {W}(u))$, где ${{P}_{z}}(.)$ – оператор проектирования пространства ${{E}^{{L + 1}}} \otimes {{E}^{L}} \supset W$на вторую компоненту ${{E}^{L}}$, содержащую $z$.

Имея субдифференциал ${{\partial }_{{{{u}^{l}}}}}I({{\rho }^{{(l)}}},u)$ можно записать общий вид субградиента ${{g}^{l}} \in {{\partial }_{u}}I({{\rho }^{{(l)}}},u)$ можно записать в виде

и использовать его в субградиентном методе минимизации по $u$ при решении задач (2.1), (3.1) по схеме, предложенной в [15].

5. СУБГРАДИЕНТНЫЙ МЕТОД В ЗАДАЧЕ (2.1), (2.2)

Введем функцию внутреннего максимума в (2.1):

Лемма 1. Справедлива формула для субдифференциала $\partial L(u)$ выпуклой функции $L(u)$

где

Доказательство следует из той же формулы для субдифференциала функции максимума из [14].

Формула (5.1) позволяет решить максиминную задачу (2.1), (2.2) определения $\bar {v}$ методом субградиентного спуска. Введем функцию в ограничении $u \in Y$:

Функция $G(u)$ будет линейной и ее градиент $\nabla G(u) = (1,\; \ldots ,\;1)$ есть постоянный вектор. Имея градиент функции в ограничении $u \in Y$ для решения задачи выпуклого программирования (2.1), можно теперь воспользоваться комбинированным методом субградиентного спуска и проекции субградиентов (см. [15, с. 259]) с программным шагом

где $s$ – номер шага; ${{h}_{s}} = D{{s}^{{ - \alpha }}}$ – программный шаг метода, $0 < \alpha < 1$ – параметр, например $\alpha = 1{\text{/}}2$; $D$ – характерный размер множества $Y$ допустимых решений задачи, например оценка диаметра; ${{r}_{s}} = \nabla G(u(s))$; ${{\nu }^{s}} \in \partial L(u(s))$ – любой субградиент, – есть оператор проектирования на отрезок $[0,N]$.

Очевидно, что множество $Y$ допустимых решений задачи вогнутого программирования (2.1), (2.2) имеет внутренние точки, тогда в силу теоремы 7 в [15, с. 259] справедлива

Теорема 2. Все предельные точки последовательности $u(s)$ в методе (5.2) являются решениями задачи (2.1), (2.2).

6. СУБГРАДИЕНТНЫЙ МЕТОД В ЗАДАЧЕ (3.1), (3.2)

Введем функцию внутреннего минимума в (3.1):

Лемма 2. Функция минимума $M({{p}^{0}})$ с распадающимися переменными будет вогнутой и ее субдифференциал $\partial M({{p}^{0}})$ определяется по формуле

где

Доказательство следует из формулы для субдифференциала функции максимума из [14].

Полученная формула позволяет решить максиминную задачу (3.1) определения ${{p}^{0}}$ методом субградиентного подъема. Введем агрегированную функцию в ограничении ${{p}^{0}} \in \Lambda $:

Имея субградиенты функции внутреннего минимума (6.1) для решения задачи выпуклого программирования (3.1), можно теперь воспользоваться комбинированным методом субградиентного спуска и проекции субградиентов (см. [15, с. 259]) с программным шагом

где $s$ – номер шага; ${{h}_{s}} = K{{s}^{{ - \alpha }}}$ – программный шаг метода, $0 < \alpha < 1$ – параметр, например $\alpha = 1{\text{/}}2$; $K$ – характерный размер множества $\Lambda $ допустимых решений задачи, например оценка диаметра; ${{r}^{s}} = \nabla D(p(s))$; ${{\nu }^{s}} \in \partial M(p(s))$ – любой субградиент, есть оператор проектирования на отрезок $[0,1]$.

Очевидно, что множество $\Lambda $ допустимых решений задачи вогнутого программирования (3.1), (3.2) имеет внутренние точки, тогда в силу теоремы 7 из [15, с. 259] справедлива

Теорема 3. Все предельные точки последовательности $p(s)$ в методе (6.4) являются решениями задачи (3.1), (3.2).

Замечание 1. Для определения некоторого решения $u(s) \in \tilde {V}({{p}^{0}}(s))$ в выпуклой задаче минимизации (6.1) на каждом шаге также можно воспользоваться методом субградиентного подъема.

Введем функцию внутреннего минимума в (6.1)

Имея субдифференциал $\partial I({{\rho }^{{(l)}}},u)$ вогнутой функции $I({{\rho }^{{(l)}}},u)$, можно вычислить субдифференциал ${{\partial }_{u}}N(p,u)$ с использованием формулы для субдифференциала суммы из [15]:

что позволяет решить задачу нахождения любого решения $u \in \tilde {Y}({{p}^{0}})$ в выпуклой задаче минимизации (6.1) методом субградиентного спуска.

Воспользуемся ранее введенной агрегированной функцией $G(u)$ в ограничении $u \in Y$. Имея субградиенты агрегированной функции $G(u)$ для решения задачи определения некоторого решения $u \in \tilde {V}({{p}^{0}})$ в выпуклой задаче минимизации (6.1), можно теперь воспользоваться комбинированным методом субградиентного спуска и проекции субградиентов (см. [15, с. 259]) с программным шагом

где $s$ – номер шага; ${{h}_{s}} = D{{s}^{{ - \alpha }}}$ – программный шаг метода, $0 < \alpha < 1$ – параметр, например $\alpha = 1{\text{/}}2$; $D$ – характерный размер множества $Y$ допустимых решений задачи, например оценка диаметра; ${{r}^{s}} = \nabla G(V(s))$; ${{\nu }^{s}} \in {{\partial }_{u}}N(p,u(s))$ – любой субградиент, ${{P}_{{ij}}}({{u}_{{ij}}})$ – оператор проектирования на отрезок $[0,N]$.

Тогда в силу теоремы 7 из [15, с. 259] все предельные точки последовательности $u(s)$ в методе (6.6) принадлежат множеству (6.3).