1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 10, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 10, стр. 1643-1655

О выборе разностных схем при решении обратных коэффициентных задач

А. Ф. Албу 1, Ю. Г. Евтушенко 1, В. И. Зубов 1, *

1 ВЦ ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия

* E-mail: zubov@ccas.ru

Поступила в редакцию 31.01.2020
После доработки 21.03.2020
Принята к публикации 09.06.2020

Полный текст (PDF)

Аннотация

В работе проведены исследования, касающиеся выбора разностной схемы для аппроксимации уравнения диффузии тепла при решении обратной коэффициентной задачи в трехмерной постановке. На примере ряда нелинейных задач для трехмерного уравнения теплопроводности, коэффициенты которого зависят от температуры, проводится сравнительный анализ нескольких схем переменных направлений: локально-одномерной схемы, схемы Дугласа–Рекфорда и схемы Писмена–Рекфорда. Каждый численный метод использовался для получения распределения температуры внутри параллелепипеда. При сравнении методов принимались во внимание точность получаемого решения и время достижения требуемой точности на компьютере. Библ. 19. Фиг. 8.

Ключевые слова: нелинейные задачи, трехмерное уравнение теплопроводности, численные методы, схемы переменных направлений.

ВВЕДЕНИЕ

В работах [1]–[7] исследовалась обратная коэффициентная задача, посвященная вопросу идентификации зависящего от температуры коэффициента теплопроводности вещества. Рассмотрение проводилось на основе первой краевой задачи для одномерного и двумерного нестационарного уравнения теплопроводности. В качестве исследуемых объектов выступали стержень и прямоугольная пластина. Обратные коэффициентные задачи сводились к вариационным задачам. В указанных выше работах был предложен эффективный алгоритм их численного решения, основанный на использовании методологии Быстрого Автоматического Дифференцирования (см. [8]–[10]).

Одномерный и двумерный варианты рассмотренных обратных коэффициентных задач, безусловно, представляют большой математический интерес. Однако на практике, при сборе экспериментальных данных, имеют дело с трехмерными объектами. Поэтому задачу идентификации коэффициента теплопроводности следует решать в трехмерной постановке. Одним из основных элементов алгоритма решения обратной коэффициентной задачи является решение прямой задачи (определение температурного поля в любой точке объекта в любой момент времени). От эффективности ее решения зависит эффективность решения обратной задачи в целом.

В том случае, когда вариационная задача решается численно с привлечением методологии Быстрого Автоматического Дифференцирования, аппроксимация сопряженной задачи однозначно определяется выбором аппроксимации прямой задачи, и, как показало исследование обратной коэффициентной задачи в двумерной постановке, при переходе от одномерного случая к многомерному случаю влияние этого выбора становится более весомым. Так, если начально-краевая задача в двумерном случае аппроксимируется неявной схемой с весами (см. [3]), аппроксимация сопряженной задачи будет представлять собой линейную систему алгебраических уравнений, для разрешения которой (в силу двумерности по пространству) также требуется строить итерационный процесс. В связи с этим для решения прямой задачи в многомерном случае было рекомендовано использовать какую-либо экономичную разностную схему (см. [11]).

В работах [4]–[6] для аппроксимации уравнения теплопроводности была выбрана схема переменных направлений Писмена–Рекфорда, которая является безусловно устойчивой при рассмотрении задачи в двумерном пространстве (см. [12]). В этом случае для решения сопряженной задачи не требуется организовывать итерационный процесс. Полученная линейная система алгебраических уравнений расщепляется на ряд подсистем, каждая из которых решается эффективным методом прогонки.

Алгоритм решения прямой задачи в трехмерном случае еще больше усложняется и требует больших затрат машинного времени. Одним из способов сокращения времени расчетов является удачный выбор аппроксимации прямой задачи. В литературе встречается большое количество численных методов, которые могут быть использованы для решения уравнения диффузии тепла в трехмерном случае. Поэтому возникает естественный вопрос: какой метод выбрать для решения конкретной задачи?

Этот вопрос исследовался в работе Жюля Тибо (Jules Thibault) [13]. Там приведено практическое сравнение девяти наиболее распространенных разностных схем решения трехмерного уравнения теплопроводности. Каждый численный метод использовался для получения распределения температуры внутри параллелепипеда. Исследованные в работе [13] разностные схемы делятся на три основных класса: явные схемы, неявные схемы и схемы альтернативных (переменных) направлений. При сравнении схем принимались во внимание точность получаемого решения, легкость программирования, время вычисления и требуемая память компьютера. В итоге самыми эффективными для решения трехмерных задач теплопроводности были признаны методы переменных направлений. Свою эффективность эти методы подтвердили также и при исследовании многих практических задач, которые были решены на протяжении большого периода времени после опубликования упомянутой выше работы.

Сравнение численных методов в работе [13] проводилось для достаточно простой задачи, в которой все коэффициенты уравнения теплопроводности являлись постоянными. При решении обратных коэффициентных задач для нестационарного уравнения теплопроводности мы имеем дело с нелинейными задачами, т.к. при этом рассматриваются зависящие от температуры коэффициенты теплопроводности вещества. Однако в литературе мы нигде не нашли рекомендации, какому методу отдать предпочтение при решении такого рода задач, и решили исследовать этот вопрос. Кроме того, хотелось отметить и тот факт, что проведенные в [13] сравнения утратили свою значимость, т.к. там аппроксимация уравнения по пространству проводилась на шаблоне, который содержал слишком мало точек по каждому направлению (5 или 10 точек). Используемая сейчас вычислительная техника позволяет решать практические задачи на гораздо более подробных сетках.

В настоящей работе на примере нескольких нелинейных задач для трехмерного уравнения теплопроводности, коэффициенты которых зависят от температуры, проводится сравнительный анализ разностных схем переменных направлений, которые, на наш взгляд, следует использовать при решении задачи идентификации коэффициента теплопроводности вещества в трехмерном случае. Использовались локально-одномерные схемы, схема Дугласа–Рекфорда, схема Писмена–Рекфорда (см. [14]–[16]). При сравнении методов принимались во внимание точность получаемого решения и время достижения требуемой точности на компьютере.

Задача идентификации коэффициента теплопроводности вещества связана с исследованием характеристик новых создаваемых материалов. При проведении экспериментальных исследований используют, как правило, образцы материала простой формы (обычно это параллелепипед). Возникающую при этом обратную коэффициентную задачу в трехмерном случае разумно рассматривать также для объекта-параллелепипеда. Поэтому все используемые в работе численные методы применялись для получения распределения температуры внутри параллелепипеда на основе первой краевой задачи для трехмерного нестационарного уравнения теплопроводности.

1. ПОСТАНОВКА ЗАДАЧИ

Пусть образец исследуемого вещества имеет форму прямого параллелепипеда длины $R$, ширины $L$ и высоты $H$. Температура $T$ этого параллелепипеда в начальный момент времени известна. Известно также, как изменяется температура параллелепипеда на его гранях. Для математического описания процесса теплопроводности в параллелепипеде введем декартовы координаты $x,y$ и $z$. Точки $s = (x,y,z)$ параллелепипеда образуют область $Q = \left\{ {(0,R) \times (0,L) \times (0,H)} \right\}$ с границей $\Gamma = \partial Q$. Распределение температурного поля в параллелепипеде в каждый момент времени описывается решением следующей начально-краевой (смешанной) задачи:

(1.1)
$C(s)\frac{{\partial T(s,t)}}{{\partial t}} = {{\operatorname{div} }_{s}}\left( {K(T(s,t)) \cdot {{\nabla }_{s}}T(s,t)} \right),\quad (s,t) \in \left\{ {Q \times (0,\Theta )} \right\},$
(1.2)
$T(s,0) = {{w}_{0}}(s),\quad \quad \quad \quad \quad s \in \bar {Q},$
(1.3)
$T(s,t) = {{w}_{\Gamma }}(s,t),\quad \quad \quad s \in \Gamma ,\quad 0 \leqslant t \leqslant \Theta .$
Здесь $t$ – время; $T(s,t) \equiv T(x,y,z,t)$ – температура вещества в точке $s$ с координатами $(x,y,z)$ в момент времени $t$; $C(s)$ – объемная теплоемкость материала; $K(T)$ – коэффициент теплопроводности; ${{w}_{0}}(s)$ – заданная температура параллелепипеда в начальный момент времени $t = 0$; ${{w}_{\Gamma }}(s,t)$ – заданная температура на границе области. Объемная теплоемкость $C(s)$ рассматривается как известная функция координат.

Если зависимость коэффициента теплопроводности $K(T)$ от температуры $T$ известна, то, решив смешанную задачу (1.1)–(1.3), найдем распределение температуры $T(s,t)$ в любой точке области $Q \times (0,\Theta )$. Задачу (1.1)–(1.3) ниже будем называть прямой задачей.

2. АЛГОРИТМ РЕШЕНИЯ ПРЯМОЙ ЗАДАЧИ

Для численного решения прямой задачи вводятся временнáя и пространственная сетки (в общем случае, неравномерные).

Временнáя сетка задается набором узловых значений $\{ {{t}^{j}}\} _{{j = 0}}^{J}$, ${{t}^{0}} = 0$, ${{t}^{J}} = \Theta $. Шаги ${{\tau }^{j}}$ этой сетки определяются соотношениями ${{\tau }^{j}} = {{t}^{{j + 1}}} - {{t}^{j}}$, $j = \overline {0,J - 1} $.

Вводятся также две пространственные сетки: основная и вспомогательная. Для построения основной пространственной сетки на отрезке $[0,R]$ выбирается система “опорных” точек $\{ {{x}_{n}}\} _{{n = 0}}^{N}$ так, что ${{x}_{0}} = 0$, ${{x}_{N}} = R$ и ${{x}_{n}} < {{x}_{{n + 1}}}$ для всех $0 \leqslant n < N$. При этом $h_{n}^{x}$ – расстояние между опорными точками ${{x}_{n}}$ и ${{x}_{{n + 1}}}$, т.е. $h_{n}^{x} = {{x}_{{n + 1}}} - {{x}_{n}}$, $n = \overline {0,N - 1} $. Аналогично на отрезках $[0,L]$ и $[0,H]$ выбирается система “опорных” точек $\{ {{y}_{i}}\} _{{i = 0}}^{I}$ и $\{ {{z}_{l}}\} _{{l = 0}}^{L}$ так, что ${{y}_{0}} = 0$, ${{y}_{I}} = L$, ${{y}_{i}} < {{y}_{{i + 1}}}$ для всех $0 \leqslant i < I$ и ${{z}_{0}} = 0$, ${{z}_{L}}$ = H, ${{z}_{l}} < {{z}_{{l + 1}}}$ для всех $0 \leqslant l < L$ соответственно. При этом $h_{i}^{y} = {{y}_{{i + 1}}} - {{y}_{i}}$, $i = \overline {0,I - 1} $, $h_{l}^{z} = {{z}_{{l + 1}}} - {{z}_{l}}$, $l = \overline {0,L - 1} $. Точки основной сетки – совокупность точек $\{ {{x}_{n}},{{y}_{i}},{{z}_{l}}\} $, где $n = \overline {0,N} $, $i = \overline {0,I} $ и $l = \overline {0,L} $.

Вспомогательная сетка $\{ {{\tilde {x}}_{n}},{{\tilde {y}}_{i}},{{\tilde {z}}_{l}}\} $, $n = \overline {0,N + 1} $, $i = \overline {0,I + 1} $, $l = \overline {0,L + 1} $, строится похожим образом. Отличие состоит лишь в выборе опорных точек:

${{\tilde {x}}_{0}} = {{x}_{0}},\quad {{\tilde {x}}_{{N + 1}}} = {{x}_{N}},\quad {{\tilde {x}}_{n}} = {{x}_{{n - 1}}} + h_{{n - 1}}^{x}{\text{/}}2,\quad n = \overline {1,N} ,$
${{\tilde {y}}_{0}} = {{y}_{0}},\quad {{\tilde {y}}_{{I + 1}}} = {{y}_{I}},\quad {{\tilde {y}}_{i}} = {{y}_{{i - 1}}} + h_{{i - 1}}^{y}{\text{/}}2,\quad i = \overline {1,I} ,$
${{\tilde {z}}_{0}} = {{z}_{0}},\quad {{\tilde {z}}_{{L + 1}}} = {{z}_{L}},\quad {{\tilde {z}}_{l}} = {{z}_{{l - 1}}} + h_{{l - 1}}^{z}{\text{/}}2,\quad l = \overline {1,L} .$
Плоскости $x = {{\tilde {x}}_{n}}$, $y = {{\tilde {y}}_{i}}$, $z = {{\tilde {z}}_{l}}$ делят объект на параллелепипеды – так называемые расчетные ячейки. Расчетной ячейке будем приписывать индексы $\left( {n,i,l} \right)$, если вершина этой ячейки, наиближайшая к началу координат, совпадает с узловой точкой $\left( {{{{\tilde {x}}}_{n}},{{{\tilde {y}}}_{i}},{{{\tilde {z}}}_{l}}} \right)$, а объем этой ячейки будем обозначать через ${{V}_{{nil}}}$, т.е.

${{V}_{{nil}}} = \frac{{h_{n}^{x} + h_{{n - 1}}^{x}}}{2}\frac{{h_{i}^{y} + h_{{i - 1}}^{y}}}{2}\frac{{h_{l}^{z} + h_{{l - 1}}^{z}}}{2},\quad n = \overline {1,N - 1} ,\quad i = \overline {1,I - 1} ,\quad l = \overline {1,L - 1} .$

В основе алгоритма численного решения прямой задачи лежит использование уравнения теплового баланса для расчетной ячейки, который состоит в том, что изменение теплосодержания вещества в объеме ${{V}_{{nil}}}$ за фиксированный промежуток времени ${{\tau }^{j}} = {{t}^{{j + 1}}} - {{t}^{j}}$ равняется количеству тепла, проходящему через поверхность ${{S}_{{nil}}}$ объема ${{V}_{{nil}}}$ за этот же промежуток времени:

$\iiint\limits_{{{V}_{{nil}}}} {[E(x,y,z,{{t}^{{j + 1}}}) - E(x,y,z,{{t}^{j}})]{\kern 1pt} dV} = \int\limits_{{{t}^{j}}}^{{{t}^{{j + 1}}}} {\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{{{S}_{{nil}}}} {K(T){{T}_{n}}dSdt} } ,$
где $E(x,y,z,t)$ – плотность теплосодержания.

Обозначим среднюю температуру в ячейке с индексами $\left( {n,i,l} \right)$ через ${{T}_{{nil}}}\left( t \right)$, а через $T_{{nil}}^{j}$ – ее значение в момент времени ${{t}^{j}}$. Тогда последнее соотношение может быть приближенно записано в виде

(2.1)
$\begin{gathered} {{C}_{{nil}}} \cdot {{V}_{{nil}}} \cdot (T_{{nil}}^{{j + 1}} - T_{{nil}}^{j}) \cong \int\limits_{{{t}^{j}}}^{{{t}^{{j + 1}}}} {{{{\left\{ {\iint\limits_{S_{{nil}}^{{x + }}} {\left. {\left( {K(T)\frac{{\partial T}}{{\partial x}}} \right)} \right|}} \right.}}_{{x = {{{\tilde {x}}}_{{n + 1}}}}}}dydz} - {{\iint\limits_{S_{{nil}}^{{x - }}} {\left. {\left( {K(T)\frac{{\partial T}}{{\partial x}}} \right)} \right|}}_{{x = {{{\tilde {x}}}_{n}}}}}dydz + \\ + \;\iint\limits_{S_{{nil}}^{{y + }}} {{{{\left. {\left( {K(T)\frac{{\partial T}}{{\partial y}}} \right)} \right|}}_{{y = {{{\tilde {y}}}_{{n + 1}}}}}}dxdz} - \iint\limits_{S_{{nil}}^{{y - }}} {{{{\left. {\left( {K(T)\frac{{\partial T}}{{\partial y}}} \right)} \right|}}_{{y = {{{\tilde {y}}}_{n}}}}}dxdz + }\iint\limits_{S_{{nil}}^{{z + }}} {{{{\left. {\left( {K(T)\frac{{\partial T}}{{\partial z}}} \right)} \right|}}_{{z = {{{\tilde {z}}}_{{n + 1}}}}}}dxdy} - \\ \, - \left. {\iint\limits_{S_{{nil}}^{{z - }}} {{{{\left. {\left( {K(T)\frac{{\partial T}}{{\partial z}}} \right)} \right|}}_{{z = {{{\tilde {z}}}_{n}}}}}dxdy}} \right\}dt. \\ \end{gathered} $
Здесь через $S_{{nil}}^{{x + }}$ обозначена часть поверхности $S_{{nil}}^{{}}$, которая принадлежит плоскости $x = {{\tilde {x}}_{{n + 1}}}$, через $S_{{nil}}^{{x - }}$ обозначена часть поверхности $S_{{nil}}^{{}}$, принадлежащая плоскости $x = {{\tilde {x}}_{n}}$. Аналогично определяются остальные части поверхности ячейки: $S_{{nil}}^{{y + }}$, $S_{{nil}}^{{y - }}$, $S_{{nil}}^{{z + }}$ и $S_{{nil}}^{{z - }}$. Тепловой поток на грани $x = {{\tilde {x}}_{{n + 1}}}$ расчетной ячейки в момент времени $t$ аппроксимируем по формуле
${{\left. {\left( {K(T)\frac{{\partial T}}{{\partial x}}} \right)} \right|}_{{x = {{{\tilde {x}}}_{{n + 1}}}}}} \cong \frac{{K({{T}_{{n + 1,il}}}(t)) + K({{T}_{{nil}}}(t))}}{2}\frac{{{{T}_{{n + 1,il}}}(t) - {{T}_{{nil}}}(t)}}{{h_{n}^{x}}}$.
Потоки тепла на остальных гранях ячейки аппроксимируются аналогичным образом. Тогда уравнение теплового баланса (2.1) может быть аппроксимировано в виде
(2.2)
${{C}_{{nil}}} \cdot {{V}_{{nil}}} \cdot (T_{{nil}}^{{j + 1}} - T_{{nil}}^{j}) = \int\limits_{{{t}^{j}}}^{{{t}^{{j + 1}}}} {[\Lambda _{x}^{{}}{{T}_{{nil}}}(t) + \Lambda _{y}^{{}}{{T}_{{nil}}}(t) + \Lambda _{z}^{{}}{{T}_{{nil}}}(t)]{\kern 1pt} dt} ,$
где
$\Lambda _{x}^{{}}{{T}_{{nil}}}(t) = \left[ {\frac{{K({{T}_{{n + 1,il}}}(t)) + K({{T}_{{nil}}}(t))}}{2}\frac{{{{T}_{{n + 1,il}}}(t) - {{T}_{{nil}}}(t)}}{{h_{n}^{x}}}} \right. - \left. {\frac{{K({{T}_{{n,il}}}(t)) + K({{T}_{{n - 1,il}}}(t))}}{2}\frac{{{{T}_{{nil}}}(t) - {{T}_{{n - 1,il}}}(t)}}{{h_{{n - 1}}^{x}}}} \right]S_{{il}}^{{yz}},$
$\Lambda _{y}^{{}}{{T}_{{nil}}}(t) = \left[ {\frac{{K({{T}_{{n,i + 1,l}}}(t)) + K({{T}_{{nil}}}(t))}}{2}\frac{{{{T}_{{n,i + 1,l}}}(t) - {{T}_{{nil}}}(t)}}{{h_{i}^{y}}}} \right. - \left. {\frac{{K({{T}_{{n,il}}}(t)) + K({{T}_{{n,i - 1,l}}}(t))}}{2}\frac{{{{T}_{{nil}}}(t) - {{T}_{{n,i - 1,l}}}(t)}}{{h_{{i - 1}}^{y}}}} \right]S_{{nl}}^{{xz}},$
$\Lambda _{z}^{{}}{{T}_{{nil}}}(t) = \left[ {\frac{{K({{T}_{{ni,l + 1}}}(t)) + K({{T}_{{nil}}}(t))}}{2}\frac{{{{T}_{{ni,l + 1}}}(t) - {{T}_{{nil}}}(t)}}{{h_{l}^{z}}}} \right. - \left. {\frac{{K({{T}_{{nil}}}(t)) + K({{T}_{{ni,l - 1}}}(t))}}{2}\frac{{{{T}_{{nil}}}(t) - {{T}_{{ni,l - 1}}}(t)}}{{h_{{l - 1}}^{z}}}} \right]S_{{ni}}^{{xy}},$
$S_{{il}}^{{yz}} = \frac{{h_{i}^{y} + h_{{i - 1}}^{y}}}{2}\frac{{h_{l}^{z} + h_{{l - 1}}^{z}}}{2},\quad S_{{nl}}^{{xz}} = \frac{{h_{n}^{x} + h_{{n - 1}}^{x}}}{2}\frac{{h_{l}^{z} + h_{{l - 1}}^{z}}}{2},\quad S_{{ni}}^{{xy}} = \frac{{h_{n}^{x} + h_{{n - 1}}^{x}}}{2}\frac{{h_{i}^{y} + h_{{i - 1}}^{y}}}{2}.$
Далее, в зависимости от того, каким образом аппроксимируется по времени уравнение (2.2), получаем ту или другую разностную схему, с помощью которой решается прямая задача (1.1)–(1.3).

Опыт исследования задачи идентификации коэффициента теплопроводности в двумерной постановке позволил сделать вывод о том, что при решении многомерных обратных коэффициентных задач желательно использовать одну из схем переменных направлений (см. [17]). Наиболее популярными среди них являются локально-одномерные схемы, схема Дугласа–Рекфорда и схема Писмена–Рекфорда. Наряду с основными значениями искомой сеточной функции $T_{{nil}}^{j}$ в указанных выше схемах используются еще два промежуточных значения $T_{{nil}}^{{j + 1/3}}$ и $T_{{nil}}^{{j + 2/3}}$ функции температуры, которые можно формально рассматривать как значения температуры в момент времени ${{t}^{j}} + {{\tau }^{j}}{\text{/}}3$ и ${{t}^{j}} + 2{{\tau }^{j}}{\text{/}}3$ (см. [11]).

Для более компактной записи разностных схем введем следующее обозначение:

$\Lambda _{{_{x}}}^{p}(T_{{nil}}^{j}) = \left[ {\frac{{K(T_{{n + 1,il}}^{p}) + K(T_{{nil}}^{p})}}{2}\frac{{T_{{n + 1,il}}^{j} - T_{{nil}}^{j}}}{{h_{n}^{x}}} - \frac{{K(T_{{nil}}^{p}) + K(T_{{n - 1,il}}^{p})}}{2}\frac{{T_{{nil}}^{j} - T_{{n - 1,il}}^{j}}}{{h_{{n - 1}}^{x}}}} \right]S_{{il}}^{{yz}},$
которое будем использовать для временнóй дискретизации оператора $\Lambda _{x}^{{}}{{T}_{{nil}}}(t)$. Аналогичные обозначения: $\Lambda _{y}^{p}{{T}_{{nil}}}$ и $\Lambda _{z}^{p}{{T}_{{nil}}}$ вводятся и для временнóй дискретизации операторов $\Lambda _{y}^{{}}{{T}_{{nil}}}(t)$ и $\Lambda _{z}^{{}}{{T}_{{nil}}}(t)$.

Локально-одномерная схема имеет вид:

$x$ – направление

$\frac{{{{V}_{{nil}}}{{C}_{{nil}}}(T_{{nil}}^{{j + 1/3}} - T_{{nil}}^{j})}}{{{{\tau }^{j}}{\text{/}}3}} = \Lambda _{{_{x}}}^{p}(T_{{nil}}^{{j + 1/3}}),$

$y$ – направление

$\frac{{{{V}_{{nil}}}{{C}_{{nil}}}(T_{{nil}}^{{j + 2/3}} - T_{{nil}}^{{j + 1/3}})}}{{{{\tau }^{j}}{\text{/}}3}} = \Lambda _{{_{y}}}^{q}(T_{{nil}}^{{j + 2/3}}),$

$z$ – направление

$\frac{{{{V}_{{nil}}}{{C}_{{nil}}}(T_{{nil}}^{{j + 1}} - T_{{nil}}^{{j + 2/3}})}}{{{{\tau }^{j}}{\text{/}}3}} = \Lambda _{{_{z}}}^{r}(T_{{nil}}^{{j + 1}})$
$(n = \overline {1,N - 1,} \;\;i = \overline {1,I - 1} ,\;\;l = \overline {1,L - 1} ,\;\;j = \overline {0,J - 1} ).$
Как отмечено в [15], при дополнительных предположениях относительно ограниченности вторых производных искомой функции эту схему можно рассматривать в двух вариантах:

а) коэффициенты теплопроводности вычисляются на предыдущем подслое времени, где значения температуры известны, т.е. $p = j,$ $q = j + 1{\text{/}}3,$ $r = j + 2{\text{/}}3$ (явная схема);

б) коэффициенты теплопроводности вычисляются на текущем подслое времени: $p = j + 1{\text{/}}3,$ $q = j + 2{\text{/}}3,$ $r = j + 1$ (неявная схема).

В первом случае на каждом этапе получаются линейные уравнения, которые решаются методом прогонки. Во втором случае на каждом этапе для определения неизвестной функции получается нелинейное уравнение, которое решается тем или иным итерационным методом. На текущей итерации коэффициенты вычисляются по значениям температуры с предыдущей итерации, а неизвестная функция определяется с помощью метода прогонки.

Схема Дугласа–Рекфорда:

$x$ – направление

$\frac{{{{V}_{{nil}}}{{C}_{{nil}}}(T_{{nil}}^{{j + 1/3}} - T_{{nil}}^{j})}}{{{{\tau }^{j}}}} = \Lambda _{{_{x}}}^{{j + 1/3}}(T_{{nil}}^{{j + 1/3}}) + \Lambda _{{_{y}}}^{j}(T_{{nil}}^{j}) + \Lambda _{{_{z}}}^{j}(T_{{nil}}^{j}),$

$y$ – направление

$\frac{{{{V}_{{nil}}}{{C}_{{nil}}}(T_{{nil}}^{{j + 2/3}} - T_{{nil}}^{{j + 1/3}})}}{{{{\tau }^{j}}}} = \Lambda _{{_{y}}}^{{j + 2/3}}(T_{{nil}}^{{j + 2/3}}) - \Lambda _{{_{y}}}^{j}(T_{{nil}}^{j}),$

$z$ – направление

$\frac{{{{V}_{{nil}}}{{C}_{{nil}}}(T_{{nil}}^{{j + 1}} - T_{{nil}}^{{j + 2/3}})}}{{{{\tau }^{j}}}} = \Lambda _{{_{z}}}^{{j + 1}}(T_{{nil}}^{{j + 1}}) - \Lambda _{{_{z}}}^{j}(T_{{nil}}^{j})$
$(n = \overline {1,N - 1,} \;\;i = \overline {1,I - 1} ,\;\;l = \overline {1,L - 1} ,\;\;j = \overline {0,J - 1} ).$
Указанные выше схемы являются устойчивыми и наиболее часто используются исследователями на практике.

Приведенная ниже схема Писмена–Рекфорда для трехмерного уравнения теплопроводности является условно устойчивой:

$x$ – направление

$\frac{{{{V}_{{nil}}}{{C}_{{nil}}}(T_{{nil}}^{{j + 1/3}} - T_{{nil}}^{j})}}{{{{\tau }^{j}}{\text{/}}3}} = \Lambda _{{_{x}}}^{j}(T_{{nil}}^{{j + 1/3}}) + \Lambda _{{_{y}}}^{j}(T_{{nil}}^{j}) + \Lambda _{{_{z}}}^{j}(T_{{nil}}^{j}),$

$y$ – направление

$\frac{{{{V}_{{nil}}}{{C}_{{nil}}}(T_{{nil}}^{{j + 2/3}} - T_{{nil}}^{{j + 1/3}})}}{{{{\tau }^{j}}{\text{/}}3}} = \Lambda _{{_{x}}}^{j}(T_{{nil}}^{{j + 1/3}}) + \Lambda _{{_{y}}}^{j}(T_{{nil}}^{{j + 2/3}}) + \Lambda _{{_{z}}}^{j}(T_{{nil}}^{{j + 1/3}}),$

$z$ – направление

$\frac{{{{V}_{{nil}}}{{C}_{{nil}}}(T_{{nil}}^{{j + 1}} - T_{{nil}}^{{j + 2/3}})}}{{{{\tau }^{j}}{\text{/}}3}} = \Lambda _{{_{x}}}^{j}(T_{{nil}}^{{j + 2/3}}) + \Lambda _{{_{y}}}^{j}(T_{{nil}}^{{j + 2/3}}) + \Lambda _{{_{z}}}^{j}(T_{{nil}}^{{j + 1}})$
$(n = \overline {1,N - 1,} \;\;i = \overline {1,I - 1} ,\;\;l = \overline {1,L - 1} ,\;\;j = \overline {0,J - 1} ).$

В работе [1], [12] с помощью критерия фон Неймана проведен анализ устойчивости разностной схемы Писмена–Рекфорда для $n$-мерного уравнения теплопроводности. Там показано, что при $n \geqslant 3$ эта схема является условно устойчивой даже в случае, когда коэффициенты уравнения не зависят от температуры. Она требует работы с гораздо более мелким шагом по времени, чем первые три схемы. Но именно этот факт позволяет использовать для определения коэффициента теплопроводности на текущем подслое известное значение температуры на предыдущем временном слое, т.е. работать с указанным выше безытерационным вариантом этой схемы.

Которой из этих схем и в каких случаях отдать предпочтение, постараемся выяснить на основе проведенных численных расчетов, результаты которых представлены ниже.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Было проведено огромное количество численных экспериментов, касающихся решения первой краевой задачи для трехмерного нелинейного уравнения теплопроводности с разными входными данными. Наиболее характерные из них приводятся в этом разделе в виде трех серий расчетов.

Во всех случаях, когда для численного решения задачи использовались итерационные разностные схемы (второй вариант локально-одномерной схемы и схема Дугласа–Рекфорда), итерации продолжались до тех пор, пока не выполнялось следующее условие: максимальное относительное отклонение температуры на текущей и на предыдущей итерации меньше, чем 10–14.

Отрезок температур $[a,b]$, на котором аппроксимировался коэффициент теплопроводности, определялся как множество значений функций ${{w}_{0}}(x,y,z)$ и ${{w}_{\Gamma }}(x,y,z,t)$. Отрезок $[a,b]$ разбивался точками ${{T}_{0}} = a$, ${{T}_{1}}$, ${{T}_{2}}$, …, ${{T}_{M}} = b$ на $M = 80$ равных частей, а функция $K(T)$ аппроксимировалась непрерывной кусочно-линейной функцией таким образом, как это показано в [4]. Если в процессе решения задачи температура в точке выходила за границы отрезка $[a,b]$, то для определения функции $K(T)$ использовалась линейная экстраполяция.

Все расчеты проводились на четырех равномерных пространственных сетках с одинаковым шагом по каждому пространственному направлению, равным ${\text{1/}}N$ (N = 25, 50, 100, 200). В тех случаях, когда для решения прямой задачи использовалась устойчивая схема, величина $\tau $ шага по времени варьировалась в довольно больших (допустимых) пределах: для каждой пространственной сетки расчеты проводились при $\tau = {\text{0}}{\text{.1}}$, 0.04, 0.02, 0.01, 0.002, 0.001. В случае использования для дискретизации по времени схемы Писмена–Рекфорда, величина временного шага $\tau $ выбиралась для каждой пространственной сетки самостоятельно c учетом выполнения критерия устойчивости. При выбранной пространственно-временной сетке с помощью описанных выше конечно-разностных схем определялось численное решение смешанной задачи, и оно сравнивалось с аналитическим решением. В качестве меры отклонения вычисленного решения от аналитического использовалась норма $C{\text{([}}a{\text{,}}\,b{\text{])}}$.

3.1. Первая серия расчетов

В первой серии расчетов рассматривался вариант, когда объемная теплоемкость $C(s) = 1$, а коэффициент теплопроводности $K(T)$ линейно зависел от $T$. Этот пример – простейший из всех рассмотренных. Целью первой серии расчетов является не только сравнить исследуемые разностные схемы, но и проверить корректность созданных машинных кодов, реализующих рассматриваемые алгоритмы.

Численные эксперименты базировались на функции

(3.1)
$T(x,y,z,t) = Ax + By + Cz + ({{A}^{2}} + {{B}^{2}} + {{C}^{2}})t + D,$
где $A$, $B$, $C$, $D$ – произвольные константы. Область $Q \times (0,\Theta )$ определения функции (3.1) и параметры $A$, $B$, $C$, $D$ выбирались так, чтобы $\forall (s,t) \in \bar {Q} \times [0,\Theta ]$ функция (3.1) была определена и положительна.

Если в качестве начальной функции ${{w}_{0}}(x,y,z)$ и граничной функции ${{w}_{\Gamma }}(x,y,z,t)$ выбрать след функции (3.1) на параболической границе области $Q \times (0,\Theta )$, то, как нетрудно проверить, функция (3.1) является решением смешанной задачи (1.1)–(1.3) при $C(s) = 1$ и $K(T) = T$.

Расчеты проводились при следующем наборе параметров: $A = B = C = 1$, $D = 0.5$, а область $Q \times (0,\Theta ) = (0,1) \times (0,1) \times (0,1) \times (0,1)\,$. При таких параметрах температура на параболической границе рассматриваемой области изменялась от $a = {\text{0}}{\text{.5}}$ до $b = 6.{\text{5}}$.

Следует отметить, что при этом средняя температура объекта в начальный момент времени $t = 0$ равна примерно 2.0, а в последний момент времени $t = 1$ примерно равна 5.0. Таким образом, температурное поле в рассматриваемом объекте на протяжении временного отрезка $[0,1]$ меняется в 2.5 раза.

В этой серии экспериментов точность получаемых численных решений с помощью всех четырех разностных схем на всех пространственных сетках оказалась очень высокая. Она варьируется от ${{10}^{{ - 14}}}$ до ${{10}^{{ - 15}}}$ в норме $C$ и зависит, в основном, от величины $\tau $ шага по времени. Что касается требуемого машинного времени, то для этого примера самой эффективной оказалась безытерационная локально-одномерная схема.

3.2. Вторая серия расчетов

Во второй серии расчетов рассматривался вариант, когда объемная теплоемкость $C(s) = 1$, а коэффициент теплопроводности $K(T) = \frac{1}{T}$.

Численные эксперименты базировались здесь на функции

(3.2)
$T(x,y,z,t) = - \frac{{(k_{1}^{2} + k_{2}^{2} + k_{3}^{2})}}{{\lambda ({{k}_{1}}x + {{k}_{2}}y + {{k}_{3}}z + \lambda t + A)}},$
где ${{k}_{1}}$, ${{k}_{2}}$, ${{k}_{3}}$, $\lambda $, $A$ – произвольные константы. Область $Q \times (0,\Theta )$ определения функции (3.2) и параметры ${{k}_{1}}$, ${{k}_{2}}$, ${{k}_{3}}$, $\lambda $, $A$ выбирались таким образом, чтобы $\forall (s,t) \in \bar {Q} \times [0,\Theta ]$ функция (3.2) была определена и положительна.

Если в качестве начальной функции ${{w}_{0}}(x,y,z)$ и граничной функции ${{w}_{\Gamma }}(x,y,z,t)$ выбрать след функции (3.2) на параболической границе области $Q \times (0,\Theta )$, то, как нетрудно проверить, функция (3.2) является решением смешанной задачи (1.1)–(1.3) при $C(s) = 1$ и $K(T) = \frac{1}{T}$.

Результаты расчетов, приведенные ниже, соответствуют следующему набору параметров: ${{k}_{1}} = {{k}_{2}} = {{k}_{3}} = 1$, $\lambda = 1.8$, $A = - 5$, а область $Q \times (0,\Theta ) = (0,1) \times (0,1) \times (0,1) \times (0,1)\,$. При таких параметрах температура на параболической границе рассматриваемой области изменяется от $a = {\text{0}}{\text{.3339}}$ до $b = {\text{8}}{\text{.3331}}$.

Следует отметить, что при этом средняя температура объекта в начальный момент времени $t = 0$ равна примерно 0.49, а в последний момент времени $t = \Theta $ равна 1.11. Таким образом, температурное поле в рассматриваемом объекте на протяжении временного отрезка $[0,1]$ меняется примерно в 2.3 раза.

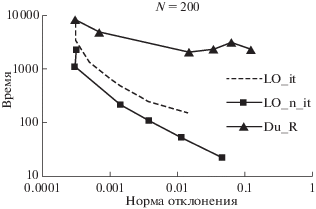
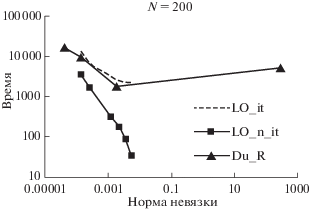
На фиг. 1–4 представлены зависимости машинного времени, затраченного на решение прямой задачи с помощью разных схем и при разных $\tau $, от точности полученного решения. На всех графиках изображены поведения трех устойчивых схем. Через LO_it обозначена неявная локально одномерная схема, через LO_n_it – явная локально одномерная схема, а через Du_R – схема Дугласа–Рекфорда. Поведение условно-устойчивой схемы Писмена–Рекфорда описывается отдельно. При построении графиков везде использовалась логарифмическая шкала формата оси.

Указанная на фигурах величина нормы отклонения зависит от величины шага по времени, при котором проводился соответственный расчет, т.е. каждая отмеченная точка на графиках была получена при некотором определенном значении $\tau $.

3.3. Третья серия расчетов

В третьей серии рассматривается уравнение теплопроводности (1.1), в которой объемная теплоемкость $C(s) = 1$ и коэффициент теплопроводности $K(T) = \alpha {{T}^{n}}$, где $\alpha > 0$ – произвольное заданное положительное число, $n \ne 0$ – произвольное заданное действительное число. Функция

(3.3)
$T(t,x,y,z) = {{\left( {\frac{{A{{n}^{2}}}}{{2(3n + 2)(B - \alpha Ant)}}({{x}^{2}} + {{y}^{2}} + {{z}^{2}})} \right)}^{{1/n}}},$
где $A$ и $B$ – произвольные действительные константы, является решением уравнения (1.1) с указанными выше коэффициентами.

Как и в предыдущих примерах, при формулировке смешанной задачи (1.1)–(1.3) в качестве начальной функции ${{w}_{0}}(x,y,z)$ и граничной функции ${{w}_{\Gamma }}(x,y,z,t)$ выбирался след функции (3.3) на параболической границе области $Q \times (0,\Theta )$.

При проведении расчетов были использованы следующие значения входных данных:

$\alpha = 1,\quad n = 2,\quad A = 1,\quad B = 3,$
$Q = \left\{ {0 < x < 1,\;1 < y < 2,\;2 < z < 3} \right\},\quad 0 < t < 1.$

Определив минимальное и максимальное значения температур на параболической границе рассматриваемой области, получаем отрезок температур, на котором аппроксимируется коэффициент теплопроводности: $[{\text{0}}{\text{.645498}},\;{\text{1}}{\text{.8708}}]$.

Температурное поле в этом примере меняется не настолько динамично, как во второй серии расчетов. Средняя температура объекта в начальный момент времени равна примерно 0.8, а на последнем временном слое – примерно 1.5, т.е. температурное поле в объекте на протяжении всего временного отрезка меняется почти в 2 раза.

На фиг. 5–8, как и выше, представлены зависимости времени расчета, необходимого для вычисления решения с заданной точностью, от этой точности.

3.4. Анализ полученных результатов

Первая серия численных экспериментов показала, что созданные расчетные коды корректны и что все рассматриваемые разностные схемы в простейших вариантах позволяют получить решение задачи с практически машинной точностью за сопоставимое машинное время.

Что касается более сложных вариантов (вторая и третья серии расчетов), то анализ результатов численных экспериментов показывает, что точности решений, получаемых с помощью локально-одномерной схемы и схемы Дугласа–Рекфорда, при одних и тех же параметрах могут сильно отличаться друг от друга, и это несмотря на то, что обе эти схемы являются устойчивыми.

Так, использование как явного, так и неявного вариантов локально-одномерной схемы на всех рассматриваемых пространственных сетках и при всех $\tau \leqslant 0.1$ позволяет получить численное решение задачи, отличающееся от точного решения не более, чем на 5%. Если же проводить расчеты с шагом по времени $\tau \leqslant 0.04$, то для всех пространственных сеток отклонения численного решения от точного составляет менее 1%.

Фиг. 1.
Фиг. 2.
Фиг. 3.
Фиг. 4.
Фиг. 5.
Фиг. 6.
Фиг. 7.
Фиг. 8.

Схема Дугласа–Рекфорда проявила себя как более “капризная”. Так, численные решения смешанной задачи (1.1)–(1.3) из второй серии расчетов, полученные с ее помощью при $\tau = 0.1$ и $N = 100$, $N = 200$, отличаются от точного решения задачи примерно на 12%. Если же соответствующие расчеты проводить с шагом по времени $\tau = 0.04$, то отклонение от точного решения составляет примерно 6%. Что касается примера из третьей серии расчетов, то в этом случае решение задачи с помощью схемы Дугласа–Рекфорда при $\tau = 0.1$ можно получить только на пространственной сетке с $N = 25$. На пространственной сетке с $N = 50$ при $\tau = 0.1$ отклонение численного решения от точного – более 80% (см. фиг. 6). На пространственной сетке с $N = 200$ нельзя использовать эту схему даже при $\tau = 0.02$ (см. фиг. 8). С другой стороны, как показывают результаты третьей серии расчетов, при небольших шагах по времени $\tau $ (например, $\tau = 0.001$) с помощью схемы Дугласа–Рекфорда на всех пространственных сетках можно получить решение задачи с точностью почти на порядок большей (точность равна примерно 0.004%), чем с помощью локально-одномерной схемы. Таким образом, точность получаемого с помощью схемы Дугласа–Рекфорда численного решения сильнее зависит от выбора шага по времени, чем в случае использования других устойчивых схем.

Сравнивая между собой локально-одномерные схемы и схему Дугласа–Рекфорда на основе результатов всех проведенных расчетов, можно сделать вывод, что свойства этих схем качественно похожи, но самой эффективной из них является безытерационная локально-одномерная схема.

Заметно отличается от них схема Писмена–Рекфорда. Эта схема является условно устойчивой, что требует использования гораздо более мелкого шага по времени, чем остальные рассматриваемые схемы. Поэтому ее целесообразно применять в тех случаях, когда расчеты проводятся на сравнительно грубых пространственных сетках (20–50 узлов по каждому направлению). Если при этом расчеты проводятся с временным шагом, лишь немного меньшим допустимого для устойчивой работы схемы, то решение задачи получается быстро и с высокой точностью. Лучший результат (точность 0.03%) для примера из второй серии расчетов получается с помощью схемы Писмена–Рекфорда (на сетке $N = 25$ при $\tau $ = 1/1050) примерно за то же время, что и с помощью локально-одномерной схемы. Схема Дугласа–Рекфорда требует заметно больше машинного времени для достижения такой точности.

Что касается примера из третьей серии расчетов, то, как было отмечено выше, лучший результат, который получен с помощью устойчивых схем – это точность 0.004% (с помощью схемы Дугласа–Рекфорда). Однако примерно за такое же машинное время с помощью схемы Писмена–Рекфорда на грубой сетке ($N = 25$) при $\tau $ = 1/3200 было получено решение задачи с точностью 0.0004%, т.е. на порядок лучше. Такая высокая точность не была получена с помощью никакой другой из указанных выше схем. Необходимо отметить, что если использовать более мелкую пространственно-временную сетку ($N = 50$), то с помощью схемы Писмена–Рекфорда можно получить решение задачи с точностью 0.00005%. Время, которое было потрачено для получения такой точности, примерно такое же, которое было потрачено для достижения точности 0.004% с помощью схемы Дугласа–Рекфорда на пространственной сетке $N = 100$.

Следует отметить также следующее. Во всех проведенных расчетах коэффициент теплопроводности $K(T)$ аппроксимировался непрерывной кусочно-линейной функцией с равноотстоящими узлами при $M = 80$. Как показали расчеты, точность получаемых результатов можно увеличить в несколько раз, если при аппроксимации коэффициента теплопроводности количество интервалов на отрезке температур увеличить в два раза ($M = 160$).

ЗАКЛЮЧЕНИЕ

Выбор эффективной разностной схемы очень важен при решении обратных и оптимизационных задач, когда прямая задача решается при разных значениях параметров большое количество раз. Эффективность той или иной схемы сильно зависит от динамики температурного поля.

Для решения трехмерного уравнения теплопроводности многие исследователи рекомендуют использовать либо один из вариантов локально одномерной схемы, либо схему Дугласа–Рекфорда, т.к. обе эти схемы являются устойчивыми. Однако результаты исследования, приведенные в этой работе, показали, что нередко самой эффективной (высокая точность при небольших затратах машинного времени) при решении прямой задачи на грубых пространственных сетках является схема Писмена–Рекфорда, несмотря на тот факт, что она требует проводить вычисления с очень мелким шагом по времени. Авторами настоящей статьи был проведен цикл работ (см., например, [18], [19]), касающихся оптимизации процесса кристаллизации металла в литейном деле. В результате многочисленных исследований для решения прямой задачи в указанных работах была выбрана именно схема Писмена–Рекфорда, которая хорошо себя зарекомендовала.

Конечно, на разных задачах рассмотренные схемы могут вести себя по-разному. Поэтому при решении конкретной обратной задачи следует выбирать подходящую разностную схему на основе решения прямых тестовых задач.

Как показали проведенные численные расчеты, схема Писмена–Рекфорда на грубых пространственных сетках при временном шаге, близком к максимально допустимому, позволяет получить высокую точность расчетов. Поэтому мы рекомендуем вначале решить обратную задачу на грубой пространственной сетке (20–30 узлов по каждому направлению), используя схему Писмена–Рекфорда. Затем, имея уже хорошее приближение к решению обратной задачи, выбирать расчетную сетку и разностную схему, исходя из требуемой точности конечного результата.

Список литературы

  1. Зубов В.И. Применение методологии быстрого автоматического дифференцирования к решению обратной коэффициентной задачи для уравнения теплопроводности // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 10. С. 1760–1774.

  2. Albu A.F., Evtushenko Y.G., Zubov V.I. Identification of Discontinuous Thermal Conductivity Coefficient Using Fast Automatic Differentiation. In: Battiti R., Kvasov D., Sergeyev Y. (eds) Learning and Intelligent Optimization. LION 2017. Lecture Notes in Computer Science, 2017. V. 10556. P. 295–300. Springer, Cham.

  3. Zubov V.I., Albu A.F. The FAD-methodology and Recovery the Thermal Conductivity Coefficient in Two Dimension Case. Proc. of the VIII Internat. Conference on Optimizat. Meth. and Appl. “Optimization and applications”. 2017. P. 39–44.

  4. Албу А.Ф., Зубов В.И. О восстановлении коэффициента теплопроводности вещества по температурному полю // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 10. С. 1642–1657.

  5. Албу А.Ф., Зубов В.И. Восстановление коэффициента теплопроводности вещества по поверхностному тепловому потоку // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 12. С. 1992–2017.

  6. Albu A., Zubov V. Identification of the thermal conductivity coefficient in two dimension case // Optim. Lett. 2018. P. 1–17.

  7. Albu A., Zubov V. On the Stability of the Algorithm of Identification of the Thermal Conductivity Coefficient. In: Evtushenko Y., Jaćimović M., Khachay M., Kochetov Y., Malkova V., Posypkin M. (eds) Optimizat. and Appl. OPTIMA 2018. Communications in Computer and Information Science, vol. 974. Springer, Cham, 2019. P. 247–263.

  8. Евтушенко Ю.Г. Оптимизация и быстрое автоматическое дифференцирование. М.: ВЦ им. А.А. Дородницына РАН, 2013. 144 с.

  9. Евтушенко Ю.Г., Зубов В.И. Об обобщенной методологии быстрого автоматического дифференцирования // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 11. С. 1847–1862.

  10. Albu A., Evtushenko Y., Zubov V. On Optimization Problem Arising in Computer Simulation of Crystal Structures. In: Jaćimović M., Khachay M., Malkova V., Posypkin M. (eds) Optimization and Applications. OPTIMA 2019. Communications in Computer and Information Science, vol 1145. Springer, Cham, 2020. P. 115–126.

  11. Самарский А.А. Теория разностных схем. М.: Наука, 1977.

  12. Gao Ch., Wang Y. A general formulation of Peaceman and Rachford ADI method for the N-dimensional heat diffusion equation // Int. Comm. Heat Mass Transfer. 1996. V. 23. № 6. P. 845–854.

  13. Thibault J. Comparison of Nine Three-Dimensional Numerical Methods for the Solution of the Heat Diffusion Equation // Numerical Heat Transfer Fundamentals. 1985. V. 8. № 3. P. 281–298.

  14. Peaceman D.W., Rachford H.H. The Numerical Solution of Parabolic and Elliptic Differential Equations. J. of the Society for Industrial and Appl. Math. 1955. V. 3. № 1. P. 28–41.

  15. Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. М.: Едиториал УРСС, 2003.

  16. Douglas J., Rachford H.H. On the numerical solution of heat conduction problems in two and three space variables. Trans. Amer. Math. Soc. 1956. V. 82. P. 421–439.

  17. Албу А.В., Зубов В.И. Опыт использования методологии быстрого автоматического дифференцирования для решения обратных коэффициентных задач // Ж. вычисл. матем. и матем. физ. 2020. Т. 60. № 1. С. 18–28.

  18. Албу А.В., Албу А.Ф., Зубов В.И. Управление процессом кристаллизации вещества в литейной форме сложной геометрии // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 12. С. 2149–2162.

  19. Албу А.Ф., Зубов В.И. Исследование задачи оптимального управления процессом кристаллизации вещества в новой постановке для объекта сложной геометрической формы // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. № 12. С. 1879–1893.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал