Журнал вычислительной математики и математической физики, 2020, T. 60, № 11, стр. 1898-1914

1.1. Солнечные вспышки и эффект магнитного пересоединения

Согласно представлениям современной астрофизики [1]–[4], вспышки на Солнце зарождаются в его короне, где плазма сильно разрежена и обладает высокой проводимостью, магнитные силы преобладают над остальными, а магнитные силовые линии “вморожены” в плазму и движутся вместе с ней [3].

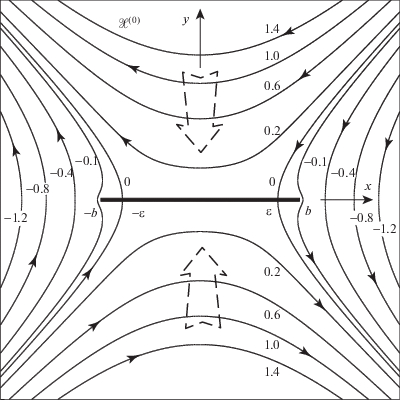
Как показано в работах [5], [6], в этих условиях в Солнечной короне возникают токовые слои. Магнитное поле в окрестности токового слоя рассматривается как плоское, ${\mathbf{B}} = ({{B}_{x}},{{B}_{y}},0)$, а величина ${{B}_{x}} - i{{B}_{y}}$ является аналитической функцией комплексного переменного $z = x + iy$. В дальнейшем саму эту функцию будем называть магнитным полем. В модели токового слоя С.И. Сыроватского [7] это поле¹¹ ${{\mathcal{F}}^{{(0)}}}(z) = {{B}_{x}}(z) - i{{B}_{y}}(z)$ было дано в виде

Картина этого поля представлена на фиг. 1; жирной линией изображен токовый слой, считающийся бесконечно тонким (это допущение обосновано в [8]), а магнитные силовые линии изображены линиями со стрелками, показывающими направление поля; $\mu $ – положительный параметр, характеризующий рост поля на бесконечности.

Согласно [1], [3], токовый слой разделяет движущиеся навстречу друг другу потоки плазмы, обозначенные на фиг. 1 двойными штриховыми стрелками. Поскольку поле противоположно направлено по разные стороны слоя, то магнитные силовые линии, приближающиеся к слою вместе с плазмой, “аннигилируют” на нем. Высвобождающаяся при этом энегрия “закачивается” в этот слой в виде электрического тока и окружающего магнитного поля. Этот эффект, обусловливающий  накопление  энергии в токовом слое, называют магнитным пересоединением [1]–[4].

Следует отметить, что ток в слое течет перпендикулярно плоскости рисунка (см. фиг. 1), причем его направление на серединном участке $( - \varepsilon ,\varepsilon )$ слоя противоположно направлению тока на концевых отрезках $( - b, - \varepsilon )$ и $(\varepsilon ,b)$; последний поэтому называют обратным током. Заметим, что в точках $z = \pm \varepsilon $, отделяющих участки обратного тока, магнитное поле обращается в нуль. Величина $\varepsilon $, как и другие параметры модели ($b$ и $\mu $), является заданной; из физических соображений полагают, что $0 < (b - \varepsilon ){\text{/}}b \ll 1$.

С течением времени, как установлено в [8], плотность плазмы вблизи токового слоя падает и развивается его неустойчивость. Это приводит к разрушению слоя, происходящему в течение короткого отрезка времени, т.е. к Солнечной вспышке, при которой накопленная энергия преобразуется в кинетическую и тепловую энергию плазмы [1], [9], [10] и в электромагнитное излучение [11], [12].

1.2. Модель Сомова магнитного пересоединения

Вычислительные эксперименты по моделированию магнитного поля в области пересоединения, выполненные в [13], [14] и др. работах, показали наличие магнитогидродинамических разрывов (т.е. МГД ударных волн) вблизи концов токового слоя. На основании этих результатов с учетом некоторых положений модели [15], в работах [16], [17] была предложена модель магнитного пересоединения (модель Сомова), являющаяся обобщением модели Сыроватского.

Модель Сомова, сохраняя токовый слой ${{\Gamma }_{0}}$ Сыроватского, присоединяет к его концам четыре МГД-разрыва ${{\Gamma }_{j}}$, $j = \overline {1,4} $, расположенных зеркально-симметрично относительно осей $x$, $y$ и изображенных на фиг. 2 в виде разрезов длины $r$, причем разрез в первом квадранте наклонен к оси $x$ под углом $\pi \alpha $. Магнитное поле, обозначаемое в этой модели через $\mathcal{F}(z) = {{B}_{x}}(z) - i{{B}_{y}}(z)$, имеет, как и поле Сыроватского (1), линейный рост на бесконечности

Принимается, что токовый слой электрически нейтрален, т.е. нормальная компонента ${{B}_{n}}$ магнитного поля на нем равна нулю, а на ударных волнах, преломляющих линии поля, она постоянна и равна заданной величине $\beta $. Выражая ${{B}_{n}}$ через $\mathcal{F}(z)$ по формуле ${{B}_{n}}(z) = \operatorname{Re} [\nu (z)\mathcal{F}(z)]$, где $\nu (z)$ – комплексная единичная нормаль, записываем эти условия в виде Конфигурацию ${{\Gamma }_{0}} \cup \Gamma $ (см. фиг. 2) называют токовой; она является поперечным сечением трехмерной поверхности, по которой, как и в модели Сыроватского, течет электрический ток перпендикулярно плоскости рисунка [1]–[4].

Поле Сомова $\mathcal{F}(z)$ удовлетворяет условиям краевой задачи Римана–Гильберта (2), (3) во внешности $\mathcal{X}$ токовой конфигурации. Эта область $\mathcal{X}$, являющаяся областью магнитного пересоединения в модели Сомова, изображена на фиг. 2; напомним, что областью пересоединения ${{\mathcal{X}}^{{(0)}}}$ в модели Сыроватского служит внешность разреза $[ - b,b]$ (см. фиг. 1). Решение задачи Римана–Гильберта (2), (3), включая магнитное поле для модели Сомова, приведенное на фиг. 3, получено в [18]–[20]. Изложение этого решения в сжатом виде дано в разд. 2.

1.3. Связь между моделями Сомова и Сыроватского

Необходимо отметить, что модели Сыроватского и Сомова различаются не только по геометрии токовой конфигурации, но и по набору параметров, т.е. величин, задаваемых исследователем и однозначно определяющих модель. Если в первой из них – это $b$, $\varepsilon $ и $\mu $, то во второй – это, кроме геометрических параметров $b$, $r$, $\alpha $ и коэффициента $\mu $ из асимптотики (2) поля на бесконечности, еще и физическая величина $\beta $, характеризующая преломление магнитного поля на ударных волнах. Кроме того, в модели Сыроватского величина $\varepsilon $ (половина длины участка прямого тока в токовом слое) является ее параметром, а в модели Сомова она находится из решения соответствующей краевой задачи и, в конечном итоге, определяется остальными параметрами модели.

В работе изучается поведение магнитного поля в модели Сомова при укорочении относительной длины $\varrho : = r{\text{/}}b$ фронта ударной волны и фиксированных остальных ($b$, $\alpha $, $\mu $) параметрах модели. В этой ситуации, чтобы подчеркнуть зависимость поля $\mathcal{F}(z)$ от $\rho $, будем обозначать его через  $\mathcal{F}(\rho ;z)$. Основным в работе является вопрос, переходит ли при $\varrho \to 0$ поле Сомова в поле Сыроватского? Математически этот вопрос сводится к получению соответствующей асимптотики функции $\mathcal{F}(\rho ;z)$ и установлению того, что главным членом этой асимптотики является ${{\mathcal{F}}^{{(0)}}}(z)$.

Отметим, что переход между областями пересоединения в моделях Сыроватского и Сомова при изменении $\rho $, т.е. переход от ${{\mathcal{X}}^{{(0)}}}$ к $\mathcal{X}$, геометрически означает сингулярное деформирование области ${{\mathcal{X}}^{{(0)}}}$ (ср. фиг. 1 и фиг. 2). При выводе искомой асимптотики использованы результаты [21] о конформном отображении сингулярно деформированных областей, а также полученное в работах [18], [22]–[25] представление решения задачи Римана–Гильберта в виде интеграла Кристоффеля–Шварца.

Проведенное исследование (разд. 3) показало, что при $\varrho \to 0$ и согласованном, порядка ${{\varrho }^{{ - 1/2}}}$, росте параметра $\beta $, входящего в граничное условие (3) на ударных волнах $\Gamma $, поле Сомова переходит в поле Сыроватского с сохранением участков обратного тока, причем поправка к полю Сыроватского имеет порядок $\rho $ и спадает как ${{z}^{{ - 1}}}$ при $z \to \infty $. Отметим, что в более простом случае отсутствия обратного тока этот вопрос был рассмотрен в работе [26].

2.1. Постановка краевой задачи

Поскольку область $\mathcal{X}$ пересоединения в модели Сыроватского и в целом задача (2), (3) в ней симметрична относительно осей $x$ и $y$, т.е.

то ее достаточно рассмотреть только в четверти исходной области, получаемой пересечением с первым квадрантом, т.е. на многоугольнике $G$, изображенном на фиг. 4а, где отмечены и его вершины²².

В области $G$, как следует из (2), (3), задача Римана–Гильберта формулируется следующим образом: найти аналитическую в $G$ и непрерывную в $\bar {G}{\backslash }A$ функцию $\mathcal{F}$, удовлетворяющую краевому условию

в котором коэффициент $h(z)$ и правая часть $c(z)$ определяются по формулам и отвечающую условию роста в бесконечности

Решение этой задачи, как можно показать с помощью [18], [22] однозначно определено. Заметим еще, что бесконечно удаленная точка $A$ является для области $G$ граничной (см. фиг. 4а), тогда как для исходной области $\mathcal{X}$ она является внутренней точкой (см. фиг. 2).

2.2. Подход к решению

Для того чтобы найти решение $w = \mathcal{F}(z)$ поставленной задачи Римана–Гильберта (5)–(7) в области $G$, воспользуемся конформным отображением $z = {{\Phi }^{{ - 1}}}(\zeta )$ верхней полуплоскости $\mathbb{H} = \{ \zeta :\operatorname{Im} \zeta > 0\} $ на область $G$. Это отображение проиллюстрировано на фиг. 4а, 4б; здесь, согласно упомянутому выше правилу, соответствующие друг другу точки на разных плоскостях обозначены одинаково. В частности, построенное в п. 2.3 отображение $z = {{\Phi }^{{ - 1}}}(\zeta )$ переводит друг в друга обозначенные через $A$ бесконечно удаленные точки областей $\mathbb{H}$ и $G$ и имеет при $\zeta \to \infty $ асимптотику ${{\Phi }^{{ - 1}}}(\zeta ) \sim 2\mathcal{K}\sqrt \zeta $, где $\mathcal{K}$ определено ниже в п. 2.3.

С помощью этого отображения сводим рассматриваемую задачу Римана–Гильберта (5)–(7) в области $G$ к аналогичной задаче относительно функции $\mathcal{P}(\zeta ): = \mathcal{F} \circ {{\Phi }^{{ - 1}}}(\zeta )$ в полуплоскости $\mathbb{H}$. Задача в ней формулируется следующим образом: найти аналитическую в $\mathbb{H}$ и непрерывную в $\bar {\mathbb{H}}{\backslash }\{ \infty \} $ функцию $\mathcal{P}(\zeta ),$ удовлетворяющую краевому условию

где данные этой задачи, т.е. коэффициент $\chi (\zeta ) = h \circ {{\Phi }^{{ - 1}}}(\zeta )$ и правая часть $\sigma (\zeta ) = c \circ {{\Phi }^{{ - 1}}}(\zeta )$ определяются по формулам и отвечающую условию роста на бесконечности

Условие (10) написано с учетом указанного поведения отображения ${{\Phi }^{{ - 1}}}(\zeta )$ на бесконечности. Задача (8)–(10), как и (5)–(7), из которой она получена, однозначно определена.

Построив решение $w = \mathcal{P}(\zeta )$ этой задачи с помощью метода [18] и возвратившись к области $G$ с помощью отображения $\zeta = \Phi (z)$, находим искомое решение задачи (5)–(7) в этой области в виде суперпозиции

Используемый метод [18] построения решения $w = \mathcal{P}(\zeta )$ задачи в $\mathbb{H}$ позволил представить его как конформное отображение полуплоскости на некоторый многоугольник – как установлено в п. 2.4, на четырехугольник $\mathcal{W}$, изображенный на фиг. 4в. Таким образом, решение $\mathcal{F}(z)$ задачи в области $G$ имеет геометрический смысл конформного отображения одного многоугольника, $G$, на другой, $\mathcal{W}$. Последний можно считать областью годографа магнитного поля для модели Сомова. Связку (11) отображений $\zeta = \Phi (z)$, $w = \mathcal{P}(\zeta )$ и $w = \mathcal{F}(z)$ иллюстрирует фиг. 4.

Построение конформного отображения $\zeta = \Phi (z)$ изложено в п. 2.3, а решение $w = \mathcal{P}(\zeta )$ задачи Римана–Гильберта (8)–(10) дано в п. 2.4.

2.3. Конформное отображение

Подчиним конформное отображение $z = {{\Phi }^{{ - 1}}}(\zeta )$ полуплоскости $\mathbb{H}$ на область $G$ (см. фиг. 4а, 4б) следующим однозначно его определяющим условиям:

Принимается, что $\alpha < 1{\text{/}}2$. Обозначим через $\omega $ и $\tau $ неизвестные координаты прообразов вершин $C$ и $E$ на плоскости $\zeta $, см. фиг. 4. Тогда согласно теории конформного отображения многоугольников [27], [28] рассматриваемое отображение $z = {{\Phi }^{{ - 1}}}(\zeta )$ записывается в виде интеграла Кристоффеля–Шварца: где, как легко убедиться, $\mathcal{K} > 0$. Из вида (13) отображения вытекает следующее его поведение и поведение обратного отображения на бесконечности:

Неизвестные параметры $\omega $, $\tau $ и $\mathcal{K}$ интеграла (13) находятся из системы трансцендентных уравнений, получаемой, как обычно (см. [27]), путем приравнивания трех заданных расстояний между вершинами многоугольной границы $\partial G$ соответствующим выражениям, вычисляемым по формуле (13). Принимая для нашего случая эти расстояния как ${\text{|}}{\kern 1pt} (BC){\kern 1pt} {\text{|}} = b$, ${\text{|}}{\kern 1pt} (CD){\kern 1pt} {\text{|}} = r$ и ${\text{|}}{\kern 1pt} (CE){\kern 1pt} {\text{|}} = 0$, получаем систему уравнений в виде

где величины ${{I}_{1}}(\omega ,\tau )$, ${{I}_{2}}(\omega ,\tau )$, ${{I}_{3}}(\omega ,\tau )$ определяются через интеграл по формулам Разделив второе уравнение системы (15) на первое, исключаем $\mathcal{K}$ и сводим ее к системе двух уравнений относительно только прообразов $\omega $ и $\tau $. После ее решения предынтегральный множитель $\mathcal{K}$ из (13) определяется по формуле легко следующей из первого уравнения системы (15).

Для того чтобы решить систему (18), приведем вначале асимптотики для искомых прообразов $\omega $ и $\tau $ при стремлении $\rho $ к бесконечности и фиксированных остальных геометрических параметрах $b$ и $\alpha $; чтобы подчеркнуть зависимость искомых $\omega $, $\tau $, $\mathcal{K}$ от $\rho $, будем их обозначать в этой ситуации через $\omega (\rho )$, $\tau (\rho )$, $\mathcal{K}(\rho )$. Асимптотики для $\omega (\rho )$, $\tau (\rho )$, построенные в [18] с использованием теории конформного отображения сингулярно деформируемых областей [21], имеют вид

Входящие сюда коэффициенты определяются по формулам где ${{\sigma }_{0}}$ и ${{\eta }_{0}}$ выражаются через гипергеометрическую функцию Гаусса $F(a,b;c;z)$: Укажем еще вытекающую из (20)–(23), используемую в дальнейшем асимптотику разности прообразов вершин $C$ и $E$ (см. фиг. 4б):

Получим асимптотику при $\rho \to 0$ для $\mathcal{K}(\rho )$. Для этого запишем величину ${{I}_{1}}(\omega ,\tau )$ в формуле (19) в виде интеграла (16) и выразим его через гипергеометрическую функцию Гаусса с помощью интегрального представления Эйлера [29] для этой функции. Подставляя асимптотики (20), (21) в найденное выражение, получаем

где величина ${{\sigma }_{0}}$ определяется из (24).

Искомые прообразы $\omega $ и $\tau $ находились в работе [18] путем решения системы уравнений (18) с помощью метода Ньютона [30], [31]. Входящие в эту систему интегралы (17) вычислялись аналитически тем же способом, который выше указан для ${{I}_{1}}(\omega ,\tau )$, т.е. через гипергеометрическую функцию и ее аналитическое продолжение [29]; начальное приближение для искомых $\omega $ и $\tau $ строилось с помощью асимптотик (20), (21).

Проведенная в [18] реализация такого численно-аналитического метода решения системы (18) показала его высокую эффективность. Так, время расчета одного варианта на персональном компьютере средней производительности составило менее $1$ с; при этом для параметров $\omega $ и $\tau $ была достигнута относительная точность не ниже ${{10}^{{ - 11}}}$. Как показали сравнительные эксперименты, этот метод на порядки превышает по точности и быстродействию обычно применяемые методы квадратур Гаусса и Гаусса–Якоби.

Отображение $\zeta = \Phi (z)$ области $S$ на полуплоскость $\mathbb{H}$ находится путем обращения функции $z = {{\Phi }^{{ - 1}}}(\zeta )$, исходя из ее представления в виде интеграла Кристоффеля–Шварца (13). Такое обращение вблизи особых точек этой функции можно выполнить аналитически с помощью теории функции Аппеля ${{F}_{1}}({{a}_{1}},{{a}_{2}};b,c;{{z}_{1}},{{z}_{2}})$ – гипергеометрической функции двух комплексных переменных ${{z}_{1}}$, ${{z}_{2}}$ (по каждой из них она имеет три особые точки $0,1,\infty $), определяемой в виде ряда [32]

и выражаемой в виде интегрального представления типа Эйлера [32]

Получим разложение для отображения $\zeta = \Phi (z)$ вблизи одной из ее особых точек – бесконечно удаленной точки $A$ (см. фиг. 4а). Для этого, воспользовавшись представлением (29), выразим интеграл Кристоффеля–Шварца (13) через функцию Аппеля. Выполнив с помощью формул из [25], [33] аналитическое продолжение функции ${{F}_{1}}({{a}_{1}},{{a}_{2}};b,c;{{z}_{1}},{{z}_{2}})$ в бесконечность по каждому из переменных ${{z}_{1}}$, ${{z}_{2}}$, находим

Выражая в этой формуле функцию Аппеля через ряд (28), приходим к следующему разложению отображения ${{\Phi }^{{ - 1}}}(\zeta )$ в окрестности точки $\zeta = \infty $: легко преобразуемому к виду обращая который в соответствии с [21], получаем требуемое представление для отображения $\zeta = \Phi (z)$ вблизи бесконечно удаленной точки $A$ (см. фиг. 4а) Фигурирующие здесь коэффициенты ${{\Lambda }_{m}}$ связаны с коэффициентами ${{\lambda }_{m}}$ из (32) формулами Воспользовавшись соотношениями (31), (32), (34), приведем три первых члена разложения (33):

Таким же методом можно получить разложения отображения $\zeta = \Phi (z)$ вблизи остальных вершин многоугольника $G$, однако для цели численного построения решения исходной задачи проще это провести другим методом, как это и было сделано в работе [18]. Для описания этого метода, обеспечивающего эффективную реализацию отображения $\zeta = \Phi (z)$ во всей области $G$, обозначим вершины $A,\;S,\;B,\;C,\;D,\;E$ многоугольника $G$ соответственно через ${{z}_{m}}$, $m = \overline {1,6} $, где $S$ – некоторая выбранная регулярная точка на стороне $AB$ (см. фиг. 4а), которую также будем считать вершиной угла раствора $\pi $. Углы в этих вершинах обозначаем через $\pi {{\beta }_{m}}$, а прообразы этих вершин – через ${{\zeta }_{m}}$.

Поскольку разложение вблизи бесконечной вершины $A = {{z}_{1}}$ уже найдено – это формула (35), то приведем далее разложения отображения $\zeta = \Phi (z)$ вблизи конечных вершин ${{z}_{m}}$, т.е. при $m = \overline {2,6} $. Разлагаем входящие в интеграл (13) биномы в биномиальный ряд вблизи выбранной ${{\zeta }_{m}}$, а полученный после их перемножения ряд почленно интегрируем и обращаем. Таким образом, приходим к требуемому разложению вблизи вершины ${{z}_{m}}$, $m = \overline {2,6} $:

где коэффициенты $\Lambda _{k}^{{(m)}}$ выражаются через параметры интеграла (13) с помощью конечных явных формул, получаемых параллельно с разложеним (37); здесь ${{R}_{m}}$ – расстояние от ${{z}_{m}}$ до ближайшей особой точки, а величины ${{\delta }_{m}}$ определяются по формулам При выбранном $m = \overline {2,6} $ ряд (37) сходится во вписанном в область $G$ секторе раствора $\pi {{\beta }_{m}}$ и радиуса ${{R}_{m}}$ с центром в вершине ${{z}_{m}}$. Множества сходимости разложений (37) для вершин ${{z}_{m}}$, $m = \overline {2,6} $, т.е. для $S,\;B,\;C,\;D,\;E$ и разложения (35) для ${{z}_{1}} = A$ покрывают в совокупности все множество $\bar {G}{\backslash }\{ \infty \} $, так что для любой его точки найдется, по крайней мере, одно из указанных разложений отображения $\zeta = \Phi (z)$, сходящееся в ней с экспоненциальной скоростью.

2.4. Решение задачи Римана–Гильберта для модели Сомова

Отметим, что задача (8)–(10) Римана–Гильберта имеет особенности – разрывы данных $\chi (\zeta )$ и $\sigma (\zeta )$ в точках $A$, $C$, $E$ и роcт искомой функции $\mathcal{P}(\zeta )$ в точке $A$, которые затрудняют применение классических методов [34], [35].

Ее решение было получено с помощью метода [18], позволяющего преодолевать подобные трудности. Заметим, что общий метод для случая произвольных разрывных (кусочно-гёльдеровых) данных задачи Римана–Гильберта и роста решения в некоторых граничных точках развит в работах [22]–[24]; он опирается на результаты [25] по теории функции Лауричеллы – гипергеометрической функции многих переменных. В случае кусочно-постоянных данных метод дает решение в форме интеграла Кристоффеля–Шварца.

В такой форме и было получено решение $\mathcal{P}(\zeta )$ задачи (8)–(10) в работе [18]:

Из выражения (38), рассматриваемого как интеграл Кристоффеля–Шварца, вытекает, что функция $w = \mathcal{P}(\zeta )$ конформно отображает полуплоскость $\mathbb{H}$ на четырехугольник, обозначенный выше через $\mathcal{W}$ и изображенный на фиг. 4в. Этот рисунок и фиг. 4б показывают, что отображение $w = \mathcal{P}(\zeta )$ переводит точки $\zeta = \infty $, $\zeta = \omega $, $\zeta = \tau $, $\zeta = \theta $, расположенные на $\partial \mathbb{H}$, соответственно в вершины $A$, $C$, $E$, $T$ многоугольника $\mathcal{W}$ с углами, равными $ - \pi {\text{/}}2$, $\pi \alpha $, $\pi (1{\text{/}}2 - \alpha )$, $2\pi $. Координаты $\omega $, $\tau $ прообразов вершин $C$, $E$ были найдены в п. 2.3, а координата $\theta $ прообраза вершины $T$ дается формулой (39). Координаты ${{w}_{C}}$ и ${{w}_{E}}$ самих вершин $C$ и $E$, как установлено в [18], равны что иллюстрируется фиг. 4в.

Найдем координату ${{w}_{T}}$ вершины $T$ многоугольника $\mathcal{W}$ (см. фиг. 4в). Поскольку из указанных величин углов и координат вершин ${{w}_{C}}$ и ${{w}_{E}}$ многоугольника $\mathcal{W}$ следует, что вершина $T$ расположена на отрицательной мнимой полуоси, то ее координату удобно обозначить через $ - it$, где $t > 0$, т.е.

Для нахождения $t$, прежде всего, выполним в формуле (38) следующие замены, не изменяющие функцию $\mathcal{P}$: нижний предел $\omega $ интеграла заменим на $\tau $, а координату ${{w}_{C}}$ $($второй член в правой части (38)$)$ – на координату ${{w}_{E}}$ из (40). Тогда получим Делая далее подстановку $s = \tau + (\theta - \tau )x$ и используя представление Эйлера для гипергеометрической функции [29], находим Аналитически продолжая гипергеометрическую функцию по формуле (29) подставляя сюда значение $\theta $ из (39) и используя соотношение получаем искомое значение величины $t$ в равенстве (41), определяющем координату вершины $T$ (см. фиг. 4в):

Далее в работе будем полагать, что $\theta $ находится на оси $\partial \mathbb{H}$ правее $\tau $ (см. фиг. 4б), условием выполнения чего является, как показано в [18], неравенство

а функцию $w = \mathcal{P}(\zeta )$ будем задавать в следующей, вытекающей из (38) форме: где $\theta $ определяется равенством (39), а $t$ – равенством (44).

Численная реализация решения $\mathcal{P}(\zeta )$ задачи (8)–(10) была выполнена в работе [18] с помощью приводимого далее набора разложений функции $\mathcal{P}(\zeta )$, области сходимости которых покрывают в совокупности всю полуплоскость $\mathbb{H}$, где она определена.

Получим вначале разложение для $w = \mathcal{P}(\zeta )$ вблизи бесконечно удаленной точки, являющейся прообразом вершины $A$ многоугольника $\mathcal{W}$ (см. фиг. 4а). Для этого каждый из биномов, входящих в подынтегральное выражение в (46), разложим в биномиальный ряд, перемножим эти ряды, а результат почленно проинтегрировав, получим

Приведем выражения для первых двух коэффициентов ряда (47): вытекающие из формулы (47).

Чтобы выписать остальные необходимые разложения функции $w = \mathcal{P}(\zeta )$, введем некоторые обозначения. Пусть $K$ и $L$ – изображенные на фиг. 4в регулярные точки соответственно границы $\partial{ \mathcal{W}}$ и области $\mathcal{W}$. Обозначим точки $A,\;C,\;E,\;T,\;K,\;L$ рассматриваемого многоугольника соответственно через ${{w}_{n}}$, $n = \overline {1,6} $, их прообразы – через ${{\zeta }_{n}}$, а углы в них – через $\pi {{\alpha }_{n}}$ (точкам $K$ и $L$ приписываем угол раствора $\pi $, так что ${{\alpha }_{5}} = {{\alpha }_{6}} = 1$). Действуя тем же путем, что и при выводе представления (47), соответствующего $n = 1$, получаем для $n = \overline {2,6} $ следующие разложения:

где коэффициенты $b_{k}^{{(m)}}$ выражаются через параметры интеграла (46) с помощью конечных явных формул, получаемых параллельно с разложеним (51) (эти формулы приведены в [18]); ${{\rho }_{n}}$ – радиус сходимости ряда в (51), являющийся расстоянием от ${{\zeta }_{n}}$ до ближайшей особой точки ${{\zeta }_{p}}$ (не совпадающей с выбранной ${{\zeta }_{n}}$); показатели ${{\gamma }_{n}}$ определяются следующим образом: ${{\gamma }_{2}} = - \alpha $, ${{\gamma }_{3}} = - 1{\text{/}}2$, ${{\gamma }_{4}} = - \alpha - 1$, ${{\gamma }_{5}}$ – деленный на $\pi $ аргумент подынтегральной функции в (38), ${{\gamma }_{6}} = 1$.

Множества сходимости разложений (47) и (51) покрывают в совокупности все множество , так что для любой его точки найдется, по крайней мере, одно из указанных разложений функции $\mathcal{P}(\zeta )$, сходящееся в ней с экспоненциальной скоростью.

Подставляя в представление (11) найденную здесь функцию $w = \mathcal{P}(\zeta )$ и построенное в п. 2.3 отображение $\zeta = \Phi (z)$, получаем решение $w = \mathcal{F}(z)$ задачи (8)–(10) в области $G$, а используя соотношения симметрии (4), приходим к решению задачи Римана–Гильберта (5)–(7) в исходной области пересоединения $\mathcal{X}$.

Проведенная в [18] реализация изложенного решения для модели пересоединения Сомова, включая вычисление магнитного поля, пример которого дан на фиг. 3, показала его высокую эффективность. Так, время расчета одного варианта магнитного поля во всей области $\mathcal{X}$ на персональном компьютере средней производительности составило менее 1 с, а достигнутая относительная точность составила ${{10}^{{ - 11}}}$.

3.1. Факторизация поля Сыроватского

Поскольку модель Сыроватского (п. 1.1) обладает той же, что и модель Сомова, симметрией относительно осей $x$, $y$ – это относится и к области ${{\mathcal{X}}^{{(0)}}}$ (см. фиг. 1), и к функции ${{\mathcal{F}}^{{(0)}}}(z)$ из (1), – то ее, как и модель Сомова, можно рассматривать лишь в четверти исходной области ${{\mathcal{X}}^{{(0)}}}$, т.е. в ${{G}^{{(0)}}}$, представляющей собой первый квадрант, изображенный на фиг. 5а. Поле ${{\mathcal{F}}^{{(0)}}}$ также можно определить как решение задачи Римана–Гильберта, которая формулируется следующим образом: найти аналитическую в ${{G}^{{(0)}}}$ и непрерывную в ${{\bar {G}}^{{(0)}}}{\backslash }({{A}^{{(0)}}} \cup {{C}^{{(0)}}})$ функцию ${{\mathcal{F}}^{{(0)}}}(z)$, удовлетворяющую краевому условию

где кусочно-постоянная функция ${{h}^{{(0)}}}(z)$ определяется равенством и отвечающую перечисляемым ниже требованиям в точках ${{A}^{{(0)}}}$, ${{N}^{{(0)}}}$ и ${{C}^{{(0)}}}$ границы $\partial {{G}^{{(0)}}}$: где постоянная ${{\mathfrak{C}}^{{(0)}}} > 0$ при $\varepsilon < b$ и ${{\mathfrak{C}}^{{(0)}}} = 0$ при $\varepsilon = b$. Можно показать, используя [22], что поставленная таким образом задача Римана–Гильберта (с необязательно заданной константой ${{\mathfrak{C}}^{{(0)}}}$) однозначно разрешима.

Поле Сыроватского (1) имеет геометрический смысл конформного отображения $w = {{\mathcal{F}}^{{(0)}}}(z)$ области ${{G}^{{(0)}}}$ на область ${{\mathcal{W}}^{{(0)}}}$ годографа магнитного поля Сыроватского, представляющую собой нижнюю полуплоскость с разрезом по отрицательной мнимой полуоси от бесконечности ($ - i\infty $) до точки ${{T}^{{(0)}}}$ (см. фиг. 5в), т.е.

Этот вид области ${{\mathcal{W}}^{{(0)}}}$ можно установить, переписав выражение (1) через функцию Жуковского ${\text{Zh}}(\eta ): = \tfrac{1}{2}(\eta + 1{\text{/}}\eta )$ в виде и использовав известные свойства конформного отображения, осуществляемого этой функцией [28]. На границе $\partial {{\mathcal{W}}^{{(0)}}}$ имеются две бесконечно удаленные точки, ${{A}^{{(0)}}}$ и ${{C}^{{(0)}}}$, расположенные на разных берегах упомянутого разреза, так что будем обозначать его через $({{C}^{{(0)}}}{{T}^{{(0)}}}{{A}^{{(0)}}})$, см. фиг. 5в.

Приведем поле Сыроватского (1) к факторизованному виду

аналогичному суперпозиции (11) для поля Сомова. Входящую в (59) функцию $\zeta = {{\Phi }^{{(0)}}}(z)$ определим как отображение удовлетворяющее нормировке близкой к условиям для отображения $\Phi (z)$, вытекающим из (12), (14). Нетрудно убедиться, что эта функция выражается формулой выполняемое ею соответствие точек приведено на фиг. 5а, 5б.

Вторая компонента суперпозиции (59) – функция ${{\mathcal{P}}^{{(0)}}}$ – имеет следующий вид, вытекающий из формул (1), (62):

Соотношения (57), (59), (60) показывают, что она осуществляет отображение которое иллюстрируют фиг. 5б, 5в. Очевидно также, что если обозначить через $\mathfrak{Z}$ пересечение малой окрестности точки $\zeta = {{\theta }^{{(0)}}}$ с полуплоскостью $\mathbb{H}$, то ${{\mathcal{P}}^{{(0)}}}(\mathfrak{Z})$ будет представлять собой некоторую окрестность образа ${{T}^{{(0)}}}$ этой точки за вычетом разреза $({{C}^{{(0)}}}{{T}^{{(0)}}}{{A}^{{(0)}}})$. Отсюда следует, что производная функции (63) обращается в нуль при $\zeta = {{\theta }^{{(0)}}}$. Из этого наблюдения получаем, что а координата $w_{T}^{{(0)}}$ конца разреза области ${{\mathcal{W}}^{{(0)}}}$ (см. фиг. 5в) есть Связка отображений $\zeta = {{\Phi }^{{(0)}}}(z)$, $w = {{\mathcal{P}}^{{(0)}}}(\zeta )$ и $w = {{\mathcal{F}}^{{(0)}}}(z)$ видна из фиг. 5.

Следует отметить, что хотя поле Сыроватского (1) не содержит параметра $\rho $, но введенные по формулам (62) и (63) функции ${{\Phi }^{{(0)}}}$ и ${{\mathcal{P}}^{{(0)}}}$, входящие в представление (59) для этого поля, зависят от $\rho $, поэтому при необходимости будем указывать для них $\rho $ как долнительный аргумент, например, писать ${{\mathcal{P}}^{{(0)}}}(\rho ;\zeta )$.

Для случая отсутствия в этой модели обратного тока, т.е. при $\varepsilon = b$, в число аргументов будем добавлять $b$. Несложный анализ формулы (1) показывает, что при $\varepsilon \to b$ функция ${{\mathcal{P}}^{{(0)}}}(\zeta )$, осуществляющая отображение (64), переходит в функцию

разрез $({{C}^{{(0)}}}{{T}^{{(0)}}}{{A}^{{(0)}}})$ согласно (66) достигает вещественной оси (см. фиг. 5в), и область ${{\mathcal{W}}^{{(0)}}}$ вырождается в ${{\mathcal{W}}^{{(0)}}}(b)$ – четвертый квадрант.

3.2. Сравнение моделей

Обратимся к основному вопросу работы: превращается ли модель Сомова в модель Сыроватского при стремлении к нулю относительной длины $\varrho : = r{\text{/}}b$ фронта ударной волны и фиксированных остальных параметрах модели $b$, $\alpha $, $\mu $? Одной из главных при этом является задача определить, какой вид в процессе такого предельного перехода должна иметь зависимость $\beta (\rho )$, чтобы при $\rho \to 0$ координата ${{w}_{T}}(\rho )$ конца разреза $T$ области $\mathcal{W}$ стремилась к значению $w_{T}^{{(0)}}$, определяемому из (66).

Убедимся, что если полагать величину $\beta $ постоянной или имеющей конечный предел при $\varrho \to 0$ и фиксированных $b$, $\alpha $, $\mu $, то требуемого превращения одной модели в другую не происходит. В этих условиях для модели Сомова обозначим через $\Phi (\rho ,z)$ и $\mathcal{P}(\rho ,z)$ компоненты суперпозиции (11), через ${{w}_{T}} = - it(\rho )$ – координату конца $T$ разреза области $\mathcal{W}$, а через $\theta (\rho )$ – координату ее прообраза (см. фиг. 4б, 4в). Тогда из выражения (39) и оценок (20), (25), (26) вытекает асимптотика

а из (44) и оценок (20), (21), (25), (26), (68) – следующая асимптотика: Подставляя в представление (46) оценки (20), (21), (26), (68) и (69), находим, что т.е. здесь главный член совпадает с полем Сыроватского при $\varepsilon = b$, что соответствует случаю отсутствия обратного тока. Это означает, что если предел величины $\beta $ при $\varrho \to 0$ конечен, то при таком предельном процессе поле Сомова $\mathcal{P}(\zeta )$ не имеет требуемого предела (63) и переходит в поле Сыроватского ${{\mathcal{P}}^{{(0)}}}(b;\zeta )$ без обратного тока, а имеющийся в области $\mathcal{W}$ разрез $(ETA)$ перерезает при $\rho \to 0$ эту область так, что от нее отпадает третий квадрант. Это ясно из асимптотики (70) для отображения и асимптотики (69) для координаты ${{w}_{T}}$ конца разреза; из последней очевидно, что эта координата стремится к нулю при $\rho \to 0$.

Если зависимость $\beta (\rho )$ задать в виде

где $\Xi = {\text{const}}$, то конец $T$ разреза $(ETA)$ не достигнет при $\rho \to 0$ вещественной оси, так как в этом случае вместо (68) получим асимптотику в которой ${{\theta }_{{(1)}}}$ определяется формулой (68), а ${{\theta }_{{(2)}}}$ – формулой здесь величины ${{\tau }_{{(1)}}}$ и ${{\tau }_{{(2)}}}$ даются равенствами (22), величины ${{\omega }_{{(1)}}}$ и ${{\omega }_{{(2)}}}$ – равенствами (23), а величины ${{\mathcal{K}}_{{(1)}}}$ и ${{\theta }_{{(1)}}}$ – равенствами (27) и (68).

Из представления (46) и оценок (20), (21), (26), (68) и (69) получаем следующую асимптотику:

Сравнивая числитель правой части (74) с числителем правой части формулы (1), определяющей поле Сыроватского, находим зависимость $\Xi (\varepsilon )$, где ${{\theta }_{{(1)}}}$ дается формулой (68), при выполнении которой $li{{m}_{{\rho \to 0}}}t(\rho ) = {{t}^{{(0)}}}$. Точнее, справедливы асимптотики вытекающие соответственно из (71), (72), (75) и из (69), (71), (75). Отметим еще, что согласно (76), $\Xi \in (0,1{\text{/}}{{\theta }_{{(1)}}})$.

3.3. Асимптотика поля Сомова при укорочении фронта ударной волны

Подставляя в разложение (32) переменное $z$ вместо ${{\Phi }^{{ - 1}}}(\zeta )$ и $\Phi (z)$ вместо $\zeta $, возвышая в квадрат, вычитая из обеих частей получаемого равенства единицу и учитывая равенство (62), приходим к разложению

где ${{\lambda }_{m}}$ – коэффициенты ряда (32). Обращая ряд (77), получаем разложение отображения $\Phi :G\;\xrightarrow{{{\text{conf}}}}\;\mathbb{H}$ области $G$ в ряд по степеням отображения ${{\Phi }^{{(0)}}}:{{G}^{{(0)}}}\;\xrightarrow{{{\text{conf}}}}\;\mathbb{H}$ области ${{G}^{{(0)}}}$, для которой $G$ получена путем ее сингулярного деформирования. Это разложение имеет вид где коэффициенты ${{M}_{m}}$ связаны с ${{\mu }_{m}}$ теми же формулами (34), которыми ${{\Lambda }_{m}}$ связаны с ${{\lambda }_{m}}$. Используя [21], где рассмотрен такой тип деформирования, находим, что ряд (79) сходится на множестве $\Phi \mathop {^{{(0)}}}\nolimits^{ - 1} ({{\mathcal{K}}_{ + }}(R))$, где $\Phi \mathop {^{{(0)}}}\nolimits^{ - 1} $ – отображение, обратное к ${{\Phi }^{{(0)}}}$,

Подставляя разложение (78) и оценку (74) в представление (11), получаем искомую асимптотику поля Сомова $\mathcal{F}(z)$ по степеням поля Сыроватского ${{\mathcal{F}}^{{(0)}}}(z)$:

где коэффициент ${{B}_{1}}$, зависящий от $\rho $, дается формулой Если в этой формуле учесть оценки при $\rho \to 0$ для величин $\mathcal{K}$, $\theta $, $\omega $, $\tau $, задаваемые равенствами (20), (23), (26), (68), то получим для этого коэффициента асимптотику а если ее подставить в соотношение (80), то придем к двойной (соответствующей $\rho \to 0$, $z \to \infty $) асимптотике вида где $\varphi (\rho ,z) = \mathcal{O}({{\rho }^{2}})$, $\rho \to 0$, и $\varphi (\rho ,z) = \mathcal{O}({\text{|}}z{\kern 1pt} {{{\text{|}}}^{{ - 1}}})$, $z \to \infty $.

Асимптотики (80), (83) показывают, что при укорочении длины ударных волн в модели Сомова она действительно при условии $\beta = \Xi {{\rho }^{{ - 1/2}}}$ переходит в модель Сыроватского, где $\Xi $ связано с $\varepsilon $ равенствами (75), (68).