Журнал вычислительной математики и математической физики, 2020, T. 60, № 11, стр. 1867-1880

1. ПРОЕКЦИИ НАЧАЛА КООРДИНАТ НА ЛИНЕЙНОЕ МНОГООБРАЗИЕ

Пусть $L$ – линейное многообразие из ${{R}^{n}}$, множество, замкнутое относительно операции аффинной комбинации векторов: если ${{x}^{1}} \in L,$ ${{x}^{2}} \in L$, то множеству $L$ должен принадлежать вектор $\lambda {{x}^{1}} + (1 - \lambda ){{x}^{2}}$ при любом вещественном $\lambda $. Будем считать, что $0 \notin L,$ $L \ne \emptyset $. Линейное подпространство, параллельное $L$ и ортогональное ему, обозначим соответственно

Наборы номеров компонент вектора $x$ c отрицательными, положительными, ненулевыми и нулевыми значениями будем обозначать ${{J}_{ - }}(x)$, ${{J}_{ + }}(x{\text{)}}$, $J(x{\text{)}}$, соответственно. Набор $J(x{\text{)}}$ называется (см. [1]) носителем вектора $x$.

Пусть $f(x{\text{)}}$ – некоторая норма вектора $x \in {{R}^{n}}$. Вектор $x$, при котором достигается решение задачи минимизации этой нормы на многообразии $L$,

будем называть проекцией начала координат на линейное многообразие $L$, порождаемой нормой $f$. В частности, могут использоваться гёльдеровские, октаэдральные или чебышёвские нормы: Здесь $p$ – заданный из открытого интервала $(1,\,\infty )$ степенной коэффициент гёльдеровской нормы, ${{h}_{j}}$ – заданные весовые коэффициенты. Весовые коэффициенты составляют вектор $h \in R_{ + }^{n}$, где $R_{ + }^{n}$ – подмножество векторов ${{R}^{n}}$ со всеми положительными компонентами.

Задача поиска гёльдеровской проекции равносильна минимизации на $L$ строго выпуклой функции

которая является результатом дифференцируемого возрастающего преобразования гёльдеровской нормы $f_{h}^{p}$. Для гёльдеровской нормы задача (1) имеет единственное решение [2], [3]. Обозначим его $x(f_{h}^{p}).$

Частным случаем гёльдеровских норм являются при $p = 2$ евклидовы нормы. Использование $f_{h}^{2}$ в качестве целевой функции задачи (1) означает, что отыскивается евклидова проекция начала координат на линейное многообразие. В этом случае задача (1) решается методом наименьших квадратов.

Поскольку могут использоваться разные значения степенных коэффициентов $p \in (1,\,\,\infty )$ и разные значения вектора весовых коэффициентов $h \in R_{ + }^{n}$, то имеем множество гёльдеровских и, при фиксированном $p = 2$, множество евклидовых норм. Они порождают множества гёльдеровских и евклидовых проекций:

Так как любая евклидова норма является гёльдеровской, то множество евклидовых проекций содержится в множестве гёльдеровских проекций. В [2], [3] доказано, что справедливо более сильное утверждение – множества гёльдеровских и евклидовых проекций совпадают,

В качестве наиболее общего подхода к постановке проблемы определения ближайших к началу координат точек линейного многообразия в [2], [3] предлагалось рассматривать множество точек линейного многообразия с парето-минимальными абсолютными значениями компонент

Множество $Q$ состоит из векторов линейного многообразия $L$, у которых нельзя уменьшить, оставаясь в рамках $L$, абсолютное значение любой из компонент без увеличения абсолютного значения какой-либо другой компоненты. Из теоремы Гордона об альтернативных системах линейных неравенств [4] вытекает следующее равносильное (7) определение:

В [3] установлены ограниченность, связность, замкнутость множества $Q$, а также его возможная невыпуклость при $\,p \geqslant 4$. Доказано [2], что евклидовы и, согласно (6), гёльдеровские проекции принадлежат $Q$:

При этом ${{P}_{2}}$ совпадает с $Q$ в том и только том случае, если оба эти множества состоят из одного вектора. Вместе с тем, как доказано в [3], множество ${{P}_{2}}$ всегда “почти” совпадает с $Q$, так как где ${\text{cl}}\,\,$ – замыкание множества. Доказано также [3], что множество ${{P}_{2}}$ является связным, проекция $x(f_{h}^{2})$ является непрерывной вектор-функцией от вектора $h \in R_{ + }^{n}$.

Важную роль в характеристике свойств наименее удаленных от начала координат точек линейного многообразия играют векторы линейного многообразия с минимальным (не сужаемым) носителем. Их множество обозначим через

Здесь и далее символ $ \subset $ обозначает строгое включение одного множества в другое в отличие от соотношения нестрогого включения $ \subseteq $. Множество $B$ состоит из конечного числа векторов [2], [3]. Их не более чем где $m$ – размерность линейного многообразия $L$. Справедливы [2], [3] соотношения где ${\text{co}}\,$ – выпуклая оболочка векторов.

Известно, что октаэдральные и чебышёвские нормы (3), (4) являются предельными значениями гёльдеровских норм. При любом $h \in R_{ + }^{n}$ для любого $x \in {{R}^{n}}$: при $p \to 1$ имеем

а при $p \to \infty $ верно

Поиск октаэдральной проекции при фиксированном векторе весовых коэффициентов может давать неединственные решения. Введем множества октаэдральных проекций при фиксированном $h \in R_{ + }^{n}$ и при всех $h \in R_{ + }^{n}$:

Как доказано в [3], множество октаэдральных проекций при любом фиксированном $h$ содержит векторы линейного многообразия с минимальным носителем, т.е. множество

при любом $h \in R_{ + }^{n}$ содержит хотя бы один вектор, Аналогичное свойство при ${{h}_{j}} = 1,$ $j = 1,...,n$, доказывалось в [5].

Свойство (13) означает, что множество $X(h)$ состоит из одного вектора в том и только том случае, если это вектор из $B$. Если множество $B(h)$ содержит несколько векторов, то, как доказано в [3], их выпуклая оболочка образует $X(h)$:

Из этого свойства и конечности числа векторов в $B$ следует, что различающихся множеств октаэдральных проекций $X(h)$ только конечное число.

При использовании чебышёвской нормы в качестве целевой функции задачи (1) также возможна ситуация неединственности решения. При этом среди решений задачи минимизации чебышёвской нормы могут оказаться не находящиеся в $Q$ векторы. В [6] рассматривался пример линейного многообразия при $n = 2$, заданного условием ${{x}_{1}} = 1$. Решением задачи (1) с чебышёвской нормой (4) будет вектор с ${{x}_{1}} = 1$ и любым значением ${{x}_{2}}$ из интервала $\left[ { - {{h}_{1}}{\text{/}}{{h}_{2}},\;{{h}_{1}}{\text{/}}{{h}_{2}}} \right]$. При этом множество $Q$, как и множество $P$, состоит из одного вектора с компонентами ${{x}_{1}} = 1,\;{{x}_{2}} = 0$.

Для избавления от проблем неоднозначности чебышёвских проекций используется условие Хаара [7], [8]. Оно состоит в требовании особых свойств от линейного многообразия. Согласно условию Хаара, линейное многообразие должно быть таким, чтобы задача поиска чебышёвской проекции имела единственное решение. Выполнение условия Хаара не всегда легко проверить. И не понятно, что делать, если это условие не выполняется.

В [6] вкратце изложен алгоритм вычисления во всех случаях однозначной чебышёвской проекции. Далее будет подробно рассмотрен этот алгоритм. Он служит одновременно и определением однозначной чебышёвской проекции.

2. МНОЖЕСТВО РЕШЕНИЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Введенному выше аксиоматическому определению линейного многообразия соответствуют различные алгебраические формы его задания. В частности, линейным многообразием является множество решений системы линейных уравнений. В этом случае имеем

где заданными являются матрица $A$ размера $m \times n$ и вектор $b$ из ${{R}^{m}}$. Условие $L \ne \emptyset $ означает совместность рассматриваемой системы линейных уравнений. Условие $0 \notin L$ означает, что система неоднородная, т.е. $b \ne 0$.

Подпространство, параллельное $L$, состоит из решений однородной системы

Ортогональное подпространство является образом матрицы, транспонированной из $A$:

К проблеме поиска решений системы линейных уравнений с минимальными абсолютными значениями компонент сводятся задачи вычисления решений моделей, имеющих вид системы линейных уравнений, максимально приближенных к заданному недопустимому решению. В частности, вид системы линейных уравнений имеет модель межотраслевого баланса (МОБ) [9]. Проблема вычисления сбалансированных показателей МОБ, максимально приближенных к заданным несбалансированным показателям, возникает как при составлении отчетного, так и при формировании перспективного МОБ [10], [11].

Пример 1. Рассмотрим двумерное линейное многообразие, заданное как множество решений системы из двух линейных уравнений с четырьмя переменными:

Подпространство $S$, параллельное этому многообразию, состоит из векторов $s \in {{R}^{4}}$, являющихся решениями однородной системы линейных уравнений Ортогональное линейное подпространство $Z$ состоит из векторов $z \in {{R}^{4}}$ с компонентами где ${{u}_{1}},\,\,{{u}_{2}}$ – любые вещественные числа.

Рассмотрим случай одинаковых весовых коэффициентов ${{h}_{j}} = 1,$ $j = 1,...,n$. В этом случае решения системы (15), (16) с минимальной чебышёвской нормой будут достигаться при значении этой нормы, равном 4. Таких решений много. В частности, ими являются векторы:

При этом любое решение системы (15), (16) с минимальной чебышёвской нормой является выпуклой комбинацией векторов ${{x}^{1}}$ и ${{x}^{5}}$, т.е. принадлежит замкнутому интервалу [${{x}^{1}},{{x}^{5}}$].

Интервал [${{x}^{1}},{{x}^{5}}$] разбивается точками ${{x}^{2}}$ и ${{x}^{4}}$ на три интервала. Векторы из двух крайних полуоткрытых интервалов не находятся в $Q$,

Для доказательства следует воспользоваться определением (7) множества $Q$. Действительно, вектор $s = (1, - 1,0,0)$ удовлетворяет условиям (17), (18). При этом для любого $x$ из интервала $[{{x}^{1}},{{x}^{2}})$ выполняются соотношения Аналогично для любого вектора $x$ из интервала $({{x}^{4}},{{x}^{5}}]$ выполняются эти же соотношения для вектора $s = ( - 1,1,0,0)$, также удовлетворяющего (17), (18).

Векторы из замкнутого интервала [${{x}^{2}},{{x}^{4}}$] находятся в $Q$. Для доказательства следует воспользоваться определением (8) множества $Q$. Для любого $x$ из [${{x}^{2}},{{x}^{4}}$] при $z$, определяемом правилом (19) для ${{u}^{1}} = {{u}^{2}} = 1$, выполняются соотношения

Интересующие нас объекты двумерного линейного многообразия представлены на фигуре. Эта фигура сделана на плоскости самого линейного многообразия. Выделенные прямые линии состоят из векторов линейного многообразия, у которых нулевое значение имеет одна из компонент. Точки пересечения прямых образуют векторы с минимальным носителем, составляющие множество $B$. Это векторы:

Их получилось на единицу меньше, чем верхняя оценка $C_{4}^{2} = 6,$ поскольку прямые ${{x}_{3}} = 0$ и ${{x}_{4}} = 0$ в данном примере не пересекаются.

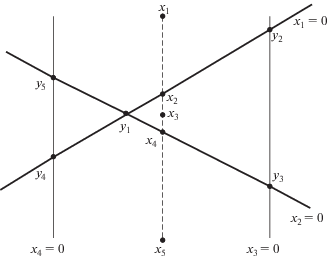
Множество векторов линейного многообразия с парето-минимальными абсолютными значениями компонент $Q$ в данном примере не выпукло. Оно состоит из объединения двух треугольников:

Поскольку точка ${{y}^{1}}$ входит в оба треугольника, то $Q$ – связное множество.

Множество евклидовых ${{P}_{2}}$-проекций состоит из относительно внутренних точек этих треугольников с добавлением точки ${{y}^{1}}$, что делает это множество связным

Здесь символ ${\text{ri}}$ обозначает относительную внутренность [1] множества. Штриховой линией изображен отрезок [${{x}^{1}},{{x}^{5}}$]. Из рисунка видно, что расположенные на этом отрезке полуоткрытые интервалы $[{{x}^{1}},{{x}^{2}})$ и $({{x}^{4}},{{x}^{5}}]$ в $Q$ не находятся. Интервал [${{x}^{2}},{{x}^{4}}$] находится в $Q$.

3. АЛГОРИТМ ВЫЧИСЛЕНИЯ ЧЕБЫШЁВСКОЙ ПРОЕКЦИИ

В данном разделе излагается алгоритм вычисления во всех случаях однозначной чебышёвской проекции. Алгоритм состоит в последовательном решении задач линейного программирования с номерами $t = 1,...,T$ при определяемом далее числе $T$. При этом в каждой из этих задач требуется находить относительно внутреннюю точку оптимальных решений, т.е. оптимальное решение с минимальным набором активных ограничений. Свойством вырабатывать именно такие оптимальные решения обладают алгоритмы метода внутренних точек [6].

Считаем заданным вектор весовых коэффициентов $h \in R_{ + }^{n}$. Положим ${{J}^{1}} = \left\{ {1,...,n} \right\},$ ${{N}^{1}} \equiv \emptyset $. Полагаем первоначально $t = 1$.

На этапе $t$ решается задача линейного программирования

Здесь $\alpha $ – дополнительная переменная, соответствующая для $t = 1$ значению минимизируемой чебышёвской нормы $f_{h}^{\infty }$ в задаче (1). Условие (22) при $t = 1$ является несущественным, поскольку ${{N}^{1}} = \emptyset .$ На последующих этапах $t > 1$ множество ${{N}^{t}}$ будет не пустым. Значения фиксированных величин ${{\bar {x}}_{j}}$ при $j \in {{N}^{t}}$ определяются из решений задач предыдущих этапов.

Обозначим через ${{\alpha }^{t}}$ – оптимальное значение целевой функции задачи (20)–(23), ${{x}^{t}}$ – оптимальное значение вектора переменных $x$ с минимальным набором активных (выполняющихся в виде равенств) ограничений (21).

Отметим, что у задачи (20)–(23) обязательно имеется оптимальное решение. Это следует из того, что имеется допустимое по условиям (22), (23) решение и из ограниченности снизу нулем допустимого по условию (21) значения $\alpha $. При $t = 1$ допустимое решение будет составлять любой вектор $x \in L$ и любое значение $\alpha $, удовлетворяющее с данным $x$ условию (21). При $t > 1$ допустимым решением будет оптимальное решение ${{\alpha }^{{t - 1}}},\;{{x}^{{t - 1}}}$ задачи (20)–(23), полученное на предыдущем этапе $t - 1$.

Если векторы $x$ и $y$ из ${{R}^{n}}$ являются оптимальными решениями задачи (20)–(23), то оптимальным решением будет и вектор $z = \gamma x + (1 - \gamma )y$ при любом $\gamma \in (0,\,\,1)$. У вектора $z$ активными будут те и только те ограничения-неравенства (21), которые активны для обоих решений $x$ и $y$. Отсюда следует существование оптимальных решений с минимальным набором активных ограничений, которые активны при любом оптимальном решении.

Введем подмножество номеров из набора ${{J}^{t}}$, представляющее активные ограничения (21) в оптимальном решении

Положим ${{\bar {x}}_{j}} = x_{j}^{t}$, $j \in {{I}^{t}}$. Набор ${{I}^{t}}$ исключим из множества ${{J}^{t}}$ и добавим к множеству ${{N}^{t}}$. Получим множества Если ${{J}^{{t + 1}}} \ne \emptyset ,$ то переходим к следующему этапу поиска относительно внутренней точки оптимальных решений задачи (20)–(23) для $t: = t + 1$.

Поскольку ${{I}^{t}} \ne \emptyset $, то ${{J}^{{t + 1}}}$ строго включено в ${{J}^{t}}$. На одном из этапов обязательно возникает ситуация ${{J}^{{t + 1}}} = \emptyset .$ Это будет последний этап вычислений с номером $t = T$.

Отметим, что именно относительно внутренняя точка оптимальных решений дает однозначный выбор набора ${{I}^{t}}$ и значений $x_{j}^{t}$ при $j \in {{I}^{t}}$. Следовательно, приведенный алгоритм будет вырабатывать однозначный вектор ${{x}^{t}}$ из ${{R}^{n}}$ при $t = T$. Этот вектор обозначим через $x(f_{h}^{\infty }).$ Его будем называть чебышёвской проекцией начала координат на линейное многообразие при использовании в чебышёвской норме вектора весовых коэффициентов $h \in R_{ + }^{n}$.

Множество вычисляемых по приведенному алгоритму чебышёвских проекций при варьировании весовых коэффициентов в чебышёвской норме представим в виде

В [6] доказано следующее утверждение, согласно которому определенная здесь чебышёвская проекция при заданном векторе весовых коэффициентов $h$ из $R_{ + }^{n}$ является вектором линейного многообразия с парето-минимальными абсолютными значениями компонент.

Теорема 1. Справедливо ${{P}_{\infty }} \subseteq Q.$

Отметим, что для примера первого раздела изложенным здесь алгоритмом будет получено единственное решение с ${{x}_{1}} = 1$, ${{x}_{2}} = 0$ при использовании любых положительных весовых коэффициентов ${{h}_{1}},\;{{h}_{2}}$. В примере предыдущего раздела изложенный алгоритм даст решение ${{x}^{3}}$.

Доказательство теоремы 1 вытекает из определения (7) множества $Q$ и приводимой ниже леммы. Отметим, что ${{\alpha }^{1}} > 0$, поскольку $0 \notin L$. Величины ${{\alpha }^{t}}$ в силу (21) неотрицательны и убывают с ростом $t$. Поэтому ${{\alpha }^{1}} > {{\alpha }^{2}} > ... > {{\alpha }^{{\text{T}}}} \geqslant 0.$ Нулевые значения может иметь (может и не иметь) только ${{\alpha }^{{\text{T}}}}$. Если ${{\alpha }^{{\text{T}}}} = 0$, то уже сам этот факт означает, что допустимые по условиям (21)–(23) при $t = T$ значения $\alpha = 0,\;x \in {{R}^{n}}$ являются относительно внутренней точкой оптимальных решений задачи (20)–(23).

Введем последовательность вложенных линейных подпространств. Пусть ${{S}^{1}} = S$,

В качестве пояснения отметим, что линейное подпространство ${{S}^{t}}$ составляют векторы $s = \lambda ({{x}^{1}} - {{x}^{2}})$, где $\lambda $ – любое вещественное число, ${{x}^{1}},\;{{x}^{2}}$ – любая пара векторов из $L$, удовлетворяющих (22) для данного $t$.

Определим множество номеров компонент векторов

Отметим, что при ${{\alpha }^{t}} > 0$ В случае ${{\alpha }^{t}} = 0$ (что, как отмечалось, возможно при $t = T$) имеем

Лемма. Необходимым и достаточным условием для того, чтобы положительная величина ${{\alpha }^{t}}$ и вектор ${{x}^{t}}$из ${{R}^{n}}$, удовлетворяющие при данном $t$ ограничениям (21)–(23), являлись оптимальным решением задачи (20)–(23) с минимальным набором активных ограничений, является отсутствие вектора $s \in {{S}^{t}}$, при котором

Доказательство. Необходимость. Пусть ${{\alpha }^{t}}$, ${{x}^{t}}$ – оптимальное решение задачи (20)–(23) с минимальным набором активных ограничений. Предположим, что существует вектор $s \in {{S}^{t}}$, удовлетворяющий (28), (29). Тогда

Вектор ${{x}^{t}} - \lambda s$ при достаточно малом положительном $\lambda $ будет удовлетворять ограничениям (21)–(23) вместе со значением $\alpha = {{\alpha }^{t}}$. При этом состав активных ограничений-неравенств сократится. Из набора $I_{ + }^{t}$ исключатся номера множества ${{J}_{ + }}(s) \cap I_{ + }^{t}$. Из набора $I_{ - }^{t}$ исключатся номера множества ${{J}_{ - }}(s) \cap I_{ - }^{t}$. В силу (30) одно из множеств ${{J}_{ - }}(s) \cap I_{ - }^{t}$ или ${{J}_{ + }}(s) \cap I_{ + }^{t}$ обязательно не пусто. Получим допустимое по условиям (21)–(23) решение $\alpha = {{\alpha }^{t}}$, $x = {{x}^{t}} - \lambda s$ при достаточно малом положительном $\lambda $ с суженным набором активных ограничений. Это противоречит исходному условию. Необходимость доказана.

Достаточность. Пусть при допустимых по условиям (21)–(23) значениях ${{\alpha }^{t}}$, ${{x}^{t}}$ для определенных по правилам (24)–(26) множеств не существует вектора $s \in {{S}^{t}}$, при котором выполняется соотношение (28), (29). Требуется доказать, что ${{\alpha }^{t}}$, ${{x}^{t}}$ – оптимальное решение задачи (20)–(23) с минимальным набором активных ограничений.

Предположим, что это не так. Тогда существует допустимое по условиям (21)–(23) решение $\tilde {\alpha } \leqslant {{\alpha }^{t}}$, $\tilde {x} \in {{R}^{n}}$, при котором либо $\tilde {\alpha } < {{\alpha }^{t}}$ (т.е. ${{\alpha }^{t}}$ и ${{x}^{t}}$ – неоптимальное решение), либо $\tilde {\alpha } = {{\alpha }^{t}}$, но при этом строго включен в ${{I}^{t}}$набор номеров

В первом случае для всех $\,j \in {{I}^{t}}$ выполнено

Вектор $s = {{x}^{t}} - \tilde {x}$, находящийся в ${{S}^{t}}$, будет удовлетворять (28), (29), что противоречит исходному условию об отсутствии таких векторов.

Во втором случае выполняются нестрогие неравенства

Дополнительно к этому для некоторого непустого подмножества $\tilde {I} \subset {{I}^{t}}$ неравенства выполняются в строгом виде: Отсюда следует, что для вектора $s = {{x}^{t}} - \tilde {x},$ справедливо Последнее из этих соотношений означает выполнение (28) для данного вектора $s$. С учетом первых двух равенств получается, что для данного $s$ выполняются соотношения (29). Так как оба вектора ${{x}^{t}}$ и $\tilde {x}$ составляют со значением $\alpha = {{\alpha }^{t}}$ допустимое по ограничениям (21)–(23) решение, то $s \in {{S}^{t}}$. Приходим к противоречию с исходным условием отсутствия вектора в ${{S}^{t}}$, удовлетворяющего (28), (29). Лемма доказана.

При доказательстве теоремы 1 используется первая часть данной леммы, необходимость отсутствия вектора $s \in {{S}^{t}}$, удовлетворяющего (28), (29). В доказательстве теоремы следующего раздела потребуется обратное утверждение данной леммы.

4. СХОДИМОСТЬ ГЁЛЬДЕРОВСКИХ ПРОЕКЦИЙ

Теорема 2. Для любого вектора весовых коэффициентов $h \in R_{ + }^{n}$ при $p \to \infty $ верно

Данная теорема может рассматриваться как еще одно подтверждение правильности введенного в предыдущем разделе определения чебышёвской проекции. Эта теорема идейно связана со сходимостью (12) гёльдеровских норм к чебышёвской норме. При этом теорема не является простым следствием этого факта.

Поскольку все гёльдеровские проекции, согласно (9), находятся в компакте $Q$, то у векторов $x(f_{h}^{p})$ существуют предельные при $p \to \infty $ точки и они находятся в $Q$. При этом априори не ясно, состоит ли множество предельных при $p \to \infty $ и фиксированном $h$ точек из одной точки? И будет ли эта точка совпадать с чебышёвской проекцией $x(f_{h}^{\infty })$?

Пример 2. Для иллюстрации потенциальной справедливости теоремы 2 рассмотрим линейное многообразие в ${{R}^{2}}$, состоящее из векторов, удовлетворяющих уравнению

Геометрически это многообразие представляется в виде прямой на плоскости, проходящей через точки

Эти точки составляют множество векторов данного линейного многообразия с минимальным носителем, обозначенное выше $B$. Множество векторов линейного многообразия с парето-минимальными абсолютными значениями компонент составляет замкнутый отрезок между этими точками, $Q = [{{x}^{1}},{{x}^{2}}].$

Можно отметить, что в этом примере для октаэдральных проекций имеется всего три варианта множеств решений. Если ${{h}_{2}} > {{h}_{1}}$, то множество октаэдральных проекций состоит из одной точки ${{x}^{1}}.$ Если ${{h}_{1}} > {{h}_{2}}$, то множество октаэдральных проекций состоит из одной точки ${{x}^{2}}.$ В случаях, когда ${{h}_{1}} = {{h}_{2}}$, множество октаэдральных проекций состоит из всего множества $Q$, $X(h) = [{{x}^{1}},{{x}^{2}}].$

Гёльдеровские проекции имеют компоненты

Множества гёльдеровских проекций при различных ${{h}_{1}} > 0,$ ${{h}_{2}} > 0$ составляют открытый интервал $({{x}^{1}},{{x}^{2}})$.

Чебышёвские проекции в данном примере имеют компоненты

Их множество при различных положительных весовых коэффициентах также составляет открытый интервал $({{x}^{1}},{{x}^{2}})$. Из приведенных выражений вытекает, что для фиксированных ${{h}_{1}},\;{{h}_{2}}$ при $p \to \infty $ Это иллюстрирует справедливость теоремы 2.

Доказательство теоремы 2. Поскольку рассматривается фиксированный вектор весовых коэффициентов $h$, то в целях упрощения записи будем использовать обозначение

Пусть $P$ – некоторая возрастающая к бесконечности последовательность степенных коэффициентов, такая что при $p \in {\rm P},\;p \to \infty $

для некоторого $\bar {x} \in Q$. Необходимо доказать, что точка $\bar {x}$ совпадает с чебышёвской проекцией, т.е. Тем самым будет доказано, что любая сходящаяся последовательность гёльдеровских проекций с данным вектором весовых коэффициентов сходится к одному и тому же вектору, к чебышёвской проекции. Следовательно, справедливо (31).

Вводимые здесь обозначения, порождаемые вектором $\bar {x}$ из (32), как будет установлено ниже, совсем не случайно будут совпадать с обозначениями, вводившимися при описании и исследовании свойств алгоритма предыдущего раздела.

Обозначим через $T$ число различающихся значений величин ${{h}_{j}}\left| {{{{\bar {x}}}_{j}}} \right|,\;j = 1,...,n.$ Упорядоченный по убыванию набор этих значений обозначим через ${{\alpha }^{t}},\;t = 1,...,T.$ Согласно этому определению все ${{\alpha }^{t}}$, кроме, быть может, ${{\alpha }^{{\text{T}}}}$, положительные, ${{\alpha }^{1}} > {{\alpha }^{2}} > ... > {{\alpha }^{{\text{T}}}} \geqslant 0.$ Далее рассматриваем ситуацию ${{\alpha }^{t}} > 0.$

Введем наборы номеров компонент векторов. Пусть

Положим

Введем последовательность вложенных линейных подпространств. Пусть ${{S}^{1}} = S,$

Поскольку ${{\alpha }^{t}} > 0$, то ${{\bar {x}}_{j}} \ne 0$ для всех $\,j \in {{I}^{t}}.$ Согласно (32), (34), (35), начиная с некоторого значения$\bar {p} \in P,$ $\bar {p} > 2$, при всех $p \geqslant \bar {p},$ $p \in P$ верно

Здесь ${\text{sign}}\,\,a$ – функция от вещественного $a$, имеющая значение 1, 0 или –1, если $a > 0,\;a = 0$ или $a < 0$ соответственно.

Из (34)–(36) следует, что при $p \geqslant \bar {p},\;p \in P$, положительна величина

Номер $j$ из ${{I}^{t}}$, на котором реализуется значение $c(t,p),$ обозначим через $l(t,p)$.

При вычислении гёльдеровской проекции, как отмечалось, в задаче (1) вместо функции $f_{h}^{p}$ можно использовать функцию $\varphi _{h}^{p}$, определенную в (5). Эту функцию можно умножить на любую положительную константу. Можно также зафиксировать на оптимальном уровне часть переменных и ограничиться оптимизацией только по оставшимся переменным. Поэтому вектор $x(p)$ при $p \in P$, $p \geqslant \bar {p}$, можно рассматривать как решение задачи

при любом $t \in \{ 1,...,T\} $. Здесь

Введем частные производные функции $g_{t}^{p}$ в точке $x(p)$:

где

Из (37) и определения $l(t,p)$ следует, что для $p \geqslant \bar {p}$, $p \in P$, справедливо

Поэтому, согласно (40), при $p \geqslant \bar {p}$, $p \in P$, справедливо неравенство Из (35), (39)–(41) следует, что при всех $p \in P$, $p \geqslant \bar {p}$, справедливо

Так как

и при этом, согласно (37), имеем $l(t,p) \in {{I}^{t}},$ то в силу (32), начиная с некоторого значения $\tilde {p} > \bar {p},$ $\tilde {p} \in P$, для всех $p \geqslant \tilde {p},$ $p \in P$ справедливо неравенство Следовательно, при некотором $\varepsilon \in (0,\,\,1)$ для всех$p \geqslant \tilde {p},$ $p \in P$, выполняются неравенства Поэтому согласно (39) при $p \in P,$ $p \to \infty $, имеем

Тот факт, что $x(p)$ является оптимальным решением задачи (38), равносилен утверждению о равенстве нулю производной функции $g_{t}^{p}$ в точке $x(p)$ по любому направлению $s \in {{S}^{t}},$

Поскольку ${{J}^{t}} = {{I}^{t}} \cup {{J}^{{t + 1}}},$ то

В силу (44) для любого $s \in {{S}^{t}}$ при $p \in P,$ $p \to \infty $, имеем

Так как при ${{\alpha }^{t}} > 0$ справедливо (35) и $I_{ + }^{t} \cap I_{ - }^{t} = \emptyset ,$ то первую составляющую в правой части (46) можно представить как сумму двух составляющих:

Докажем теперь, используя лемму предыдущего раздела, что вектор $\bar {x}$ из (36) и величина ${{\alpha }^{t}}$, определенная на основе этого вектора, составляют оптимальное решение задачи (20)–(23) с минимальным набором активных ограничений последовательно для $t = 1,...,T.$ При $t > 1$ считаем, что этот факт доказан для предыдущих значений $t$. Возможный случай ${{\alpha }^{t}} = 0$ при $t = T$ не рассматривается, так как при нем доказанный факт следует непосредственно из значения ${{\alpha }^{t}} = 0$. Итак, считаем, что ${{\alpha }^{t}} > 0$.

Доказываемый факт означает, что последовательно для $t = 1,...,T$ определенная здесь величина ${{\alpha }^{t}}$ совпадает с обозначенной также величиной из алгоритма предыдущего раздела. Определенные здесь множества номеров ${{I}^{t}},\;I_{ + }^{t},\;I_{ - }^{t},\;{{J}^{t}},\;{{N}^{t}}$ совпадают с обозначенными также множествами номеров в предыдущем разделе. Последовательно для $t = 1,...,T$ будут совпадать компоненты ${{\bar {x}}_{j}}$ при $j \in {{I}^{t}}.$ В результате получим совпадение числа этапов $T$ и значений всех компонент вектора $\bar {x}$, т.е. доказываемое равенство (33) верно.

Предположим, что существует вектор $\bar {s}$ в ${{S}^{t}}$, при котором выполняются соотношения (28), (29) и, следовательно, соотношение (30). Из (42), (43), (48) следует, что для некоторого $M > 0$ и всех $p \geqslant \bar {p},$ $p \in P$, выполняется неравенство

Из (29), (30), (46), (47), (49) следует, что для данного $\bar {s}$ при всех $p \in P$ соотношение (45) выполняться не может. Предположение не верно.

Из леммы предыдущего раздела получаем, что вектор $\bar {x}$ является относительно внутренней точкой оптимальных решений задачи (20)–(23) последовательно при всех $t = 1,...,T$. Это и требовалось доказать. Теорема доказана.

5. ОБСУЖДЕНИЯ

1. Принципиально новыми результатами в данной статье являются доказательства теоремы о сходимости гёльдеровских проекций к чебышёвской проекции и леммы, содержащей критерий для выявления относительно внутренней точки оптимальных решений задачи (20)–(23). Этот критерий использовался здесь для теоретических исследований. В вычислительных алгоритмах для выявления относительно внутренних точек оптимальных решений можно пользоваться условием дополняющей нежесткости в строгой форме. Приведем его для случая, когда в формулировке задачи линейного программирования (20)–(23) линейное многообразие задачи определено в виде решений системы линейных уравнений (14). Пусть ${{a}_{{ij}}}$ – коэффициенты матрицы $A$. Переменные ${{x}_{j}}$ для $j \in {{N}^{t}}$ заданы равными ${{\bar {x}}_{j}}$. Положим

Задача (20)–(23) приобретает вид

Пусть ${{u}_{i}}$ для $i = 1,...,m,\;{{{v}}_{j}},\;{{\omega }_{j}}$ для $j \in {{J}^{t}}$ – множители Лагранжа ограничений (51)–(53). Двойственной будет следующая задача линейного программирования:

Чтобы располагаемые допустимые по ограничениям решения исходной и двойственной задач были относительно внутренними точками оптимальных решений этих задач, необходимо и достаточно [4] выполнения для них следующих условий, которые и называются условиями дополняющей нежесткости в строгой форме:

2. Установленную в теореме 2 связь гёльдеровских проекций с чебышёвской можно рассматривать как важный аспект в обосновании правильности введенного первоначально определения чебышёвской проекции через алгоритм лексикографической оптимизации. Доказанный в теореме 2 факт может использоваться как еще одно, равносильное первоначальному, определение чебышёвской проекции.

Возможно, эта теорема будет полезна и для конструирования новых алгоритмов вычисления чебышёвской проекции путем итеративного (например, методом Ньютона) уточнения гёльдеровской проекции и повышения в этом итеративном процессе степенных коэффициентов гёльдеровских норм. Конечно, такой путь вычислений нуждается в конкретизации и проработке проблем связанных с устойчивостью результатов вычислений к погрешностям счета.

3. Линейное многообразие может быть задано как сдвиг на заданный вектор $r \in {{R}^{n}}$ образа некоторой матрицы $G$ размера $m \times n$,

В таком виде представляется множество невязок задачи линейной аппроксимации. В этом случае $i = 1,...,m$ – номера факторов, $j = 1,...,n$ – номера наблюдений, ${{g}_{{ij}}}$ – коэффициенты матрицы $G$, являющейся значением измерения фактора $i$ в наблюдении $j$, ${{r}_{j}}$ – значение результирующего показателя в $j$-м наблюдении. Компоненты вектора $\lambda $ являются искомыми коэффициентами линейной регрессии.

Компоненты вектора $x$ должны быть по возможности минимальны по абсолютной величине. В частности, может минимизироваться чебышёвская норма $f_{h}^{\infty }$, что означает использование чебышёвской линейной аппроксимации.

Традиционно чебышёвская аппроксимация используется в задаче поиска наилучшего приближения функции через комбинации заданного набора функций [7], [12] . Пусть заданная на отрезке $[a,b]$ при $a < b$ непрерывная функция одной переменной ${v}(t)$ аппроксимируется линейной комбинацией непрерывных линейно независимых на этом отрезке функций ${{\omega }_{i}}(t),\;i = 1,...,m.$ Например, это могут быть степенные функции, тогда речь идет о поиске полинома наилучшего приближения.

Задана непрерывная функция весовых коэффициентов $h(t) > 0$ для $t \in [a,b]$. Требуется найти вещественные коэффициенты ${{\lambda }_{i}}$, чтобы было минимально значение функции

Для решения такой задачи обычно используется ее дискретизация [7], [12] . Задается возрастающий набор значений ${{t}_{j}},\;j = 1,...,n$, из интервала $[a,b]$. Затем вычисляются компоненты векторов $h,\;r$ и коэффициенты матрицы $G$:

Приходим к задаче линейной дискретной аппроксимации

где $L$ определяется условием (54).

Условие Хаара для рассматриваемой проблемы означает [7], [8], что при любом $\lambda \in {{R}^{m}},$ $\lambda \ne 0$ функция

должна иметь на отрезке $[a,b]$ не более чем $m - 1$ нулей. Отсюда следует, что получаемая в результате дискретизации задача (55) должна иметь единственное решение. Набор функций ${{\omega }_{i}}$, при которых выполняется условие Хаара, принято называть чебышёвской системой. Изложенный здесь алгоритм вычисления чебышёвской проекции применительно к дискретной задаче чебышёвской аппроксимации позволяет однозначно решать задачу чебышёвского приближения независимо от того, выполняется условие Хаара или нет. При этом само чебышёвское приближение, опираясь на доказанную здесь теорему 2, можно определить как предел гёльдеровских приближений при стремлении к бесконечности степенных коэффициентов гёльдеровской нормы.