Журнал вычислительной математики и математической физики, 2020, T. 60, № 7, стр. 1248-1267

Численное моделирование переноса пассивного скаляра в мелкой воде с использованием квазигазодинамического подхода

Т. Г. Елизарова^1, *, А. В. Иванов^1, **

¹ ИПМ им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия

^* E-mail: telizar@mail.ru
^** E-mail: alexvladiv@mail.ru

Поступила в редакцию 13.08.2019
После доработки 13.01.2020
Принята к публикации 10.03.2020

DOI: 10.31857/S0044466920070066

Аннотация

Изложен новый метод численного решения уравнения переноса пассивного скаляра в рамках системы уравнений гидродинамики в приближении мелкой воды. Метод основан на разработанных ранее квазигазодинамических алгоритмах для численного моделирования течений сжимаемого газа. Построены сглаженные уравнения и выписана их разностная аппроксимация, в том числе и для течений с источником примеси. Апробация численных алгоритмов представлена на примерах одномерных и двумерных течений. В качестве примера применения алгоритма приведено решение задачи о циркуляции воды в озере Валунден. Дано обобщение построенного подхода для численного моделирования переноса пассивного скаляра в рамках приближения вязкой несжимаемой жидкости. Библ. 21. Фиг. 21.

Ключевые слова: уравнения мелкой воды, перенос примеси, регуляризованные уравнения, метод конечного объема, источник, озеро Валунден.

1. ВВЕДЕНИЕ

Моделирование переноса пассивного скаляра в рамках уравнений гидродинамики имеет широкое практическое применение, при этом в качестве скаляра могут рассматриваться примесь, соленость или температура. Рассмотрим гидродинамическую систему уравнений в приближении мелкой воды (МВ), которая включает в себя перенос примеси. Пусть концентрация примеси характеризуется величиной $C$. В таком случае математическая модель представляет собой систему уравнений МВ:

(1)

$\frac{{\partial h}}{{\partial t}} + {\text{div}}\left( {h{\mathbf{u}}} \right) = 0,$

(2)

$\frac{{\partial \left( {h{\mathbf{u}}} \right)}}{{\partial t}} + {\text{div}}\left( {h{\mathbf{u}} \otimes {\mathbf{u}}} \right) + \nabla \frac{{g{{h}^{2}}}}{2} = h({\mathbf{f}} - g\nabla b),$

которая дополняется уравнением для описания переноса примеси. Уравнение переноса можно записать в двух вариантах:

(3)

$\frac{{\partial Ch}}{{\partial t}} + {\text{div}}\left( {{\mathbf{u}}Ch} \right) = {\text{div}}\left( {Dh\nabla C} \right),$

(4)

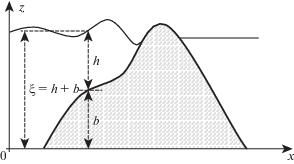
$\frac{{\partial C}}{{\partial t}} + {\text{div}}\left( {{\mathbf{u}}C} \right) = {\text{div}}\left( {D\nabla C} \right).$

Используемые обозначения поясняет фиг. 1, здесь $h({\mathbf{x}},t)$ – толщина слоя воды, отсчитываемая от дна; $b({\mathbf{x}})$ – уровень дна; ${\mathbf{u}}({\mathbf{x}},t)$ – вектор горизонтальных скоростей; $g$ – ускорение силы тяжести, направленное вниз вдоль оси $z$; ${\mathbf{f}}({\mathbf{x}},t)$ – вектор объемной внешней силы, действующей по всей глубине, например, силы Кориолиса; $C({\mathbf{x}},t)$ – пассивный скаляр, роль которого может играть концентрация примеси, соленость или температура (далее, не ограничивая общности, мы будем подразумевать под этим обозначением именно концентрацию примеси); $D$ – коэффициент диффузии примеси; $\xi ({\mathbf{x}},t) = h({\mathbf{x}},t) + b({\mathbf{x}})$ – уровень поверхности воды.

Фиг. 1.

Схематическое изображение используемых обозначений.

Уравнение переноса пассивного скаляра в виде (3) часто используется в задачах гидрологии и позволяет учитывать величину так называемого “живого сечения”, т.е. площадь сечения потока, перпендикулярного к направлению скорости.

Уравнение (4) – это классическое уравнение переноса, где предполагается, что загрязнитель пассивен и не взаимодействует с течением. Однако в некоторых случаях необходимо учитывать другие явления, например такие, как осаждение, источник или сток примеси, эрозия, которые в приведенных уравнениях не рассматриваются.

Поскольку в практических расчетах чаще всего используется уравнение вида (3), далее, говоря о переносе пассивного скаляра в мелкой воде, мы будем подразумевать систему (1)–(3).

Разработка эффективного и точного численного алгоритма для решения системы уравнений (1)–(3) представляет собой сложную задачу. В первую очередь – это обусловлено тем, что решения данной системы, как правило, не являются гладкими: они могут содержать как гидродинамические разрывы и волны разрежения для уравнений (1), (2), так и разрывы в решении для уравнения переноса (3). Помимо этого, в задачах часто встречаются случаи, в которых коэффициент диффузии $D$ очень мал. Это приводит к тому, что многие схемы для численного решения уравнения переноса оказываются неустойчивыми или излишне диссипативными, что усложняет численное моделирование и поднимает вопрос о разработке методов для решения этой проблемы. Одним из подходов является применение специализированного отдельного алгоритма для решения уравнения переноса. Последнее делает численное решение системы уравнений (1)–(3) неоднородным. Такой подход был реализован, например в [1], [2], где совмещаются метод частиц для расчета уравнения переноса и метод конечного объема для решения уравнений мелкой воды. Существуют и другие методы, например, также широко развит подход использования конечно-разностных TVD-схем (схем с невозростанием полной вариации) [3]–[6], помимо этого, для решения системы уравнения переноса в мелкой воде применяются кинетические алгоритмы [7], [8], схемы Годунова [9], методы типа конечного объема [10], схемы Лакса–Фридрихса совместно с центрально-разностной аппроксимацией для уравнения переноса [11] и др.

В данной работе предлагается к рассмотрению новый однородный алгоритм для моделирования процессов переноса пассивного скаляра в мелкой воде, основанный на совместном решении системы уравнений гидродинамики и уравнения переноса. В основе метода для решения рассматриваемой системы как целого лежит квазигазодинамический подход [12]–[14].

В разд. 2 описан алгоритм построения регуляризованного уравнения переноса. В разд. 3 и 4 приведены специфические тесты, использованные для апробации численного алгоритма. Для моделирования одномерных течений это задачи: о распространении примеси течением над неровным дном [1]; классическая задача о распаде разрыва [1], [4], [8]; задача Римана с разбегающейся жидкостью [8]. В последней точным решением для уравнения переноса является стационарное распределение концентрации в виде ступеньки, что достаточно сложно удается получить в численном расчете. Дополнительной сложностью в этой задаче является описание формирования “сухой зоны” в центральной части расчетной области.

В качестве двумерных тестов, рассмотренных в разд. 4 и 5, использовались примеры, приведенные в [2]: задача прорыва симметричной плотины на плоском дне, которая также приведена в [4], и задача о разрушении дамбы над неровным дном при наличии источника. В частности, в разд. 5 рассматривается случай решения системы уравнений переноса в мелкой воде при наличии источника. Задачи с источником очень важны, поскольку применяются для моделирования, например, аварий танкеров в прибрежной зоне и распространения загрязнений вдоль берега и прилегающей акватории.

Разд. 6 посвящен задаче воспроизведения динамики течений озера Валунден, Шпицберген. В нем приводятся результаты моделирования, поясняющие экспериментальные данные, полученные в ходе исследований озера сотрудниками института океанологии им. П.П. Ширшова РАН [15], [16].

Стоит отметить, что сложности, связанные с решением уравнения переноса пассивного скаляра в рамках гидродинамических уравнений, проявляются как в модели мелкой воды, так и при рассмотрении задач в приближении вязкой несжимаемой жидкости. Авторы продемонстрировали одно из возможных решений данной проблемы на примере уравнений гидродинамики в приближении МВ. В заключение показан способ регуляризации уравнения переноса пассивного скаляра для гидродинамических уравнений, описывающих течение вязкой несжимаемой жидкости.

2. ПОСТРОЕНИЕ СИСТЕМЫ СГЛАЖЕННЫХ УРАВНЕНИЙ

Рассматривается система регуляризованных уравнений мелкой воды (далее РУМВ), описанная в [17]:

(5)

$\frac{{\partial h}}{{\partial t}} + \operatorname{div} {{{\mathbf{j}}}_{{\mathbf{m}}}} = 0,$

(6)

$\frac{{\partial \left( {h{\mathbf{u}}} \right)}}{{\partial t}} + {\text{div}}\left( {{{{\mathbf{j}}}_{m}} \otimes {\mathbf{u}}} \right) + \nabla \frac{{g{{h}^{2}}}}{2} = h{\text{*}}\left( {{\mathbf{f}} - g\nabla b} \right) + \operatorname{div} \Pi ,$

(7)

$h{\text{*}} = h - \tau {\text{div}}\left( {h{\mathbf{u}}} \right),$

(8)

${{{\mathbf{j}}}_{m}} = h\left( {{\mathbf{u}} - {\mathbf{w}}} \right),$

(9)

${\mathbf{w}} = \frac{\tau }{h}\left[ {{\text{div}}\left( {h{\mathbf{u}} \otimes {\mathbf{u}}} \right) + gh\nabla \left( {b + h} \right) - h{\mathbf{f}}} \right],$

(10)

$\Pi = {{\Pi }_{{NS}}} + \tau {\mathbf{u}} \otimes \left[ {h\left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}} + gh\nabla \left( {b + h} \right) - h{\mathbf{f}}} \right] + \tau I\left[ {gh\operatorname{div} \left( {h{\mathbf{u}}} \right)} \right],$

где $\tau > 0$ – параметр регуляризации с размерностью времени, ${{\Pi }_{{NS}}}$ – тензор вязких напряжений Навье–Стокса, который при необходимости в ряде задач рассматривается как дополнительный регуляризатор и может быть включен или отброшен, см., например, [17], [18]. Коэффициент кинематической вязкости жидкости $\mu $ считается искусственным и вычисляется через параметр $\tau $:

(11)

${{\Pi }_{{NS}}} = \mu \frac{h}{2}[(\nabla \otimes {\mathbf{u}}) + {{(\nabla \otimes {\mathbf{u}})}^{{\text{T}}}}],\quad \mu = \tau gh.$

Добавим к системе уравнений (5)–(10) регуляризованное уравнение переноса. Для этого запишем уравнение (3) в интегральном виде, интегрируя его и усредняя по промежутку времени от $t$ до $t + \Delta t$:

$\frac{{\widehat C\widehat h - Ch}}{{\Delta t}} + \frac{1}{{\Delta t}}\int\limits_t^{t + \Delta t} \,{\text{div}}\left( {{\mathbf{u}}Ch} \right)dt{\text{'}} = \frac{1}{{\Delta t}}\int\limits_t^{t + \Delta t} \,{\text{div}}\left( {Dh\nabla C} \right)dt{\text{'}},$

величины $\widehat C$, $\widehat h$ взяты в момент времени $t + \Delta t$. Воспользуемся теоремой о среднем значении, тогда имеем

(12)

$\frac{{\widehat C\widehat h - Ch}}{{\Delta t}} + {\text{div}}({\mathbf{u}}{\text{*}}C{\text{*}}h{\text{*}}) = {\text{div}}(Dh{\text{*}}\nabla C{\text{*}}).$

Величины $h{\text{*}}({\mathbf{x}},t) = h({\mathbf{x}},t{\text{*}})$, ${\mathbf{u}}{\text{*}}({\mathbf{x}},t) = {\mathbf{u}}({\mathbf{x}},t{\text{*}})$ и $C{\text{*}}({\mathbf{x}},t) = C({\mathbf{x}},t{\text{*}})$ определены на промежуточном слое по времени: $t < t{\text{*}} < \Delta t$. Предполагается, что за малое время $\Delta t$ значения этих величин изменяются, причем изменение мало, и, при условии существования и достаточной гладкости производной, его можно оценить, ограничиваясь первым членом ряда в разложении по времени.

Построение регуляризатора выглядит следующим образом. Выпишем значения величин на временном слое $t{\text{*}}$, как и указывалось только с первым порядком по времени, где $\tau \sim \Delta t$:

${\mathbf{u}}{\text{*}} = {\mathbf{u}} + \tau \frac{{\partial {\mathbf{u}}}}{{\partial t}},\quad h{\text{*}} = h + \tau \frac{{\partial h}}{{\partial t}},\quad C{\kern 1pt} {\text{*}} = C + \tau \frac{{\partial C}}{{\partial t}}.$

Далее, по аналогии с построением КГД уравнений выразим производные по времени из исходной системы уравнений. Возьмем $\tfrac{{\partial C}}{{\partial t}}$ из уравнения (3), раскрыв производную по времени:

$h\frac{{\partial C}}{{\partial t}} + C\frac{{\partial h}}{{\partial t}} = - {\text{div}}\left( {{\mathbf{u}}hC} \right) + {\text{div}}\left( {Dh\nabla C} \right) = - C{\text{div}}\left( {{\mathbf{u}}h} \right) - \left( {{\mathbf{u}}h \cdot \nabla C} \right) + {\text{div}}\left( {Dh\nabla C} \right),$

где, подставив $\tfrac{{\partial h}}{{\partial t}}$ из (1), получим

$\frac{{\partial C}}{{\partial t}} = - \left( {{\mathbf{u}} \cdot \nabla C} \right) + \frac{1}{h}{\text{div}}\left( {Dh\nabla C} \right),$

откуда имеем

$C{\text{*}} = C - \tau \left( {{\mathbf{u}} \cdot \nabla C} \right) + O({{\tau }^{2}}),$

где слагаемое с $\tau D$ пренебрежимо мало по сравнению $O(\tau )$.

Как видно из (5), получаем

$h{\text{*}}{\mathbf{u}}{\text{*}} = h\left( {{\mathbf{u}} - {\mathbf{w}}} \right) + O({{\tau }^{2}}).$

Тогда, возвращаясь к уравнению (12), отбрасывая слагаемые порядка $O({{\tau }^{2}})$ и заменяя разностную производную по времени ее дифференциальным аналогом, получим конечный вид регуляризованного уравнения переноса:

(13)

$\frac{{\partial Ch}}{{\partial t}} + {\text{div}}\left( {{{{\mathbf{j}}}_{m}}C} \right) = {\text{div}}\left( {Dh\nabla C + \tau {\mathbf{u}}h\left( {{\mathbf{u}} \cdot \nabla C} \right)} \right).$

Сглаженное по времени уравнение (4) имеет вид

$\frac{{\partial C}}{{\partial t}} + {\text{div}}\left( {C\left[ {{\mathbf{u}} - {\mathbf{w}} + \tau \frac{{\mathbf{u}}}{h}\left( {{\mathbf{u}} \cdot \nabla h} \right)} \right]} \right) = {\text{div}}\left( {D\nabla C + \tau {\mathbf{u}}\left( {{\mathbf{u}} \cdot \nabla C} \right)} \right).$

Для расчетов далее, как уже говорилось, мы будем использовать уравнение (13) в качестве сглаженного уравнения переноса.

Алгоритм, использующий регуляризацию только уравнений гидродинамики, без включения в него регуляризации уравнения переноса, оказывается плохо устойчивым. Его сравнение с предложенным выше вариантом рассмотрено в [19].

3. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ОДНОМЕРНЫХ ТЕЧЕНИЙ

Система РУМВ совместно с уравнением переноса, записанная для плоского одномерного течения без учета внешних сил, имеет следующий вид:

(14)

$\frac{{\partial h}}{{\partial t}} + \frac{{\partial {{j}_{m}}}}{{\partial x}} = 0,$

(15)

$\frac{{\partial hu}}{{\partial t}} + \frac{{\partial {{j}_{m}}u}}{{\partial x}} + \frac{\partial }{{\partial x}}\left( {\frac{{g{{h}^{2}}}}{2}} \right) + gh\frac{{\partial b}}{{\partial x}} = \frac{{\partial \Pi }}{{\partial x}},$

(16)

$\frac{{\partial Ch}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {{{j}_{m}}C} \right) = \frac{\partial }{{\partial x}}\left( {h(D + \tau {{u}^{2}})\frac{{\partial C}}{{\partial x}}} \right),$

где

(17)

${{j}_{m}} = h\left( {u - w} \right),$

(18)

$w = \frac{\tau }{h}\left[ {\frac{{\partial (h{{u}^{2}})}}{{\partial x}} + gh\frac{\partial }{{\partial x}}\left( {h + b} \right)} \right],$

(19)

$\Pi = \tau hu\left[ {u\frac{{\partial u}}{{\partial x}} + g\frac{\partial }{{\partial x}}\left( {h + b} \right)} \right] + \tau gh\frac{{\partial \left( {hu} \right)}}{{\partial x}}.$

В этом разделе не используется дополнительная вязкость (11), т.е. $\mu = 0$.

Для численного решения регуляризованных уравнений МВ (14)–(19), подобно методам, разработанным для квазигазодинамических уравнений [17], используем явную по времени разностную схему с аппроксимацией всех пространственных производных центральными разностями, верхний индекс $k$ говорит о том, что значение рассматриваемых величин берется на $k$-м шаге по времени, для упрощения записи он опущен в правой части уравнений, где значения всех величин взяты на текущем временном шаге, т.е. ${{u}_{{i + 1/2}}} = u_{{i + 1/2}}^{k}$. Значения искомых переменных $h(x,t)$, $u(x,t)$ и $C(x,t)$ зададим в узлах пространственной сетки $i$. Значения переменных в полуцелых пространственных точках $i + 1{\text{/}}2$ находятся как среднее арифметическое значений в соседних точках:

(20)

$\begin{gathered} {{b}_{{i + 1/2}}} = \frac{{{{b}_{i}} + {{b}_{{i + 1}}}}}{2},\quad {{\tau }_{{i + 1/2}}} = \frac{{{{\tau }_{i}} + {{\tau }_{{i + 1}}}}}{2}, \\ {{h}_{{i + 1/2}}} = \frac{{{{h}_{i}} + {{h}_{{i + 1}}}}}{2},\quad {{u}_{{i + 1/2}}} = \frac{{{{u}_{i}} + {{u}_{{i + 1}}}}}{2},\quad {{C}_{{i + 1/2}}} = \frac{{{{C}_{i}} + {{C}_{{i + 1}}}}}{2}; \\ {{w}_{{i + 1/2}}} = \frac{{{{\tau }_{{i + 1/2}}}}}{{{{h}_{{i + 1/2}}}}}\left( {\frac{{{{h}_{{i + 1}}}u_{{i + 1}}^{2} - {{h}_{i}}u_{i}^{2}}}{{\Delta x}} + g{{h}_{{i + 1/2}}}\frac{{{{h}_{{i + 1}}} + {{b}_{{i + 1}}} - {{h}_{i}} - {{b}_{i}}}}{{\Delta x}}} \right); \\ \end{gathered} $

(21)

${{\Pi }_{{i + 1/2}}} = {{\tau }_{{i + 1/2}}}{{u}_{{i + 1/2}}}{{h}_{{i + 1/2}}}\left( {{{u}_{{i + 1/2}}}\frac{{{{u}_{{i + 1}}} - {{u}_{i}}}}{{\Delta x}} + g\frac{{{{h}_{{i + 1}}} + {{b}_{{i + 1}}} - {{h}_{i}} - {{b}_{i}}}}{{\Delta x}}} \right) + {{\tau }_{{i + 1/2}}}g{{h}_{{i + 1/2}}}\frac{{{{h}_{{i + 1}}}{{u}_{{i + 1}}} - {{h}_{i}}{{u}_{i}}}}{{\Delta x}};$

(22)

${{j}_{{m,i + 1/2}}} = {{h}_{{i + 1/2}}}\left( {{{u}_{{i + 1/2}}} - {{w}_{{i + 1/2}}}} \right);$

(23)

$\frac{{h_{i}^{{k + 1}} - h_{i}^{k}}}{{\Delta t}} + \frac{{{{j}_{{m,i + 1/2}}} - {{j}_{{m,i - 1/2}}}}}{{\Delta x}} = 0;$

(24)

$\frac{{h_{i}^{{k + 1}}u_{i}^{{k + 1}} - h_{i}^{k}u_{i}^{k}}}{{\Delta t}} + \frac{{{{u}_{{i + 1/2}}}{{j}_{{m,i + 1/2}}} - {{u}_{{i - 1/2}}}{{j}_{{m,i - 1/2}}}}}{{\Delta x}} + \frac{g}{2}\frac{{h_{{i + 1/2}}^{2} - h_{{i - 1/2}}^{2}}}{{\Delta x}} = - gh_{i}^{*}\frac{{{{b}_{{i + 1/2}}} - {{b}_{{i - 1/2}}}}}{{\Delta x}} + \frac{{{{\Pi }_{{i + 1/2}}} - {{\Pi }_{{i - 1/2}}}}}{{\Delta x}};$

(25)

$\begin{gathered} \frac{{C_{i}^{{k + 1}}h_{i}^{{k + 1}} - C_{i}^{k}h_{i}^{k}}}{{\Delta t}} + \frac{{{{j}_{{m,i + 1/2}}}{{C}_{{i + 1/2}}} - {{j}_{{m,i - 1/2}}}{{C}_{{i - 1/2}}}}}{{\Delta x}} = \\ = \frac{1}{{\Delta x}}\left( {{{h}_{{i + 1/2}}}\frac{{{{C}_{{i + 1}}} - {{C}_{i}}}}{{\Delta x}}(D + {{\tau }_{{i + 1/2}}}u_{{i + 1/2}}^{2}) - {{h}_{{i - 1/2}}}\frac{{{{C}_{i}} - {{C}_{{i - 1}}}}}{{\Delta x}}(D + {{\tau }_{{i - 1/2}}}u_{{i - 1/2}}^{2})} \right). \\ \end{gathered} $

Здесь подразумевается, что

(26)

$h_{i}^{*} = {{h}_{i}} - {{\tau }_{i}}\frac{{{{h}_{{i + 1/2}}}{{u}_{{i + 1/2}}} - {{h}_{{i - 1/2}}}{{u}_{{i - 1/2}}}}}{{\Delta x}}.$

Устойчивость численного алгоритма обеспечивается слагаемыми с коэффициентом регуляризации $\tau $, который определяется в виде

(27)

$\tau = \alpha \frac{l}{c},$

где $l$ – характерный размер пространственной ячейки, который используется в численном алгоритме, например, в виде $l = \sqrt s $, где $s$ – площадь ячейки, $c = \sqrt {gh} $ – скорость распространения длинной волны, $\alpha $ – численный коэффициент, выбираемый из условий точности и устойчивости счета. Как правило, 0 < $\alpha $ < 1, и в качестве базового значения можно выбирать $\alpha = 0.5$. В одномерных расчетах характерный размер полагается равным шагу пространственной сетки, $l = \Delta x$.

Условие устойчивости имеет вид условия Куранта–Фридрихса–Леви, где шаг по времени выбирается по формуле

(28)

$\Delta t = \beta \mathop {\left( {\frac{{\Delta x}}{c}} \right)}\nolimits_{{\text{min}}} ,\quad 0 < \beta < 1.$

Значение числа Куранта, $\beta $ во всех нижеперечисленных тестах: $\beta = 0.1$ (либо это оговорено). Все тестовые расчеты рассматривают задачи, в которых $D = 0$. Также во всех тестах (за исключением задач, в которых это оговорено) используются граничные условия сноса для высоты, скорости и концентрации на левой и правой границах:

$\frac{{\partial h}}{{\partial x}} = 0,\quad \frac{{\partial u}}{{\partial x}} = 0,\quad \frac{{\partial C}}{{\partial x}} = 0.$

Далее приведены примеры численного решения тестовых задач, выполненные с помощью изложенного выше разностного алгоритма. Во всех расчетах использованы равномерные пространственные сетки. Поскольку рассматривались только модельные задачи, то все величины являются безразмерными. Ряд дополнительных результатов по одномерным расчетам приведен в [19].

3.1. Адвекция загрязнения над неровным дном

Пример взят из [1]. Начальные условия изображены на фиг. 2, область $x \in [0,1]$. Рассматривается начальный уровень поверхности воды $\xi (x,0) \equiv 1$. Значение потока в начальный момент времени $Q(x,0) = h(x,0)u(x,0) = 0.1$ и полагается, что $g = 1$. Начальное распределение концентрации ограничивается областью $[0.4,0.5]$, где $C(x,0) = 1$, в остальной части области $C(x,0) = 0$. Функция дна имеет вид

$b(x) = \left\{ \begin{gathered} 0.25(cos(10\pi (x - 0.5)) + 1),\quad 0.4 \leqslant x \leqslant 0.6, \hfill \\ 0,\quad x \notin [0.4,0.6]. \hfill \\ \end{gathered} \right.$

Фиг. 2.

Начальные условия. (а) Распределение концентрации; (б) график распределения уровня поверхности воды, скорости и неровности дна.

Нетрудно видеть, что включенные в уравнение (16) регуляризирующие добавки отличны от нуля только в областях, где есть градиенты скорости и концентрации примеси. Замечено, что если в начальный момент возникает осцилляция численного решения за счет неаккуратного задания начальных условий для концентрации, то далее в областях решения с постоянной концентрацией или скоростью эти осцилляции не разглаживаются и переносятся течением без изменений. Поэтому для корректного моделирования задачи требуется аккуратное задание начального возмущения. В данном случае для этого используется сглаживание начального возмущения по сетке, а именно, начальные значения для концентрации на границе разрыва задаются в трех точках: левая (${{C}_{l}}$) и правая (${{C}_{r}}$) граница разрыва и точка между ними как полусумма граничных значений, $\tfrac{{{{C}_{l}} + {{C}_{r}}}}{2} = 0.5$.

Согласно [1], модельным решением данной задачи является перемещение начального возмущения концентрации примеси вправо по времени с сохранением его высоты $C = 1$.

На фиг. 3а приведены результаты для $t = 0$, $2$ и $4$, $\Delta x = 3.125 \times {{10}^{{ - 4}}}$, $\alpha = 0.5$.

Фиг. 3.

Распределение концентрации, $\alpha = 0.5$, $\beta = 0.1$. (а) Для различных моментов времени, $\Delta x = 3.125 \times {{10}^{{ - 4}}}$; (б) для различных значений $\Delta x$, $t = 4$.

В [1] приводится сравнение метода конечного объема (FV – Finite-Volume) и метода частиц совместно с методом конечного объема (FVP – Finite-Volume-Particle), где число частиц примеси было равно 20, оба метода рассчитывались на сетке $\Delta x = 0.005$ с применением центральной схемы с разностями против потока. При сравнении расчета, полученного с применением модели РУМВ, видно, что он соответствует результатам для FV и FVP модели в [1].

На фиг. 3б приведены результаты для различных значений $\Delta x$ при $\alpha = 0.5$, $\beta = 0.1$. Можно увидеть, что наблюдается сходимость решения при сгущении сетки.

3.2. Прорыв плотины на плоском дне

Рассмотрим классическую задачу распада разрыва на плоском дне, постановка которой взята из [8]. В данной задаче концентрация примеси, как и уровень жидкости, имеет разрыв в точке обрушения дамбы, см. фиг. 4, область $x \in [0,2000]$. Начальные значения задаются в виде $(h,u,C) = (1.0,0,0.7)$, $x \in [0,1000]$; $(h,u,C) = (0.5,0,0.5)$, $x \in [1000,2000]$. Аналогично предыдущему случаю, значения для концентрации и высоты на границе разрыва задаются в трех точках: левая и правая граница разрыва и точка между ними как полусумма граничных значений.

Фиг. 4.

Распределение концентрации и уровня поверхности воды в начальный момент времени.

Численное решение данной задачи для $\xi $ состоит из трех плоских зон – двух исходных неактивных зон по краям и промежуточной зоны, которые разделены двумя простыми волнами: волной разрежения, идущей влево, и ударной волной, идущей вправо, при этом скачок концентрации просто переносится со скоростью промежуточной плоской зоны.

Зависимость численного решения для уровня воды от коэффициента регуляризации $\alpha $ представлена на фиг. 5а, $\Delta x = 5$. При приближении к $\alpha = 0.1$ наблюдаются появление осцилляций и последующее нарушение устойчивости численного решения. Далее $\alpha = 0.3$.

Фиг. 5.

Распределение для $t = 240$, $\beta = 0.1$ (а) уровня поверхности жидкости для различных значений коэффициента $\alpha $, $\Delta x = 5$; (б) концентрации для различных сгущений разностной сетки, $\alpha = 0.3$.

На фиг. 5б демонстрируется сходимость решения для концентрации примеси при сгущении разностной сетки.

В [8] представлены результаты с использованием двухстадийной по времени кинетическoй схемы, имеющей второй порядок точности, $\Delta x = 20$. Они практически совпадают с расчетами, полученными с применением регуляризованных уравнений с использованием схемы первого порядка точности, фиг. 6.

Фиг. 6.

Распределение концентрации и уровня поверхности жидкости для $t = 240$, $\Delta x = 5$, $\alpha = 0.3$, $\beta = 0.1$.

3.3. Задача Римана с разбегающейся жидкостью

В соответствии с постановкой [4] рассматривается область $x \in [0,50]$. Начальные условия представляют собой две разбегающиеся волны от центра разрыва, расположенного в координате ${{x}_{0}} = 25$, фиг. 7. Значения слева от разрыва: $(h,u,C) = (1, - 5,1),\;x \in [0,25]$; значения справа: $(h,u,C) = (1,5,0),\;x \in [25,50]$. Время расчета $t = 2.5$. Скорость и концентрация на границе разрыва задавались в двух точках, т.е. без промежуточного сглаживания.

Фиг. 7.

Начальное распределение скорости, концентрации и уровня поверхности воды.

В момент времени $t = 2.5$ в центре области образуется так называемая зона “сухого дна”. Для описания “сухих областей” используется распространенный подход, детально описанный, например, в [20]. При этом выбирается параметр отсечения $\varepsilon $, который задает минимальное значение толщины слоя жидкости $h$, которое вычисляется на основе разностного алгоритма.

В данной задаче дно является плоским, и в качестве параметра отсечения используется постоянная величина, равная $\varepsilon = 0.001$.

В областях сухого дна жидкость покоится, поэтому при малых $h$ ставится ограничение для $\tau $ и $u$ в виде

(29)

$\tau = \left\{ \begin{gathered} \alpha \Delta x{\text{/}}\sqrt {gh} ,\quad h > \varepsilon , \hfill \\ 0,\quad h \leqslant \varepsilon , \hfill \\ \end{gathered} \right.$

(30)

${\text{если}}\;h < \varepsilon ,\quad h = \varepsilon \;{\text{и}}\;u = 0.$

Подобная задача без учета распространения примеси была рассмотрена в рамках РУМВ, ее решение, а также описание методики расчета зон обводнения/осушки приведены в [20].

В [4] указано, что для данной задачи точным решением для распределения концентрации примеси $C$ является стационарный разрыв, который в большинстве численных схем воспроизводится весьма трудоемкими методами.

Результаты для распределения $\xi $ и $C$ на момент времени $t = 2.5$, $\Delta x = 0.1$, $\alpha = 0.3$ представлены на фиг. 8. Подчеркнем, что использованный авторами алгоритм позволяет воспроизвести точное решение для распределения концентрации для любых разбиений по сетке в течение всего времени расчета.

Фиг. 8.

Результаты расчета для $t = 2.5$, $\Delta x = 0.1$, $\alpha = 0.3$. (а) График распределения уровня поверхности воды; (б) распределение концентрации.

4. РАЗНОСТНЫЙ АЛГОРИТМ ДЛЯ МОДЕЛИРОВАНИЯ ПРОСТРАНСТВЕННЫХ ТЕЧЕНИЙ И ПРИМЕР РАСЧЕТА ЗАДАЧИ О РАЗРУШЕНИИ ДАМБЫ

Разностный алгоритм для моделирования пространственных течений строится аналогично алгоритму расчета одномерных течений. Система уравнений (5)–(13) аппроксимируется с помощью метода конечного объема, причем все пространственные производные аппроксимируются центральными разностями со вторым порядком точности. Разностные схемы для РУМВ были неоднократно приведены в публикациях, например в [17]–[20]. Здесь приведем лишь аппроксимацию уравнения переноса. Отметим, что здесь для расчета двумерных течений регуляризатор Навье–Стокса (11) не отбрасывался.

Для плоской геометрии уравнение для концентрации в системе РУМВ запишется в виде

(31)

$\frac{{\partial Ch}}{{\partial t}} + \frac{{\partial {{j}_{{mx}}}C}}{{\partial x}} + \frac{{\partial {{j}_{{my}}}C}}{{\partial y}} = \frac{\partial }{{\partial x}}\left( {h(D + \tau u_{x}^{2})\frac{{\partial C}}{{\partial x}} + \tau {{u}_{x}}{{u}_{y}}h\frac{{\partial C}}{{\partial y}}} \right) + \frac{\partial }{{\partial y}}\left( {h(D + \tau u_{y}^{2})\frac{{\partial C}}{{\partial y}} + \tau {{u}_{x}}{{u}_{y}}h\frac{{\partial C}}{{\partial x}}} \right).$

Соответствующая разностная реализация имеет вид

$\begin{gathered} \widehat C\widehat h = Ch - \frac{{\Delta t}}{{\Delta x}}(j_{{i + 1/2,j}}^{x}{{C}_{{i + 1/2,j}}} - j_{{i - 1/2,j}}^{x}{{C}_{{i - 1/2,j}}}) - \frac{{\Delta t}}{{\Delta y}}(j_{{i,j + 1/2}}^{y}{{C}_{{i,j + 1/2}}} - j_{{i,j - 1/2}}^{y}{{C}_{{i,j - 1/2}}}) + \\ + \;\frac{{\Delta t}}{{\Delta x}}\left( {{{h}_{{i + 1/2,j}}}\frac{{{{C}_{{i + 1,j}}} - {{C}_{{i,j}}}}}{{\Delta x}}(D + {{\tau }_{{i + 1/2,j}}}{{{(u_{{i + 1/2,j}}^{x})}}^{2}}) + } \right.{{\tau }_{{i + 1/2,j}}}u_{{i + 1/2,j}}^{x}u_{{i + 1/2,j}}^{y}{{h}_{{i + 1/2,j}}}\frac{{{{C}_{{i + 1/2,j + 1/2}}} - {{C}_{{i + 1/2,j - 1/2}}}}}{{\Delta y}} - \\ \end{gathered} $

$\, - {{h}_{{i - 1/2,j}}}\frac{{{{C}_{{i,j}}} - {{C}_{{i - 1,j}}}}}{{\Delta x}}(D + {{\tau }_{{i - 1/2,j}}}{{(u_{{i - 1/2,j}}^{x})}^{2}}) - \left. {{{\tau }_{{i - 1/2,j}}}u_{{i - 1/2,j}}^{x}u_{{i - 1/2,j}}^{y}{{h}_{{i - 1/2,j}}}\frac{{{{C}_{{i - 1/2,j + 1/2}}} - {{C}_{{i - 1/2,j - 1/2}}}}}{{\Delta y}}} \right) + $

$\begin{gathered} \, + \frac{{\Delta t}}{{\Delta y}}\left( {{{h}_{{i,j + 1/2}}}\frac{{{{C}_{{i,j + 1}}} - {{C}_{{i,j}}}}}{{\Delta y}}(D + {{\tau }_{{i,j + 1/2}}}{{{(u_{{i,j + 1/2}}^{y})}}^{2}})} \right. + {{\tau }_{{i,j + 1/2}}}u_{{i,j + 1/2}}^{x}u_{{i,j + 1/2}}^{y}{{h}_{{i,j + 1/2}}}\frac{{{{C}_{{i + 1/2,j + 1/2}}} - {{C}_{{i - 1/2,j + 1/2}}}}}{{\Delta x}} - \\ \, - {{h}_{{i,j - 1/2}}}\frac{{{{C}_{{i,j}}} - {{C}_{{i,j - 1}}}}}{{\Delta y}}(D + {{\tau }_{{i,j - 1/2}}}{{(u_{{i,j - 1/2}}^{y})}^{2}}) - \left. {{{\tau }_{{i,j - 1/2}}}u_{{i,j - 1/2}}^{x}u_{{i,j - 1/2}}^{y}{{h}_{{i,j - 1/2}}}\frac{{{{C}_{{i + 1/2,j - 1/2}}} - {{C}_{{i - 1/2,j - 1/2}}}}}{{\Delta x}}} \right). \\ \end{gathered} $

Для демонстрации эффективности двумерного алгоритма было выбрано два характерных теста, результаты расчета которых описаны далее. Поскольку задачи модельные, то все величины являются безразмерными. Некоторые предварительные результаты по данным расчетам приведены в [19].

4.1. Задача прорыва симметричной дамбы на плоском дне

Постановка и численное моделирование данной задачи изложены в [2] и [4].

Рассматривается квадратная область $[0,1400] \times [0,1400]$, разделенная стенкой посередине. В начальный момент времени центральная секция стенки разрушается, и из-за разности уровней происходит разлив воды. На фиг. 9 изображены начальные условия для высоты уровня жидкости, скорости и концентрации. Вода вытекает через отверстие, находящееся между координатами $y = 560$ и $y = 840$; координата стенки: $x = 700$.

Фиг. 9.

Начальное распределение (а) уровня поверхности воды и скорости; (б) уровня поверхности воды с наложенной картой распределения концентрации.

Функция, описывающая начальные условия для концентрации примеси, выглядит следующим образом:

$C(x,y,t = 0) = \left\{ \begin{gathered} {{e}^{{ - 0.0001[{{{(x - 650)}}^{2}} + {{{(y - 600)}}^{2}}]}}},\quad 0 \leqslant x \leqslant 700,\quad 0 \leqslant y \leqslant 1400, \hfill \\ 0.5,\quad 700 \leqslant x \leqslant 1400,\quad 0 \leqslant y \leqslant 1400. \hfill \\ \end{gathered} \right.$

Заметим, что начальное распределение концентрации примеси несимметрично относительно положения стенки.

Условия на границах, соответствующих $x = 0$ и $x = 1400$, ставились в виде условий сноса:

$\frac{{\partial h}}{{\partial x}} = 0,\quad \frac{{\partial C}}{{\partial x}} = 0,\quad \frac{{\partial {{u}_{x}}}}{{\partial x}} = 0,\quad \frac{{\partial {{u}_{y}}}}{{\partial x}} = 0.$

Условия отражения ставились для стенок $y = 0$, $y = 1400$:

$\frac{{\partial h}}{{\partial y}} = 0,\quad \frac{{\partial C}}{{\partial y}} = 0,\quad \frac{{\partial {{u}_{x}}}}{{\partial y}} = 0,\quad {{u}_{y}} = 0,$

а также на внутренних стенках:

$\frac{{\partial h}}{{\partial x}} = 0,\quad \frac{{\partial C}}{{\partial x}} = 0,\quad {{u}_{x}} = 0,\quad \frac{{\partial {{u}_{y}}}}{{\partial x}} = 0.$

Результаты для $t = 200$ представлены на фиг. 10 и 11 . Коэффициенты $\alpha = 0.5$, $\beta = 0.2$. Число разбиений по сетке: ${{N}_{x}} = {{N}_{y}} = 500$, что соответствует: $\Delta x = \Delta y = 2.8$, такие же разбиения сетки используются в [2] и [4].

Фиг. 10.

Результаты расчета для распределения уровня поверхности воды. (а) В трехмерном виде; (б) изолинии уровня и линии тока.

Фиг. 11.

Результаты расчета для распределения концентрации примеси. (а) В трехмерном виде; (б) в проекции на плоскость $Oxy$.

В [2] приводится сравнение метода конечного объема (FV – Finite-Volume) и метода частиц совместно с методом конечного объема (FVP – Finite-Volume-Particle). Поэтому далее результаты расчета с применением РУМВ будут сравниваться с этими двумя моделями.

Расчеты хорошо согласуются с [2] и [4]. При уменьшении $\alpha $ до $0.2$ увеличивается амплитуда вихрей, что соответствует картине, представленной в [2], [4]. Также из фиг. 10 видно, что решение для поверхности жидкости хорошо демонстрирует картину как кругового гидравлического скачка, так и вихрей, образованных по обе стороны от разрыва. Аналогично для концентрации – фиг. 11 – можно наблюдать четкое расположение фронтов и структур внутри вихрей, как и в [2].

Присутствуют незначительные осцилляции концентрации примеси в малом вихре, которые, однако, встречаются и в [2] для FV метода. В случае же FVP метода вихрь неестественно сглажен, что вызывает сомнения с точки зрения корректности решения из [2].

5. ЗАДАЧА О РАЗРУШЕНИИ ДАМБЫ НАД НЕРОВНЫМ ДНОМ ПРИ НАЛИЧИИ ИСТОЧНИКА

Аналогичным образом, применяя квазигазодинамический подход, приведенная выше система РУМВ с учетом переноса примеси была обобщена на случай переноса при наличии источника примеси. Уравнения МВ с учетом источника примеси отличаются от классических уравнений (1)–(4) наличием источника массы $S$ в правой части уравнения (1) и источником примеси в правой части уравнений (3) или (4), см., например, [4], [8].

Система РУМВ вместе с уравнением переноса при наличии источника примеси и без учета внешних сил имеет вид

(32)

$\frac{{\partial h}}{{\partial t}} + \operatorname{div} {{{\mathbf{j}}}_{{\mathbf{m}}}} = S,$

(33)

(34)

$\frac{{\partial Ch}}{{\partial t}} + {\text{div}}\left( {{{{\mathbf{j}}}_{m}}C} \right) = {\text{div}}\left( {Dh\nabla C + \tau {\mathbf{u}}\left[ {\left( {{\mathbf{u}}h \cdot \nabla C} \right) + CS - {{T}_{s}}S} \right]} \right) + {{T}_{s}}S,$

где

(35)

$h{\text{*}} = h - \tau \left( {{\text{div}}\left( {h{\mathbf{u}}} \right) - S} \right),$

(36)

${{{\mathbf{j}}}_{m}} = h\left( {{\mathbf{u}} - {\mathbf{w}}} \right),$

(37)

${\mathbf{w}} = \frac{\tau }{h}\left[ {{\text{div}}\left( {h{\mathbf{u}} \otimes {\mathbf{u}}} \right) + gh\nabla \left( {b + h} \right)} \right],$

(38)

$\Pi = {{\Pi }_{{NS}}} + \tau {\mathbf{u}} \otimes \left[ {h\left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}} + gh\nabla \left( {b + h} \right) + S{\mathbf{u}}} \right] + \tau I\left[ {gh\left( {{\text{div}}\left( {h{\mathbf{u}}} \right) - S} \right)} \right].$

Обозначения, принятые в РУМВ, остаются без изменений. Помимо этого, в уравнении присутствуют: $S({\mathbf{x}},t)$ – источник жидкости, и ${{T}_{s}}$ – значение концентрации примеси в источнике $S$.

Регуляризатор (35)–(38) для системы уравнений (32)–(34) построен с учетом включенного в систему источника примеси. Как показали дальнейшие численные эксперименты, включение источника $S$ в формулы для дополнительной диссипации не влияeт на результат численного решения представленной далее задачи. Тем не менеe, как отмечено в [4] и [8], для системы уравнений с источником появляется необходимость выполнения нетривиальных условий баланса и законов сохранения, чего добиваются не все схемы. Для оценки влияния этого фактора на решение системы (32)–(38) возможно обобщение энергетической оценки решения из [21].

Для апробации алгоритма был взят тест, приведенный в [2].

Рассматривается квадратная область: $[0,1400] \times [0,1400]$, в ней имеется разрыв сложной формы, который начинает распадаться начиная со времени $t = 0$. Начальное распределение глубины и скоростей показанo на фиг. 12. Граница двух областей описывается следующей функцией:

$\Gamma (y) = \left\{ \begin{gathered} min\left[ {500 + \tfrac{{{{{(y - 700)}}^{2}}}}{{400}},900} \right],\quad 0 \leqslant y \leqslant 700, \hfill \\ 500,\quad 700 \leqslant y \leqslant 1400. \hfill \\ \end{gathered} \right.$

Фиг. 12.

Начальное распределение уровня поверхности воды и потоков.

Дно в этой задаче имеет форму трех эллиптических гауссианов:

$b(x,y) = 4.5\left[ {{{e}^{{ - {{\kappa }_{1}}{{{(x - 800)}}^{2}} - {{\kappa }_{2}}{{{(y - 700)}}^{2}}}}} + {{e}^{{ - {{\kappa }_{2}}{{{(x - 600)}}^{2}} - {{\kappa }_{1}}{{{(y - 600)}}^{2}}}}} + {{e}^{{ - {{\kappa }_{2}}{{{(x - 1000)}}^{2}} - {{\kappa }_{1}}{{{(y - 700)}}^{2}}}}}} \right],$

где ${{\kappa }_{1}} = {{10}^{{ - 4}}}$, ${{\kappa }_{2}} = {{10}^{{ - 3}}}$.

Начальное условие для концентрации: $C(x,y,t = 0) = 0$, но в дальнейшем, из-за наличия источника, задаваемого формулой:

$S(x,y,t) = 0.5{{e}^{{ - 0.5{{{(t - 8)}}^{2}} - 0.00001{{{(x + y - 1300)}}^{2}} - 0.0005{{{(x - y - 100)}}^{2}}}}},$

концентрация примеси в котором ${{T}_{s}} = 25$, концентрация $C$ возрастает.

На границах ставились условия сноса:

$\frac{{\partial h}}{{\partial {\mathbf{n}}}} = 0,\quad \frac{{\partial C}}{{\partial {\mathbf{n}}}} = 0,\quad \frac{{\partial {{u}_{n}}}}{{\partial {\mathbf{n}}}} = 0,\quad \frac{{\partial {{u}_{\tau }}}}{{\partial {\mathbf{n}}}} = 0,$

здесь индексы $n$ и $\tau $ соответствуют нормальным и тангенциальным направлениям к границе области соответственно.

Результаты моделирования представлены на фиг. 13, 14 и 15 для времени расчета $t = 30$ и $\alpha = 0.5$, $\beta = 0.2$, ${{N}_{x}} = {{N}_{y}} = 500$, что соответствует: $\Delta x = \Delta y = 2.8$.

Фиг. 13.

Результаты расчета. Изолинии уровня поверхности жидкости.

Фиг. 14.

РУМВ: Изолинии распределения концентрации примеси для различных моментов времени. (а) $t = 7.5$; (б) $t = 15$; (в) $t = 22.5$; (г) $t = 30$.

Фиг. 15.

Сравнение расчетов для 2D проекции концентрации примеси ($C(y)$) на момент времени $t = 30$ для РУМВ ($\beta = 0.2$, $\alpha = 0.5$, ${{N}_{x}} = {{N}_{y}} = 500$), FV и FVP из [2].

В [2] приводится сравнение метода конечного объема (FV – Finite-Volume) и метода частиц совместно с методом конечного объема (FVP – Finite-Volume-Particle) для такого же разбиения по сетке ${{N}_{x}} = {{N}_{y}} = 500$. Поэтому результаты расчета с применением РУМВ будут сравниваться с этими двумя моделями.

На фиг. 13 приведен результат для распределения уровня поверхности воды. Можно заметить, что столкновение искривленной ударной волны начального распределения с неровностями дна приводит к довольно сложным волновым структурам. Полученное распределение соответствует расчету, приведенному в [2].

Результаты для РУМВ эволюции изменения концентрации примеси во времени изображены на фиг. 14 на те же моменты времени, что и в работе [2]. Подчеркнем, что оба расчета выполнены на одинаковых пространственных сетках, при этом метод РУМВ имеет первый порядок точности по пространству, а метод из [2] – как минимум второй. Визуальное сопоставление результатов РУМВ и [2] показывает их близкое соответствие.

На фиг. 15 можно увидеть сравнение результатов расчетов для концентрации в двумерной проекции на оси $(C,y)$, выполненное путем наложения изображений. Как видно, результат, полученный с помощью модели РУМВ ($\beta = 0.2$, $\alpha = 0.5$, ${{N}_{x}} = {{N}_{y}} = 500$), находится между методами FV и FVP из [2]. Как и в приведенном выше расчете задачи о разрушении дамбы, метод FVP из [2] представляется излишне сглаженным.

Также на фиг. 16 приводятся зависимость численного решения от сгущения сетки ($\beta = 0.2$, $\alpha = 0.5$) и изменения параметра $\alpha $ (${{N}_{x}} = {{N}_{y}} = 400$, $\beta = 0.2$). Из приведенных фигур ясно видны сходимость численного решения при сгущении пространственной сетки и улучшение разрешения особенностей распределения концентрации при уменьшении параметра регуляризации $\alpha $.

Фиг. 16.

РУМВ: 2D проекция концентрации примеси ($C(y)$), $\beta = 0.2$. (а) Для различных разбиений сетки, $\alpha = 0.5$; (б) для различных значений $\alpha $, ${{N}_{x}} = {{N}_{y}} = 400$.

6. РАСЧЕТ ЦИРКУЛЯЦИИ ОЗЕРА ВАЛУНДЕН

Рассматривается озеро Валунден, Шпицберген, 77°53$\prime $ N, 16°46$\prime $ E, [15], [16], фиг. 17. Размеры озера порядка 1300 на 700 м. Дно достаточно ровное, с быстро нарастающей глубиной. Глубина в центре озера порядка 10–12 м. Озеро сообщается с морским заливом – фьордом – через узкий пролив, глубина которого около 1 м. Из-за сильных приливов, которые сопровождаются колебаниями уровня воды во фьорде, достигающим 2 м, в канале, соединяющем фьорд и озеро, возникает нестационарное течение со скоростями до 1 м/с. Известно, что втекающий в озеро поток имеет более низкую температуру, чем вода в озере. Это реальная практическая задача, поэтому все величины указаны в единицах СИ, кроме концентрации примеси, о которой будет сказано ниже.

Фиг. 17.

Озеро Валунден: (а) схема расположения озера, взятая из [15]; (б) снимок со спутника, взятый из сети Интернет.

Целью работы был расчет течений в озере, которые возникают во время притока/оттока воды из фиорда. Помимо этого, требовалось выяснить, как втекающая вода может влиять на образование льда в холодное время. Для упрощенной модели этого процесса использовалось уравнение переноса, в котором втекающая вода низкой температуры рассматривалась как “примесь”. Распределение концентрации “примеси” в таком случае можно сопоставить с толщиной льда, который нарастает в озере в холодное время года и оказывается более толстым вблизи входа в канал по сравнению с его толщиной в остальной части озера. Поэтому далее концентрация $С$ указана в абстрактных безразмерных единицах.

Для физически корректного моделирования озера в качестве внешней силы была добавлена сила Кориолиса:

${{f}_{x}} = {{f}^{c}}{{u}_{y}},\quad {{f}_{y}} = - {{f}^{c}}{{u}_{x}}.$

Параметр Кориолиса ${{f}^{c}} = 2\Omega sin\phi $, где $\Omega = 7.2921 \times {{10}^{{ - 5}}}$ с^–1 – угловая скорость вращения Земли, был взят константой для всей области на географической широте $\phi = {{77.866667}^{{^{ \circ }}}}$.

Для батиметрии озера была построена следующая модель, см. фиг. 18а: глубина воды во входном канале 1 м, однако имеется возвышенность в точке соединения канала с озером, фиг. 18б, ширина канала приблизительно 10–12 м, длина всего канала составляет примерно 200 м, глубина самого озера – 10 м, высота берегов над озером – 2 м.

Фиг. 18.

(а) Модель батиметрии озера; (б) место входа канала в озеро в разрезе, $L$ – расстояние вдоль оси канала, голубым цветом обозначен уровень воды ($\xi = 10$ м).

Поскольку ось $y$ совпадает с направлением нормали к границе вычислительной области, то для моделирования притока холодной воды в озеро, на границе впадающего в озеро канала ($x = 1300$, фиг. 18б) были заданы следующие граничные условия:

$\frac{{\partial h}}{{\partial y}} = 0,\quad {{u}_{y}} = - sin\left( {\frac{{\pi t}}{6}} \right)\;{\text{м/с}},\quad {{u}_{x}} = 0\;{\text{м/с}},\quad C = 1,$

где время $t$ указано в часах. Профиль нормальной компоненты скорости на границе канала продемонстрирован на фиг. 19.

Фиг. 19.

Значение скорости ${{u}_{n}} = - {{u}_{y}}$ на границе втекающего канала.

Для других границ в роли граничного условия выступало условие “сухого дна”: (29), (30).

Поскольку коэффициент диффузии “примеси”, т.е. в данном случае коэффициент температуропроводности воды $D$, очень мал (для 0°С $D \sim 13.2 \times {{10}^{{ - 8}}}$ м²/с), для расчета циркуляции, помимо дополнительного регуляризатора типа Навье–Стокса (11) в уравнении (10), к коэффициенту $D$ в (13) была внесена искусственная добавка $\delta \mu $, где $\delta $ – безразмерный коэффициент, выбираемый из условий устойчивости и точности расчета, а $\mu $ – коэффициент вязкости, взятый из (11):

$D \to D + \delta \mu ,\quad \mu = \tau gh.$

Необходимость такой добавки в данной задаче обусловлена малым значением скоростей, вследствие чего диссипативное слагаемое $ \sim {\kern 1pt} \tau h{{u}^{2}}$ в (13) оказывается малым.

Численные параметры представленных ниже расчетов следующие:

${{N}_{x}} = 247,\quad \Delta x \simeq 4.1\;{\text{м,}}$

${{N}_{y}} = 234,\quad \Delta y \simeq 5.4\;{\text{м,}}$

$\alpha = 0.3,\quad \beta = 0.2,\quad \delta = 0.1,\quad \varepsilon = 0.01.$

На фиг. 20 изображена картина течения и линии уровня абсолютного значения скорости ${\text{|}}u{\text{|}} = \sqrt {u_{x}^{2} + u_{y}^{2}} $ для двух значений времени 3 и 9 ч, которые соответствуют максимуму и минимуму скорости втекания воды в озеро. Распределение величины скорости – порядка нескольких сантиметров в секунду вдали от канала – согласуется с экспериментальными наблюдениями [16]. Также можно заметить отчетливую картину образования кругового вихря диаметром 200–300 м, что также соответствует экспериментальным наблюдениям.

Фиг. 20.

Циркуляция, образованная на озере, а также линии уровня абсолютного значения скорости ${\text{|}}u{\text{|}}$ для (а) $t = 3$ ч; (б) $t = 9$ ч.

На фиг. 21 приведено распределение концентрации примеси, втекающей в озеро для моментов времени $t = 3$ ч и $t = 15$ ч, соответствующим двум максимумам значения скорости втекания. Концентрация втекающей холодной воды определяет формирование и распределение толщины льда при замерзании озера.

Фиг. 21.

Распределение концентрации примеси в озере для (а) $t = 3$ ч; (б) $t = 15$ ч.

В целом в решении действительно образуется завихрение, причем численные эксперименты показали, что наличие силы Кориолиса не влияет на образование циркуляции, т.е. циркуляция образуется исключительно за счет формы озера и положения втекающего потока.

Холодная вода концентрируется вблизи зоны входа канала в озеро, и, как показывают данные многолетних наблюдений [15], [16], это соответствует реальной картине распределения толщины льда – лед значительно толще в области формирования вихря.

7. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

В работе впервые построены регуляризованные уравнения гидродинамики совместно с уравнением для переноса пассивного скаляра, которым может быть, в частности, концентрация примеси в жидкости. В численных экспериментах на примере течений в приближении мелкой воды показано, что наличие дополнительной регуляризации в уравнении для переноса скаляра существенно улучшает устойчивость численного решения для уравнения переноса по сравнению с использованием регуляризации только для уравнений неразрывности и импульса.

Аналогичный прием можно применить и для решения уравнений Навье–Стокса для описания течения неизотермической вязкой несжимаемой жидкости, рассматривая уравнение теплопроводности как уравнение переноса пассивного скаляра с концентрацией $C$. В этом случае регуляризованный вид системы запишется как

(39)

$\nabla \cdot ({\mathbf{u}} - {\mathbf{w}}) = 0,$

(40)

$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \nabla \cdot \left( {\left( {{\mathbf{u}} - {\mathbf{w}}} \right) \otimes {\mathbf{u}}} \right) - \nu ((\nabla \otimes {\mathbf{u}}) + {{(\nabla \otimes {\mathbf{u}})}^{{\text{T}}}}) - \nabla \cdot ({\mathbf{u}} \otimes {\mathbf{w}}) = - \frac{1}{{{{\rho }_{0}}}}\nabla p + {\mathbf{f}},$

где скорость

(41)

${\mathbf{w}} = \tau (({\mathbf{u}} \cdot \nabla ){\mathbf{u}} + \frac{1}{{{{\rho }_{0}}}}\nabla p - {\mathbf{f}}),$

а регуляризованный вид уравнения переноса примеси есть

(42)

$\frac{{\partial C}}{{\partial t}} + \nabla \cdot \left( {({\mathbf{u}} - {\mathbf{w}})C} \right) = \nabla \cdot \left( {\frac{\nu }{{Sc}}\nabla C + \tau {\mathbf{u}}\left( {\nabla \cdot {\mathbf{u}}C} \right)} \right).$

Здесь $\tfrac{\nu }{{Sc}}$ – коэффициент диффузии примеси, или, для теплопроводной жидкости, коэффициент температуропроводности.

Отметим, что ранее уравнение вида (42) записывалось без учета слагаемого с градиентом $C$ в правой части, что приводило к существенным осцилляциям численного решения при моделировании течений с большими скоростями потока.

В заключение авторы выражают благодарность А.А. Злотнику за конструктивные замечания по поводу вида регуляризованных уравнений и за плодотворные идеи по постановке начальных условий в задачах переноса, а также Е.Г. Морозову за постановку задачи об озере Валунден и советы по интерпретации результатов.

Список литературы

Chertock A., Kurganov A., Petrova G. Finite-volume-particle methods for models of transport of pollutant in shallow water // J. of Scientific Comput. 2006. V. 27. P. 189–199.
Chertock A., Kurganov A. On a hybrid finite-volume-particle method // ESAIM: M2AN. 2004. Vol. 38. № 6. P. 1071–1091.
Квон В.И., Квон Д.В., Зонов С.Д. и др. Численный расчет течений и дальнего переноса примеси в равнинных речных водохранилищах // Прикл. матем. и теор. физ. 2003. Т. 44. № 6. С. 158–163.
Delis A.I., Katsaounis T. A generalized relaxation method for transport and diffusion of pollutant models in shallow water // Computational Methods in Applied Mathematics. 2004. V. 4. №. 4. P. 410–430.
Benkhaldoun F., Elmahi I., Seaid M. Well-balanced finite volume schemes for pollutant transport on unstructured meshes // J. of Comput. Physics. 2007. V. 226. P. 180–203.
Chaabelasri E.M., Elmah I., Abdellaoui R. et al. Well balanced adaptive simulation of pollutant transport by shallow water flows: application to the bay of Tangier // Internat. J. of Hydraulic Enging. 2014. V. 3. №. 1. P. 10–23.
Bristeau M.-O., Perthame B. Transport of pollutant in shallow water using kinetic schemes // ESAIM: Proc. 2001. V. 10. P. 9–21.
Audusse E., Bristeau M.-O. Transport of pollutant in shallow water a two time steps kinetic method // ESAIM: M2AN. 2003. V. 37. №. 2. P. 389–416.
Fernandez-Nieto E.D., Narbona-Reina G. Extension of WAF type methods to non-homogeneous shallow water equations with pollutant // J. of Scientific Comput. 2008. V. 36. P. 193–217.
Чуруксаева В.В., Михайлов М.Д. Численное моделирование потока жидкости над рельефом дна // Вестн. Том. гос. ун-та. Матем. и механ. 2014. № 1(27). С. 51–60.
Chaabelasri E.M., Elmah I., Abdellaoui R. et al. Numerical solution of advection diffusion reaction equation coupled with shallow water equation // Internat J. of Scientific & Enging Research. 2017. V. 8. P. 256–262.
Четверушкин Б.Н. Кинетические схемы и квазигазодинамическая система уравнений. М.: Макс-Пресс, 2004. С. 332.
Шеретов Ю.В. Динамика сплошных сред при пространственно-временном осреднении. Москва–Ижевск: НИЦ “Регулярная и хаотическая динамика”. 2009. С. 400.
Елизарова Т.Г. Квазигазодинамические уравнения и методы расчета вязких течений. М.: Научный мир, 2007. С. 351.
Marchenko A.V., Morozov E.G. Asymmetric tide in Lake Vallunden (Spitsbergen) // Nonlinear Process. Geophys. Discuss. 2013. V. 20. P. 935–944. URL: https://doi.org/10.5194/npg-20-935-2013
Morozov E.G., Marchenko A.V., Filchuk K.V. et al. Sea ice evolution and internal wave generation due to a tidal jet in a frozen sea // Applied Ocean Research. 2019. V. 87. P. 179–191. URL: https://doi.org/10.1016/j.apor.2019.03.024.
Булатов О.В., Елизарова Т.Г. Регуляризованные уравнения мелкой воды и эффективный метод численного моделирования течений в неглубоких водоемах // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. № 1. С. 170–184.
Шеретов Ю.В. Регуляризованные уравнения гидродинaмики. Тверь: Тверской государственный университет, 2016. С. 222.
Елизарова Т.Г., Иванов А.В. Метод регуляризации для численного моделирования переноса примеси в мелкой воде // Препринты ИМП им. М.В. Келдыша. 2019. № 27. С. 1–28.
Булатов О.В., Елизарова Т.Г. Регуляризованные уравнения мелкой воды для численного моделирования течений с подвижной береговой линией // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 4. С. 665–684.
Злотник А.А. О построении квазигазодинамических систем уравнений и баротропной системы с потенциальной массовой силой // Матем. моделирование. 2012. Т. 24. № 4. С. 65–79.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал