Журнал вычислительной математики и математической физики, 2020, T. 60, № 9, стр. 1620-1638

1. ВВЕДЕНИЕ

Исследование операций как совокупных целенаправленных действий включает в себя и математическую теорию принятия решений, к которой относится данная статья. Большинство задач принятия управляющих решений в реальных системах характеризуется множественностью целей. Часть имеющихся целей удается ранжировать и затем вводить самые существенные из них в ограничения, часть целей удается “свернуть” – агрегировать в более общие, используя весовые коэффициенты [1]. Однако довести задачу до однокритериальной оптимизации, как правило, не получается по следующей объективной причине.

Процесс принятия решений в сложных системах является коллективным: различные члены коллектива могут иметь разные цели, и каким будет компромисс между ними, заранее не известно [2]. Даже если коллектив устроен иерархически и в нем существует лицо, принимающее решение в последней инстанции, традиционно называемое ЛПР, то ЛПР вряд ли сформулирует свою точную цель системному аналитику. В теории исследования операций, как и в практике управления, ЛПР и исследователь операции (ИО) специально разделены, поскольку именно за ЛПР должна оставаться функция окончательного выбора, неотделимая от ответственности [1].

Тем не менее круг целей операции обычно удается очертить, и задача ИО как разработчика системы поддержки принятия решений состоит не в том, чтобы путем оптимизации заданных критериев некоторое решение выбрать, но в том, чтобы отбросить заведомо неоптимальные решения и получить по данным критериям представительное множество оценок возможных результатов коллектива, причем, вообще говоря, в условиях, когда не все зависит лишь от их действий. Из-за необходимости учета неконтролируемых факторов при оценке последствий различных решений эта задача оказывается неординарной даже в постановочном плане.

В наиболее простых случаях в исследовании операций принимается модель трактовки неконтролируемых факторов как неопределенных, и при оценке предлагаемого решения используются наихудшие их значения. Но зачастую такие оценки получаются малоинформативными: тривиальными, излишне пессимистичными и пр. Тогда необходимо строить модель неконтролируемых факторов, в том числе пытаться их разделить, классифицировать причины их возникновения, уточнять параметры. В данной работе подобному моделированию уделяется довольно много внимания. Покажем, что разные модели неопределенности и неконтролируемости приводят к различающимся результатам, поэтому адекватность модели для анализируемой операции является первоочередным условием успешности ее применения.

В однокритериальных задачах ситуация существенно упрощается, когда можно обосновать случайность неконтролируемых факторов и получить информацию о виде (а лучше и о параметрах) их функций распределения. В таком варианте общепринято осреднение критериев (но не ограничений, которые должны выполняться с заданной вероятностью, в частности с вероятностью 1, при любых значениях случайных факторов), что сводит анализ к более или менее стандартным оптимизационным постановкам [3]. В многокритериальных (МК) задачах проблема учета случайных факторов остается открытой. Она не решается путем осреднения, аналогичного скалярному, поскольку для каждой компоненты вектор-функции выигрышей ее среднее значение достигается на своей реализации случайного фактора, и неясно, на какую именно реализацию ориентироваться при оптимизации вектора в целом. Модельные вопросы отношения к случайным факторам в МК-оптимизации поднимались в наших работах [4], [5]. Отчасти затронем их в разд. 4 в контексте оценки использования ЛПР смешанных стратегий.

Еще одна принятая в исследовании операций модель неслучайных неконтролируемых факторов – это их трактовка как целенаправленных действий противника. Такая игровая трактовка в скалярных задачах приводит к тому же результату, что и в первой модели – с неопределенностью, но только пессимистичное значение уже получает содержательное объяснение. В МК-задачах указанная трактовка меняет сам результат, а именно, искомые оценки достижимых значений вектора критериев. В разд. 2, 3 анализируются и формально сопоставляются соответствующие две модели в терминах МК-игр с фиксированным порядком ходов, чтобы отделить постановки, в которых наибольший гарантированный выигрыш максимизирующего игрока автоматически совпадает с наименьшим гарантированным проигрышем минимизирующего, от тех, где это возможно лишь в вырожденных случаях. В разд. 4–6 обсуждаются понятия решения и значения МК-игры преимущественно для второй постановки, изучаются свойства введенных понятий. Предложена параметризация решения и значения МК-игры с помощью обратной логической свертки (ОЛС) [6] на базе скаляризации по Гермейеру [1]. Проведено сравнение с линейной скаляризацией для МК-обобщения Шепли [7] равновесия Нэша.

2. МК-ЗАДАЧА С НЕОПРЕДЕЛЕННЫМИ ФАКТОРАМИ

Предположим, что цель принятия решений (цель операции [1], [3]) сформулирована в виде МК-задачи [1], [2], [8] максимизации вектор-функции $\Phi (x,y)$ = $({{\varphi }_{1}}(x,y), \ldots ,{{\varphi }_{n}}(x,y))$ путем выбора управляющего параметра $x \in X$ с учетом наличия неконтролируемого фактора $y \in Y$. Отметим, что, строго говоря, наличие векторного критерия свидетельствует о неясности цели и, согласно [1], ее необходимо уточнять. Однако, как уже упоминалось выше, уточнение цели – прерогатива участника-ЛПР, который формирует цель иногда уже в процессе объявления решения. С точки зрения ИО (а на его стороне и авторы статьи) имеется неявная цель, заданная набором ${{\varphi }_{i}}$, $i = \overline {1,n} $.

Пусть без ограничения общности $\Phi (x,y) \geqslant 0$. Здесь и далее стандартные знаки неравенств для векторов понимаются в смысле покомпонентных неравенств, а перечеркнутый знак служит для обозначения отрицания соответствующего векторного неравенства. Множества $X$ и $Y$ будем полагать конечными или компактными в евклидовом пространстве, в последнем случае функции ${{\varphi }_{i}}$ считаем непрерывными по совокупности переменных. В данном разделе рассмотрим операцию, в которой параметр $y$ моделирует неопределенный фактор, принимающий произвольные значения из множества $Y$, и никаких вероятностных характеристик для него не задано.

Если ИО рассчитывает иметь информацию о конкретном реализовавшемся значении ${{y}^{1}}$ параметра $y$ до принятия решения о выборе $x \in X$, то, отбросив заведомо неоптимальные решения, он рекомендует ЛПР выбирать $x$ из множества неулучшаемых по векторному критерию стратегий, т.е. из тех $x$, на которых достигается $\mathop {{\text{Max}}}\limits_{x \in X} \,\Phi (x,{{y}^{1}})$. (Всюду в работе с помощью максимума или минимума с большой буквы обозначается множество максимальных/минимальных элементов в смысле отношения $ < $ между векторами, так что речь, как правило, идет о множестве Слейтера [8].) Но заранее гарантировать ЛПР векторы $\varphi {\text{*}} \in \mathop {{\text{Max}}}\limits_{x \in X} \,\Phi (x,{{y}^{1}})$ ИО не может, поскольку выбор ${{y}^{1}}$ ему еще не известен, и оценить возможные значения $\varphi {\text{*}}$ ИО должен из расчета на допустимость любых ${{y}^{1}} \in Y$. Гарантированные МК-оценки вводятся следующим образом.

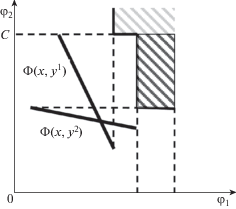
Если какое-либо значение $\varphi $ векторного критерия $\Phi (\, \cdot \,)$ ИО может гарантировать, то с учетом заинтересованности ЛПР в максимизации $\Phi $ будем считать гарантированной и любую оценку МК-результата ЛПР, не превышающую $\varphi $ ни по одной компоненте. Тем самым предполагается, что возможность получить по частному критерию, например ${{\varphi }_{i}}$, результат $\varphi _{i}^{*}$ автоматически означает для ЛПР достижимость и всех оценок ${{\psi }_{i}} < \varphi _{i}^{*}$ критерия ${{\varphi }_{i}}$ путем реализации более высокой оценки $\varphi _{i}^{*}$. Подчеркнем разницу между достижимым значением векторного критерия и достижимой оценкой получаемых значений (при конкретном ${{y}^{1}} \in Y$). А именно, значение $\varphi $ векторного критерия достигается, если существует $x \in X$: $\Phi (x,{{y}^{1}}) = \varphi $, оценка $\psi $ векторного критерия для максимизирующего его ЛПР достигается, если существует $x \in X$: $\Phi (x,{{y}^{1}}) \geqslant \psi $. (На фиг. 1а показано соответствующее различие.)

Теперь выпишем множество

достижимых МК-оценок векторного критерия $\Phi $ при известном $y$. Тогда при априорной возможности любого $y \in Y$ ИО может гарантировать ЛПР лишь оценки из пересечения $\bigcap\nolimits_{y \in Y} {{{\Psi }_{1}}(y)} $ указанных множеств. Наилучший гарантированный результат (НГР) в этом случае определяется неулучшаемыми из гарантированных МК-оценок – задается формулой Следуя логике [8]–[13], множество (2.1) можно рассматривать как НГР информированного, т.е. делающего свой ход вторым, игрока-ЛПР в антагонистической МК-игре (которую строго определим в разд. 3). Появление множества в качестве значения максимума в (2.1) характерно для МК-задач в силу неполного порядка, формируемого среди векторных оценок $\psi \in {{\mathbb{R}}^{n}}$ отношением $ < $ (см. фиг. 1б, в).

Если ИО не уверен, что до принятия решения о выборе $x \in X$ станет известным конкретное реализовавшееся значение параметра $y$, то какое бы решение ${{x}^{0}}$ ни оказалось выбранным ЛПР, никакие оценки вектора критериев, не входящие в множество

ИО гарантировать не может. Всe множество гарантированных оценок вектора критериев, т.е. оценок, на которые допустимо рассчитывать в подобной ситуации, задается формулой $\bigcup\nolimits_{x \in X} {{{\Psi }_{2}}(x)} $. И поскольку аналогично предыдущему случаю НГР определяется неулучшаемыми из гарантированных МК-оценок, выводим следующую формулу для значения НГР неинформированного ЛПР: Множество (2.2) – НГР игрока, делающего ход первым в антагонистической МК-игре [8]–[13]. Пара множеств (2.1) и (2.2) представляет собой МК-аналог понятий минимакса и максимина для максимизирующего ЛПР (в разд. 3 покажем, что для минимизирующего ЛПР они будут выглядеть иначе – в отличие от скалярных случаев).

Вопросам формализации значений МК-максимина и МК-минимакса и получения МК-гарантированных оценок при наличии неопределенных факторов посвящено довольно много работ (кроме уже упоминавшихся), в том числе для динамических постановок задач. Из последних отметим [14] на базе подхода, предложенного в [15]. Связь (2.1), (2.2) с построениями из [15] подробно обсуждалась в [16] и останавливаться на нюансах их различий в настоящей работе не будем, приняв за основу наиболее распространенные определения [8]. К тому же для данных формулировок (в отличие от [14]) справедливо [16] обобщение скалярного соотношения “максимин не больше минимакса”, отражающего одно из принципиальных положений исследования операций, что информированность не может ухудшить результат [1]. (Вся имеющаяся и ожидаемая информация должна быть использована в модели при вычислении НГР.)

Для того чтобы в операции с векторным критерием учесть, что неконтролируемый фактор вызван действиями другого ЛПР, преследующего собственные цели, в разд. 3, 4 изучим МК-игру с нулевой суммой согласно [13] и ее отличие от антагонистической в общей логике противоположности интересов. При этом, независимо от порядка ходов, игрока-ЛПР, максимизирующего векторный критерий, будем считать игроком 1 (1-м игроком), а его противника – игроком 2, или 2-м игроком (ЛПР 2).

3. МОДЕЛИ НЕКОНТРОЛИРУЕМЫХ ФАКТОРОВ, ОБУСЛОВЛЕННЫХ ДЕЙСТВИЯМИ ЛПР

Рассмотрим обобщенную операцию, в которой участвуют со своими коллективами два ЛПР (1-й и 2-й), также называемые игроками. Пусть векторные критерии эффективности действий каждого из них зависят еще и от действий партнера/противника. Эту операцию назовем МК-игрой (двух лиц). В принципе, можно говорить о двух операциях с двумя ЛПР и двумя ИО, но для анализа взаимосвязи удобнеe объединить их в одно целое, чтобы интерпретировать неконтролируемый фактор как результат частичной операции (целенаправленных действий, хотя и с неявной целью).

В МК-игре с противоположными интересами предполагается, что выбор значений неконтролируемого фактора $y \in Y$ осуществляет 2-й игрок-ЛПР, исходя из стремления к минимизации вектор-функции $\Phi (x,y)$, которую максимизирует 1-й ЛПР. Формально МК-игру двух лиц с противоположными интересами запишем как $\Gamma = \left\langle {X,Y,\Phi } \right\rangle $, где $X$ – множество стратегий 1-го игрока, $Y$ – 2-го, и при выборе игроками пары $(x,y) \in X \times Y$ 1-й получит вектор выигрышей $\Phi (x,y) = ({{\varphi }_{1}}(x,y), \ldots ,{{\varphi }_{n}}(x,y))$, а 2-й получит этот же вектор $\Phi (x,y)$ как вектор проигрышей. К сожалению, сказанного недостаточно для описания результата подобной МК-игры, поскольку не конкретизирована интерпретация игроками-ЛПР своего векторного критерия.

Согласно [1] неединственность оптимизируемой функции соответствует субъективной неопределенности в цели оптимизации. При этом отношение игроков к такой внутренней неопределенности, вообще говоря, может быть различным. Традиционная векторная оптимизация (см., например, в [8]) полагает, что наличие многих критериев подразумевает стремление к оптимизации их всех. Менее распространенная интерпретация множественности критериев, восходящая к [10], сводится к тому, что игроку надо оптимизировать какой-нибудь критерий из заданного набора. В играх с векторной функцией выигрышей правомерно использование обеих интерпретаций [17]. Для того чтобы выявить их влияние на результат игры, в [13] введены два вида МК-игр $\Gamma $ с противоположными интересами: антагонистическая (${{\Gamma }^{A}}$) и с нулевой суммой (${{\Gamma }^{0}}$).

В антагонистической игре считается, что один игрок является антагонистом другого, т.е. его цель – в том, чтобы помешать партнеру достичь своей цели. Так, предположив в записи $\Gamma $, что цель 1-го игрока заключается в максимизации вектора выигрышей $({{\varphi }_{1}}, \ldots ,{{\varphi }_{n}})$, получаем, что в антагонистической МК-игре ${{\Gamma }^{A}}$ целью 2-го игрока будет минимизация хотя бы одного из ${{\varphi }_{1}}, \ldots ,{{\varphi }_{n}}$, какого придется. Очевидно, что при этом 1-й игрок также оказывается антагонистом по отношению ко 2-му. Любой из ЛПР в антагонистической постановке игры с противоположными интересами олицетворяет для партнера источник неопределенных факторов (природной неопределенности), что отчасти было рассмотрено в разд. 2.

В игре с нулевой суммой цель одного игрока совпадает с целью другого со знаком “минус”. А именно, если целью 1-го игрока является максимизация вектора выигрышей $({{\varphi }_{1}}, \ldots ,{{\varphi }_{n}})$, то целью 2-го игрока в игре с нулевой суммой ${{\Gamma }^{0}}$ будет максимизация вектора $( - {{\varphi }_{1}}, \ldots , - {{\varphi }_{n}})$, т.е. минимизация вектора проигрышей $({{\varphi }_{1}}, \ldots ,{{\varphi }_{n}})$. Если целью 1-го игрока является максимизация хотя бы одного из ${{\varphi }_{1}}, \ldots ,{{\varphi }_{n}}$, какого придется, то и целью 2-го в игре ${{\Gamma }^{0}}$ будет минимизация хотя бы одного из ${{\varphi }_{1}}, \ldots ,{{\varphi }_{n}}$, какого придется. (Причем не обязательно, что оба игрока выберут один и тот же частный критерий.) Название “с нулевой суммой” здесь весьма условно и принято для данной постановки, чтобы подчеркнуть, что никакого другого аспекта противоположности интересов в ней нет, в отличие от антагонистической игры, где противоположно все, в том числе и интерпретация многокритериальности.

Строгие определения игр ${{\Gamma }^{A}}$ и ${{\Gamma }^{0}}$ вытекают из следующей формальной конструкции [13], [8], основанной на указанных выше двух базовых интерпретациях векторной оптимизации. Отметим, что возможны и промежуточные интерпретации МК-задач, когда одна группа частных критериев оптимизируется в совокупности, а из другой группы достаточно оптимизации произвольного критерия, но далее столь общих постановок рассматривать не будем, ограничившись крайними случаями. Существенно, что и при допустимости подобных расширенных интерпретаций векторной оптимизации принципиально различаются только два вида МК-игр с противоположными интересами согласно определению 2 ниже.

Определение 1. В МК-задаче на максимум назовем для любого $z \in {{\mathbb{R}}^{n}}$ гарантированными оценками значения $z$ элементы множества $\{ \psi \in \mathbb{R}_{ + }^{n}\,{\text{|}}\,\psi \leqslant z\} $, а слабыми оценками значения $z$ – векторы из $\{ \xi \in \mathbb{R}_{ + }^{n}\,{\text{|}}\,\xi \not { > }z\} $. Для оценок в МК-задаче на минимум знаки неравенств меняются на противоположные (см. пример на фиг. 2).

Гарантированные оценки были рассмотрены в разд. 2. Смысл использования слабых оценок похож. Пусть $z$ – векторный выигрыш 1-го игрока. Тогда компоненты ${{z}_{i}}$ – достигнутые им значения по каждому частному критерию ${{\varphi }_{i}}$ (одновременно). А так как 1-й игрок заинтересован в максимизации вектора из ${{\varphi }_{i}}$, то и все “меньшие” $z$ векторные оценки оказываются уже достигнутыми. Множество слабых оценок характеризует те величины, которые максимизирующий игрок считает достигнутыми при получении им выигрыша $z$, если для сравнения векторов-выигрышей он применяет бинарное отношение $\not { > }$ (в отличие от отношения $ \leqslant $, применяемого им при использовании гарантированных оценок). И аналогично для 2-го игрока – в задаче минимизации. Из определения 1 следует, что любая гарантированная оценка $\psi $ для $z$ не лучше векторного результата $z$ по всем критериям, а любая слабая оценка $\xi $ не лучше $z$ хотя бы по одному критерию (но не фиксируется по какому, и в этом – суть многокритериальности).

Определение 2. МК-игрой с нулевой суммой ${{\Gamma }^{0}}$ называется игра с противоположными интересами ($\Gamma $), в которой оба игрока пользуются одним и тем же типом оценок значений векторного критерия. Игра $\Gamma $, в которой игроки ориентируются на взаимодополняющие оценки, называется антагонистической (${{\Gamma }^{A}}$).

Указанные формулировки игры с нулевой суммой и антагонистической охватывают случаи применения 1-м игроком (максимизирующим) не только гарантированных, как в рассмотренных примерах, но и слабых оценок. Все основные свойства введенных классов игр не зависят от того, кто из игроков какими именно оценками руководствуется, важно – одинаковыми или разными. Следуя исходной постановке разд. 2, будем предполагать для 1-го игрока использование гарантированных оценок (из результатов [13], [16] вытекает, что и для противоположного случая приводимые утверждения по большей части сохраняются). При этом мы также учли, что термин “МК-игра с нулевой суммой” в литературе встречается чаще для гарантированных оценок.

Замечание 1. Для антагонистической игры, где 1-й игрок ориентируется на гарантированные оценки, можно дать следующее модельное пояснение. У ЛПР 1 два вида неконтролируемых факторов $y$ и $i$, и по обоим он придерживается принципа гарантированности результата. У ЛПР 2 индекс $i$ – управление, поэтому ему достаточно слабых оценок. Такое поведение соответствует модели “оборона против нападения” [1]. Однако для игры с нулевой суммой нужен иной пример, когда 2-й игрок тоже воспринимает индекс критерия как неконтролируемый фактор и использует гарантированные оценки. Здесь уже речь идет не о прямом конфликте, и можно себе представить игру-соревнование по ряду показателей, задаваемых индексом $i$ (в простейшем случае ${{\varphi }_{i}} = {{x}_{i}} - {{y}_{i}} + C$), либо модельную игру из [4], [5], где каждый игрок заботится о своих интересах, но их векторы оказались противоположно направленными. Поэтому формальное разделение $\Gamma $ на игру ${{\Gamma }^{A}}$, в которой предпочтения игроков противоположны, и игру ${{\Gamma }^{0}}$, в которой противоположны вектор-функции выигрышей, является содержательно обусловленным. Отметим, что в [7] под МК-игрой понимается второй вариант – с гарантированными оценками (и оптимизацией всех критериев), а в [10]–[12] – первый (в связи с моделированием коалиций в скалярных играх многих лиц без побочных платежей), в [8], [9], [13] допускается и та, и другая интерпретация.

Как и для 1-го игрока в разд. 2, НГР 2-го игрока в роли самостоятельного ЛПР зависит от его информированности. Рассмотрим два варианта информированности в игре $\Gamma $: ${{\Gamma }_{{12}}}$ и ${{\Gamma }_{{21}}}$. В игре ${{\Gamma }_{{12}}}$ первым делает ход 1-й игрок, а вторым – 2-й, уже зная ход 1-го. Значение такого МК-максимина для 2-го (минимизирующего) игрока [16] отличается от аналогичного значения (2.2), построенного для 1-го игрока, и будет равно

либо в зависимости от типа оценки значений векторного критерия 2-м игроком. Множество (3.1) считается наименьшим гарантированным проигрышем, или НГР, игрока 2 в МК-игре с противоположными интересами при фиксированном порядке ходов “1-й, 2-й” для постановки с нулевой суммой ($\Gamma _{{12}}^{0}$), а (3.2) – для антагонистической ($\Gamma _{{12}}^{A}$).

И также в МК-игре ${{\Gamma }_{{21}}}$ при фиксированном порядке ходов “2-й, 1-й” НГР 2-го игрока задается значениями его векторных минимаксов, которые определяются в виде

в постановке игры с нулевой суммой $\Gamma _{{21}}^{0}$ или (см. фиг. 2 в) в антагонистической постановке $\Gamma _{{21}}^{A}$. Сравнивая с НГР 1-го игрока (2.1) и (2.2), сформулируем следующее правило определения НГР. По своим стратегиям игроки берут объединение, а по стратегиям противника пересечение – множеств соответствующих оценок вектора критериев. Порядок переменных определен порядком ходов. Игрок 1 выбирает максимальные по Слейтеру оценки, а игрок 2 – минимальные.

В [16] доказаны тождества (для иллюстрации ср. фиг. 1 в и 2 в)

означающие, что в антагонистической МК-игре с фиксированным порядком ходов наибольший гарантированный выигрыш 1-го игрока всегда равен наименьшему гарантированному проигрышу 2-го, т.е. им нет смысла договариваться – у игры существует цена, равная НГР. В итоге получается, что в антагонистической МК-игре, как и в обычной однокритериальной, 2-й игрок служит эквивалентом природной неопределенности и не имеет никаких специфических свойств сознательного противника. Указанный случай уже описан в разд. 2. Поэтому далее МК-игры будем преимущественно изучать в постановке с нулевой суммой, полагая, что отличие противника-ЛПР от неопределенного фактора проявляется как раз для них.

Для МК-игр с нулевой суммой аналогичные (3.4) тождества не выполнены, и даже их ослабление на паретовские значения справедливо лишь для игр, фактически эквивалентных независимому набору однокритериальных. А именно, обозначим через ${{P}_{{max}}}(W)$ и ${{P}_{{min}}}(W)$ границы Парето множества $W \subset \mathbb{R}_{ + }^{n}$ в МК-задачах на максимум или на минимум. Тогда ${{\mathcal{F}}_{ \leqslant }} \cap {{\mathcal{F}}_{ \geqslant }} \ne \not {0} \Leftrightarrow {{P}_{{max}}}({{\mathcal{F}}_{ \leqslant }}) = {{P}_{{min}}}({{\mathcal{F}}_{ \geqslant }})( = {{\psi }^{{21}}})$ [18] и ${{f}_{ \leqslant }} \cap {{f}_{ \geqslant }} \ne \not {0} \Leftrightarrow {{P}_{{max}}}({{f}_{ \leqslant }}) = {{P}_{{min}}}({{f}_{ \geqslant }})( = {{\psi }^{{12}}})$ [13], где

Таким образом, в МК-игре с нулевой суммой при фиксированном порядке ходов игроков наибольший гарантированный выигрыш ЛПР 1 пересекается с наименьшим гарантированным проигрышем ЛПР 2, если и только если паретовское значение НГР каждого игрока состоит из единственного вектора. Получается, что на общий МК-случай ${{\Gamma }^{0}}$ нельзя распространить теорему Гермейера о существовании решения в играх с полной информированностью о действиях противника [1], гарантирующую для скалярных таких игр равенство максимина и минимакса (в стратегиях – отображениях).

Условие единственности оптимума по Парето в задаче МК-оптимизации равносильно отсутствию конкуренции между частными критериями, т.е. возможности оптимизировать каждый из них независимо от других. МК-игра $\Gamma $ при этом тоже распадается на $n$ отдельных скалярных игр. В остальных случаях МК-игра с нулевой суммой при фиксированном порядке ходов не имеет решения в смысле, принятом для скалярных игр. Наибольший гарантированный выигрыш 1-го игрока в ${{\Gamma }^{0}}$ будет по некоторой компоненте строго меньше наименьшего гарантированного проигрыша 2-го, поскольку гарантированная оценка для хотя бы одной из сторон окажется хуже (по крайней мере, по одному из критериев и не лучше по другим), чем значение векторного критерия, которое будет игроком получено. Гарантированные оценки в МК-играх, где многокритериальность существенна, являются пессимистичными в том смысле, что нет таких действий противника, которые бы к ним приводили (независимо от порядка ходов игроков) – см. пример на фиг. 3. Это говорит о потенциальной возможности поиска компромисса в МК-игре с нулевой суммой. Рассмотрим ее в разд. 5, 6, а в следующем разделе обсудим МК-постановки игры в нормальной форме и различные определения ее решения.

4. СПЕЦИФИКА ПРИНЯТИЯ РЕШЕНИЙ ДЛЯ МК-ИГР В НОРМАЛЬНОЙ ФОРМЕ

Для игр в нормальной форме принятие решений осложняется тем, что игроки выбирают свои стратегии одновременно, не зная хода противника [19]. В скалярном случае игра с нулевой суммой в нормальной форме (в отличие от игр с фиксированным порядком ходов) имеет решение не всегда, а лишь когда максимин функции выигрышей равен минимаксу, т.е. НГР каждого из игроков не зависит от порядка их ходов [1]. Тогда игроки могут одновременно выбрать свои гарантирующие стратегии и получить решение и значение (цену) игры, т.е. НГР – одинаковый у обоих игроков.

В МК-играх с нулевой суммой НГРы игроков, как правило, не пересекаются (см. разд. 3), однако можно говорить об условиях независимости НГР каждого из них от порядка ходов. Это означает равенство ${{f}_{ \leqslant }} = {{\mathcal{F}}_{ \leqslant }}$ для 1-го игрока и (или) ${{\mathcal{F}}_{ \geqslant }} = {{f}_{ \geqslant }}$ – для 2-го. Назовем такую ситуацию наличием одностороннего решения. “Одностороннего” потому, что равенство может выполняться для одного игрока. Кроме того, даже когда оно справедливо для обоих, односторонняя цена игры, т.е. значение НГР (оценка выигрыша ЛПР), будет своей для каждого игрока. Термин “решение” применен потому, что указанная оценка и оптимальные стратегии игрока не связаны с его информированностью о действиях партнера. Хорошим свойством МК-игр ${{\Gamma }^{0}}$ с односторонним решением является отсутствие борьбы за порядок ходов (как и в скалярном случае [19]).

Для антагонистической игры в нормальной форме наличие одностороннего решения у одного игрока эквивалентно его наличию у другого – на основе тождеств (3.4). Следовательно, существование одностороннего решения в ${{\Gamma }^{A}}$ обусловливает существование и ее классического решения в смысле, принятом для скалярных игр и означающем равенство всех НГР. (Для МК-игр с нулевой суммой это не так.) По определению антагонистической игры один из игроков в ней руководствуется гарантированными оценками. Наличие одностороннего решения для него не зависит от того, в какой именно игре он участвует. Тем  самым данное свойство оказывается характеризующим для ${{\Gamma }^{A}}$. Оно также важно для ${{\Gamma }^{0}}$ и для принятия решений в МК-задачах с неопределенностью. Исследуем условия существования одностороннего решения для максимизирующего и для минимизирующего игрока в произвольной МК-постановке. (Впервые вопрос о классе игр с противоположными интересами, для которых ${{f}_{ \leqslant }} = {{\mathcal{F}}_{ \leqslant }}$, рассмотрен в [10] в контексте трактовки ${{\Gamma }^{A}}$ – при анализе кооперативных игр.)

Критерии совпадения ${{f}_{ \leqslant }}$ и ${{\mathcal{F}}_{ \leqslant }}$ или ${{\mathcal{F}}_{ \geqslant }}$ и ${{f}_{ \geqslant }}$ (МК-максимина и МК-минимакса любого игрока) получены в [13], [20] в форме, соответствующей использованию игроками-ЛПР скаляризации по Гермейеру [1], или обратной логической свертки (ОЛС) [6]. В частности, для равенства двух множеств ${{f}_{ \leqslant }} = {{\mathcal{F}}_{ \leqslant }}$, или

МК-максимина и МК-минимакса 1-го игрока необходимо и достаточно, чтобы $\forall \mu \in M\;\mathop = \limits^{{\text{def}}} \;\left\{ {\mu \geqslant 0\,{\text{|}}\,\sum\nolimits_{i = 1}^n {{{\mu }_{i}} = 1} } \right\}$ выполнялись числовые равенства где $I(\mu )\;\mathop = \limits^{{\text{def}}} \;\{ i = \overline {1,n} \,{\text{|}}\,{{\mu }_{i}} > 0\} $. Условия (4.2) основаны на представлении множеств максимизируемых оценок в левой и правой части (4.1) с помощью ОЛС согласно [20]: где ${{\theta }^{ - }}$, ${{\theta }^{ + }}$ определены в (4.2). И также для минимизирующего ЛПР [13]: МК-максимин совпадает с МК-минимаксом в гарантированных оценках игрока 2, т.е. ${{f}_{ \geqslant }} = {{\mathcal{F}}_{ \geqslant }}$, или тогда и только тогда, когда $\forall \mu \in M$ выполняются равенства Подчеркнем различие знаков минимума и максимума в определениях ОЛС для игроков 1 и 2 (значения ОЛС выделены в (4.2) и (4.5) фигурными скобками).

Других общих условий для (4.1), (4.4) авторам неизвестно. По крайней мере, использование линейной свертки [1], [8] не дает адекватной параметризации НГР [4] и не позволяет получить критерии их равенств. Выполнение при всех $\mu \in M$ (4.2) или (4.5) влечет за собой и равенства

т.е. существование решений скалярных игр с любым из частных критериев. Но как показывают примеры из [10], последнего условия недостаточно для справедливости (4.1). Недостаточно его и для (4.4). Так что для существования одностороннего решения у конечной МК-игры в нормальной форме недостаточно (см. [10], [11], [13], [21]) перехода к смешанным стратегиям, хотя они и обеспечивают равенство максимина и минимакса по каждому отдельному осредненному ${{\varphi }_{i}}$. Применение ЛПР смешанных стратегий расширяет множества гарантированных для него оценок (т.е. левые части (4.3), если взять игрока 1), оптимальные из которых определяют его НГР. Однако это не обязательно приводит к равенствам (4.2) или (4.5). Дело в том, что наличие внутреннего минимума или максимума по $i \in I(\mu )$ при ${\text{|}}I(\mu ){\text{|}} > 1$ нарушает привычную билинейность по смешанным стратегиям свертки математических ожиданий. Функция в фигурных скобках в (4.2) или (4.5) становится после осреднения частных критериев не выпукло-вогнутой, а вогнутой или выпуклой по стратегиям сразу двух игроков.

Таким образом, стандартная техника смешанного расширения МК-игры не подходит для вывода при каждом $\mu \in M$ условий (4.2) и (4.5) существования решений соответствующих скалярных игр с функцией выигрышей, равной минимуму или максимуму по $i \in I(\mu )$, т.е. не дает соотношений типа (4.1), (4.4). Иная ситуация возникает при осреднении не частных критериев, а их свертки в случае применения ОЛС соответствующим игроком-ЛПР. Тогда билинейность математического ожидания ОЛС обеспечивает равенство максимина и минимакса при всех $\mu \in M$. Выпукло-вогнутость осредненной функции свертки Гермейера сохраняется также при использовании математических ожиданий частных критериев по своим смешанным стратегиям и математического ожидания свертки – по чужим, как предложено в [5]. Тем самым, если при переходе к смешанным стратегиям в МК-игре не подменять сразу частные критерии их средними значениями, но пересмотреть понятие НГР для этого случая (с учетом изменения смешанного расширения), то можно получить одностороннее решение игры.

Формализуем последнюю идею для конечной МК-игры с нулевой суммой, в которой 1-й игрок руководствуется ОЛС при принятии решений. Поскольку существование одностороннего решения для одного игрока не зависит от другого, то необязательно уточнять принцип оптимальности за минимизирующего игрока, но для определенности будем считать его аналогичным. Предположим, что исходно $X$ и $Y$ – конечные, а $p$ и $q$ – смешанные стратегии игроков на этих множествах. Обозначим через $P$ и $Q$ множества соответствующих смешанных стратегий. Теперь допустим, что ЛПР 1 и 2 оценивают свои МК-средние выигрыши и проигрыши с помощью следующих средних ОЛС с параметрами $\mu $ и $\nu \in M$:

Целевая вектор-функция для каждого ЛПР заменена параметрическим семейством скалярных функций свертки, первые из которых максимизирует 1-й игрок, а вторые минимизирует 2-й. Модельное обоснование использования именно этого правила осреднения для МК-игр в ОЛС дано в [5] (оно позволяет ЛПР избежать излишне оптимистичных оценок, возникающих, когда игроки придерживаются линейных сверток вслед за [7]).

Математически – введем согласованное с ОЛС смешанное расширение исходной МК-игры ${{\Gamma }^{0}}$ как параметрическое семейство скалярных игр в нормальной форме

Отсюда для ЛПР 1 его МК-средние максимин и минимакс определим путем параметризации с помощью максиминов и минимаксов ОЛС, но не после осреднения исходных частных критериев ${{\varphi }_{i}}(x,y)$ по $p$ и $q$ [7], а применив предложенные средние ОЛС: Получим, что в силу вогнутости по $p$ и линейности по $q$ функции ${{G}_{1}}(p,q)[\mu ]$ выполнено Равенства (4.7) влекут за собой и равенство ${{\bar {f}}_{ \leqslant }} = {{\bar {\mathcal{F}}}_{ \leqslant }}$, соответствующее наличию одностороннего решения в смешанных стратегиях при использовании ОЛС 1-м ЛПР и осреднении им свертки по смешанной стратегии противника для оценки своего МК-среднего НГР. Сделанный вывод в силу его важности повторим в виде отдельного утверждения.

Утверждение 1. В МК-игре $\overline \Gamma _{G}^{0}$ существует одностороннее решение в смешанных стратегиях для 1-го игрока.

Для 2-го игрока вывод тот же, поэтому не будем на нем останавливаться. Отметим лишь, что скалярные игры семейства $\overline \Gamma _{G}^{0}$ оказываются играми с непротивоположными интересами даже при $\mu = \nu $ из-за различия ОЛС. Противоположность интересов при одинаковых коэффициентах свертки возникает в играх аналогичного расширения $\overline \Gamma _{G}^{A}$ антагонистической МК-игры, поскольку для минимизирующего игрока, принимающего решения на основе слабых оценок, ОЛС задается с помощью минимума из частных критериев (приведенных к коэффициентам свертки), совпадающего с ОЛС максимизирующего игрока, ориентирующегося на гарантированные оценки. Пусть

где Как и для игры $\overline \Gamma _{G}^{0}$, в игре $\overline \Gamma _{G}^{A}$ существует одностороннее решение не только для 1-го, но и для 2-го игрока, если перейти для него к МК-среднему НГР по аналогии с (4.6). Кроме того, для рассматриваемого МК-осреднения можно обобщить равенства (3.4). Однако, чтобы не загромождать изложение, не будем приводить здесь все выкладки, а просто с учетом разд. 3 и на основании существования одностороннего решения для минимизирующего ЛПР в игре $\overline \Gamma _{G}^{A}$ сформулируем конечный результат.

Утверждение 2. Для $\overline \Gamma _{G}^{A}$ существует классическое решение МК-игры в нормальной форме.

Классическое решение МК-игры здесь понимается, как и выше, в полном соответствии с решением скалярной игры в нормальной форме, но с учетом введенного МК-смешанного расширения. Отсюда следует, что МК-средний наименьший гарантированный проигрыш 2-го игрока в слабых оценках ($\not { < }$) совпадает с МК-средним НГР 1-го (4.6) независимо от порядка ходов (поскольку ${{\bar {f}}_{ \leqslant }} = {{\bar {\mathcal{F}}}_{ \leqslant }}$ для игры $\overline \Gamma _{G}^{A}$, как и для $\overline \Gamma _{G}^{0}$). Напомним, что без осреднения ОЛС одностороннего решения МК-игры в смешанных стратегиях может не быть [11], [10]. Поэтому на произвольные антагонистические МК-игры в нормальной форме утверждение 2 не распространяется.

Для МК-игры с нулевой суммой даже при наличии односторонних решений единой цены игры, как правило, не будет. Так что у противников найдется непустое переговорное множество, несмотря на противоположность их выигрышей. Выше упоминалось, что наличие нескольких критериев у ЛПР соответствует неопределенности. В играх с неопределенными факторами противоположность целевых функций оказывается неоднозначной [22] (см. также замечание 1 в разд. 3). Если отношения игроков-ЛПР к субъективной неопределенности не противоположны, а одинаковы, как в играх с нулевой суммой, то возможны решения, которые лучше обоих НГР (см., например, на фиг. 3). Содержательно для МК-игр это можно пояснить, воспользовавшись методологией исследования операций.

Два игрока представляют собой два коллектива с двумя ЛПР и двумя ИО, осуществляющими поддержку принятия решений в своих коллективах. С точки зрения ИО любое совместное решение (исход игры), которое обеспечивает их коллективам результат не хуже НГР и является недоминируемым ответом на стратегию противника, может служить основой для компромисса. Такой подход (рассмотрим его подробнее в разд. 5) развивает понятие равновесия по Нэшу, предложенное в [7] для МК-игры с нулевой суммой, и обобщает понятие дележа скалярной игры двух лиц [19]. Дележ в играх двух лиц определяется как Парето-оптимальный исход, который для обоих игроков оказывается не хуже, чем их НГР в отсутствие информированности. В контексте дальнейшего сравнения с дележом заметим, что, как и в скалярном случае, любой исход МК-игры с нулевой суммой – Парето-оптимальный по системе всех частных критериев обоих игроков. Поэтому в качестве дополнительного ограничения указанное условие не вводится.

5. ПРИМЕНЕНИЕ ОЛС ДЛЯ АНАЛИЗА РАВНОВЕСИЯ В МК-ИГРЕ

Согласно [7] ситуацией равновесия для МК-игры с нулевой суммой ${{\Gamma }^{0}}$ является любая пара стратегий (${{x}^{0}},{{y}^{0}}$), для которой

Такие пары называются равновесными по Шепли или просто равновесными (в МК-случаях). В зависимости от способа скаляризации МК-максимума и минимума по Слейтеру множество точек (5.1) сводится к соответствующему набору равновесий в скалярных играх двух лиц с функциями выигрышей – свертками частных критериев при всех вариантах коэффициентов свертки у каждого из игроков. Тем самым выбор скаляризации задает определенную параметризацию для множества (5.1). Проанализируем возможность добавить к (5.1) сравнение с НГР для получения равновесного дележа как решения игры ${{\Gamma }^{0}}$.

Воспользуемся при описании НГР 1-го игрока представлением (4.3) множеств гарантированных оценок и предположим выполнение стандартных условий регулярности

обозначая символом ${\text{cl}}$ замыкание в ${{\mathbb{R}}^{n}}$. Тогда согласно [20] имеем где ${{\theta }^{ - }}$, ${{\theta }^{ + }}$ определены в (4.2). (В отсутствие регулярности правые части равенств в (5.3) не содержат ряда незначимых элементов множеств, стоящих в левых частях, а именно, некоторых слейтеровских точек, не являющихся паретовскими [18], [20].)

Для задания НГР 2-го игрока докажем аналогичное (4.3) представление. Введем $n$-мерный вектор $\overline c $ с одинаковыми компонентами

и не будем рассматривать для 2-го игрока оценки, превосходящие $\bar {c}$, в силу их неинформативности. Тогда переобозначим (3.1), (3.3) через

Утверждение 3. Справедливо представление НГР игрока 2 с помощью ОЛС:

Доказательство приведем схематично – без излишних подробностей. Непосредственным повторением выкладок из [1], [6] убеждаемся в правомерности параметризации с помощью логической свертки и ОЛС в МК-задачах за максимизирующего игрока для векторного критерия со всеми неположительными компонентами. Также на случай неположительности частных критериев переносятся результаты [20]. Теперь обоснование (5.4), (5.5) вытекает из (4.3), если принять, что 2-й игрок максимизирует по $y \in Y$ вектор-функцию $ - \Phi (x,y)$, а 1-й игрок ее минимизирует по $x \in X$.

Действительно, поменяв максимизирующего и минимизирующего игроков в (4.3), запишем по отношению к критерию $ - \Phi (x,y)$ на базе второго равенства в (4.3), что

где пересечение с неотрицательным ортантом заменено условием “не меньше $ - \bar {c}$” в силу неположительности функции выигрышей $ - \Phi (x,y)$. По тем же причинам для компонент, не входящих в ОЛС с данным $\nu $, вместо 0-х значений подставлены $ - C$ (для чего пришлось выделить компоненты из общего декартового произведения). Для остальных компонент в правой части воспользуемся преобразованием

После чего, сделав замену переменных $\chi $ на $\psi \;\mathop = \limits^{{\text{def}}} \; - \chi $ в левой и правой частях для перехода к неотрицательным величинам в задаче за минимизирующего $\Phi (x,y)$ игрока 2, получаем (5.4). (Вырожденный отрезок $[C,C]$ записали одним числом $\{ C\} $.) Формулу (5.5) выводим из первого равенства в (4.3) аналогично (пример, иллюстрирующий формулу (5.5), см. на фиг. 4).

При наличии регулярности для представления НГР игрока 2 с помощью ОЛС можно выписать аналог (5.3). Но для дальнейших построений такая конкретизация не понадобится. Укажем, что условия регулярности (5.2) допускают ослабление для учета случаев, когда некоторые из множеств оценок в левой части (4.3) имеют пустую внутренность. Эта возможность подробно разобрана в [20], где обоснован переход в пространства меньшей размерности. Так что предположения регулярности являются не слишком ограничительными.

В регулярном случае для описания множества точек (5.1) применима его параметризация с помощью ОЛС, как предложено в [23], поскольку условия (5.1) на равновесные исходы можно согласно [1], [6] выразить в форме $({{x}^{0}},{{y}^{0}}) \in {{R}^{0}}$, где

(в нерегулярном случае ${{R}^{0}}$ (5.6) уже, чем определено (5.1), за счет незначимых точек Слэйтера – не являющихся паретовскими). При этом для исходов из ${{R}^{0}}$ выполнено и так же для ЛПР 2: Получили, что любая пара стратегий из ${{R}^{0}}$ (равновесная по Шепли в МК-игре) дает каждому игроку результат не хуже оценки, которая гарантируется информированному такому игроку, причем для тех же параметров свертки по Гермейеру его частных критериев. Введем формальное определение, позволяющее сравнивать множества в критериальном пространстве игрокам, применяющим гарантированные оценки.

Определение 3 (см. [2]). Оболочкой по Эджворту и Парето произвольного множества $Z \subset \mathbb{R}_{ + }^{n}$ называется множество $\{ \psi \in \mathbb{R}_{ + }^{n}\,{\text{|}}\,\exists z \in Z{\kern 1pt} :\;\psi \leqslant z\} $ в задаче на максимум или $\{ \psi \in {{\mathbb{R}}^{n}}\,{\text{|}}\,\exists z \in Z{\kern 1pt} :\;\psi \geqslant z\} $ в задаче на минимум. Соответствующие множества будем обозначать через $\mathop {{\text{eph}}}\nolimits_ \leqslant (Z)$ и $\mathop {{\text{eph}}}\nolimits_ \geqslant (Z)$.

Определим понятие равновесного значения МК-игры ${{\Gamma }^{0}}$ как множества ${{Z}^{0}}\;\mathop = \limits^{{\text{def}}} \;\{ \Phi ({{x}^{0}},{{y}^{0}})\,|\,({{x}^{0}},{{y}^{0}}) \in {{R}^{0}}\} $ ${{Z}^{0}}\;\mathop = \limits^{{\text{def}}} \;\{ \Phi ({{x}^{0}},{{y}^{0}})\,|\,({{x}^{0}},{{y}^{0}}) \in {{R}^{0}}\} $ . Тогда из полученных неравенств следует

Утверждение 4. В случае ${{Z}^{0}} \ne \not {0}$:

Доказательство. Для любого $\psi $ из левой части (4.3), а значит, и для $\psi \in {{\mathcal{F}}_{ \leqslant }}$ выполнено согласно (4.3), что $\exists \mu \in M$: $\forall i = \overline {1,n} $ ${{\psi }_{i}} \leqslant {{\theta }^{ + }}[\mu ]{{\mu }_{i}}$. Имеем

как показано выше. Так что $\forall i \in I(\mu )$: ${{\psi }_{i}} \leqslant {{\mu }_{i}}{{\varphi }_{i}}({{x}^{0}},{{y}^{0}}){\text{/}}{{\mu }_{i}}$ = ${{\varphi }_{i}}({{x}^{0}},{{y}^{0}})$, а для ${{\psi }_{k}} = 0$, и, значит, $\psi \leqslant \Phi ({{x}^{0}},{{y}^{0}})$ (в силу неотрицательности $\Phi $), т.е. $\psi \in \mathop {{\text{eph}}}\nolimits_ \leqslant ({{Z}^{0}})$. Аналогично, для $\psi \in {{f}_{ \geqslant }}$ из (5.4) имеем ${{\psi }_{k}} = C \geqslant {{\varphi }_{k}}({{x}^{0}},{{y}^{0}})$ при ${{\nu }_{k}} = 0$ и для остальных индексов критериев – $i \in I(\nu )$, что дает и правое включение в (5.7).

Добавив к (5.7) полученные в [13] соотношения ${{f}_{ \leqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{\mathcal{F}}_{ \leqslant }})$, ${{\mathcal{F}}_{ \geqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \geqslant ({{f}_{ \geqslant }})$, которые еще раз подчеркивают сутевое отличие рассматриваемой трактовки МК-максимина и МК-минимакса (как для максимизирующего, так и для минимизирующего ЛПР) от их аналогов из [14], подытожим специфику многокритериальности в игре с нулевой суммой. По классификации скалярных игр двух лиц из [19] исходы, являющиеся дележами (т.е. приводящие для обоих игроков к результатам не хуже их НГР в отсутствие информированности), составляют $\alpha $-ядро игры, а $\beta $-ядром называется подмножество таких исходов из $\alpha $-ядра, которые для обоих игроков дают результаты, не худшие, чем НГР в условиях информированности о ходе партнера. Исходы из ${{R}^{0}}$ (а в регулярном случае и все равновесные по Шепли) в МК-игре можно отнести и к $\alpha $-, и к$\beta $-ядру, если эти понятия обобщить на МК-случай, заменяя неравенства на принадлежность оболочке Эджворта–Парето. С одной стороны, здесь отмечается соответствие значению скалярной игры с нулевой суммой, которое совпадает с максимином и минимаксом целевой функции в предположении их равенств, т.е. решение такой игры включается и в $\alpha $-, и в $\beta $-ядро. Но, с другой стороны, (5.7) справедливо и в отсутствие равенств МК-максимина МК-минимаксу у любого из игроков, а равенство МК-НГР между игроками возможно лишь в вырожденном случае. В разд. 6 покажем, что непустота ${{R}^{0}}$ не является редкостью, т.е. хорошие свойства множества ${{R}^{0}}$ как решения МК-игры ${{\Gamma }^{0}}$ (и множества ${{Z}^{0}}$ как ее равновесного значения) во многом обусловлены пессимистичностью МК-НГР.

В антагонистической МК-игре оценка результата для информированного 2-го игрока представима (с учетом непревышения $\bar {c}$) в виде

где в отличие от (5.4) внутренний максимум по индексам частных критериев для нижних границ перемножаемых отрезков заменен на минимум. Отсюда с помощью (4.3) и определения ${{\theta }^{ - }}[\mu ]$ еще раз можно вывести равенство ${{f}_{{\not { < }}}} = {{f}_{ \leqslant }}$, т.е. существование решения для антагонистической МК-игры $\Gamma _{{12}}^{A}$ (и также для $\Gamma _{{21}}^{A}$). Чтобы определить аналог МК-равновесия по Шепли для антагонистической МК-игры в нормальной форме, можно во втором включении в (5.1) заменить слейтеровский МК-минимум слабыми оценками (см. определение 1). Однако, не останавливаясь на обобщении стандартного определения (далее не используемого), сразу применим ОЛС и введем множество в качестве равновесного решения МК-игры ${{\Gamma }^{A}}$. Для ее равновесного значения ${{Z}^{A}}\;\mathop = \limits^{{\text{def}}} \;\left\{ {\Phi ({{x}^{A}},{{y}^{A}})\,{\text{|}}\,({{x}^{A}},{{y}^{A}}) \in {{R}^{A}}} \right\}$ ${{Z}^{A}}\;\mathop = \limits^{{\text{def}}} \;\left\{ {\Phi ({{x}^{A}},{{y}^{A}})\,{\text{|}}\,({{x}^{A}},{{y}^{A}}) \in {{R}^{A}}} \right\}$ докажем вполне ожидаемое

Утверждение 5. В случае ${{Z}^{A}} \ne \not {0}$: ${{\mathcal{F}}_{ \leqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{Z}^{A}})$, ${{f}_{{\not { < }}}} \subseteq \mathop {{\text{eph}}}\nolimits_{\not { < }} ({{Z}^{A}})$, где $\mathop {{\text{eph}}}\nolimits_{\not { < }} (Z)\;\mathop = \limits^{{\text{def}}} $ $\mathop = \limits^{{\text{def}}} \;\left\{ {\psi \in {{\mathbb{R}}^{n}}\,{\text{|}}\,\exists z \in Z\,:\psi \not { < }z} \right\}$.

Доказательство. Первое включение доказывается как и первое включение в утверждении 4 с заменой верхних индексов 0 на $A$. Для доказательства второго включения выберем $\psi \in {{f}_{{\not { < }}}}$ и получим из (5.8), что ${{\psi }_{k}} = C \geqslant {{\varphi }_{k}}({{x}^{A}},{{y}^{A}})$ при ${{\nu }_{k}} = 0$ и

для индекса ${{i}^{0}} \in I(\nu )$, реализующего минимум ${{\varphi }_{j}}({{x}^{A}},{{y}^{A}}){\text{/}}{{\nu }_{j}}$. Первое равенство вытекает из (5.9). Неравенство для ${{i}^{0}}$ обосновывает второе включение в утверждении 5.

Таким образом, и для антагонистической МК-игры в нормальной форме, определив для нее МК-равновесие по аналогии с (5.6), получили такое же свойство, как и (5.7), показывающее, что равновесные исходы дают обоим игрокам результат не хуже их НГР. Наличие равновесия в игре ${{\Gamma }^{A}}$ накладывает на ее параметры определенные условия, так как равенство ${{f}_{{\not { < }}}} = {{f}_{ \leqslant }}$, наряду с включением ${{f}_{ \leqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{\mathcal{F}}_{ \leqslant }})$, приводит к следствию из утверждения 5: ${{f}_{ \leqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_ \leqslant ({{Z}^{A}})$ и ${{f}_{ \leqslant }} \subseteq \mathop {{\text{eph}}}\nolimits_{\not { < }} ({{Z}^{A}})$. Отсюда вытекает непустота пересечения $\mathop {{\text{eph}}}\nolimits_ \leqslant ({{Z}^{A}})\bigcap {{\text{ep}}{{{\text{h}}}_{{\not { < }}}}({{Z}^{A}})} $ в случае ${{Z}^{A}} \ne \not {0}$. (Для примера с фиг. 2, 3 это видно на фиг. 5.)

Изучим условия существования равновесия, уделяя основное внимание МК-игре с нулевой суммой, поскольку нас в первую очередь интересует существование решения у нее. Под решением игр ${{\Gamma }^{0}}$ и ${{\Gamma }^{A}}$ в разд. 6 будем понимать именно равновесия ${{R}^{0}}$ и ${{R}^{A}}$ в силу доказанных свойств (5.7) и утверждения 5 для равновесных значений ${{Z}^{0}}$ и ${{Z}^{A}}$.

6. СУЩЕСТВОВАНИЕ РАВНОВЕСИЯ В МК-ИГРАХ

В разд. 5 свели вопрос о существовании равновесного дележа-решения МК-игры с нулевой суммой к непустоте ${{R}^{0}}$ (5.6). При этом если не говорить о применении смешанных стратегий, то не важно, какую свертку используют игроки-ЛПР, в регулярном случае параметризация множества исходов (5.1) с помощью ОЛС (5.6) сохраняется. На базе данной параметризации можно видеть, что условие, определяющее (5.6), в отличие от условий (4.2), (4.5), характеризующих наличие односторонних решений, следует из существования решения скалярной игры с хотя бы одним частным критерием. Действительно, достаточно выбрать в (5.6) в качестве $\mu $ и $\nu $ вектор с единицей именно на месте такого частного критерия, чтобы обеспечить включение в ${{R}^{0}}$ решения указанной скалярной игры. То же решение будет принадлежать и ${{R}^{A}}$ по определению (5.9). Покажем формально, что условие в (5.6) слабее наличия одностороннего решения.

Утверждение 6. Если для некоторого вектора $\mu \in M$ ситуация $(x{\text{*}},y{\text{*}})$ является решением скалярной игры с нулевой суммой на $X \times Y$ с функцией выигрышей в форме ОЛС за максимизирующего игрока:

то $(x{\text{*}},y{\text{*}}) \in {{R}^{0}}$ – оказывается исходом из решения МК-игры ${{\Gamma }^{0}}$ в смысле (5.6) и (5.1).

Доказательство. По определению решения скалярной игры с (6.1) имеем

Пусть Тогда т.е. для $\nu = {{\nu }^{0}}$ с $\nu _{{{{i}^{0}}}}^{0} = 1$ имеем И с учетом получили для $(x{\text{*}},y{\text{*}})$ выполнение (5.6) с соответствующим $\mu $ и $\nu = {{\nu }^{0}}$.

Заметим, что указанная в утверждении 6 для максимизирующего игрока в игре ${{\Gamma }^{0}}$ ОЛС (6.1) совпадает с ОЛС минимизирующего игрока в игре ${{\Gamma }^{A}}$. Поэтому ситуация $(x{\text{*}},y{\text{*}})$ будет равновесным исходом и для антагонистической МК-игры на основании (5.9).

Аналогично утверждению 6 доказывается симметричное утверждение для ОЛС за минимизирующего игрока в игре ${{\Gamma }^{0}}$. Оно дает еще одно достаточное условие существования МК-равновесия в ОЛС и набор равновесных исходов из ${{R}^{0}}$.

Утверждение 7. Если для некоторого вектора параметров $\nu \in M$ ситуация $(x{\text{**}},y{\text{**}})$ является решением скалярной игры с нулевой суммой на $X \times Y$ с функцией выигрышей в форме ОЛС за минимизирующего игрока в МК-игре ${{\Gamma }^{0}}$:

то $(x{\text{**}},y{\text{**}}) \in {{R}^{0}}$ – оказывается исходом из решения игры ${{\Gamma }^{0}}$ в смысле (5.6) и (5.1).

Отметим, что предположений из обоих утверждений 6 и 7 недостаточно для существования одностороннего решения МК-игры, так как не требуется наличия решений скалярных игр при всех коэффициентах свертки. С другой стороны, условия (5.6) (и (5.1)) явно дают слишком широкое множество. Несмотря на предпринятую в разд. 5 попытку ввести содержательные дополнительные требования для того, чтобы построить решение как собственное подмножество стратегий, равновесных по Шепли, она не привела к сужению ${{R}^{0}}$ в силу (5.7). Для примера, рассмотренного в [5], множество исходов (5.1) было вообще неизбирательным. Для произвольной МК-игры с нулевой суммой непустоту ${{R}^{0}}$ легко обеспечить путем перехода к смешанным стратегиям, поскольку, как показано выше, достаточно, чтобы решение имела скалярная игра с одним из частных критериев. И эти свойства не зависят от вида свертки, используемой для описания множеств Слейтера в (5.1). Стандартным подходом является применение линейной свертки [7], но согласно [24] множество (5.1), параметризованное с помощью линейной свертки, наиболее широкое, значит, не уже (5.6). На самом деле в регулярном и выпуклом случае эти множества одинаковы, так как для любых $({{x}^{0}},{{y}^{0}})$, удовлетворяющих (5.1), существуют параметры $\mu $, $\nu \in M$, с которыми выполнены условия в (5.6). Причем перебор коэффициентов свертки при параметризации на базе ОЛС можно даже сократить. Пусть для простоты $\Phi (x,y) > 0$ (тогда автоматически выполняются условия регулярности).

Утверждение 8: ${{R}^{0}} = \{ ({{x}^{0}},{{y}^{0}}) \in X \times Y\,{\text{|}}\,\exists \mu \in M$:

Доказательство. Для любой пары $({{x}^{0}},{{y}^{0}})$, удовлетворяющей (5.1), выберем

Имеем из (5.1) $\forall x \in X$ $\exists {{i}^{0}} \in I({{\mu }^{0}})$ (= $\{ 1, \ldots ,n\} $): ${{\varphi }_{{{{i}^{0}}}}}(x,{{y}^{0}}) \leqslant {{\varphi }_{{{{i}^{0}}}}}({{x}^{0}},{{y}^{0}})$. А значит, Последняя величина равна ${{\varphi }_{i}}({{x}^{0}},{{y}^{0}}){\text{/}}\mu _{i}^{0}$ $\forall i \in I({{\mu }^{0}})$, так что и минимуму по $i \in I({{\mu }^{0}})$. Получили, что ${{x}^{0}}$ реализует максимум этой свертки.

С другой стороны, $\forall y \in Y$ $\exists {{i}^{1}} \in I({{\mu }^{0}})$: ${{\varphi }_{{{{i}^{1}}}}}({{x}^{0}},y) \geqslant {{\varphi }_{{{{i}^{1}}}}}({{x}^{0}},{{y}^{0}})$, а значит,

$\forall i \in I({{\mu }^{0}})$, т.е. равенство и максимуму по $i \in I({{\mu }^{0}})$. Отсюда ${{y}^{0}}$ является минимизатором ОЛС 2-го игрока с ${{\mu }^{0}}$ для данного ${{x}^{0}}$. Что в силу (5.6) завершает доказательство.

Для антагонистической МК-игры непустота (5.9) также обеспечивается переходом к смешанным стратегиям (в отличие от существования одностороннего решения). Для одностороннего решения требуется, чтобы были решения скалярных игр (6.1) при любых $\mu \in M$. Но это не достигается путем использования смешанных стратегий, если не применять МК-смешанного расширения с осреднением ОЛС, рассмотренного в разд. 4. В свою очередь, предложенная концепция МК-осреднения свертки для получения решения конечной МК-игры в смешанных стратегиях позволяет задействовать математический аппарат ОЛС для параметризации и анализа структуры МК-равновесия, причем с сохранением хороших свойств, отмечаемых у стандартной линейной свертки. Тем самым увеличивается конкурентоспособность логической свертки и ОЛС, имеющих большое распространение в исследовании операций.

7. ЗАКЛЮЧЕНИЕ

Полученные результаты, несмотря на описание разнообразных подходов к формализации решения МК-игры, скорее говорят о том, что оно еще нуждается в уточнении. Это следует и из отличия понятий одностороннего решения и равновесия, одно из которых представляется слишком узким, а другое слишком широким. Но главное – из-за того, что не удается получить решение, приемлемое с позиций исследования операций, в котором отражались бы все возможности компромисса, обусловленного исключительно многокритериальностью, т.е. субъективной неопределенностью в целеполагании. Интуитивно понятное определение решения имеется лишь для антагонистических МК-игр с фиксированным порядком ходов, в которых, к слову, нет места компромиссу. Для МК-игр с нулевой суммой, где традиционно предлагается применять равновесие, настораживает его неизбирательность (так, на фиг. 5 ${{Z}^{0}} = {{Z}^{A}} = \{ \Phi (x,y)\,{\text{|}}\,x \in X,y \in Y\} $).

Конечно, есть возможность априорного сокращения набора коэффициентов свертки ($\mu $, $\nu \in M$ для ОЛС), например, с помощью выявления относительной важности для ЛПР частных критериев [25]. Такой подход ведет к выбору не всех недоминируемых точек в исходных задачах (2.1), (2.2), (3.1)–(3.3), а сообразующихся с системой предпочтений, задаваемой некоторой лексикографией среди ряда критериев. Учет подобной дополнительной информации при анализе МК-игр с противоположными интересами ранее не рассматривался и представляет самостоятельный предмет для изучения.

Любопытный способ сужения (5.1) путем наложения добавочных ограничений вытекает из построений [26] (определение 2.13 и теорема 2.14) для смешанных расширений конечных МК-игр. Указанный способ базируется на концепции set optimization (вводятся отношения частичного порядка между множествами достижимых оценок по типу отношений включения их оболочек Эджворта–Парето). Интересно было бы оценить, на сколько ограничения из [26] позволяют сократить набор альтернатив для ИО.

Кроме того, для задания более жестких ограничений на равновесия с целью получения более адекватного решения МК-игры с противоположными интересами можно пойти по пути обобщения на МК-игры понятий $\gamma $-ядра и $g$-ядра из [19], взяв за основу результаты [27]. Смысл в том, что указанные понятия ядра-решения скалярной игры базируются на ее информационных расширениях, т.е. на учете обмена информацией между игроками в процессе проведения игры (другой, принятый в русскоязычной литературе, термин – иерархические игры [22]). Конкретно $\gamma $ (или $g$)-ядро состоит из дележей, равновесных по Штакельбергу (или по Гермейеру). Их построение предполагает разработку стратегий априорного информирования, включающих сценарии угроз, предупреждений [19] или наказания [22], что улучшает НГР применяющего их игрока. В результате более значимым становится условие “не хуже НГР”, принятое во всех концепциях ядра. Подобные расширения перспективны также для динамических игр, отражая, к примеру, процесс ведения переговоров.

Однако вопросы МК-формализации переговорного процесса между двумя ЛПР, которые представляют векторы интересов своих коллективов, на данный момент остались вне поля зрения исследователей. Отчасти это связано с тем, что указанные выше стратегии требуют конкретизации предположений об информированности обоих ЛПР о параметрах свертки друг у друга и об отношении партнера к неопределенности. И потому дальнейшее развитие теории иерархических игр с неконтролируемыми факторами в направлении, вынесенном в заголовок, не вписывается в рамки данной статьи. Отметим, что утверждения 4 и 5 позволяют воспользоваться из этой теории идеей переговорного множества – основополагающей для скалярных игр с непротивоположными интересами [22], свойства которых проявились и в МК-играх с нулевой суммой. А именно, можно ввести понятия переговорных оценок: в МК-игре ${{\Gamma }^{0}}$ как ${{Z}^{0}}{\backslash }\left\{ {\mathop {{\text{eph}}}\nolimits_ \leqslant ({{\mathcal{F}}_{ \leqslant }})\bigcup {{\text{ep}}{{{\text{h}}}_{ \geqslant }}({{f}_{ \geqslant }})} } \right\}$, и в ${{\Gamma }^{A}}$ – как ${{Z}^{A}}{\backslash }\left\{ {\mathop {{\text{eph}}}\nolimits_ \leqslant ({{\mathcal{F}}_{ \leqslant }})\bigcup {{\text{ep}}{{{\text{h}}}_{{\not { < }}}}({{f}_{{\not { < }}}})} } \right\}$. Для случая конечной МК-игры, когда игроки применяют ОЛС, для МК-смешанного расширения $\overline \Gamma _{G}^{0}$ есть шанс еще сильнее сузить множество равновесных исходов до кандидатов на решение игры, выбрав в соответствующем множестве переговорных оценок векторы, не доминируемые в критериальном пространстве ни для одного из игроков.

Вопрос о непустоте множества переговорных оценок при непустоте ${{Z}^{0}}$, ${{Z}^{A}}$ и о выделении в случае непустоты из ${{R}^{0}}$, ${{R}^{A}}$ переговорного множества исходов является предметом ближайшего изучения. Планируется развить указанную идею и посмотреть (в том числе на конкретных примерах), к чему она приводит, если заранее рассчитывать на использование ОЛС игроками-ЛПР. Тогда параметризация НГР и равновесных значений с помощью ОЛС даст их наглядное описание (с разложением по коэффициентам свертки) и укажет игрокам потенциально компромиссные варианты, т.е. предоставит больше возможности договориться, а ИО – несколько уменьшить множество (в критериальном пространстве), составляющее априорную оценку результата ЛПР в МК-игре с противоположными интересами.

Авторы выражают свою благодарность Владимиру Викторовичу Морозову за полезное обсуждение предварительной версии статьи.