Журнал вычислительной математики и математической физики, 2021, T. 61, № 3, стр. 504-518

ВВЕДЕНИЕ

Постоянно возрастающий мировой спрос на электроэнергию в условиях ограниченных энергоресурсов стимулирует не только развитие нетрадиционной энергетики, но и более рациональное использование произведенной энергии. Одним из направлений для повышения эффективности энергетических систем является использование хранилищ энергии (см. [1]), которые позволяют накапливать излишки энергии и отдавать их при пиковом энергопотреблении. Особенно необходимыми такие устройства становятся при использовании нетрадиционной энергетики (солнечной, ветряной), которая отличается сильно неравномерным производством энергии. Вместе с тем использование хранилищ энергии в комбинации с традиционными электростанциями также позволяет существенно повысить их эффективность. Перспективным способом хранения энергии являются воздушно-аккумулирующие газотурбинные электростанции (ВАГТЭ) (см. [2]). В них избыточная электроэнергия направляется на компрессоры, которые закачивают сжимаемый воздух в специальные резервуары, а при пиковом энергопотреблении сжатый воздух выходит из резервуаров и раскручивает турбины, вырабатывающие электроэнергию. ВАГТЭ характеризуются высокой надежностью, экономичностью и низким воздействием на окружающую среду; они могут быть как малогабаритные, так и крупномасштабные. Однако в этих устройствах образующееся при сжатии воздуха тепло не используется, при этом на нагрев расширяющегося воздуха, выходящего из резервуаров, расходуется топливо. Данные недостатки устраняются в разрабатываемых ВАГТЭ нового типа – бестопливных адиабатических, в которых тепло сжатого воздуха сохраняется и используется при его расширении (см. [3]). Адиабатичность можно достичь за счет использования в ВАГТЭ накопителей тепловой энергии на основе гранулированного или капсулированного теплоаккумулирующего материала (ТАМ) с фазовым переходом, в частицах которого происходит плавление и кристаллизация вещества без нарушения их целостности (см. [4]). Гранулированные ТАМ выпускаются в промышленных масштабах (см. [5]) и представляют собой неорганические несущие матрицы размером несколько миллиметров, внутри которых содержится органическое вещество, претерпевающее фазовые переходы (плавление/кристаллизация), но не вытекающее в жидком состоянии за счет адсорбции. Заметим, что указанные гранулированные или капсулированные ТАМ могут применяться не только в составе перспективных ВАГТЭ, но и в иных энергетических системах, и являются весьма перспективными материалами для различных приложений (см. [6]).

Настоящая работа посвящена численному моделированию течений газа через слой гранулированного или капсулированного материала с фазовым переходом. Такие материалы при относительно малых размерах составляющих их частиц могут описываться, с точки зрения механики, как сплошные многокомпонентные среды. Использование подхода взаимодействующих взаимопроникающих континуумов подразумевает пространственное осреднение и позволяет отказаться от детального описания процессов в каждой частице (см. [7]); данный подход прекрасно зарекомендовал себя при моделировании различных гранулированных и пористых сред. Фазовые превращения в гранулированных ТАМ не могут описываться классической задачей Стефана (см. [8]), так как в таких материалах отсутствует четко выраженная граница фазовых переходов. Из-за интенсивного теплообмена между протекающим газом и твердым пористым каркасом в гранулированных и капсулированных ТАМ зона фазового перехода становится не поверхностью, а протяженной областью – двухфазной зоной (см. [9], [10]), в которой присутствует плавящееся вещество в двух фазах. Особенности процессов в ТАМ с газовым теплоносителем, таким образом, затрудняют применение при их моделировании известных численных методов (см. [11]). Вместе с тем актуальность задачи стимулировала активные исследования в области численного моделирования гранулированных или капсулированных ТАМ (см. [12]–[15]). В [16], [17] были предложены и апробированы математическая модель и оригинальный численный метод для исследования одномерных течений газа через слой гранулированного материала с фазовым переходом. Анализ сходимости численного метода и сравнение результатов расчета с известными экспериментами, подробно описанные в [17], показали работоспособность предложенной численной модели даже при расчете малоразмерных теплоаккумуляторов. В [18] исследовано влияние сжимаемости газа при моделировании процессов в гранулированных плавящихся ТАМ и показано, что распространенное пренебрежение сжимаемостью при моделировании указанных ТАМ может приводить к значительным неточностям в решении задачи, а также не может гарантировать верхнюю или нижнюю оценку для реального времени протекания процесса. Заметим, что предложенные в [16], [17] модель и метод расчета являются модификацией моделей и алгоритмов для исследования как нестационарных процессов охлаждения пористых саморазогревающихся объектов при заданном давлении газа на их открытых границах (см. [19], [20]), так и нестационарных процессов фильтрационного горения твердых пористых сред в условиях естественной конвекции и принудительной фильтрации (см. [21], [22]).

В настоящей работе для моделирования двумерных плоских нестационарных течений газа через гранулированные материалы с фазовым переходом предложены математическая модель и численный метод, являющиеся развитием модели и метода, подробно описанных в [17]. На последовательности сгущающихся сеток экспериментально исследована сходимость метода. Рассмотрены задачи о нагреве теплового аккумулятора на основе гранулированного материала с фазовым переходом, имеющего боковые границы плавно сужающейся и плавно расширяющейся формы.

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Рассмотрим пористый объект, имеющий как открытые, так и непроницаемые границы. Конденсированная среда в этом объекте представляет собой засыпку частиц гранулированного теплоаккумулирующего материала, в которых происходит плавление/кристаллизация без нарушения их целостности. Указанный фазовый переход протекает при определенной фиксированной температуре. Газ втекает в объект через открытую границу при заданных температуре и давлении, проходит через гранулированную засыпку и вытекает через проницаемую поверхность в открытое пространство с заданным давлением. Отметим, что при плавлении и затвердевании материалов в общем случае меняются их плотность и размеры. Однако в реальных теплоаккумулирующих материалах, используемых в накопителях тепловой энергии, такие изменения, как правило, малы, поэтому изменением пористости, плотности конденсированной фазы, а также ее движением можно пренебречь.

Математическая модель описанного процесса строится в рамках модели взаимодействующих взаимопроникающих континуумов (см. [7]) и включает в себя уравнения неразрывности, движения и внутренней энергии газа, уравнение внутренней энергии теплоаккумулирующего материала, а также уравнение состояния совершенного газа. В уравнении энергии ТАМ учитываются его теплопроводность, контактный теплообмен с газом, который полагается пропорциональным разнице их температур в рассматриваемой точке среды, а также поглощение/выделение энергии в результате плавления/кристаллизации материала, интенсивность которого пропорциональна скорости изменения доли расплавившегося вещества материала по аналогии с теорией двухфазной зоны (см. [9], [10], [23], [24]). В уравнении внутренней энергии газа учитываются теплопроводность и теплообмен с теплоаккумулирующим материалом. Для описания динамики газа используется уравнение сохранения импульса для пористых сред (см. [7]), которое может рассматриваться как обобщение классического закона Дарси. Так как в [25] было показано, что учет температурной зависимости динамической вязкости при моделировании течения газа через пористые тепловыделяющие объекты может изменять решение не только качественно, но и количественно, то в настоящей работе также будем полагать, что вязкость газа зависит от его температуры по формуле Сазерленда. Так как теплоаккумулирующий материал полагается неподвижным и с постоянной плотностью, то уравнения движения и неразрывности для него вырождаются. Таким образом, система уравнений, описывающая нестационарные течения газа через гранулированные материалы с фазовым переходом, в общем случае может быть записана следующим образом:

где a – пористость, с – удельная теплоемкость, с_s1, c_s2 – константы в формуле Сазерленда,  f – доля жидкой фазы в теплоаккумулирующем материале, g – ускорение силы тяжести, k₁ – коэффициент проницаемости пористой среды, k₂ – коэффициент инерционного сопротивления пористой среды, p – давление газа, Q – удельная теплота плавления материала, R – газовая постоянная, Т – температура, t – время, u – скорость фильтрации газа, α – константа, определяющая интенсивность межфазного теплообмена, Δ – оператор Лапласа, λ – коэффициент теплопроводности, μ – коэффициент динамической вязкости газа, ρ – плотность, χ – коэффициент, учитывающий инерционное взаимодействие сред при их относительном ускоренном движении (см. [7]), $\nabla $ – оператор набла. Индексы в обозначениях указывают на следующее: с – теплоаккумулирующий (конденсированный) материал, g – газ, p – значение при постоянном давлении, ph – значение при фазовом переходе.

Далее при описании двумерных плоских течений газа в гранулированном материале будем использовать эйлеровы декартовы координаты x_i и обозначать индексом 1 – горизонтальную компоненту, а индексом 2 – вертикальную компоненту векторных величин. Введем безразмерные переменные следующим образом: ${{\tilde {x}}_{i}} = {{x}_{i}}{\text{/}}H$, $i = 1,\;2$, ${\mathbf{\tilde {u}}} = {\mathbf{u}}{\text{/}}{{u}_{*}}$, $\tilde {t} = t{\text{/}}{{t}_{*}}$, $\tilde {p} = p{\text{/}}{{p}_{*}}$, $\tilde {\rho } = \rho {\text{/}}{{\rho }_{*}}$, ${{\tilde {T}}_{c}} = {{T}_{c}}{\text{/}}{{T}_{*}}$, ${{\tilde {T}}_{g}} = {{T}_{g}}{\text{/}}{{T}_{*}}$, где H – высота рассматриваемого пористого объекта, ${{u}_{*}}$, ${{t}_{*}}$ – характерные значения скорости фильтрации газа и времени соответственно, ${{p}_{*}}$, ${{\rho }_{*}}$, ${{T}_{*}}$ – значения давления, плотности и температуры газа при “нормальных” условиях. Подставляя новые переменные в (1.1)–(1.5) и опуская тильду, можем переписать систему (1.1)–(1.5) в безразмерном виде в декартовых координатах:

В системе (1.6)–(1.10) используются следующие параметры подобия:

Расчет фазового перехода в системе (1.6)–(1.10) происходит следующим образом. Уравнение внутренней энергии теплоаккумулирующего материала (1.6) при решении распадается на два уравнения, последовательно используемых для определения двух функций: T_c и f. Когда температура материала не равна температуре его плавления, слагаемое с f обнуляется, и мы получаем следующее уравнение, из которого определяется функция T_c:

Когда температура материала достигает точки плавления/кристаллизации, начинается фазовый переход. При постоянной температуре фазового перехода левая часть уравнения энергии материала обнуляется, и мы получаем следующее уравнение для определения функции $f$: Уравнение (1.12) используется, пока  f  не достигнет своих экстремальных значений, соответствующих окончанию фазового перехода: 0 – при кристаллизации и 1 – при плавлении. Далее возвращаемся к уравнению (1.11). Представленный подход позволяет описывать процессы при произвольной скорости фазового превращения и не требует наличия четкой границы фазовых переходов.

Граничные условия для системы (1.6)–(1.10) следующие. На входе в пористый объект (т.е. на открытой границе, через которую газ втекает в объект) известны давление и температура газа, на выходе (т.е. на открытой границе, через которую газ вытекает из объекта) известно давление газа. На открытых и непроницаемых границах также известны условия теплообмена. Таким образом, граничные условия для системы (1.6)–(1.10) могут быть записаны в виде

Здесь G₁ и G₂ – соответственно открытые границы, через которые газ втекает и вытекает из объекта, G₃ – непроницаемые границы объекта, n – вектор внешней нормали к границе объекта, ${{p}_{0}}$, ${{T}_{{g0}}}$ – заданные значения давления и температуры газа на входе в пористый объект соответственно, ${{T}_{a}}$ – температура внешней среды, ${\text{B}}{{{\text{i}}}_{o}} = {{{{\beta }_{o}}H} \mathord{\left/ {\vphantom {{{{\beta }_{o}}H} {{{\lambda }_{c}}}}} \right. \kern-0em} {{{\lambda }_{c}}}}$, ${\text{B}}{{{\text{i}}}_{w}} = {{{{\beta }_{w}}H} \mathord{\left/ {\vphantom {{{{\beta }_{w}}H} {{{\lambda }_{c}}}}} \right. \kern-0em} {{{\lambda }_{c}}}}$, где β₀ и β_w – коэффициенты, определяющие интенсивность теплообмена с внешней средой через открытые и непроницаемые границы соответственно.

Для решения системы (1.6)–(1.10) с условиями (1.13)–(1.15) необходимо задать значения искомых величин в начальный момент времени.

2. ЧИСЛЕННЫЙ МЕТОД

Система уравнений (1.6)–(1.10), описывающая двумерное плоское течение газа через слой гранулированного материала с фазовым переходом, является нелинейной смешанной гиперболически-параболической системой уравнений и в общем случае не может быть решена аналитически. Для ее решения предлагается численный метод, основанный на комбинации явных и неявных конечно-разностных схем. В соответствии с идеей метода уравнения внутренней энергии и движения газа преобразовываются в явные конечно-разностные уравнения, из которых определяются температура и компоненты скорости фильтрации газа соответственно. Уравнение энергии теплоаккумулирующего материала также преобразовывается в конечно-разностное уравнение, из которого по явной схеме определяются функции T_c и f, согласно описанному в предыдущем разделе алгоритму. Уравнение неразрывности преобразуется в неявное конечно-разностное уравнение, из которого методом прогонки (см. [26]) с учетом уравнения состояния совершенного газа определяется давление. Далее из уравнения состояния совершенного газа определяется плотность газа.

Рассмотрим равномерную прямоугольную сетку с шагом по пространству h и шагом по времени τ = rh². Для сокращения записей здесь и далее будем полагать, что открытые границы объекта являются только горизонтальными, а непроницаемые границы – только вертикальными (для других случаев все соотношения можно выписать по аналогии с данным случаем). Заменяя частные производные в (1.6)–(1.10) конечными разностями и обозначая продвижение по временной координате верхними индексами, а продвижение по пространственным координатам – нижними, выпишем следующую систему конечно-разностных уравнений, аппроксимирующую исходную систему (1.6)–(1.10):

Система конечно-разностных уравнений (2.1)–(2.7) аппроксимирует исходную систему (1.6)–(1.10) со вторым порядком точности по h и первым порядком по τ, в чем несложно убедиться с помощью разложения искомых функций в ряд Тейлора. В уравнении (2.3) вариация знака при аппроксимации конвективной производной температуры газа обусловлена направлением скорости фильтрации газа: при положительном значении соответствующей компоненты скорости фильтрации выбирается верхний знак, при отрицательном значении – нижний. Для схем четного порядка точности типично преобладание дисперсионной ошибки (см. [26]), которая может приводить к осцилляциям решения и потере устойчивости. Поэтому в уравнения (2.4)–(2.6) добавлены демпфирующие члены, которые имеют четвертый порядок и не изменяют формальную точность метода. Эти слагаемые определяются следующим образом:

Краевые условия для сеточных функций получим из (1.13)–(1.15), используя для аппроксимации производных по координатам конечные разности второго порядка. На открытых границах объекта при определении температур газа и теплоаккумулирующего материала будем использовать трехточечную аппроксимацию производной по вертикальной координате

где вместо φ подставляется соответствующая сеточная функция, верхний знак выбирается при наибольшем значении индекса m, нижний знак – при наименьшем.

Добавим также фиктивные точки (узлы сетки), расположенные за пределами открытых границ. Компоненты скорости фильтрации газа на открытых границах и в фиктивных точках, а также температура газа в фиктивных точках определяются из условия равенства нулю их первых производных по вертикальной координате в соответствующих узлах сетки, аппроксимированных по формуле (2.8). Давление газа в фиктивных точках будем определять из условия равенства нулю на границе его второй производной по вертикальной координате, которую аппроксимируем по формуле

Для нахождения температур газа и теплоаккумулирующего материала на непроницаемых стенках используется аналогичная (2.8) формула для определения производной по горизонтальной координате

где вместо φ подставляется соответствующая сеточная функция, верхний знак выбирается при наибольшем значении индекса l, нижний знак – при наименьшем. Добавим также дополнительные условия для давления и вертикальной (тангенциальной) компоненты скорости фильтрации газа на непроницаемых стенках, которые задаются исходя из равенства нулю их первых производных по нормали, записанных в виде (2.9). В добавляемых фиктивных точках, расположенных за пределами непроницаемой границы, задаются давление, температура газа и компоненты скорости фильтрации, которые определяются, согласно условию отражения (см. [26]), из их значений в приграничных узлах сетки.

Опишем алгоритм нахождения искомых сеточных функций из системы (2.1)–(2.7) на каждом временном слое. Пусть в начальный момент времени значения температуры в пористом объекте отличаются от температуры плавления теплоаккумулирующего материала. Фиксируя индекс l и последовательно меняя индекс m, решаем уравнения (2.1), (2.3)–(2.5); затем из граничных условий определяем значения искомых функций на открытых границах. Далее методом прогонки решаем уравнение (2.6), затем тривиально решаем уравнение (2.7). Выполнив описанную процедуру для всех “внутренних” значений индекса l, определяем значения всех искомых функций на боковых стенках и в фиктивных точках. Таким образом, задавая начальные условия и последовательно продвигаясь по временным слоям, найдем значения всех искомых функций в требуемый момент времени.

Когда при выполнении описанного алгоритма в каком-то узле сетки температура ТАМ переходит через точку плавления, алгоритм корректируется следующим образом: в данном узле сетки температура ТАМ приравнивается температуре фазового перехода и учитывается энергия, которая в данном узле на данном временном шаге должна быть затрачена на совершение фазового перехода:

где $f_{{l,m}}^{n}$ равно 0 – при плавлении и 1 – при кристаллизации. Далее алгоритм нахождения искомых функций аналогичен описанному выше, но уравнение (2.1) теперь заменяется уравнением (2.2).

Когда при выполнении алгоритма в каком-то узле сетки доля жидкой фазы переходит через свое допустимое экстремальное значение (1 – при плавлении и 0 – при кристаллизации), алгоритм снова корректируется: в данном узле сетки значение доли жидкой фазы приравнивается соответствующему экстремальному значению и учитывается энергия, которая в данном узле на данном временном шаге должна быть затрачена на нагрев либо охлаждение ТАМ:

где  f_ex равно 1 – при плавлении и 0 – при кристаллизации. Затем уравнение (2.2) заменяется уравнением (2.1). Дальнейший процесс отыскания неизвестных величин идентичен описанному выше.

Система разностных уравнений (2.1)–(2.7) может применяться для моделирования нестационарных течений газа в тепловых аккумуляторах на основе гранулированного или капсулированного материала с фазовым переходом, конфигурация которых позволяет описывать их в рамках двумерного плоского приближения. Достоинством предложенного численного метода является то, что он не требует наличия четких границ раздела фаз, позволяя описывать процессы при произвольной скорости фазового перехода, а также позволяет избежать решения сложных систем уравнений, благодаря чему возможно распараллеливание алгоритма путем геометрической декомпозиции.

3. ИССЛЕДОВАНИЕ СХОДИМОСТИ ЧИСЛЕННОГО МЕТОДА

Доказать аналитически сходимость численного решения системы (2.1)–(2.7) к точному решению системы (1.6)–(1.10) не представляется возможным. Отметим, что так как система (1.6)–(1.10) является нелинейной, то доказательство устойчивости, если бы такое было возможным, также не гарантировало бы сходимость. Экспериментальное исследование сходимости показало, что сходимость имеет место при некотором ограничении на r.

Численный эксперимент показал, что точность предлагаемого метода зависит от геометрии пористого объекта. В случае, когда задача может быть сведена к одномерной нестационарной, результаты вычислений были сопоставлены с решением, полученным из описанного в [17] численного метода для одномерного течения, и показано полное совпадение. В [17] точность метода была подтверждена сравнением с экспериментальными данными из [14], [27], а также проверкой сходимости на последовательности сгущающихся сеток. Данная проверка показала, что описывающий одномерные течения метод имеет первый порядок сходимости, но при этом порядок сходимости во внутренних точках может приближаться ко второму. Соответственно, точно такой же порядок сходимости имеет предлагаемый в настоящей работе метод при расчете одномерных течений.

Для пористых объектов иных конфигураций исследования сходимости проводились на последовательности сгущающихся сеток. Такой численный анализ показал, что значительной чувствительностью к шагу сетки обладают локальные экстремумы компонент скорости фильтрации газа, которые могу возникать при огибании газом горизонтальных препятствий. Погрешность вычислений таких пиковых значений на грубых сетках может оказаться достаточно большой. Однако, если основной интерес представляет нахождение распределений температур, плотности, давления, доли жидкой фазы, то для объектов таких форм грубые сетки позволяют получить достаточно точный результат вычислений данных величин. В случае же отсутствия горизонтальных препятствий для движения газа в пористом объекте, как правило, можно использовать достаточно грубые сетки (h = 0.025). Но заметим, что при наличии больших градиентов каких-либо величин (например, температур в пристеночных областях при сильном внешнем теплообмене через эти стенки) может оказаться, что грубая сетка не в состоянии корректно учесть эти градиенты, что может привести к существенным погрешностям в таких локальных областях. Однако, если первоочередная задача состоит в определении каких-либо интегральных параметров, то в этом случае грубые сетки позволяют получить достаточно точный результат.

При проверке порядка сходимости предложенного численного метода было обнаружено, что общий порядок сходимости, который определяется скоростью сходимости времени полного плавления ТАМ и скоростью сходимости искомых функций в узлах сетки, близок к первому, как и в одномерных задачах (см. [17]). Однако порядок сходимости для внутренних точек сетки может быть выше. Продемонстрируем это на ряде модельных задач. Рассмотрим функцию ${{t}_{{ml}}} = {{t}_{{ml}}}\left( {{{x}_{1}},{{x}_{2}}} \right)$ – время расплавления ТАМ в точке $\left( {{{x}_{1}},{{x}_{2}}} \right)$, т.е. время, когда функция f в точке $\left( {{{x}_{1}},{{x}_{2}}} \right)$ становится равной 1. Рассмотрим также отклонения этой функции:

где ${{t}_{{ml}}}\left[ {{{h}_{k}}} \right]$ – значение времени плавления ТАМ в точке $\left( {{{x}_{1}},{{x}_{2}}} \right)$, полученное на сетке с шагом ${{h}_{k}} = {{h}_{0}}{{2}^{{ - k}}},$ ${{h}_{0}} = 0.05$. По определению сходимости введенные в (3.1) отклонения должны удовлетворять соотношению где параметр b₀ и скорость сходимости b не зависят от h.

Рассмотрим течение газа в пористом объекте, который имеет форму прямоугольного параллелепипеда с проницаемыми горизонтальными и непроницаемыми вертикальными стенками, при этом две боковые параллельные друг другу стенки теплоизолированы, а другие две – нет. Расстояние между вертикальными стенками, через которые может осуществляться теплообмен с внешней средой, обозначим через L. Течение газа в таком объекте может считаться плоским и описываться системой (1.6)–(1.10) с условиями (1.13)–(1.15). Зададим следующие значения безразмерных параметров:

которые соответствуют значениям размерных параметров

Пусть $L = 0.5$. В начальный момент времени ${{T}_{c}} = {{T}_{g}} = 1$, $f = {{u}_{1}} = {{u}_{2}} = 0$, а $p$ и ${{\rho }_{g}}$ соответствуют условиям равновесия газа в пористом объекте. Рассмотрим два предельных типа граничных условий для температур ТАМ на непроницаемой поверхности G₃. Первое условие соответствует адиабатической стенке $\left( {{{{\left. {{{\partial {{T}_{c}}} \mathord{\left/ {\vphantom {{\partial {{T}_{c}}} {\partial n}}} \right. \kern-0em} {\partial n}}} \right|}}_{{{{G}_{3}}}}} = 0} \right)$ и может быть получено из (1.15) при ${\text{B}}{{{\text{i}}}_{w}} = 0$, а второе – изотермической стенке, оно может быть получено из (1.15) как предел при ${\text{B}}{{{\text{i}}}_{w}} \to \infty $, из которого получаем ${{\left. {{{T}_{c}}} \right|}_{{{{G}_{3}}}}} = {{T}_{a}}$, где положим ${{T}_{a}} = 1$.

Таблицы 1 и 2 демонстрируют значения времен плавления в разных точках и их отклонений, а также значения b₀ и b, полученные для (3.2) методом наименьших квадратов. Заметим, что параметры течения газа в описанном пористом объекте с адиабатическими стенками не изменяются по оси ${{x}_{1}}$, поэтому в табл. 1 представлены данные только для плоскости симметрии объекта. Из табл. 1 и 2 видно, что порядок сходимости b может значительно отличаться в разных точках расчетной области, причем порядок сходимости во внутренних точках в среднем близок к 1.5, а в точках, принадлежащих границе области, – к 1. Это соответствует выводу, сделанному в [17] при исследовании одномерных задач, о том, что общий порядок сходимости численного метода близок к 1, хотя во внутренних точках он может быть выше.

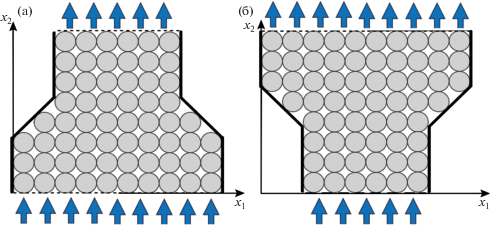
Далее рассмотрим течение газа в пористом объекте на основе гранулированного ТАМ с фазовым переходом с теплоизолированными боковыми стенками, но имеющими более сложную, чем в предыдущем случае, конфигурацию. Пусть горизонтальные поверхности объекта проницаемы, две боковые непроницаемые стенки параллельны, а другие две боковые непроницаемые стенки им ортогональны, параллельны только в нижней и верхней областях, а в средней части плавно сужаются либо плавно расширяются по направлению движения газа (фиг. 1). Течения газа через такие объекты могут быть описаны системой (1.6)–(1.10) с условиями (1.13)–(1.15). При решении указанной системы будем использовать значения параметров (3.3) и ${\text{B}}{{{\text{i}}}_{w}} = 0$. Пусть в начальный момент времени ${{T}_{c}} = {{T}_{g}} = 1$, $f = {{u}_{1}} = {{u}_{2}} = 0$, а $p$ и ${{\rho }_{g}}$ соответствуют условиям равновесия газа в пористом объекте.

Геометрию пористого объекта с плавно сужающимися стенками определим следующим образом. Пусть расстояние L₁ между стенками на высоте ${{x}_{2}} = 1$ в два раза меньше расстояния L₀ между ними на высоте ${{x}_{2}} = 0$, плоскость ${{x}_{1}} = {{{{L}_{0}}} \mathord{\left/ {\vphantom {{{{L}_{0}}} 2}} \right. \kern-0em} 2}$ является плоскостью симметрии объекта, плавное сужение стенок начинается с высоты ${{x}_{2}} = 0.25$ и заканчивается при ${{x}_{2}} = 0.75$. Таким образом, боковые стенки имеют наклон ${\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ к оси ${{x}_{1}}$. Значения времен плавления ТАМ и его отклонений в разных точках при разных шагах сетки, а также значения b и b₀ из (3.2) для такого объекта при L₀ = 2 представлены в табл. 3.

Рассмотрим также течение газа в плавно расширяющемся пористом объекте. Пусть теперь ${{L}_{0}} = {{{{L}_{1}}} \mathord{\left/ {\vphantom {{{{L}_{1}}} 2}} \right. \kern-0em} 2}$, плоскостью симметрии объекта является плоскость ${{x}_{1}} = {{{{L}_{1}}} \mathord{\left/ {\vphantom {{{{L}_{1}}} 2}} \right. \kern-0em} 2}$, плавное расширение стенок начинается с высоты ${{x}_{2}} = 0.25$ и заканчивается при ${{x}_{2}} = 0.75$. Таким образом, боковые стенки имеют наклон $ - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ к оси ${{x}_{1}}$. Значения времен плавления ТАМ и его отклонений в разных точках при разных шагах сетки и значения параметров b и b₀ из (3.2) при L₁ = 2 представлены в табл. 4.

Из табл. 3 и 4 видно, что так же, как и в рассмотренных выше случаях, скорость сходимости решения задачи выше во внутренних точках расчетной области, чем в граничных точках, причем на границе b в среднем близко к 1, а внутри – к 1.5. В ходе вычислительных экспериментов было обнаружено, что при течении газа через пористые объекты сложной геометрической конфигурации порядок сходимости в некоторых граничных точках может быть и ниже 1. Проведенные расчеты подтверждают сделанный ранее вывод о том, что скорость сходимости предлагаемого численного метода во внутренних точках выше, чем на границе.

Таким образом, общий порядок сходимости предложенного численного метода близок к первому, но во внутренних точках пористого объекта скорость сходимости может быть выше.

4. ТЕЧЕНИЯ ГАЗА ЧЕРЕЗ ПЛАВНО СУЖАЮЩИЕСЯ И ПЛАВНО РАСШИРЯЮЩИЕСЯ ПОРИСТЫЕ ОБЪЕКТЫ С ГРАНУЛИРОВАННЫМ ПЛАВЯЩИМСЯ ТАМ

Для демонстрации работы предложенного численного метода рассмотрим течение газа через пористые объекты плавно сужающейся и плавно расширяющейся формы, описанные в предыдущем разделе и схематично изображенные на фиг. 1. Систему (1.6)–(1.10) и условия (1.13)–(1.15) также будем рассматривать при значениях параметров (3.3), ${\text{B}}{{{\text{i}}}_{w}} = 0$ и при следующих начальных условиях: ${{T}_{c}} = {{T}_{g}} = 1$, $f = {{u}_{1}} = {{u}_{2}} = 0$, $p$ и ${{\rho }_{g}}$ соответствуют условиям равновесия газа в пористом объекте. Заметим, что такая постановка задачи соответствует процессу “зарядки” теплового аккумулятора, при котором в нем происходит накопление энергии.

На фиг. 2 приведены распределения искомых величин в плавно сужающемся пористом объекте при L₀ = 2 через время t = 2. Для лучшей визуализации все графики кроме поля скоростей развернуты на 180°; длина стрелки на фиг. 2е пропорциональна модулю скорости. Из фиг. 2 следует, что, охлаждаясь в результате движения через объект, газ хуже нагревает гранулированный ТАМ, поэтому по направлению к выходу из объекта температуры газа и ТАМ падают. Более эффективный нагрев ТАМ происходит в центральной части объекта (в окрестности плоскости симметрии ${{x}_{1}} = {{{{L}_{0}}} \mathord{\left/ {\vphantom {{{{L}_{0}}} 2}} \right. \kern-0em} 2}$), так как здесь газ движется более быстро, чем у боковых стенок, сужение которых создает дополнительное сопротивление потоку и приводит к замедлению движения газа вблизи них. Из-за этого в пристеночных областях наблюдается заметное отставание температуры ТАМ, доли жидкой фазы и температуры газа от их значений в центральной части объекта. Встречая на своем пути наклонные стенки, газ стремится обогнуть их, поэтому вблизи сужающихся стенок наблюдается повышенное давление газа, а плотность увеличивается значительно. В самом конце сужающейся зоны наблюдаются пиковые значения скорости фильтрации газа. Попадая вновь в зону с параллельными стенками, газ стремится течь вертикально вверх, а давление газа стремится выровняться по горизонтальной оси.

Далее рассмотрим течение газа в плавно расширяющемся пористом объекте. На фиг. 3 приведены распределения искомых величин в описанном пористом объекте при L₁ = 2 через время t = 2. Для лучшей визуализации все графики кроме поля скоростей повернуты на 180°. Из фиг. 3 следует, что так же, как в рассмотренном выше случае, более эффективный нагрев ТАМ происходит в центральной части объекта (в окрестности плоскости симметрии ${{x}_{1}} = {{L}_{1}}{\text{/}}2$), так как здесь газ движется быстрее, чем у боковых стенок. Входя в расширяющуюся часть объекта, газ стремится заполнить увеличивающееся пространство, перетекая от центральной части к боковым стенкам, вблизи которых наблюдается пониженное давление. В самом начале расширяющейся зоны скорость фильтрации газа имеет пиковые значения. Аналогично рассмотренному выше случаю, в пристеночных областях наблюдается заметное отставание температуры ТАМ, доли жидкой фазы и температуры газа от их значений в центральной части объекта. Попадая после расширяющейся части в зону с параллельными стенками, газ стремится течь вертикально вверх, а давление газа стремится выровняться по горизонтальной оси. Нагрев ТАМ вблизи боковых стенок возле выхода из объекта происходит намного хуже, чем в предыдущем случае, из-за чего плотность в этих областях падает очень медленно и долго остается достаточно высокой.

Таким образом, при течении горячего газа как через сужающиеся, так и через расширяющиеся пористые объекты на основе гранулированных ТАМ с фазовым переходом нагрев вблизи наклонных стенок объекта происходит медленнее, чем в его центральной части, даже при отсутствии теплообмена через боковые стенки.

ЗАКЛЮЧЕНИЕ

Для моделирования двумерных плоских течений газа через тепловые аккумуляторы на основе гранулированных или капсулированных материалов с фазовым переходом предложены математическая модель и численный метод. Экспериментальное исследование сходимости метода показало, что общий порядок сходимости близок к первому, однако во внутренних точках расчетной области скорость сходимости может быть выше. С использованием предложенной численной модели решена задача о течении горячего газа через пористые плавно сужающиеся и плавно расширяющиеся объекты, состоящие из гранулированного материала с фазовым переходом. Показано, что как при сужении, так и при расширении объекта нагрев теплоаккумулирующего материала и его плавление вблизи боковых стенок происходят медленнее, чем в центральной части объекта.

Вычисления проведены на оборудовании ЦКП “Дальневосточный вычислительный ресурс” ИАПУ ДВО РАН. Авторы выражают благодарность В.А. Левину за оказанную поддержку при проведении настоящего исследования.