1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 7, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 7, стр. 1172-1178

Нейронная сеть с гладкими функциями активации и без узких горловин почти наверное является функцией Морса

С. В. Курочкин *

Нац. исследовательский ун-т “Высшая школа экономики”
109028 Москва, Покровский бул., 11, Россия

* E-mail: skurochkin@hse.ru

Поступила в редакцию 15.12.2019
После доработки 15.12.2019
Принята к публикации 15.09.2020

Полный текст (PDF)

Аннотация

Доказано, что нейронная сеть с функциями активации типа сигмоидной является функцией Морса для почти всех, в смысле меры Лебега, наборов своих параметров (весов) в случае, когда архитектура сети не предусматривает сужений – слоев, в которых количество нейронов меньше, чем в соседних. На примерах показано, что требование отсутствия горловин является существенным. Библ. 16. Фиг. 1.

Ключевые слова: нейронная сеть, функции Морса.

1. ВВЕДЕНИЕ

Искусственные нейронные сети стали весьма распространенным и во многих случаях эффективным инструментом для решения различных задач анализа данных. Возможность с их помощью распознавать/аппроксимировать сложные нелинейные зависимости в данных подтверждена практикой. Теоретическим подкреплением такой достаточно универсальной применимости нейронных сетей выступает так называемая теорема Цыбенко (см. [1], [2]) – ряд результатов, полученных независимо различными авторами в конце 1980-х годов, по смыслу близких к классической теореме Соуна–Вейерштрасса в применении к конкретному множеству аппроксимируемых и запасу аппроксимирующих функций.

Предметом настоящей работы является теоретическое обоснование другого реально наблюдаемого и используемого свойства функций, получаемых в результате аппроксимации точечных или дискретных данных посредством нейросетей: возможности получать информацию об исследуемом объекте, анализируя структуру линий уровня и/или индексы критических точек аппроксимирующей функции. Целесообразность такого подхода проявляется, например, в задачах анализа изображений: согласно современным представлениям, как зрение человека (см. [3]), так и наиболее продвинутые системы машинного зрения (см. [4, гл. 4, 5]) существенно используют анализ контуров. Пример результата такого типа описан в [5], где предложен метод распознавания гомотопического типа объекта через степень аппроксимирующего отображения.

Среди всех вообще дифференцируемых функций нескольких переменных (и функций на многообразиях) функции Морса выделяются именно регулярным устройством своих линий уровня, их перестройкой при изменении уровня, а в количестве и индексах их критических точек содержится важная информация (см., например, [6]–[8]). Свойство быть функцией Морса является свойством общего положения: такие функции образуют открытое всюду плотное множество в пространстве дифференцируемых функций (точные формулировки см. в указанных и многих других текстах по теории Морса). Для применения в прикладных задачах, где пространство всевозможных функций описывается конечным (возможно, как в случае нейронных сетей, очень большим) числом параметров, такой результат представляется недостаточным. Желательно иметь уверенность в том, что в данном пространстве дополнение к функциям Морса имеет нулевую меру. Практически это будет означать, что при решении реальной задачи функции, получаемые на всех шагах так называемого обучения нейронной сети (и, разумеется, сама обученная сеть), будут функциями Морса, и это даст дополнительные возможности для анализа.

В данной работе получено условие на архитектуру нейронной сети, при котором для почти всех наборов параметров (так называемых весов) реализуемое сетью отображение будет функцией Морса. Смысл условия в том, что в сети не должно быть узких горловин (bottleneck) – когда в каком-то слое количество нейронов строго меньше, чем в слоях по обе стороны от данного. Сети с горловиной (обычно, одной) используются в специальных целях, в частности, как автокодировщики, когда требуется понизить размерность задачи путем выбора меньшего количества признаков (features), чем размерность входного вектора. Сети без горловин являются обычной практикой, они же фигурируют в теоремах об универсальной аппроксимации (см. [1]). Также на примере показано, что уже простейшая сеть с горловиной может не быть функцией Морса для множества параметров положительной меры.

Возможно, наиболее близким по смыслу известным автору результатом является утверждение, что почти все (в смысле меры Лебега в пространстве коэффициентов) многочлены нескольких переменных являются функциями Морса (см. [9], [10]).

Структура работы следующая. В разд. 2 даны терминология по нейронным сетям и необходимые сведения из дифференциальной топологии. В разд. 3 сформулирован основной результат. Далее в основном тексте дано его доказательство на примере сети классической архитектуры – с одним скрытым слоем. Основная идея работает уже на этом случае, и ход рассуждения можно проследить наглядно. Доказательство в общем случае технически несколько сложнее и вынесено в Приложение. В Заключении сформулированы выводы и возможные открытые вопросы. В Приложении также приведены доказательства основной теоремы и двух лемм.

2. ТЕРМИНОЛОГИЯ И ПОСТАНОВКА ЗАДАЧИ

2.1. Нейронные сети

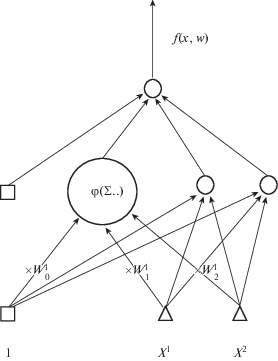
В математических терминах нейронная сеть – это вещественнозначная функция нескольких вещественных переменных, являющаяся композицией (последовательным применением) нескольких отображений вида: аффинное преобразование, затем покоординатное применение фиксированной нелинейной функции (так называемой функции активации). Коэффициенты аффинных преобразований являются настраиваемыми параметрами сети и называются весами. Иногда те из них, которые являются свободными членами соответствующих выражений, называются порогами или смещениями. Каждое отдельное взятие аффинной формы с последующим преобразованием посредством функции активации называется нейроном. В качестве функций активации могут выбираться различные варианты. На первом этапе развития теории использовались ступенчатые функции (Хевисайда), что давало возможность строить универсальные классификаторы, однако итоговое отображение получается разрывным, и задача нахождения наилучших весов имеет экспоненциальную сложность. Затем было предложено использовать сглаженные аналоги, в частности: сигмоидную, или логистическую $\varphi (x) = 1{\text{/}}\left[ {1 + {\text{exp}}( - x)} \right]$, арктангенс, гиперболический тангенс и некоторые другие. Использование дифференцируемых функций активации, вместе с простым способом вычисления градиента по весам от функции ошибок сети (так называемый метод обратного распространения ошибки), дало существенное продвижение и обусловило по сей день широкое применение именно таких сетей. При этом, как было доказано теоретически и как показала практика, конкретный выбор функции активации, хотя и доступен в применяемых программных реализациях, не влияет на результат сколько-нибудь существенным образом, важны лишь общие свойства таких функций: дифференцируемость, строгая монотонность, ограниченность, унимодальность первой производной. Также в последнее время в связи с резко возросшим объемом задач анализа дискретных данных используются недифференцируемые функции, например, $\operatorname{Re} LU(x) = max(0,x)$. На фиг. 1 представлен пример нейронной сети, на вход которой подается двумерный вектор, его координаты преобразуются независимо тремя нейронами промежуточного, или скрытого, слоя, выходы которых, в свою очередь, суммируются и преобразуются выходным нейроном (архитектура 2-3-1). Как это обычно делается для единообразия и наглядности, на фиг. 1 добавлены условные входы, тождественно равные единице, которые умножатся на пороги нейронов. В результате получается функция $f(x,w)$ двух переменных $x = ({{x}^{1}},{{x}^{2}})$, зависящая от $3 \times 3 + 4 = 13$ параметров-весов (объединенных в вектор $w$). Большое количество настраиваемых параметров характерно для нейронных сетей вообще и особенно для таких, где аффинное+нелинейное преобразование (называется слоем сети) последовательно делается много раз (такие сети называются глубокими или глубинными). Задача нахождения наилучшего (или удовлетворительного) набора весов ставится как задача минимизации ошибки аппроксимации на заданном (обучающем) наборе данных, который содержит входные векторы ${{x}_{k}}$, $k = 1,2, \ldots ,N$, и соответствующие им целевые значения ${{y}_{k}}$, $N$ – количество наблюдений. Эта задача глобальной безусловной невыпуклой оптимизации решается методами типа градиентного спуска, иногда второго порядка (с использованием гессиана), с регуляризацией, препятствующей чрезмерной подгонке к данным (переобучение, overfitting), и в сочетании с методами стохастической оптимизации. Подробно тема изложена во многих источниках (см., например, [11]). Итерации процесса оптимизации называются шагами обучения, которое для больших задач может занимать длительное время даже на мощных процессорах. Естественно, при таком подходе внимания требуют методы эффективного вычисления градиента и гессиана (см., например, [12]). Однако и то и другое берется по отношению к весам $w$, а не по аргументу $x$, и соответствующие результаты не удается применить к рассматриваемой здесь задаче.

Фиг. 1.

Пример искусственной нейронной сети. Для одного из нейронов скрытого слоя (выделен) показан принцип преобразования входного сигнала.

2.2. Сведения из дифференциальной топологии

Здесь кратко сформулированы начальные понятия и результаты дифференциальной топологии, необходимые для изложения. Подробно материал изложен во многих высококачественных текстах (см., например, [6]–[8]). Пусть $U \subset {{\mathbb{R}}^{n}}$ – область, $f:U \to \mathbb{R}$ – дифференцируемая функция. Точка $x \in U$ называется регулярной, если градиент $f$ в этой точке не равен нулю, и критической – в противном случае. Число $y \in \mathbb{R}$ является критическим значением для $f$, если $y = f(x)$ для некоторой критической точки $x$. Если в ${{f}^{{ - 1}}}(y)$ нет критических точек (в частности, если прообраз пуст), то такое значение $y$ называется регулярным для $f$. Все остальные значения являются критическими. Важный результат – теорема Сарда: множество критических значений имеет меру ноль. Критическая точка называется невырожденной, если в этой точке гессиан $f$ является невырожденной матрицей. Невырожденные критические точки изолированы. В окрестности такой точки после подходящей замены координат в векторе $x$ функция представляется в виде $f(x) = - {{({{x}^{1}})}^{2}} - \ldots - {{({{x}^{q}})}^{2}} + {{({{x}^{{q + 1}}})}^{2}} + \ldots + {{({{x}^{n}})}^{2}}$ (лемма Морса), число $q$ называется индексом этой критической точки. Если функция имеет только невырожденные критические точки, то она называется функцией Морса. Функции Морса существуют и всюду плотны в пространстве дифференцируемых функций. В силу своих хороших дифференциальных свойств, отмеченных во Введении, они представляют вполне прикладной интерес. Но с наибольшей силой это понятие работает, когда функция определена не на подмножестве ${{\mathbb{R}}^{n}}$, а на многообразии: количество и индексы критических точек произвольной функции Морса связаны с топологией многообразия.

Вопрос, рассматриваемый в данной работе, формулируется так: дана архитектура нейронной сети; можно ли, и при каких условиях, утверждать, что для почти всех наборов весов (в смысле меры Лебега в пространстве весов) соответствующая сеть является функцией Морса. В следующем разделе будет получен такой критерий, а также рассмотрены контрпримеры.

Очевидно, что “почти всех” нельзя заменить на “всех” – любая нейронная со всеми весами, равными нулю, дает на выходе константу.

3. КРИТЕРИЙ ТОГО, ЧТО НЕЙРОННАЯ СЕТЬ ЯВЛЯЕТСЯ ФУНКЦИЕЙ МОРСА

Теорема. Пусть $f(x,w)$ – нейронная сеть с произвольным количеством слоев и нейронов в слоях, функциями активации $\varphi $ типа сигмоидной и условием, что в ней нет такого промежуточного слоя, количество нейронов в котором строго меньше, чем в некоторых слоях по обе стороны от него (условие отсутствия горловины; при этом входной вектор в данном случае также считается слоем с количеством нейронов, равным размерности пространства признаков). Считаем, что $f:U \times W \to \mathbb{R}$, $x \in U \subset {{\mathbb{R}}^{n}}$, $w \in W \subset {{\mathbb{R}}^{p}}$, $U$, $W$ – области соответственно в пространстве признаков и пространстве весов. Тогда для почти всех $w$ для любого $x$ частная производная ${{\partial }^{2}}f(x,w){\text{/}}\partial w\partial x$, рассматриваемая как линейное отображение $\partial (\partial f(x,w){\text{/}}\partial x){\text{/}}\partial w:{{\mathbb{R}}^{p}} \to {{\mathbb{R}}^{n}}$ (пространство ${{\mathbb{R}}^{n}}$ отождествляется со своим сопряженным) является сюрьекцией в точке $(x,w)$.

Доказательство. Здесь будет рассмотрен случай сети архитектуры 2-3-1 (фиг. 1). Доказательство для общего случая вынесено в Приложение.

На вход $i$-го, $i = 1,2,3$, нейрона скрытого слоя подается вектор $({{x}^{1}},{{x}^{2}})$. От него берутся аффинные формы ${{s}^{i}} = w_{0}^{i} + w_{1}^{i}{{x}_{1}} + w_{2}^{i}{{x}_{2}}$, $i = 1,2,3$, затем результат покоординатно преобразуется функцией активации $\varphi $. От полученных выходов ${{y}^{1}}$, ${{y}^{2}}$, ${{y}^{3}}$ берется аффинная форма $\tilde {s} = {{\tilde {w}}_{0}} + {{\tilde {w}}_{1}}{{y}_{1}} + {{\tilde {w}}_{2}}{{y}_{2}} + {{\tilde {w}}_{3}}{{y}_{3}}$ и окончательно, $f(x,w) = \varphi (\tilde {s})$. Имеем

(1)
$\frac{{\partial f(x,w)}}{{\partial x}} = \varphi {\kern 1pt} '(\tilde {s})({{\tilde {w}}_{1}},{{\tilde {w}}_{2}},{{\tilde {w}}_{3}})\operatorname{diag} (\varphi {\kern 1pt} '({{s}^{1}}),\varphi {\kern 1pt} '({{s}^{2}}),\varphi {\kern 1pt} '({{s}^{3}}))\left( {\begin{array}{*{20}{c}} {w_{1}^{1}}&{w_{2}^{1}} \\ {w_{1}^{2}}&{w_{2}^{2}} \\ {w_{1}^{3}}&{w_{2}^{3}} \end{array}} \right)$
(произведение скаляра, $1 \times 3$-строки, $3 \times 3$-матрицы и $3 \times 2$-матрицы, результат – $1 \times 2$-строка). Тогда, например, для производной по порогу первого нейрона скрытого слоя имеем
(2)
$\frac{{{{\partial }^{2}}f(x,w)}}{{\partial w_{0}^{1}\partial x}} = \frac{\partial }{{\partial {{s}^{1}}}}[\varphi {\kern 1pt} '(\tilde {s})({{\tilde {w}}_{1}},{{\tilde {w}}_{2}},{{\tilde {w}}_{3}})\operatorname{diag} (\varphi {\kern 1pt} '({{s}^{1}}),\varphi {\kern 1pt} '({{s}^{2}}),\varphi {\kern 1pt} '({{s}^{3}}))]\left( {\begin{array}{*{20}{c}} {w_{1}^{1}}&{w_{2}^{1}} \\ {w_{1}^{2}}&{w_{2}^{2}} \\ {w_{1}^{3}}&{w_{2}^{3}} \end{array}} \right).$
Для краткости записи выражение в квадратных скобках (это $1 \times 3$-строка) обозначим через $u(x,w)$. Далее
(3)
$\frac{{{{\partial }^{2}}f(x,w)}}{{\partial w_{1}^{1}\partial x}} = {{x}^{1}}\frac{\partial }{{\partial {{s}^{1}}}}u(x,w)\left( {\begin{array}{*{20}{c}} {w_{1}^{1}}&{w_{2}^{1}} \\ {w_{1}^{2}}&{w_{2}^{2}} \\ {w_{1}^{3}}&{w_{2}^{3}} \end{array}} \right) + u(x,w)\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \\ 0&0 \end{array}} \right),$
и аналогично для производной по $w_{2}^{1}$ и для производных по весам двух других нейронов 1-го (скрытого) слоя. Вычитая выражение (2), домноженное на ${{x}^{i}}$, из выражения (3) для соответствующего веса, получаем, что уже только вариация весов $w_{i}^{j}$ скрытого слоя позволяет получать в образе касательного пространства $w$ при отображении ${{\partial }^{2}}f(x,w){\text{/}}\partial w\partial x$ всевозможные строки вида $uA$, где $A$ – произвольная $3 \times 2$-матрица. При этом всегда $\varphi {\kern 1pt} ' \ne 0$ и для почти всех (в смысле меры Лебега) наборов весов ${{\tilde {w}}_{i}}$ строка $(\mathop {\tilde {w}}\nolimits_1 ,\mathop {\tilde {w}}\nolimits_2 ,\mathop {\tilde {w}}\nolimits_3 )$, а тем самым и строка $u$, ненулевая. Следовательно, для почти всех наборов весов в виде $uA$ можно представить любую $1 \times 2$-строку.

Далее потребуется следующий факт из дифференциальной топологии.

Лемма 1. Пусть $U$, $W$ – области соответственно в ${{\mathbb{R}}^{n}}$ и ${{\mathbb{R}}^{p}}$, $p \geqslant n$, $f(x,w)$ – дифференцируемая функция, $f:U \times W \to \mathbb{R}$. Обозначим ${{f}_{w}}(x) = f(x,w)$, ${{f}_{w}}:U \to \mathbb{R}$, $d{{f}_{w}}:U \to {{\mathbb{R}}^{n}}$ – ее производная по $x$,

$d{{f}_{w}}(x) = \left( {\frac{{\partial {{f}_{w}}(x)}}{{\partial {{x}_{1}}}}, \ldots ,\frac{{\partial {{f}_{w}}(x)}}{{\partial {{x}_{n}}}}} \right),$
и $F(x,w) = d{{f}_{w}}(x)$, $F:U \times W \to {{\mathbb{R}}^{n}}$. Пусть известно, что в любой точке $(x,w)$ производная от $F$ по $w$ является сюрьекцией. Тогда для почти всех $w$ (в смысле обычной меры Лебега в ${{\mathbb{R}}^{p}}$) ${{f}_{w}}$ является функцией Морса.

Это утверждение может быть получено из [4, теорема 1.2.4]. Для замкнутости изложения в Приложении приведено краткое доказательство.

Непосредственное применение леммы 1 дает

Следствие. Нейронная сеть, удовлетворяющая условиям теоремы, для почти всех наборов весов $w$ является функцией Морса.

Замечание 1. Приведенное выше доказательство годится не только для конкретной сети на фиг. 1, но и для любой сети с одним промежуточным слоем: при произвольной размерности входного вектора и любом количестве нейронов в слое.

Следующий пример демонстрирует связь между наличием горловины и возможностью существования вырожденных критических точек.

Контрпример. Рассмотрим сеть архитектуры 2-1-2-1:

$f(x,w) = \varphi ({{\hat {w}}_{0}} + {{\hat {w}}_{1}}\varphi (\tilde {w}_{0}^{1} + \tilde {w}_{1}^{1}\varphi ({{w}_{0}} + {{w}_{1}}{{x}^{1}} + {{w}_{2}}{{x}^{2}})) + \mathop {\hat {w}}\nolimits_2 \varphi (\tilde {w}_{0}^{2} + \tilde {w}_{1}^{2}\varphi ({{w}_{0}} + {{w}_{1}}{{x}^{1}} + {{w}_{2}}{{x}^{2}}))).$

Поскольку при преобразовании в первом слое размерность входного вектора понижается, все критические точки $f$, если они есть, обязаны быть вырожденными. Пусть в качестве функции активации $\varphi $ будет, например, сигмоидная, и рассмотрим следующий набор весов: ${{w}_{0}} = 0$, ${{w}_{1}} = 1$, ${{w}_{2}} = 0$, $\tilde {w}_{0}^{1} = - 10$, $\tilde {w}_{1}^{1} = 1$, $\tilde {w}_{0}^{2} = 10$, $\tilde {w}_{1}^{2} = - 1$, ${{\hat {w}}_{0}} = 0$, ${{\hat {w}}_{1}} = 1$, ${{\hat {w}}_{2}} = 1$. Тогда точка $x = (0,0)$ является локальным минимумом, который устойчив, т.е. существует и мало меняется, при произвольных малых возмущениях всех весов. Таким образом, в пространстве весов существует множество положительной меры такое, что все соответствующие сети имеют вырожденную критическую точку.

Замечание 2. Из этого примера можно сконструировать другие, демонстрирующие различные дифференциальные свойства нейронных сетей как отображений.

1. Если убрать один слой со стороны входа, т.е. взять 1-2-1-сеть, то она почти для всех весов будет функцией Морса и при этом для множества весов положительной меры будет иметь критические точки.

2. Если убрать еще один слой, то полученная 2-1-сеть для всех ненулевых наборов весов будет иметь только регулярные значения.

4. ЗАКЛЮЧЕНИЕ

Использование дифференциальных свойств функций для исследования топологии объекта, на котором они заданы или который они аппроксимируют, успешно применяется в математике, прежде всего, дифференциальной топологии и геометрии, и в прикладных областях, таких так топологический анализ данных. Искусственные нейронные сети являются в настоящее время общеупотребительным универсальным аппроксиматором. Полученный в данной работе критерий того, что сеть является функцией Морса, дает теоретическое основание для примерения дифференциально-топологических методов в широком классе прикладных задач. Дальнейшие вопросы теоретического свойства, по-видимому, могут быть связаны с получением различных явных соотношений между дифференциальными характеристиками сети как функции, топологической (конкретно, клеточной) структурой поверхностей уровня и топологической структурой исследуемого объекта.

Список литературы

  1. Cybenko G.V. Approximation by Superpositions of a Sigmoidal function // Math. Control Signals Systems. 1989. V. 2. № 4. P. 303–314.

  2. Pinkus A. Approximation theory of the MLP model in neural networks // Acta Numerica. 1999. V. 8. P. 143–195.

  3. Dagnelie G. (ed.) Visual Prosthetics. Springer, 2011.

  4. Szeliski R. Computer Vision. Springer, 2011.

  5. Курочкин С.В. Распознавание гомотопического типа объекта с помощью дифференциально-топологических инвариантов аппроксимирующего отображения // Компьютерная оптика. 2019. Т 43. 4. (в печати)

  6. Хирш М. Дифференциальная топология М.: Мир, 1979.

  7. Постников М.М. Введение в теорию Морса. М.: Наука, 1971.

  8. Прасолов В.В. Элементы комбинаторной и дифференциальной топологии. М.: МЦНМО, 2014.

  9. Le C. A note on optimization with Morse polynomials // Commun. Korean Math. Soc. 2018. V. 33. № 2. P. 671–676.

  10. Banyaga A., Hurtubise D. Lectures on Morse Homology. Kluwer Texts Math. Sci. V. 29, Kluwer Acad. Publ. Dordrecht, 2004.

  11. Гудфеллоу Я., Бенджио И., Курвилль А. Глубокое обучение. М.: ДМК Пресс, 2017.

  12. Bishop C. Exact Calculation of the Hessian Matrix for the Multi-layer Perceptron // Neur. Computat. 1992. V. 4. № 4. P. 494–501.

  13. Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning. N.Y.: Springer, 2009. ISBN 978-0-387-84857-0.

  14. Nicolaescu L. An Invitation to Morse Theory. Springer, 2011. ISBN 978-1-4614-1105-5

  15. Baksalary J.K., Kala R. The matrix equation AX – YB = C // Linear Algebra and its Applicat. 1979. V. 30. P. 41–43.

  16. Прасолов В.В. Задачи и теоремы линейной алгебры. М.: МЦНМО, 2015.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал