Журнал вычислительной математики и математической физики, 2021, T. 61, № 9, стр. 1556-1570

1. ВВЕДЕНИЕ

Под магнитным торнадо в широком смысле понимаются вихревые высокоскоростные потоки проводящего электрический ток газа в электромагнитном поле. Такие потоки неоднократно наблюдались в солнечной плазме [1]–[4]. Есть основания считать [5], что магнитные торнадо, зарождающиеся в хромосфере Солнца, образуют канал для транспортировки энергии из нижних слоев Солнца в солнечную корону и являющиеся причиной ее аномального разогрева, возникновения солнечных пятен и генерации солнечного ветра.

При построении математической теории магнитного торнадо естественно использовать опыт математического моделирования торнадо в атмосферном воздухе Земли. К настоящему времени считается, что торнадо порождается вихревым движением в материнском (смерчевом) облаке. Судя по наблюдениям [6], [7], вихрь, порождающий торнадо, имеет сложную трехмерную структуру, состоящую из одновременной циркуляции воздуха в полоидальном и азимутальном направлениях и образующую изогнутый тор (вихревое кольцо). Причины возникновения вихревого кольца, равно как и механизм генерации им торнадо, плохо изучены. Прямое математическое моделирование торнадо, основанное на численном решении уравнений газовой динамики применительно к воздушной атмосфере Земли с учетом трехмерности движения, турбулентности воздушных течений, зависимости динамической вязкости воздуха от водяной и песчаной пыли и т.д. [8]–[11], наталкивается на ряд серьезных проблем, главной из которых следует считать выбор начальных и граничных условий. Экстраполяция последних по данным наблюдений неизбежно приводит к большим погрешностям, обесценивающим результаты вычислений параметров торнадо. В этой связи в [12], [13] была предложена простая математическая модель, позволяющая исследовать причинно-следственную связь между наличием вихревого движения в материнском облаке и возникновением закрученного восходящего потока воздуха. Эта модель абстрагируется от ряда важных особенностей торнадо, снимает остроту проблемы выбора граничных условий и позволяет дать теоретическое решение задачи предсказания и предотвращения торнадо – где и когда могут возникнуть торнадо и какова их мощность, какие меры необходимо предпринять для предотвращения возможного или нейтрализации уже случившегося торнадо? Для практического ответа на эти вопросы на базе простой модели [12], [13] необходим дополнительный анализ данных мониторинга вихревых образований в верхних слоях атмосферы и распределения давления в атмосферном воздухе.

Прямое математическое моделирование магнитного торнадо на Солнце на базе численного решения уравнений классической МГД [14] сопряжено с дополнительной проблемой выбора счетной области. Поскольку Солнце – это огромный плазменный шар, в котором отсутствуют твердая поверхность Солнца и атмосфера, то при исследовании магнитного торнадо исчезают естественные границы типа поверхности Земли и верхних слоев атмосферы, которые имели место при изучении торнадо в атмосферном воздухе Земли и на которых ставились граничные условия. Неопределенность в задании границ счетной области существенно усугубляет проблему выбора начальных и граничных условий при прямом математическом моделировании магнитного торнадо. В этой связи в настоящей статье обобщаются идеи работ [12], [13] для исследования магнитных торнадо на Солнце. При этом делается ряд предположений. Во-первых, считается, что среда, где возникает магнитное торнадо, является плазмой, динамика которой подчиняется уравнениям классической МГД теории Х. Альфвена. Во-вторых, магнитным торнадо будем называть стационарное течение солнечной плазмы, гидродинамические и электродинамические параметры которого обладают осевой симметрией относительно некоторой вертикальной прямой, а вертикальная скорость имеет конечный и положительный предел при $z \to + \infty $. Здесь $z$ – координата на вертикальной прямой, которая однозначно определяется лучом, исходящим из центра Солнца, причем координата $z$ отсчитывается от солнечного центра. В этом определении специально не предполагается вращение плазмы вокруг вертикальной прямой, чтобы единой теорией охватить магнитные торнадо различной природы. Например, если солнечная плазма в силу различных причин аксиально симметричным образом сжимается к некоторой вертикальной оси с координатой $z$, то в возникающем z-пинче, как известно [15], имеет место эффект аномального ускорения частиц плазмы вдоль вертикальной прямой, что приводит к появлению магнитного торнадо в указанном выше смысле.

В настоящей работе анализируется другой возможный механизм возникновения магнитного торнадо, обусловленный наличием плазменного вихря в фотосфере или хромосфере в плоскости, ортогональной некоторой вертикальной прямой, центр которого лежит на этой прямой, и перепада плазменного давления периферия-центр (к образованию плазменного вихря могут привести различные причины, например, электрический дрейф плазмы в скрещенных электромагнитных полях). Согласно [12], [13], перечисленные причины приводят к появлению гидродинамического торнадо, однако возникает вопрос, насколько совместимо существование этого торнадо с магнитным полем, взаимодействующим с плазменным веществом?

Цель работы – дать теоретическое подтверждение существования наблюдаемых магнитных торнадо и указать пути математического исследования этого явления. Первая задача решается изучением специальных классов точных решений уравнений классической МГД, среди которых содержатся течения типа магнитных торнадо. Вторая сводится к построению специального математического аппарата – уравнений магнитного торнадо, численное и аналитическое решение которых позволяет практически искать магнитные торнадо.

2. УРАВНЕНИЯ МАГНИТНОГО ТОРНАДО

Рассмотрим динамику плазменной среды, подчиненной уравнениям классической МГД для несжимаемой вязкой плазмы с конечной проводимостью в постоянном гравитационном поле [16]:

где $\mu = {\text{const}}$, $\sigma = {\text{const}}$ – гидродинамическая вязкость и проводимость плазмы, ${\mathbf{g}}$ – постоянное ускорение силы тяжести, ${{{\text{I}}}_{3}}$ – единичный трехмерный тензор, $\operatorname{def} {\mathbf{U}}$ – тензор скоростей деформаций векторного поля ${\mathbf{U}}$.

В осесимметричном случае, $\partial {\text{/}}\partial \varphi = 0$, система (1) в цилиндрических координатах примет вид

где в цилиндрических координатах ${\mathbf{g}} = (0,0, - g)$.

Последняя система допускает частные решения вида

где функции $A$, $B$, $C$, $P$, $S$, $G$, $Q$, $\Phi $ подлежат нахождению. В этом несложно убедиться, подставляя выражения (2) в систему (1), записанную в цилиндрических координатах. Тогда получим следующий результат.

Теорема 1. В случае осевой симметрии функции (2) являются решением системы (1) тогда и только тогда, когда комплексные функции $u = A + {\text{i}}B$, $w = P + {\text{i}}S$ и вещественные функции $C$ и $G$ удовлетворяют системе уравнений

где ${{\gamma }_{0}}(t)$ – произвольная вещественная функция, ${{\nu }_{{\text{m}}}} = {{c}^{2}}{\text{/}}(4\pi \sigma )$ – магнитная вязкость, $\operatorname{Re} $ – символ вещественной части комплексного числа. По решению системы (3) функция $Q$ ищется из равенстваа функция $\Phi $ однозначно, с точностью до произвольной константы, из уравнения

Функции (2) в достаточно малой окрестности оси симметрии сколь угодно точно аппроксимируют любое осесимметричное течение плазмы, не имеющее особенностей на оси. Действительно, раскладывая параметры течения в степенные ряды по радиусу $r$ и ограничиваясь при достаточно малом $r$ первыми, главными членами разложений, приходим к формулам (2). При этом надо учесть, что радиальные и азимутальные компоненты векторных величин являются нечетными функциями радиуса, а осевые компоненты и термодинамические параметры – четными.

Теорема 2. 1) Любое решение системы (3) удовлетворяет системе уравнений

2) Любое решение системы (5), для которого при некотором ${{z}_{0}}$ тождественно по $t$ выполнено равенство

удовлетворяет системе (3).

3) Если для решения системы (5) условие (6) выполнено в некоторой точке ${{z}_{0}}$, то круглая скобка в левой части равенства (6) тождественно равна нулю для всех $t$ и $z$.

Система (5) называется уравнениями магнитного торнадо. Согласно теореме 2, физический смысл имеют только решения (5), удовлетворяющие условию (6) в некоторой точке ${{z}_{0}}$, в качестве которой надо взять граничную точку области по $z$, где решаются системы (3), (5), ${{z}_{0}} \leqslant z < + \infty $. Поэтому ниже условие (6) называется граничным и для простоты считается ${{z}_{0}} = 0$. Достаточным условием справедливости (6) являются, очевидно, соотношения

В частном случае $w = 0$, $G = 0$ (отсутствует магнитное поле) граничное условие (6) выполнено, а система (5) дает Система (7) называется уравнениями торнадо и позволяет исследовать явление торнадо в атмосферном воздухе [12], [13]. Ниже существенно используются результаты этого исследования. В безразмерном виде система (5) и граничное условие (6) запишутся следующим образом: где $R = \rho {{L}_{0}}{{U}_{0}}{\text{/}}\mu $, ${{R}_{{\text{m}}}} = {{L}_{0}}{{U}_{0}}{\text{/}}{{\nu }_{{\text{m}}}}$ – числа Рейнольдса (гидродинамическое и магнитное), ${{M}_{{\text{A}}}} = {{{v}}_{{\text{A}}}}{\text{/}}{{U}_{0}}$ – альфвеновское число Маха, ${{{v}}_{{\text{A}}}} = {{H}_{0}}{\text{/}}\sqrt {4\pi \rho } $ – альфвеновская скорость, $\Gamma = \Gamma (t) = 2{{\gamma }_{0}}(t)t_{0}^{2}{\text{/}}\rho $, ${{t}_{0}} = {{L}_{0}}{\text{/}}{{U}_{0}}$, ${{L}_{0}}$, ${{H}_{0}}$, ${{U}_{0}}$, – характерные значения длины, напряженности магнитного поля и скорости.

Система (8) в матричной форме имеет тот же вид, что и уравнение торнадо (7). Введем комплексный и вещественный векторы ${\mathbf{u}} = {{(u,w)}^{{\text{т}}}}$, ${\mathbf{c}} = {{(C,G)}^{{\text{т}}}}$ и для вектора ${\mathbf{x}} = {{(x,y)}^{{\text{т}}}}$ рассмотрим 2×2-матрицу $A({\mathbf{x}})$:

Тогда система (8) равносильна нелинейной системе уравнений относительно векторных функций – комплекснозначной ${\mathbf{u}}(t,z)$ и вещественнозначной ${\mathbf{c}}(t,z)$:

Рассмотрим специальные решения системы (8).

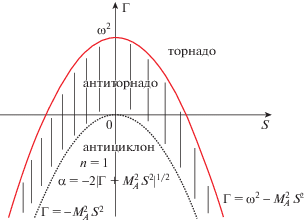
Определение. 1) Магнитным торнадо (антиторнадо) называется стационарное решение системы (8), (9), для которого существует конечный передел и верно неравенство $\mathop {\lim }\limits_{z \to + \infty } C(z) > 0$ ($\mathop {\lim }\limits_{z \to + \infty } C(z) < 0$).

2) Магнитным циклоном (антициклоном) называется стационарное решение системы (8), (9), для которого справедливо асимптотическое равенство (эквивалентность в смысле матанализа) $C(z)\sim \alpha {{z}^{n}}$, $z \to + \infty $, для некоторых $\alpha > 0$ ($\alpha < 0$) и $n \geqslant 0$, зависящих от стационарного решения; если при этом $\Gamma > 0$ ($\Gamma < 0$), то стационарное решение называется магнитным циклоном (антициклоном) гидродинамического типа. Числа $\alpha $, $n$ называются показателями циклона или антициклона.

Показатели $\alpha $ и $n$ характеризуют силу циклона или антициклона – чем больше $\left| \alpha \right|$ и $n$, тем выше энергия этих течений. Ниже чаще всего $n = 0$ или $n = 1$. Магнитным циклоном (антициклоном) с показателем $n = 0$ является любое магнитное торнадо (антиторнадо). Другой пример дают точные стационарные решения системы (8), (9) вида ${{u}_{0}}(z) \equiv {{A}_{0}} + {\text{i}}{{B}_{0}}$, ${{w}_{0}}(z) \equiv {{P}_{0}} + {\text{i}}S$, ${{C}_{0}}(z) = - 2{{A}_{0}}z$, ${{G}_{0}}(z) = - 2{{P}_{0}}z$, где постоянные комплексные числа ${{A}_{0}} + {\text{i}}{{B}_{0}}$, ${{P}_{0}} + {\text{i}}{{S}_{0}}$ подчинены условию ${{({{A}_{0}} + {\text{i}}{{B}_{0}})}^{2}} + \Gamma = M_{{\text{A}}}^{2}{{({{P}_{0}} + {\text{i}}{{S}_{0}})}^{2}}$. Тогда при ${{A}_{0}} > 0$ имеем антициклон, а при ${{A}_{0}} < 0$ – циклон – оба с показателем $n = 1$.

Система уравнений магнитного торнадо (8) должна быть дополнена начальными и граничными условиями. При рассмотрении стационарных течений начальные условия теряют актуальность, а граничные условия для $u$ и $w$ ставятся в точках $z = 0$ и $z = \infty $, а для $C$ и $G$ – в точке $z = 0$. Как уже отмечалось, по данным наблюдений за солнечной плазмой трудно сделать осмысленный выбор граничных условий. Разумеется, надо использовать граничное условие (9), но его недостаточно. Дополнительные соображения можно извлечь из экспериментального исследования закрученных потоков в ртутной плазме [17], порождаемых вращающимся диском, обобщающего работу Т. Кармана [18] на случай плазменных течений [19], [20].

Ниже рассматриваются два класса решений уравнений магнитного торнадо (8), (9), анализ которых приводит к важным выводам, в частности, показывает, что течения типа магнитных торнадо, антиторнадо, циклона, антициклона теоретически существуют и приводят к появлению высокоскоростных потоков плазмы с огромными напряженностями магнитного поля. При этом граничные условия выбирались так, чтобы гарантировать при численном решении существование и единственность решения рассматриваемых краевых задач на полупрямой.

3. ДВА КЛАССА ЧАСТНЫХ РЕШЕНИЙ УРАВНЕНИЙ МАГНИТНОГО ТОРНАДО

Рассмотрим решения системы (8) с $G = 0$ и чисто мнимой функцией $w$. Тогда $w = {\text{i}}S$, граничное условие (9) выполнено и система (8) упрощается:

Система (10) описывает взаимодействие чисто азимутального (${{H}_{r}} = {{H}_{z}} = 0$) магнитного поля, для которого ${{H}_{\varphi }} = rS(t,z)$, с осесимметричными течениями плазмы вида (2). Ограничимся еще более частным случаем $S = {\text{const}}$, тогда второе уравнение в (10) выполнено тождественно и система (10) сводится к следующей: которая отличается от уравнений торнадо (7) заменой $\Gamma \to M_{{\text{A}}}^{2}{{S}^{2}} + \Gamma $. Случай $S = {\text{const}}$ соответствует осесимметричному чисто азимутальному магнитному полю без особенностей на оси, создаваемому однородным осевым током, ${{j}_{r}} = {{j}_{\varphi }} = 0$, ${{j}_{z}} = {\text{const}}$, причем ${{j}_{z}}$ связано с $S$ соотношением ${{j}_{z}} = 2S$. Система (11) позволяет исследовать влияние указанного магнитного поля на осесимметричные течения плазмы вида (2), при этом движущаяся плазма на магнитное поле не воздействует. Ниже рассмотрены стационарные решения (11) для определенных граничных условий.

Второй класс стационарных решений системы (8), (9) образован течениями плазмы вида (2) вдоль силовых линий магнитного поля. Известно [21], что интегрирование уравнений классической МГД может быть сведено к интегрированию уравнений обычной гидродинамики в случае стационарных течений плазмы, когда магнитное поле и гидродинамическая скорость параллельны друг другу. Рассмотрим стационарные решения системы (8) с ${{R}_{{\text{m}}}} = \infty $ (идеально проводящая плазма), для которых $w = ku$, $G = kC$, где $k$ – произвольная заданная вещественная константа. Для таких решений граничное условие (9) выполнено, а система (8) сводится к следующей:

Комбинация ${{k}^{2}}M_{{\text{A}}}^{2}$ ниже называется параметром замагниченности и характеризует роль магнитного поля при движении плазменного вещества. Нетрудно проверить, что ${{k}^{2}}M_{{\text{A}}}^{2}$ равно отношению энергии магнитного поля к кинетической энергии плазмы, отнесенных к единице объема, ${{k}^{2}}M_{{\text{A}}}^{2} = {{H}^{2}}{\text{/}}(8\pi ):\rho {{U}^{2}}{\text{/}}2$. При ${{k}^{2}}M_{{\text{A}}}^{2} \to 0$ влияние магнитного поля на движение плазмы исчезающе мало. При ${{k}^{2}}M_{{\text{A}}}^{2} \to + \infty $ и, что самое интересное, ${{k}^{2}}M_{{\text{A}}}^{2} \to 1$ это влияние резко возрастает, и значение ${{k}^{2}}M_{{\text{A}}}^{2} = 1$ является бифуркационным, разделяющим разные типы стационарных течений (см. разд. 5). При ${{k}^{2}}M_{{\text{A}}}^{2} = 1$ система (12) становится линейной и легко интегрируется: где ${{K}_{0}}$, ${{K}_{1}}$, ${{K}_{2}}$ – произвольные постоянные. Формулы (13) задают пятимерное вещественное пространство, состоящее при $\Gamma \ne 0$ из циклонов или антициклонов с показателями $\alpha = - R\Gamma {\text{/}}3$, $n = 3$, заведомо не относящиеся к гидродинамическому типу в смысле данного выше определения.

При ${{k}^{2}}M_{{\text{A}}}^{2} \ne 1$ система (12) следующим образом редуцируется к уравнениям торнадо (7). При ${{k}^{2}}M_{{\text{A}}}^{2} < 1$ заменой переменных

система (12) сводится к виду который совпадает с системой (7) в безразмерном виде при $\partial {\text{/}}\partial t = 0$.

При ${{k}^{2}}M_{{\text{A}}}^{2} > 1$ заменой переменных

где черта означает комплексное сопряжение, система (12) сводится к виду который совпадает с системой (7) для $\partial {\text{/}}\partial t = 0$, где $\Gamma $ заменено на $ - \Gamma $.

Итак, исследование стационарных осесимметричных течений плазмы вида (2) вдоль силовых линий магнитного поля полностью редуцируется к исследованию стационарных решений уравнений торнадо (7).

4. СТАЦИОНАРНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ТОРНАДО

Рассмотрим уравнения торнадо (7) в безразмерном виде

Система (18) нелинейная, и в нашем распоряжении нет математической теоремы, позволяющей определить граничные условия, для которых возникающая краевая задача для системы (18) имеет и притом единственное решение. Физические соображения [12], [13] приводят к следующим граничным условиям: Факт существования и единственности стационарного решения задачи (18), (19) устанавливается численно посредством изложенного ниже метода установления.

Выберем счетную область $[0,L]$ на оси $z$ с достаточно большим $L$ (результаты проводимых расчетов существенно не меняются при увеличении $L$) и равномерную сетку ${{z}_{k}} = kh$, $0 \leqslant k \leqslant N$, $h = L{\text{/}}N$, $N > 1$ – натуральное. Рассмотрим неявную разностную схему

из которой значения $u_{k}^{1}$, $0 < k < N$, на верхнем слое ищутся по значениям $u_{k}^{0}$, $0 < k < N$, на нижнем слое прогонкой при решении системы линейных уравнений: После этого величины $C_{k}^{1}$ на верхнем слое ищутся решением задачи Коши на отрезке $[0,L]$: с учетом того, что правая часть (22) задана в узлах ${{z}_{k}}$. Поскольку порядок аппроксимации разностной схемы (20) равен $O(\tau + {{h}^{2}})$ при численном решении задачи Коши (22), можно использовать метод счета невысокого порядка. Достаточно, например, рассмотреть метод Рунге–Кутты второго порядка точности, который в данном случае сводится к квадратурной формуле трапеций: Условие устойчивости прогонки выполнено при наличии диагонального преобладания (по строкам) матрицы коэффициентов системы (21) Последнее условие, нетрудно убедиться, заведомо выполнено, если Неравенства (24) дают ограничения на временной шаг $\tau $.

По разностной схеме (20), (23) вычисления ведутся до момента установления, т.е. пока не будет выполнено условие

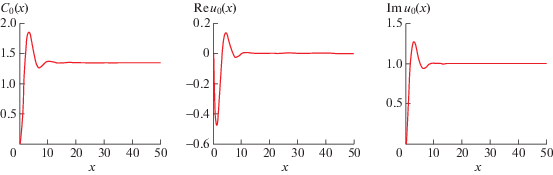
где $\varepsilon > 0$ – задаваемая до начала счета малая положительная величина. Для шагов $h = {{10}^{{ - 2}}}$, $h = {{10}^{{ - 3}}}$ минимальное значение $\varepsilon = {{10}^{{ - 9}}}$. При выполнении неравенства (25) вычисления прекращаются, а $u_{k}^{1}$, $C_{k}^{1}$, $0 \leqslant k \leqslant N$, рассматриваются как сеточные аппроксимации искомого стационарного решения. От выбора начальных значений функций $u$ и $C$ результат расчета не зависит, но существенно зависит время установления. Для его минимизации начальные функции $u(z)$, $C(z)$ следует выбирать так, чтобы $u(z)$ удовлетворяло граничным условиям (19), а $C(z)$ – граничному условию (19) и уравнению $dC{\text{/}}dz = - 2\operatorname{Re} u(z)$. Мы использовали простейшие аппроксимации В частности, в узлах сетки $C({{z}_{k}})$ вычислялись по формулам (23): $C({{z}_{k}}) = C({{z}_{{k - 1}}}) - h({{A}_{k}} + {{A}_{{k - 1}}})$, $k = 1,\; \ldots ,\;N$, $C({{z}_{0}}) = 0$, ${{A}_{k}} = \operatorname{Re} u({{z}_{k}})$.

Построенный выше алгоритм нахождения стационарных решений краевой задачи (18), (19) значительно проще прямых методов – типа метода стрельбы [22] или метода квазилинеаризации Р. Беллмана [23] – решения краевой задачи на полупрямой для нелинейной системы ОДУ пятого порядка, которая получится, если в (18) положить $\partial {\text{/}}\partial t = 0$ и перейти к вещественным неизвестным функциям $A$, $B$, $C$. Частным случаем последней задачи, для $\Gamma = 0$, ${{u}_{0}} = {\text{i}}$, $R = 1$, является известная задача Т. Кармана [18] о бесконечном плоском диске, погруженнoм в вязкую несжимаемую жидкость и вращающимся с постоянной угловой скоростью. Требуется определить скорость жидкости, приводимой в движение указанным диском. Решение этой задачи известно [24], [25] (в частности, $C(\infty ) = - 0.886$) и использовалось в качестве одного из тестов для предложенного выше алгоритма.

Существование и единственность стационарного решения краевой задачи (18), (19) и тип этого решения зависят от граничного условия ${{u}_{0}}$ в нуле. Характер этой зависимости до конца не ясен и требует дополнительного исследования. Ниже мы ограничимся важнейшим частным случаем граничного условия (19), когда ${{u}_{0}} = {\text{i}}\omega $, $\omega > 0$:

Стационарное решение краевой задачи (18), (26) зависит от трех вещественных параметров $\omega > 0$, $R > 0$, $\Gamma $. Преобразованием подобия эта зависимость сводится к одному параметру, что важно для численного исследования.

Теорема 3. Пусть $\omega > 0$ и

Тогда функции $u$, $C$ от $(t,z)$ удовлетворяют системе (18) тогда и только тогда, когда функции $\tilde {u}$, $\tilde {C}$ от $(\tau ,x)$ удовлетворяют системе уравнений

В переменных $\tilde {u}$, $\tilde {C}$ краевая задача (18), (26) равносильна задаче (28), (29)

решения которой зависят, очевидно, от одного параметра $\Gamma {\text{/}}{{\omega }^{2}}$ и позволяют восстановить решение краевой задачи (18), (26) посредством преобразования (27).

Рассмотрим краевые условия

причем в (30) берется арифметическое значение корня. Численные расчеты на установление по приведенному выше алгоритму приводят к следующим результатам:

1) при $\Gamma > 1$ краевая задача (18), (30) имеет стационарное решение типа торнадо;

2) при $0 \leqslant \Gamma < 1$ краевая задача (18), (30) имеет стационарное решение типа антиторнадо;

3) при $\Gamma = 1$ краевая задача (18), (30) имеет точное решение $u(z) \equiv {\text{i}}$, $C(z) \equiv 0$;

4) при $\Gamma < 0$ краевая задача (18), (31)

имеет стационарное решение типа антициклон с показателями $\alpha = - 2\sqrt {\left| \Gamma \right|} $, $n = 1$, в частности $C(z)\sim - 2\sqrt {\left| \Gamma \right|} z$, $z \to + \infty $.

Графическая иллюстрация результатов 1)–4) приведена в [12], [26]. Численные расчеты на установление для различных начальных условий не обнаружили неединственность стационарных решений указанных выше краевых задач. Из обратного преобразования подобия (27) отсюда следует, что для краевого условия (26), где для $\Gamma \geqslant 0$ берется арифметическое значение корня, а при $\Gamma < 0$ считается ${\text{i}}\sqrt \Gamma = \sqrt {\left| \Gamma \right|} $, имеет место следующий

Вывод. Существует критическое значение ${{\Gamma }_{{{\text{кр}}}}} = {{\omega }^{2}}$, для которого при $\Gamma > {{\Gamma }_{{{\text{кр}}}}}$ краевая задача (18), (26) имеет стационарное решение типа торнадо, а при $0 \leqslant \Gamma < {{\Gamma }_{{{\text{кр}}}}}$ – типа антиторнадо; при $\Gamma = {{\Gamma }_{{{\text{кр}}}}}$ стационарное решение суть $u(z) = {\text{i}}\omega $, $C(z) = 0$. Наконец, при $\Gamma < 0$ краевая задача (18), (26) имеет стационарное решение типа антициклон с показателями $\alpha = - 2\sqrt {\left| \Gamma \right|} $, $n = 1$.

В заключение укажем на источник важных приближенных формул для так называемых мощных торнадо, под которыми ниже подразумеваются стационарные решения краевой задачи (18), (19) с $\Gamma > 0$ (арифметическим значением корня в (19)) и $\left| {{{u}_{0}}} \right|{{\Gamma }^{{ - 1/2}}} \ll 1$. Из формулы (4) следует, что $\Gamma $ в чисто гидродинамическом случае ($w = 0$, $G = 0$) определяет перепад гидродинамического давления в центре торнадо ($r = 0$) и на его периферии ($r = \infty $). Интуитивно ясно, что чем больше $\Gamma $ и, значит, указанный перепад давления, тем с большей скоростью потоки воздуха будут стремиться к оси $z$ и тем сильнее они должны закручиваться вокруг оси и приобретать бо́льшую вертикальную скорость, что приводит к значительному росту кинетической энергии воздушных масс такого торнадо и оправдывает для него эпитет “мощный”. Вероятно, все воздушные по шкале Фуджиты [7] торнадо, представляющие основную опасность, относятся к мощным. Оценим величину $\left| {{{u}_{0}}} \right|{{\Gamma }^{{ - 1/2}}}$ для ${{u}_{0}} = {\text{i}}\omega $. Тогда под $\omega $ надо понимать угловую скорость вращения ${{\omega }_{{\text{K}}}}$, с которой сила Кориолиса закручивает радиальные потоки воздуха у поверхности Земли. Из физических соображений $u(\infty ) = {\text{i}}\Omega $, где $\Omega $ – угловая скорость вращения воздуха в вихревом кольце материнского облака (см. Введение). Из (19) следует, что $\Omega = \sqrt \Gamma $ и, значит, $\left| {{{u}_{0}}} \right|{{\Gamma }^{{ - 1/2}}} = \left| {{{\omega }_{{\text{K}}}}{\text{/}}\Omega } \right|$. Нетрудно установить [7], что ${{\omega }_{{\text{K}}}} = {{\Omega }_{{\text{З}}}}\sin \varphi $, где ${{\Omega }_{{\text{З}}}} = 7.3 \times {{10}^{{ - 5}}}$ с^–1 – угловая скорость вращения Земли, $\varphi $ – широта местности возникновения торнадо. По данным наблюдений [6], [7] для разрушительных торнадо с типичными значениями скорости воздуха $U = 100$ м/с и радиуса $r = 10$ км вихревого кольца материнского облака получим $\Omega = U{\text{/}}r = {{10}^{{ - 2}}}$ с^–1 и $\left| {{{u}_{0}}} \right|{{\Gamma }^{{ - 1/2}}} = 7.3 \times {{10}^{{ - 3}}}$. Таким образом, для разрушительных торнадо, действительно, можно считать $\left| {{{u}_{0}}} \right|{{\Gamma }^{{ - 1/2}}} \ll 1$.

Для получения приближенных формул воспользуемся преобразованием подобия.

Теорема 4. Пусть $\Gamma > 0$ и

Тогда функции $u$, $C$ от $(t,z)$ удовлетворяют системе (18) тогда и только тогда, когда функции $\tilde {u}$, $\tilde {C}$ от $(\tau ,x)$ удовлетворяют системе

Если $u(z)$, $C(z)$ – стационарное решение краевой задачи (18), (19), то, согласно теореме 4,

есть стационарное решение системы (33) с граничными условиями $\tilde {u}(0) = {{u}_{0}}{{\Gamma }^{{ - 1/2}}}$, $\tilde {u}(\infty ) = {\text{i}}$, $\tilde {C}(0) = 0$. Если $\left| {{{u}_{0}}} \right|{{\Gamma }^{{ - 1/2}}} \ll 1$, то, предполагая аналитическую зависимость стационарного решения системы (33) с указанными краевыми условиями от граничного условия для $\tilde {u}$ в нуле, можно построить теорию возмущений по граничному условию для $\tilde {u}$ в нуле [26] и сколь угодно точно вычислить функции $\tilde {u}(x)$, $\tilde {C}(x)$, а значит, используя преобразование (32), и функции $u(z)$, $C(z)$. При этом функции $\tilde {u}(x)$, $\tilde {C}(x)$ рассматриваются как возмущения функций ${{u}_{0}}(x)$, ${{C}_{0}}(x)$, являющихся стационарным решением системы (33) для невозмущенных граничных условий $\tilde {u}(0) = 0$, $\tilde {C}(0) = 0$, $\tilde {u}(\infty ) = {\text{i}}$. Графики этих функций, полученные численно и представленные на фиг. 1, показывают, что это решение имеет тип торнадо. Ограничимся ниже нулевым приближением, считая $\tilde {u}(x) \cong {{u}_{0}}(x)$, $\tilde {C}(x) \cong {{C}_{0}}(x)$, что дает приближенные формулы $u(z) \cong {{\Gamma }^{{1/2}}}{{u}_{0}}\left( {z{{\Gamma }^{{1/4}}}{{R}^{{1/2}}}} \right)$, $C(z) \cong {{\Gamma }^{{1/4}}}{{R}^{{ - 1/2}}}{{C}_{0}}\left( {z{{\Gamma }^{{1/4}}}{{R}^{{1/2}}}} \right)$, которые не зависят от граничного условия $u(0) = {{u}_{0}}$, и чья точность возрастает при ${{u}_{0}}{{\Gamma }^{{ - 1/2}}} \to 0$. Вторая формула позволяет вычислить $C(\infty ) \cong {{\Gamma }^{{1/4}}}{{R}^{{ - 1/2}}}{{C}_{0}}(\infty )$. Последнее равенство можно уточнить [26], показав, что имеет место асимптотика $C(\infty )\sim {{\Gamma }^{{1/4}}}{{R}^{{ - 1/2}}}{{C}_{0}}(\infty )$, ${{u}_{0}}{{\Gamma }^{{ - 1/2}}} \to 0$. Из графиков на фиг. 1 следует, что ${{C}_{0}}(\infty ) \cong 1.35$, поэтому окончательно получим важную асимптотическую формулу В частности, $C(\infty )$ растет пропорционально ${{\Gamma }^{{1/4}}}$ при $\Gamma \to + \infty $ и фиксированном ${{u}_{0}}$, что подтверждается численными расчетами.

5. РОЛЬ АЗИМУТАЛЬНОГО МАГНИТНОГО ПОЛЯ

Проанализируем течения из первого класса разд. 3, задаваемого решениями системы (11) и позволяющего исследовать влияние чисто азимутального магнитного поля, порождаемого постоянным однородным осевым током, на осесимметричные течения плазмы. Рассмотрим решения системы (11), подчиненные краевым условиям

Из результатов 1)–4) разд. 4 следует, что стационарные решения задачи (11), (35) существуют и относятся к типам торнадо, антиторнадо или антициклон в зависимости от значений $\Gamma $ и $S$, как это указано на фиг. 2, где приведены показатели $\alpha $ и $n$ антициклона и граничные параболы $\Gamma = - M_{{\text{A}}}^{2}{{S}^{2}}$, $\Gamma = {{\omega }^{2}} - M_{{\text{A}}}^{2}{{S}^{2}}$, разделяющие различные типы течений. Парабола $\Gamma = - M_{{\text{A}}}^{2}{{S}^{2}}$ входит в область антиторнадо, а парабола $\Gamma = {{\omega }^{2}} - M_{{\text{A}}}^{2}{{S}^{2}}$ состоит из точек, задающих равномерное вращение плазмы вокруг вертикальной оси с постоянной угловой скоростью $\omega $. Разумеется, система (11) имеет и другие решения, определяемые более общими граничными условиями в нуле $u(0) = {{u}_{0}} \in \mathbb{C}$, $C(0) = {{C}_{0}} \in \mathbb{R}$.$\mathbb{R}$ Как отмечалось выше, для более общих граничных условий классификация решений системы (11) неизвестна и требует дополнительного исследования. Скорее всего, основные типы решений – торнадо, антиторнадо, антициклон останутся, но области на плоскости $(S,\Gamma )$, определяемые этими решениями, усложнятся; не исключено также появление на плоскости $(S,\Gamma )$ “мертвой зоны”, где решения краевой задачи для системы (11) не существует.

Полученные результаты приводят к трем важным выводам:

1) азимутальное магнитное поле смещает в сторону уменьшения границы, разделяющей три типа течений – торнадо ($\Gamma > {{\Gamma }_{{{\text{кр}}}}} = {{\omega }^{2}} - M_{{\text{A}}}^{2}{{S}^{2}}$), антиторнадо (${{\Gamma }_{{{\text{кр}}}}} > \Gamma \geqslant - M_{{\text{A}}}^{2}{{S}^{2}}$) и антициклон ($\Gamma < - M_{{\text{A}}}^{2}{{S}^{2}}$);

2) в сильном азимутальном магнитном поле $\left| S \right| > \omega {\text{/}}{{M}_{{\text{A}}}}$ течение типа торнадо возникает и для $\Gamma < 0$, т.е. когда суммарное (магнитное и гидродинамическое) давление в центре торнадо больше, чем на его периферии;

3) для $\omega {{\left( {\Gamma + M_{{\text{A}}}^{2}} \right)}^{{ - 1/2}}} \ll 1$ стационарное решение задачи (11), (35) имеет тип торнадо, вертикальная скорость которого на бесконечности, согласно (34), приближенно равна $C(\infty ) \cong 1.35{{\left( {\Gamma + M_{{\text{A}}}^{2}{{S}^{2}}} \right)}^{{1/4}}}{{R}^{{ - 1/2}}}$, в частности, азимутальное магнитное поле ${{H}_{\varphi }} = rS$ вызывает генерацию (увеличение) вертикальной скорости торнадо на бесконечности.

Дополнительное обсуждение содержится в [27].

6. ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ ПЛАЗМЫ ВДОЛЬ СИЛОВЫХ ЛИНИЙ МАГНИТНОГО ПОЛЯ

Рассмотрим течения из второго класса разд. 3, задаваемые решениями системы (12) и описывающие осесимметричные потоки плазмы вида (2) вдоль силовых линий магнитного поля, для которых магнитные и гидродинамические параметры пропорциональны, $w = ku$, $G = kC$, $k = {\text{const}}$.

Согласно результатам 1)–4) разд. 4, система (15) имеет решения для граничных условий

а система (17) имеет решения для граничных условий принадлежащих к одному из трех типов – торнадо, антиторнадо, антициклон. Применяя преобразования (14), (16), заключаем, что исследуемая система (12) при ${{k}^{2}}M_{{\text{A}}}^{2} \ne 1$ имеет решения для граничных условий принадлежащих к одному из четырех типов – торнадо, антиторнадо, циклон, антициклон, в зависимости от значений $\Gamma $ и $k$, как это показано на фиг. 3. Интервал $\left( { - M_{{\text{A}}}^{{ - 1}},M_{{\text{A}}}^{{ - 1}}} \right)$ на оси $k$ входит в область антиторнадо, а бесконечные интервалы $\left( { - \infty , - M_{{\text{A}}}^{{ - 1}}} \right)$, $\left( {M_{{\text{A}}}^{{ - 1}}, + \infty } \right)$ – в область торнадо, точки параболы $\Gamma = {{\omega }^{2}}\left( {1 - {{k}^{2}}M_{{\text{A}}}^{2}} \right)$, не лежащие на оси $k$, соответствуют решениям системы (12), задающим вращение плазмы вокруг оси $z$ с постоянной угловой скоростью $\omega $. При $\omega {{\left| {1 - {{k}^{2}}M_{{\text{A}}}^{2}} \right|}^{{1/2}}}{{\left| \Gamma \right|}^{{ - 1/2}}} \ll 1$ решение краевой задачи (12), (36) имеет тип торнадо или антиторнадо, вертикальная скорость которого на бесконечности, согласно (34), равна Система (12) имеет, разумеется, и другие решения, определяемые более общими граничными условиями в нуле $u(0) = {{u}_{0}} \in \mathbb{C}$, $C(0) = {{C}_{0}} \in \mathbb{R}$, но их классификация в общем случае неизвестна и требует дополнительного исследования. Скорее всего, основные типы решений – торнадо, антиторнадо, циклон, антициклон остаются, но области на плоскости $(k,\Gamma )$, определяемые этими решениями, существенно изменятся.

Проведем некоторые вычисления. Имеем для торнадо и антиторнадо с учетом формулы (36):

где ${{\Gamma }_{{{\text{кр}}}}}$ – граница, отделяющая на прямой $\Gamma $ область торнадо от области антиторнадо (см. фиг. 3). Пусть $u(z)$, $C(z)$ – стационарное решение задачи (18), (26) для $\Gamma \geqslant 0$, ${{u}_{0}}(z)$, ${{C}_{0}}(z)$ – указанное решение для $\Gamma = 0$, являющееся антиторнадо, ${{u}_{{{\text{Kar}}}}}(z)$, ${{C}_{{{\text{Kar}}}}}(z)$ – решение этой задачи для $\omega = 1$, $R = 1$, $\Gamma = 0$, полученное  Карманом.  В частности,  ${{C}_{{{\text{Kar}}}}}(\infty ) = - 0.886$ [24].  В  [12]  показано, что $C(\infty )$ – монотонно возрастающая непрерывная функция от $\Gamma $, в частности, $\mathop {\lim }\limits_{\Gamma \to 0} C(\infty ) = {{C}_{0}}(\infty )$. Из теоремы 3 следует ${{u}_{0}}(z) = \omega {{u}_{{{\text{Kar}}}}}\left( {\sqrt {\omega R} z} \right)$, ${{C}_{0}}(z) = \sqrt {\omega {\text{/}}R} {{C}_{{{\text{Kar}}}}}\left( {\sqrt {\omega R} z} \right)$, откуда ${{C}_{0}}(\infty ) = \sqrt {\omega {\text{/}}R} {{C}_{{{\text{Kar}}}}}(\infty ) = - 0.886\sqrt {\omega {\text{/}}R} $. Вычислим теперь предельные значения ${{H}_{z}}(\infty )$ при $\left| {k{{M}_{{\text{A}}}}} \right| \to 1 \pm 0$. При $\left| {k{{M}_{{\text{A}}}}} \right| \to 1 - 0$ для торнадо имеем где $\tilde {C}(x)$ – решение (15), $ \pm $ совпадает с $\operatorname{sgn} k$ и использованы преобразования (14) и асимптотическая формула (34). При $\left| {k{{M}_{{\text{A}}}}} \right| \to 1 + 0$ для антиторнадо имеем аналогичную выкладку где $\tilde {C}(x)$ – решение (17). При $\left| k \right| \to + \infty $ для торнадо имеем где $\tilde {C}(x)$ – решение (17). Отсюда следует $\mathop {\lim }\limits_{\left| k \right| \to + \infty } C(\infty ) = 0$, а из (36) вытекает соотношение $\mathop {\lim }\limits_{\left| k \right| \to + \infty } u(\infty ) = 0$.

Полученные результаты приводят к следующим выводам.

1. Существует критическое (бифуркационное) значение параметра замагниченности, равное 1, разделяющее типы течений плазмы – торнадо от циклонов, антиторнадо от антициклонов. При стремлении точки $(k,\Gamma )$ к бифуркационным прямым $k = \pm M_{{\text{A}}}^{{ - 1}}$ различия между указанными типами течений не стираются, а усиливаются, что выражается, во-первых, согласно формулам (36), (37), в неограниченном возрастании скорости плазмы – вертикальной и угловой скорости вращения торнадо и антиторнадо, а также радиальной скорости и показателя $\alpha $ циклона и антициклона и, во-вторых, согласно формулам (39), (40), в генерации сколь угодно сильного осевого магнитного поля. В частности, существуют сверхмощные магнитные торнадо, в которых плазма течет вдоль магнитного поля и имеет конечную замагниченность.

2. В сильном магнитном поле с параметром замагниченности, большим 1, существуют плазменные течения типа торнадо и для $\Gamma < 0$, т.е. когда суммарное (гидродинамическое и магнитное) давление в центе торнадо больше, чем на его периферии.

3. Для фиксированного $\Gamma $ при стремлении параметра замагниченности к бесконечности скорость плазмы в циклонах и торнадо, согласно (36), (37), стремится к нулю, а осевое магнитное поле имеет конечный предел, вычисляемый по (41), в частности, сильное магнитное поле препятствует возникновению магнитных торнадо и циклонов.

4. В слабом магнитном поле ($\left| {k{{M}_{{\text{A}}}}} \right| < 1$), согласно (38), происходит усиление (для торнадо) или ослабление (для антиторнадо) в $\sqrt {\Gamma {\text{/}}{{\Gamma }_{{{\text{кр}}}}}} $ раз азимутального магнитного поля на бесконечности по сравнению с азимутальным магнитным полем при $z = 0$; в сильном магнитном поле ($\left| {k{{M}_{{\text{A}}}}} \right| > 1$), наоборот, происходит ослабление (для торнадо) или усиление (для антиторнадо) в $\sqrt {\Gamma {\text{/}}{{\Gamma }_{{{\text{кр}}}}}} $ раз ${{H}_{\varphi }}(\infty )$ по сравнению с ${{H}_{\varphi }}(0)$.

7. ЗАКЛЮЧЕНИЕ

В статье рассмотрено математическое моделирование явления торнадо применительно к солнечной плазме посредством точных решений специального вида уравнений классической МГД. Выведены уравнения магнитного торнадо. Комплексификация уравнений и преобразования подобия позволили редуцировать уравнения магнитного торнадо к удобной для построения алгоритмов их численного решения форме, сводящейся к нелинейной системе двух уравнений теплопроводности относительно комплексных “температур”, и понизить размерность задачи.

Рассмотрены два класса решений уравнений магнитного торнадо, содержащих течения плазмы типа торнадо, исследование которых удается редуцировать к уравнениям торнадо в атмосферном воздухе. Рассмотрен численный метод установления нахождения стационарных решений уравнений торнадо. Полученные классы точных решений являются тестами при численном исследовании уравнений магнитного торнадо. Анализ решения указанных классов, с одной стороны, дает теоретическое доказательство существования магнитных торнадо в плазме, а с другой, – позволяет обнаружить ряд важных закономерностей взаимодействия магнитного поля с плазмой торнадо. Достоверность полученных результатов такая же, как и уравнений классической МГД, применимость которых к анализу явлений в солнечной плазме общепринята.