Журнал вычислительной математики и математической физики, 2022, T. 62, № 10, стр. 1620-1631
Анизотропная адаптация подвижной неструктурированной сетки к телам сложной формы, заданным интерполяционным восьмеричным деревом
Т. К. Козубская 1, Л. Н. Кудрявцева 1, 2, В. О. Цветкова 1, *
1 ИПМ им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия
2 ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 44/2, Россия
* E-mail: lera.tsvetkova@gmail.com
Поступила в редакцию 30.09.2021
После доработки 02.04.2022
Принята к публикации 08.06.2022
- EDN: LHOAYQ
- DOI: 10.31857/S0044466922100076
Аннотация
В статье предлагается методика анизотропной адаптации подвижной неструктурированной сетки к поверхности объекта произвольной формы с учетом возможности его перемещения. Сеточная адаптация разрабатывается с целью ее применения в задачах внешнего обтекания, в которых обтекаемые тела моделируются как области сплошной среды со слабой проницаемостью согласно методу погруженных границ. Такой подход определяет задачу в односвязной области и позволяет использовать при динамической адаптации технику перераспределения сеточных узлов с сохранением топологии исходной сетки. Базовым входным параметром адаптации является функция расстояния до поверхности тела, а ее анизотропный характер определяется вычисляемыми полями кривизны, ассоциированными с его геометрией. Все параметры адаптации задаются в узлах заранее построенного восьмеричного дерева, являющегося атрибутом тела и носителем его геометрии. В статье дается подробное описание метода анизотропной адаптации и приводятся примеры его работы. Библ. 22. Фиг. 12.
ВВЕДЕНИЕ
Задача обтекания подвижных тел имеет исключительно важное значение для современной вычислительной аэродинамики. Интерес в одновременном рассмотрении двух или более обтекаемых объектов, каждый из которых движется по своим законам, стимулирует развитие различных методов моделирования и техники соответствующей работы с геометрией. В данной работе предлагается новая методика сеточной анизотропной адаптации с целью ее дальнейшего использования в комбинации с методом погруженных границ при решении задач обтекания тел сложной формы. Среди алгоритмов погруженных границ в настоящей статье мы ориентируемся на метод штрафных функций Бринкмана [1], [2], в рамках которого обтекаемый объект моделируется внесением дополнительных источниковых членов в газодинамические уравнения, в качестве которых мы подразумеваем уравнения Эйлера, Навье–Стокса и осредненные по Рейнольдсу уравнения Навье–Стокса для описания течений вязкого сжимаемого газа. Источники в уравнениях определяют тело как сплошную среду со слабой проницаемостью, их величины отличны от нуля только в точках, лежащих внутри геометрического положения движущегося объекта. Таким образом, метод погруженных границ позволяет определять задачу внешнего обтекания в односвязной области, что, в свою очередь, открывает возможность использования техники перераспределения узлов при сохранении сеточной топологии для уточнения локализации поверхности обтекаемых объектов.
Для расчета задач внешнего обтекания при “классическом” подходе, т.е. на сетках, граничные узлы (или элементы) которой согласованы с границей тела, существует ряд известных методов. Среди них сеточная деформация [3] является наименее вычислительно затратным алгоритмом. Она позволяет достаточно быстро менять геометрию сетки для нового положения тела на каждом шаге по времени. Недостатком сеточной деформации является тот факт, что при больших амплитудах движения качество сетки становится слабо контролируемым вплоть до разрывов и перепутываний, а потому для больших смещений этот подход не годится. Альтернативный подход, основанный на перестроении сетки [4], как локальном, так и глобальном, в том числе и на доразбиении [5], хотя и может быть достаточно быстрым, однако требует вовлечения в численный алгоритм нежелательной интерполяции, а также заметно усложняет процесс распараллеливания, так как топология и размер сетки могут со временем меняться. Метод Химеры [6], подразумевающий наличие двух или нескольких наложенных сеток, также требует интерполяции и усложненной реализации обмена расчетных данных между сетками.
В статьях [7]–[10] разрабатываются и исследуются алгоритмы для адаптации сетки с использованием управляющей функции или метрик. Существуют работы по подбору метрики и для анизотропных сеток как в контексте генерации или доразбиения сетки [5], так и для подвижных адаптивных сеток [11]. Способы задания различных управляющих метрик в различных методах адаптации обсуждаются в работе [12]. Как правило, все представленные в литературе алгоритмы подразумевают оценку апостериорной ошибки, на основе которой и строится метрический тензор.
Следует отметить, что адаптация подвижной сетки в задачах вычислительной газовой динамики при использовании метода погруженных границ использовалась и ранее (см., например, работы [13], [14]). Отличительной чертой предлагаемой нами методики сеточной адаптации является, как уже отмечено выше, возможность использования техники перераспределения узлов с сохранением топологии исходной сетки. Это свойство адаптации позволяет избежать снижения точности численного результата из-за интерполяции, сохраняет структуру алгоритма и, как следствие, сильно упрощает реализацию параллельной версии. Одной из трудностей при таком подходе применительно к реальным промышленно-ориентированным задачам для высокоскоростных течений является обеспечение необходимого сеточного разрешения в пристеночной области. При этом требуемое разрешение должно сохраняться независимо от возможных перемещений обтекаемого тела. При построении подхода мы предполагаем, что исходная сетка весьма умеренных размеров в начале расчета сгущается к поверхности “погруженного” в расчетную область объекта, а затем начинает передвигаться вместе с ним. Желаемая степень сеточного сгущения к поверхности тела при этом определяется требованием размера шага сетки в нормальном направлении внутри пристеночного пограничного слоя. Толщина же пограничного слоя уменьшается с ростом числа Рейнольдса, характеризующим уровень турбулентности течения. Это приводит к жесткому ограничению на малость шага сетки вблизи поверхности. В настоящей работе, посвященной только методу адаптации как таковому, не исследуется вопрос о достижимости нужного разрешения сетки в пограничном слое. Безусловно, ответ на этот вопрос зависит от количества узлов исходной сетки и, в общем случае, от их начального распределения, т.е. от тех параметров, которые можно регулировать на стадии препроцессинга. При этом стоит заметить, что, в случае недостатка узлов и недостаточного разрешения погранслойной области сеткой, при моделировании турбулентных течений мы предполагаем использовать технику пристеночных функций.
Практически во всех методах адаптации к поверхности тела, в том числе и в нашем подходе, главным входным параметром для адаптации выступает функция расстояния. Понятно, что в задачах с подвижными объектами скорость вычисления расстояния в узлах динамически изменяемой сетки становится критической с точки зрения обеспечения эффективности всего алгоритма в целом. Для минимизации вычислительной стоимости этой процедуры мы предлагаем хранить все параметры геометрии обтекаемого тела и, в первую очередь, поле расстояния до его поверхности в узлах восьмеричного дерева, называемом далее интерполяционной решеткой [15]. Такое дерево является атрибутом тела и строится один раз на этапе подготовки геометрии. Далее интерполяционная решетка движется вместе с телом и позволяет вычислить новое расстояние в любой точке расчетной области за конечное время. Такая методика уже тестировалась на различных конфигурациях и использовалась при численном решении двумерных задач внешнего обтекания подвижных тел [16], [17]. Решение же существенно трехмерных задач вычислительной газовой динамики потребовало дальнейшего развития предлагаемого подхода. Дело в том, что изотропный характер ранее предложенной адаптации, определяемой лишь расстоянием до поверхности тела, не дает возможности построения сильно анизотропных сеток вдоль поверхности обтекаемого тела, характерных для численного решения широкого класса задач внешнего обтекания с высокими числами Рейнольдса. Действительно, изотропное сгущение сетки к поверхности, обеспечивающее требуемую малость пристеночного шага, с неизбежностью приводит к построению сеток чрезмерно большой размерности даже в двумерном случае и неприемлемо большой размерности – в трехмерном. Это обстоятельство потребовало учета в разработанном алгоритме анизотропии геометрии. Для качественной реализации анизотропной адаптации для тел сложной формы, особенно в трехмерной постановке, помимо функции расстояния, необходимо учитывать информацию более высоких порядков для входящей геометрии. В настоящей работе описывается наша реализация метода учeта кривизны при построении управляющей метрики адаптации. Кривизна рассчитывается для триангулированной поверхности подвижного тела, а ее значения записываются в вершины интерполяционной решетки. В процессе сеточной адаптации эта информация используется для настройки управляющих параметров метрики. В статье методика анизотропной адаптации формулируется как для двумерной, так и трехмерной постановки.
Для обеспечения динамического сгущения сетки к поверхности тела при решении задач внешнего обтекания, сеточная адаптация должна удовлетворять ряду дополнительных критериев. Помимо сохранения изначально заданной степень сгущения сетки в нормальном направлении к поверхности, управление адаптацией также не должно допускать резкого роста размеров сеточных элементов. Эти условия требуется выполнять (или стремиться выполнять), используя имеющееся в исходной сетке количество сеточных узлов. Еще одним требованием в ряде задач является обеспечение неподвижности узлов сетки в заранее отмеченных подобластях расчeтной области. Перечисленные требования к адаптации существенным образом влияют на выбор еe управляющих параметров и также определяют новизну предлагаемого метода.
В статье дается подробное описание методики анизотропной адаптации подвижной неструктурированной сетки к границе обтекаемого тела с использованием функций расстояния и кривизны, обсуждаются связанные с данной техникой проблемы и приводятся примеры ее использования.
1. МЕТОД АДАПТАЦИИ ПОДВИЖНОЙ НЕСТРУКТУРИРОВАННОЙ СЕТКИ
В методе адаптации подвижной сетки расчетная сетка рассматривается как упругий материал, который подвергается сжатию вблизи границы движущегося тела. Упругая деформация, зависящая от времени, задается d-мерным отображением $x(\xi ,t)\,:{{R}^{d}} \times R \to {{R}^{d}} \times R$.
Пусть $C$ обозначает матрицу Якоби отображения $x(\xi ,.)$, где ${{c}_{{ij}}} = {{\partial {{x}_{i}}} \mathord{\left/ {\vphantom {{\partial {{x}_{i}}} {\partial {{\xi }_{j}}}}} \right. \kern-0em} {\partial {{\xi }_{j}}}}$. Пусть ${{x}^{n}}(\xi )$ – отображение исходной сетки в сетку на момент времени ${{t}^{n}}$.
Чтобы сформулировать вариационную задачу для сеточной адаптации на дифференциальном уровне, нужно ввести предположение, что ${{x}^{n}}(\xi )$ – квазиизометрический диффеоморфизм. Деформация на момент времени ${{t}^{{n + 1}}}$ определяется решением вариационной задачи [18]
(1)
$F\left( {x(\xi ,t),{{x}^{n}}(\xi )} \right) = \mathop \smallint \limits_{{{\Omega }_{\xi }}} W\left( {Q({{x}^{n}},t){{\nabla }_{\xi }}x\left( {\xi ,t} \right)H{{{(\xi )}}^{{ - 1}}}} \right)\det Hd\xi .$(2)
$W(C) = (1 - \theta )\frac{{\left( {\frac{1}{d}\operatorname{tr} ({{C}^{{\text{т}}}}C)} \right)}}{{\det {{C}^{{2/d}}}}} + \frac{1}{2}\theta \left( {\frac{1}{{\det C}} + \det C} \right).$Пусть граница подвижного деформируемого тела в момент времени t задается в виде нулевой изоповерхности скалярной функции $u(x,t)$. Предполагается, что $u(x,t)$ близка к функции расстояния со знаком от границы тела, поскольку в реальных задачах вычисление точной функции расстояния, как правило, не имеет смысла, а используются ее различные приближенные варианты.
Метрический тензор ${{G}_{x}}$ может быть записан в виде ${{G}_{x}} = U{{\Sigma }^{2}}{{U}^{{\text{т}}}}$, где столбцы $U$ являются собственными векторами ${{G}_{x}}$, а ${{\Sigma }^{2}}$ – диагональная матрица с элементами на диагонали $\sigma _{i}^{2}$, т.е. собственными значениями ${{G}_{x}}$. В каждой точке расчетной области можно задать локально оптимальные координаты с помощью аффинного преобразования с матрицей $Q = \Sigma {{U}^{{\text{т}}}}$. Говорят, что расчетная сетка оптимальна (изометрична), если после, применяя данное аффинное преобразование к ячейкам полученной сетки, получится начальная сетка, или
где V – произвольная ортогональная матрица.Метрика адаптации $G = {{G}_{x}}$ требует задания нормального и тангенциального направлений в каждой точке $p$ (столбцы матрицы $U$), которые в свою очередь определяются изоповерхностью функции $u(x,t)$, проходящей через $p$ , а также коэффициентов растяжения ${{\sigma }_{i}}$ вдоль этих направлений. Чем больше значение ${{\sigma }_{i}}$, тем меньше размер ячейки в направлении столбца ${{u}_{i}}$. Соотношение ${{\max }_{{i,j}}}\frac{{{{\sigma }_{i}}}}{{{{\sigma }_{j}}}} - 1$ определяет степень анизотропии. Функция ${{\sigma }_{1}} = {{\sigma }_{{{\text{normal}}}}}(x,t)$ определяет растяжение сетки вдоль направления, нормального к телу, а ${{\sigma }_{2}} = {{\sigma }_{{{\text{tangential}}}}}(x,t)$ (${{\sigma }_{{2,3}}}$ в 3D) определяет пространственное распределение анизотропии. В узком слое на границе тела анизотропия максимальна и стремится к нулю вдали от тела.
Очень часто некорректно построенная метрика может приводить к резкому росту константы квазиизометрии, скачкам размеров ячеек и визуальным “разрывам” в сетке. Оптимальная метрика, которая дает наименьшую константу квазиизометрии, не известна даже для простых тел. В данной работе используются некоторые эвристические правила задания метрики, когда растяжение ${{\sigma }_{1}}$ принимается константой в слое на границе тела и убывает по гиперболе при отдалении от него, а тангенциальное растяжение определяется кривизной поверхности и постепенно уменьшает свое влияние вдали от границы. Для тела задается некоторое пятно радиуса $D$, за пределами которого метрика ${{G}_{x}}$ равна единичной матрице.
Метрика изотропной адаптации определяется соотношением
где ${{\sigma }_{1}}(x,t) = \phi \left( {u(x,t)} \right)$ – сеточная плотность. В данном случае степень анизотропии равна нулю. Использование изотропной метрики во всей расчетной области возможно только для небольших значений ${{\sigma }_{1}}$, так как решением вариационной задачи в этом случае является отображение, при котором прообраз тела почти в ${{\sigma }_{1}}$ раз больше размера тела в эйлеровой системе координат. Это приводит к стягиванию внутрь тела большого числа точек расчетной области.Анизотропная версия метрического тензора определяется соотношением
(4)
$G(x,t) = \sigma _{1}^{2}I + (\sigma _{2}^{2} - \sigma _{1}^{2}){{\nabla }_{x}}u{{\nabla }_{x}}{{u}^{{\text{т}}}}\frac{1}{{{{{\left| {{{\nabla }_{x}}u} \right|}}^{2}}}}.$К функционалу (1) применяется стандартная конечно-элементная дискретизация. Метрический тензор ${{G}_{{}}}$ хранится в узлах сетки, что критично для стабильности тонких и сильно сжатых сеточных слоев. Для решения задачи оптимизации на каждом шаге по времени применяется техника градиентного спуска с предобуславливателем [19], где направление минимизации определяется приближенным решением линейной системы с усеченной матрицей Гессе функционала (3), в которой отброшены члены, потенциально приводящие к потере положительной определенности. Итоговое смещение вдоль направления минимизации находится одномерным поиском.
2. ЗАДАНИЕ ФУНКЦИИ РАССТОЯНИЯ И ДРУГИХ ПАРАМЕТРОВ АДАПТАЦИИ
Пересчет значений функции расстояния необходим на каждом шаге по времени, поэтому его реализация должна быть эффективной и не вносить существенного вклада в расчетное время. В представленной работе используется дополнительная фоновая сетка, называемая нами интерполяционной решеткой и представляющая собой восьмеричное дерево (см. фиг. 1). Вершины этого дерева хранят точное расстояние до поверхности тела. Дерево движется вместе с телом, и с помощью линейной интерполяции в любой момент времени можно найти расстояния в любой точке расчетной области. В процессе совершенствования алгоритма адаптации стало ясно, что информации о расстоянии до границ тела недостаточно для построения как минимум анизотропной сетки, а тем более сетки, учитывающей особенности геометрии. На данный момент вершины фоновой сетки хранят значения и градиенты функции расстояния, а также значения кривизны. В трехмерной постановке информация о кривизне задана главными направлениями кривизны и главными кривизнами.
Методика построения восьмеричного дерева приведена в [15]. Начальная фоновая сетка разбивается до тех пор, пока минимальный размер ребра не будет меньше минимального сеточного размера желаемой адаптивной сетки.
Приближенные значения кривизны поверхности тела вычисляются на этапе подготовки фоновой сетки. Предполагается, что тело задано хорошо разрешенной триангулированной поверхностью. Для всех точек поверхностной сетки рассчитывается приближенное значение кривизны с использованием метода из работ [20], [21] (детальное описание дается в следующем разделе). Каждой вершине фонового восьмеричного дерева приписывается значение радиуса кривизны в ближайшей к данной вершине точке граничного контура/поверхности (см. фиг. 2).
3. МЕТОДИКА РАСЧЕТА ПОЛЕЙ КРИВИЗНЫ
Поскольку аналитическая функция задания поверхности не всегда доступна, то в общем случае используется подробная триангуляция поверхности подвижного тела. В [20] рассматриваются различные методы расчета кривизны для дискретно заданных поверхностей. Для каждой вершины сетки строится приближение к соприкасающемуся параболоиду поверхности. Для нахождения элементов квадратичной формы используются вершины сетки первого или второго порядка соседства. Переопределенная система уравнений решается методом наименьших квадратов. Соответственно, для каждой точки вычисляются главные направления и главные кривизны (см. фиг. 3).
4. ВЫБОР УПРАВЛЯЮЩИХ ПАРАМЕТРОВ
Каждой точке границы двумерного или трехмерного тела можно приписать некоторый минимальный масштаб. Это может быть минимальный радиус кривизны, который локально описывает форму поверхности, либо минимальное расстояние до некоторого подмножества медиальных осей, которое описывает локальный параметр толщины тела или поведение вблизи негладкого участка границы.
При задании сжатия в тангенциальном направлении требуется учет как кривизны границы тела, так и расстояния до медиальной оси. Использование только кривизны может приводить к резким переходам степени сжатия и, потенциально, к сеточным разрывам, особенно на внутренних углах (см. фиг. 4). Если расстояние до медиальной оси меньше, чем величина пограничного слоя в логическом пространстве, ${{\sigma }_{2}}$ на границе тела увеличивается, чтобы избежать “разрыва” сетки внутри тела. Увеличение ${{\sigma }_{2}}$ приводит к увеличению прообраза пограничного слоя в лагранжевых координатах, что приводит к увеличению числа вершин адаптивной сетки внутри области и около ее границы.
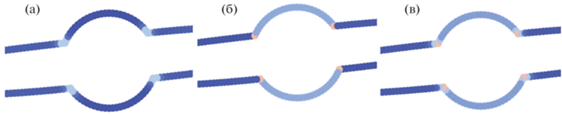
Фиг. 4.
Распределение параметра ${{\sigma }_{2}}$ на границе тестового тела, определяемое медиальными осями (а), кривизной (б) и комбинацией этих значений (в).
Рассмотрим алгоритм вычисления поля параметра ${{\sigma }_{1}}$, т.е. сжатия в нормальном направлении, где d – значение функции расстояния без знака до границы тела, h – длина ребра исходной сетки, оба параметра нормированы на L – величину по нормали адаптивной зоны:
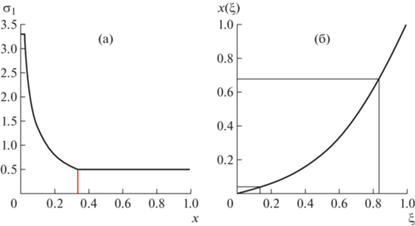
Фиг. 5.
(а) – распределение параметра ${{\sigma }_{1}}$ вдоль нормального направления. Показаны значения D – толщина переходного участка, (б) – функция обратного размера $d(\xi )$ и значения $d({{\xi }_{\delta }}) = \delta $, $d({{\xi }_{D}}) = D$.
Для задания поля параметра ${{\sigma }_{2}}$ выполняются следующие вычисления.
Рассмотрим функцию для произвольного R:
где $L$ – размер по нормали адаптивной зоны, т.е. области, где узлы подвижны. Фиг. 6 иллюстрирует связь параметров из формулы (5), а именно: ${{\tilde {\sigma }}_{2}}(x,R) = {{l}_{\xi }}{\text{/}}{{l}_{x}}$.Функция (5) имеет максимум не на границе. Чтобы это исправить, находим ${{d}_{{{\text{max}}}}}$ такое, что ${{\tilde {\sigma }}_{2}}({{d}_{{{\text{max}}}}}) = \max {{\tilde {\sigma }}_{2}}(d,~R)~$. Корректируем формулу (5):
(6)
${{\sigma }_{2}}(d,R) = \left\{ \begin{gathered} \frac{{\frac{R}{L} + \xi }}{{\frac{R}{L} + d}},\quad d \geqslant {{d}_{{{\text{max}}}}}, \hfill \\ {\text{\;}}{{{\tilde {\sigma }}}_{2}}({{d}_{{{\text{max}}}}}),\quad d < {{d}_{{{\text{max}}}}}{{.}_{~}} \hfill \\ \end{gathered} \right.$В трехмерной постановке добавляется третий параметр ${{\sigma }_{3}}$. Тогда построение полей ${{\sigma }_{2}}$ и ${{\sigma }_{3}}$ происходит аналогично, используя для задания $R$ значения главных кривизн.
6. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
6.1. Аэродинамический профиль NACA0016
В качестве двумерной тестовой задачи рассмотрим построение секи, сгущенной к поверхности профиля NACA0016. В рассматриваемой геометрии есть два сложных участка, которые требуют более изотропного разрешения: передняя скругленная кромка и законцовка с острыми ребрами. В результате сгущения исходной сетки в 30 раз анизотропия сеточных элементов оказалась распределена желаемым образом, т.е. параметр ${{\sigma }_{2}}$ максимален вблизи кромок профиля, а значит, и сеточные элементы ближе к изотропной форме. Утверждение проиллюстрировано на фиг. 8. На фиг. 8в также можно заметить увеличение параметра ${{\sigma }_{2}}$ к внутреннему углу геометрии. Такое поведение обусловлено обратной связью между расчетной сеткой и фоновой адаптивной решеткой. Величина сжатия в тангенциальном направлении в вершинах восьмеричного дерева увеличивается, если в процессе адаптации происходит “разрыв” сетки.
6.2. Сечение в плоскости вращения винта квадрокоптера
Поскольку в будущем планируется адаптация сетки к сложной трехмерной геометрии винта дрона (см. фиг. 9а) [22], полезной тестовой задачей в двумерной постановке выступает горизонтальное сечение этого винта (фиг. 9б). Для этого контура требуется разрешить сеткой углы на законцовках, а также место соединения лопасти со втулкой. Особенность данной формы еще и в близком расположении соседних стенок, что также характерно для изначальной геометрии. Фиг. 10 приводит распределение радиуса кривизны в расчетной области. На фиг. 11 показаны фрагменты адаптивной сетки: элементы вблизи углов близки к изотропным, анизотропия увеличивается при приближении к более прямым участкам контура.
6.3. Эллипсоид
В трехмерном случае управляющие параметры метрики строятся также как на плоскости, только в тангенциальном направлении используются два параметра растяжения ${{\sigma }_{2}}$ и ${{\sigma }_{3}}$, определяемые главными кривизнами и главными направлениями. Для теста рассматриваем эллипсоид с осями $a = 0.5$, $b = 0.25$, $c = 0.075$. Требуется сгустить сеточные элементы вдоль сильно скривленных кромок эллипсоида. На фиг. 12 показаны поверхности, составленные из граней адаптивной сетки, на которых значение функции расстояния минимально. Метод, основанный на использовании кривизны, обеспечивает эффективное разрешение острых кромок эллипсоида, см. фиг. 12б.
ЗАКЛЮЧЕНИЕ
В работе предложена новая методика анизотропной адаптации подвижной неструктурированной сетки к неявно заданной поверхности тела. Входными параметрами методики являются поля расстояния до поверхности тела и поля кривизны поверхности обтекаемого тела, приближенно рассчитываемые по предложенным алгоритмам.
Важно отметить, что в данной работе методика разрабатывается применительно к постановкам задач вычислительной газовой динамики, подразумевающих использование метода погруженных границ для описания обтекаемых объектов. Этот подход позволяет определить задачу в односвязной области, что, в свою очередь, открывает возможность использования методов адаптации подвижной сетки для отслеживания движущегося по сетке тела. Вместе с тем адаптация к поверхности перемещающегося в газовом потоке тела существенно осложняется жесткими требованиями по разрешению пограничных слоев и гладкости сетки, а потому границы ее применимости для сеток приемлемой размерности все еще остаются не до конца определенными.
На данном этапе работы мы не решали задачи вычислительной газовой динамики, рассматривая только метод сеточной адаптации как таковой. Будущие же исследования в данном направлении мы планируем посвятить апробации разработанной методики при решении задач внешнего обтекания трехмерных тел сложной конфигурации и систем тел, оценке применимости методики, а также ее оптимизации по вычислительной стоимости и обеспечению устойчивой работы метода.
Список литературы
Angot Ph., Bruneau C.-H., Fabrie P., A penalization method to take into account obstacles in incompressible viscous flows. Numer.Math. 1999. V. 81. № 4. P. 497–520.
Abalakin I.V., Kozubskaya T.K., Zhdanova N.S., Immersed boundary penalty method for compressible flows over moving obstacles // ECCM 6/ECFD 7. 2018. P. 1797.
Бобков В.Г., Вершков В.А., Козубская Т.К., Цветкова В.О. Методика деформации неструктурированных сеток в задачах определения аэродинамических характеристик тел при малых перемещениях // Матем. моделирование. 2021. Т. 33. № 3. С. 109–132.
Koobus B., Hascoët L., Alauzet F., Loseille A., Mesri Y., Dervieux, A. Continuous mesh adaptation models for CFD, 2008.
Leicht T., Hartmann R. Error estimation and anisotropic mesh refinement for 3d laminar aerodynamic flow simulations // J. of Comput. l Phys. 2010. V. 229. Iss. 19. P. 7344–7360.
Steger J., Dougherty F.C., Benek J.A. A chimera grid scheme // Advances in Grid Generat. 1983. № 5. P. 59–69.
Лисейкин В.Д., Паасонен В.И. Адаптивные сетки и высокоточные схемы для решения сингулярно-возмущенных задач // Сиб. журнал вычисл. матем. 2021. Т. 24. № 1. С. 77–92.
Agouzal A., Lipnikov K., Vassilevski Yu. Adaptive generation of quasi-optimal tetrahedral meshes // East west journal of numerical math. 1999. V. 7. № 4. P. 223–244.
Lipnikov K., Vassilevski Yu. An adaptive algorithm for quasioptimal mesh generation // Comput. Math. and math. Phys.1999. V. 39. № 9. P. 1468–1486.
Bogomolov K.L., Degtyarev L.M., Tishkin V.F. A variational method for generation of high aspect-ratio regular adaptive grids// Matem. Mod. 2001. V. 13. № 5. P. 11–28.
Chiappa A.S., Micheletti S., Peli R., Perotto S., Mesh adaptation-aided image segmentation // Communications in Nonlinear Science and Numerical Simulation. 2019. V. 74. P. 147–166.
Arpaia L., Beaugendre H., Cirrottola L., Froehly A., Lorini M., Nouveau L., Ricchiuto M. h- and r- adaptation on simplicial meshes using MMG tools. 2021. arXiv:2109.08451
Минаков А.В., Гаврилов А.А., Дектерев А.А. Численный алгоритм решения пространственных задач гидродинамики с подвижными твердыми телами и свободной поверхностью // Сиб. журнал индустриальной матем. 2008. Т. 11. № 4 (36). С. 94–104.
Filimonov S.A., Gavrilov A.A., Dekterev A.A. Implementation of the immersed boundary method for solving problems of fluid dynamics with moving bodies // J. Phys. Conf. Ser. 2019. V. 1359. P. 012073.
Суков С.А. Комбинированный алгоритм вычисления расстояния со знаком для задач численного моделирования физических процессов и визуализации движения твердых тел // Научная визуализация. 2020. Т. 12. № 5. С. 86–101.
Цветкова В.О., Абалакин И.В., Бобков В.Г., Жданова Н.С., Козубская Т.К., Кудрявцева Л.Н. Моделирование обтекания винта на адаптивной неструктурированной сетке с использованием метода погруженных // Матем. моделирование. 2021. Т. 33. № 8. С. 59–82.
Tsvetkova V., Kozubskaya T., Kudryavtseva L., Zhdanova N. On mesh adaptation for supercomputer simulation of flows around solid bodies defined by immersed boundary method // Proc. Computer Science.2020. V. 178. P. 404–413.
Garanzha V.A., Kudryavtseva L. Moving Deforming Mesh Generation Based on the Quasi-Isometric Functional // In: Garanzha V.A., Kamenski L., Si H. (eds) Numerical Geometry, Grid Generation and Scientific Computing. Lecture Notes in Comput. Science and Engng, Vol. 143. Springer, Cham.
Kaporin I.E., Milyukova O.Yu. MPI + OpenMP implementation of the BiCGStab method with explicit preconditioning for the numerical solution of sparse linear systems // Numerical meth. and program. 2019. № 20. P. 516–527.
Garimella R., Swartz B. Curvature Estimation for Unstructured Triangulations of Surfaces. Technical Report LA-UR-03-8240, Los Alamos National Lab, 2003.
Petitjean S., Boyer E. Regular and non-regular point sets: properties and reconstruction // Comput. Geometry. 2001. V. 19. P. 101–126.
Brandt J.B. Small-scale propeller performance at low speeds: диc. – University of Illinois at Urbana-Champaign, 2005.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики












