Журнал вычислительной математики и математической физики, 2022, T. 62, № 3, стр. 499-520
Вариант замыкания системы моментных уравнений произвольного порядка
Ю. А. Никитченко *
МАИ
125993 Москва, Волоколамское ш., 4, Россия
* E-mail: nikitchenko7@yandex.ru
Поступила в редакцию 18.05.2021
После доработки 20.07.2021
Принята к публикации 17.11.2021
- EDN: AROHGJ
- DOI: 10.31857/S0044466922030127
Аннотация
Предложен метод замыкания системы моментных уравнений порядка выше второго, не использующий аппроксимирующую функцию распределения молекул по скоростям. Замыкающие систему моменты построены в виде комбинаций моментов низших порядков. Построены системы моментных уравнений до шестого порядка включительно. На примере задачи о профиле ударной волны показано, что повышение порядка системы моментных уравнений не приводит к улучшению решения. Это объясняется тем, что члены уравнений замыкающего момента, которые не могут быть выражены через низшие моменты, вносят погрешность, соизмеримую с величиной замыкающего момента. Для тестирования решений использовано модельное кинетическое уравнение многоатомных газов. Библ. 18. Фиг. 10.
1. ВВЕДЕНИЕ
Одной из актуальных задач газовой динамики является описание течений, в которых существенное изменение газодинамических параметров происходит на расстояниях порядка длины свободного пробега молекул или на интервалах времени порядка времени их свободного пробега. Состояние газа описывается функцией распределения молекул по скоростям, значительно отличающейся от локально-максвелловской, равновесной функции распределения.
Такие неравновесные состояния характерны для течений разреженных газов, так как эффективными масштабами этих течений являются длина и время свободного пробега молекул. Другой тип неравновесных течений – высоко градиентные области, возникающие в плотных газах, например, ударные волны. Ширина профиля ударной волны составляет несколько десятков длин пробега молекулы, в то время, как температура и давление увеличиваются многократно.
Процессы хемосорбции или криоконденсации газа на обтекаемой поверхности приводят к возникновению разрыва функции распределения на границе раздела фаз. Эти разрывы реализуются в пристеночном кнудсеновском слое протяженностью в несколько длин свободного пробега молекул, что способствует возникновению неравновесной области течения.
Наиболее популярная и широко используемая модель течения газа – модель Навье–Стокса–Фурье (НСФ) теоретически обоснована только в слабонеравновесных условиях, когда квадратами неравновесных величин, т.е. величин, обращающихся в ноль в условиях равновесия, можно пренебречь, см., например, [1], [2]. К таким неравновесным величинам относятся: девиатор напряжений (неравновесные напряжения), тепловой поток, разность энергии теплового движения молекул на поступательных, вращательных и колебательных степенях свободы и ряд других моментов неравновесной функции распределения.
Физико-математические модели молекулярно-кинетической теории, такие как прямое статистическое моделирование или модельные кинетические уравнения, весьма ограничены в отношении степени разреженности газовой среды и для течений плотных газов практически не используются.
В середине прошлого века стало развиваться научное направление [3], [4], часто называемое методом Грэда, использующее принципы молекулярно-кинетической теории для получения систем дифференциальных уравнений в частных производных. В основе метода лежит интегрирование кинетического уравнения Больцмана, домноженного на некоторый молекулярный признак, по пространству скоростей.
Если в качестве молекулярного признака используются масса, импульс (момент импульса) или энергия молекулы, то интеграл столкновений кинетического уравнения обращается в ноль, а само уравнение сводится к констатации соответствующего закона сохранения. Для других молекулярных признаков законов сохранения не существует и для вычисления момента интеграла столкновений приходится прибегать к дополнительным допущениям.
Грэд сделал два сильных допущения: первое – относительно закона межмолекулярного взаимодействия, второе – относительно функции распределения молекул по скоростям. Отметим, что функция распределения определяет основные свойства газа, являясь его фазовой функцией состояния. Задание какого-либо конкретного вида этой функции в неравновесных условиях предписывает газу не характерные для него свойства. Используемое Грэдом разложение функции распределения около состояния равновесия является хорошей аппроксимацией только в слабо неравновесной среде, когда реальная функция близка к равновесной. Отметим, что в этих условиях хорошо работает модель НСФ, которая существенно проще моментных систем [3].
Используя “модельную” функцию распределения, Грэд записал аппроксимации моментов четвертого порядка, при помощи которых замкнул систему моментных уравнений третьего порядка. Была получена 20-моментная система уравнений. В целях сокращения количества уравнений делается еще одно сильное допущение: моменты третьего порядка заменяются “симметричной суммой” их сверток [3]. Основанием для этого служит предположение о близости состояния газа к состоянию равновесия. Таким образом была получена 13-моментная система уравнений – неполная система моментных уравнений третьего порядка.
При решении задачи о структуре ударной волны аналитически было показано, что 13-моментная система не имеет решений при числах Маха M > 1.65 (см. [5]), а 20-моментная система – при M > 1.851 (см. [1]). Численные решения, полученные при больших числах Маха, содержали на профиле ударной волны физически неадекватные области – субскачки.
Дальнейшее развитие 13-моментная система получила в виде регуляризованной системы моментных уравнений R13 (cм. [6], [7]). Как отмечалось выше, 20-моментная система замкнута аппроксимациями моментов четвертого порядка, а переход к 13-моментной системе осуществлен при помощи аппроксимации моментов третьего порядка. В работе [6] были записаны моментные уравнения для поправок к аппроксимациям моментов третьего и четвертого порядков. Затем в предположении малости поправок, к их моментным уравнениям применялась процедура Чепмена–Энскога.
Полученная в результате модель R13 по порядку приближения соответствует модели Барнетта, модели второго приближения, с характерным для этого приближения громоздким комплексом смешанных производных. Особенностью второго приближения является то, что третьи степени неравновесных величин принимаются пренебрежимо малыми, в то время как вторые степени этих величин учитываются наравне с основными членами моментных уравнений. Таким образом, имеет место весьма специфическое описание течения.
В настоящей работе предпринята попытка расширения области применимости системы моментных уравнений за счет повышения ее порядка. Еще в начале исследований моментных уравнений, см., например, [3], высказывалось мнение, что повышение порядка системы моментных уравнений должно приближать ее решения к решению уравнения Больцмана. Обнадеживающими в этом плане выглядели результаты работы [8], в которой была получена система моментных уравнений четвертого порядка. В задаче о структуре ударной волны удалось получить гладкое, без субскачка, решение при М ≈ 2.2.
В настоящей работе предложен метод замыкания системы моментных уравнений произвольного порядка, не использующий какую-либо модельную функцию распределения. Записаны в явной форме системы пятого и шестого порядков. Проанализированы возможности применения систем высокого порядка для описания течений высокой степени неравновесности.
2. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Специфические операции.
Для операции свертки используются греческие индексы, например:
Подстрочный символ “звездочка” обозначает операцию компактного симметрирования, т.е. симметрирования с исключением повторений тождественных по значению членов, аналог “симметричной суммы” [3]. Количество звездочек в одночлене соответствует рангу тензорного уравнения. Например, для симметричных тензоров ${{A}_{{ijk}}}$ и ${{B}_{{ijk}}}$:
Основные символы и специфические термины:
${{\delta }_{{ij}}}$ – символ Кронекера;
t, ${{x}_{i}}$ – время и координата геометрического пространства;
${{\xi }_{i}} = {{c}_{i}} + {{u}_{i}}$ – молекулярная, тепловая и групповая (макроскопическая) скорости;
${{m}_{0}}$, $\varepsilon $ – масса и энергия вращения молекулы;
$f \equiv f(t,{{x}_{1}},{{x}_{2}},{{x}_{3}},{{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}},\varepsilon )$ – одночастичная функция распределения, фазовое пространство которой дополнено пространством энергий вращения молекулы $\varepsilon $;
$M_{{ijk...}}^{{\left( N \right)}} = \int {{{m}_{0}}{{c}_{i}}{{c}_{j}}{{c}_{k}}\; \ldots \;fd{\mathbf{c}}d\varepsilon } $ – поступательные моменты N-го порядка;
$M_{{i...}}^{{r\left( N \right)}} = \int {\varepsilon {{c}_{i}}\; \ldots \;fd{\mathbf{c}}d\varepsilon } $ – вращательные моменты N-го порядка (ранг тензора $N - 2$);
$d{\mathbf{c}} = d{{c}_{1}}d{{c}_{2}}d{{c}_{3}}$ – элемент пространства тепловых скоростей;
$m_{{ijk...}}^{{\left( N \right)}}$ и $m_{{ijk...}}^{{r\left( N \right)}}$ – корректирующие члены моментов порядка $N > 3$, см. (3.12);
$\rho = \int {{{m}_{0}}fd{\mathbf{c}}d\varepsilon } = {{M}^{{\left( 0 \right)}}}$ – плотность газа;
${{P}_{{ij}}} = M_{{ij}}^{{\left( 2 \right)}} = \int {{{m}_{0}}{{c}_{i}}{{c}_{j}}fd{\mathbf{c}}d\varepsilon } $ – тензор напряжений, момент второго порядка;
${{T}_{{ij}}} = \frac{{{{P}_{{ij}}}}}{\rho }$ – тензор удельных напряжений;
$p = {{{{P}_{{\alpha \alpha }}}} \mathord{\left/ {\vphantom {{{{P}_{{\alpha \alpha }}}} 3}} \right. \kern-0em} 3}$ – механическое давление;
${{T}_{t}} = \frac{p}{{\rho R}}$ – температура поступательных степеней свободы, поступательная температура;
${{E}_{r}} = {{M}^{{r\left( {\text{2}} \right)}}} = \int {\varepsilon fd{\mathbf{c}}d\varepsilon } = \left( {{{c}_{{v}}} - \frac{3}{2}{\text{R}}} \right)\rho {{T}_{r}} = \rho {{R}_{{\text{r}}}}{{T}_{r}}$ – энергия вращения молекул в единице объема;
${{T}_{r}} = \frac{1}{{\rho {{R}_{{\text{r}}}}}}\int {\varepsilon \,fd{\mathbf{c}}d\varepsilon } $ – температура вращательных степеней свободы, вращательная температура;
$T = \frac{3}{2}\left( {\gamma - 1} \right){{T}_{t}} + \frac{{\left( {5 - 3\gamma } \right)}}{2}{{T}_{r}}$ – термодинамическая температура;
$\theta = {{T}_{t}} - {{T}_{r}}$;
$p_{{ij}}^{{}} = {{P}_{{ij}}} - {{\delta }_{{ij}}}p$ – тензор неравновесных напряжений (девиатор напряжений);
$2{{\varphi }_{{ijk}}} = M_{{ijk}}^{{\left( 3 \right)}} = \int {{{m}_{0}}{{c}_{i}}{{c}_{j}}{{c}_{k}}fdcd\varepsilon } $ – поступательный момент третьего порядка;
${{\varphi }_{i}} = {{\varphi }_{{i\alpha \alpha }}}$ – вектор теплового потока, создаваемого поступательным движением молекул;
${{\omega }_{i}} = M_{i}^{{r\left( 3 \right)}} = \int {{{c}_{i}}\varepsilon \,fd{\mathbf{c}}d\varepsilon } $ – вектор теплового потока, создаваемого переносом энергии вращения молекул, вращательный момент третьего порядка;
${{\psi }_{{ijk}}} = {{2{{\varphi }_{{ijk}}}} \mathord{\left/ {\vphantom {{2{{\varphi }_{{ijk}}}} \rho }} \right. \kern-0em} \rho }$ и ${{\varpi }_{i}} = {{{{\omega }_{i}}} \mathord{\left/ {\vphantom {{{{\omega }_{i}}} \rho }} \right. \kern-0em} \rho }$ – удельные значения моментов третьего порядка;
τ – время релаксации функции распределения;
${{\tau }_{p}}$ – время релаксации напряжений;
${{\tau }_{\varphi }}$ – время релаксации теплового потока, создаваемого поступательным движением молекул;
${{\tau }_{\omega }}$ – время релаксации теплового потока, обусловленного переносом энергии вращения молекул;
${{\tau }_{\theta }}$ – время релаксации разности температур $\theta $ или время поступательно-вращательной релаксации;
${{\tau }_{N}}$ – время релаксации поступательных моментов N-го порядка ($N \geqslant 4$);
$\tau _{N}^{r}$ – время релаксации вращательных моментов N-го порядка ($N \geqslant 4$);
$r_{{ij}}^{{\left( 2 \right)}} = \frac{{T_{{ij}}^{ + } - {{T}_{{ij}}}}}{\tau } = - \frac{{{{p}_{{ij}}}}}{{\rho {{\tau }_{p}}}} - {{\delta }_{{ij}}}\frac{{5 - 3\gamma }}{2}R\frac{\theta }{{Z\tau }}$ – релаксационный член второго порядка (3.34);
${{r}^{{r\left( 2 \right)}}} = {{R}_{r}}\frac{{T_{{\text{r}}}^{ + } - {{T}_{r}}}}{\tau } = \frac{3}{2}\left( {\gamma - 1} \right){{R}_{r}}\frac{\theta }{{Z\tau }}$ – релаксационный член второго порядка (3.33);
$r_{{ijk}}^{{\left( 3 \right)}} = \frac{{\psi _{{ijk}}^{ + } - {{\psi }_{{ijk}}}}}{\tau } = - \frac{2}{3}\frac{{{{\psi }_{{ijk}}}}}{{{{\tau }_{p}}}}$ – релаксационный член третьего порядка (3.35);
${{r}_{i}}^{{r\left( 3 \right)}} = \frac{{\varpi _{{\text{i}}}^{ + } - {{\varpi }_{i}}}}{\tau } = - \frac{{{{\varpi }_{i}}}}{{{{\tau }_{p}}}}$ – релаксационные члены третьего порядка (3.36);
μ – коэффициент вязкости;
Z – среднее количество межмолекулярных столкновений, приходящихся на одно неупругое столкновение;
s – показатель степени температуры в аппроксимациях $\mu = cT_{t}^{s}$, где c – константа.
Физические константы и критерии подобия:
k – постоянная Больцмана;
${{c}_{p}}$, ${{c}_{{v}}}$ – удельные изобарная и изохорная теплоемкости;
$R = {k \mathord{\left/ {\vphantom {k {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}}$ – удельная газовая постоянная;
${{R}_{r}} = \left( {{{c}_{{v}}} - \frac{3}{2}R} \right) = \frac{{\left( {5 - 3\gamma } \right)}}{{2\left( {\gamma - 1} \right)}}R$;
$\gamma = {{{{c}_{p}}} \mathord{\left/ {\vphantom {{{{c}_{p}}} {{{c}_{{v}}}}}} \right. \kern-0em} {{{c}_{{v}}}}}$ – показатель адиабаты;
$Pr$ – число Прандтля;
$M$ – число Маха;
Аббревиатуры:
НСФ – модель Навье–Стокса–Фурье;
МКУ – модельное кинетическое уравнение;
S3, S4, S5, S6 – системы моментных уравнений третьего, …, шестого порядков.
3. СИСТЕМЫ МОМЕНТНЫХ УРАВНЕНИЙ
3.1. Метод построения системы моментных уравнений
Будем строить моментные уравнения на базе модельного кинетического уравнения релаксационного типа:
(3.1)
$\frac{{\partial f}}{{\partial t}} + {{\xi }_{\alpha }}\frac{{\partial f}}{{\partial {{x}_{\alpha }}}} = \frac{{{{f}^{ + }} - f}}{\tau }.$Использование МКУ (3.1) вместо уравнения Больцмана обусловлено тем, что в дальнейшем нас будут интересовать только моменты интеграла столкновений, а не сам интеграл столкновений кинетического уравнения. Будем считать, что ${{f}^{ + }}$ и τ подобраны настолько удачно, что моменты интеграла столкновений (3.1) близки к их реальным значениям.
Традиционное вычисление моментов больцмановского интеграла связано с выбором некоторой, в большинстве случаев достаточно грубой, модели молекулы. Достоверность строгих аналитических выводов, имеющих в своей основе весьма неточные данные, видимо, не лучше достоверности сделанного выше предположения о выборе ${{f}^{ + }}$ и τ.
Проинтегрируем уравнение (3.1) по пространству скоростей и энергии вращения молекул, предварительно умножив его на молекулярные признаки в виде массы и импульса молекулы, т.е. ${{m}_{0}}$ и ${{m}_{0}}{{\xi }_{{\text{i}}}}$. Получим моментные уравнения нулевого и первого порядков, выражающие законы сохранения массы и импульса:
(3.2)
$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {{u}_{\alpha }}}}{{\partial {{x}_{\alpha }}}} = 0; \\ \frac{{\partial \rho {{u}_{i}}}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {\rho {{u}_{i}}{{u}_{\alpha }} + {{P}_{{i\alpha }}}} \right) = 0. \\ \end{gathered} $Моментное уравнение порядка $N \geqslant 2$, полученное интегрированием (3.1) с соответствующим молекулярным признаком, имеет вид
(3.3)
$\frac{{\partial M_{{ijk...}}^{{\left( N \right)}}}}{{\partial t}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}M_{{ijk...}}^{{\left( N \right)}}} \right) + M_{{***...\alpha }}^{{\left( N \right)}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} - \frac{{M_{{***...}}^{{\left( {N - 1} \right)}}}}{\rho }\frac{{\partial P_{{*\alpha }}^{{}}}}{{\partial {{x}_{\alpha }}}} + \frac{{\partial M_{{ijk...\alpha }}^{{\left( {N + 1} \right)}}}}{{\partial {{x}_{\alpha }}}} = \frac{1}{\tau }\left( {M_{{ijk...}}^{{\left( N \right) + }} - M_{{ijk...}}^{{\left( N \right)}}} \right).$Уравнения моментов второго порядка $M_{{ij}}^{{\left( 2 \right)}} = {{P}_{{ij}}}$ и ${{M}^{{r\left( 2 \right)}}} = {{E}_{r}}$ следуют непосредственно из (3.3) с учетом того, что $M_{i}^{{\left( 1 \right)}} = \int {{{m}_{0}}{{c}_{i}}fd{\mathbf{c}}d\varepsilon } \equiv 0$, а $M_{i}^{{{\text{r}}\left( 1 \right)}}$ не существует:
(3.4)
$\frac{\partial }{{\partial t}}{{P}_{{ij}}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}{{P}_{{ij}}}} \right) + {{P}_{{*\alpha }}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + 2\frac{{\partial {{\varphi }_{{ij\alpha }}}}}{{\partial {{x}_{\alpha }}}} = \frac{1}{\tau }\left( {P_{{ij}}^{ + } - {{P}_{{ij}}}} \right),$(3.5)
$\frac{\partial }{{\partial t}}{{E}_{{\text{r}}}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}{{E}_{r}}} \right) + \frac{{\partial {{\omega }_{\alpha }}}}{{\partial {{x}_{\alpha }}}} = \frac{1}{\tau }\left( {E_{r}^{ + } - {{E}_{r}}} \right) = \Xi .$Правая часть (3.4) с учетом ${{P}_{{ij}}} = {{p}_{{ij}}} + {{\delta }_{{ij}}}p$, где $p = {{{{P}_{{\alpha \alpha }}}} \mathord{\left/ {\vphantom {{{{P}_{{\alpha \alpha }}}} 3}} \right. \kern-0em} 3}$ – механическое давление, а $p_{{ij}}^{{}}$ – неравновесное напряжение, может быть преобразована следующим образом:
(3.6)
$P_{{ij}}^{ + } - {{P}_{{ij}}} = \left( {p_{{ij}}^{ + } + {{\delta }_{{ij}}}{{p}^{ + }}} \right) - \left( {p_{{ij}}^{{}} + {{\delta }_{{ij}}}p} \right) = - \left( {p_{{ij}}^{{}} - p_{{ij}}^{ + }} \right) - {{\delta }_{{ij}}}\left( {p - {{p}^{ + }}} \right) = - \left( {1 - \Pi } \right)p_{{ij}}^{{}} - {{\delta }_{{ij}}}\frac{2}{3}\tau \Xi .$Рационально положить, что в процессе пространственно однородной релаксации векторы, отображающие неравновесные величины, например, вектор теплового потока, не меняют своего направления. Направление главных осей тензоров также остается неизменным. Из этого положения следует, что отношение ${{p_{{ij}}^{ + }} \mathord{\left/ {\vphantom {{p_{{ij}}^{ + }} {p_{{ij}}^{{}}}}} \right. \kern-0em} {p_{{ij}}^{{}}}}$ и фигурирующие ниже ${{\varphi _{{ijk}}^{ + }} \mathord{\left/ {\vphantom {{\varphi _{{ijk}}^{ + }} {{{\varphi }_{{ijk}}}}}} \right. \kern-0em} {{{\varphi }_{{ijk}}}}}$ и ${{\omega _{i}^{ + }} \mathord{\left/ {\vphantom {{\omega _{i}^{ + }} {{{\omega }_{i}}}}} \right. \kern-0em} {{{\omega }_{i}}}}$ не зависят от значений индексов, т.е. являются скалярами. Например, для вектора ${{\omega }_{i}}$ отношения ${{\omega _{1}^{ + }} \mathord{\left/ {\vphantom {{\omega _{1}^{ + }} {{{\omega }_{1}}}}} \right. \kern-0em} {{{\omega }_{1}}}} = {{\omega _{2}^{ + }} \mathord{\left/ {\vphantom {{\omega _{2}^{ + }} {{{\omega }_{2}}}}} \right. \kern-0em} {{{\omega }_{2}}}} = {{\omega _{3}^{ + }} \mathord{\left/ {\vphantom {{\omega _{3}^{ + }} {{{\omega }_{3}}}}} \right. \kern-0em} {{{\omega }_{3}}}}$ представляют собой параметр сокращения длины вектора в процессе пространственно-однородной релаксации. Это положение, очевидно, распространяется на все неравновесные величины, независимо от ранга соответствующего тензора.
Отмеченное свойство релаксирующих величин является основой применяемого метода построения моментных уравнений для функции распределения общего вида. Кроме этого, благодаря данному свойству правые части моментных уравнений могут быть представлены в виде релаксационных членов без использования какой-либо модели межмолекулярного взаимодействия.
Очевидно, что при таком подходе время релаксации τ может быть определено только из каких-то дополнительных соображений. Например, оно может быть принято равным среднему времени свободного пробега молекулы. Неопределенными останутся также $\Xi $, ${{p_{{ij}}^{ + }} \mathord{\left/ {\vphantom {{p_{{ij}}^{ + }} {p_{{ij}}^{{}}}}} \right. \kern-0em} {p_{{ij}}^{{}}}}$, и аналогичные отношения, определяющие быстроту релаксации неравновесных величин.
Запишем уравнения неравновесных величин 2-го и 3-го порядков. Преобразуем (3.4) с учетом (3.6):
(3.7)
$\frac{\partial }{{\partial t}}{{P}_{{ij}}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}{{P}_{{ij}}}} \right) + {{P}_{{*\alpha }}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + 2\frac{{\partial {{\varphi }_{{ij\alpha }}}}}{{\partial {{x}_{\alpha }}}} = - \frac{{p_{{ij}}^{{}}}}{{{{\tau }_{p}}}} - {{\delta }_{{ij}}}\frac{2}{3}\Xi {\kern 1pt} .$Произведем свертку этого выражения. Учтем, что ${{P}_{{\alpha \alpha }}} = 3p$, ${{p}_{{\alpha \alpha }}} \equiv 0$, ${{\varphi }_{{i\alpha \alpha }}} = {{\varphi }_{i}}$. В результате получим уравнение механического давления:
(3.8)
$\frac{\partial }{{\partial t}}p + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}p} \right) + \frac{2}{3}{{P}_{{\beta \alpha }}}\frac{{\partial {{u}_{\beta }}}}{{\partial {{x}_{\alpha }}}} + \frac{2}{3}\frac{\partial }{{\partial {{x}_{\alpha }}}}{{\varphi }_{\alpha }} = - \frac{2}{3}\Xi .$(3.9)
$\frac{\partial }{{\partial t}}p_{{ij}}^{{}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}p_{{ij}}^{{}}} \right) + {{P}_{{*\alpha }}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} - {{\delta }_{{ij}}}\frac{2}{3}{{P}_{{\alpha \beta }}}\frac{{\partial {{u}_{\beta }}}}{{\partial {{x}_{\alpha }}}} + 2\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{\varphi }_{{ij\alpha }}} - {{\delta }_{{ij}}}\frac{1}{3}{{\varphi }_{\alpha }}} \right) = - \frac{{p_{{ij}}^{{}}}}{{{{\tau }_{p}}}}.$Уравнения моментов третьего порядка следуют непосредственно из (3.3):
(3.10)
$\frac{\partial }{{\partial t}}{{\varphi }_{{ijk}}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}{{\varphi }_{{ijk}}}} \right) + {{\varphi }_{{**\alpha }}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} - \frac{1}{2}{{T}_{{**}}}\frac{{\partial {{P}_{{*\alpha }}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{2}\frac{\partial }{{\partial {{x}_{\alpha }}}}M_{{ijk\alpha }}^{{\left( 4 \right)}} = - \frac{{{{\varphi }_{{ijk}}}}}{\varphi };$(3.11)
$\frac{\partial }{{\partial t}}{{\omega }_{i}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}{{\omega }_{i}}} \right) + {{\omega }_{\alpha }}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{\alpha }}}} - {{R}_{r}}{{T}_{r}}\frac{\partial }{{\partial {{x}_{\alpha }}}}{{P}_{{i\alpha }}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}M_{{i\alpha }}^{{r\left( 4 \right)}} = - \frac{{{{\omega }_{i}}}}{{{{\tau }_{\omega }}}}.$3.2. Вариант замыкания системы моментных уравнений
Из полученных выше уравнений можно составить систему моментных уравнений третьего порядка. Однако эта система останется незамкнутой, пока в уравнениях моментов третьего порядка (3.10) и (3.11) не определены замыкающие систему моменты четвертого порядка. Истинные значения этих моментов можно определить только в том случае, если известно решение кинетического уравнения.
Аппроксимации моментов порядка N, полученные интегрированием модельных функций распределения того или иного вида, приводят к той или иной комбинации моментов порядков N – 1 и ниже. Одни из первых таких аппроксимаций были предложены Грэдом. Таким образом, естественным способом замыкания системы уравнений является выражение замыкающих моментов в виде комбинаций моментов, уже определенных системой.
Отметим общие свойства моментов функции распределения:
– момент – симметричный тензор;
– масса молекулы или энергия ее вращения входит в определение момента только один раз;
– момент первого порядка, определяемый в системе координат, движущейся вместе с газом, тождественно равен нулю.
Кроме этого, учтем, что в моментном уравнении (3.3) искомый момент определяется только компактно симметрированными линейными комбинациями других моментов.
Будем считать, что все моменты до третьего порядка включительно, определены точно. Выразим момент порядка N > 3 в виде суммы аппроксимирующего и корректирующего членов:
(3.12)
$M_{{ijk...}}^{{...\left( N \right)}} = A_{{ijk...}}^{{...\left( N \right)}} + \rho m_{{ijk...}}^{{...\left( N \right)}}.$Выпишем моменты до седьмого порядка, составленные по указанному выше правилу. Моменты поступательных степеней свободы:
(3.13)
$M_{{ijk{\text{l}}}}^{{\left( 4 \right)}} = \rho {{T}_{{**}}}{{T}_{{**}}} + \rho m_{{ijkl}}^{{\left( 4 \right)}},$(3.14)
$M_{{ijk...}}^{{\left( 5 \right)}} = \rho {{T}_{{**}}}{{\psi }_{{***}}} + \rho m_{{ijk...}}^{{\left( 5 \right)}},$(3.15)
$M_{{ijk...}}^{{\left( 6 \right)}} = \rho \left( {{{T}_{{**}}}{{T}_{{**}}}{{T}_{{**}}} + {{\psi }_{{***}}}{{\psi }_{{***}}} + {{T}_{{**}}}m_{{****}}^{{\left( 4 \right)}}} \right) + \rho m_{{ijk...}}^{{\left( 6 \right)}},$(3.16)
$M_{{ijk...}}^{{\left( 7 \right)}} = \rho \left( {{{T}_{{**}}}{{T}_{{**}}}{{\psi }_{{***}}} + {{\psi }_{{***}}}m_{{****}}^{{\left( 4 \right)}} + {{T}_{{**}}}m_{{*****}}^{{\left( 5 \right)}}} \right) + \rho m_{{ijk...}}^{{\left( 7 \right)}}$(3.17)
$M_{{ij}}^{{r\left( 4 \right)}} = \rho {{R}_{r}}{{T}_{r}}{{T}_{{ij}}} + \rho m_{{ij}}^{{r\left( 4 \right)}},$(3.18)
$M_{{ijk}}^{{r\left( 5 \right)}} = \rho \left( {{{R}_{r}}{{T}_{r}}{{\psi }_{{ijk}}} + {{T}_{{**}}}{{\varpi }_{*}}} \right) + \rho m_{{ijk}}^{{r\left( 5 \right)}},$(3.19)
$M_{{ijkl}}^{{r\left( 6 \right)}} = \rho \left( {{{R}_{r}}{{T}_{r}}{{T}_{{**}}}{{T}_{{**}}} + {{\psi }_{{***}}}{{\varpi }_{*}} + {{R}_{r}}{{T}_{r}}m_{{ijkl}}^{{\left( 4 \right)}} + {{T}_{{**}}}m_{{**}}^{{r\left( 4 \right)}}} \right) + \rho m_{{ijkl}}^{{r\left( 6 \right)}},$(3.20)
$M_{{ijk...}}^{{r\left( 7 \right)}} = \rho \left( {{{R}_{r}}{{T}_{r}}{{T}_{{**}}}{{\psi }_{{***}}} + {{T}_{{**}}}{{T}_{{**}}}{{\varpi }_{*}} + {{\psi }_{{***}}}m_{{**}}^{{r\left( 4 \right)}} + {{\varpi }_{*}}m_{{****}}^{{\left( 4 \right)}} + {{T}_{{**}}}m_{{***}}^{{r\left( 5 \right)}} + {{R}_{r}}{{T}_{r}}m_{{ijk...}}^{{\left( 5 \right)}}} \right) + \rho m_{{ijk...}}^{{r\left( 7 \right)}}$Нетрудно убедиться, что в условиях равновесия представленные аппроксимации моментов соответствуют их точным значениям при любых значениях индексов.
Если (3.13) и (3.17) подставить в (3.10) и (3.11), приняв $m_{{ijkl}}^{{\left( 4 \right)}} = 0$ и $m_{{ij}}^{{r\left( 4 \right)}} = 0$, система моментных уравнений третьего порядка S3 будет замкнута. Уравнения моментов третьего порядка примут следующий вид:
(3.21)
$\frac{\partial }{{\partial t}}{{\varphi }_{{ijk}}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}{{\varphi }_{{ijk}}}} \right) + {{\varphi }_{{**\alpha }}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + \frac{R}{2}{{P}_{{*\alpha }}}\frac{{\partial {{T}_{{**}}}}}{{\partial {{x}_{\alpha }}}} = - \frac{{{{\varphi }_{{ijk}}}}}{{{{\tau }_{\varphi }}}};$(3.22)
$\frac{\partial }{{\partial t}}{{\omega }_{i}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{u}_{\alpha }}{{\omega }_{i}}} \right) + {{\omega }_{\alpha }}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{\alpha }}}} + {{R}_{r}}{{P}_{{i\alpha }}}\frac{{\partial {{T}_{r}}}}{{\partial {{x}_{\alpha }}}} = - \frac{{{{\omega }_{i}}}}{{{{\tau }_{\omega }}}}.$Отметим, что (3.21) существенно проще соответствующего уравнения 20-моментной системы Грэда, хотя аппроксимация момента четвертого порядка
3.3. Время релаксации неравновесных величин
Времена релаксации ${{\tau }_{p}}$, ${{\tau }_{\varphi }}$, ${{\tau }_{\omega }}$ могут быть определены в гидродинамическом приближении с использованием законов Стокса и Фурье для напряжений и теплового потока. В этом приближении время релаксации τ и совпадающие с ним по порядку величины ${{\tau }_{p}}$, ${{\tau }_{\varphi }}$, ${{\tau }_{\omega }}$, рассматриваются как малые величины. Основные параметры газа: ρ, u, p, T считаются величинами порядка единицы.
Члены левых частей уравнений (3.9), (3.21), (3.22), не содержащие неравновесных величин, очевидно, имеют порядок единицы. Релаксационный член должен иметь тот же порядок величины. Отсюда следует, что все неравновесные величины, за некоторым несущественным в данном случае исключением, имеют порядок τ.
После домножения (3.9) на ${{\tau }_{p}}$ и исключения слагаемых, содержащих неравновесные величины (после домножения их порядок станет равным ${{\tau }^{2}}$), получим выражение для неравновесных напряжений в гидродинамическом приближении. В целях сокращения записи рассмотрим только касательные напряжения ($i \ne j$):
(3.23)
$p_{{ij}}^{{}} = - {{\tau }_{p}}p\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right).$В законе трения Стокса касательные напряжения выражаются в виде
(3.24)
$p_{{ij}}^{{}} = - \mu \left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right).$Аналогичным образом определяется время релаксации теплового потока. В левой части (3.21) отбрасываются слагаемые с неравновесными величинами. Учитывается, что в гидродинамическом приближении ${{T}_{{ii}}}\sim {{T}_{t}}\sim T$, и ${{T}_{{ij}}} = 0$ при $i \ne j$. Моменты третьего порядка, выраженные через старшие члены (3.21):
Два последних уравнения позволяют получить выражение теплового потока поступательных степеней свободы в гидродинамическом приближении:
(3.26)
${{\varphi }_{i}} = {{\varphi }_{{i\alpha \alpha }}} = - {{\tau }_{\varphi }}\frac{5}{2}Rp\frac{{\partial T}}{{\partial {{x}_{i}}}}.$Из закона Фурье:
Так как рассматриваются только поступательные степени свободы, то
(3.27)
${{c}_{p}} = 5{\text{/}}2R,\quad Pr = 2{\text{/}}3,\quad {\text{т}}{\text{.е}}{\text{.}}\quad {{\varphi }_{i}} = - \frac{{15}}{4}R\mu \frac{{\partial T}}{{\partial {{x}_{i}}}}.$В многоатомном газе к составляющей ${{\varphi }_{i}}$ добавляется составляющая ${{\omega }_{i}}$. Главные члены (3.22), с учетом того, что в рассматриваемом приближении ${{T}_{{\text{r}}}}\sim T$:
В законе Фурье на долю внутренних степеней свободы отводится часть полного теплового потока:
(3.35)
${{\omega }_{i}} = - \left( {\frac{{{{c}_{p}}}}{{\Pr }} - \frac{{15}}{4}R} \right)\mu \frac{{\partial T}}{{\partial {{x}_{i}}}} = - \frac{{\left( {5 - 3\gamma } \right)}}{{2\left( {\gamma - 1} \right)}}R\mu \frac{{\partial T}}{{\partial {{x}_{i}}}} = - {{R}_{{\text{r}}}}\mu \frac{{\partial T}}{{\partial {{x}_{i}}}}.$(3.29)
${{\tau }_{\omega }} = {\mu \mathord{\left/ {\vphantom {\mu p}} \right. \kern-0em} p} = {{\tau }_{p}}.$Выразим быстроту поступательно-вращательного энергообмена $\Xi $ в виде релаксационного члена разности поступательной и вращательной температур $\theta = {{T}_{t}} - {{T}_{r}}$. В (3.5) и (3.6) $\Xi $ представлена как $\Xi = {{\left( {E_{r}^{ + } - {{E}_{r}}} \right)} \mathord{\left/ {\vphantom {{\left( {E_{r}^{ + } - {{E}_{r}}} \right)} \tau }} \right. \kern-0em} \tau }$ и $\Xi = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}\,{{\left( {p - {{p}^{ + }}} \right)} \mathord{\left/ {\vphantom {{\left( {p - {{p}^{ + }}} \right)} \tau }} \right. \kern-0em} \tau }$. С учетом того, что в терминах температуры ${{E}_{r}} = \rho {{R}_{r}}{{T}_{r}}$, $p = \rho R{{T}_{t}}$, а плотность газа не изменяется в процессе релаксации, т.е. ${{\rho }^{ + }} \equiv \rho $, после несложных преобразований получаем
где ${{\tau }_{\theta }} = {\tau \mathord{\left/ {\vphantom {\tau {\left( {1 - {{{{\theta }^{ + }}} \mathord{\left/ {\vphantom {{{{\theta }^{ + }}} \theta }} \right. \kern-0em} \theta }} \right)}}} \right. \kern-0em} {\left( {1 - {{{{\theta }^{ + }}} \mathord{\left/ {\vphantom {{{{\theta }^{ + }}} \theta }} \right. \kern-0em} \theta }} \right)}}$.Для времени поступательно-вращательной релаксации ${{\tau }_{\theta }}$ существуют приближения разных порядков, см., например, [9], [10]. Если в качестве времени релаксации функции распределения $\tau $ принять среднее время свободного пробега молекулы, то для ${{\tau }_{\theta }}$ можно использовать аппроксимацию
где Z – среднее количество межмолекулярных столкновений, приходящихся на одно неупругое столкновение.3.4. Системы моментных уравнений высших порядков
Выпишем систему моментных уравнений третьего порядка S3. Уравнение сохранения массы (3.2) оставим без изменений, а остальные уравнения выразим относительно величин, не содержащих плотность газа, т.е. удельных величин. В уравнениях моментов второго и третьего порядка учтем выражения для релаксационного члена (3.30) и времен релаксации (3.25), (3.28), (3.29), (3.31):
(3.2)
$\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {{u}_{\alpha }}}}{{\partial {{x}_{\alpha }}}} = 0,$(3.32)
$\frac{{\partial {{u}_{i}}}}{{\partial t}} + {{u}_{\alpha }}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{\rho }\frac{{\partial {{P}_{{i\alpha }}}}}{{\partial {{x}_{\alpha }}}} = 0,$(3.33)
$\frac{{\partial {{T}_{{\text{r}}}}}}{{\partial t}} + {{u}_{\alpha }}\frac{{\partial {{T}_{r}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{{{{R}_{r}}\rho }}\frac{{\partial {{\omega }_{\alpha }}}}{{\partial {{x}_{\alpha }}}} = \frac{3}{2}\left( {\gamma - 1} \right)\frac{\theta }{{Z\tau }} = \frac{{{{r}^{{r\left( 2 \right)}}}}}{{{{R}_{r}}}},$(3.34)
$\frac{{\partial {{T}_{{ij}}}}}{{\partial t}} + {{u}_{\alpha }}\frac{{\partial {{T}_{{ij}}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{*\alpha }}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{\rho }\frac{{\partial \rho {{\psi }_{{ij\alpha }}}}}{{\partial {{x}_{\alpha }}}} = - \frac{{{{p}_{{ij}}}}}{{\rho {{\tau }_{p}}}} - {{\delta }_{{ij}}}\frac{{5 - 3\gamma }}{2}R\frac{\theta }{{Z\tau }} = r_{{ij}}^{{\left( 2 \right)}},$(3.35)
$\frac{{\partial {{\psi }_{{ijk}}}}}{{\partial t}} + {{u}_{\alpha }}\frac{{\partial {{\psi }_{{ijk}}}}}{{\partial {{x}_{\alpha }}}} + {{\psi }_{{ * * \alpha }}}\frac{{\partial {{u}_{ * }}}}{{\partial {{x}_{\alpha }}}} + {{{\text{T}}}_{{ * \alpha }}}\frac{{\partial {{T}_{{**}}}}}{{\partial {{x}_{\alpha }}}} + \left\{ {\frac{1}{\rho }\frac{{\partial \rho m_{{ijk\alpha }}^{{\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right\} = - \frac{2}{3}\frac{{{{\psi }_{{ijk}}}}}{{{{\tau }_{p}}}} = r_{{ijk}}^{{\left( 3 \right)}},$(3.36)
$\frac{\partial }{{\partial t}}{{\varpi }_{i}} + {{u}_{\alpha }}\frac{{\partial {{\varpi }_{i}}}}{{\partial {{x}_{\alpha }}}} + {{\varpi }_{\alpha }}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{\alpha }}}} + {{R}_{r}}{{T}_{{i\alpha }}}\frac{{\partial {{T}_{r}}}}{{\partial {{x}_{\alpha }}}} + \left\{ {\frac{1}{\rho }\frac{{\partial \rho m_{{i\alpha }}^{{r\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right\} = - \frac{{{{\varpi }_{i}}}}{{{{\tau }_{p}}}} = {{r}_{i}}^{{r\left( 3 \right)}}.$Как отмечалось выше, система S3 будет замкнутой, если $m_{{ijkl}}^{{\left( 4 \right)}} = 0$ и $m_{{ij}}^{{r\left( 4 \right)}} = 0$. Здесь и ниже члены, которыми мы пренебрегаем при замыкания системы, будут выделяться фигурными скобками. Это правило, очевидно, относится только к замыкающим систему уравнениям.
Для сокращения дальнейших выкладок удобно преобразовать (3.3) относительно моментов, не содержащих плотность газа:
(3.37)
$\frac{\partial }{{\partial t}}\left( {\frac{{M_{{ijk...}}^{{\left( N \right)}}}}{\rho }} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {\frac{{M_{{ijk...}}^{{\left( N \right)}}}}{\rho }} \right) + \frac{{M_{{***...\alpha }}^{{\left( N \right)}}}}{\rho }\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} - \frac{{M_{{***...}}^{{\left( {N - 1} \right)}}}}{{{{\rho }^{2}}}}\frac{{\partial \rho {\text{T}}_{{*\alpha }}^{{}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{\rho }\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {M_{{ijk...\alpha }}^{{\left( {N + 1} \right)}}} \right) = \frac{1}{\tau }\left( {\frac{{M_{{ijk...}}^{{\left( N \right) + }}}}{\rho } - \frac{{M_{{ijk...}}^{{\left( N \right)}}}}{\rho }} \right).$Моментные уравнения четвертого порядка могут быть получены подстановкой (3.13), (3.14) и (3.17), (3.18) в общее моментное уравнение (3.37):
(3.38)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{T}_{{**}}}{{T}_{{**}}} + m_{{ijkl}}^{{\left( 4 \right)}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{{**}}}{{T}_{{**}}} + m_{{ijkl}}^{{\left( 4 \right)}}} \right) + \left( {{{T}_{{ * \alpha }}}{{T}_{{**}}} + m_{{***\alpha }}^{{\left( 4 \right)}}} \right)\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} - \frac{{{{\psi }_{{ * * * }}}}}{\rho }\frac{{\partial \rho T_{{*\alpha }}^{{}}}}{{\partial {{x}_{\alpha }}}} + \\ + \;\frac{1}{\rho }\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {\rho \left( {{{T}_{{**}}}{{\psi }_{{**\alpha }}} + {{T}_{{*\alpha }}}{{\psi }_{{***}}} + m_{{ijk...\alpha }}^{{\left( 5 \right)}}} \right)} \right) = \frac{1}{\tau }\left( {T_{{**}}^{ + }T_{{**}}^{ + } - {{T}_{{**}}}{{T}_{{**}}} + m_{{ijkl}}^{{\left( 4 \right) + }} - m_{{ijkl}}^{{\left( 4 \right)}}} \right); \\ \end{gathered} $(3.39)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{R}_{r}}{{T}_{r}}{{T}_{{ij}}} + m_{{ij}}^{{r\left( 4 \right)}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{R}_{r}}{{T}_{r}}{{T}_{{ij}}} + m_{{ij}}^{{r\left( 4 \right)}}} \right) + \left( {{{R}_{r}}{{T}_{r}}{{T}_{{ * \alpha }}} + m_{{ * \alpha }}^{{r\left( 4 \right)}}} \right)\frac{{\partial {{u}_{ * }}}}{{\partial {{x}_{\alpha }}}} - \frac{{{{\varpi }_{ * }}}}{\rho }\frac{{\partial \rho T_{{*\alpha }}^{{}}}}{{\partial {{x}_{\alpha }}}} + \\ + \;\frac{1}{\rho }\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {\rho \left( {{{R}_{r}}{{T}_{r}}{{\psi }_{{ij\alpha }}} + {{T}_{{*\alpha }}}{{\varpi }_{ * }} + {{T}_{{ij}}}{{\varpi }_{\alpha }} + m_{{ij\alpha }}^{{r\left( 5 \right)}}} \right)} \right) = \frac{1}{\tau }\left( {{{R}_{r}}\left( {T_{r}^{ + }T_{{ij}}^{ + } - {{T}_{r}}{{T}_{{ij}}}} \right) + m_{{ij}}^{{r\left( 4 \right) + }} - m_{{ij}}^{{r\left( 4 \right)}}} \right). \\ \end{gathered} $При переходе к системе четвертого порядка достаточно определить только корректирующие члены $m_{{ijkl}}^{{\left( 4 \right)}}$ и $m_{{ij}}^{{r\left( 4 \right)}}$, опущенные в системе третьего порядка. Определения полных моментов $M_{{ijkl}}^{{\left( 4 \right)}}$ и $M_{{ij}}^{{r\left( 4 \right)}}$ не требуется.
Умножим (3.34) на ${{T}_{{kl}}}$. Затем (3.34), записанное с индексами k и l, умножим на ${{T}_{{ij}}}$ и почленно сложим полученные выражения. В результате получим
Проделаем эту операцию для других сочетаний индексов, соответствующих компактно симметрированной сумме ${{T}_{{ * * }}}{{T}_{{ * * }}}$, например ${{T}_{{ik}}}{{T}_{{jl}}}$ и ${{T}_{{il}}}{{T}_{{jk}}}$. Проведя почленное сложение, приходим к уравнению:
(3.40)
$\frac{\partial }{{\partial t}}\left( {{{T}_{{ * * }}}{{T}_{{ * * }}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{{ * * }}}{{T}_{{ * * }}}} \right) + {{T}_{{\alpha *}}}{{T}_{{ * * }}}\frac{{\partial {{u}_{ * }}}}{{\partial {{x}_{\alpha }}}} + \frac{{{{T}_{{ * * }}}}}{\rho }\frac{{\partial \rho {{\psi }_{{ * * \alpha }}}}}{{\partial {{x}_{\alpha }}}} = \frac{{T_{{ * * }}^{{}}T_{{ * * }}^{ + } - 2{{T}_{{ * * }}}{{T}_{{ * * }}}}}{\tau }.$Аналогичным образом из зависимостей (3.33), (3.34), домноженных на ${{T}_{r}}$ и ${{T}_{{ij}}}$, можно получить
(3.41)
$\frac{\partial }{{\partial t}}\left( {{{T}_{r}}{{T}_{{ij}}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{r}}{{T}_{{ij}}}} \right) + {{T}_{r}}{{T}_{{*\alpha }}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{\rho }\left( {{{T}_{r}}\frac{{\partial \rho {{\psi }_{{ij\alpha }}}}}{{\partial {{x}_{\alpha }}}} + \frac{{{{T}_{{ij}}}}}{{{{R}_{r}}}}\frac{{\partial \rho {{\varpi }_{\alpha }}}}{{\partial {{x}_{\alpha }}}}} \right) = \frac{{{{T}_{r}}T_{{ij}}^{ + } + T_{r}^{ + }T - 2{{T}_{r}}{{T}_{{ij}}}}}{\tau }.$Уравнения (3.40) и (3.41) являются точными, в том смысле, что соответствуют функции распределения общего вида. Вычтем (3.40) и (3.41) из (3.38) и (3.39) соответственно. В результате получим моментные уравнения четвертого порядка, записанные для корректирующих членов:
(3.42)
$\frac{{\partial m_{{ijkl}}^{{\left( 4 \right)}}}}{{\partial t}} + {{u}_{\alpha }}\frac{{\partial m_{{ijkl}}^{{\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}} + m_{{***\alpha }}^{{\left( 4 \right)}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{*\alpha }}}\frac{{\partial {{\psi }_{{***}}}}}{{\partial {{x}_{\alpha }}}} + {{\psi }_{{**\alpha }}}\frac{{\partial {{T}_{{**}}}}}{{\partial {{x}_{\alpha }}}} + \left\{ {\frac{1}{\rho }\frac{{\partial \rho m_{{ijkl\alpha }}^{{\left( 5 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right\} = - \frac{{m_{{ijkl}}^{{\left( 4 \right)}}}}{{{{\tau }_{4}}}} + \tau r_{{ * * }}^{{\left( 2 \right)}}r_{{ * * }}^{{\left( 2 \right)}},$(3.43)
$\frac{{\partial m_{{ij}}^{{{\text{r}}\left( 4 \right)}}}}{{\partial t}} + {{u}_{\alpha }}\frac{{\partial m_{{ij}}^{{r\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}} + m_{{*\alpha }}^{{r\left( 4 \right)}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + {{\psi }_{{ij\alpha }}}\frac{{\partial {{R}_{r}}{{T}_{r}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{*\alpha }}}\frac{{\partial {{\varpi }_{*}}}}{{\partial {{x}_{\alpha }}}} + {{\varpi }_{\alpha }}\frac{{\partial {{T}_{{ij}}}}}{{\partial {{x}_{\alpha }}}} + \left\{ {\frac{1}{\rho }\frac{{\partial \rho m_{{ij\alpha }}^{{r\left( 5 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right\} = - \frac{{m_{{ij}}^{{r\left( 4 \right)}}}}{{\tau _{4}^{r}}} + \tau r_{{ij}}^{{\left( 2 \right)}}{{r}^{{r\left( 2 \right)}}}.$На примере зависимости (3.42) поясним вид релаксационных членов уравнений (3.42) и (3.43). После почленного вычитания (3.40) из (3.38) правая часть уравнения принимает вид
Времена релаксации ${{\tau }_{4}}$ и $\tau _{4}^{{\text{r}}}$ в (3.42) и (3.43) определены аналогично ${{\tau }_{p}}$, ${{\tau }_{\varphi }}$, ${{\tau }_{\omega }}$:
Система S3, дополненная уравнениями (3.42) и (3.43), образует систему моментных уравнений четвертого порядка – S4. Эта система будет замкнута, если пренебречь корректирующими членами $m_{{ijk...}}^{{\left( 5 \right)}}$ и $m_{{ijk}}^{{{\text{r}}\left( 5 \right)}}$, т.е. ограничиться только аппроксимирующими членами моментов пятого порядка (3.14), (3.18).
Расширим систему моментных уравнений до пятого порядка, повторив описанные выше процедуры для моментов (3.14), (3.15) и (3.18), (3.19). Моментные уравнения пятого порядка:
(3.44)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{T}_{{**}}}{{\psi }_{{***}}} + m_{{i...}}^{{\left( 5 \right)}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{{**}}}{{\psi }_{{***}}} + m_{{i...}}^{{\left( 5 \right)}}} \right) + \left( {{{T}_{{*\alpha }}}{{\psi }_{{***}}} + {{T}_{{**}}}{{\psi }_{{**\alpha }}} + m_{{*...\alpha }}^{{\left( 5 \right)}}} \right)\frac{{\partial {{u}_{ * }}}}{{\partial {{x}_{\alpha }}}} - \\ - \;\frac{{{{T}_{{**}}}{{T}_{{**}}} + m_{{****}}^{{\left( 4 \right)}}}}{\rho }\frac{{\partial \rho T_{{*\alpha }}^{{}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{\rho }\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {\rho \left( {{{T}_{{**}}}{{T}_{{**}}}{{T}_{{*\alpha }}} + {{T}_{{*\alpha }}}m_{{****}}^{{\left( 4 \right)}} + {{T}_{{**}}}m_{{***\alpha }}^{{\left( 4 \right)}} + {{\psi }_{{***}}}{{\psi }_{{**\alpha }}} + m_{{i..\alpha }}^{{\left( 6 \right)}}} \right)} \right) = \\ = \;\frac{1}{\tau }\left( {T_{{**}}^{ + }\psi _{{**}}^{ + } - {{T}_{{**}}}{{\psi }_{{**}}} + m_{{i...}}^{{\left( 5 \right) + }} - m_{{i...}}^{{\left( 5 \right)}}} \right), \\ \end{gathered} $(3.45)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{T}_{{**}}}{{\varpi }_{*}} + {{R}_{r}}{{T}_{r}}{{\psi }_{{ijk}}} + m_{{ijk}}^{{r\left( 5 \right)}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{{**}}}{{\varpi }_{*}} + {{R}_{r}}{{T}_{r}}{{\psi }_{{ijk}}} + m_{{ijk}}^{{r\left( 5 \right)}}} \right) + \\ + \;\left( {{{T}_{{ * \alpha }}}{{\varpi }_{*}} + {{T}_{{**}}}{{\varpi }_{\alpha }} + {{R}_{r}}{{T}_{r}}{{\psi }_{{ * * \alpha }}} + m_{{ * * \alpha }}^{{r\left( 5 \right)}}} \right)\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} - \frac{1}{\rho }\left( {{{R}_{r}}{{T}_{r}}{{T}_{{**}}} + m_{{**}}^{{r\left( 4 \right)}}} \right)\frac{{\partial \rho T_{{*\alpha }}^{{}}}}{{\partial {{x}_{\alpha }}}} + \\ + \;\frac{1}{\rho }\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {\rho \left( {{{R}_{r}}{{T}_{r}}\left( {{{T}_{{**}}}{{T}_{{ * \alpha }}} + m_{{ilk\alpha }}^{{\left( 4 \right)}}} \right) + {{T}_{{**}}}m_{{ * \alpha }}^{{r\left( 4 \right)}} + {{T}_{{ * \alpha }}}m_{{**}}^{{r\left( 4 \right)}} + {{\psi }_{{ * * \alpha }}}{{\varpi }_{*}} + {{\psi }_{{ijk}}}{{\varpi }_{\alpha }} + m_{{ijk\alpha }}^{{r\left( 6 \right)}}} \right)} \right) = \\ = \;\frac{1}{\tau }\left( {T_{{ * * }}^{ + }\varpi _{ * }^{ + } - T_{{ * * }}^{{}}\varpi _{ * }^{{}} + {{R}_{r}}\left( {T_{r}^{ + }\psi _{{ijk}}^{ + } - T_{r}^{{}}\psi _{{ijk}}^{{}}} \right) + m_{{ijk}}^{{r\left( 5 \right) + }} - m_{{ijk}}^{{r\left( 5 \right)}}} \right). \\ \end{gathered} $Комбинации моментных уравнений ${{T}_{r}}$ (3.33),${{T}_{{ij}}}$ (3.34), ${{\psi }_{{ijk}}}$ (3.35) и ${{\varpi }_{i}}$ (3.36) дают
(3.46)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{T}_{{ * * }}}{{\psi }_{{ * * * }}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{{ * * }}}{{\psi }_{{ * * * }}}} \right) + \left( {{{T}_{{ * \alpha }}}{{\psi }_{{ * * * }}} + {{T}_{{ * * }}}{{\psi }_{{ * * \alpha }}}} \right)\frac{{\partial {{u}_{ * }}}}{{\partial {{x}_{\alpha }}}} + \frac{{{{\psi }_{{ * * * }}}}}{\rho }\frac{{\partial \rho {{\psi }_{{ * * \alpha }}}}}{{\partial {{x}_{\alpha }}}} + \\ + \;{{T}_{{ * * }}}{{T}_{{ * \alpha }}}\frac{{\partial {{T}_{{ * * }}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{\rho }{{T}_{{ * * }}}\frac{{\partial \rho m_{{ * * * \alpha }}^{{\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}} = \frac{1}{\tau }\left( {T_{{ * * }}^{ + }{{\psi }_{{ * * * }}} + T_{{ * * }}^{{}}\psi _{{ * * * }}^{ + } - 2{{T}_{{ * * }}}{{\psi }_{{ * * * }}}} \right), \\ \end{gathered} $(3.47)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{T}_{{ * * }}}{{\varpi }_{ * }} + {{R}_{r}}{{T}_{r}}{{\psi }_{{ijk}}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{{ * * }}}{{\varpi }_{ * }} + {{R}_{r}}{{T}_{r}}{{\psi }_{{ijk}}}} \right) + \left( {{{T}_{{ * \alpha }}}{{\varpi }_{{ * * }}} + {{T}_{{ * * }}}{{\varpi }_{\alpha }} + {{R}_{r}}{{T}_{r}}{{\psi }_{{ * \alpha }}}} \right)\frac{{\partial {{u}_{ * }}}}{{\partial {{x}_{\alpha }}}} + \\ + \;{{R}_{r}}{{T}_{{ * * }}}{{T}_{{ * \alpha }}}\frac{{\partial {{T}_{r}}}}{{\partial {{x}_{\alpha }}}} + {{R}_{r}}{{T}_{r}}{{T}_{{ * \alpha }}}\frac{{\partial {{T}_{{ * * }}}}}{{\partial {{x}_{\alpha }}}} + \frac{{{{\varpi }_{ * }}}}{\rho }\frac{{\partial \rho {{\psi }_{{ * * \alpha }}}}}{{\partial {{x}_{\alpha }}}} + \frac{{{{\psi }_{{ijk}}}}}{\rho }\frac{{\partial \rho {{\varpi }_{\alpha }}}}{{\partial {{x}_{\alpha }}}} + \frac{{{{T}_{{ * * }}}}}{\rho }\frac{{\partial \rho m_{{ * \alpha }}^{{r\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}} + {{R}_{r}}\frac{{{{T}_{r}}}}{\rho }\frac{{\partial \rho m_{{ijk\alpha }}^{{\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}} = \\ = \;\frac{1}{\tau }\left( {T_{{ * * }}^{ + }\varpi _{ * }^{{}} + T_{{ * * }}^{{}}\varpi _{ * }^{ + } - 2T_{{ * * }}^{{}}\varpi _{ * }^{{}} + {{R}_{r}}\left( {T_{r}^{{}}\psi _{{ijk}}^{ + } + T_{r}^{ + }\psi _{{ijk}}^{{}} - 2T_{r}^{{}}\psi _{{ijk}}^{{}}} \right)} \right). \\ \end{gathered} $Вычтем (3.46) и (3.47) из (3.44) и (3.45) соответственно. В результате получим моментные уравнения пятого порядка, выраженные в виде корректирующих членов:
(3.48)
$\begin{gathered} \frac{{\partial m_{{i...}}^{{\left( 5 \right)}}}}{{\partial t}} + {{u}_{\alpha }}\frac{{\partial m_{{i...}}^{{\left( 5 \right)}}}}{{\partial {{x}_{\alpha }}}} + m_{{ * ...\alpha }}^{{\left( 5 \right)}}\frac{{\partial {{u}_{ * }}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{*\alpha }}}\frac{{\partial m_{{ * * * м}}^{{\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}} + m_{{ * * * \alpha }}^{{\left( 4 \right)}}\frac{{\partial {{T}_{{ * * }}}}}{{\partial {{x}_{\alpha }}}} + \\ + \;{{\psi }_{{ * * \alpha }}}\frac{{\partial {{\psi }_{{ * * * }}}}}{{\partial {{x}_{\alpha }}}} + \left\{ {\frac{1}{\rho }\frac{{\partial \rho m_{{i...\alpha }}^{{\left( 6 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right\} = - \frac{{m_{{i...}}^{{\left( 5 \right)}}}}{{{{\tau }_{5}}}} + \tau r_{{ * * }}^{{\left( 2 \right)}}r_{{ * * * }}^{{\left( 3 \right)}}, \\ \end{gathered} $(3.49)
$\begin{gathered} \frac{{\partial m_{{ijk}}^{{{\text{r}}\left( 5 \right)}}}}{{\partial t}} + {{u}_{\alpha }}\frac{{\partial m_{{ijk}}^{{r\left( 5 \right)}}}}{{\partial {{x}_{\alpha }}}} + m_{{ * * \alpha }}^{{r\left( 5 \right)}}\frac{{\partial {{u}_{ * }}}}{{\partial {{x}_{\alpha }}}} + m_{{ijk\alpha }}^{{\left( 4 \right)}}\frac{{\partial {{R}_{r}}{{T}_{r}}}}{{\partial {{x}_{\alpha }}}} + {{\psi }_{{ * * \alpha }}}\frac{{\partial {{\varpi }_{*}}}}{{\partial {{x}_{\alpha }}}} + {{\varpi }_{\alpha }}\frac{{\partial {{\psi }_{{ijk}}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{*\alpha }}}\frac{{\partial m_{{ * * }}^{{r\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}} + \\ + \;m_{{ * \alpha }}^{{r\left( 4 \right)}}\frac{{\partial {{T}_{{ * * }}}}}{{\partial {{x}_{\alpha }}}} + \left\{ {\frac{1}{\rho }\frac{{\partial \rho m_{{ijk\alpha }}^{{{\text{r}}\left( 6 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right\} = - \frac{{m_{{ijk}}^{{r\left( 5 \right)}}}}{{\tau _{5}^{r}}} + \tau r_{{ijk}}^{{\left( 3 \right)}}{{r}^{{r\left( 2 \right)}}} + \tau r_{{ * * }}^{{\left( 2 \right)}}r_{ * }^{{r\left( 3 \right)}}. \\ \end{gathered} $Система S4, дополненная зависимостями (3.48) и (3.49), образует систему моментных уравнений пятого порядка S5.
Для дальнейшего расширения системы моментных уравнений подставим в общее уравнение (3.37) уравнения шестых и седьмых моментов (3.15), (3.16) и (3.19), (3.20):
(3.50)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{T}_{{**}}}{{T}_{{**}}}{{T}_{{**}}} + {{\psi }_{{***}}}{{\psi }_{{***}}} + {{T}_{{**}}}m_{{****}}^{{\left( 4 \right)}} + m_{{i...}}^{{\left( 6 \right)}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{{**}}}{{T}_{{**}}}{{T}_{{**}}} + {{\psi }_{{***}}}{{\psi }_{{***}}} + {{T}_{{**}}}m_{{****}}^{{\left( 4 \right)}} + m_{{i...}}^{{\left( 6 \right)}}} \right) + \\ + \;\left( {{{T}_{{**}}}{{T}_{{**}}}{{T}_{{*\alpha }}} + {{\psi }_{{***}}}{{\psi }_{{**\alpha }}} + {{T}_{{*\alpha }}}m_{{****}}^{{\left( 4 \right)}} + {{T}_{{**}}}m_{{***\alpha }}^{{\left( 4 \right)}} + m_{{i...\alpha }}^{{\left( 6 \right)}}} \right)\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} - \frac{1}{\rho }\left( {{{T}_{{**}}}{{\psi }_{{***}}} + m_{{*****}}^{{\left( 5 \right)}}} \right)\frac{{\partial \rho T_{{ * \alpha }}^{{}}}}{{\partial {{x}_{\alpha }}}} + \\ + \;\frac{1}{\rho }\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {\rho \left( {{{T}_{{**}}}{{T}_{{*\alpha }}}{{\psi }_{{***}}} + {{T}_{{**}}}{{T}_{{**}}}{{\psi }_{{**\alpha }}} + {{\psi }_{{**\alpha }}}m_{{****}}^{{\left( 4 \right)}} + {{\psi }_{{***}}}m_{{***\alpha }}^{{\left( 4 \right)}} + {{T}_{{*\alpha }}}m_{{*****}}^{{\left( 5 \right)}} + {{T}_{{**}}}m_{{****\alpha }}^{{\left( 5 \right)}} + m_{{i..\alpha }}^{{\left( 7 \right)}}} \right)} \right) = \\ = \;\frac{1}{\tau }\left( {T_{{**}}^{ + }T_{{**}}^{ + }T_{{**}}^{ + } + \psi _{{***}}^{ + }{{\psi }_{{***}}} + T_{{**}}^{ + }m_{{****}}^{{ + \left( 4 \right)}} - {{T}_{{**}}}{{T}_{{**}}}{{T}_{{**}}} - {{\psi }_{{***}}}{{\psi }_{{***}}} - {{T}_{{**}}}m_{{****}}^{{\left( 4 \right)}} + m_{{ijk...}}^{{ + \left( 6 \right)}} - m_{{ijk...}}^{{\left( 6 \right)}}} \right); \\ \end{gathered} $(3.51)
$\begin{gathered} + \;\left( {{{R}_{r}}{{T}_{r}}{{T}_{{**}}}{{T}_{{*\alpha }}} + {{\psi }_{{**\alpha }}}{{\varpi }_{*}} + {{\psi }_{{***}}}{{\varpi }_{\alpha }} + {{R}_{r}}{{T}_{r}}m_{{***\alpha }}^{{\left( 4 \right)}} + {{T}_{{*\alpha }}}m_{{**}}^{{r\left( 4 \right)}} + {{T}_{{**}}}m_{{*\alpha }}^{{r\left( 4 \right)}} + m_{{**\alpha }}^{{r\left( 6 \right)}}} \right)\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} - \\ - \;\frac{1}{\rho }\left( {{{R}_{r}}{{T}_{r}}{{\psi }_{{***}}} + {{T}_{{**}}}{{\varpi }_{*}} + m_{{***}}^{{r\left( 5 \right)}}} \right)\frac{{\partial \rho {\text{T}}_{{*\alpha }}^{{}}}}{{\partial {{x}_{\alpha }}}} + \\ \end{gathered} $Сумма комбинаций моментных уравнений ${{T}_{{ij}}}$ (3.34), ${{\psi }_{{ijk}}}$ (3.35), и $m_{{ijkl}}^{{\left( 4 \right)}}$ (3.42):
(3.52)
$\begin{gathered} \;\quad \frac{\partial }{{\partial t}}\left( {{{T}_{{**}}}{{T}_{{**}}}{{T}_{{**}}} + {{\psi }_{{***}}}{{\psi }_{{***}}} + {{T}_{{**}}}m_{{****}}^{{\left( 4 \right)}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{{**}}}{{T}_{{**}}}{{T}_{{**}}} + {{\psi }_{{***}}}{{\psi }_{{***}}} + {{T}_{{**}}}m_{{****}}^{{\left( 4 \right)}}} \right) + \quad \quad \sum\limits_{}^{} {} \\ + \;\left( {{{T}_{{**}}}{{T}_{{**}}}{{T}_{{*\alpha }}} + {{\psi }_{{***}}}{{\psi }_{{**\alpha }}} + {{T}_{{*\alpha }}}m_{{****}}^{{\left( 4 \right)}} + {{T}_{{**}}}m_{{***\alpha }}^{{\left( 4 \right)}}} \right)\frac{{\partial {{u}_{ * }}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{*\alpha }}}{{T}_{{**}}}\frac{{\partial {{\psi }_{{***}}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{*\alpha }}}{{\psi }_{{***}}}\frac{{\partial {{T}_{{**}}}}}{{\partial {{x}_{\alpha }}}} + \\ + \;{{T}_{{**}}}{{\psi }_{{**\alpha }}}\frac{{\partial {{T}_{{**}}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{\rho }\left( {{{T}_{{**}}}{{T}_{{**}}}\frac{{\partial \rho {{\psi }_{{**\alpha }}}}}{{\partial {{x}_{\alpha }}}} + m_{{****}}^{{\left( 4 \right)}}\frac{{\partial \rho {{\psi }_{{**\alpha }}}}}{{\partial {{x}_{\alpha }}}} + {{\psi }_{{***}}}\frac{{\partial \rho m_{{***\alpha }}^{{\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{**}}}\frac{{\partial \rho m_{{****\alpha }}^{{\left( 5 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right) = \\ = \;\frac{1}{\tau }\left( {T_{{**}}^{{}}T_{{**}}^{{}}T_{{**}}^{ + } - 2{{T}_{{**}}}{{T}_{{**}}}{{T}_{{**}}} + {{\psi }_{{***}}}\psi _{{***}}^{ + } - 2{{\psi }_{{***}}}{{\psi }_{{***}}} + T_{{**}}^{{}}m_{{****}}^{{ + \left( 4 \right)}} + T_{{**}}^{ + }m_{{****}}^{{\left( 4 \right)}} - 2{{T}_{{**}}}m_{{****}}^{{\left( 4 \right)}}} \right). \\ \end{gathered} $Комбинации моментных уравнений ${{T}_{r}}$ (3.33), ${{T}_{{ij}}}$ (3.34), ${{\psi }_{{ijk}}}$ (3.35), ${{\varpi }_{i}}$ (3.36), $m_{{ijkl}}^{{\left( 4 \right)}}$ (3.42), $m_{{ij}}^{{r\left( 4 \right)}}$ (3.43), соответствующие (3.51), представим раздельно:
(3.53a)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{T}_{r}}{{T}_{{**}}}{{T}_{{**}}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{r}}{{T}_{{**}}}{{T}_{{**}}}} \right) + {{T}_{r}}{{T}_{{**}}}{{T}_{{*\alpha }}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{\rho }\left( {{{T}_{r}}{{T}_{{**}}}\frac{{\partial \rho {{\psi }_{{**\alpha }}}}}{{\partial {{x}_{\alpha }}}} + \frac{{{{T}_{{**}}}{{T}_{{**}}}}}{{{{R}_{r}}}}\frac{{\partial \rho {{\varpi }_{\alpha }}}}{{\partial {{x}_{\alpha }}}}} \right) = \\ = \;\frac{1}{\tau }\left( {T_{r}^{ + }T_{{**}}^{{}}T_{{**}}^{{}} + T_{r}^{{}}T_{{**}}^{{}}T_{{**}}^{ + } - 2{{T}_{r}}{{T}_{{**}}}{{T}_{{**}}}} \right), \\ \end{gathered} $(3.53б)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{\psi }_{{***}}}{{\varpi }_{*}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{\psi }_{{***}}}{{\varpi }_{*}}} \right) + \left( {{{\psi }_{{**\alpha }}}{{\varpi }_{*}} + {{\psi }_{{***}}}{{\varpi }_{\alpha }}} \right)\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{*\alpha }}}{{\varpi }_{*}}\frac{{\partial {{T}_{{**}}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{*\alpha }}}{{\psi }_{{***}}}\frac{{\partial {{R}_{r}}{{T}_{r}}}}{{\partial {{x}_{\alpha }}}} + \\ + \;\frac{1}{\rho }{{\varpi }_{*}}\frac{{\partial \rho m_{{**\alpha }}^{{\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}} = \frac{1}{\tau }\left( {\psi _{{***}}^{ + }\varpi _{*}^{{}} + \psi _{{***}}^{{}}\varpi _{*}^{ + } - 2{{\psi }_{{***}}}{{\varpi }_{*}}} \right), \\ \end{gathered} $(3.53в)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{T}_{r}}m_{{ijkl}}^{{\left( 4 \right)}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{r}}m_{{ijkl}}^{{\left( 4 \right)}}} \right) + {{T}_{r}}m_{{ * * * \alpha }}^{{\left( 4 \right)}}\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{r}}\left( {{{T}_{{ * \alpha }}}\frac{{\partial {{\psi }_{{ * * * }}}}}{{\partial {{x}_{\alpha }}}} + {{\psi }_{{ * * \alpha }}}\frac{{\partial {{T}_{{ * * }}}}}{{\partial {{x}_{\alpha }}}}} \right) + \\ + \;\frac{1}{\rho }\left( {\frac{{m_{{ijkl}}^{{\left( 4 \right)}}}}{{{{R}_{r}}}}\frac{{\partial \rho {{\varpi }_{\alpha }}}}{{\partial {{x}_{\alpha }}}} + {{T}_{r}}\frac{{\partial \rho m_{{ijkl\alpha }}^{{\left( 5 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right) = \frac{1}{\tau }\left( {T_{r}^{ + }m_{{ijkl}}^{{\left( 4 \right)}} + T_{r}^{{}}m_{{ijkl}}^{{\left( 4 \right) + }} - 2{{T}_{r}}m_{{ijkl}}^{{\left( 4 \right)}}} \right), \\ \end{gathered} $(3.53г)
$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{T}_{{ * * }}}m_{{ * * }}^{{r\left( 4 \right)}}} \right) + {{u}_{\alpha }}\frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{T}_{{ * * }}}m_{{ * * }}^{{r\left( 4 \right)}}} \right) + \left( {{{T}_{{ * * \alpha }}}m_{{ * * }}^{{r\left( 4 \right)}} + {{T}_{{ * * }}}m_{{ * \alpha }}^{{r\left( 4 \right)}}} \right)\frac{{\partial {{u}_{*}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{ * * }}}{{\psi }_{{ * * \alpha }}}\frac{{\partial {{R}_{r}}{{T}_{r}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{ * * }}}{{T}_{{ * \alpha }}}\frac{{\partial {{\varpi }_{ * }}}}{{\partial {{x}_{\alpha }}}} + \\ + \;{{T}_{{ * * }}}{{\varpi }_{\alpha }}\frac{{\partial {{T}_{{ * * }}}}}{{\partial {{x}_{\alpha }}}} + \frac{1}{\rho }\left( {m_{{ * * }}^{{r\left( 4 \right)}}\frac{{\partial \rho {{\psi }_{{ * * \alpha }}}}}{{\partial {{x}_{\alpha }}}} + {{T}_{{ * * }}}\frac{{\partial \rho m_{{ * * \alpha }}^{{r\left( 5 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right) = \frac{1}{\tau }\left( {T_{{ * * }}^{ + }m_{{ * * }}^{{r\left( 4 \right)}} + T_{{ * * }}^{{}}m_{{ * * }}^{{r\left( 4 \right) + }} - 2{{T}_{{ * * }}}m_{{ * * }}^{{r\left( 4 \right)}}} \right). \\ \end{gathered} $Вычтем (3.52) и (3.53) из (3.50) и (3.51) соответственно. В результате получим моментные уравнения шестого порядка, выраженные в виде корректирующих членов
Система S5, дополненная двумя последними уравнениями, образует систему моментных уравнений шестого порядка S6.
4. АНАЛИЗ ЧИСЛЕННЫХ РЕШЕНИЙ СИСТЕМ МОМЕНТНЫХ УРАВНЕНИЙ
4.1. Тестовая задача и вспомогательные модели течения
Одним из основных дефектов систем моментных уравнений третьего и четвертого порядка является их коротковолновая неустойчивость, проявляющаяся в возникновении физически неадекватной области в задаче о профиле ударной волны. Для анализа систем моментных уравнений высших порядков естественно использовать именно эту задачу.
Задача о профиле плоской ударной волны формулируется следующим образом. Рассматривается движение газа вдоль декартовой оси 0X. На верхней границе вычислительной области выставляются условия невозмущенного потока, а на нижней – условия Ренкина–Гюгонио. На обеих границах газ находится в равновесии. Рассматривается начально-краевая задача с граничными условиями Дирихле.
Для решения систем моментных уравнений используется схема Лакса–Вендроффа (Lax–Wendroff scheme). Производные аппроксимируются асимметричным, смещенным вверх по потоку конечно-разностным шаблоном, построенным на четырех узлах расчетной сетки.
В качестве эталонной модели течения принималось МКУ [11]. Для одномерного течения имеем
(4.1)
$\frac{\partial }{{\partial t}}\left| {\begin{array}{*{20}{c}} {{{f}_{t}}} \\ {{{f}_{r}}} \end{array}} \right| + {{\xi }_{x}}\frac{\partial }{{\partial x}}\left| {\begin{array}{*{20}{c}} {{{f}_{t}}} \\ {{{f}_{r}}} \end{array}} \right| = \frac{p}{\mu }\left| {\begin{array}{*{20}{c}} {f_{t}^{ + } - {{f}_{t}}} \\ {f_{r}^{ + } - {{f}_{r}}} \end{array}} \right|,$Характерной особенностью модели (4.1) является соотношение времен релаксации: $\tau = {{\tau }_{p}} = {\mu \mathord{\left/ {\vphantom {\mu p}} \right. \kern-0em} p}$. Это соотношение было принято и при проведении тестовых расчетов моментных систем.
При расчете профилей ударных волн в аргоне и азоте свободные параметры s и Z МКУ, как и в [11], “настраивалась” по экспериментальным данным [12]–[14]. Параметр s в коэффициенте вязкости $\mu = \mu \left( {T_{t}^{s}} \right)$ принимался s = 0.78 для аргона и s = 0.75 для азота. Параметр $Z = 1.3\left( {1 + 0.75{{{{T}_{r}}} \mathord{\left/ {\vphantom {{{{T}_{r}}} {{{T}_{t}}}}} \right. \kern-0em} {{{T}_{t}}}}} \right)$. Эти значения параметров s и Z принимались для всех моделей течения.
Для численной реализации МКУ использовались решения 4-диагональных матриц с нестационарным членом. Разностные шаблоны и алгоритм решения подробно описаны в [11].
Помимо МКУ рассматривалась модель НСФ в интерпретации [2]:
(4.2)
$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {{u}_{x}}}}{{\partial x}} = 0, \\ \frac{{\partial {{u}_{x}}}}{{\partial t}} + {{u}_{x}}\frac{{\partial {{u}_{i}}}}{{\partial x}} + \frac{1}{\rho }\frac{{\partial {{P}_{{xx}}}}}{{\partial x}} = 0, \\ \frac{{\partial T}}{{\partial t}} + {{u}_{x}}\frac{{\partial T}}{{\partial x}} + \left( {\gamma - 1} \right)\frac{{{{P}_{{xx}}}}}{{\rho R}}\frac{{\partial {{u}_{x}}}}{{\partial x}} + \frac{1}{{{{c}_{v}}\rho }}\frac{{\partial {{q}_{x}}}}{{\partial x}} = 0. \\ \end{gathered} $Для решения (4.2) использовался алгоритм Томаса (Thomas algorithm), реализуемый на 3-диагональной матрице.
4.2. Результаты численных тестов
Расчеты проводились для одно- и двухатомных газов. Физически неадекватные участки на профиле ударной волны возникали примерно при одинаковых числах Маха как для одноатомных, так и для двухатомных газов. Ниже приводятся графики только для двухатомных газов, полученные при $\tau _{N}^{r} = {{\tau }_{N}}$.
Во всех графических материалах физические величины представлены в безразмерном виде. Плотность отнесена к ее значению в невозмущенном потоке ρ∞, групповая скорость ux – к $\sqrt {R{{T}_{\infty }}} $. Остальные моменты функции распределения порядка N отнесены к ${{\left( {R{{T}_{\infty }}} \right)}^{{{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}}}}$. В качестве единицы геометрического размера принималась длина свободного пробега в невозмущенном потоке: ${{\lambda }_{\infty }} = \frac{{16{{\mu }_{\infty }}}}{{5{{\rho }_{\infty }}}}\sqrt {2\pi R{{T}_{\infty }}} $. На всех графиках ноль геометрической шкалы соответствует трансзвуковому течению $M = 1$.
На фиг. 1 приведены профили основных газодинамических параметров при ${{M}_{\infty }} = 1.7$.
Фиг. 1.
Профили плотности, скорости и температуры, ${{M}_{\infty }} = 1.7$. Сплошные линии – модель S3; штриховые линии – МКУ; штрихпунктирные линии – НСФ.

Профили трех рассмотренных моделей течения достаточно близки. Обращает на себя внимание, что модель НСФ лучше согласуeтся с кинетической моделью, чем модель S3. Отметим, что индивидуальная настройка свободных параметров s и Z для моделей S3 и НСФ позволяет получить несколько лучшее соответствие с моделью МКУ, но такие настройки сами по себе не являются предметом настоящего исследования.
Повышение интенсивности ударной волны до ${{M}_{\infty }} = 2$ приводит к появлению на профилях модели S3 физически неадекватных участков, см. фиг. 2. Вместе с тем наблюдается хорошее согласование профилей НСФ и МКУ.
Фиг. 2.
Профили плотности, скорости и температуры, ${{M}_{\infty }} = 2$. Сплошные линии – модель S3; штриховые линии – МКУ; штрихпунктирные линии – НСФ.

Система S3 замкнута уравнениями моментов третьего порядка (3.35) и (3.36). Эти уравнения не содержат членов в фигурных скобках. Для момента третьего порядка ${{\psi }_{{xxx}}}$ опущенный член имеет вид
На фиг. 3 показан профиль момента ${{\psi }_{{xxx}}}$, вычисленного различными способами. Кривые 1 и 2 соответствуют кинетическому решению: 1 – решение (4.1), 2 – результат вычисления ${{\psi }_{{xxx}}}$ по следующему уравнению, полученному преобразованием стационарного одномерного варианта (3.35):
(4.4)
${{\psi }_{{xxx}}} = - \frac{3}{2}{{\tau }_{p}}\left( {{{u}_{x}}\frac{{\partial {{\psi }_{{xxx}}}}}{{\partial x}} + 3{{\psi }_{{xxx}}}\frac{{\partial {{u}_{x}}}}{{\partial x}} + 3{{T}_{{xx}}}\frac{{\partial {{T}_{{xx}}}}}{{\partial x}} + \frac{1}{\rho }\frac{{\partial \rho m_{{xxxx}}^{{\left( 4 \right)}}}}{{\partial {{x}_{\alpha }}}}} \right).$Фиг. 3.
Профиль момента ${{\psi }_{{xxx}}}$, ${{M}_{\infty }} = 2$. 1 – пунктир – МКУ; 2 – штрихи – уравнение (4.4); 3 – модель S3; 4 – выражение (4.3).

Кривая 3 на фиг. 3 – решение модели S3, т.е. системы уравнений (3.2), (3.32), …, (3.36).
Почти полное совпадение кривых 1 и 2 предсказуемо, и следует из того, что моментное уравнение (3.35) получено формальным интегрированием кинетического уравнения (4.1). Небольшое расхождение графиков обусловлено разными конечно-разностными аппроксимациями производных, используемыми в (4.1) и (4.4). Кривая 2 в данном случае демонстрирует согласование численного решения кинетического уравнения и соответствующего ему моментного уравнения.
Профиль модели S3 существенно отличается от кинетического решения, причем положение “изломов” на профиле ${{\psi }_{{xxx}}}$ соответствуют положению аналогичных дефектов профилей ρ, ux, T на фиг. 2. Кривая 4 на фиг. 3 изображает профиль члена (4.3), отсутствующего в модели S3. Профиль рассчитан по данным кинетического решения. По своей величине член (4.3) не уступает моменту ${{\psi }_{{xxx}}}$ модели S3. Этот факт приводит к выводу о том, что аппроксимация четвертого момента (3.13), и, по-видимому, (3.17), уже при ${{M}_{\infty }} = 2$ недостаточно точна.
Рассмотрим модели более высоких порядков. Предварительно отметим, что любая из систем моментных уравнений порядка $N > 3$ содержит дополнительный свободный параметр ${{\tau }_{N}}$ (и $\tau _{N}^{r}$ для многоатомных газов). Этот параметр соответствует времени релаксации $m_{{i...}}^{{\left( N \right)}}$, т.е. разности между истинным значением момента и его аппроксимацией. Оценка времени релаксации такой математической абстракции как $m_{{i...}}^{{\left( N \right)}}$ на основе эмпирических данных, очевидно, невозможна. В дальнейшем будем подбирать значения ${{\tau }_{N}}$ (и $\tau _{N}^{r}$) из соображений наилучшего совпадения с профилями МКУ.
На фиг. 4 представлены профили модели S4 для двух значений ${{\tau }_{4}}$ при ${{M}_{\infty }} = 2$.
Фиг. 4.
Профили плотности и скорости, ${{M}_{\infty }} = 2$. Сплошные линии – модель S4: 1 и 3 – ${{\tau }_{4}} = \tau $, 2 и 4 – ${{\tau }_{4}} = 0.35\tau $. Штриховые линии – МКУ; штрихпунктирные линии – НСФ.
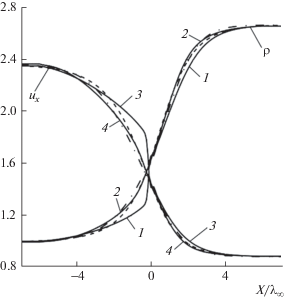
Графики показывают, что при ${{\tau }_{4}} = 0.35\tau $ модель S4 позволяет получать гладкие профили, почти совпадающие с профилями модели НСФ. Однако увеличение числа Маха приводит к появлению новых дефектов профиля, не устраняемых уменьшением ${{\tau }_{4}}$. Для ${{M}_{\infty }} = 3$ данные представлены на фиг. 5.
Фиг. 5.
Профили плотности и скорости, ${{M}_{\infty }} = 3$. Сплошные линии – модель S4, ${{\tau }_{4}} = 0.35\tau $. Штриховые линии – МКУ; штрихпунктирные линии – НСФ.

Модель S5, графики которой показаны на фиг. 6, только отчасти улучшает решение.
Фиг. 6.
Профили плотности и скорости, ${{M}_{\infty }} = 3$. Сплошные линии – модель S5, ${{\tau }_{4}} = 0.35\tau $, ${{\tau }_{5}} = 0.25\tau $. Штриховые линии – МКУ; штрихпунктирные линии – НСФ.

Модель S6 не позволяет улучшить решение модели S5 при этом числе Маха, см. фиг. 7.
Фиг. 7.
Профили плотности и скорости, ${{M}_{\infty }} = 3$. Сплошные линии – модель S6, ${{\tau }_{4}} = 0.35\,\tau $, ${{\tau }_{5}} = 0.1\,\tau $, ${{\tau }_{6}} = 0.005\,\tau $. Штриховые линии – МКУ; штрихпунктирные линии – НСФ.

Возможным объяснением неспособности рассмотренных систем моментных уравнений физически адекватно описывать высоко неравновесные течения могут служить большие погрешности аппроксимаций замыкающих моментов (3.13), …, (3.20). На фиг. 8 на примере модели S4 показаны профили $m_{{x...x}}^{{\left( 4 \right)}}$ и выражения
Это выражение, отсутствующее в моментном уравнении (3.42) модели S4, определено погрешностью аппроксимации замыкающего момента $M_{{x...x}}^{{\left( 5 \right)}}$. Оба профиля взяты из “точного” кинетического решения.Фиг. 8.
Модель S4. ${{M}_{\infty }} = 3$. Сплошная линия – $m_{{x...x}}^{{\left( 4 \right)}}$, штриховая линия – (4.5).

На фиг. 9 и фиг. 10 для моделей S5 и S6 профили корректирующих членов $m_{{x...x}}^{{\left( 5 \right)}}$ и $m_{{x...x}}^{{\left( 6 \right)}}$ сопоставлены с выражениями
Здесь, как и выше, профили взяты из кинетического решения.Фиг. 9.
Модель S5. ${{M}_{\infty }} = 3$. Сплошная линия – $m_{{x...x}}^{{\left( 5 \right)}}$, штриховая линия – (4.6).

Фиг. 10.
Модель S6. ${{M}_{\infty }} = 3$. Сплошная линия – $m_{{x...x}}^{{\left( 6 \right)}}$, штриховая линия – (4.7).

Из трех последних фигур следует, что погрешность, вносимая в замыкающее систему уравнение, превышает величину определяемого этим уравнением параметра. По мере повышения порядка уравнения преобладание погрешности над определяемым параметром возрастает. Видимо, дальнейшее повышение порядка системы моментных уравнений не приведет к существенному улучшению решения.
5. ЗАКЛЮЧЕНИЕ
Результаты проведенных тестовых расчетов позволяют сделать вывод о том, что повышение порядка системы моментных уравнений не позволяет получать физически адекватные решения в области сильнонеравновесных течений. Причиной этого является увеличение вклада замыкающего момента в решение системы и, как следствие, увеличение влияния погрешности аппроксимации этого момента. Разумеется, что погрешность аппроксимации определена методом замыкания системы.
Хотя предложенный метод построения и замыкания системы моментных уравнений носит достаточно общий характер, он не исчерпывает всех методов. Возможно, методы, лучше учитывающие реальные свойства неравновесных процессов и дающие лучшие аппроксимации замыкающих моментов, позволят получать решения, близкие к кинетическим. Специально отметим два основных недостатка предложенного метода.
– Предложенный метод замыкания системы моментных уравнений основан на чисто формальных свойствах моментов функции распределения молекул по скоростям.
– Времена релаксации напряжений и тепловых потоков рассмотрены в гидродинамическом приближении. Вопрос о применимости такого приближения к сильно-неравновесным течениям остается открытым.
Анализ систем моментных уравнений проводился на основе численных решений. Как известно, применяемый метод численного решения может существенно влиять на результат. В настоящей работе для решения систем моментных уравнений использовалась условно устойчивая численная схема. Не применялись схемы, использующие искусственное сглаживание решений, например, схемы с искусственной вязкостью. В настоящем исследовании нас интересовали преимущественно “естественные” свойства систем моментных уравнений. Применение упомянутых схем позволяет получать гладкие решения, однако соответствие этих решений реальным физическим процессам будет по меньшей мере неочевидным.
Проведенные численные тесты, а также ряд известных работ, например [15], [16], показывают также, что модель НСФ не хуже, чем моментные системы высоких порядков, согласуется с кинетическим решением. Сама модель НСФ представляет собой неполную систему моментных уравнений второго порядка, так как распространена не выше свертки моментных уравнений второго порядка. Замыкающие систему НСФ зависимости для неравновесных напряжений и тепловых потоков имеют убедительное теоретическое и эмпирическое обоснование в области слабо неравновесных течений.
Как отмечалось выше, сильно неравновесные области, в которых модель НСФ дает большие погрешности, обладают, как правило, небольшой протяженностью. Их характерный размер составляет несколько десятков длин свободного пробега молекулы. Современные вычислительные средства позволяют решать модельные кинетические уравнения в столь узких областях. В этом плане представляют интерес, и не только теоретический, комбинации кинетического и гидродинамического решений, см., например [17], [18] и приведенный в этих работах список публикаций.
Автор выражает благодарность Алене Васильевне Тихоновец за всестороннюю помощь в написании и оформлении текста статьи.
Список литературы
Коган М.Н. Динамика разреженного газа. М.: Наука, 1967. 440 с.
Никитченко Ю.А. О целесообразности учета коэффициента объемной вязкости в задачах газовой динамики // Изв. РАН, МЖГ. 2018. № 2. С. 128–138.
Grad H. On the kinetic theory of rarefied gases // Communication on Pure and Applied Math. 1949. V. 2. № 4. P. 331–407.
Grad H. Principles of Kinetic Theory of Gases. Handbuch der Physik / Ed. S. Flügge, Berlin: Springer, 1958. V. 12.
Grad H. The profile of a steady plane shock wave // Communication on Pure and Applied Math. 1952. V. 5. № 3. P. 257–300.
Struchtrup H., Torrilhon M. Regularization of grad’s 13moment equations: Derivation and linear analysis // Physics of Fluids. 2003. V. 15. P. 2668–2680.
Timokhin M.Yu., Struchtrup H., Kokhanchik A.A., Bondar Ye.A. Different variants of R13 moment equations applied to the shock-wave structure // Physics of Fluids, American Institute of Physics. V. 29. № 4. P. 049901.
Никитченко Ю.А. Снижение коротковолновой неустойчивости системы моментных уравнений за счет ее расширения // Уч. зап. ЦАГИ. 2015. Т. 46. № 1. С. 72–84.
Lordi J.A., Mates R.E. Rotational relaxation in nonpolar diatomic gases // Physics of Fluids. 1970. V. 13. № 2. P. 291–308.
Bird G.A. Molecular gas dynamics and the direct simulation of gas flows. Oxford: Clarendon Press, 1994.
Никитченко Ю.А. Модельное кинетическое уравнение многоатомных газов // Ж. вычисл. матем. и матем. физ. 2017. Т. 57. № 11. С. 1882–1894.
Holtz T., Muntz E.P. Molecular velocity distribution functions in an argon normal shock wave at Mach number 7 // Phys. Fluids. 1983. V. 26. № 9. P. 2425–2436.
Alsmeyer H. Density profiles in argon and nitrogen shock waves measured by the absorption of an electron beam // J. Fluid Mech. 1976. V. 74. Pt. 3. P. 497–513.
Robben F., Talbot L. Experimental study of the rotational distribution function of nitrogen in a shock wave // Phys. Fluids. 1966. V. 9. № 4. P. 653–662.
Elizarova T.G., Shirokov I.A., Montero S. Numerical simulation of shock-wave structure for argon and helium // Physics of Fluids. 2005. 17. 068101.
Elizarova T.G., Khokhlov A.A., Montero S. Numerical simulation of shock wave structure in nitrogen // Physics of fluids. 2007. V. 19. 068102.
Никитченко Ю.А., Попов С.А., Тихоновец А.В. Комбинированная кинетико-гидродинамическая модель течения многоатомного газа // Матем. моделирование. 2019. Т. 31. № 2. С. 18–32.
Никитченко Ю.А., Тихоновец А.В. Тестирование кинетико-гидродинамической модели на примере расчета обтекания поглощающей поверхности // Матем. моделирование. 2020. Т. 32. № 9. С. 103–119.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики


