1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 62, № 5, 2022

Журнал вычислительной математики и математической физики, 2022, T. 62, № 5, стр. 872-888

О моделировании цилиндрической медленной необыкновенной волны в холодной магнитоактивной плазме

А. А. Фролов 1, *, Е. В. Чижонков 2, **

1 Физический институт им. П.Н. Лебедева РАН
119991 Москва, Ленинский пр-т, 53, Россия

2 МГУ им. М.В. Ломоносова
119899 Москва, Ленинские горы, Россия

* E-mail: frolovaa@lebedev.ru
** E-mail: chizhonk@mech.math.msu.su

Поступила в редакцию 12.09.2021
После доработки 10.11.2021
Принята к публикации 14.01.2022

Полный текст (PDF)

Аннотация

Исследовано влияние внешнего магнитного поля на нерелятивистские цилиндрические плазменные колебания. Для инициализации медленной необыкновенной волны в магнитоактивной плазме предложен способ построения недостающих начальных условий на основе решения линейной задачи в виде рядов Фурье–Бесселя. С целью численного моделирования нелинейной волны построена схема метода конечных разностей второго порядка точности типа Мак-Кормака. Показано, что при учете внешнего магнитного поля ленгмюровские колебания трансформируются в медленную необыкновенную волну. При этом скорость волны увеличивается с ростом внешнего постоянного поля, что способствует выносу энергии из первоначальной области локализации колебаний. По этой причине известный эффект внеосевого опрокидывания наблюдается с запаздыванием по времени, а начиная с некоторого критического значения внешнего поля, перестает реализовываться совсем, т.е. формируется глобальное по времени гладкое решение. Библ. 22. Фиг. 12.

Ключевые слова: магнитоактивная плазма, плазменные колебания, медленная необыкновенная волна, ряды Фурье–Бесселя, численное моделирование, метод конечных разностей, эффект опрокидывания.

ВВЕДЕНИЕ

Полностью ионизованная плазма является сильно нелинейной средой, в которой даже относительно небольшие начальные коллективные смещения частиц могут приводить к колебаниям и волнам большой амплитуды [1]. Численному моделированию колебаний в холодной плазме, а также кильватерных волн, возбуждаемых коротким мощным лазерным импульсом, посвящена монография [2].

Сложность и разнообразие постановок задач резко возрастают, если рассматривать динамику магнитоактивной плазмы, т.е. плазмы, помещенной во внешнее магнитное поле. Даже в случае малых возмущений магнитоактивной плазмы, т.е. при рассмотрении только линейных волн, в классических учебниках и монографиях (см., например, [3], [4]) вводится их специальная классификация. В частности, в высокочастотной области спектра существуют три волны: обыкновенная, а также быстрая и медленная необыкновенная. Следут отметить, что внешнее магнитное поле порождает (индуцирует) магнитное поле в самой плазме, что требует соответствующего задания начальных условий для рассматриваемых дифференциальных уравнений. Эти условия в общем случае не могут быть произвольными. Например, в работе [5] показано, что при инициализации медленных необыкновенных волн (МНВ) тривиальные условия допустимы только в случае слабых внешних полей; в противном случае динамика волны может быть сильно искажена “неестественными” начальными условиями. По существу, такая ситуация приводит к постановке новой вспомогательной задачи о разумной постановке недостающих (по сравнению с инициализацией колебаний без внешнего магнитного поля) начальных условий. В настоящей работе такая задача сначала формулируется, а затем решается в терминах рядов Фурье–Бесселя [6].

Следует также обратить внимание, что даже в случае зависимости решения от одной пространственной переменной, т.е. при наличии аксиальной симметрии, дифференциальные уравнения модели холодной плазмы достаточно сложны и громоздки. По этой причине возможности аналитического и асимптотического подходов здесь сильно ограничены, а в качестве основного инструмента исследования выступает численное моделирование. В свою очередь, это требует применения надежных и эффективных алгоритмов расчета. В настоящей работе с этой целью построена модификация классической схемы Мак-Кормака второго порядка точности, анализ и тестирование которой в плоском случае приведены в [7]. Напомним, что для колебаний и волн в случае аксиальной симметрии в плазме без магнитного поля характерным является эффект внеосевого опрокидывания [8], наблюдаемый по истечении нескольких периодов, что накладывает дополнительные требования на качество численного алгоритма [2].

Наконец, отметим актуальность тематики, связанной с МНВ. Их изучению в последнее время уделяется повышенное внимание (см., например, [9], [10]). Это напрямую связано с интенсивными экспериментальными и теоретическими исследованиями взаимодействия мощных лазерных импульсов с плазмой, которое имеет множество практических приложений от ядерной физики до медицины.

Статья имеет следующую структуру. Сначала приведена постановка задачи в эйлеровых переменных, включая начальные и асимптотические граничные условия, необходимые для описания временной эволюции плазменных колебаний и волн, порождаемых мощным коротким лазерным импульсом. Этих условий недостаточно для однозначного определения решения, поэтому в следующем разделе рассматривается вспомогательная задача. На основании ее решения с помощью рядов Фурье–Бесселя можно описать линейную МНВ, дискретный аналог которых хорошо приспособлен для практических вычислений недостающих начальных условий. В следующем разделе приводится описание численного метода решения нелинейной системы уравнений в частных производных типа Мак-Кормака, имеющего на гладких решениях второй порядок точности относительно параметров дискретизации. Наконец, самый большой раздел посвящен численным экспериментам. В нем приводятся примеры построенных начальных данных, которые зависят от напряженности внешнего магнитного поля и инициализируют МНВ. Далее в терминах функции, описывающей энергию линейной волны, иллюстрируется ее динамика во времени во внешнем магнитном поле различной напряженности. Особое внимание уделяется расчетам нелинейной нерелятивистской МНВ и ее сравнению с линейным случаем. Представляет отдельный интерес влияние внешнего магнитного поля на эффект внеосевого опрокидывания волны. Показано, что при значении магнитного поля, превышающего критическое, решение носит глобально гладкий по времени и пространству характер. В заключениe систематизируются результаты проведенных исследований.

1. ОСНОВНЫЕ УРАВНЕНИЯ

Будем считать плазму холодной нерелятивистской электронной жидкостью, пренебрегая рекомбинационными эффектами и движением ионов. Тогда в векторной форме система описывающих ее гидродинамических уравнений совместно с уравнениями Максвелла будет иметь вид

(1)
$\begin{gathered} \frac{{\partial n}}{{\partial t}} + {\text{div}}(nV) = 0,\quad \frac{{\partial V}}{{\partial t}} + \left( {V \cdot \nabla } \right)V = \frac{e}{m}\left( {E + \frac{1}{c}\left[ {V \cdot B} \right]} \right), \\ \frac{1}{c}\frac{{\partial E}}{{\partial t}} = - \frac{{4\pi }}{c}enV + {\text{rot}}\;B,\quad \frac{1}{c}\frac{{\partial B}}{{\partial t}} = - {\text{rot}}\;E,\quad {\text{div}}\;B = 0, \\ \end{gathered} $
где e, m – заряд и масса электрона (здесь заряд электрона имеет отрицательный знак: $e < 0$), c – скорость света; n, V – плотность и скорость электронов; E, B – векторы электрического и магнитного полей.

Система уравнений (1) является одной из простейших моделей плазмы, которую часто называют уравнениями гидродинамики “холодной” плазмы; она хорошо известна и достаточно подробно описана в учебниках и монографиях (см., например, [3], [4], [11], [12]).

Получим из базовых уравнений рассматриваемой модели плазмы (1) систему, решения которой обладают аксиальной (цилиндрической) симметрией. Будем обозначать независимые переменные в цилиндрической системе координат обычным образом – $(r,\varphi ,z)$ и примем допущение, что плазма находится во внешнем магнитном поле ${{B}_{0}}$, которое направлено вдоль оси z и не зависит от времени и пространства.

С целью проведения численного моделирования одномерных цилиндрических плазменных колебаний и волн во внешнем поле ${{B}_{0}} \equiv {\text{const}}$ базовые уравнения (1) можно существенно упростить. Будем считать, что

– решение определяется только r- и φ-компонентами вектор-функций V, E, а также z-компонентой вектора магнитного поля B; при этом ${{B}_{z}} = {{B}_{0}} + {{B}_{p}}$, где ${{B}_{p}}$ – индуцированное магнитное поле в плазме;

– зависимость во всех указанных функциях и в электронной плотности n от переменных φ и z отсутствует, т.е. соответствующие частные производные равны нулю: $\partial {\text{/}}\partial \varphi = \partial {\text{/}}\partial z = 0$. Напомним, что ${{B}_{0}} \equiv {\text{const}}$.

Качественная структура искомого решения представлена на фиг. 1, где $B(r,t) \equiv {{B}_{p}}(r,t)$. В рассматриваемом случае из системы (1) следуют нетривиальные уравнения:

(2)
$\begin{gathered} \frac{{\partial n}}{{\partial t}} + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {rn{{V}_{r}}} \right) = 0,\quad \frac{{\partial {{V}_{r}}}}{{\partial t}} + {{v}_{r}}\frac{{\partial {{V}_{r}}}}{{\partial r}} - \frac{{V_{\varphi }^{2}}}{r} = \frac{e}{m}\left[ {{{E}_{r}} + \frac{1}{c}{{V}_{\varphi }}\left( {{{B}_{0}} + {{B}_{p}}} \right)} \right], \\ \frac{{\partial {{V}_{\varphi }}}}{{\partial t}} + {{V}_{r}}\frac{{\partial {{V}_{\varphi }}}}{{\partial r}} + \frac{{{{V}_{r}}{{V}_{\varphi }}}}{r} = \frac{e}{m}\left[ {{{E}_{\varphi }} - \frac{1}{c}{{V}_{r}}\left( {{{B}_{0}} + {{B}_{p}}} \right)} \right], \\ \frac{1}{c}\frac{{\partial {{B}_{p}}}}{{\partial t}} + \frac{1}{r}\frac{{\partial \left( {r{{E}_{\varphi }}} \right)}}{{\partial r}} = 0,\quad \frac{{\partial {{E}_{r}}}}{{\partial t}} = - 4\pi en{{V}_{r}},\quad \frac{1}{c}\frac{{\partial {{E}_{\varphi }}}}{{\partial t}} = - \frac{{4\pi e}}{c}n{{V}_{\varphi }} - \frac{{\partial {{B}_{p}}}}{{\partial r}}. \\ \end{gathered} $
Фиг. 1.

Искомые функции и их зависимость от координат.

Введем безразмерные величины

$\begin{gathered} \rho = {{k}_{p}}r,\quad \theta = {{\omega }_{p}}t,\quad \hat {N} = n{\text{/}}{{n}_{0}},\quad {{{\hat {V}}}_{r}} = \frac{{{{V}_{r}}}}{c},\quad {{{\hat {V}}}_{\varphi }} = \frac{{{{V}_{\varphi }}}}{c}, \\ {{{\hat {E}}}_{r}} = - \frac{{e{{E}_{r}}}}{{mc{{\omega }_{p}}}},\quad {{{\hat {E}}}_{\varphi }} = - \frac{{e{{E}_{\varphi }}}}{{mc{{\omega }_{p}}}},\quad \hat {B} = - \frac{{eB}}{{mc{{\omega }_{p}}}},\quad \hat {B} = {{{\hat {B}}}_{0}} + {{{\hat {B}}}_{p}}, \\ \end{gathered} $
где ${{\omega }_{p}} = {{\left( {4\pi {{e}^{2}}{{n}_{0}}{\text{/}}m} \right)}^{{1/2}}}$ – плазменная частота, ${{n}_{0}}$ – значение невозмущенной электронной плотности, ${{k}_{p}} = {{\omega }_{p}}{\text{/}}c$.

В новых переменных система (2) примет вид

(3)
$\begin{gathered} \frac{{\partial{ \hat {N}}}}{{\partial \theta }} + \frac{1}{\rho }\frac{\partial }{{\partial \rho }}\left( {\rho \hat {N}{{{\hat {V}}}_{r}}} \right) = 0, \\ \frac{{\partial {{{\hat {V}}}_{r}}}}{{\partial \theta }} + {{{\hat {V}}}_{r}}\frac{{\partial {{{\hat {V}}}_{r}}}}{{\partial \rho }} - \frac{{\hat {V}_{\varphi }^{2}}}{\rho } = - {{{\hat {E}}}_{r}} - {{{\hat {V}}}_{\varphi }}\left( {{{{\hat {B}}}_{0}} + {{{\hat {B}}}_{p}}} \right), \\ \frac{{\partial {{{\hat {V}}}_{\varphi }}}}{{\partial \theta }} + {{{\hat {V}}}_{r}}\frac{{\partial {{{\hat {V}}}_{\varphi }}}}{{\partial \rho }} + \frac{{{{{\hat {V}}}_{r}}{{{\hat {V}}}_{\varphi }}}}{\rho } = - {{{\hat {E}}}_{\varphi }} + {{{\hat {V}}}_{r}}\left( {{{{\hat {B}}}_{0}} + {{{\hat {B}}}_{p}}} \right), \\ \frac{{\partial {{{\hat {B}}}_{p}}}}{{\partial \theta }} + \frac{1}{\rho }\frac{{\partial \left( {\rho {{{\hat {E}}}_{\varphi }}} \right)}}{{\partial \rho }} = 0,\quad \frac{{\partial {{{\hat {E}}}_{r}}}}{{\partial \theta }} = \hat {N}{{{\hat {V}}}_{r}},\quad \frac{{\partial {{{\hat {E}}}_{\varphi }}}}{{\partial \theta }} = \hat {N}{{{\hat {V}}}_{\varphi }} - \frac{{\partial {{{\hat {B}}}_{p}}}}{{\partial \rho }}. \\ \end{gathered} $

Из полученных уравнений

$\frac{{\partial{ \hat {N}}}}{{\partial \theta }} + \frac{1}{\rho }\frac{\partial }{{\partial \rho }}\left( {\rho \hat {N}{{{\hat {V}}}_{r}}} \right) = 0,\quad \frac{{\partial {{{\hat {E}}}_{r}}}}{{\partial \theta }} = \hat {N}{{\hat {V}}_{r}}$
следует

$\frac{\partial }{{\partial \theta }}\left[ {\hat {N} + \frac{1}{\rho }\frac{{\partial \left( {\rho {{{\hat {E}}}_{r}}} \right)}}{{\partial \rho }}} \right] = 0.$

Это соотношение справедливо как при отсутствии плазменных колебаний ($\hat {N} \equiv 1$, ${{\hat {E}}_{r}} \equiv 0$), так и при их наличии. Поэтому в традиционном предположении однородной плотности фонового заряда неподвижных ионов отсюда следует более простое выражение для электронной плотности $\hat {N}(\rho ,\theta )$:

(4)
$\hat {N}(\rho ,\theta ) = 1 - \frac{1}{\rho }\frac{{\partial \left( {\rho {{{\hat {E}}}_{r}}} \right)}}{{\partial \rho }}.$

Воспользовавшись им, приходим к уравнениям, описывающим цилиндрические одномерные нерелятивистские плазменные колебания и волны:

(5)
$\begin{gathered} \frac{{\partial {{V}_{r}}}}{{\partial \theta }} + {{V}_{r}}\frac{{\partial {{V}_{r}}}}{{\partial \rho }} - \frac{{V_{\varphi }^{2}}}{\rho } = - {{E}_{r}} - {{V}_{\varphi }}\left( {{{B}_{0}} + B} \right),\quad \frac{{\partial {{V}_{\varphi }}}}{{\partial \theta }} + {{V}_{r}}\frac{{\partial {{V}_{\varphi }}}}{{\partial \rho }} + \frac{{{{V}_{r}}{{V}_{\varphi }}}}{\rho } = - {{E}_{\varphi }} + {{V}_{r}}\left( {{{B}_{0}} + B} \right), \\ \frac{{\partial B}}{{\partial \theta }} + \frac{1}{\rho }\frac{{\partial \left( {\rho {{E}_{\varphi }}} \right)}}{\rho } = 0,\quad \frac{{\partial {{E}_{r}}}}{{\partial \theta }} + \frac{{{{V}_{r}}}}{\rho }\frac{{\partial \left( {\rho {{E}_{r}}} \right)}}{{\partial \rho }} = {{V}_{r}},\quad \frac{{\partial {{E}_{\varphi }}}}{{\partial \theta }} + \frac{{{{V}_{\varphi }}}}{\rho }\frac{{\partial \left( {\rho {{E}_{r}}} \right)}}{{\partial \rho }} + \frac{{\partial B}}{{\partial \rho }} = {{V}_{\varphi }}. \\ \end{gathered} $

Здесь для удобства у всех безразмерных искомых функций убран символ “крышка”, а также – нижний индекс “p” у индуцированного магнитного поля в плазме. Система (5) является основной для численного моделирования в настоящей работе. Отметим, что в дальнейшем будет использоваться полезная формула электронной плотности (4), в которой также убран символ “крышка”.

Приведем следствие уравнений (4), (5) – закон сохранения энергии (см. [13]):

(6)
$\frac{\partial }{{\partial \theta }}\left\{ {\frac{{E_{r}^{2} + E_{\varphi }^{2} + B_{z}^{2}}}{2} + N\frac{{V_{r}^{2} + V_{\varphi }^{2}}}{2}} \right\} + \frac{1}{\rho }\frac{\partial }{{\partial \rho }}\left\{ {\rho \left[ {{{E}_{\varphi }}{{B}_{z}} + N{{V}_{r}}\frac{{V_{r}^{2} + V_{\varphi }^{2}}}{2}} \right]} \right\} = 0.$

Здесь в качестве ${{B}_{z}}$ можно понимать не только индуцированное поле $B(\rho ,\theta )$, но и полное поле ${{B}_{0}} + B(\rho ,\theta )$, так как способ получения уравнения (6) допускает оба варианта без изменения формы записи.

2. ЛИНЕЙНАЯ МЕДЛЕННАЯ НЕОБЫКНОВЕННАЯ ВОЛНА

2.1. Начальные и граничные условия

Рассмотрим возбуждение колебаний в постоянном внешнем магнитном поле ${{B}_{0}} \equiv {\text{const}}$ в окрестности прямой $\rho = 0$. Положим, что скорость электронов ${{V}_{r}}$ в начальный момент времени ($\theta = 0$) равна нулю

(7)
${{V}_{r}}(\rho ,\theta = 0) = 0,$
а колебания инициализируются электрическим полем ${{E}_{r}}$ следующего вида:
(8)
${{E}_{r}}(\rho ,\theta = 0) = {{\left( {\frac{{{{a}_{*}}}}{{{{\rho }_{*}}}}} \right)}^{2}}\rho \exp \left\{ { - 2\frac{{{{\rho }^{2}}}}{{\rho _{*}^{2}}}} \right\},$
где параметры ${{\rho }_{*}}$ и ${{a}_{*}}$ характеризуют масштаб области локализации и максимальную величину ${{E}_{{\max }}} = {{a_{*}^{2}} \mathord{\left/ {\vphantom {{a_{*}^{2}} {\left( {{{\rho }_{*}}2\sqrt {\text{e}} } \right)}}} \right. \kern-0em} {\left( {{{\rho }_{*}}2\sqrt {\text{e}} } \right)}} \approx {{0.3a_{*}^{2}} \mathord{\left/ {\vphantom {{0.3a_{*}^{2}} {{{\rho }_{*}}}}} \right. \kern-0em} {{{\rho }_{*}}}}$ электрического поля (8) соответственно. Здесь и далее ${\text{e}} = 2.71\; \ldots $ – основание натурального логарифма. Вид функции (8) выбран из соображений, что подобные колебания могут возбуждаться в разреженной плазме (${{\omega }_{l}} \gg {{\omega }_{p}}$) лазерным импульсом с частотой ${{\omega }_{l}}$ при его фокусировке сферической линзой, когда фокальное пятно имеет форму круга.

Если электрическое поле лазерного излучения имеет аксиальную симметрию и гауссово распределение по пространственным координатам и времени

(9)
${{E}_{L}}(\rho ,z,t) = {{E}_{{0L}}}\exp \left\{ { - \frac{{{{\rho }^{2}}}}{{\rho _{*}^{2}}} - \frac{{\omega _{p}^{2}}}{{\tau _{*}^{2}}}{{{\left( {t - \frac{z}{c}} \right)}}^{2}}} \right\}\cos \left[ {{{\omega }_{l}}\left( {t - \frac{z}{c}} \right)} \right],$
где ${{\tau }_{*}} = {{\omega }_{p}}{{\tau }_{p}}$, ${{\rho }_{*}} = {{k}_{p}}{{R}_{p}}$ – безразмерные значения длительности ${{\tau }_{p}}$ и радиуса фокального пятна ${{R}_{p}}$ лазерного импульса, то в некоторой точке z, удаленной от заднего фронта импульса на расстояние, превышающее длину плазменной волны (${{k}_{p}}\left| z \right| \gg 1$), справедливо следующее соотношение, связывающее величину ${{a}_{*}}$ с параметрами лазерного импульса [8]
(10)
$a_{*}^{2} = a_{0}^{2}{{\tau }_{*}}\sqrt {\pi {\text{/}}2} \exp \left( { - {{\tau _{*}^{2}} \mathord{\left/ {\vphantom {{\tau _{*}^{2}} 8}} \right. \kern-0em} 8}} \right),$
где ${{a}_{0}} = e{{E}_{{0L}}}{\text{/}}(m{{\omega }_{l}}c)$ – нормированная амплитуда лазерного поля. В условиях оптимального возбуждения кильватерной волны (${{\tau }_{*}} = 2$), когда ее амплитуда максимальна, соотношение (10) принимает вид $a_{*}^{2} = a_{0}^{2}\sqrt {2\pi {\text{/e}}} \approx 1.52a_{0}^{2}$.

Заметим, что на больших расстояниях от прямой $\rho = 0$, в силу начального условия (8), плазменные колебания не возбуждаются. Поэтому будем считать, что выполнены следующие условия:

(11)
$\begin{array}{*{20}{c}} {{{V}_{r}}(\rho \to \infty ,\theta ) = {{V}_{\varphi }}(\rho \to \infty ,\theta ) = 0,} \\ {{{E}_{r}}(\rho \to \infty ,\theta ) = {{E}_{\varphi }}(\rho \to \infty ,\theta ) = B(\rho \to \infty ,\theta ) = 0.} \end{array}$

Кроме того, аксиальная симметрия решения предусматривает выполнение следующих условий на оси $\rho = 0$:

(12)
$\begin{gathered} {{V}_{r}}(\rho = 0,\theta ) = {{V}_{\varphi }}(\rho = 0,\theta ) = 0, \\ {{E}_{r}}(\rho = 0,\theta ) = {{E}_{\varphi }}(\rho = 0,\theta ) = 0. \\ \end{gathered} $

Таким образом, учитывая специфику цилиндрической системы координат ($\rho \geqslant 0$), будем изучать в первом квадранте $\{ (\rho ,\theta ):0 \leqslant \rho < \infty ,\;\theta > 0\} $ решения системы (5), определяемые начальными и граничными условиями (7), (8), (11), (12) при наличии внешнего магнитного поля ${{B}_{0}}$, не зависящего ни от времени, ни от пространственной координаты.

В целях моделирования локализованного в пространстве решения системы (13) примéним следующий подход ограничения области. Зафиксируем область определения решения по переменной ρ с помощью параметра d, т.е. отрезок $[0,d]$. Предполагается, что в течение времени наблюдения решение не успеет достигнуть границы d и отразиться от нее. Из явного вида начальной функции (8) следует, что если положить $d \approx 4.5{{\rho }_{*}}$, то вне отрезка $[0,d]$ функция ${{E}_{r}}(\rho ,\theta = 0)$ не будет по порядку превышать величину 10–18. Поэтому указанного значения d достаточно для наблюдения за ленгмюровскими колебаниями, т.е. когда внешнее магнитное поле ${{B}_{0}}$ отсутствует. В рассматриваемом случае возбуждения волны необходим запас для ее распространения в пространстве, следовательно, параметр d надо брать бóльшим. Как правило, его примерного удвоения бывает достаточно, т.е. параметр d можно выбирать как $d = 10{{\rho }_{*}}$. Конечно, здесь речь идет об ориентировочном значении, так как при необходимости d можно и нужно увеличивать.

2.2. Ряды Фурье–Бесселя

Рассмотрим систему (5) в предположении малости возмущений относительно нулевого фона. После отбрасывания слагаемых второго порядка малости получим

(13)
$\begin{array}{*{20}{c}} {\frac{{\partial V_{r}^{l}}}{{\partial \theta }} = - E_{r}^{l} - V_{\varphi }^{l}{{B}_{0}},\quad \frac{{\partial V_{\varphi }^{l}}}{{\partial \theta }} = - E_{\varphi }^{l} + V_{r}^{l}{{B}_{0}},} \\ {\frac{{\partial {{B}^{l}}}}{{\partial \theta }} + \frac{1}{\rho }\frac{{\partial \left( {\rho E_{\varphi }^{l}} \right)}}{\rho } = 0,\quad \frac{{\partial E_{r}^{l}}}{{\partial \theta }} = V_{r}^{l},\quad \frac{{\partial E_{\varphi }^{l}}}{{\partial \theta }} + \frac{{\partial {{B}^{l}}}}{{\partial \rho }} = V_{\varphi }^{l}.} \end{array}$

Верхний индекс l здесь обозначает принадлежность к решению линеаризованной задачи.

Отметим, что для (13) имеет место закон сохранения энергии (см. [13]):

(14)
$\frac{1}{2}\frac{\partial }{{\partial \theta }}\left\{ {{{{\left( {E_{r}^{l}} \right)}}^{2}} + {{{\left( {E_{\varphi }^{l}} \right)}}^{2}} + {{{\left( {B_{z}^{l}} \right)}}^{2}} + {{{\left( {V_{r}^{l}} \right)}}^{2}} + {{{\left( {V_{\varphi }^{l}} \right)}}^{2}}} \right\} + \frac{1}{\rho }\frac{\partial }{{\partial \rho }}\left\{ {\rho E_{\varphi }^{l}B_{z}^{l}} \right\} = 0,$
где, как и ранее, в качестве $B_{z}^{l}$ можно понимать не только индуцированное поле ${{B}^{l}}(\rho ,\theta )$, но и полное поле ${{B}_{0}} + {{B}^{l}}(\rho ,\theta )$, так как способ получения уравнения (14) допускает оба варианта без изменения формы записи.

Далее будем учитывать условия (11) и (12), представляя искомое решение задачи в виде сходящихся рядов Фурье по функциям Бесселя на отрезке $[0,d]$, безусловно, предполагая его достаточную гладкость. С этой целью определим два набора базисных функций $\left\{ {{{Y}_{k}}(\rho )} \right\}_{{k = 1}}^{\infty }$ и $\left\{ {{{Z}_{k}}(\rho )} \right\}_{{k = 1}}^{\infty }$, что связано с различной четностью искомых функций относительно оси симметрии $\rho = 0$. Пусть ${{\mu }_{k}}$, $k = 1,\;2,\; \ldots $ – нули функции Бесселя ${{J}_{1}}(t),$ т.е. ${{J}_{1}}({{\mu }_{k}}) = 0.$ Положим ${{\kappa }_{k}} = {{\mu }_{k}}{\text{/}}d$, тогда на отрезке $[0,d]$ для функций

${{Z}_{k}}(\rho ) = {{J}_{1}}({{\kappa }_{k}}\rho )\frac{{\sqrt 2 }}{{d\left| {{{J}_{0}}({{\mu }_{k}})} \right|}},\quad {{Y}_{k}}(\rho ) = {{J}_{0}}({{\kappa }_{k}}\rho )\frac{{\sqrt 2 }}{{d\left| {{{J}_{0}}({{\mu }_{k}})} \right|}}$
справедливы условия ортогональности
$\int\limits_0^d {\rho {{Z}_{k}}(\rho ){{Z}_{l}}(\rho )d\rho } = \delta _{k}^{l},\quad \int\limits_0^d {\rho {{Y}_{k}}(\rho ){{Y}_{l}}(\rho )d\rho } = \delta _{k}^{l},$
где $\delta _{k}^{l}$ – символ Кронеккера.

Легко проверить полезные соотношения, связывающие функции из обеих наборов:

$Y_{k}^{'}(\rho ) = - {{\kappa }_{k}}{{Z}_{k}}(\rho ),\quad \frac{1}{\rho }\frac{d}{{d\rho }}\left( {\rho {{Z}_{k}}(\rho )} \right) = {{\kappa }_{k}}{{Y}_{k}}(\rho ),\quad k = 1,\;2,\; \ldots \;.$

Используя полноту, ортогональность и полезные свойства базисных функций (см., например, [6]), имеем формальное представление решения системы (13) в виде рядов Фурье–Бесселя:

$\begin{gathered} E_{r}^{l}(\rho ,\theta ) = \sum\limits_{k = 1}^\infty {{{E}_{r}}} (k){{Z}_{k}}(\rho )\cos \left( {\omega (k)\theta } \right), \\ V_{r}^{l}(\rho ,\theta ) = \sum\limits_{k = 1}^\infty {{{V}_{r}}(k)} {{Z}_{k}}(\rho )\sin \left( {\omega (k)\theta } \right), \\ \end{gathered} $
(15)
$E_{\varphi }^{l}(\rho ,\theta ) = \sum\limits_{k = 1}^\infty {{{E}_{\varphi }}} (k){{Z}_{k}}(\rho )\sin \left( {\omega (k)\theta } \right),$
$\begin{gathered} V_{\varphi }^{l}(\rho ,\theta ) = \sum\limits_{k = 1}^\infty {{{V}_{\varphi }}} (k){{Z}_{k}}(\rho )\cos \left( {\omega (k)\theta } \right), \\ {{B}^{l}}(\rho ,\theta ) = \sum\limits_{k = 1}^\infty B (k){{Y}_{k}}(\rho )\cos \left( {\omega (k)\theta } \right). \\ \end{gathered} $

Подстановка (15) в (13) порождает формулу зависимости частоты от номера гармоники и напряженности внешнего магнитного поля

(16)
$\omega (k) = \sqrt {1 + \frac{{\kappa _{k}^{2} + B_{0}^{2}}}{2} \pm \sqrt {B_{0}^{2} + {{{\left( {\frac{{\kappa _{k}^{2} - B_{0}^{2}}}{2}} \right)}}^{2}}} } $
и явные выражения для коэффициентов Фурье–Бесселя:
(17)
$\begin{gathered} {{V}_{r}}(k) = - {{E}_{r}}(k), \\ {{E}_{\varphi }}(k) = - {{B}_{0}}{{E}_{r}}(k)\frac{{\omega (k)}}{{1 + \kappa _{k}^{2} - {{\omega }^{2}}(k)}}, \\ {{V}_{\varphi }}(k) = {{B}_{0}}{{E}_{r}}(k)\frac{{\kappa _{k}^{2} - {{\omega }^{2}}(k)}}{{1 + \kappa _{k}^{2} - {{\omega }^{2}}(k)}}, \\ B(k) = - {{B}_{0}}{{E}_{r}}(k)\frac{{{{\kappa }_{k}}}}{{1 + \kappa _{k}^{2} - {{\omega }^{2}}(k)}}, \\ \end{gathered} $
где коэффициенты ${{E}_{r}}(k)$, $k = 1,\;2,\; \ldots $, определяются равенством

(18)
$E_{r}^{l}(\rho ,\theta = 0) \equiv {{\left( {\frac{{{{a}_{*}}}}{{{{\rho }_{*}}}}} \right)}^{2}}\rho \exp \left\{ { - 2\frac{{{{\rho }^{2}}}}{{\rho _{*}^{2}}}} \right\} = \sum\limits_{k = 1}^\infty {{{E}_{r}}} (k){{Z}_{k}}(\rho ).$

Обратим внимание, что в данном случае объект МНВ [3], [4] соответствует распространению возмущений в направлении, ортогональном вектору магнитного поля, и удовлетворяет только одному из двух соотношений (16), а именно – со знаком минус. В частности, при отсутствии внешнего магнитного поля из (16) следует формула для частоты ленгмюровских колебаний в холодной изотропной плазме $\omega (k) \equiv 1$ (в размерных переменных – $\omega (k) \equiv {{\omega }_{p}}$), т.е. уравнения (13) в этом случае порождают решение хорошо известной задачи. С другой стороны, при $k \to \infty $ справедливо $\omega (k) \to {{\omega }_{{up}}}$, где $\omega _{{up}}^{2} = 1 + B_{0}^{2}$, т.е. решение системы (13) может быть в этом случае приближенно описано так называемыми верхнегибридными колебаниями (см. [3, с. 112–113]).

Таким образом, построенное аналитическое решение дает возможность определить из (15) необходимые начальные условия для инициализации нелинейной МНВ, которая при достаточно малом внешнем поле ${{B}_{0}}$ будет близка к линейной. Отметим также, что замена бесконечной области по переменной ρ на конечную, позволяет вместо преобразования Ханкеля (в цилиндрических координатах – аналог интегрального преобразования Фурье) использовать в расчетах ряды Фурье–Бесселя, что может быть реализовано гораздо эффективнее с помощью библиотек стандартных программ численного анализа.

3. ЧИСЛЕННЫЙ АЛГОРИТМ ВТОРОГО ПОРЯДКА ТОЧНОСТИ

Пусть исходное уравнение имеет вид

(19)
$\frac{{\partial U}}{{\partial \theta }} + \frac{{\partial F(U)}}{{\partial \rho }} = S(U,\rho ,\theta ),$
где U, F, S – вектор-функции, рассматриваемые в полуплоскости $\{ (\rho ,\theta ):\theta \geqslant 0,\;\rho \in \mathbb{R}\} $, и в момент времени $\theta = 0$ заданы начальные условия

(20)
$U(\rho ,\theta = 0) = {{U}^{0}}(\rho ),\quad \rho \in \mathbb{R}.$

Будем считать, что нас интересует приближенное решение задачи Коши, определенной соотношениями (19), (20), про которое известно, что оно существует, единственно и обладает достаточной гладкостью.

Определим дискретизацию независимых переменных с помощью постоянных параметров τ и h так, что

${{\theta }^{n}} = n\tau ,\quad n \geqslant 0,\quad {{\rho }_{i}} = ih,\quad i = 0,\;1,\;2,\; \ldots ,$
и будем обозначать зависимую переменную $U(\rho ,\theta )$ в узле сетки $({{\rho }_{i}},{{\theta }^{n}})$ как $U_{i}^{n}$. Стандартная схема Мак-Кормака [14] состоит из двух этапов вычислений, известных как предиктор и корректор, и может быть представлена в виде
(21)
$U_{i}^{p} = U_{i}^{n} - \frac{\tau }{h}\left( {F_{{i + 1}}^{n} - F_{i}^{n}} \right) + \tau S_{i}^{n},$
(22)
$U_{i}^{c} = U_{i}^{n} - \frac{\tau }{h}\left( {F_{i}^{p} - F_{{i - 1}}^{p}} \right) + \tau S_{i}^{p},$
где верхний индекс p обозначает шаг предиктор (c – корректор) или n – временной слой ${{\theta }^{n}}$.

Окончательная формула, формирующая решение на следующем временном слое $(n + 1)$, имеет вид:

(23)
$U_{i}^{{n + 1}} = \frac{{U_{i}^{p} + U_{i}^{c}}}{2}.$

Приведенная схема хорошо известна и давно используется в вычислительной практике. Ее свойства представлены в популярных монографиях, посвященных численному анализу и математическому моделированию (см., например, [15], [16]). Напомним, что на гладких решениях схема Мак-Кормака имеет порядок аппроксимации $O\left( {{{\tau }^{2}} + {{h}^{2}}} \right)$ и условие устойчивости $\tau = O(h)$, поэтому ее традиционно относят к схемам второго порядка точности.

Важным отличием системы (5) от традиционной формы записи уравнений (19) являются недивергентные слагаемые следующего вида:

${{V}_{r}}\frac{{\partial {{E}_{r}}}}{{\partial \rho }},\quad {{V}_{r}}\frac{{\partial {{V}_{\varphi }}}}{{\partial \rho }},\quad {{V}_{\varphi }}\frac{{\partial {{E}_{r}}}}{{\partial \rho }}.$

Например, одно из них присутствует в уравнении, описывающем динамику r − компоненты электрического поля

$\frac{{\partial {{E}_{r}}}}{{\partial \theta }} + {{V}_{r}}\frac{{\partial {{E}_{r}}}}{{\partial \rho }} = {{V}_{r}} - \frac{{{{V}_{r}}{{E}_{r}}}}{\rho }.$

В работе [7] был предложен подход для устранения трудности с недивергентной формой слагаемых при сохранении прежнего (второго) порядка точности разностной схемы Мак-Кормака. В дальнейшем он хорошо зарекомендовал себя при расчетах плоских МНВ [5], [17], поэтому на его деталях здесь останавливаться не будем.

Существенным отличием обсуждаемой схемы от плоского случая является необходимость расчетов на оси симметрии $\rho = 0$. В частности, речь идет об уравнении для индуцированного магнитного поля в системе (5):

(24)
$\frac{{\partial B}}{{\partial \theta }} + \frac{1}{\rho }\frac{{\partial \left( {\rho {{E}_{\varphi }}} \right)}}{\rho } = 0.$

Функция $B(\rho ,\theta )$ является единственной функцией, которая не обращается в нуль на оси симметрии, поэтому для вычислений особенность в нуле требует модификации уравнения. Учитывая условие из (12), т.е. ${{E}_{\varphi }}(\rho = 0,\theta ) = 0$, в пределе при $\rho \to 0$ из (24) имеем

$\frac{{\partial B}}{{\partial \theta }} + 2\frac{{\partial {{E}_{\varphi }}}}{{\partial \rho }} = 0.$

В свою очередь, соотношения предиктор и корректор для этого уравнения примут вид

(25)
$\left( B \right)_{0}^{p} = \left( B \right)_{0}^{n} - 2\frac{\tau }{h}\left( {{{E}_{\varphi }}} \right)_{1}^{n},\quad \left( B \right)_{0}^{c} = \left( B \right)_{0}^{n} - 2\frac{\tau }{h}\left( {{{E}_{\varphi }}} \right)_{1}^{p}.$

Нижние индексы 0 и 1 обозначают дискретные значения функций на оси ($\rho = 0$) и в соседней точке ($\rho = h$).

Отметим также, что при $\rho = d$ вычисления не производятся совсем: просто функции ${{E}_{r}}$, ${{V}_{r}}$, ${{E}_{\varphi }}$, ${{V}_{\varphi }}$ полагаются равными нулю, как и производная $\partial B{\text{/}}\partial \rho $, в силу достаточной удаленности границы d.

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Процесс опрокидывания нерелятивистских ленгмюровских колебаний при учете аксиальной симметрии рассматривался в [8], [18], в свою очередь, трансформация плоских колебаний в МНВ – в работе [5]. Поэтому в целях сохранения преемственности с приведенными в них результатами расчетов зафиксируем значения параметров в начальном условии (8): ${{a}_{*}} = 0.365$, ${{\rho }_{*}} = 0.6$. Выберем параметр d, характеризующий искусственную границу, равным 7. При этом характерное значение параметра дискретизации по пространственной переменной, использовавшееся в расчетах, равно $h = 0.25 \times {{10}^{{ - 3}}}$. Шаг интегрирования по времени $\tau $ из соображений устойчивости выбирался равным $h{\text{/}}2$, а в целях контроля точности регулярно проводились расчеты с сеточными параметрами в два раза меньшими, чем основные (рабочие).

4.1. Расчет начальных данных

Выбор начальных данных для инициализации МНВ представляет определенные трудности. Дело в том, что в соответствии с формулами (15) начальные условия (7), (8) порождают ненулевые функции ${{V}_{\varphi }}$ и B при $\theta = 0$. Причем определяются они в терминах коэффициентов рядов Фурье–Бесселя, зависящих от функции ${{E}_{r}}$ в начальный момент времени. Как правило, чтобы избежать проблем с недостающими начальными условиями, волны в магнитоактивной плазме рассматривают либо в электростатическом приближении [1], [19], либо полагают недостающие начальные функции ${{V}_{\varphi }}$ и B тождественно нулевыми. При использовании слабых магнитных полей ${{B}_{0}} \ll 1$ последнее вполне допустимо, однако в общем случае пространственная форма волны может быть сильно искажена тривиальными начальными данными (см. детали в [5]).

Заметим, что вышесказанное порождает определенную новизну в постановке задачи, так как при отсутствии внешнего магнитного поля начальных условий (7), (8) вполне достаточно для однозначного определения ленгмюровских колебаний в произвольный момент времени.

Приведем пример, иллюстрирующий согласование начальных данных в медленной необыкновенной волне. Для одного и того же пространственного распределения функции ${{E}_{r}}(\rho ,\theta = 0)$, инициирующего волну в соответствии с (8) на фиг. 2 и фиг. 3 изображены начальные распределения функций $B(\rho ,\theta = 0)$ и ${{V}_{\varphi }}(\rho ,\theta = 0)$, определяемые решением (15) при различных внешних полях ${{B}_{0}} \in \{ 0.25,\;0.5,\;1\} $.

Фиг. 2.

Начальное индуцированное магнитное поле ${{B}_{{{\text{init}}}}}(\rho ) = B(\rho ,\theta = 0)$ для различных значений ${{B}_{0}}$: сплошная линия – ${{B}_{0}} = 0.25$, пунктирная – ${{B}_{0}} = 0.5$, штриховая – ${{B}_{0}} = 1$.

Фиг. 3.

Начальная φ-компонента скорости электронов ${{V}_{{\varphi ,{\text{init}}}}}(\rho ) = {{V}_{\varphi }}(\rho ,\theta = 0)$ для различных значений ${{B}_{0}}$: сплошная линия – ${{B}_{0}} = 0.25$, пунктирная – ${{B}_{0}} = 0.5$, штриховая – ${{B}_{0}} = 1$.

Процедура их расчета базировалась на использовании пакетов QUADPACK [20] (библиотека SLATEC) и FUNPACK [21], реализующих вычисление определенных интегралов и работу с функциями Бесселя. На отрезке $[0,d]$ вычислялись коэффициенты Фурье–Бесселя ${{E}_{r}}(k)$ из разложения (18). Далее с помощью формул (15) при $\theta = 0$ и (16) вычислялись искомые коэффициенты функций ${{B}^{l}}(\rho ,\theta = 0)$ и $V_{\varphi }^{l}(\rho ,\theta = 0)$, которые использовались для определения на сетке недостающих начальных данных. Количество коэффициентов определялось параметром MCOEF, характерное значение которого полагалось 40. Для контрольных расчетов, как правило, значение параметра удваивалось.

Легко заметить, что диапазон изменения этих начальных функций вполне соизмерим с диапазоном ${{E}_{r}}(\rho ,\theta = 0) \in [0,\;0.068]$. Это дает основание для вывода, что как полагать обе начальные функции нулевыми, так и совсем пренебрегать индуцированным магнитным полем (случай электростатического приближения или верхнегибридных колебаний), при рассмотрении МНВ с начальным возмущением (7), (8) было бы не вполне оправдано.

Отметим, что речь о согласовании начальных данных идет только в смысле сохранения физического смысла решения МНВ, так как, в силу гиперболичности исходной системы (5), с математической точки зрения все наборы достаточно гладких начальных условий являются равноправными.

4.2. Линейная МНВ

Для иллюстраций динамики линейной волны выберем функцию, характеризующую ее энергию с точностью до множителя 1/2,

(26)
$E{{n}_{{{\text{lin}}}}}(\rho ,\theta ) = E_{r}^{2}(\rho ,\theta ) + E_{\varphi }^{2}(\rho ,\theta ) + {{B}^{2}}(\rho ,\theta ) + V_{r}^{2}(\rho ,\theta ) + V_{\varphi }^{2}(\rho ,\theta ).$

Из соотношения (14) следует, что интеграл по отрезку $[0,d]$ с весом ρ от функции $E{{n}_{{{\text{lin}}}}}(\rho ,\theta )$ равен константе, поэтому ее пространственные распределения в различные моменты времени могут иллюстрировать волновой характер переноса энергии в пространстве.

Сравним поведение волны для различных внешних полей ${{B}_{0}} \in \{ 0.25,\;0.5,\;1\} $. Выберем с этой целью характерные моменты времени – $\theta \in \{ 0,\;40\pi ,\;80\pi \} $ и рассмотрим для них функцию $E{{n}_{{{\text{lin}}}}}$.

На фиг. 4 приведены пространственные распределения энергии для слабого внешнего магнитного поля ${{B}_{0}} = 0.25$. Легко заметить, что волна очень похожа на неподвижную, т.е. перемещение экстремальных значений энергии практически незаметно. Однако пусть медленно, но энергия перемещается в пространстве, о чем свидетельствует ее монотонное увеличение на периферии волны в зависимости от времени. Конечно, в силу закона сохранения, эта монотонность полностью компенсируется соответствующим убыванием максимальных значений. Поэтому можно сказать, что для слабых внешних полей происходит медленное “расплывание” энергии практически без изменения ее начальной формы.

Фиг. 4.

Энергия линейной волны во внешнем поле ${{B}_{0}} = 0.25$ для различных значений θ: сплошная линия – $\theta = 0$, пунктирная – $\theta = 40\pi $, штриховая – $\theta = 80\pi $.

Влияние значимого увеличения внешнего поля представлено на фиг. 5. При ${{B}_{0}} = 0.5$ со временем происходит изменение формы волны, связанное с заметным перемещением энергии на периферии волны. Легко заметить, что скорость этого изменения при этом увеличивается. Другими словами, в умеренных внешних полях скорость переноса энергии линейной волны со временем возрастает, хотя максимальные значения энергии при этом монотонно убывают. Отметим, что фиг. 4 и 5 являются замечательной иллюстрацией “медленности” рассматриваемой необыкновенной волны.

Фиг. 5.

Энергия линейной волны во внешнем поле ${{B}_{0}} = 0.5$ для различных значений θ: сплошная линия – $\theta = 0$, пунктирная – $\theta = 40\pi $, штриховая – $\theta = 80\pi $.

Наконец, динамика энергии волны в сильном магнитном поле ${{B}_{0}} = 1$ представлена на фиг. 6. Представленные пространственные распределения функции $E{{n}_{{{\text{lin}}}}}$ наглядно иллюстрируют волновой характер – скорость переноса энергии достаточно велика, а амплитуда уменьшается при выполнении закона сохранения, т.е. наблюдаются одновременно две тенденции: ускорение переноса энергии и немонотонное “расплывание” формы волны.

Фиг. 6.

Энергия линейной волны во внешнем поле ${{B}_{0}} = 1$ для различных значений θ: сплошная линия – $\theta = 0$, пунктирная – $\theta = 40\pi $, штриховая – $\theta = 80\pi $.

Уточним, что представленные выше графики получены одновременно как с помощью формул (15), так и при использовании численного алгоритма из разд. 3, упрощенного для линейных уравнений (13). В силу второго порядка точности приближенного метода и малости параметров дискретизации, заметить визуально различия в графиках функции $E{{n}_{{{\text{lin}}}}}$, полученных различными способами, не представляется возможным.

4.3. Нелинейная МНВ

Наиболее интересным свойством нелинейной МНВ, в отличие от линейной, является ее опрокидывание по прошествии некоторого количества периодов. Аналогичный эффект имеет место и в случае отсутствия внешнего магнитного поля, т.е. в случае аксиально симметричных ленгмюровских колебаний [8], [18].

Краткое изложение эффекта опрокидывания в рамках рассматриваемой модели холодной плазмы (без внешнего магнитного поля) состоит в следующем. Начальное пространственное распределение электронной плотности N, как следствие формул (4) и (8), приводит к избытку положительного заряда в начале координат (при $\rho = 0$). По этой причине начинается движение электронов в направлении центра области, что через половину периода колебаний порождает распределение плотности с глобальным максимумом также при $\rho = 0$. Если бы нелинейные плазменные колебания сохраняли во времени свою пространственную форму, то описанные распределения плотности электронов регулярно меняли бы друг друга через каждую половину периода, порождая в центре области строго периодическую последовательность экстремумов с неизменными амплитудами. Однако с течением времени происходит постепенное формирование абсолютного максимума плотности, расположенного вне оси и сравнимого по величине с осевыми. После возникновения этого внеосевого максимума наблюдается резкое возрастание его по величине и достаточно быстро (часто через период – другой) на его месте возникает сингулярность электронной плотности. Численному моделированию этого процесса посвящена монография [2], кроме того, графики для аксиально-симметричного случая и используемых в настоящей статье параметров имеются в [18]. Уточним, что здесь речь идет о колебаниях, которые существуют на протяжении нескольких периодов во времени.

Приведем иллюстрации влияния умеренного по напряженности внешнего магнитного поля ${{B}_{0}} = 0.5$ на эффект опрокидывания, в данном случае, уже МНВ. На фиг. 7 пунктиром изображено для электронной плотности изменение во времени в начале координат, а сплошной линией – динамика максимального по области значения. Влияние внешнего поля приводит к значительному (практически в два раза) уменьшению амплитуды колебаний на оси симметрии по сравнению с его отсутствием. Сначала колебания носят регулярный характер, т.е. глобальные по области максимумы и минимумы плотности сменяют друг друга через половину периода и располагаются в начале координат. После четвертого регулярного (центрального) максимума в момент времени $\theta \approx 19$ возникает новая структура – внеосевой максимум электронной плотности, по величине сравнимый с ближайшим регулярным. Далее в течение двух следующих периодов он монотонно возрастает, а затем в ${{\theta }_{{br}}} \approx 35.1$ на его месте возникает сингулярность электронной плотности.

Фиг. 7.

Динамика плотности плазмы $N$ при ${{B}_{0}} = 0.5$: сплошная линия – максимум по области, пунктирная линия – ось симметрии.

Распределения компонент скорости ${{V}_{r}}$ и электрического поля ${{E}_{r}}$ в момент опрокидывания изображены на фиг. 8. Отметим, что в окрестности сингулярности плотности функция скорости имеет скачок производной, а функция электрического поля принимает ступенчатый характер. Именно такие качественные характеристики и обеспечивают опрокидывание колебаний в момент ${{\theta }_{{br}}} \approx 35.1$. Важно отметить, что опрокидывание носит характер “градиентной катастрофы”, т.е. сами функции ${{E}_{r}}$ и ${{V}_{r}}$ при этом остаются ограниченными. Для внеосевого опрокидывания подобные распределения являются характерными и в большом количестве представлены в [2].

Фиг. 8.

Пространственные распределения r-компонент скорости и электрического поля в момент опрокидывания для ${{B}_{0}} = 0.5$: сплошная линия – ${{E}_{r}}$, пунктирная линия – ${{V}_{r}}$.

Распределения φ-компонент скорости и электрического поля, а также индуцированное магнитное поле в момент опрокидывания изображены на фиг. 9–11. В окрестности сингулярности плотности их поведение качественно сходно с r-компонентами: функция скорости ${{V}_{\varphi }}$ принимает ступенчатый характер, а функция электрического поля ${{E}_{\varphi }}$ имеет скачок производной. В свою очередь, функция B имеет скачок производной, а в окрестности начала координат $\rho = 0$ практически совпадает с константой. Отметим, что все представленные на фиг. 9–11 функции также ограничены, а их изображения ранее в научной литературе не встречались.

Фиг. 9.

Пространственное распределение φ-компоненты скорости в момент опрокидывания для ${{B}_{0}} = 0.5$.

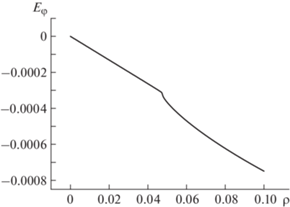
Фиг. 10.

Пространственное распределение φ-компоненты электрического поля в момент опрокидывания для ${{B}_{0}} = 0.5$.

Фиг. 11.

Пространственное распределение индуцированного магнитного поля в момент опрокидывания для ${{B}_{0}} = 0.5$.

Следует обратить внимание, что для колебаний и волн, порождаемых узким импульсом (в данном случае ${{\rho }_{*}} = 0.6$), абсолютные значения φ-компоненты скорости и индуцированного магнитного поля по порядку меньше абсолютных значений скорости ${{V}_{r}}$ и электрического поля ${{E}_{r}}$. В свою очередь, абсолютные значения электрического поля ${{E}_{\varphi }}$ еще примерно на порядок меньше, чем ${{V}_{\varphi }}$. Тем не менее такие малые возмущения, сформировавшиеся при ${{B}_{0}} = 0.5$, привели к опрокидыванию волны примерно на 10 безразмерных единиц времени (около 20%) быстрее, чем при ${{B}_{0}} = 0$, т.е. при тождественно нулевых ${{V}_{\varphi }}$, ${{E}_{\varphi }}$, B.

Ожидаемое влияние внешнего магнитного поля на ленгмюровские колебания плазмы сводится к двум процессам: возбуждение бегущей волны при любом ${{B}_{0}}$ и пресечение ее опрокидывания при достаточно большом ${{B}_{0}}$. Аналогичное влияние оказывало увеличение температуры электронов на релятивистские колебания, рассмотренное в [22]. Причиной является схожесть физических факторов: увеличение внешнего магнитного поля, как и температуры, приводит к увеличению групповой скорости плазменных волн, что способствует выносу энергии из первоначальной области локализации колебаний. В случае нагревания плазмы в слабо-нелинейном приближении удалось в явной форме получить условие, при выполнении которого может наблюдаться эффект опрокидывания. Это было связано с монотонным увеличением времени опрокидывания в зависимости от температуры электронов. В рассматриваемом случае магнитоактивной плазмы подобного условия вывести не удалось, и это имеет вескую причину. Дело в том, что внешнее поле влияет на время опрокидывания МНВ немонотонным образом: в слабых полях процесс опрокидывания ускоряется, а затем – при увеличении поля – процесс замедляется, вплоть до полного прекращения, которое достаточно сложно отследить по причине необходимости моделирования волны на больших временах.

Асимптотическое запаздывание по времени эффекта опрокидывания легко заметить при увеличении внешнего поля. Качественно процесс опрокидывания, если он имеет место, практически не изменяется. Сначала наблюдаются регулярные максимумы плотности на оси симметрии, которые сопровождаются небольшим затуханием. Затем формируется практически неподвижный внеосевой максимум, который располагается вблизи оси симметрии, монотонно возрастает и приводит к сингулярности. Увеличение внешнего магнитного поля ${{B}_{0}}$ “растягивает” этот процесс во времени. Качественныe отличия самих пространственных распределений в момент опрокидывания от представленных на фиг. 8–11 не обнаружены. Как и выше, опрокидывание носит характер “градиентной катастрофы”, т.е. все функции, кроме электронной плотности, при этом остаются ограниченными.

На фиг. 12 изображена зависимость времени опрокидывания от величины ${{B}_{0}}$ при взятых параметрах ${{a}_{*}}$ и ${{\rho }_{*}}$. Спадание времени опрокидывания при малых значениях напряженности магнитного поля связано с ненулевым значением φ-компоненты скорости электронов, которая увеличивается с ростом магнитного поля. Последующее нарастание времени опрокидывания с ростом напряженности магнитного поля связано с увеличением групповой скорости медленной необыкновенной волны, которая выносит энергию из области первоначальной локализации колебаний. Подобный эффект уже наблюдался в процессе опрокидывания плоской релятивистской МНВ [17], однако формальное аналитическое обоснование его пока получить не удалось. Дополнительное увеличение внешнего поля приводит к резкому увеличению времени опрокидывания. Например, при ${{B}_{0}} = 2.5$ опрокидывание наблюдается при ${{\theta }_{{br}}} \approx 193.3$, а при ${{B}_{0}} = 3$ имеем ${{\theta }_{{br}}} \approx 375.9$. Отображение этих данных на фиг. 12 сильно бы ухудшило наглядность представленного графика.

Фиг. 12.

Зависимость времени опрокидывания колебаний ${{\theta }_{{br}}}$ от внешнего поля ${{B}_{0}}$.

Следует отметить, что расчеты эффекта опрокидывания подвергались строгому контролю, так как в этом процессе из гладкого решения формировалась так называемая градиентная катастрофа. При уменьшении/увеличении параметров дискретизации, размеров области и количества слагаемых в рядах в два раза (контрольные расчеты) пространственно-временные координаты опрокидывания изменялись на доли процентов.

ЗАКЛЮЧЕНИЕ

В работе исследовано влияние внешнего магнитного поля на цилиндрические нерелятивистские нелинейные плазменные колебания и волны, порождаемые мощным лазерным импульсом. В результате согласованного взаимодействия электромагнитных полей и частиц в магнитоактивной плазме формируется медленная необыкновенная волна. Для ее инициализации использован метод построения недостающих начальных условий на основе решения линейной задачи в рядах Фурье–Бесселя, которые несложно адаптировать к их дискретному аналогу по пространству. Реализация дискретных преобразований осуществляется с помощью стандартных пакетов программ численного анализа.

С целью численного моделирования нерелятивистской волны построена схема метода конечных разностей второго порядка точности типа Мак-Кормака на основе эйлеровых переменных. В силу новизны постановки задачи результаты расчетов подвергались тщательному контролю. Если внешнее магнитное поле отсутствует, то в соответствии с начальными условиями колебания сосредоточены в окрестности начала координат и продолжаются там до их опрокидывания. Эффект опрокидывания характеризуется формированием внеосевого максимума плотности по истечении нескольких периодов колебаний, затем – быстрым ростом этого максимума, и, наконец, сингулярностью плотности, что связано с пересечением траекторий соседних частиц. В случае учета внешнего магнитного поля ленгмюровские колебания трансформируются в медленную необыкновенную волну. При этом групповая скорость волны увеличивается с ростом внешнего постоянного поля, что способствует выносу энергии из первоначальной области локализации колебаний. По этой причине, начиная с некоторого критического значения внешнего поля, эффект опрокидывания уже перестает наблюдаться, т.е. формируется глобальное по времени гладкое решение. Представленная динамика электронной плотности и пространственные распределения энергиии хорошо иллюстрируют опрокидывание медленной необыкновенной волны.

Полученные результаты можно использовать для моделирования более сложных по структуре волн в магнитоактивной плазме, например, при релятивистских скоростях электронов или при дополнительном учете температуры электронов. Учитывая малость угловой компоненты электрического поля в момент опрокидывания, представляют определенный интерес моделирование электростатических верхнегибридных колебаний [1] и сравнение их опрокидывания с представленным в работе. Кроме того, возможно обобщение полученных данных на случай намагниченной квантовой плазмы, а также они могут быть полезны при обсуждении различных физических эффектов, связанных с плазменными колебаниями и волнами.

Список литературы

  1. Davidson R.C. Methods in nonlinear plasma theory. New York: Academic Press, 1972. P. 33–53.

  2. Чижонков Е.В. Математические аспекты моделирования колебаний и кильватерных волн в плазме. М.: Физматлит, 2018. С. 12–240.

  3. Александров А.Ф., Богданкевич Л.С., Рухадзе А.А. Основы электродинамики плазмы. М.: Высшая школа, 1988. С. 102–113.

  4. Гинзбург В.Л., Рухадзе А.А. Волны в магнитоактивной плазме. М.: Наука, 1975. С. 112–124.

  5. Фролов А.А., Чижонков Е.В. О численном моделировании медленной необыкновенной волны в магнитоактивной плазме // Вычисл. методы и программирование. 2020. Т. 21. С. 420.

  6. Джексон Д. Ряды Фурье и ортогональные полиномы. М.: ГИТТЛ, 1948. С. 124–129.

  7. Чижонков Е.В. О схемах второго порядка точности для моделирования плазменных колебаний // Вычисл. методы и программирование. 2020. Т. 21. С. 115.

  8. Горбунов Л.М., Фролов А.А., Чижонков Е.В., Андреев Н.Е. Опрокидывание нелинейных цилиндрических колебаний плазмы // Физ. плазмы. 2010. Т. 36. № 4. С. 375.

  9. Borhanian J. Extraordinary electromagnetic localized structures in plasmas: Modulational instability, envelope solitons, and rogue waves // Physics Letters A. 2015. V. 379. № 6. P. 595.

  10. Moradi A. Energy behaviour of extraordinary waves in magnetized quantum plasmas // Phys. of Plasmas. 2018. V. 25. P. 052123.

  11. Силин В.П. Введение в кинетическую теорию газов. М.: Наука, 1971. С. 119.

  12. Силин В.П., Рухадзе А.А. Электромагнитные свойства плазмы и плазмоподобных сред. М.: Книжный дом “ЛИБРОКОМ”, 2012. С. 104–110.

  13. Фролов А.А., Чижонков Е.В. О применении закона сохранения энергии в модели холодной плазмы // Ж. вычисл. матем. и матем. физ. 2020. Т. 60. № 3. С. 503.

  14. MacCormack R.W. The effect of viscosity in hypervelocity impact cratering // J. Spacecr. Rockets. 2003. V. 40. № 5. P. 757.

  15. Шокин Ю.И., Яненко Н.Н. Метод дифференциального приближения. Применение к газовой динамике. Новосибирск: Наука, 1985. С. 251–252.

  16. Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. Т. 1. М.: Мир, 1990. С. 179–180.

  17. Фролов А.А., Чижонков Е.В. Об опрокидывании медленной необыкновенной волны в холодной магнитоактивной плазме // Матем. моделирование. 2021. Т. 33. № 6. С. 3.

  18. Фролов А.А., Чижонков Е.В. Влияние электрон-ионных соударений на опрокидывание цилиндрических плазменных колебаний // Матем. моделирование. 2018. Т. 30. № 10. С. 86.

  19. Maity C. Lagrangian Fluid Technique to Study Nonlinear Plasma Dynamics. PHD Thesis. Kolkata, India: Saha Institute of Nuclear Physics, 2013.

  20. de Doncker E. An adaptive extrapolation algorithm for automatic integration // SIGNUM Newsletter. 1978. № 13. P. 12.

  21. Cody W.J. The FUNPACK package of special function subroutines // ACM Trans. Math. Soft. 1975. № 1. P. 13.

  22. Chizhonkov E.V., Frolov A.A. Influence of electron temperature on breaking of plasma oscillations // Russ. J. Numer. Anal. Math. Modelling. 2019. V. 34. № 2. P. 71.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал