1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 62, № 7, 2022

Журнал вычислительной математики и математической физики, 2022, T. 62, № 7, стр. 1209-1223

О возбуждении и развитии неустойчивости в пограничном слое сжимаемого газа, наблюдаемых при высокоточном численном моделировании без введения искусственных возмущений

А. И. Толстых 1, *, Д. А. Широбоков 1, **

1 Федеральный исследовательский центр “Информатика и управление” РАН
119333 Москва, Вавилова, 40, Россия

* E-mail: tol@ccas.ru
** E-mail: shibo2506@yandex.ru

Поступила в редакцию 12.11.2021
После доработки 12.11.2021
Принята к публикации 10.01.2022

Полный текст (PDF)

Аннотация

Приводятся численные решения нестационарных уравнений Навье–Стокса в задаче о неустойчивости пограничного слоя на пластине, мгновенно введенной в дозвуковой поток, полученные на основе схемы с мультиоператорными аппроксимациями 16-го порядка. Использовалась традиционная постановка задачи без введения каких-либо источников возбуждения неустойчивости. Неустойчивые моды возникали вследствие наличия контролируемого фона малых возмущений точных решений, создаваемого аппроксимационными погрешностями схемы. Представленные решения описывают сценарий возникновения пакетов волн Толмина–Шлихтинга в окрестности передней кромки с зависящей от времени интенсивностью и их распространения вниз по потоку с возрастающими амплитудами. Оценивается влияние спектрального состава диссипативной части схемы на волновые числа и амплитуды волновых пакетов. Обсуждается соответствие развития неустойчивости в полученных решениях основным результатам линейной теории. Библ. 22. Фиг. 12.

Ключевые слова: дозвуковой пограничный слой, неустойчивость, волны Толмина–Шлихтинга, уравнения Навье–Стокса, мультиоператоры, схема 16-го порядка.

1. ВВЕДЕНИЕ

Возникновение неустойчивости течений в пограничных слоях, приводящей к ламинарно-турбулентному переходу, явилось предметом многочисленных теоретических, экспериментальных и численных исследований. Основной вклад в понимание причин возникновения неустойчивости внесла классическая теория волн Tолмина–Шлихтинга [1]. Ее основные выводы были подтверждены рядом экспериментов, указанных в [1], а также классическими экспериментами, описанными в [2]. В этих экспериментах изучалось естественное возбуждение неустойчивых мод управляемой фоновой турбулентностью, а также искусственное возбуждение в виде вибрирующих полос на поверхности обтекаемой пластины. В дальнейшем искусственные воздействия на пограничные слои такого и других типов использовались в различных экспериментах, внесших значительный вклад в описание явления неустойчивости и перехода ламинарного пограничного слоя в турбулентный (см. [3]–[6]). Введение искусственных возбудителей различных типов (например, в виде периодических локальных вдувов-отсосов через твердую поверхность) широко использовалось в многочисленных исследованиях, основанных на численном моделировании течений в пограничных слоях (главным образом, течений несжимаемой жидкости). Не перечисляя большое количество работ, посвященных этой теме, отметим статьи [8]–[11] и содержащиеся в них ссылки.

Введение искусственных возмущений осуществлялось также при численном моделировании течений в пограничных слоях при сверхзвуковом обтекании [12], [13]. Гиперзвуковые режимы были рассмотрены в [14], [15].

Использование возбудителей неустойчивости в численных исследованиях обычно связано либо с изучением восприимчивости ламинарного пограничного слоя, либо с получением лишь стационарных решений при отсутствии этих возбудителей.

В последнем случае можно задаться вопросом, не обусловлены ли набюдаемые стационарные решения без признаков неустойчивости свойствами используемых схем, числом узлов сетки, а также критерием выхода на стационарный режим. В этой связи можно рассуждать следующим образом.

Обычным теоретическим подходом к исследованию устойчивости является введение малых возмущениий того или иного типа в точные решения исходных уравнений или их упрощений. С другой стороны, отличие численного решения устойчивой схемы от точного в узлах сетки является малыми возмущениями последнего. Можно также говорить о том, что действие разностного оператора на точное решение, рассматриваемое в узлах сетки, есть действие аппроксимируемого оператора на это решение плюс погрешность аппроксимации, а погрешность аппроксимации можно рассматривать как некоторый источник, добавляемый к исходным уравнениям и возмущающий последние.

В случае устойчивости точного решения нормы этих сеточных функций характеризуют точность численных решений. В случае неустойчивого точного решения малые отклонения от этого решения в зависимости от их спектрального состава могут образовывать начальные данные для развития неустойчивых мод. Возможность численных решений различать эти моды и описывать их развитие в процессе интегрирования по времени (возможно длительного) зависит от спектральных свойств используемых схем и подробности сеток.

При использовании мультиоператорных схем высоких порядков для прямого численного моделирования неустойчивых течений в дозвуковых струях [16], недорасширенных сверхзвуковых струях [17], а также в случае изолированных вихрей [18], [19], было замечено, что кажущиеся не меняющимися в течение достаточно большого интервала времени численные решения уравнений Навье–Стокса или Эйлера внезапно переходили в квазипериодические нестационарные режимы.

Идея численного моделирования неустойчивых течений на основе уравнений Эйлера или Навье–Стокса без введения каких-либо механизмов возбуждения неустойчивости была использована в [20], где для исследования неустойчивости двумерного пограничного слоя при дозвуковом обтекании плоской пластины применялась мультиоператорная схема 16 -го порядка [21], снабженная диссипативным механизмом с контролируемыми спектральными свойствами.

Оказалось, что на используемой сетке численное решение нестационарных уравнений Навье–Стокса в окрестности передней кромки в процессе интегрирования по времени выходило на решение, похожее на стационарное решение Блазиуса. Однако внизу по течению после достижения некоторого времени стали наблюдаться наложенные на это решение распространяющиеся вниз по потоку пакеты волн Tолмина–Шлихтинга. На достаточном расстоянии от передней кромки наблюдались значительные возмущения решений с образованием локальных отрывных зон. Спектры этих возмущений показали хорошее соответствие с диаграммой неустойчивости теории волн Tолмина–Шлихтинга [1]. Поскольку схема была оптимизирована с целью минимизации фазовых ошибок аппроксимаций производных в широком диапазоне длин волн [21], основной вклад в погрешность аппроксимации и соответствующий фон малых возмущений вносился дополнительной диссипативной составляющей схемы в виде члена 15-го порядка малости относительно шага сетки с самосопряженным положительным оператором. Спектры его действия на сеточные функции имели широкополосный характер, что предположительно послужило основой для образования неустойчивых мод. Можно предположить, что здесь имеется некоторая аналогия с возбуждением неустойчивости фоновой турбулентностью в экспериментах [2].

Поскольку результаты [20] выявили четкий сценарий возбуждения и развития волн неустойчивости при конкретных параметрах сетки и конкретном фоне малых возмущений, остался открытым вопрос, насколько он изменится, если значительно уменьшить влияние этого фона.

Целью данной работы является исследование неустойчивости при входных данных задачи [20] с той разницей, что параметры диссипативного оператора выбраны таким образом, чтобы он генерировал фурье-гармоники с заметной амплитудой лишь в узкой области самых коротких волн, поддерживаемых сеткой. Последние заведомо находятся вне области неустойчивости линейной теории и можно предположить, что условная фоновая турбулентность с широкополосным спектром в этом случае очень мала.

Статья организована следующим образом. В разд. 2 описаны постановка задачи и детали используемой схемы. Численные результаты представлены в разд. 3. Разд. 4 содержит обсуждения и выводы.

2. ПОСТАНОВКА ЗАДАЧИ И СХЕМА

Как и в случае расчетов [20], рассматривалось течение вязкого сжимаемого газа, описываемого уравнениями Навье–Стокса, в прямоугольной области $0 \leqslant x \leqslant {{x}_{{\max }}},{\kern 1pt} $ $0 \leqslant y \leqslant {{y}_{{\max }}}$. При приведении уравнений к безразмерному виду в качестве характерных значений скорости использовалась скорость звука в невозмущенном потоке ${{c}_{\infty }}$, так что характерное значение времени $t$ оказывалось равным $L{\text{/}}{{c}_{\infty }}$. В качестве характерной длины использовалась длина $L$, для которой число Рейнольдса, вычисленное по параметрам невозмущенного потока, равнялось $5 \times {{10}^{5}}$. При этом полагалось, что ${{x}_{{\max }}},{\kern 1pt} {{y}_{{\max }}} = 0.2$. На левой границе задавались параметры невозмущенного потока с числом Маха ${\text{M}} = 0.5$, на верхней границе использовались характеристические условия, предполагающие распространение возмущений только изнутри области. Пластиной считалась нижняя граница области при $x \geqslant 0.25$ с условиями прилипания и заданной температурой, равной температуре торможения. На правой границе значения искомых функций определялись экстраполяцией решений внутри области.

Расчетная область покрывалась сеткой с числом узлов $3000 \times 100$. Ее шаги вдоль координаты $x$ были постоянными и равными $h = 5 \times {{10}^{{ - 3}}}$ до некоторого значения $x = {{x}_{*}}$, после которого они плавно увеличивались, способствуя таким образом гашению исходящих из области $x \leqslant 14.5$ волн. Вдоль $y$ осуществлялось сгущение сетки, при котором минимальный шаг около нижней границы был равен $0.0001$.

В начальный момент времени $t = 0$ предполагалось, что течение является невозмущенным во всей области, кроме поверхности пластины с нулевыми скоростями и заданной температурой. Это можно интерпретировать, как мгновенное введение пластины в равномерный поток.

Для  численного  решения  сформулированной  выше задачи использовалась схема с мультиоператорными аппроксимациями 16-го порядка гиперболической части нестационарных уравнений Навье–Стокса, записанных в дивергентной форме [21]. Общая теория мультиоператоров изложена в [22].

Поясним конструкцию мультиоператорной схемы на примере модельного уравнения ${{u}_{t}} + f{{(u)}_{x}} = 0$. Для аппроксимации производной по $x$ на сетке с шагом $h$ будем использовать линейную комбинацию базисных операторов, полученных из однопараметрического семейства операторов компактных аппроксимаций $l(c)$ путем задания различных значений параметра $c$:

(1)
$\frac{\partial }{{\partial x}} \approx {{L}_{M}}({{c}_{1}},{{c}_{2}}, \ldots ,{{c}_{M}}) = \sum\limits_{i = 1}^M \,{{\gamma }_{i}}l({{c}_{i}}),\quad \sum\limits_{i = 1}^M \,{{\gamma }_{i}} = 1.$
Коэффициенты ${{\gamma }_{i}}$ этой комбинации, названной мультиоператором, определяются из условия обращения в ноль $M - 1$ низших членов разложения в ряд Tейлора в погрешности аппроксимации (1). Используя задаваемые значения параметра, можно управлять спектральными свойствами мультиоператора и добиться того, чтобы его фурье-образ был близок к образу оператора первой производной в области коротковолновых гармоник.

В данном исследовании базисные операторы определялись полусуммой $l(c) = ({{L}_{l}}(c) + {{L}_{r}}(c)){\text{/}}2$, где левые и правые операторы ${{L}_{l}}$ и ${{L}_{r}}$ являются суперпозициями двухточечных операторов вида

${{L}_{l}}(c) = \frac{1}{h}{{R}_{l}}{{(c)}^{{ - 1}}}{{\Delta }_{ - }},\quad {{L}_{r}}(c) = \frac{1}{h}{{R}_{r}}{{(c)}^{{ - 1}}}{{\Delta }_{ + }},\quad {{R}_{l}}(c) = I + c{{\Delta }_{ - }},\quad {{R}_{r}}(c) = I - c{{\Delta }_{ + }},$
где ${{\Delta }_{ - }}$ и ${{\Delta }_{ + }}$ – операторы левых и правых двухточечных разностей (${{\Delta }_{ - }}{{u}_{j}} = {{u}_{j}} - {{u}_{{j - 1}}},$ ${{\Delta }_{ + }}{{u}_{j}} = {{u}_{{j + 1}}} - {{u}_{j}}$). Значения ${{c}_{i}},i = 1,2, \ldots ,8$, в (1) в рассматриваемой схеме распределены равномерно между своими минимальным и максимальным значениями ${{c}_{{\min }}}$ и ${{c}_{{\max }}}$, ${{\bar {c}}_{{\min }}} > - 1{\text{/}}2 + \delta ,$ $\delta > 0$. Число базисных операторов полагалось равным восьми. Поскольку разложения для действий базисных операторов на достаточно гладкие функции содержат только четные степени, имеем
${{L}_{M}}{{u}_{j}} = [{{u}_{x}}{{]}_{j}} + O({{h}^{{16}}}).$
Параметры ${{c}_{{\min }}},\;{{c}_{{\max }}}$ являются свободными параметрами. Они управляют свойствами мультиоператора и задаются таким образом, чтобы минимизировать дисперсионные погрешности мультиоператорной схемы для уравнения переноса.

В схемах высокого порядка для уравнений Эйлера или Навье–Стокса обычно требуется присутствие диссипативного механизма, способствующего подавлению паразитических осцилляций численных решений. Tакой механизм может быть представлен мультиоператорами с базисными операторами, определяемыми однопараметрическим семейством ${{D}_{0}}(c) = {{L}_{l}}(c) - {{L}_{r}}(c)$. Задавая набор параметров ${{\bar {c}}_{i}},i = 1,2, \ldots ,8$, и считая для удобства исследования, что они равномерно распределены между своими минимальным и максимальным значениями ${{\bar {c}}_{{\min }}},\;{{\bar {c}}_{{\max }}}$, построим мультиоператор

(2)
${{D}_{M}}({{\bar {c}}_{{{\text{min}}}}},{{\bar {c}}_{{{\text{max}}}}}) = \sum\limits_{i = 1}^8 \,{{\gamma }_{i}}{{D}_{0}}({{\bar {c}}_{i}}),\quad {{\bar {c}}_{{{\text{min}}}}} > - 1{\text{/}}2 + \delta ,\quad \delta > 0,$
такой, что ${{D}_{M}}{{u}_{j}} = O({{h}^{{15}}})$. Параметры ${{\bar {c}}_{{\min }}},\;{{\bar {c}}_{{\max }}}$ должны быть выбранными таким образом, чтобы мультиоператор был положительным в гильбертовом пространстве сеточных функций со скалярным произведением двух функций ${{u}_{h}}$ и ${{v}_{h}}$ вида $({{u}_{h}},{{v}_{h}}) = h\sum\nolimits_{j = - \infty }^\infty \,{{u}_{j}}{{v}_{j}}$.

При использовании мультиоператоров (1) и (2) полудискретизованная схема для модельного уравнения

(3)
$\frac{{\partial u}}{{\partial t}} + \frac{{\partial f(u)}}{{\partial x}} = 0,$
приобретает вид
(4)
$\frac{{\partial u}}{{\partial t}} + {{L}_{M}}f(u) + C{{D}_{M}}u = 0,\quad C = {\text{const}} \geqslant 0.$
Она устойчива в приближении замороженных коэффициентов как схема с положительными операторами.

Схема (4) легко обобщается на случаи, когда в уравнении (3) функции $f$ и $u$ являются векторными. При этом постоянную $C$ достаточно заменить на единичную матрицу, умноженную на некоторую постоянную. В случае нескольких пространственных переменных для производных по этим переменным строится свой мультиоператор.

2.1. Роль контролируемой диссипации

В случае устойчивых решений роль диссипативной добавки в виде третьего слагаемого в (4) сводится к демпфированию паразитических осцилляций численных решений, вызванных немонотонностью схемы. При этом он является добавкой к погрешности аппроксимации производной (в случае уравнений газовой динамики – к аппроксимации всех их членов) и вносит вклад высокого порядка малости в погрешность решения. В случае неустойчивых решений, как отмечалось во Введении, он может одновременно играть роль при создании фона малых возмущений, из которого возникают неустойчивые моды. Для оценки обеих возможностей в последнем случае рассмотрим его спектральные свойства.

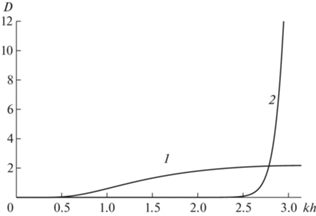
Представление $D = {{\hat {D}}_{M}}(\alpha ;{{\bar {c}}_{{\min }}},{{\bar {c}}_{{\max }}})$ оператора ${{D}_{M}}$ в пространстве Фурье (его фурье-образ) в силу его самосопряженности является вещественной функцией безразмерного волнового числа $\alpha = kh$. При некоторых значениях параметров (${{\bar {c}}_{{\min }}},{{\bar {c}}_{{\max }}}$), рассматриваемых как допустимые, эта функция положительна в диапазоне волновых чисел $\alpha \in [0,\pi ]$ гармоник, поддерживаемых сеткой с шагом $h$. Первый член ее разложния по $\alpha $ в окрестности нуля имеет вид $c({{\bar {c}}_{{\min }}},{{\bar {c}}_{{\max }}}){{\alpha }^{{2M - 1}}}$, указывающий на очень быстрое стремление к нулю этой функции при уменьшении $\alpha $. На фиг. 1 представлены функции $D(\alpha )$ для двух вариантов выбора параметров, использовавшихся в [20] (кривая 1) и в данном исследовании (кривая 2).

Фиг. 1.

Фурье-образы диссипативных операторов двух типов.

В спектрах волн неустойчивоcти в численных решениях [20] при используемых шагах сетки доминировали гармоники с длинами волн, для которых $\alpha = kh \approx 0.25$. При этом значения $\alpha $ для самых коротких волн с очень маленькими амплитудами, наблюдаемых в спектрах, достигали величин порядка $0.5$. Согласно фиг. 1, интервал $\alpha \in [0,0.5]$ – это приблизительно тот интервал, в котором значения $D(\alpha )$ визуально равны нулю (на самом деле очень малы). В полном согласии с этим фактом численные решения из [20] указывают на то, что декременты затухания гармоник, обусловленные диссипативными добавками, оказались значительно меньшими инкремента их возрастания вследствие неустойчивости Tолмина–Шлихтинга. В расчетах, представленных ниже, значения декрементов в этом интервале, как показывает их подробный анализ, оказываются на много порядков меньшими, сохраняя при этом свои малые значения вплоть до достаточно больших значений $\alpha $.

Для оценки роли диссипативной добавки в случае неустойчивости решений исходных уравнений обратимся снова к схеме (4) . Будем рассматривать входящие в нее сеточные функции как проекции на сетку функций непрерывного аргумента из пространства Гильберта. Произведя линеаризацию исходного уравнения, перейдем в пространство Фурье. При этом будем считать для простоты, что мультиоператор ${{L}_{M}}$ заменен на дифференциальный оператор первой производной, т.е. прeнебрежем вносимой им погрешностью аппроксимации (она мала при $\alpha < 2.5$ вследствие оптимизации мультиоператора). В результате получим обыкновенное дифференциальное уравнение вида

(5)
$\hat {u}{{(k)}_{t}} + ika\hat {u}(k) + C{{\hat {D}}_{M}}(kh)\hat {u}(k) = 0,$
где $\hat {u}(k)$ – преобразование Фурье функции $u(x)$ и $a = f_{u}^{'} = {\text{const}}$. В соответствии с предыдущими оценками будем рассматривать третье слагаемое как малое возмущение, представимое в виде
$\epsilon {{d}_{M}}(kh)\hat {u}(k),\quad \epsilon \ll 1.$
Представив решение уравнения (5) в виде $\hat {u}(k) = {{u}_{0}} + \epsilon v$, где ${{u}_{0}}(k)$ – решение этого уравнения при $C = 0$, получим для $v(k,t)$ уравнение вида ${{v}_{t}} + ikav = - {{d}_{M}}{{u}_{0}} = - f(k)$. Решая его, найдем для добавки $\delta u(x,t)$ к $u(x,t)$, возникающей при $C \ne 0$, выражение вида
(6)
$\delta u(x,t) = \epsilon \int\limits_{ - \infty }^\infty {(f(k){\text{/}}iak){{e}^{{ik(x - at)}}}dk} - \epsilon \int\limits_{ - \infty }^\infty {(f(k){\text{/}}iak){{e}^{{ikx}}}dk} .$
Первое слагаемое в правой части (6) указывает на возбуждение возмущений, распространяющихся с фазовой скоростью $a$, а второе – на возбуждение независимых от времени возмущений. В случае устойчивого решения исходного дифференциального уравнения структура вносимых возмущений не представляет особого интереса, поскольку они являются погрешностями численного решения. В случае неустойчивого решения эти малые возмущения могут создать условия для образования неустойчивых мод. Во всех случаях возникающий фон малых возмущений определяется произведением ${{\hat {D}}_{M}}(kh){{u}_{0}}(k)$ на интервале волновых чисел гармоник, разрешаемых схемой на сетке с шагом $h$.

Приведенные выше соображения и оценки направлены на попытку объяснить кажущееся самовозбуждение неустойчивости в численных решениях уравнений Навье–Стокса. Чтобы подтвердить их, в данном исследовании использовался выбор параметров оператора ${{D}_{M}}$, соответствующий кривой 2 на фиг. 1. В этом случае ввиду пренебрежимо малых значений ${{\hat {D}}_{M}}$ на “актуальном” интервале волновых чисел создаваемый им фон ожидается быть пренебрежимо малым. Условно две возможные ситуации можно сопоставить с наличием и отсутствием (или очень слабой) турбулентности в реальных условиях обтекания.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Численные решения уравнений Навье–Стокса с использованием оператора ${{D}_{M}}$ второго типа (т.е. соответствующего кривой 2 на фиг. 1) показали, что характер возникновения и развития неустойчивости во многом аналогичен описанному в [20] при значительно меньших амплитудах возникающих и распространяющихся волн Tолмина–Шлихтинга. Его можно охарактеризовать следующим образом. В течение начального интервала времени (приблизительно $t < 60$) в окрестности передней кромки происходит релаксация начально невозмущенного потока к течению типа Блазиуса в пограничном слое несжимаемой жидкости. В течение всего времени расчета течение в этой окрестности характеризуется устойчивыми малыми колебаниями типа стоячих волн. В полном соответствии с линейной теорией устойчивости, начиная с некоторого расстояния от передней кромки, т.е. начиная с некоторого значения числа Рейнольдса ${\text{R}}{{{\text{e}}}_{\delta }}$, вычисленного по толщине вытеснения и этому расстоянию, устойчивые колебания переходят в распространяющиеся вниз по потоку пакеты волн Tолмина–Шлихтинга. Начальные амплитуды этих пакетов меняются с течением времени, создавая видимость “прерывистости” возникающих возмущений. Амплитуды пакетов как функции их координат $x(t)$ возрастают до момента их выхода из области с постоянными шагами сетки (приблизительно до $x < 14.5$) и перехода в область их демпфирования в остальной части расчетной области с возрастающими шагами сетки.

Существенные отличия численных решений для вариантов с диссипациями первого и второго типа (в соответствии с обозначениями на фиг. 1) отчетливо проявляются при вычислении коэффициентов трения на поверхности пластины $f$. На фиг. 2 их распределения вдоль пластины в момент времени $t = 140$ показаны вместе с решением Блазиуса в случае несжимаемой жидкости. Для варианта 1 эти решения взяты из [20], а для варианта 2 они получены в рамках данного исследования.

Фиг. 2.

Cравнение распределений коэффициентов трения вдоль поверхности пластины; сплошная линия – результаты из [20], пунктирная линия – результаты данных расчетов, маркеры – решение Блазиуса для несжимаемой жидкости.

На фиг. 2 видно, что отличия от решения Блазиуса незначительны для обоих диссипаций при $x < 5$ и во всей области для диссипации второго типа. На рисунке при $x > 8$ видна мгновенная картина волновых пакетов, являющихся проявлеием неустойчивости Tолмина–Шлихтинга в случае диссипации первого типа, не заметного в случае диссипации второго типа. Tаким образом, фигура сразу же подтверждает предположение о том, что существенную роль в возбуждении неустойчивости в решениях [20] играет фон малых возмущений, возникающий при использовании диссипации первого типа.

В дальнейшем, следуя многим экспериментальным и теоретическим исследованиям, будем характеризовать неустойчивость пограничного слоя возмущениями скорости около поверхности тела (см., например, классичские эксперименты [2]). Соответственно, основной интерес в данном исследовании будет представлять в фиксированные моменты $t$ продольная скорость $U(t,x) = u(t,x,{{y}_{*}})$, где ${{y}_{*}} = 5.7 \times {{10}^{{ - 4}}}$ суть расстояние от поверхности пластины близкого к ней узла сетки. Непосредственное рассмотрение полученных значений функции $U(t,x)$ позволяет проследить развитие волновых пакетов с достаточно большими амплитудами (как это видно на фиг. 2), однако оно оказывается неэффективным при описании ее малых и очень малых возмущений. Следуя [20], для выявления таких возмущений будет использоваться следующий прием. На отдельных интервалах $[{{x}_{i}},{{x}_{j}}]$ строятся полиномы наилучшего среднеквадратичного приближения к функции $U$ с базисными функциями, являющимися полиномами Чебышёва для этих интервалов. Затем рассматриваются отклонения $\delta U$ полученных локальных аппроксимаций от $U$. Оказалось, что функции $\delta U(x)$ позволяют обнаруживать хорошо организованные волновые структуры с очень малыми колебаниями около меняющихся с координатой $x$ средними значениями $U(x)$ и вычислять их спектры. При этом следует иметь в виду, что амплитуды колебаний $\delta U(x)$ есть амплитуды в обычно принятом смысле только при U(x) = const. В противном случае они лишь характеризуют пульсации скорости на отдельных интервалах изменения $x$.

3.1. Возмущения в окрестности передней кромки

В отличие от численных решений [20], визуализировать волновые процессы в случае диссипации второго типа во всей расчетной области удается лишь с применением описанного выше подхода. Вычисление функций $\delta U(x)$ для различных моментов времени $t$ показало, что их изменения имеют на локальных интервалах изменения $x$ колебательный характер и, в частности, описывают хорошо организованные волновые пакеты. В окрестности передней кромки аппроксимирующие полиномы являются быстро убывающими функциями, что приводит к необходимости использовать последовательность интервалов сравнительно небольшой длины.

На фиг. 3 для диссипации второго типа и нескольких значений времени $t$ представлены зависимости $\delta U(x)$ для интервалов $x \in [1,2],\;[2,3],\;[3,5],\;[5,8]$, в каждом из которых вычислялись свои полиномы наилучшего среднеквадратичного приближения. Как видно, первый интервал характеризуется визуально независимыми от времени колебаниями $\delta U(x)$ с длинами волн порядка $0.25$, на которые наложены убывающие с $x$ коротковолновые осцилляции типа “пилы”. Последние естественно считать паразитическими осцилляциями, характерными для схем высокого порядка, возникающими вследствие больших градиентов параметров потока около острой передней кромки. При этом несущие относительно длинные волны стоячего типа, как можно предположить, характеризуют численные решения уравнений Навье–Стокса в окрестности острой кромки. Они визуально не зависят от времени и можно считать, что при $x < 2$ течение является устойчивым. Заметим, что число Рейнольдса ${\text{R}}{{{\text{e}}}_{\delta }}$, вычисленное по толщине вытеснения, в данных расчетах при $x = 2$ равно приблизительно 1800. Хотя оно больше критического числа ${\text{R}}{{{\text{e}}}_{\delta }}$ в линейной теории для несжимаемой жидкости [1], устойчивость течения при меньших значения этого числа согласуется с результатом этой теории.

Фиг. 3.

Образование волновых пакетов в окрестности передней кромки в данных расчетах. Интервал $x \in [1,8]$ разбит на четыре части с разными порядками амплитуд отклонений от усредненных распределений.

Более подробное изучение длинноволновых колебаний показывает, что расстояние между их пиками уменьшается с увеличением расстояния от кромки ( это видно, в частности, на интервале $x \in [1,2]$). Пространственные амплитудные спектры, вычисленные для этого интервала в различные моменты времени, имеют пики в диапазоне волновых чисел $k$ приблизительно от $k = 9$ до $k = 25$. В координатах (${\text{R}}{{{\text{e}}}_{\delta }},k\delta $) эти числа располагаются около нижней ветви нейтральной кривой диаграммы неустойчивости [1].

В нижнем по течению интервале $[2,3]$ с увеличенными значениями ${\text{R}}{{{\text{e}}}_{\delta }}$ наблюдаются зависящие от времени колебания с заметными различиями амплитуд. Их визуализация с малыми интервалами изменения времени показывает, что они распространяются вниз по течению, характеризуя начало конвективной неустойчивости. На последующих интервалах видны хорошо организованные волновые пакеты. Их наполнения можно рассматривать как признаки возникающих волн Tолмина–Шлихтинга. Пакеты на интервалах [3, 5] и [5, 8] являются развитием пакетов, образовавшихся ранее при меньших значениях координаты $x$. Чтобы проследить эволюцию конкретного пакета во времени и пространстве, на фиг. 4 показаны функции $\delta U(x)$ в последовательные моменты времени на одном и том же интервале. Видно, что пакет, наблюдаемый при $t = 30$, за 12 единиц времени переместился вниз по потоку в слегка модифицированном виде приблизительно на 2 единицы расстояния. Это позволяет грубо оценить его групповую скорость ${{v}_{g}}$ как ${{v}_{g}} \approx 0.17$. В процессе этого движения пакета максимальные амплитуды колебаний возросли приблизительно в три раза. При $t = 54$ на рассматриваемом интервале пакет отсутствует – он переместился за его пределы, однако заметен новый пакет с на четыре порядка меньшими амплитудами (его не было видно на фоне доминирующего пакета в предыдущие моменты времени).

Фиг. 4.

Развитие волнового пакета во времени и пространстве внизу по течению в данных расчетах.

Для сравнения полученных решений с решениями из [20] на фиг. 5 представлены функции $\delta U(x)$ в случае диссипации первого типа для моментов времени из фиг. 3. При $x < 5$ на рисунке видны визуально стационарные длинноволновые колебания с наложенными на них убывающими паразитическими колебаниями, аналогичные представленным на фиг. 3. Как и в случае диссипации второго типа, внизу по течению наблюдаются сформированные волновые пакеты с сильно меняющимися со временем амплитудами.

Фиг. 5.

Образование волновых пакетов в окрестности передней кромки в расчетах [20].

Неравномерный, “прерывистый”, характер возбуждения волн Tолмина–Шлихтинга, а также их рост и перемещение иллюстрирует фиг. 6. Tам показаны максимальные значения амплитуд колебаний $\delta U(x)$ на интервалах $x \in [4,6]$ и $x \in [5,7]$ как функции времени при наличии и отсутствии фона малых возмущений, создаваемого диссипацией первого типа. Видны черты сходства изменения со временем максимальных значений в обоих случаях при существенно больших значениях последних при наличии фона. Видно также, что в обоих случаях пики максимальных значений перемещаются вниз по потоку, причем это перемещение приблизительно соответствует оценкам групповой скорости пакетов.

Фиг. 6.

Максимальные значения амплитуд колебаний на интервалах $x$ [4, 6] (сплошные линии) и [5, 7] (штриховые линии); (a) – в данных расчетах, (б) – в расчетах [20].

Пространственные спектры для интервала $x \in [5,7]$, вычисленные при $t = 50$ и $t = 150$, приведены на фиг. 7. Они имеют похожие формы, но сильно отличаются амплитудами. Их максимальные значения, в соответствии с фиг. 6, оказываются на несколько порядков большими в случае диссипации первого типа.

Фиг. 7.

Амплитудные спектры на интервале $x \in [5,8]$; кривые 1 и 2 соответствуют расчетам [20] и данным расчетам.

Оба типа спектров характеризуются пиками в области небольших значений волнового числа $k$, отнесенного к ${{L}^{{ - 1}}}$, где $L$ – длина, по которой вычислено число Рейнольдса ${\text{Re}} = 5 \times {{10}^{5}}$. Эти пики в кривых 1 и 2 расположены в окрестности $k = 50$ и $k = 35$ соответственно. Переходя к безразмерным волновым числам $k\delta $, где $\delta $ – толщина вытеснения, можно усмотреть, что при $x = 6$ гармоникам с такими волновыми числами соответствуют точки внутри области неустойчивости линейной теории.

Следуя линейной теории устойчивости, на основании анализа численных решений в окрестности передней кромки естественно предположить следующее.

В ближайшей окрестности кромки, где числа ${\text{R}}{{{\text{e}}}_{\delta }}$ достаточно малы, волновые числа длинноволновых колебаний в координатах диаграммы неустойчивости лежат несколько ниже нижней ветви нейтральной кривой. Это объясняет устойчивость этих колебаний. При увеличении координаты $x$ толщина вытеснения и с ней ${\text{R}}{{{\text{e}}}_{\delta }}$ возрастают; при этом волновые числа $k\delta $ попадают в область неустойчивости несколько выше этой ветви. Отсюда следует распространение пакетов вниз по течению с возрастанием амплитуд гармоник.

На основании представленных выше результатов можно заключить, что независимо от наличия или отсутствия фона малых возмущений, создаваемого диссипацией первого типа, возбудителями конвективной неустойчивости в численных решениях уравнений Навье–Стокса являются малые длинноволновые колебания вдоль оси $x$ в ближайшей окрестности передней кромки пластины. Влияние этого фона в этой области проявляется в значительном увеличении интенсивности пульсаций и небольшом смещении спектра в сторону более коротких волн.

3.2. Распространение возмущений вниз по потоку

В полном соответствии с линейной теорией, анализ численных решений в данных расчетах, как и в расчетах [20], указывает на распространение вниз по потоку сформировавшихся в окрестности передней кромки волновых пакетов различной интенсивности с заметным увеличением амплитуд их наполнений. Однако увидеть их можно только, рассматривая отклонения $\delta u(x)$ от усредненных значений $U(x)$ на определенных интервалах. Если это не делать, то получаемые решения с точностью до ${{10}^{{ - 4}}}$ кажутся стационарными. Примеры функций $\delta u(x)$ при $x > 8$ в последовательные моменты времени приведены на фиг. 8. В верхней части фигуры показаны положения одного из пакетов при $t = 46$, 62, 82 на интервале $x \in [8,14]$. Сравнивая положения пакетов, можно приблизительно оценить групповую скорость их распрoстранения как ${{v}_{g}} \approx 0.15$. На основании этого можно заключить, что первоначальное положение и форма этого пакета изображены на фиг. 6 при $t = 30$. На фигуре также видно, что за 20 единиц времени максимальные значения амплитуд его наполнения увеличились приблизительно в два раза. Назовем этот пакет пакетом A. Чтобы отобразить следующий за ним пакет B, имеющий меньшие амплитуды, в средней части фигуры показаны функции $\delta u(x)$ на разных интервалах в моменты времени $t = 70$, 76, 82. Нижняя часть фигуры иллюстрирует более сложную форму пакетов и их эволюцию на более поздних временах. В соответствии с малыми амплитудами пульсаций в окрестности передней кромки при $t > 100$, максимальные амплитуды этих пакетов весьма малы. Tем не менее они указывают на их существенное возрастание (на несколько порядков) при распространении пакетов вниз по потоку.

Фиг. 8.

Волновые пакеты в последовательные моменты времени в данных численных решениях.

На фиг. 9 приведены спектры пакетов при $t = 62,$ $t = 76,$ $t = 140$, изображенных на фиг. 8 в средней ее части. Видно, что эти спектры с волновыми числами пиков в окрестности $k = 30$ достаточно узкие; они близки к спектрам в окрестности передней кромки. Это указывает на то, что в процессе распространения пакетов почти не появлялись новые гармоники с волновыми числами в области неустойчивости линейной теории.

Фиг. 9.

Спектры волновых пакетов, изображенных на фиг. 4; кривые 1, 2, 3 соответствуют временам $t = 30$, 42, 54.

В случае численных решений из [20] интенсивные пульсации продольной скорости можно непосредственно наблюдать, рассматривая функцию $U(x)$. Картины волновых пакетов в фиксированные моменты времени в этих решениях приведены на фиг. 10. В верхней части фигуры ($t \leqslant 82$) показано распространение вниз по потоку пакета с наибольшими амплитудами, образовавшегося при небольших временах в окрестности передней кромки. Сравнивая картину его развития с аналогичной картиной эволюции пакета в верхней части фиг. 5, можно увидеть, что при приблизительно одинаковой групповой скорости, пакеты существенно различаются. Помимо большой разницы в амплитудах колебаний функций $U(x)$ и $\delta u(x)$, пакет во втором случае в процессе перемещения вниз по потоку почти не меняет своей формы с максимальными амплитудами в своем центре; при этом расстояния между пиками колебаний в нем кажутся постоянными. Пакет на фиг. 10 лишь на малых временах имеет такую простую форму. В процессе его перемещения максимальные амплитуды смещаются в его переднюю часть, а характер наполнения становится менее регулярным.

Фиг. 10.

Развитие волновых пакетов внизу по течению в численных решениях [20].

Сравнение максимальных значений функций $\delta u(x)$ на интервале $[13,14]$ как функций времени приведены на фиг. 11 для обоих типов диссипаций. Их повышенные значения в обоих случаях наблюдаются приблизительно на временах, соответствующих прибытию из окрестности передней кромки пакетов с наиболее интенсивными пульсациями.

Фиг. 11.

Максимальные значения амплитуд на интервале $x \in [13,14]$ как функций времени; (a) – в данных расчетах, (б) – в расчетах [20].

Спектры функции $\delta u(x)$ в случае диссипации из [20], вычисленные для интервала $[8,14.5]$ в различные моменты времени, приведены на фиг. 12. В отличие от спектров при отсутствии фона малых возмущений, создаваемого диссипацией второго типа, они имеют более широкую полосу пиковых волновых чисел. Они отличаются также большей изменчивостью и на порядки большими значениями максимальных амплитуд. При этом максимальные пики наблюдаются при больших волновых числах (приблизительно в окрестности $kP$). Расширение спектров и увеличение амплитуд пульсаций указывают на возбуждение новых неустойчивых мод с большими начальными амплитудами. Tаким образом, находит подтверждение предположение о том, что источником неустойчивости являются малые возмущения с достаточно широким спектром, создаваемые диссипацией первого типа.

Фиг. 12.

Спектры волновых пакетов на интервале $x \in [8,14.5]$ в расчетах [20].

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ И ВЫВОДЫ

В данном исследовании представлены численные решения уравнений Навье–Стокса, описывающие возбуждение и развитие волн Tолмина–Шлихтинга без применения искусственного возбуждения неустойчивости в случае пластины, внезапно введенной в дозвуковой поток. Эти решения были получены на основе мультиоператорной схемы 16 -го порядка с управляемым диссипативным механизмом. В случае гладких функций он вносит вклад в погрешность аппроксимации порядка $O({{h}^{{15}}})$, но при этом может играть роль малых возмущений точных решений, из которых рождаются волны неустойчивости. Были рассмотрены два типа диссипативного оператора. В одном случае его действие характеризуется широким спектром фурье-гармоник, создающих возбуждающий фон для возникновения неустойчивости. В другом случае он действовал только на гармоники с самыми короткими длинами волн, поддерживаемыми сетками. Оказалось, что в обоих случаях наблюдается один и тот же сценарий возникновения и распространения волн Tолмина–Шлихтинга. Согласно численным решениям, в окрестности передней кромки в процессе релаксации к течению, близкому к течению Блазиуса, наблюдаются длинноволновые пространственные колебания придонной продольной скорости, напоминающие стоячие волны. Они имеют малые амплитуды, не возрастающие с течением времени. Это соответствует выводам линейной теории об устойчивости течения при малых числах Рейнольдса, вычисленных по толщине вытеснения пограничного слоя. С увеличением расстояния от передней кромки, когда это число возрастает, наблюдается переход колебаний стационарного типа в пакеты волн, распространяющихся вниз по потоку с увеличением амплитуд. Волновые числа этих волн приблизительно соответствуют волновым числам неустойчивых мод, описываемых линейной теорией. Можно показать, что групповые скорости в численных решениях близки к фазовым скоростям индивидуальных гармоник в линейной теории.

Разница в решениях для двух типов диссипации состоит в следующем. В случае отсутствия фона малых возмущений, создаваемого диссипацией первого типа, начальные амплитуды волн Tолмина–Шлихтинга весьма малы (отклонения от усредненных продольных распределений скорости около твердой поверхности имеют порядки ${{10}^{{ - 9}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 7}}}$). Соответственно, максимальные значения амплитуд на больших расстояниях от передней кромки несмотря на их возрастания также малы (поядка ${{10}^{{ - 4}}}$). Пространственные спектры волновых пакетов в течение всего времени своего развития имеют достаточно узкий характер, не сильно отличаясь от начальных спектров; это указывает на отсутствие появления новых неустойчивых мод.

Существование этого фона в численных решениях характеризуется двояким воздействием. Во-первых, начальные значения амплитуд оказываются на порядки большими и после их возрастания внизу по потоку наблюдаются локальные отрицательные скорости. Во-вторых, спектры значительно расширяются, приобретая широкополосный характер. Это указывает на появление новых неустойчивых мод, генерируемых фоном. Приблизительные оценки их волновых чисел как функций числа Рейнольдса указывают на соответствие (на качественном уровне) с диаграммой неустойчивости в линейной теории.

Можно предположить, что при аналогичном изучении пространственного течения наличие возбуждающего фона с широкополосным спектром может служить некоторой имитацией фоновой турбулентности в реальных условиях.

Список литературы

  1. Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1969.

  2. Schubauer G.B., Scramstad H.K. Laminar-boundary-layer oscillations and transition on a flat plate. 1948; NACA Rep. 909.

  3. Klebanoff P.S., Tidstrom K.D., Sargent L.M. Numerical simulation of transition in wall-bounded shear flows // Annu. Rev. Fluid Mech. 1962. V. 23. P. 495–537.

  4. Gaster M., Grant I. An experimental investigation of the formation and development of a wavepacket in a laminar boundary layer // Proc. R. Soc. Lond. A. 1975. V. 347. P. 253–269.

  5. Качанов Ю.С., Козлов В.В., Левченко В.Я. Нелинейное развитие волны в пограничном слое // Изв. АН СССР. МЖГ. 1977. T. 3. С. 49–58.

  6. Бородулин В.И., Качанов Ю.С. Формироваие и развитие когерентных структур в переходном пограничном слое // Ж. прикл. механ. и техн. физ. 1995. Т. 36. № 4. С. 60–97.

  7. Cleiser L., Zang T.A. Numerical simulation of transition in wall-bounded shear flows. Annu. Rev. Fluid Mech. 1991. V. 23. P. 495–537.

  8. Rist U., Fasel H. Direct numerical simulation of controlled transition in a flat-plate boundary layer. J. Fluid Mech. 1995. V. 298. P. 211–248.

  9. Borodulin V.I., Gaponenko V.R., Kachanov Y.S. et al. Late-Stage Transitional Boundary-Layer Structures. Direct Numerical Simulation and Experiment // Theoret. Comput. Fluid Dynamics. 2002. V. 15. P. 317–337.

  10. Yeo K.C., Zhao X., Wang Z.Y., Ng K.C. DNS of wavepacket evolution in a Blasius boundary layer // J. Fluid Mech. 2010. V. 652. P. 333–372.

  11. Bhaumik S., Sengupta T. Receptivity to harmonic excitation following nonimpulsive start for boundary-layer flows // AIAA Journal. 2017. V. 55. P. 3233–3238.

  12. Muppidi S., Mahesh K. DNS of transition in supersonic boundary layers // AIAA paper, 2010-4440.

  13. Liu C., Lu P. DNS Study on Physics of Late Boundary Layer Transition // AIAA paper, 2012-0083.

  14. Егоров И.В., Новиков А.В. Прямое численное моделирование ламинарно-турбулентного обтекания плоской пластины при гиперзвуковых скоростях потока // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 6. С. 1064–1081.

  15. Егоров И.В., Новиков А.В., Федоров А.В., Прямое численное моделирование ламинарно-турбулентного перехода при гиперзвуковых скоростях потока на супер-ЭВМ // Ж. вычисл. матем. и матем. физ. 2017. Т. 57. № 8. С. 1347–1373.

  16. Липавский М.В., Tолстых А.И. Об одной мультиоператорной схеме десятого порядка и ее применение в прямом численном моделировании поля // Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 4. С. 600–614.

  17. Tolstykh A.I., Shirobokov D.A. Fast calculations of screech using highly accurate multioperators-based schemes // Applied Acoustics. 2013. V. 74. P. 102–109.

  18. Tolstykh A.I., Lipavskii M.V. Instability and acoustic fields of the Rrankine vortex as seen from long-term calculations with the tenth-order multioperators-based scheme // Mathematics and Computers in Simulation. 2018. V. 147. P. 301–320.

  19. Tolstykh A.I., Lipavskii M.V. General scenario and fine details of compressible Gaussian vortex unforced instability // European Journal of Mechanics – B/Fluids. 2021. V. 87. P. 161–170.

  20. Tolstykh A.I., Shirobokov D.A. Observing production and growth of Tollmien-Schlichting waves in subsonic flat plate boundary layer via exciters-free high fidelity numerical simulation // J. of Turbulence. V. 21. № 11. P. 632–649.

  21. Tolstykh A.I. 16th and 32nd multioperators based schemes for smooth and discontinuous solutions // Commun. in Comput. Phys. 2017. V. 45. P. 33–45.

  22. Tолстых А.И. Компактные и мультиоператорные аппроксимации высокой точности для уравнений в частных производных. М.: Наука, 2015.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал