Журнал вычислительной математики и математической физики, 2023, T. 63, № 1, стр. 43-50

1. ВВЕДЕНИЕ

Несмотря на то что алгоритмический подход к символьному суммированию имеет длинную историю [1], [2], стандартные алгоритмы суммирования и их реализации в системах компьютерной алгебры обладают тем недостатком, что они могут без необходимости требовать времени выполнения, которое экспоненциально зависит от размера входа. Это происходит из-за хорошо известного эффекта “разбухания промежуточных выражений”.

Одним из важных промежуточных представлений, возникающих в алгоритмах символьного суммирования, является т.н. форма Госпера–Петковшека рациональной функции [2], [3]. Современный термин для этого представления – полиномиальная нормальная форма (далее ПНФ [3]). Одна из проблем с ПНФ заключается в том, что степень одного из образующих эту форму полиномов может экспоненциально зависеть от размера числителя и знаменателя данной рациональной функции. Поскольку степень ПНФ определяет временную сложность выполнения алгоритмов суммирования, это напрямую влияет на эффективность их реализации в системах компьютерной алгебры.

Далее будет показано, как, используя компактное представление ПНФ, можно избежать разбухания промежуточных выражений и существенно понизить сложность алгоритма Госпера [2] для суммируемых гипергеометрических термов. В разд. 2 даются необходимые предварительные сведения и определения. В разд. 3 кратко описывается алгоритм Госпера. В разд. 4 предлагается основанная на компактном представлении модификация этого алгоритма, а в разд. 5 рассматриваются примеры, основанные на реализации предложенных алгоритмов в системе компьютерной алгебры Мэйпл [4].

2. ФАКТОРИАЛЬНЫЕ ПОЛИНОМЫ И ПНФ

Пусть $\mathbb{K}$ – поле нулевой характеристики, $x$ – независимая переменная, $E$ – оператор сдвига относительно $x$, т.е. $Ef(x) = f(x + 1)$ для произвольной функции $f(x)$. Ненулевое выражение $F(x)$ называется гипергеометрическим термом над $\mathbb{K}$, если существует рациональная функция $r(x) \in \mathbb{K}(x)$ такая, что $EF(x){\text{/}}F(x) = r(x)$. Обычно $r(x)$ называют рациональным сертификатом терма $F(x)$.

Задача неопределенного гипергеометрического суммирования: по гипергеометрическому терму $F(x)$ найти гипергеометрический терм $G(x)$, удовлетворяющий линейному разностному уравнению первого порядка

Если такой терм найден, результат неопределенного суммирования записывается в виде где $c$ – произвольная постоянная или периодическая функция $x$ с периодом 1.

Например, $\frac{{{{4}^{x}}{{x}^{4}}}}{{\left( {\begin{array}{*{20}{c}} {2{\kern 1pt} x} \\ x \end{array}} \right)}}$ является гипергеометрическим термом с сертификатом $\frac{{2{{{\left( {x + 1} \right)}}^{5}}}}{{{{x}^{4}}\left( {2{\kern 1pt} x + 1} \right)}}$ и суммой

(произвольная постоянная обычно опускается).

Для ненулевых полиномов $p(x)$ и $q(x)$ дисперсионным множеством называется множество натуральных чисел $h$ таких, что $p(x)$ и $q(x + h)$ имеют нетривиальный общий делитель ($\deg ({\text{НОД}}(p(x),q(x + h)) > 0$). Если это множество непусто, то дисперсией $p(x)$ и $q(x)$ является его наибольший элемент, в противном случае дисперсия $p(x)$ и $q(x)$ полагается равной $ - \infty $ [1].

Два полинома $u(x),{v}(x) \in \mathbb{K}[x]$ называются эквивалентными по сдвигу, если существует 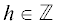такое, что $u(x + h) = v(x)$. Установление эквивалентности по сдвигу двух полиномов не составляет труда [5]. Имея несколько различных эквивалентных по сдвигу полиномов ${{u}_{1}}(x), \ldots ,{{u}_{t}}(x)$, легко перечислить их в порядке от “крайнего левого” до “крайнего правого”, т.е. переупорядочить их как ${{v}_{1}}(x), \ldots ,{{v}_{t}}(x)$ таким образом, что для любых индексов $i,j \in \{ 1, \ldots ,t\} ,$ $i < j$, ${{v}_{j}}(x + {{h}_{{ij}}}) = {{v}_{i}}(x)$ и ${{h}_{{ij}}} > 0$ . Мы ссылаемся на ${{v}_{1}}(x)$ как на наименьший и на ${{v}_{t}}(x)$ как на наибольший элемент класса сдвиговой эквивалентности, образованного полиномами ${{u}_{1}}(x), \ldots ,{{u}_{t}}(x)$.

3. АЛГОРИТМ ГОСПЕРА

В [2] Госпер описал процедуру суммирования гипергеометрического терма, которая широко используется в системах компьютерной алгебры. Алгоритм основан на простом наблюдении: если заданный гипергеометрический терм $F(x)$ имеет гипергеометрическую сумму $G(x)$, то термы $G(x)$ и $F(x)$ подобны: существует функция $Y(x) \in \mathbb{K}(x)$ такая, что $G(x) = Y(x)F(x)$. Это сводит исходную задачу суммирования к задаче нахождения рационального решения $Y(x)$ уравнения

где $r(x)$ – рациональный сертификат терма $F(x)$.

Для решения (5) рациональный сертификат преобразуется к ПНФ $(z,A(x),B(x),C(x))$ и поиск суммы сводится к отысканию полиномиального решения $y(x)$ ключевого уравнения:

Если $y(x)$ найдено, то Чтобы решить (6), можно найти верхнюю оценку степени решения и использовать (например) метод неопределенных коэффициентов, сведя задачу поиска к стандартной процедуре линейной алгебры. Одним из факторов, влияющих на эту оценку (и, как следствие, размер решаемой линейной системы) является степень полинома $C(x)$ в (6).

Иногда полином $C(x)$ из (6) называют универсальным знаменателем. Известная проблема с алгоритмом Госпера состоит в том, что универсальный знаменатель может иметь пессимистически завышенную степень (т.е. $C(x)$ и $y(x)$ могут иметь общий множитель высокой степени, который сократится после подстановки решения $y(x)$ уравнения (6) в (7)). Это, в свою очередь, может привести к экспоненциальной зависимости времени выполнения алгоритма Госпера от размера входных данных, даже когда вход и выход малы.

Рассмотрим применение адгоритма Гоcпера к гипергеометрическому терму

с рациональным сертификатом дисперсия числителя и знаменателя которого равна 32. После построения ПНФ получаем ключевое уравнение с правой частью степени 31. Это уравнение имеет полиномиальное решение степени 29 После подстановки $y(x)$ в (7) факториальный полином в $C(x)$ сокращается и окончательный результат суммирования имеет вид

Покажем, как с помощью небольших дополнительных усилий можно (после получения оценки степени решения (6)) удалить “лишние” множители в универсальном знаменателе $C(x)$ перед решением ключевого уравнения.

4. ПОНИЖЕНИЕ СТЕПЕНИ РЕШЕНИЯ КЛЮЧЕВОГО УРАВНЕНИЯ

Предположим, что заданный гипергеометрический терм $F(x)$ не является рациональной функцией и суммируем, т.е. уравнение (6) имеет полиномиальное решение $y(x)$. Сокращение в (7) происходит, когда решение $y(x)$ и правая часть $C(x)$ уравнения (6) имеют общий множитель. Предположим, что $C(x) = [p(x{{)]}_{k}}\tilde {C}(x)$ и решение $y(x)$ также имеет множитель ${{[p(x)]}_{k}}$. Тогда подстановка

в (6) дает новое уравнение имеющее полиномиальное решение $\tilde {y}(x)$, и можно $y(x)$ в (7) заменить на $\tilde {y}(x)$, $C(x)$ в (7) заменить на $\tilde {C}(x)$ (по сути неявно реализуя сокращение ненужного общего множителя в числителе и знаменателе (7)). Если верхняя оценка степени решения $y(x)$ в (6) равна $N$, то оценка степени решения $\tilde {y}(x)$ в (11) уменьшится до $N - k\deg p(x)$.

Возвращаясь к примеру (8), если установлено, что в решение ключевого уравнения входит множитель ${{\left[ {x + \frac{{88}}{3}} \right]}_{{28}}}$, то подстановка в это уравнение $y(x) = {{\left[ {x + \frac{{88}}{3}} \right]}_{{29}}}\tilde {y}(x)$ дает модифицированное ключевое уравнение:

с верхней границей степени решения $ < {\kern 1pt} 3$. Решение $\tilde {y}(x) = 1{\text{/}}3$ последнего уравнения дает тот же результат, что и в (9), без дополнительных затрат на сокращение числителя и знаменателя (7) на их наибольший общий делитель.

Заметим, что из-за природы ПНФ факториальные полиномы появляются только в правой части ключевого уравнения (6). Более того, число этих факториальных полиномов ограничено степенями числителя и знаменателя рационального сертификата $r(x)$ и не зависит от величины дисперсии. С другой стороны, каждый входящий в $C(x)$ множитель вида ${{\left[ {p(x)} \right]}_{k}}$ добавляет значение $k\deg p(x)$ к оценке верхней границы степени решения $y(x)$, которая может быть такой большой, как значение дисперсии числителя и знаменателя сертификата $r(x)$, домноженное на $\deg p(x)$. Поэтому такие множители являются подходящими кандидатами на проверку их сократимости в (7), приводящей к избавлению от несущественной зависимости времени выполнения алгоритма от значения дисперсии. Рассмотрение в качестве кандидатов на сокращение других множителей не приведет к изменению асимптотической сложности алгоритма.

Покажем, как можно эффективно отыскать те из множителей вида ${{\left[ {p(x)} \right]}_{k}}$ в правой части (6), которые также являются множителями решения $y(x)$. Для упрощения изложения предположим, что все полиномы, входящие в (6), разложены на неприводимые множители (позже будет показано, что это предположение не является обязательным). В дальнейшем пусть ${{\left[ {p(x)} \right]}_{k}}$ – один из множителей $C(x)$ в (6), т.е. $C(x) = {{\left[ {p(x)} \right]}_{k}}\tilde {C}(x)$. Наш подход основан на компактном представлении факториальных полиномов, “ленивых” вычислениях последовательных значений $y(x)$ в (6) и простых структурных свойствах полиномиальных решений уравнения (6):

1. Выражение ${{\left[ {p(x)} \right]}_{k}}$ обращается в ноль на любом корне $\alpha $ полинома $p(x)$, а также при $x = \alpha + 1, \ldots ,\alpha + k - 1$.

2. Выражения $A(x)$ и $B(x - 1)$ не могут обращаться в ноль при $x = \alpha ,\alpha + 1, \ldots ,\alpha + k - 1$. Это следует из требования (iii) в определении ПНФ.

3. Если решение $y(x)$ уравнения (6) обращается в ноль в любой из точек $\alpha ,\alpha + 1, \ldots ,\alpha + k$ (где $\alpha $ – корень $p(x)$), то $y(x)$ обращается в ноль во всех этих точках. Это значит, что полином ${{\left[ {p(x)} \right]}_{{k + 1}}}$ входит как множитель в $y(x)$ и факториальный полином ${{\left[ {p(x)} \right]}_{k}}$ из $C(x)$ сокращается при подстановке $y(x)$ в (7).

4. Если полиномы $A(x)$ и $B(x - 1)$ не имеют множителей, эквивалентных по сдвигу полиному $p(x)$, то выражение ${{\left[ {p(x)} \right]}_{k}}$ гарантированно является множителем решения $y(x)$ уравнения (6). Это свойство выполняется только для нерациональных гипергеометрических термов и следует из доказанного в [8] факта, что однородное уравнение

соответствующее уравнению (6), имеет только тривиальное решение, если $z,A(x)$ и $B(x)$ получены при построении ПНФ для гипергеометрического терма, не являющегося рациональной функцией.

5. Любой множитель $A(x)$ (соответственно $B(x - 1)$) из (6), эквивалентный по сдвигу полиному $p(x)$, дает начальное значение решения $y(x)$ при $x = \beta $ (соответственно, при $x = \beta + 1$), где $\beta $ является корнем этого множителя. Вычисления, необходимые для обнаружения равенства или неравенства $y(x)$ нулю в последовательных точках, начинающиеся с $x = \beta $ (соответственно, с $x = \beta + 1$), можно выполнить “лениво”. Раскрытие скобок в ${{\left[ {p(x)} \right]}_{k}}$ или знание самого корня $\beta $ для этого не требуется.

Поясним последнее утверждение. Пусть $C(x) = [p(x{{)]}_{k}}\tilde {C}(x)$, где ${{[p(x)]}_{k}}$ – единственный факториальный полином в правой части (6), а $b(x)$ – множитель $B(x - 1)$, эквивалентный по сдвигу $p(x)$ (т.е. $p(x + h) = b(x),h > 0$). Принимая $b(x) = 0$, получаем

что дает значение решения $y(x)$ при $x = \beta + 1$, где $\beta $ – любой корень $b(x)$. Теперь из (6) можно выразить Значение $y(\beta + 2)$ будет равно нулю если и только если выражение в квадратных скобках равно нулю. Для проверки этого равенства не требуется полное вычисление значения правой части. Достаточно разделить полином в квадратных скобках в (12) на полином $b(x)$ и проверить равенство нулю полученного остатка. Продолжая вычисления по модулю полинома $b(x)$ подобным образом, дойдем до значения $y(x + h)$ и если оно равно нулю, то множитель ${{[p(x)]}_{k}}$ входит в решение $y(x)$ и может быть сокращен, как показано выше. Заметим, что вычисление $A{{(x)}^{{ - 1}}}$ по модулю $b(x)$ в квадратных скобках в (12) не представляет проблем, так как по условию (ii) из определения ПНФ полиномы $A(x),A(x + 1), \ldots ,A(x + h)$ обратимы по модулю полинома $b(x)$.

Возвращаясь к примеру (8), для установления того, что факториальный полином ${{\left[ {x + \frac{{88}}{3}} \right]}_{{28}}}$ являетстя множителем решения $y(x)$ уравнения (6), воспользуемся множителем $\left( {x + 94{\text{/}}3} \right)$ полинома $B(x - 1)$, эквивалентным по сдвигу полиному $x + \frac{{88}}{3}$, что даст значение $y(x)$ для $x = - 91{\text{/}}3$. Одного шага вычислений по рекурренции (12) оказывается достаточным, чтобы определить равенство $y(x) = 0$ при $x = - 88{\text{/}}3$.

Если наряду с ${{[p(x)]}_{k}}$ правая часть (6) содержит и другие факториальные полиномы ${{[u(x)]}_{\ell }}$, ${{[{v}(x)]}_{m}}, \ldots $, то проверка сократимости ${{[p(x)]}_{k}}$ будет такой же, как показано выше: просто в (12) нужно заменить $p(x - k + 1)$ на $p(x - k + 1)u(x - \ell + 1){v}(x - m + 1) \ldots $, а $p(x + 1)$ на $p(x + 1)u(x + 1){v}(x + 1) \ldots $, домножить правую часть (12) на ${{[u(x)]}_{{\ell - 1}}}{{[{v}(x)]}_{{m - 1}}} \ldots $, и учитывать, что любой факториальный полином ${{[q(x)]}_{n}}$ обращается в 1 при $n \leqslant 0$.

Аналогичной (12) рекурренцией можно воспользоваться и в случае, когда $A(x)$ в (6) содержит множитель, эквивалентный по сдвигу полиному $p(x)$. Если же оба полинома $A(x)$ и $B(x - 1)$ в (6) содержат множители, эквивалентные по сдвигу полиному $p(x)$, можно минимизировать количество промежуточных ленивых шагов при тестировании вхождения ${{[p(x)]}_{k}}$ в решение $y(x)$. Пусть, например, $C(x) = [p(x{{)]}_{k}}\tilde {C}(x)$, $b(x)$ – множитель $B(x - 1)$ эквивалентный по сдвигу $p(x)$, а $a(x)$ – множитель $A(x)$ эквивалентный по сдвигу $p(x)$. Отметим, что $a(x)$ является наименьшим, а $b(x)$ – наибольшим элементом класса сдвиговой эквивалентности, образованного полиномами $a(x),p(x - k + 1),p(x - k + 2), \ldots ,p(x),b(x)$. Если вычисление значений $y(x)$ начинается в нуле полинома $b(x)$ (соответственно в нуле полинома $a(x)$), то количество промежуточных шагов для установления равенства нулю решения $y(x)$ на нулях полинома ${{[p(x)]}_{k}}$ равно дисперсии полиномов $b(x)$ и $p(x)$ (соответственно дисперсии полиномов $p(x - k + 1)$ и $a(x)$). Меньшее из этих значений дает минимальное число промежуточных шагов.

Если $C(x)$ в (6) содержит несколько множителей вида ${{[p(x)]}_{k}}$, то проверку вхождения этих множителей в решение $y(x)$ можно проводить в произвольном порядке (это следует из локальных свойств ПНФ, установленных в [9]). Отметим, что если дисперсия равна $d$, то число промежуточных шагов при проверке не может превышать $d - k$, т.е., чем выше факториальная степень проверямого множителя, тем меньшее число шагов потребуется в худшем случае. Это наблюдение позволяет избегать проверки множителей, избавление от которых не уменьшает асимптотическую сложность алгоритма (например, не проверять множители с факториальной степенью того же порядка, что и максимальная из степеней числителя и знаменателя сертификата).

5. РЕАЛИЗАЦИЯ И ЗАКЛЮЧЕНИЕ

Описанные выше свойства решений ключевого уравнения (6) позволяют внести простые изменения в алгоритм Госпера. Первое изменение не связяано напрямую с самим алгоритмом – оно вносится в процедуру построения ПНФ и обеспечивает получение результата в компактном виде.

Второе изменение вносится в алгоритм сразу после построения ключевого уравнения (6) и задействуется только в том случае, когда правая часть (6) содержит факториальные полиномы. Для каждого множителя вида ${{[p(x)]}_{k}}$ в правой части (6) проверяется, входит ли он в решение $y(x)$ (как показано выше) и отбираются те факториальные полиномы, для которых получен положительный ответ. После этого для отобранных факториальных полиномов проводятся подстановки вида (10), дающие новое ключевое уравнение, которое передается на последний этап стандартной процедуры Госпера. Задействованные при этом вычисления используют те же средства, что и построение ПНФ (вычисление дисперсионного множества полиномов, НОД полиномов и т.д.). При этом часто можно воспользоваться результатами, полученными при построении ПНФ, например, для поиска множителей $A(x)$ или $B(x - 1)$, эквивалентных по сдвигу $p(x)$.

Внесенные изменения не ухудшают асимптотическую сложность процедуры суммирования, но могут привести к весьма заметному сокращению времени ее выполнения для суммируемых термов с большим значением дисперсии рационального сертификата (фактически, в этом случае модифицированный алгоритм Госпера имеет время выполнения, полиномиальное по размеру входа [10], тогда как оригинальный алгоритм имеет экспоненциальное по размеру входа время выполнения).

Реализация описанной модификации в системе Мэйпл подтверждает улучшения временных характеристик работы алгорима. Так, например, у суммируемого гипергеометрического терма

величина дисперсии сертификата равна $\rho + 2$, а $C(x)$ в (6) включает множители ${{\left[ {x + \rho - 2{\text{/}}3} \right]}_{{\rho - 2}}}$ и ${{\left[ {x + \rho - 18{\text{/}}5} \right]}_{{\rho - 3}}}$. Время выполнения стадартного алгоритма Госпера в системе Мэйпл для $\rho = 100,200,400$ и 800 равно, соответственно, 1.163, 7.503, 58.626 и 510.230 с, тогда как время выполнения модифицированного алгоритма для тех же значаний $\rho $ остается неизменным $ \approx {\kern 1pt} 0.02$ с, подтверждая, что внесенная модификация убирает несущественную зависимость времени выполнения алгоритма от величины дисперсии сертификата.

В тех случаях, когда понизить оценку степени решения (6) не удается, время выполнения модифицированного алгоритма практически не отличается от времени выполнения стандартного алгоритма Госпера. Это очевидно для cлучаев, когда ключевое уравнение (6) не содержит факториальных полиномов в правой части, как в примере (2): в этом случае оба алгоритма возвращают результат, затратив около 10 мс. Если же (6) содержит факториальный полином высокой степени, который не сокращается в (7), то затраты на проверку сократимости (число шагов) не превышают значения дисперсии уменьшенного на факториальную степень, решаемая система линейных уравнений имеет размер, пропорциональный значению дисперсии, и время решения системы является доминирующим. Например, для суммируемого гипергеометрического терма $F(x + \rho ) - F(x)$, где $F(x) = x!{\text{/}}(3x + 1)$ – величина дисперсии сертификата равна $\rho + 1$, а $C(x)$ в (6) включает множитель ${{\left[ {x + \rho - 2{\text{/}}3} \right]}_{{\rho - 1}}}$, который не входит в решение (6). Время выполнения стандартного алгоритма Госпера в системе Мэйпл для $\rho = 100,200$ и 400 равно, соответственно, 0.843, 5.699 и 62.856 с, тогда как время выполнения модифицированного алгоритма для тех же значаний $\rho $ равно, соответственно, 0.939, 5.817 и 63.001 с, подтверждая, что дополнительные затраты незначительны и проверка сократимости в (7) несущественно ухудшает общее время работы алгоритма.

Сделанное ранее предположение, что все полиномы, входящие в (6), разложены на неприводимые множители можно ослабить. Пусть полином $p(x)$ в ${{\left[ {p(x)} \right]}_{k}}$ не является неприводимым, а полиномы $A(x)$ и $B(x - 1)$ не разложены на множители. Построим дисперсионные множества ${{S}_{A}}$ и ${{S}_{B}}$ для пар полиномов $p(x),A(x)$ и $B(x - 1),p(x)$. Если оба эти множества пусты, то ${{\left[ {p(x)} \right]}_{k}}$ входит в решение уравнения (6) и разложения $p(x)$ на неприводимые множители не требуется. В противном случае максимальный или минимальный элемент $h$ множества ${{S}_{A}}$ (соответственно множества ${{S}_{B}}$) можно использовать для получения нетривиального множителя $q(x)$ полинома $p(x)$ и эквивалентного ему по сдвигу множителя $a(x)$ полинома $A(x)$ (соответственно $b(x)$ полинома $B(x - 1)$), для чего достаточно вычислить ${\text{НОД}}(p(x),A(x + h))$ (соответственно ${\text{НОД}}(p(x),B(x - h - 1))$). Это выделит из ${{\left[ {p(x)} \right]}_{k}}$ множитель ${{\left[ {q(x)} \right]}_{k}}$, для которого и проводится проверка вхождения в решение уравнения (6). Полученный полином $q(x)$ может не быть неприводимым, но дальнейшее его разложение не требуется. Таким образом, для реализации предложенных модификаций факторизация полиномов, вообще говоря, не требуется. Заметим, однако, что используемый в системе Мэйпл алгоритм построения дисперсионного множества полиномов основан на факторизации. Поэтому попытка избежать факторизации при построении ключевого уравнения и понижении степени его решения не приводит к заметному уменьшению времени выполнения реализованных программ. Гораздо более практичным оказывается подход, при котором результаты факторизации числителя и знаменателя сертификата сохраняются и используются при построении ПНФ и ключевого уравнения. Описываемая здесь реализация включает обе возможности и позволяет модифицировать ключевое уравнение без привлечения факторизации (это сделано на случай внесения изменений в алгоритм вычисления дисперсии в системе Мэйпл).

Отметим, что предложенные здесь модификации алгоритма Госпера сохраняют свою работоспособность и для суммируемых гипергеометрических термов, зависящих от многих переменных, когда суммирование проводится по одной из них. Это показывает практичность предложенных модификаций, поскольку при использовании алгоритма Госпера в более сложных задачах, включающих несколько независимых переменных, нередкой является ситуация, когда получаемый на промежуточном этапе гипергеометрический терм гарантированно является суммируемым по выделенной переменной и требуется найти его сумму.

Для установления несуммируемости гипергеометрического терма с помощью алгоритма Госпера можно использовать описанное выше понижение степени универсального знаменателя $C(x)$ для таких множителей вида ${{\left[ {p(x)} \right]}_{k}}$, входящих в $C(x)$, для которых ни $A(x)$, ни $B(x - 1)$ не содержит множителей, эквивалентных $p(x)$ по сдвигу. Если (6) не имеет полиномиального решения, то и (11) не может иметь полиномиального решения, но уравнение (11) имеет меньшую степень правой части. Это означает, что все такие множители в правой части (6) избыточны и их удаление с помощью подстановки (10) не помешает установить факт отсутствия решения у ключевого уравнения.

Вопрос о том, можно ли использовать сходные методы для полного устранения несущественной зависимости времени выполнения алгоритма Госпера от значения дисперсии для несуммируемых гипергеометрических термов, требует дальнейшего изучения.

Автор выражает свою признательность П.У. Макаули (Университет Ватерлоо, Канада) за его вклад в реализацию предложенных методов, а также Х. Хуанг (Даляньский Технологический Университет, Китай) и рецензентам за полезные и конструктивные замечания по первоначальной версии настоящей работы.