Журнал вычислительной математики и математической физики, 2023, T. 63, № 4, стр. 639-656

О модельных двумерных течениях газа без давления: вариационное описание и численный алгоритм в рамках динамики прилипания

Н. В. Клюшнев^1, *, Ю. Г. Рыков¹

¹ ИПМ им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия

Поступила в редакцию 17.05.2022
После доработки 24.10.2022
Принята к публикации 15.12.2022

EDN: IPHKRD
DOI: 10.31857/S0044466923040105

Аннотация

Изучаются обобщенные решения системы уравнений газовой динамики без давления в случае двух пространственных измерений. Работа имеет теоретический характер и рассматривает указанную систему уравнений с точки зрения общей математической теории законов сохранения. Сделан акцент на важной отличительной особенности данной системы уравнений – возникновении сильных особенностей плотности вдоль многообразий разной размерности. Данное свойство характеризовано как возникновение иерархии особенностей. В более ранних работах прикладной направленности (например, А.Н. Крайко и др., в том числе, и для более сложных случаев трехмерных течений двухфазных сред) указанное свойство изучалось на физическом уровне строгости. В настоящей статье возникновение иерархии особенностей рассмотрено с математической точки зрения, поскольку строго обосновать, например, существование решения с сильной особенностью в точке (для двумерного случая) оказывается не так просто. Поэтому для формирования математических гипотез о поведении решения используется специальный численный алгоритм. С теоретической точки зрения рассмотрены подходы к построению вариационного принципа для обобщенных решений. С вычислительной точки зрения реализован алгоритм на основе варианта приближенной динамики прилипания в многомерном случае. Алгоритм верифицирован на ряде примеров (двумерная задача Римана) с точки зрения внутренней сходимости и сравнения с математическими результатами, в том числе, и других авторов. Библ. 30. Фиг. 8. Табл. 4.

Ключевые слова: законы сохранения, газовая динамика без давления, вариационный принцип, динамика прилипания, соотношения Ренкина–Гюгонио, иерархия особенностей.

1. ВВЕДЕНИЕ

Интерес к средам с отсутствием собственного перепада давления (кратко: среды без давления) возник при попытках описания сложных физических явлений, таких как эволюция многофазных потоков, движение дисперсных сред, в частности пылевых частиц или капель, взаимодействие гиперзвуковых потоков в некоторых предельных случаях и т.п. В работе А.Н. Крайко [1], касавшейся указанных прикладных задач, было показано, что в средах без давления возникает новый тип скачков с концентрацией вещества на, вообще говоря, гиперповерхностях. В этой работе также были получены законы эволюции подобных гиперповерхностей на физическом уровне строгости.

Основным прикладным аспектом моделей сред без собственного давления являются течения в твердотопливных ракетных двигателях с двухфазными продуктами сгорания, где одна фаза является обычным газом, а другая – средой твердых частиц с нулевым давлением. Здесь имеется обширная литература, посвященная как описанию возникновения, в том числе, специфических особенностей различных типов в среде без давления, обозначаемых как “пелены” и “шнуры”, в более сложной ситуации взаимодействия с газом и в трехмерной постановке, так и соответствующему численному моделированию. Направленность статьи не предполагает какого-либо обзора прикладных работ, поэтому, для примера, в дополнение к [1] упомянем только работы [2, 3].

Подчеркнем, что настоящая работа имеет теоретический характер и рассматривает систему уравнений газовой динамики без давления с точки зрения общей математической теории законов сохранения. В этом отношении все особенности, возникающие вследствие пересечения каких-либо полей характеристик, мы будем называть “ударными волнами”, не останавливаясь на выделении каких-либо их типов. Работа практически не касается прикладных аспектов, разве только с иллюстративной целью. Представленный ниже специальный численный метод используется только для формирования математических гипотез о поведении решения и в данном варианте не предназначен для практических расчетов.

Отметим, что еще одной существенной областью приложения моделей сред без давления является астрофизика. А именно, законы крупномасштабного распределения вещества во Вселенной (см., например, [4]).

Система уравнений газовой динамики без давления представляет собой обычную систему уравнений газовой динамики, в которой формально давление положено равным нулю. Ниже мы явно запишем данную систему в случае двух пространственных переменных. Исследование задачи Римана для этого случая при условии образования особенностей не только вдоль поверхностей, но и вдоль кривых в пространстве $(t,x,y)$, как с теоретической, так и численной точек зрения, является основной целью настоящей статьи. Пусть $(t,x,y) \in {{\mathbb{R}}_{ + }} \times {{\mathbb{R}}^{2}}$, тогда интересующая нас система уравнений выглядит следующим образом:

(1)

$\frac{{\partial \varrho }}{{\partial t}} + \frac{{\partial (\varrho u)}}{{\partial x}} + \frac{{\partial (\varrho {v})}}{{\partial y}} = 0,\quad \frac{{\partial (\varrho u)}}{{\partial t}} + \frac{{\partial (\varrho {{u}^{2}})}}{{\partial x}} + \frac{{\partial (\varrho u{v})}}{{\partial y}} = 0,\quad \frac{{\partial (\varrho {v})}}{{\partial t}} + \frac{{\partial (\varrho u{v})}}{{\partial x}} + \frac{{\partial (\varrho {{{v}}^{2}})}}{{\partial y}} = 0,$

где $\varrho $ – плотность, а $(u,{v})$ – вектор скорости.

Система (1) представляет собой нестрого гиперболическую систему законов сохранения с тремя совпадающими собственными значениями и неполным набором собственных векторов. Вследствие этого в (1) образуются сильные $\delta $-особенности на поверхностях разной коразмерности в пространстве $(t,x,y)$. Мы будем рассматривать задачу Коши для (1) с начальными условиями

(2)

$\varrho (0,x,y) = {{\varrho }_{0}}(x,y) \geqslant 0,\quad u(0,x,y) = {{u}_{0}}(x,y),\quad {v}\left( {0,x,y} \right) = {{{v}}_{0}}(x,y),$

где функции ${{\varrho }_{0}},\;{{u}_{0}},\;{{{v}}_{0}}$ являются произвольными ограниченными измеримыми функциями, но ниже будут принадлежать гораздо более узкому классу кусочно-постоянных функций. Более конкретно, нас будет интересовать решение задачи Римана для (1). Оговорим заранее, что обобщенные решения системы (1) будут, вообще говоря, пониматься в смысле мер Радона и, соответственно, также будут пониматься начальные данные. А именно, начальные данные Коши будут задаваться как меры Радона ${{P}_{0}}\left( {dx,dy} \right),$ ${{I}_{0}}\left( {dx,dy} \right),$ ${{J}_{0}}\left( {dx,dy} \right)$, определенные на борелевских подмножествах ${{\mathbb{R}}^{2}}$. При этом ${{P}_{0}} \geqslant 0$ и в смысле Радона–Никодима существуют $d{{I}_{0}}{\text{/}}d{{P}_{0}} = {{u}_{0}}\left( {x,y} \right)$ и $d{{J}_{0}}{\text{/}}d{{P}_{0}} = {{{v}}_{0}}\left( {x,y} \right)$. В случае начальных условий (2) соответствующие меры ${{P}_{0}},\;{{I}_{0}},\;{{J}_{0}}$ будут абсолютно непрерывными относительно стандартной меры Лебега.

Работа [5] обозначила новый всплеск роста интереса к математическому осмыслению моделей сред без давления. С этого времени появилось достаточно много публикаций, изучающих систему типа (1), но, главным образом, в случае одного пространственного переменного. Никоим образом не претендуя на полноту обзора, отметим несколько характерных работ. В [6] и [7] разными методами было доказано существование обобщенных решений в пространстве мер, и далее в [8] развернуто описан вариационный принцип, который использовался для доказательства существования решения. Вариационный подход будет активно обсуждаться и в настоящей статье. Из-за вырожденного характера системы уравнений газовой динамики без давления условия единственности решений имеют неоднозначный характер. Вопросы, связанные и с существованием, и с единственностью обобщенных решений в случае одной пространственной переменной рассматривались, например, в [9], [10], где единственность обеспечивалась выполнением условия типа $E$, предложенного в свое время О.А. Олейник, и той или иной формой запрета распада вещества. Наконец, в недавних работах [11], [12] рассмотрено влияние внешних сил и обобщен вариационный подход на системы без давления с нетривиальной правой частью.

В отличие от одномерного случая случай многих пространственных переменных гораздо менее изучен. Это, по-видимому, связано с тем, что, вообще говоря, при эволюции начальных функций возникает иерархия особенностей плотности, сосредоточенных на многообразиях разной размерности. Опять же не претендуя на полноту, отметим ряд публикаций на эту тему. В [13] для случая двух пространственных переменных было получено обобщение соотношений Ренкина–Гюгонио в дифференциальной форме на случай сильных особенностей на поверхностях в пространстве $\left( {t,x,y} \right)$ системы уравнений газовой динамики без давления, и исследованы решения двумерной задачи Римана, которые такие особенности содержат. Это было сделано в рамках изучения решений двумерной задачи Римана для уравнений газовой динамики в целом. В [14] и более развернуто в [15] были также получены формулы для соотношений Ренкина–Гюгонио при возникновении концентраций плотности на поверхностях, но и в форме интегральных соотношений, отражающих процессы концентрации вещества, и в дифференциальной форме на основе теории новых обобщенных функций Ж.Ф. Коломбо (см., например, [16]). Дополнительно был сделан вывод о существовании концентрации вещества не только вдоль поверхностей, но и вдоль кривых в пространстве $\left( {t,x,y} \right)$. Подробное исследование решений двумерной задачи Римана для системы уравнений газовой динамики без давления, включающей также и уравнение для энергии, представлено в [17]. Однако там также не была рассмотрена возможность возникновения концентрации плотности вдоль кривых.

В многомерном случае концентрация вещества на гиперповерхностях коразмерности один изучалась, например, в [18–20]. Форма вариационного принципа в многомерном случае анонсирована в [21]. Также в [22], [23] рассмотрены тонкие вопросы распространения векторного поля скоростей на пространственно-временные точки, находящиеся внутри особенностей разных размерностей, в ситуации, когда система (1) может быть записана как уравнение Гамильтона–Якоби.

В отличие от большинства работ по данной тематике настоящая публикация акцентирует внимание на важности построения иерархии особенностей на поверхностях разных размерностей при построении решений многомерных систем уравнений газовой динамики без давления. При этом мы ограничимся двумерным случаем, уже для которого построение точных решений с особенностями разного типа приводит к заметным трудностям. Поэтому мы рассмотрим эвристический метод построения оценок, описывающих качественное поведение обобщенных решений, на основе вариационного подхода, а также предложим численный метод решения двумерной системы уравнений газовой динамики без давления. При построении численного метода будем руководствоваться принципом наибольшей простоты и робастности даже в ущерб минимизации вычислительных затрат. Вследствие достаточной сложности возникающих иерархий особенностей, особенно в многомерном случае, на который в дальнейшем планируется обобщить предлагаемую методику, необходимо иметь алгоритм, с наибольшей вероятностью воспроизводящий реальную структуру решений, в которых важную роль может играть, например, динамика отдельных точек на плоскости $\left( {x,y} \right)$. Возможная иерархическая структура системы уравнений газовой динамики без давления в двухмерном и трехмерном случаях была описана в [24], а в более ранней работе [25] приведен эвристический вывод условий согласования особенностей в двумерном случае.

Статья организована следующим образом. Раздел 2 посвящен теоретическому описанию эвристического метода построения оценок, демонстрирующих качественное поведение обобщенных решений задачи Римана в двумерном случае, на основе вариационных техник, предложенных в [24]. Применение данной методологии в определенных случаях приводит к появлению иерархии особенностей в отличие от, например, [17], где подобная ситуация не рассматривалась. Однако на данном этапе разработанный метод касается только процесса возникновения особенностей при отсутствии вакуума. В разд. 3 приведено детальное описание численного алгоритма расчета для обобщенных решений системы уравнений газовой динамики без давления, построенного на основе результатов [26]. Расчету обобщенных решений задачи Римана без образования вакуума и их верификации с помощью признака внутренней сходимости и сравнения с теоретическими формулами и с расчетами в [17] посвящен разд. 4. В разд. 5 приводятся численные расчеты задачи Римана и верификация их качественного поведения в соответствии с [17] в случае образования вакуума. Также приводится расчет, демонстрирующий возможность отображения крупномасштабной структуры Вселенной. Наконец, в Заключении полученные результаты резюмируются и намечаются направления дальнейших исследований.

2. ОПИСАНИЕ ОСОБЕННОСТЕЙ РЕШЕНИЯ ЗАДАЧИ РИМАНА В ДВУМЕРНОМ СЛУЧАЕ ПРИ ОТСУТСТВИИ ВАКУУМА

Вначале проведем ряд предварительных рассмотрений. Обозначим ${\mathbf{x}} \equiv \left( {x,y} \right)$, $d{\mathbf{x}} \equiv \left( {dx,dy} \right)$, ${\mathbf{u}}\left( {t,{\mathbf{x}}} \right) \equiv \left( {u\left( {t,{\mathbf{x}}} \right),{v}\left( {t,{\mathbf{x}}} \right)} \right)$, ${{{\mathbf{I}}}_{t}}\left( {d{\mathbf{x}}} \right) \equiv \left( {{{I}_{t}}\left( {dx,dy} \right),{{J}_{t}}\left( {dx,dy} \right)} \right)$.

Определение 1. Пусть ${{P}_{t}}\left( {d{\mathbf{x}}} \right)$, ${{{\mathbf{I}}}_{t}}\left( {d{\mathbf{x}}} \right)$ – семейства мер Радона, определенные на борелевских подмножествах ${{\mathbb{R}}^{2}}$, слабо непрерывные по $t$, и, кроме того, ${{P}_{t}} \geqslant 0$, а мера ${{{\mathbf{I}}}_{t}}$ абсолютно непрерывна относительно ${{P}_{t}}$ для почти всех $t > 0$. Определим вектор-функцию ${\mathbf{u}}\left( {t,{\mathbf{x}}} \right)$ как производную Радона–Никодима ${\mathbf{u}}\left( {t,{\mathbf{x}}} \right) = d{{{\mathbf{I}}}_{t}}{\text{/}}d{{P}_{t}}$. Тогда ${{P}_{t}},\;{{{\mathbf{I}}}_{t}}$ назовем обобщенным решением задачи Коши (1), (2), если: 1) для любых функций $f,g,h \in C_{0}^{1}({{\mathbb{R}}^{2}})$ и любых $0 < {{t}_{1}} < {{t}_{2}} < + \infty $

$\int \int \,f\left( {\mathbf{x}} \right){{P}_{{{{t}_{2}}}}}\left( {d{\mathbf{x}}} \right) - \int \int \,f\left( {\mathbf{x}} \right){{P}_{{{{t}_{1}}}}}\left( {d{\mathbf{x}}} \right) = \int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\int \int \,\nabla f \cdot {{{\mathbf{I}}}_{\tau }}\left( {d{\mathbf{x}}} \right)d\tau } ,$

(3)

$\int \int \,g\left( {\mathbf{x}} \right){{I}_{{{{t}_{2}}}}}\left( {d{\mathbf{x}}} \right) - \int \int \,g\left( {\mathbf{x}} \right){{I}_{{{{t}_{1}}}}}\left( {d{\mathbf{x}}} \right) = \int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\int \int \,\nabla g \cdot {\mathbf{u}}{{I}_{\tau }}\left( {d{\mathbf{x}}} \right)d\tau } ,$

$\int \int \,h\left( {\mathbf{x}} \right){{J}_{{{{t}_{2}}}}}\left( {d{\mathbf{x}}} \right) - \int \int \,h\left( {\mathbf{x}} \right){{J}_{{{{t}_{1}}}}}\left( {d{\mathbf{x}}} \right) = \int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\int \int \,\nabla h \cdot {\mathbf{u}}{{J}_{\tau }}\left( {d{\mathbf{x}}} \right)d\tau } ,$

где $\int \int $ обозначает интегрирование по ${{\mathbb{R}}^{2}}$; 2) в слабом смысле при $t \to + 0$, ${{P}_{t}} \to {{P}_{0}}$, ${{{\mathbf{I}}}_{t}} \to {{{\mathbf{I}}}_{0}}$.

В случае одной пространственной переменной (см. [8], [9]) обобщенное решение задачи (1), (2) можно строить с помощью следующего вариационного принципа. Вначале следует найти глобальный минимум $a\left( {t,x} \right)$ по переменной $a$ у функции

(4)

$F\left( {t,x;a} \right) = \int\limits_{0 - 0}^{a - 0} {\left( {{{u}_{0}}\left( \sigma \right)t + \sigma - x} \right){{P}_{0}}\left( {d\sigma } \right)} .$

Если такой минимум единственный, то $u\left( {t,x} \right) = \left( {x - a\left( {t,x} \right)} \right){\text{/}}t$ и является непрерывной, а мера ${{P}_{t}}\left( {dx;x} \right)$ является абсолютно непрерывной по отношению к мере Лебега и имеет плотность $\varrho $ такую, что $\varrho \left( {t,x} \right)dx = {{P}_{0}}\left( {da} \right)$. Если же минимумов $F$ несколько, то имеет место разрыв скорости $u$, и ${{P}_{t}}\left( {dx;x} \right) = \int_{{{a}_{{\min }}}\left( {t,x} \right)}^{{{a}_{{\max }}}\left( {t,x} \right)} {\kern 1pt} {{P}_{0}}\left( {da} \right)$. Отметим для полноты, что в [27] и [28] рассматривались неклассические решения одномерной системы уравнений газовой динамики без давления, которые не удовлетворяют описанному выше вариационному принципу.

В многомерном случае особенности плотности могут возникать на поверхностях в пространстве $\left( {t,x,y} \right)$, а также вдоль кривых. При эволюции особенности вдоль поверхности характеристики системы (1) должны приходить на эту поверхность с разных ее сторон. Обозначим эти стороны как “+” и “–”. Пусть поверхность концентрации плотности задается параметрически как ${\mathbf{x}} = {\mathbf{X}}\left( {t,l} \right)$, ${\mathbf{X}} \equiv \left( {\chi ,\gamma } \right)$. Приходящие характеристики определяют соответствующие точки в лагранжевых координатах как ${\mathbf{a}}\left( {t,l} \right)$, ${\mathbf{a}} \equiv \left( {a,b} \right)$, ${\mathbf{X}}\left( {t,l} \right) = {\mathbf{a}}\left( {t,l} \right) + t{{{\mathbf{u}}}_{0}}\left( {{\mathbf{a}}(t,l)} \right)$. Как показано в [14], [15], справедлива следующая интегральная форма для обобщенных соотношений Ренкина–Гюгонио на особых поверхностях для системы (1):

(5)

$\begin{gathered} \int\limits_{{{t}_{0}}}^t \left[ {{\mathbf{X}}(t,l) - {{{\mathbf{a}}}^{ + }}(\tau ,l) - t{\mathbf{u}}_{0}^{ + }(\tau ,l)} \right]{{\varrho }_{0}}({{{\mathbf{a}}}^{ + }})\left[ {{{{({{a}^{ + }})}}_{\tau }}{{{({{b}^{ + }})}}_{l}} - {{{({{b}^{ + }})}}_{\tau }}{{{({{a}^{ + }})}}_{l}}} \right]d\tau = \\ = \int\limits_{{{t}_{0}}}^t \left[ {{\mathbf{X}}(t,l) - {{{\mathbf{a}}}^{ - }}(\tau ,l) - t{\mathbf{u}}_{0}^{ - }(\tau ,l)} \right]{{\varrho }_{0}}({{{\mathbf{a}}}^{ - }})\left[ {{{{({{a}^{ - }})}}_{\tau }}{{{({{b}^{ - }})}}_{l}} - {{{({{b}^{ - }})}}_{\tau }}{{{({{a}^{ - }})}}_{l}}} \right]d\tau , \\ \end{gathered} $

где равенства (5) выполняются покомпонентно, ${{t}_{0}} > 0$ – фиксированный момент времени, а $l$ – некоторый параметр вдоль сечения поверхности плоскостью $t = {{t}_{0}}$. То есть в двумерном случае справедливы два соотношения, определяющие поверхность концентрации вещества.

В [25] в случае двух пространственных измерений фактически приведено схематическое доказательство следующей теоремы.

Теорема 1. Пусть имеется только конечное число кусочно-непрерывно дифференцируемых поверхностей, а также конечное число кусочно-непрерывно дифференцируемых кривых концентрации меры ${{P}_{t}}\left( {d{\mathbf{x}}} \right)$. Пусть вне этих поверхностей и кривых меры ${{P}_{t}}\left( {d{\mathbf{x}}} \right)$, ${{{\mathbf{I}}}_{t}}\left( {d{\mathbf{x}}} \right)$ кусочно абсолютно непрерывны по отношению к мере Лебега с кусочно-непрерывно дифференцируемой плотностью. Тогда указанные меры являются обобщенными решениями системы (1) в смысле oпределения 1 прямой, если: а) вне многообразий концентрации меры ${{P}_{t}}\left( {d{\mathbf{x}}} \right)$ уравнения (1) удовлетворяются в обычном обобщенном смысле; б) на поверхностях концентрации меры ${{P}_{t}}\left( {d{\mathbf{x}}} \right)$ выполняются соотношения (5); в) вдоль кривых концентрации меры ${{P}_{t}}\left( {d{\mathbf{x}}} \right)$, заданных в виде ${\mathbf{x}} = {\mathbf{s}}(t) \equiv \left( {{{s}_{1}}(t),{{s}_{2}}(t)} \right)$, выполняются соотношения

(6)

${\mathbf{\dot {s}}} = {{{\mathbf{I}}}_{t}}\left( {d{\mathbf{x}};{\mathbf{s}}(t)} \right){\text{/}}{{P}_{t}}\left( {d{\mathbf{x}};{\mathbf{s}}(t)} \right).$

Условие (5) в интегральной форме является прямым обобщением условия равенства минимумов функции $F$ в (4). Однако проверять выполнение этого условия часто удобнее, когда оно записано в дифференциальной форме (об эквивалентности этих форм см. [15])

(7)

${{\dot {P}}_{t}} = {{\chi }_{l}}\left\{ {V[\varrho ] - [\varrho {v}]} \right\} - {{\gamma }_{l}}\left\{ {U[\varrho ] - [\varrho u]} \right\},\quad {{{\mathbf{\dot {I}}}}_{t}} = {{\chi }_{l}}\left\{ {V[\varrho {\mathbf{u}}] - [\varrho {v}{\mathbf{u}}]} \right\} - {{\gamma }_{l}}\left\{ {U[\varrho {\mathbf{u}}] - [\varrho u{\mathbf{u}}]} \right\},$

где $\left( {U,V} \right) \equiv d{{{\mathbf{I}}}_{t}}{\text{/}}d{{P}_{t}}$, и для любой величины $f$ обозначено $[f] \equiv {{f}^{ + }} - {{f}^{ - }}$.

Теперь перейдем к построению эвристических оценок для решений задачи Римана. Во-первых, отметим, что при изучении возникновения иерархии особенностей оказывается важным следить за эволюцией в координатах Лагранжа. В [25], [24] было показано, что в двумерном случае вместо функции (4) следует рассмотреть вектор-функцию

(8)

${\mathbf{F}} \equiv \mathop {\int \int }\limits_A \left( {{{{\mathbf{u}}}_{0}}({\mathbf{a}})t + {\mathbf{a}} - {\mathbf{x}}} \right){{\varrho }_{0}}({\mathbf{a}})dadb \equiv \mathop {\int \int }\limits_A {\mathbf{S}}({\mathbf{a}})\frac{{\partial (a,b)}}{{\partial (\tau ,l)}}d\tau dl,$

где $A$ – некоторая область в лагранжевых переменных $\left( {a,b} \right)$, $\left( {a(\tau ,l),b(\tau ,l)} \right)$ – параметризация этой области, а $\partial (a,b){\text{/}}\partial (\tau ,l) \equiv \left( {{{a}_{\tau }}{{b}_{l}} - {{b}_{\tau }}{{a}_{l}}} \right)$. Там же сформулирован следующий признак возникновения концентрации плотности $\varrho $, т.е. меры ${{P}_{t}}\left( {d{\mathbf{x}}} \right)$, вдоль некоторой поверхности $\Gamma \equiv \left( {t,{\mathbf{X}}(t,l)} \right)$. Пусть на некотором компакте $K \subset {{\mathbb{R}}^{2}}$ определены кусочно-непрерывно дифференцируемые функции ${\mathbf{a}}(\tau ,l)$ в пространстве лагранжевых переменных. Определим следующую вектор-функцию:

(9)

$\Phi (\tau ,l) \equiv \left( {{{\Phi }_{1}},{{\Phi }_{2}}} \right) \equiv \int\limits_{}^\tau {{\mathbf{S}}({\mathbf{a}})\frac{{\partial (a,b)}}{{\partial (\alpha ,l)}}d\alpha } {\kern 1pt} ,$

где ${\mathbf{S}}({\mathbf{a}})$ определена в (8). Тогда условие возникновения особенности на поверхности $\Gamma $ выглядит следующим образом. Для любого $l$ существуют такие ${{\tau }_{1}}(l)$, ${{\tau }_{2}}(l)$, что

(10)

$\frac{{\partial \Phi }}{{\partial \tau }}\left( {{{\tau }_{1}},l} \right) = \frac{{\partial \Phi }}{{\partial \tau }}\left( {{{\tau }_{2}},l} \right) = 0,\quad \Phi ({{\tau }_{1}},l) = \Phi ({{\tau }_{2}},l).$

Замечание 1. При соответствующих ограничениях на рост функций ${{\varrho }_{0}},\;{\mathbf{u}},\;{\mathbf{a}}$ условия (10) можно интерпретировать как поиск покомпонентных глобальных экстремумов функции $\Phi $ из (9), которая является аналогом функции (4). Таким образом, условия (10) предполагают процедуру поиска обобщенных решений с концентрацией особенностей, обобщающую соответствующий вариационный принцип в случае одной пространственной переменной.

Далее, условие возникновения особенности вдоль кривой в пространстве $\left( {t,{\mathbf{x}}} \right)$ предполагает, что на плоскости лагранжевых координат существует область $D(t)$, ограниченная частями границ областей $K$ для разных $\Gamma $, и таких, что

(11)

$\mathop {\int \int }\limits_{D(t)} {\mathbf{S}}({\mathbf{a}})dadb = 0\;,$

где в функцию ${\mathbf{S}}$ из (8) подставлена траектория особенности ${\mathbf{x}} = {\mathbf{s}}(t)$.

Замечание 2. Только что кратко изложенные подходы работы [24] обусловлены, в том числе, тем фактом, что произвольно построенная система движущихся частиц, которая в одномерном случае использовалась для построения приближенного решения, в двумерном случае ведет себя довольно нерегулярным образом. Так, например, возможны ситуации не существования и неединственности (см. [29]), а также скрещивания большинства траекторий для полного по некоторой мере набора начальных расположений частиц (см. [30]). Фактически в [24] сделана попытка сформулировать альтернативный принцип построения решений.

Рассмотрим задачу Римана для (1). Задачей Римана называется такая задача Коши, когда в каждом квадранте начальной плоскости $\left( {x,y} \right)$ при $t = 0$ начальные функции ${{\varrho }_{0}},\;{{u}_{0}},\;{{{v}}_{0}}$ постоянны, т.е. координатные оси служат линиями разрыва начальных данных. В дальнейшем будем нумеровать квадранты плоскости стандартным образом с помощью индекса $i = 1,2,3,4$, и этим же индексом будем отмечать значения соответствующих величин, в частности, начальных данных.

Предварительно рассмотрим более простую задачу, для которой конкретизируем приведенные выше соотношения (9), (10). А именно, пусть при $t = 0$ имеется прямая $\mu y - \nu x = 0$ с положительной нормалью $\left( { - \nu ,\mu } \right)$. В соответствии с направлением положительной нормали данная прямая делит ${{\mathbb{R}}^{2}}$ на две полуплоскости: положительную $\mathbb{R}_{ + }^{2}$, которую будем обозначать индексом “+”, и отрицательную $\mathbb{R}_{ - }^{2}$, которую будем обозначать индексом “–”. Пусть ${{\varrho }_{0}} = {{\varrho }^{ + }} = {\text{const}},$ ${{{\mathbf{u}}}_{0}} = {{{\mathbf{u}}}^{ + }} = {\text{const}}$ при $\mu y - \nu x > 0$ и ${{\varrho }_{0}} = {{\varrho }^{ - }} = {\text{const}},$ ${{{\mathbf{u}}}_{0}} = {{{\mathbf{u}}}^{ - }} = {\text{const}}$ при $\mu y - \nu x < 0$. При $t = 0$ плоскость $\left( {x,y} \right)$ является плоскостью Лагранжевых координат, которую мы для удобства будем обозначать как $\left( {a,b} \right)$. Введем в полуплоскостях $\mathbb{R}_{ \pm }^{2}$ наборы аффинных координат $\left( {\tau ,l} \right)$ по формулам

(12)

$a = {{\alpha }^{ \pm }}\tau + {{\gamma }^{ \pm }}l,\quad b = {{\beta }^{ \pm }}\tau + {{\delta }^{ \pm }}l.$

Определение 2. Системы координат (12) называются а) допустимыми, если

${{D}^{ \pm }} \equiv {{\alpha }^{ \pm }}{{\delta }^{ \pm }} - {{\beta }^{ \pm }}{{\gamma }^{ \pm }} \ne 0,\quad \mu {{\beta }^{ \pm }} - \nu {{\alpha }^{ \pm }} \ne 0\;,$

и б) согласованными, если

$\frac{{\nu {{\gamma }^{ + }} - \mu {{\delta }^{ + }}}}{{\mu {{\beta }^{ + }} - \nu {{\alpha }^{ + }}}} = \frac{{\nu {{\gamma }^{ - }} - \mu {{\delta }^{ - }}}}{{\mu {{\beta }^{ - }} - \nu {{\alpha }^{ - }}}} \equiv {{\zeta }_{0}}\;.$

Теорема 2. Существуют такие допустимые и согласованные системы координат (12), что выполняются условия (10), а поверхность $\Gamma $ и плотность сконцентрированного вещества ${{P}_{t}}$ задаются формулами

(13)

${\mathbf{X}}(t,l) = t\frac{{{{{\mathbf{u}}}^{ + }}\sqrt {{{\varrho }^{ + }}} + {{{\mathbf{u}}}^{ - }}\sqrt {{{\varrho }^{ - }}} }}{{\sqrt {{{\varrho }^{ + }}} + \sqrt {{{\varrho }^{ - }}} }} + l\left( {\mu ,\nu } \right),\quad {{P}_{t}} = t\left( {\nu [u] - \mu [{v}]} \right)\sqrt {{{\varrho }^{ + }}{{\varrho }^{ - }}} .$

Замечание 3. В отличие от, например, [13], [17], для вывода формул (13) в теореме 2 не использовалось никаких дифференциальных соотношений. Это свойство лежит в основе возможности использования результатов теоремы 2 для получения эвристических оценок в более сложных ситуациях с возникновением концентрации вещества вдоль кривой. Дополнительно можно видеть, что соотношения (13) удовлетворяют системе (7), а значит, и (5), т.е. в соответствии с теоремой 1 вектор-функция $\left( {\varrho ,{\mathbf{u}}} \right)$, представляющая собой области постоянных значений плотности и скорости, разделенные поверхностью (13), является обобщенным решением системы (1).

Доказательство. Введем обозначения ${\mathbf{A}} \equiv \left( {\alpha ,\beta } \right)$, ${\mathbf{B}} \equiv \left( {\gamma ,\delta } \right)$. Тогда, учитывая структуру начальных данных, функция $\Phi $ из (9) имеет вид

(14)

$\Phi = \left\{ \begin{gathered} \int\limits_{{{\zeta }_{0}}l}^\tau {(t{{{\mathbf{u}}}^{ - }} - {\mathbf{x}} + {{{\mathbf{A}}}^{ - }}\tau + {{{\mathbf{B}}}^{ - }}l){{\varrho }^{ - }}{{D}^{ - }}d\tau } \quad {\text{при}}\quad \tau \leqslant {{\zeta }_{0}}l, \hfill \\ \int\limits_{{{\zeta }_{0}}l}^\tau {(t{{{\mathbf{u}}}^{ + }} - {\mathbf{x}} + {{{\mathbf{A}}}^{ + }}\tau + {{{\mathbf{B}}}^{ + }}l){{\varrho }^{ + }}{{D}^{ + }}d\tau } \quad {\text{при}}\quad \tau \geqslant {{\zeta }_{0}}l. \hfill \\ \end{gathered} \right.$

Непосредственные вычисления дают следующие условия наличия экстремумов у функций ${{\Phi }_{1}},\;{{\Phi }_{2}}$:

${\text{если}}\quad \tau _{1}^{ - } = \frac{{x - t{{u}^{ - }} - {{\gamma }^{ - }}l}}{{{{\alpha }^{ - }}}} < {{\zeta }_{0}}l,\quad {\text{то}}\quad \Phi _{{1,{\text{extr}}}}^{ - } = - {{\varrho }^{ - }}{{D}^{ - }}{{(x - t{{u}^{ - }} - {{\gamma }^{ - }}l - {{\alpha }^{ - }}{{\zeta }_{0}}l)}^{2}}{\text{/}}(2{{\alpha }^{ - }});$

(15)

$\begin{gathered} {\text{если}}\quad \tau _{1}^{ + } = \frac{{x - t{{u}^{ + }} - {{\gamma }^{ + }}l}}{{{{\alpha }^{ + }}}} > {{\zeta }_{0}}l,\quad {\text{то}}\quad \Phi _{{1,{\text{extr}}}}^{ + } = - {{\varrho }^{ + }}{{D}^{ + }}{{(x - t{{u}^{ + }} - {{\gamma }^{ + }}l - {{\alpha }^{ + }}{{\zeta }_{0}}l)}^{2}}{\text{/}}(2{{\alpha }^{ + }}); \\ {\text{если}}\quad \tau _{2}^{ - } = \frac{{y - t{{{v}}^{ - }} - {{\delta }^{ - }}l}}{{{{\beta }^{ - }}}} < {{\zeta }_{0}}l,\quad {\text{то}}\quad \Phi _{{2,{\text{extr}}}}^{ - } = - {{\varrho }^{ - }}{{D}^{ - }}{{(y - t{{{v}}^{ - }} - {{\delta }^{ - }}l - {{\beta }^{ - }}{{\zeta }_{0}}l)}^{2}}{\text{/}}(2{{\beta }^{ - }}); \\ \end{gathered} $

${\text{если}}\quad \tau _{2}^{ + } = \frac{{y - t{{{v}}^{ + }} - {{\delta }^{ + }}l}}{{{{\beta }^{ + }}}} > {{\zeta }_{0}}l,\quad {\text{то}}\quad \Phi _{{2,{\text{extr}}}}^{ + } = - {{\varrho }^{ + }}{{D}^{ + }}{{(y - t{{{v}}^{ + }} - {{\delta }^{ + }}l - {{\beta }^{ + }}{{\zeta }_{0}}l)}^{2}}{\text{/}}(2{{\beta }^{ + }}).$

В соответствии с условиями (10) концентрация вдоль поверхности возникает при выполнении следующих соотношений:

(16)

$\tau _{1}^{ - } = \tau _{2}^{ - } < {{\zeta }_{0}}l,\tau _{1}^{ + } = \tau _{2}^{ + } > {{\zeta }_{0}}l;\quad \Phi _{{1,{\text{extr}}}}^{ - } = \Phi _{{1,{\text{extr}}}}^{ + },\Phi _{{2,{\text{extr}}}}^{ - } = \Phi _{{2,{\text{extr}}}}^{ + }.$

Введем обозначения ${{X}^{ \pm }} \equiv x - t{{u}^{ \pm }} - {{\gamma }^{ \pm }}l$, ${{Y}^{ \pm }} \equiv y - t{{{v}}^{ \pm }} - {{\delta }^{ \pm }}l$. Тогда соотношения (16) примут вид

(17)

$\begin{gathered} {{\alpha }^{ + }}{{\varrho }^{ - }}{{D}^{ - }}{{({{X}^{ - }} - {{\alpha }^{ - }}{{\zeta }_{0}}l)}^{2}} = {{\alpha }^{ - }}{{\varrho }^{ + }}{{D}^{ + }}{{({{X}^{ + }} - {{\alpha }^{ + }}{{\zeta }_{0}}l)}^{2}},\quad {{\beta }^{ - }}{{X}^{ - }} = {{\alpha }^{ - }}{{Y}^{ - }}; \\ {{\beta }^{ + }}{{\varrho }^{ - }}{{D}^{ - }}{{({{Y}^{ - }} - {{\beta }^{ - }}{{\zeta }_{0}}l)}^{2}} = {{\beta }^{ - }}{{\varrho }^{ + }}{{D}^{ + }}{{({{Y}^{ + }} - {{\beta }^{ + }}{{\zeta }_{0}}l)}^{2}},\quad {{\beta }^{ + }}{{X}^{ + }} = {{\alpha }^{ + }}{{Y}^{ + }}. \\ \end{gathered} $

Из (17) следуют соотношения

(18)

$\frac{{{{\beta }^{ - }}}}{{{{\alpha }^{ - }}}} = \frac{{{{\beta }^{ + }}}}{{{{\alpha }^{ + }}}},\quad t\left\{ {[u]\frac{{{{\beta }^{ \pm }}}}{{{{\alpha }^{ \pm }}}} - [{v}]} \right\} + l\left\{ {[\gamma ]\frac{{{{\beta }^{ \pm }}}}{{{{\alpha }^{ \pm }}}} - [\delta ]} \right\} = 0.$

Принимая во внимание тот факт, что (18) должно выполняться при всех $t,l$, окончательно получаем из (17)

(19)

$\begin{gathered} {{\beta }^{ - }}{{\alpha }^{ + }} = {{\beta }^{ + }}{{\alpha }^{ - }},\quad [u]{\kern 1pt} {{\beta }^{ \pm }} = [{v}]{{\alpha }^{ \pm }},\quad [\gamma ]{\kern 1pt} {{\beta }^{ \pm }} = [\delta ]{{\alpha }^{ \pm }}{\kern 1pt} , \\ \left[ u \right]y = [{v}](x - t{{u}^{ - }} - {{\gamma }^{ - }}l) + [u]{\kern 1pt} (t{{{v}}^{ - }} + {{\delta }^{ - }}l), \\ {{\alpha }^{ + }}{{\varrho }^{ - }}{{D}^{ - }}{{({{X}^{ - }} - {{\alpha }^{ - }}{{\zeta }_{0}}l)}^{2}} = {{\alpha }^{ - }}{{\varrho }^{ + }}{{D}^{ + }}{{({{X}^{ + }} - {{\alpha }^{ + }}{{\zeta }_{0}}l)}^{2}}. \\ \end{gathered} $

Непосредственно проверяется, что ${{\alpha }^{ + }}{{D}^{ - }} = {{\alpha }^{ - }}{{D}^{ + }}$ и из последнего соотношения (19) следует уравнение для $x(t,l)$:

(20)

${{x}^{2}}[\varrho ] - 2x[t\varrho u + l\varrho (\gamma + {{\zeta }_{0}}\alpha )] + \left[ {\varrho {{{\left( {ut + l(\gamma + {{\zeta }_{0}}\alpha )} \right)}}^{2}}} \right] = 0.$

Решая квадратное уравнение (19), придем к следующему выражению:

(21)

$[\varrho ]х - t[\varrho u] - l\left[ {\varrho (\gamma + {{\zeta }_{0}}\alpha )} \right] = \pm \sqrt {{{\varrho }^{ + }}{{\varrho }^{ - }}} \left( {t[u] + l[\gamma + {{\zeta }_{0}}\alpha ]} \right){\kern 1pt} .$

Из условий согласованности рассматриваемых систем координат из определения 2 следует, что

(22)

$({{\gamma }^{ \pm }} + {{\zeta }_{0}}{{\alpha }^{ \pm }})\left( {\mu [{v}] - \nu [u]} \right) = \mu ({{\gamma }^{ \pm }}[{v}] - {{\delta }^{ \pm }}[u]){\kern 1pt} .$

Выполнение начального условия $x(0,l) = \mu l$ предполагает, что

(23)

${{\gamma }^{ \pm }}[{v}] - {{\delta }^{ \pm }}[u] = \mu [{v}] - \nu [u]{\kern 1pt} .$

Принимая во внимание неравенства в (15) и учитывая (22), (23), придем к формулам для ${\mathbf{X}}(t,l)$ в (13).

С учетом ориентации масса, которая будет сконцентрирована на поверхности ${\mathbf{X}}(t,l)$, может быть вычислена так:

(24)

$\begin{gathered} {{P}_{t}} = \int\limits_{{{\zeta }_{0}}l}^{\tau _{1}^{ - }} {{{\varrho }^{ - }}{{D}^{ - }}d\tau } + \int\limits_{\tau _{1}^{ + }}^{{{\zeta }_{0}}l} {{{\varrho }^{ + }}{{D}^{ + }}d\tau } = ({{\varrho }^{ - }}{{D}^{ - }}{\text{/}}{{\alpha }^{ - }})(x - t{{u}^{ - }} - \mu l) - ({{\varrho }^{ + }}{{D}^{ + }}{\text{/}}{{\alpha }^{ + }})(x - t{{u}^{ + }} - \mu l) = \\ = - ({{D}^{ \pm }}{\text{/}}{{\alpha }^{ \pm }})\left( {[\varrho ](x - \mu l) - t[\varrho u]} \right) = t({{\delta }^{ \pm }}[u] - {{\gamma }^{ \pm }}[{v}])\sqrt {{{\varrho }^{ + }}{{\varrho }^{ - }}} . \\ \end{gathered} $

Далее, используя соотношение (23), придем к формуле для ${{P}_{t}}$ из (13).

Теорема доказана.

Теперь вернемся к рассмотрению двумерной задачи Римана и сформулируем эвристический метод получения оценок, описывающих качественное поведение решений задачи Римана при отсутствии зон вакуума, т.е. зон, где $\varrho = 0$.

Как следует из постановки задачи Римана, которая была приведена выше, в начальный момент времени имеют место разрывы начальных функций на прямых $x = 0$ и $y = 0$. Поскольку в каждом квадранте $i = 1,2,3,4$ заданы свои постоянные значения ${{\varrho }_{i}},{{{\mathbf{u}}}_{i}}$, то при $t > 0$, вообще говоря, возникнет попарное взаимодействие между всеми квадрантами с образованием поверхностей разрыва в соответствии с формулами теоремы 2. Обозначим эти поверхности разрыва как ${{{\mathbf{X}}}_{{i - j}}}$, где $i,j$ – номера соответствующих квадрантов. При этом на лагранжевой плоскости ${\mathbf{a}}$ возникнут области ${{A}_{{i - j}}}$ точек, которые концентрируются на поверхностях ${{{\mathbf{X}}}_{{i - j}}}$ до возникновения взаимодействий этих поверхностей. Наличие соприкосновения областей ${{A}_{{i - j}}}$ свидетельствует о возникновении новой поверхности концентрации, эволюция которой определяется более сложными законами, чем формулы (13) теоремы 2 (скорее всего, решения будут автомодельными). Этим поверхностям также будут соответствовать некоторые области $\tilde {A}$ на плоскости ${\mathbf{a}}$. Если же найдется еще одна область, которая будет охватываться (см. [24]) областями $\tilde {A}$, то это сигнализирует о возникновении концентрации на линии, т.е. возникновении иерархии особенностей.

Конкретные примеры качественного описания обобщенных решений на основе выделенных выше признаков будут приведены в разд. 4. Упор будет сделан на ситуации с возникновением иерархии особенностей, поскольку в отсутствие такой иерархии достаточно подробное исследование было выполнено в [13], [17].

3. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ ДИНАМИКИ ПРИЛИПАНИЯ И ОБЩИЙ АЛГОРИТМ РАСЧЕТА

Для задачи Коши (1), (2) в одномерном случае обоснован метод слипающихся частиц (adhesion dynamics) (см. [6–8]), выражающий входящие в систему (1) законы сохранения массы и импульса. Этот метод состоит в рассмотрении эволюции набора отдельных частиц, претерпевающих абсолютно неупругие столкновения, т.е. слипающихся при столкновениях. В одномерном случае рассмотрение слипающихся частиц позволяет доказать теоремы существования и единственности энтропийных решений, а также получить компактное представление этих решений (вариационный принцип), описывающее все типичные особенности. Как уже отмечалось, в двумерном случае поведение соответствующей системы частиц не обладает теми свойствами, которые присущи ей в одномерном случае (см. [29], [30]). Однако сложности, возникающие при строгом математическом описании, можно преодолеть, перейдя к приближенному описанию и используя его для построения численного алгоритма. Динамика прилипания сохраняется, просто она описывается более сложным образом (см., например, [24]).

Таким образом, в настоящей работе используется численная реализация метода слипающихся частиц для двумерного случая, основанная на подходе, описанном в [26]. Выбор численного метода (без построения сеток и использования конечно-разностных аппроксимаций) обусловлен возникновением иерархии сильных особенностей и, соответственно, необходимостью получения точной картины взаимодействия ударных волн. Здесь мы сконцентрируемся, в основном, на воспроизводстве качественного поведения обобщенных решений задачи Римана. Для точного воспроизводства количественных закономерностей необходимо существенно увеличить количество исходных частиц и использовать параллельную реализацию на высокопроизводительных вычислительных системах, что предполагается сделать в дальнейшем. Кроме того, мы приведем пример расчета, качественно демонстрирующего возможность получения картины крупномасштабного распределения вещества во Вселенной. Для подобных расчетов, основанных на физических данных, также необходимо привлечение суперкомпьютерных мощностей. В этом разделе мы опишем основные этапы алгоритма получения численного решения задачи Коши (1), (2) с помощью указанной выше реализации метода слипающихся частиц.

Во всех экспериментах, результаты которых будут обсуждаться в следующих разделах, расчетная область $\Omega $ представляет собой прямоугольник. Для получения начального распределения частиц в $\Omega $ строится вспомогательная прямоугольная сетка с количеством ячеек ${{N}_{x}} \times {{N}_{y}}$. Затем в каждой ячейке начальная плотность $\varrho (0,x,y)$ (см. (2)), интегрируется с помощью двумерной формулы трапеций, результирующая масса присваивается частице, помещенной в центр ячейки, и компоненты ее скорости выбираются равными значениям функций $u(0,x,y)$ и ${v}(0,x,y)$ в центре ячейки. Таким образом, количество частиц в начальный момент времени равно ${{N}_{x}}{{N}_{y}}$. Отметим, что в данной работе все численные эксперименты (кроме эксперимента 6) представляют собой решения двумерной задачи Римана, т.е. соответствующие начальные данные составлены из констант, поэтому выбор, например, квадратурной формулы для получения массы не играет роли.

Далее мы рассчитываем эволюцию полученной системы частиц. Частица движется во времени $t$ по прямой в соответствии с имеющейся скоростью. Каждая итерация цикла продвижения по времени устроена следующим образом: находятся попарные расстояния между траекториями частиц как функции времени, вычисляется их минимум при $t > 0$: если он меньше, чем критическое значение ${{d}_{{{\text{cr}}}}}$, то частицы считаются столкнувшимися. Выбирается ближайшее по времени столкновение и обрабатываются все частицы, столкнувшиеся в этот момент в этой или других точках области $\Omega $. Все столкновения считаются абсолютно неупругими, т.е. масса, скорость и координата результирующей точки для каждого столкновения вычисляются следующим образом:

${{{\mathbf{x}}}_{{{\text{new}}}}} = \frac{{\sum\limits_i {{{m}_{i}}{{{\mathbf{x}}}_{i}}} }}{{\sum\limits_i {{{m}_{i}}} }},\quad {{{\mathbf{u}}}_{{{\text{new}}}}} = \frac{{\sum\limits_i {{{m}_{i}}{{{\mathbf{u}}}_{i}}} }}{{\sum\limits_i {{{m}_{i}}} }},\quad {{m}_{{{\text{new}}}}} = \sum\limits_i \,{{m}_{i}},$

где ${{m}_{i}}$ обозначает массу, ${{{\mathbf{u}}}_{i}}$ – скорость, ${{{\mathbf{x}}}_{i}}$ – положение частицы, а суммирование ведется по всем частицам, столкнувшимся в данной точке. Затем для полученного набора новых частиц описанный процесс начинается с начала.

Одной из сложностей численной реализации двумерного метода слипающихся частиц является обеспечение достаточно высокой вероятности взаимодействия отдельных частиц. Дело в том, что на плоскости вероятность столкновения двух геометрических точек (не имеющих площади и линейных размеров) равна нулю, и чтобы это изменить, необходимо присвоить им некий эффективный “размер”. Обычно для этого вводится критическая величина расстояния ${{d}_{{{\text{cr}}}}}$, описанная выше. Существуют способы дополнительного увеличения вероятности взаимодействия частиц, например, специальное восстановление скорости (см. [26]). Однако мы провели серии отдельных расчетов, чтобы подобрать оптимальное ${{d}_{{{\text{cr}}}}}$ для рассматриваемого класса задач. Подробнее об этом будет сказано в следующем разделе.

Чтобы получить поле плотности в заданный момент времени, его необходимо восстановить из распределения частиц. Основной интерес представляют $\delta $-особенности плотности, т.е. концентрация вещества вдоль поверхностей или кривых в пространстве $\left( {t,x,y} \right)$. Для восстановления этих особенностей в выбранный момент времени среди частиц выделяются два класса: как минимум на порядок более тяжелые и как минимум на три порядка более тяжелые, чем самая легкая частица при $t = 0$. Первый класс считается относящимся к особенности вдоль поверхности, а второй класс – к особенности вдоль кривой. Значение плотности восстанавливается следующим образом:

$\varrho ({{{\mathbf{x}}}_{i}}) = \frac{{{{m}_{i}}}}{{{{d}_{i}}}},$

где ${{{\mathbf{x}}}_{i}}$ – координаты частицы с массой ${{m}_{i}}$, а ${{d}_{i}}$ для частицы первого класса равно расстоянию до ближайшей частицы первого или второго класса, а для частицы второго класса ${{d}_{i}} = 1$.

С теоретической точки зрения представляют интерес области начальных данных, с которых масса собирается со временем в $\delta $-особенности плотности. Для нахождения и отображения этих областей на каждой итерации алгоритма (т.е. для каждого обработанного столкновения) проводятся дополнительные операции и сохраняется дополнительный массив данных.

4. ЧИСЛЕННЫЙ РАСЧЕТ РЕШЕНИЙ БЕЗ ОБРАЗОВАНИЯ ВАКУУМА

В этом разделе мы рассмотрим результаты численного решения задач Коши (1), (2) для ряда начальных данных, не приводящих к образованию областей с $\varrho = 0$.

Во всех численных экспериментах ниже расчетная область $\Omega $ представляет собой прямоугольник $(x,y) \in [ - l,l] \times [ - l,l]$, где $l$ – выбранный масштаб длины. Количество частиц в начальный момент времени по направлениям $x$ и $y$ выбирается одинаковым, будем обозначать его через $N = {{N}_{x}} = {{N}_{y}}$. Во всех случаях, кроме эксперимента 6, решается задача Римана, т.е. начальные данные в каждой четверти координатной плоскости составлены из констант. Компоненты начальных данных будем обозначать через ${{\varrho }_{i}},\;{{u}_{i}},\;{{{v}}_{i}}$, где $i$ – номер четверти. Четверти нумеруются традиционно: с первой по четвертую против часовой стрелки, начиная с правой верхней. Для фиксированного $t$ будем называть для краткости $\delta $-особенности плотности вдоль поверхности и вдоль кривой в пространстве $\left( {t,x,y} \right)$ “тяжелой линией” и “тяжелой точкой” соответственно, имея в виду проекции соответствующих поверхностей и кривых на плоскости $t = $ const. Через ${{M}_{h}}$ будем обозначать массу тяжелой точки. Таких тяжелых точек во всех рассмотренных экспериментах наблюдается не более одной.

Конкретный выбор масштаба длины $l$ не имеет значения в качественном смысле, а лишь накладывает ограничение на максимальное время ${{t}_{{\max }}}$, для которого результаты расчета могут трактоваться как приближенное решение задачи Коши (1), (2) в некой части расчетной области $\Omega $. Оценка сверху для этого максимального времени имеет следующий вид:

${{t}_{{\max }}} < {{\tilde {t}}_{{\max }}} = \frac{l}{{\mathop {\max }\limits_i \{ {{u}_{i}},{{{v}}_{i}}\} }}.$

При $t = {{\tilde {t}}_{{\max }}}$ все частицы из начального распределения для как минимум одной из четвертей расчетной области заведомо покинут эту четверть либо столкнутся с другими частицами. Во всех рассмотренных экспериментах $l$ выбиралось равным ${{10}^{{ - 2}}}$, и все рассмотренные фиксированные моменты времени удовлетворяли $t < {{\tilde {t}}_{{\max }}}$.

Теоретические оценки этого раздела основаны на методике, описанной в разд. 2.

4.1. Эксперимент 1

Вначале рассмотрим симметричный пример концентрации массы в неподвижной точке, расположенной в начале координат. Начальные данные имеют следующий вид: ${{\varrho }_{i}} = 1\;\forall i$, ${{u}_{1}} = {{u}_{4}} = - 1$, ${{u}_{2}} = {{u}_{3}} = 1$, ${{{v}}_{1}} = {{{v}}_{2}} = - 1$, ${{{v}}_{3}} = {{{v}}_{4}} = 1$.

С теоретической точки зрения формулы (13) приводят к возникновению неподвижной иерархии особенностей. При этом плотность концентрации вещества на поверхностях равна $2t$, а масса, сосредоточенная на кривой, равна $4{{t}^{2}}$.

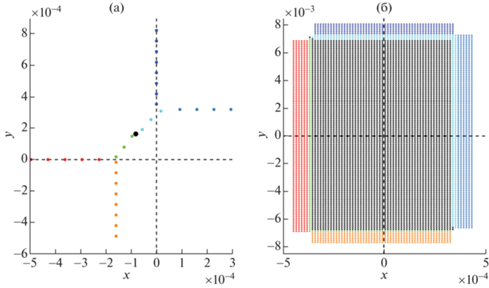
На фиг. 1 изображены рассчитанные в соответствии с описанным выше алгоритмом $\delta $-особенности плотности, а также области начальных данных, с которых масса собралась в эти особенности.

Фиг. 1.

Для эксперимента 1 и $t = 0.005$ изображены: (а) – $\delta $-особенности плотности (тяжелая точка черным цветом, тяжелые линии другими цветами), (б) – области начальных данных, соответствующие этим особенностям (теми же цветами).

В табл. 1 для разных значений $N$ представлены масса тяжелой точки, а также величина ${{\rho }_{{ij}}}$ – постоянная линейная плотность тяжелой линии, разделяющей $i$-ю и $j$-ю четверти расчетной плоскости. Из-за симметрии задачи все расчетные плотности вдоль тяжелых линий получаются одинаковые. Видно, что полученные данные согласуются с приведенными выше формулами, и наблюдается сходимость с увеличением $N$.

Таблица 1.

Сходимость различных величин с увеличением количества частиц в начальный момент времени для эксперимента 1 и $t = 0.005$

$N$	${{M}_{h}}$	${{\rho }_{{12}}}$	${{\rho }_{{23}}}$
75	$9.47 \times {{10}^{{ - 5}}}$	$9.73 \times {{10}^{{ - 3}}}$	$9.73 \times {{10}^{{ - 3}}}$
150	$9.74 \times {{10}^{{ - 5}}}$	$9.87 \times {{10}^{{ - 3}}}$	$9.87 \times {{10}^{{ - 3}}}$
299	$9.87 \times {{10}^{{ - 5}}}$	$9.93 \times {{10}^{{ - 3}}}$	$9.93 \times {{10}^{{ - 3}}}$
Теория	$1 \times {{10}^{{ - 4}}}$	$1 \times {{10}^{{ - 2}}}$	$1 \times {{10}^{{ - 2}}}$

Отметим, что этот эксперимент был использован для поиска оптимального ${{d}_{{{\text{cr}}}}}$ – критического расстояния слипания частиц. Для этого в симметричное расположение частиц в начальный момент времени вводились возмущения (разные в различных четвертях расчетной области) и сравнивалось, насколько полученные данные были близки к полученным аналитически значениям. В результате серии экспериментов было выбрано значение ${{d}_{{{\text{cr}}}}} = 0.7{{d}_{{{\text{min}}}}}$, где ${{d}_{{{\text{min}}}}}$ – минимальное расстояние между частицами в начальный момент времени. Такое ${{d}_{{{\text{cr}}}}}$ использовалось во всех экспериментах, которые будут рассмотрены далее. Можно рассмотреть и более сложные подходы к подбору ${{d}_{{{\text{cr}}}}}$, например, связывая эту величину с массой образующегося кластера, однако расчеты показали, что для рассмотренных примеров такой выбор позволяет получить достаточно устойчивые и согласующиеся с теоретическими оценками результаты.

4.2. Эксперимент 2

Начальные данные имеют следующий вид: ${{\varrho }_{i}} = 1\;\forall i$, ${{u}_{1}} = {{u}_{2}} = - 1$, ${{u}_{3}} = {{u}_{4}} = 2$, ${{{v}}_{1}} = {{{v}}_{4}} = - 1$, ${{{v}}_{2}} = {{{v}}_{3}} = 1$.

В данной вырожденной ситуации область ${{A}_{{1 - 3}}}$ имеет две компоненты, которые пересекаются в одной точке. То есть возможно появление автомодельного решения. Такое решение существует, и его можно получить из системы (7). Оно имеет вид

(25)

$\begin{gathered} x(t,l) = t{\text{/}}2 + l,\quad y = - 2l{\text{/}}3,\quad - 3t{\text{/}}2 \leqslant l \leqslant 3t{\text{/}}2, \\ P(t,l)dl = \left\{ {(4t + 8l{\text{/}}3)dl\;\;{\text{при}}\;\; - {\kern 1pt} 3t{\text{/}}2 \leqslant l \leqslant 0;\quad (4t - 8l{\text{/}}3)dl\;\;{\text{при}}\;\;0 \leqslant l \leqslant 3t{\text{/}}2} \right\}, \\ \end{gathered} $

где $l$ – параметр вдоль сечения поверхности концентрации вещества плоскостью $t = $const. Формулы (13) теоремы 2 дают оценку плотности, равную $4t$, лишь в окрестности точки $l = 0$.

На фиг. 2 изображена рассчитанная в соответствии с описанным выше алгоритмом $\delta $-особенность плотности, а также области начальных данных, с которых масса собралась в эту особенность. В данном случае образуется одна тяжелая линия без тяжелой точки. На фиг. 3 сравнивается плотность вдоль тяжелой линии, полученная с помощью формул (25) (при этом плотность была выражена через величину $x$, которая играла роль параметра), c полученными численно при разных количествах частиц в начальный момент времени. Видно, что с увеличением количества начальных частиц расчетные данные приближаются к аналитическому решению. Интеграл от модуля разности между численным и аналитическим решением для количества частиц в начальный момент времени $75$, $150$ и $299$ равен $4.9 \times {{10}^{{ - 6}}}$, $3.1 \times {{10}^{{ - 6}}}$ и $9.8 \times {{10}^{{ - 7}}}$ соответственно. В данном случае плотность была восстановлена следующим образом: диапазон значений $x$ был разбит точками на равномерные отрезки, плотность в каждой точке полагалась равной отношению массы, заключенной в двух соседних отрезках, и их суммарной длины.

Фиг. 2.

Для эксперимента 2 и $t = 0.002$ изображены: (а) – $\delta $-особенность плотности (тяжелая линия) различными цветами, (б) – область начальных данных, соответствующая этой особенности (теми же цветами).

Фиг. 3.

Для эксперимента 2 и $t = 0.002$ изображена плотность вдоль тяжелой линии, полученная аналитически (зеленый) и рассчитанная при количестве частиц в начальный момент времени $75$ (красный), $150$ (синий) и $299$ (черный).

4.3. Эксперимент 3

Рассмотрим начальные данные, записанные в следующем виде: ${{\varrho }_{i}} = \varrho > 0,$ $i = 1,2,3;$ ${{\varrho }_{4}} = R > \varrho $, ${{u}_{1}} = {{u}_{4}} = - u$, ${{u}_{2}} = {{u}_{3}} = u$, ${{{v}}_{1}} = {{{v}}_{2}} = - {v}$, ${{{v}}_{3}} = {{{v}}_{4}} = {v}$, $u > 0,$ ${v} > 0$.

Для таких начальных данных рассмотрим более подробно расположение областей ${{A}_{{i - j}}}$ на лагранжевой плоскости $(a,b)$. Обозначим

$\lambda \equiv \frac{{\sqrt R - \sqrt \varrho }}{{\sqrt R + \sqrt \varrho }},\quad \theta \equiv \frac{{2\sqrt \varrho }}{{\sqrt R + \sqrt \varrho }},\quad \Theta \equiv \frac{{2\sqrt R }}{{\sqrt R + \sqrt \varrho }}.$

При данной конфигурации начальных данных области ${{A}_{{1 - 3}}},\;{{A}_{{2 - 4}}}$ можно не рассматривать, поскольку частицы, расположенные в соответствующих квадрантах, не успеют взаимодействовать между собой. Рассмотрим области ${{A}_{{1 - 2}}},{{A}_{{2 - 3}}},{{A}_{{3 - 4}}},{{A}_{{4 - 1}}}$, они имеют вид

$\begin{gathered} {{A}_{{1 - 2}}} = \left\{ {(a,b): - tu < a < tu,b > \Theta t{v}} \right\};\quad {{A}_{{2 - 3}}} = \left\{ {(a,b):a < - \Theta tu, - t{v} < b < t{v}} \right\}; \\ {{A}_{{3 - 4}}} = \left\{ {(a,b): - \Theta tu < a < \theta tu,b < - t{v}} \right\};\quad {{A}_{{1 - 4}}} = \left\{ {(a,b):a > tu, - \theta t{v} < b < \Theta t{v}} \right\}. \\ \end{gathered} $

Этим областям соответствуют поверхности концентрации вещества в пространстве $(t,x,y)$ согласно формулам (13). А именно, области ${{A}_{{1 - 2}}}$ соответствует $x = 0,$ $y > \lambda t{v}$; области ${{A}_{{2 - 3}}}$ соответствует $y = 0,$ $x < - \lambda tu$; области ${{A}_{{3 - 4}}}$ соответствует $x = - \lambda tu,$ $y < 0$; области ${{A}_{{1 - 4}}}$ соответствует $x > 0,$ $y = \lambda t{v}$.

Далее на плоскости $(a,b)$ можно выделить области ${{\tilde {A}}_{1}},\;{{\tilde {A}}_{2}}$:

$\begin{gathered} {{{\tilde {A}}}_{1}} = \left\{ { - \Theta tu < a < - tu, - t{v} < b < t{v}} \right\} \cup \left\{ { - tu < a < \theta tu, - t{v} < b < - \theta t{v}} \right\}, \\ {{{\tilde {A}}}_{2}} = \left\{ {\theta tu < a < tu, - \theta t{v} < b < t{v}} \right\} \cup \left\{ { - tu < a < \theta tu,t{v} < b < \Theta t{v}} \right\}, \\ \end{gathered} $

которые формируют предположительно автомодельные поверхности концентрации вещества. В соответствии с законами сохранения можно дать оценку общей массы ${{M}_{k}}$ и интегрального импульса ${{\Im }_{k}}$, $k = 1,2$, этих поверхностей:

$\begin{gathered} {{{\tilde {A}}}_{1}}:{{M}_{1}} = \lambda {{t}^{2}}u{v}(3\varrho + R\theta ),\quad {{\Im }_{1}} = \left( {\lambda {{t}^{2}}{{u}^{2}}{v}(3\varrho - R\theta ),\lambda {{t}^{2}}u{{{v}}^{2}}(\varrho + R\theta )} \right), \\ {{{\tilde {A}}}_{2}}:{{M}_{2}} = \lambda {{t}^{2}}u{v}(3\varrho + R\theta ),\quad {{\Im }_{2}} = \left( { - \lambda {{t}^{2}}{{u}^{2}}{v}(\varrho + R\theta ),\lambda {{t}^{2}}u{{{v}}^{2}}( - 3\varrho + R\theta )} \right). \\ \end{gathered} $

Для возникающей линии концентрации вещества справедливы следующие оценки величин массы и вектор-импульса соответственно:

${{t}^{2}}u{v}\left( {\varrho + 2\varrho \theta + R{{\theta }^{2}}} \right),\quad \left( {{{t}^{2}}{{u}^{2}}{v}(\varrho - R{{\theta }^{2}}),{{t}^{2}}u{{{v}}^{2}}(R{{\theta }^{2}} - \varrho )} \right).$

Дополнительно подчеркнем, что полученные выше выражения являются только оценками для описания качественной структуры решения. Получить аналитическое решение данной задачи на основе уравнений (7) и (6) неожиданно оказывается довольно сложно.

Для численных экспериментов были выбраны следующие начальные данные: $\varrho = {{\varrho }_{i}} = 1,$ $i = 1,2,3;$ $R = {{\varrho }_{4}} = 1.2$, ${{u}_{1}} = {{u}_{4}} = - 1$, ${{u}_{2}} = {{u}_{3}} = 1$, ${{{v}}_{1}} = {{{v}}_{2}} = - 2$, ${{{v}}_{3}} = {{{v}}_{4}} = 2$. На фиг. 4 изображены рассчитанные в соответствии с описанным выше алгоритмом $\delta $-особенности плотности, а также области начальных данных, с которых масса собралась в эти особенности. В табл. 2 приведено сравнение рассчитанных величин массы и компонент импульса с полученными по приведенным выше формулам. Индекс $1$ соответствует тяжелой линии, расположенной ниже тяжелой точки (желтый цвет на фиг. 4), индекс $2$ соответствует тяжелой линии, расположенной выше тяжелой точки (бирюзовый цвет на фиг. 4). Видно, что с увеличением $N$ полученные численно значения приближаются к теоретическим оценкам.

Фиг. 4.

Для эксперимента 3 и $t = 0.0035$ изображены: (а) – $\delta $-особенности плотности (тяжелая точка черным цветом, тяжелые линии другими цветами), (б) – области начальных данных, соответствующие этим особенностям (теми же цветами).

5. ЧИСЛЕННЫЙ РАСЧЕТ РЕШЕНИЙ С ОБРАЗОВАНИЕМ ВАКУУМА

В этом разделе будут рассмотрены результаты численного решения задачи Коши (1), (2) для начальных данных, приводящих к образованию областей с $\varrho = 0$. Как уже было сказано во Введении, качественное поведение решений совпало с теоретическими построениями из [17].

Также приводится пример расчета, который достаточно хорошо отображает современные представления о крупномасштабной структуре Вселенной (см., например, [4]).

5.1. Эксперимент 4

Начальные данные имеют следующий вид: ${{\varrho }_{i}} = 1\;\forall i$, ${{u}_{1}} = - 1$, ${{u}_{2}} = 1$, ${{u}_{3}} = - 2$, ${{u}_{4}} = - 3$, ${{{v}}_{1}} = - 3$, ${{{v}}_{2}} = - 1$, ${{{v}}_{3}} = 1$, ${{{v}}_{4}} = - 2$. Такие значения подходят под п. $4.2(i)$ работы [17], в которой аналитически исследовалось качественное поведение решений задачи Коши, эквивалентной задаче (1), (2) в смысле переменных $(\varrho ,u,{v})$. Поведение полученного нами численного решения (см. фиг. 5) качественно согласуется со структурой решения, схематически приведенного в [17] (см. фиг. 6а). В табл. 3 для этого эксперимента показана сходимость характерных величин с увеличением количества частиц в начальный момент времени. Индекс $12$ относится к вертикальной линии между первой и второй четвертями (черный цвет на фиг. 5), индекс $23$ относится к горизонтальной линии между второй и третьей четвертями (красный цвет), $34$ – к вертикальной линии снизу (зеленый цвет). В последних двух столбцах приведены интегралы от модуля разности координаты $y$ и плотности $\varrho $ как функций $x$, восстановленных на этой и предыдущей по мелкости сетках, вдоль верхнего криволинейного участка особенности (светло-голубой цвет на фиг. 5). Координата $y$ приближалась полиномом третьей степени в смысле наименьших квадратов, а плотность была восстановлена так же, как описано для эксперимента 2.

Фиг. 5.

Для эксперимента 4 и $t = 0.002$ изображены: (а) – $\delta $-особенности плотности (тяжелые линии) различными цветами, (б) – области начальных данных, соответствующие этим особенностям (теми же цветами).

Фиг. 6.

Качественное поведение решения, приведенное в [17] для случаев, соответствующих эксперименту 4 (а) и эксперименту 5 (б).

Таблица 2.

Сравнение массы и импульса частей особенности при разном количестве точек в начальный момент времени со значениями, полученными аналитически, для эксперимента 3 при $t = 0.0035$

$N$	${{M}_{h}}$	$\Im _{h}^{x}$	$\Im _{h}^{y}$	${{M}_{1}}$	$\Im _{1}^{x}$	$\Im _{1}^{y}$	${{M}_{2}}$	$\Im _{2}^{x}$	$\Im _{2}^{y}$
75	9.934	–0.07305	0.4967	0.5654	0.3550	0.4003	0.7641	–0.3842	–0.7217
150	9.983	–0.08782	0.7232	0.2880	0.1813	0.1991	0.6805	–0.3996	–0.5163
299	9.781	–0.2633	0.4330	0.5324	0.2622	0.5063	0.5380	–0.3029	–0.4339
Теория	9.805	–0.2282	0.4565	0.4626	0.2070	0.4788	0.4626	–0.2394	–0.4139

Примечание. Все значения нормированы на $1 \times {{10}^{{ - 5}}}$.

5.2. Эксперимент 5

Начальные данные имеют следующий вид: ${{\varrho }_{i}} = 1\;\forall i$, ${{u}_{1}} = - 1$, ${{u}_{2}} = 1$, ${{u}_{3}} = 1.7$, ${{u}_{4}} = - 1.5$, ${{{v}}_{1}} = - 1$, ${{{v}}_{2}} = 0.5$, ${{{v}}_{3}} = 1$, ${{{v}}_{4}} = 1$. Такие значения подходят под п. $4.2(iii)$ работы [17]. Поведение полученного нами численного решения (см. фиг. 7) качественно согласуется со структурой решения, схематически приведенного в [17] (см. фиг. 6б). В табл. 4 для этого эксперимента также показана сходимость характерных величин с увеличением количества частиц в начальный момент времени. Индекс $34$ относится к вертикальной линии между третьей и четвертой четвертями (красный цвет на фиг. 7), индекс $41$ относится к горизонтальной линии между четвертой и первой четвертями (синий цвет). В последних двух столбцах приведены интегралы от модуля разности координаты $y$ и плотности $\varrho $ как функций $x$, восстановленных на этой и предыдущей по мелкости сетках, вдоль нижнего криволинейного участка особенности (черный цвет на фиг. 7). В данном случае была взята лишь часть этого участка, чтобы сохранить однозначность упомянутых функций. Координата $y$ приближалась полиномом третьей степени в смысле наименьших квадратов, а плотность была восстановлена так же, как описано для эксперимента 2.

Фиг. 7.

Для эксперимента 5 и $t = 0.002$ изображены: (а) – $\delta $-особенности плотности (тяжелые линии) различными цветами, (б) – области начальных данных, соответствующие этим особенностям (теми же цветами).

Таблица 3.

Сходимость различных величин с увеличением количества частиц в начальный момент времени для эксперимента 4 при $t = 0.002$

$N$	${{\varrho }_{{12}}}$	${{\varrho }_{{23}}}$	${{x}_{{34}}}$	$\left\| {y{{{(x)}}_{{{\text{upper}}}}}} \right\|$	$\left\| {\varrho {{{(x)}}_{{{\text{upper}}}}}} \right\|$
75	$3.78 \times {{10}^{{ - 3}}}$	$4.32 \times {{10}^{{ - 3}}}$	–$4.94 \times {{10}^{{ - 3}}}$	–	–
150	$4.00 \times {{10}^{{ - 3}}}$	$4.00 \times {{10}^{{ - 3}}}$	–$5.00 \times {{10}^{{ - 3}}}$	$9.71 \times {{10}^{{ - 8}}}$	$5.98 \times {{10}^{{ - 6}}}$
299	$4.03 \times {{10}^{{ - 3}}}$	$4.03 \times {{10}^{{ - 3}}}$	–$5.00 \times {{10}^{{ - 3}}}$	$1.63 \times {{10}^{{ - 8}}}$	$4.81 \times {{10}^{{ - 6}}}$

5.3. Эксперимент 6

Наконец, приведем результат расчета, который имеет отношение к моделированию формирования крупномасштабной структуры Вселенной.

Таблица 4.

Сходимость различных величин с увеличением количества частиц в начальный момент времени для эксперимента 5 при $t = 0.002$

$N$	${{\varrho }_{{41}}}$	${{\varrho }_{{34}}}$	${{x}_{{34}}}$	$\left\| {y{{{(x)}}_{{{\text{lower}}}}}} \right\|$	$\left\| {\varrho {{{(x)}}_{{{\text{lower}}}}}} \right\|$
75	$3.78 \times {{10}^{{ - 3}}}$	$6.49 \times {{10}^{{ - 3}}}$	$1.99 \times {{10}^{{ - 4}}}$	–	–
150	$4.00 \times {{10}^{{ - 3}}}$	$6.40 \times {{10}^{{ - 3}}}$	$1.99 \times {{10}^{{ - 4}}}$	$3.29 \times {{10}^{{ - 8}}}$	$9.57 \times {{10}^{{ - 6}}}$
299	$4.03 \times {{10}^{{ - 3}}}$	$6.44 \times {{10}^{{ - 3}}}$	$2.00 \times {{10}^{{ - 4}}}$	$5.49 \times {{10}^{{ - 9}}}$	$6.52 \times {{10}^{{ - 6}}}$

Начальные плотность и компоненты скоростей задавались следующим образом: $\varrho = N(1,0.3)$, $u = N(0,0.3)$, ${v} = N(0,0.3)$, где $N(\mu ,\sigma )$ – случайная величина, имеющая нормальное распределение с математическим ожиданием $\mu $ и дисперсией $\sigma $. Крайние значения распределений были “обрезаны” так, чтобы $\varrho \in [0,2]$, $u \in [ - 1,1]$, ${v} \in [ - 1,1]$. На фиг. 8 изображено распределение частиц для различных моментов времени, масса отражена размером точек. Видно, что начальные данные в виде случайных распределений приводят с течением времени к формированию структур, состоящих из массивных кластеров, соединенных связями, имеющими вид кривых.

Фиг. 8.

Распределение частиц для эксперимента 6 при разных значениях времени $t$. Размер точек пропорционален их массе.

ЗАКЛЮЧЕНИЕ

В работе рассмотрена двумерная система уравнений газовой динамики без давления как с теоретической, так и с численной точек зрения. В отличие от многих других работ в данном направлении в настоящей публикации сделан акцент на важной отличительной особенности данной системы уравнений – возникновении особенностей плотности не только вдоль поверхностей, но и вдоль кривых в пространстве $(t,x,y)$. Образование такой иерархии особенностей, т.е. особенностей, сосредоточенных на многообразиях разной размерности, по-видимому, характерно для общего многомерного случая и не имеет аналогов в случае одной пространственной переменной.

В многомерном случае для строгого математического анализа нет возможности опираться на систему движущихся частиц, по аналогии с одномерным случаем, так как столкновения таких частиц оказываются редкими для большинства начальных данных. В настоящей работе показано, что, тем не менее, можно искать обобщения на уровне вариационных принципов, по крайней мере, для специальных видов течений. Полученные обобщения качественно характеризуют ситуацию возникновения иерархии особенностей и позволяют делать эвристические оценки.

Вследствие трудностей теоретического описания в настоящей статье также предложен численный метод на основе реализации динамики прилипания (adhesion dynamics), который позволяет получать достаточно сложные структуры взаимодействия волн при наличии особенностей на поверхностях различной коразмерности. Приведен достаточно представительный набор экспериментов, подтверждающий робастность разработанного метода. А именно, для ряда расчетов (двумерная задача Римана) показана сходимость результатов с увеличением количества частиц в начальный момент времени, а также их приближение к значениям, полученным теоретически. Для более сложных структур, связанных с образованием вакуума (областей с плотностью, равной нулю), показано совпадение качественного поведения численного решения с известными результатами. Это позволяет обосновать высокую вероятность воспроизведения с помощью предложенного численного метода реальной структуры решений исследуемой системы. Также в качестве направления непосредственных дальнейших приложений приведен пример расчета, отражающий современные представления о крупномасштабной структуре Вселенной.

В дальнейшем предполагается расширить имплементацию предложенного метода на архитектуры высокопроизводительных вычислительных средств, в частности, с использованием графических плат, что позволит значительно увеличить количество частиц в начальный момент времени и достичь таким образом более точного воспроизведения мелкомасштабной структуры особенностей решений, что, в свою очередь, играет важную роль для углубления теоретического анализа многомерной системы уравнений газовой динамики без давления.

В заключение авторы приносят благодарность А.И. Аптекареву за полезные замечания и обсуждение результатов.

Список литературы

Крайко А.Н. О поверхностях разрыва в среде, лишенной собственного давления // Приклад. матем. и мех. 1979. Т. 43. № 3. С. 500–510.
Крайко А.Н., Сулайманова С.М. Двужидкостные течения смеси газа и твердых частиц с “пеленами”и “шнурами”, возникающими при обтекании непроницаемых поверхностей // ПММ. 1983. Т. 47. № 4. С. 619–630.
Крайко А.Н. Математические модели для описания течений газа и инородных частиц и нестационарной фильтрации жидкости и газа в пористых средах // Вестник ЮУрГУ. Сер. Матем. моделирование и программирование. 2014. Т. 7. № 1. С. 34–48.
Гурбатов С.Н., Саичев А.И., Шандарин С.Ф. Крупномасштабная структура Вселенной. Приближение Зельдовича и модель слипания // Успехи физ. наук. 2012. Т. 182. № 3. С. 233–261.
Bouchut F. On zero-pressure gas dynamics // in: B. Perthame (Ed.), Advances in Kinetic Theory and Computing, Ser. Adv. Math. Appl. Sci. Singapore.: World Sci. 1994. V. 22. P. 171–190.
И В., Рыков Ю.Г., Синай Я.Г. Вариационный принцип Лакса-Олейник для некоторых одномерных систем квазилинейных уравнений // Успехи матем. наук. 1995. Т. 50. № 1. С. 193–194.
Grenier E. Existence globale pour la systeme des gaz sans pression // C.R. Acad. Sci. Ser. 1. Math. 1995. V. 321. № 2. P. 171–174.
E W., Rykov Yu.G., Sinai Ya.G. Generalized variational principles, global weak solutions and behavior with random initial data for systems of conservation laws arising in adhesion particle dynamics // Comm. Math. Phys. 1996. V. 177 P. 349–380.
Huang F., Wang Z. Well posedness for pressureless flow // Comm. Math. Phys. 2001. V. 222. № 1. P. 117–146.
Li J. and Warnecke G. Generalized characteristics and the uniqueness of entropy solutions to zero-pressure gas dynamics // Adv. Differential Equations. 2003. V. 8. № 8. P. 961–1004.
Hynd R. Sticky particle dynamics on the real line // Not. Am. Math. Soc. 2019. V. 66. № 2. P. 162–168.
Hynd R. A trajectory map for the pressureless Euler equations // Transact. Am. Math. Soc. 2020. V. 373. № 10. P. 6777–6815.
Li J., Zhang T., Yang S.L. The Two-Dimensional Riemann Problem in Gas Dynamics. London: Longman, 1998.
Рыков Ю.Г. Особенности типа ударных волн в среде без давления, решения в смысле теории меры и в смысле Коломбо // Препринты ИПМ им. М.В. Келдыша. 1998. № 30. URL: https://library.keldysh.ru/preprint.asp?id_1998-30.
Rykov Yu.G. On the nonhamiltonian character of shocks in 2-D pressureless gas // Boll. Unione Mat. Ital. Sez. B. Ser. 8. 2002. V. 5-B. P. 55–78.
Colombeau J.F. Elementary introduction to new generalized functions. North-Holland Math. Studies. V. 113, 1985.
Pang Y. The Riemann problem for the two-dimensional zero-pressure Euler equations // J. Math. Anal. Appl. 2019. V. 472. № 2. P. 2034–2074.
Li J., Yang H. Delta-shock waves as limits of vanishing viscosity for multidimensional zero-pressure gas dynamics // Quart. Appl. Math. 2001. V. LIX. P. 315–342.
Шелкович В.М. Сингулярные решения систем законов сохранения типа δ и δ'-ударных волн и процессы переноса и концентрации // Успехи матем. наук. 2008. Т. 63. Вып. 3. С. 73–146.
Albeverio S., Rozanova O.S., Shelkovich V.M. Transport and concentration processes in the multidimensional zero-pressure gas dynamics model with energy conservation law // https://arxiv.org /abs/1101.5815.
Аптекарев А.И., Рыков Ю.Г. Вариационный принцип для многомерных законов сохранения и среды без давления // Успехи матем. наук. 2019. Т. 74. Вып. 6. С. 159–160.
Khanin K., Sobolevski A. Particle dynamics inside shocks in Hamilton-Jacobi equations // Phil. Trans. Roy. Soc. A. 2010. V. 368. P. 1579–1593.
Khanin K., Sobolevski A. On Dynamics of Lagrangian Trajectories for Hamilton–Jacobi Equations // Arch. Ration. Mech. Anal. 2016. V. 219. Iss. 2. P. 861–885.
Аптекарев А.И., Рыков Ю.Г. Детализация механизма образования особенностей в системе уравнений газовой динамики без давления // Докл. РАН. 2019. Т. 484. № 6. С. 655–658.
Рыков Ю.Г. Двумерная газовая динамика без давления и вариационный принцип // Препринты ИПМ им. М.В. Келдыша. 2016. № 94. URL: https://library.keldysh.ru/preprint.asp?id 16-94.
Chertock A., Kurganov A., Rykov Yu. A new sticky particle method for pressureless gas dynamics // SIAM J. N-umer. Anal. 2007. V. 45. №6. P. 2408–2441.
Рыков Ю.Г. Решения с распадом вещества в системе уравнений газовой динамики без давления // М-атем. заметки. 2020. Т. 108. № 3. С. 477–480.
Klyushnev N.V., Rykov Yu.G. Non-conventional and conventional solutions for one-dimensional pressureless gas // Lobachevskii J. Math. 2021. V. 42. № 11. P. 2615–2625.
Bressan A., Nguyen T. Non-existence and non-uniqueness for multidimensional sticky particle systems // K-inetic and Relatet Model. 2014. V. 7 (2), P. 205–218.
Bianchini S., Daneri S. On the sticky particle solutions to the multi-dimensional pressureless Euler equations // Preprint arXiv:2004.06557 (2020).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал