Журнал вычислительной математики и математической физики, 2023, T. 63, № 4, стр. 667-677
Определение высот энергетических барьеров молекулы циклогексена с использованием процедуры стохастической аппроксимации
1 Институт математических проблем биологии РАН –
филиал Института прикладной математики им. М.В. Келдыша РАН
142290 Пущино, М.о., ул. проф. Виткевича, 1, Россия
* E-mail: tepl@impb.ru
Поступила в редакцию 05.07.2022
После доработки 05.07.2022
Принята к публикации 15.12.2022
- EDN: IPOLXU
- DOI: 10.31857/S0044466923040154
Аннотация
Методом Монте-Карло (стохастическая аппроксимация) выполнен расчет относительных значений плотности состояний молекулы циклогексена в пространстве координат Кремера–Попла. С помощью этих данных были оценены высоты энергетических барьеров, разделяющие стереоизомеры молекулы. Библ. 49. Фиг. 7.
ВВЕДЕНИЕ
Много лет конформационный анализ успешно применяется в изучении изменений физико-химических свойств и реакционной способности молекул, сопровождающих взаимопревращения стереоизомеров [1]. Работы в этой области проводятся и экспериментальными, и теоретическими методами. В последние десятилетия, благодаря взрывному росту производительности вычислительной техники, компьютерное моделирование с использованием методов квантовой химии, классической молекулярной динамики и Монте-Карло [2–4] находит широкое применение в исследованиях конформационного пространства молекул. В связи с этим особую важность приобретает поиск эффективных решений “обратной задачи”, состоящей в определении параметров силовых полей молекулярных моделей, позволяющих с высокой точностью воспроизводить имеющиеся экспериментальные данные.
В предыдущей работе [5], посвященной параметризации торсионных потенциалов ковалентных связей в молекулах углеводородов, мы столкнулись с серьезными трудностями при определении высоты потенциальных барьеров, разделяющих конформеры. Дело в том, что в этой работе мы использовали стандартную процедуру Метрополиса и др. [6] для расчета структурных и энергетических характеристик молекул путем усреднения по статистически значимой выборке из канонического ансамбля молекулярных конфигураций при комнатной температуре. При такой постановке “вычислительного эксперимента” вероятность выбора конфигурации пропорциональна соответствующему ей больцмановскому фактору. Ясно, что репрезентативность выборки в области переходных состояний может оказаться очень низкой, поэтому для того чтобы поднять точность оценок высоты потенциальных барьеров до приемлемого уровня, необходимо либо работать с очень большими выборками, либо выбрать иное, наиболее подходящее для решения этой задачи средство, обратившись к богатому арсеналу методов вычислительной статистики [7], применяемых в современном молекулярном моделировании [8], [9]. Так, в работе [5], чтобы избежать задержки при подготовке данных к публикации, нам пришлось отказаться от использования алгоритма Метрополиса и др. [6] для расчета характеристик молекулы циклогексена, воспользовавшись более подходящей в данном случае процедурой Ванга–Ландау [10], [11].
Тем не менее, следует отметить, что метод Ванга–Ландау [10], [11] имеет несколько серьезных недостатков, ограничивающих его применение. Так, установлено (см. [12]), что после некоторого числа итераций статистическая точность оценок этим методом перестает улучшаться, поскольку из-за очень быстрого уменьшения величины модификационного фактора вклад всей оставшейся части выборки становится несущественным. Как было показано в работах [13], [14], эту проблему можно устранить, применив другое правило для изменения модификационного фактора, а именно после выполнения некоторого числа итераций метода [10], [11] вместо экспоненциального закона использовать формулу 1/t. К сожалению, в этом случае алгоритм вычислений не только усложняется, но и появляются дополнительные параметры, чьи величины иначе как методом проб и ошибок определить не получится. Следует отметить, что и сам термин “время t”, фигурирующий в статьях [13], [14], допускает множественное толкование. Добавим также, что для перехода к очередной стадии вычислений алгоритмы [10], [11] и [13], [14] требуют проверки “критерия плоскостности”, устанавливаемого опытным путем. Помимо всего этого необходимо задать точные границы заполняемых в процессе расчетов гистограмм, а в случае многомерных гистограмм, такую работу сделать очень сложно.
В [15] предложен более простой метод, основанный на теории процедур стохастической аппроксимации [16–18]. В настоящее время этот подход, обозначаемый в текстах статей аббревиатурой SAMC, активно используется в изучении строения и физико-химических свойств полимеров [19–21]. Цель настоящей статьи – продемонстрировать возможности метода SAMC [15] для решения задач конформационного анализа и разработки наборов параметров силовых полей молекулярных моделей. В последующих разделах будет дано описание выбранной нами модели молекулы циклогексена, рассмотрены основные этапы вычислительного алгоритма SAMC и представлены данные о высотах энергетических барьеров, полученные в результате исследования конформационного пространства этой молекулы.
1. МЕТОДИКА МОДЕЛИРОВАНИЯ
Как и прежде [5], [22], наша модель молекулы циклогексена представляет собой систему конфигурационно жестких фрагментов (четыре CH2-группы и CH=CH, о фрагментах и фрагментации молекул подробно рассказано в работе [22]) соединенных одинарными связями в соответствии с химической структурой этой молекулы. Для длин химических связей CH и C=C взяты значения 1.085 и 1.34 Å (экспериментальные данные [23]: |HCsp3| = 1.092 Å, |HCsp2| = 1.083 Å, |Csp2 = Csp2| = 1.326 Å), угол HCH равен 109.47°, а HC = C – 120° (стандартные значения для sp3 и sp2-гибридизации).
Потенциальная энергия, характеризующая конформацию молекулы циклогексена, приобретается за счет невалентных взаимодействий атомов ее фрагментов (потенциалы Леннард-Джонса и Кулона), энергии деформации межфрагментных ковалентных связей и смежных с ними валентных углов, а также торсионных потенциалов, затрудняющих вращение молекулярных фрагментов вокруг этих связей. Параметры потенциальных функций Леннард-Джонса такие же, как в работе [22], парциальные заряды на атомах (в единицах элементарного заряда: фрагмент CH=CH qC = –0.094, qH = 0.057, у соседних с ним CH2-групп qC = –0.084, qH = 0.058, а у дальних CH2-групп – qC = –0.103, qH = 0.054) и параметры торсионных потенциалов взяты из работы [5]. Энергия деформации пропорциональна квадрату отклонения длин связей и величин углов от их равновесных значений с коэффициентами 310 ккал/моль/Å2 и 40 ккал/моль/рад2 соответственно. Для равновесных длин химических связей Csp3–Csp3 и Csp3–Csp2 взяты значения 1.526 и 1.51 Å, а для углов – 109.47° (Csp3) и 120° (Csp2). Такой выбор был в значительной степени мотивирован параметрами силовых полей, представленных в статьях [24], [25]. Атомы соседних фрагментов, соединенные ковалентной связью друг с другом или через третий атом, не участвуют во взаимодействиях, описываемых потенциалом Леннард-Джонса.
Размерность конфигурационного пространства нашей модели молекулы циклогексена в системе координат одного из ее фрагментов равна 24 (5 × 6–6), поэтому проводить конформационный анализ в терминах декартовых координат и углов Эйлера, по меньшей мере, не рационально. В подобных ситуациях следует перейти от описания в системе большого числа эквивалентных координат к представлению с помощью обобщенных координат, причем таких, что только одна-две из них (в крайнем случае, три), сублимировав большой объем структурной информации, позволяют уверенно локализовать все особые точки гиперповерхности потенциальной энергии и обратным преобразованием с высокой точностью восстановить декартовы координаты всех атомов любого из конформеров. Для циклогексена такая возможность может быть реализована на основе концепции псевдовращения [26], если в рамках формализма Кремера–Попла [27–29] перейти к описанию конформационного многообразия молекулы в сферических координатах Q, θ и φ (см. [30]).
В общем случае конформационный анализ в редуцированном до трех измерений пространстве может оказаться весьма трудоемким, но для циклогексена работа сильно упрощается из-за обособленности первой координаты в этой тройке. В самом деле, амплитуда Q характеризует степень складчатости молекулы циклогексена, выражая свое среднее значение как радиус “конформационного глобуса” (см. [31, фиг. 3.19 ]), а оставшиеся две: фазовые углы θ и φ – определяют тип конформации и задают ее положение на этом глобусе. Таким образом, одну сложную задачу мы разделим на несколько более простых задач, чьи решения допускают прямое сопоставление с экспериментальными данными. К таковым можно отнести расчет зависимости конформационной энергии от амплитуды складчатости Q, построение поверхности потенциальной энергии в координатах θ и φ и др.
Потенциальную энергию, которой обладает молекула циклогексена в состоянии теплового равновесия при температуре T в моменты, когда амплитуда складчатости равна Q, можно выразить статистическим интегралом по всему диапазону значений конформационной энергии E, реализующихся в соответствующем каноническом ансамбле:
Так как символьное выражение для функции $w(E\,{\text{|}}\,Q)$ нам не известно, будем вычислять отношение этих интегралов численно по формуле трапеций. Для этого разобьем выбранный для анализа диапазон энергий на N смежных интервалов и сопоставим каждому из них Ei – среднее арифметическое величин энергии на концах соответствующего интервала (i – его порядковый номер). Вообще, при выборе границ диапазона полезно ориентироваться на уже известные данные о высотах потенциальных барьеров, иначе придется действовать методом проб и ошибок, а задавая N, следует искать разумный баланс между точностью и трудоемкостью вычислений. Далее, после преобразования в дискретную форму имеем для практического применения следующую формулу:
В этом месте, отдавая дань уважения труду первопроходцев, нельзя не упомянуть работу [32], авторы которой, смоделировав на компьютере случайное блуждание в той части конфигурационного пространства, где потенциальная энергия изучаемой системы не превышает заданного уровня, смогли оценить относительные значения статистических весов и рассчитать с их помощью термодинамические характеристики газофазного аргона.
Для определения значений g мы будем использовать многостадийную процедуру стохастической аппроксимации [15]. В ее основе лежит общая для методов [10], [13], [15] идея организовать в конфигурационном пространстве изучаемой модели случайное блуждание с переходными вероятностями обратно пропорциональными итерационно уточняемым статистическим весам $w({{E}_{i}}\,{\text{|}}\,Q)$ макросостояний в исследуемой области значений энергии. В терминах статистической механики это макросостояния, каждому из которых соответствует огромное число микросостояний в конфигурационном пространстве молекулярной модели. Для контроля можно построить гистограмму, где каждый столбик показывает количество случаев, когда мгновенная потенциальная энергия молекулы оказывалась в диапазоне значений соответствующего интервала. Вычисления считаются успешно завершенными, если на некоторой итерации значения конформационной энергии станут появляться с примерно равной частотой во всех интервалах. В этом случае огибающая вершин столбцов гистограммы для {Ei} будет выглядеть как ровная горизонтальная линия.
Стохастическая процедура [15], реализуемая на дискретном множестве состояний, не является цепью Маркова в строгом смысле [33], но имеет с ней много общего. Более того, на завершающих стадиях, когда модифицирующий фактор практически равен единице, их можно считать эквивалентными. Учитывая это обстоятельство, необходимую для наших расчетов и общую для методов [10], [13], [15] формулу переходной вероятности, можно вывести из теорем теории цепей Маркова [34], используя логическую схему [35], [36] и аргументацию, представленную в оригинальных работах [6], [37], [38].
Выберем в качестве прототипа цепи Маркова, обладающие свойством обратимости [34]. Цепи этого класса следуют принципу детального баланса [36], связывающему общим уравнением $\pi $ (инвариантное распределение состояний) и p – вероятность переходов между ними: $\pi (s1) \cdot p(s1 \to s2) = \pi (s2) \cdot p(s2 \to s1)$. Функциональное уравнение такого вида имеет много решений для заданного (целевого) распределения $\pi $. Как было показано в работе [39], оптимальным среди них является функция Метрополиса и др. (см. [6]) $p(s1 \to s2) = \min [1,{{\pi (s2)} \mathord{\left/ {\vphantom {{\pi (s2)} {\pi (}}} \right. \kern-0em} {\pi (}}s1)]$. В нашей задаче, как и в работах [10], [13], [15], целевое распределение вероятностей можно выразить формулой $\pi ({{E}_{i}}\,{\text{|}}\,Q) = Z{\text{/}}w({{E}_{i}}\,{\text{|}}\,Q) = Z{\text{/}}{{w}_{i}}$, где Z – неизвестная нормировочная константа. Таким образом, для вычисления значений переходных вероятностей мы будем использовать выражение
В целом кривую, изображающую зависимость конформационной энергии от амплитуды Q, можно построить, разбив весь диапазон вариации Q на M смежных интервалов и сопоставив каждому из них Qj – среднее арифметическое значений на концах соответствующего интервала. Средние энергии в этом случае рассчитываются по формуле:
Ядро алгоритма для расчета {g(i, j)} состоит из двух этапов, выполняемых последовательно в цикле: реализация очередного макросостояния (Eij,Qj) в конфигурационном пространстве изучаемой модели и модификация значения соответствующего элемента двумерного массива g(i, j). Эти два этапа составляют один шаг вычислительной процедуры.
В начале первого этапа готовится пробная конформация молекулы: случайно выбранный фрагмент сдвигается на случайный вектор и поворачивается на случайный угол (вместо полярного угла используется случайное значение его косинуса) вокруг своего геометрического центра как твердое тело. “Случайные” величины, упомянутые здесь, имеют равномерное распределение и вычисляются с помощью алгоритма для генерации псевдослучайных чисел [40]. Амплитуда перемещений (0.025 Å на каждую координату) и поворотов (1.3° на каждый угол Эйлера) за один шаг процедуры постоянна в течение всего вычислительного эксперимента.
Далее рассчитывается потенциальная энергия молекулы E и определяется амплитуда складчатости Q. Пробная конформация принимается в качестве реализации макросостояния s2 на этом шаге вычислительной процедуры, если $g({{i}_{{s2}}},{{j}_{{s2}}}) < g({{i}_{{s1}}},{{j}_{{s1}}})$ или, в противном случае, если $\exp \left[ {g\left( {{{i}_{{s1}}},{{j}_{{s1}}}} \right) - g\left( {{{i}_{{s2}}},{{j}_{{s2}}}} \right)} \right] \geqslant \xi $. Здесь $\xi $ – случайное число, равномерно распределенное в интервале (0,1), а s1 – макросостояние на предыдущем шаге. Если эти условия не выполнены, а также в случаях, когда величины E и Q выходят за границы заданного диапазона или когда длины ковалентных связей отклоняются от равновесных значений больше чем на 0.12 Å, а валентные углы – больше чем на 12°, переход в новое макросостояние не осуществляется, но еще раз используется s1. Амплитуда перемещений и поворотов молекулярных фрагментов за один шаг процедуры (см. выше) подбирается заранее так, чтобы принималось около 35% пробных конформаций.
На втором этапе выполняется модификация элемента массива g(i, j), соответствующего макросостоянию, реализованному на первом этапе этого шага вычислительной процедуры: $g\left( {i,j} \right) = g\left( {i,j} \right) + \gamma $. Здесь $\gamma $ – логарифм модифицирующего фактора. Напомним, что перед началом расчетов массив g необходимо инициализировать, присвоив всем его элементам значение 0 (как и в [10], мы считаем, что в этот момент статистические веса всех макросостояний одинаковы и равны 1). Величина $\gamma $ определяется по формуле (см. [15]): $\gamma \left( t \right) = {{t}_{0}}{\text{/}}\max \left( {{{t}_{0}},t} \right)$, где $t = 1,2,...$ – порядковый номер итерации. Для выбора конкретного значения параметра ${{t}_{0}}$ в [15] не оставили какого-либо рецепта, ограничившись указанием, что его величина должна соответствовать сложности задачи, а также количеству элементов массива g(i, j). В то же время еще одна неопределенность, заключающаяся в том, как соотносятся “итерации” и “шаги” вычислительной процедуры [15], дает стимул к разработке оптимальных алгоритмов. В этой ситуации большую помощь может оказать информация об условиях, влияющих на сходимость процессов стохастической аппроксимации [41].
Учитывая случайный характер модификаций, вычислительная процедура должна работать так, чтобы в среднем изменения g(i, j) происходили в правильном направлении. Для этого необходимо выполнить два условия [16], [41]. Во-первых, фактор случайности не должен быть настолько сильным, чтобы происходило накопление ошибок, следовательно, ряд $\sum\nolimits_{t = 1}^\infty {{{\gamma }^{2}}\left( t \right)} $ должен сходиться. Во-вторых, величина $\gamma $ не может уменьшаться слишком быстро, иначе элементы массива g(i, j) перестанут существенно изменяться задолго до того, как они приблизятся к искомым значениям (основной недостаток метода [10]). Таким образом, ряд $\sum\nolimits_{t = 1}^\infty {\gamma \left( t \right)} $ должен расходиться. Нетрудно убедиться, что зависимость типа $\gamma \left( t \right) = {{t}_{0}}{\text{/}}\max \left( {{{t}_{0}},t} \right)$ (см. [13], [15]) вполне удовлетворяет этим условиям.
Несмотря на концептуальную простоту, практическое применение метода SAMC [15] для изучения молекулярных моделей сопряжено с некоторыми неудобствами. Затруднения возникают не только на этапе планирования общей стратегии проведения вычислительного эксперимента, но и в конкретных ситуациях, из-за аномалий при заполнении массива g(i, j). Различные способы решения этих проблем рассмотрены в статье [20].
В нашей работе параметр ${{t}_{0}}$ равен 10. Диапазон конформационных энергий E (0–100 ккал/моль) разбит на 200, а диапазон амплитуд Q (0–1.12 Å) – на 120 интервалов. Таким образом, 24 тысячи элементов массива g(i, j) хранят всю необходимую информацию об относительных значениях плотности состояний. В соответствии с рекомендациями [15], на каждой итерации выполнялось 120 тысяч шагов вычислительной процедуры (см. выше). Здесь мы учли, что наша модель молекулы циклогексена состоит из пяти фрагментов. Всего для расчета $E\left( Q \right)$ было выполнено 33 миллиона итераций, при этом $\gamma $ уменьшился от 1 до $3.03 \times {{10}^{{ - 7}}}$. На самом деле для этой задачи достаточно 1 миллиона итераций, но мы решили убедиться в надежности результатов. Поверхность, изображающая функцию g(E, Q) после завершения итераций, показана на фиг. 1. На фиг. 2 представлена двумерная гистограмма, высота каждого столбца которой равна количеству случаев, когда реализовывалось соответствующее ему макросостояние (Eij, Qj). Эти данные собраны на последних 250 тысячах итераций. Хорошо видно, что гистограмма стала практически плоской, за исключением отдельных пиков в областях, не оказывающих существенное влияние на результат.
Фиг. 1.
Зависимость логарифма плотности состояний g от конформационной энергии E и амплитуды складчатости Q.

Фиг. 2.
H – количество реализаций макросостояний с энергией E и амплитудой складчатости Q на заключительных итерациях.

Чтобы определить, как конформационная энергия E зависит от фазовых углов θ и φ, был проведен новый вычислительный эксперимент для расчета значений логарифма статистических весов в трехмерном пространстве макросостояний $\left( {{{E}_{{ijk}}},\;{{\theta }_{j}},\;{{\varphi }_{k}}} \right)$. В этот раз параметр ${{t}_{0}}$ снова равен 10. Диапазон конформационных энергий E (0–100 ккал/моль) разбит на 200 интервалов, а диапазоны фазовых углов θ (0°–180°) и φ (0°–360°) – на 36 и 72 интервала соответственно. Массив g(i, j, k) состоит из 518 400 элементов, поэтому на каждой итерации выполнялось 2592 тысяч шагов вычислительной процедуры. Для расчета $E\left( {\theta ,\varphi } \right)$ было выполнено 6.7 миллиона итераций, при этом $\gamma $ уменьшился от 1 до $1.49 \times {{10}^{{ - 6}}}$. Контроль сходимости осуществлялся путем построения и визуального анализа 36 двумерных гистограмм, отображающих количество случаев, когда в слое ${{\theta }_{j}}$ реализовывалось макросостояние с Eijk и ${{\varphi }_{k}}$.
Карту средних значений амплитуды $Q$ в координатах θ и φ, необходимую для полного описания, также можно построить с помощью g(i, j, k), но для этого нужна дополнительная информация об амплитудах Qijk. Такие данные были получены нами на последних 50 тысячах итераций простым усреднением величин $Q$ у конформеров, соответствующих конкретному макросостоянию $\left( {{{E}_{{ijk}}},\,{{\theta }_{j}},\,{{\varphi }_{k}}} \right)$.
2. РЕЗУЛЬТАТЫ РАСЧЕТОВ
В результате экспериментальных исследований циклогексена [42–45] установлено, что наиболее стабильный его конформер – полукресло, перекрученная форма, обладающая симметрией C2 (фиг. 3). Благодаря тепловым флуктуациям молекула способна осуществить инверсию шестичленного кольца, временно трансформировавшись в энергетически невыгодную конфигурацию типа ванны (симметрия CS). Активационная энтальпия этого процесса (энергетический барьер инверсии) занимает диапазон 5.3–10.3 ккал/моль по экспериментальным данным [42], [46] или 5.2–6.28 ккал/моль согласно квантово-химическим расчетам [47–49]. Помимо этого, переход в еще одну неустойчивую форму (симметрия C2V) с плоским шестичленным кольцом требует по разным оценкам 10.4 [47] –13.4 [46] ккал/моль.
Фиг. 3.
Стереоизомеры циклогексена: (a) – перекрученная форма (полукресло, симметрия C2), (б) – конфигурация типа ванны (симметрия CS).

В рамках формализма Кремера-Попла [27–29] инверсионная пара стабильных конформеров циклогексена (форма C2) может быть отображена на гиперповерхности потенциальной энергии парой точек с координатами θ = 52.7°, φ = 210°, Q = 0.4574 Å и θ = 127.3°, φ = 30°, Q = 0.4574 Å, а соответствующая пара переходных структур (CS-ванны) точками θ = 90°, φ = 300°, Q = 0.634 Å и θ = 90°, φ = 120°, Q = 0.634 Å (см. [31]). Форму C2V с плоским шестичленным кольцом в этой системе представляет точка в начале координат.
На фиг. 4 показаны кривые, изображающие зависимость рассчитанной нами средней потенциальной энергии $E$ молекулы циклогексена от амплитуды складчатости Q при разных температурах. Как видно на этом рисунке, переход к форме C2V с плоским шестичленным кольцом (Q = 0 Å) увеличивает среднюю потенциальную энергию этой молекулы на 9.58–7.82 ккал/моль (8.72 ккал/моль при $T = 300$ К). Снижение барьера перехода к плоской форме при повышении температуры указывает на то, что в этих условиях тепловые флуктуации длин ковалентных связей и углов между ними дают больше возможностей избежать стерических напряжений. Для неплоских структур ($Q > 0.35$ Å) влияние температуры выражено слабее. Излом линий при Q = = 0.76 Å говорит о резком изменении характера деформаций молекулы для очень больших значений конформационной энергии. Ясно, что исследование этой особенности выходит за рамки данной работы, поскольку требует использования силовых полей, адекватно воспроизводящих поведение химических связей при высоких температурах.
Фиг. 4.
Зависимость средней потенциальной энергии E молекулы циклогексена от амплитуды складчатости Q при трех значениях абсолютной температуры.

Согласно нашим оценкам, распределения значений амплитуды Q имеют форму гауссовой кривой во всем диапазоне рассмотренных температур (фиг. 5). Таким образом, можно предположить, что основное состояние конфигурационного ансамбля молекул циклогексена реализуется стереоизомерами типа полукресло (симметрия C2), у которых амплитуда Q равна 0.485 ± 0.006 Å, а переход в плоскую форму C2V – очень редкое событие.
Барьер инверсии форм C2 молекулы циклогексена можно оценить по карте потенциальной энергии при температуре 300 K (фиг. 6), рассчитанной нами в зависимости от θ и φ. Координаты двух минимумов и двух седловых участков на этой карте с высокой точностью соответствуют позициям конформеров C2 и переходных форм CS на “конформационном глобусе” циклогексена (см. [31, фиг. 3.19 ]), а среднее значение высоты перевалов на пути между минимумами (энергия активации процесса инверсии при температуре 300 K) равно 7.35 ккал/моль. С понижением температуры высота энергетического барьера растет, а при повышении, наоборот, снижается. Так, при 100 K она достигает 7.51 ккал/моль, а при 500 K – опускается до 7.2 ккал/моль.
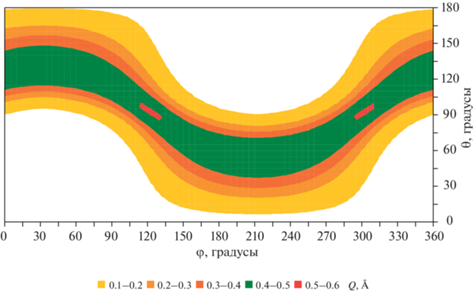
Фиг. 6.
Потенциальная энергия E молекулы циклогексена как функция фазовых углов псевдовращения φ и θ.

Зависимость средней амплитуды складчатости Q молекулы циклогексена от фазовых углов θ и φ при температуре 300 K показана на фиг. 7. Хорошо видно, что максимумы с Q = 0.51 Å расположены в центрах двух областей этой карты (θ = 90°, φ = 120° и θ = 90°, φ = 300°), занимаемых переходными структурами типа ванны (симметрия CS). В зонах стабильных конформеров (полукресло, симметрия C2, центры зон имеют координаты θ = 53°, φ = 210° и θ = 127°, φ = 30°) амплитуда Q близка к своему равновесному значению 0.485 Å. Следует отметить, что при увеличении температуры от 100 до 500 K характер рельефа карты, изображенной на фиг. 7, практически не меняется, демонстрируя лишь небольшой (0.05 Å) общий рост уровня средних значений Q.
ЗАКЛЮЧЕНИЕ
Метод SAMC [15], удачно сочетающий простоту алгоритма Ванга-Ландау [10], [11] и точность процедур стохастической аппроксимации [17], [41], имеет высокий потенциал для решения широкого спектра задач конформационного анализа и параметризации силовых полей, используемых в молекулярном моделировании.
Список литературы
Eliel E.L., Allinger N.L., Angyal S.J., Morrison G.A. Conformational Analysis. New York: Interscience-Wiley, 1965.
Leach A.R. Molecular Modeling: Principles and Applications. Harlow: Pearson Education Ltd., 2001.
Hinchliffe A. Molecular Modelling for Beginners. Chichester: John Wiley & Sons Ltd, 2008.
Jensen F. Introduction to Computational Chemistry. Chichester: John Wiley & Sons Ltd, 2007.
Teplukhin A.V. Parametrization of the torsion potential in all-atom models of hydrocarbon molecules using a simplified expression for the deformation energy of valence bonds and angles // J. Struct. Chem. 2021. V. 62. P. 1653.
Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller A.H., Teller E. Equation of state calculations by fast computing machines // J. Chem. Phys. 1953. V. 21. P. 1087.
Liang F., Liu C., Carroll R.J. Advanced Markov Chain Monte Carlo Methods: Learning from Past Samples. Chichester: John Wiley & Sons Ltd, 2010.
Singh S., Chopra M., de Pablo J.J. Density of States–Based Molecular Simulations // Annu. Rev. Chem. Biomol. Eng. 2012. V. 3. P. 369.
Janke W., Paul W. Thermodynamics and structure of macromolecules from flat-histogram Monte Carlo simulations // Soft Matter. 2016. V. 12. P. 642.
Wang F., Landau D.P. Efficient, multiple-range random walk algorithm to calculate the density of states // Phys. Rev. Lett. 2001. V. 86. P. 2050.
Landau D.P., Tsai S.-H., Exler M. A new approach to Monte Carlo simulations in statistical physics: Wang-Landau sampling // Am. J. Phys. 2004. P. 72. P. 1294.
Yan Q., de Pablo J.J. Fast calculation of the density of states of a fluid by Monte Carlo simulations // Phys. Rev. Lett. 2003. V. 90. P. 035701.
Belardinelli R.E., Pereyra V.D. Fast algorithm to calculate density of states // Phys. Rev. E. 2007. V. 75. P. 046701.
Belardinelli R.E., Pereyra V.D. Wang-Landau algorithm: A theoretical analysis of the saturation of the error // J. Chem. Phys. 2007. V. 127. P. 184105.
Liang F., Liu C., Carroll R.J. Stochastic approximation in Monte Carlo computation // J. Am. Statist. Assoc. 2007. V. 102. P. 305.
Robbins H., Monro S. A Stochastic Approximation Method // Ann. Math. Statist. 1951. V. 22. P. 400.
Wasan M.T. Stochastic Approximation. New York: Cambridge University Press, 1969.
Lai T.L. Stochastic approximation // Ann. Statist. 2003. V. 31. P. 391.
Werlich B., Shakirov T., Taylor M.P., Paul W. Stochastic approximation Monte Carlo and Wang–Landau Monte Carlo applied to a continuum polymer model // Comput. Phys. Commun. 2015. V. 186. P. 65.
Zablotskiy S.V., Martemyanova J.A., Ivanov V.A., Paul W. Stochastic approximation Monte Carlo algorithm for calculation of diagram of states of a single flexible-semiflexible copolymer chain // Polym. Sci. ser. A. 2016. V. 58. P. 899.
Shakirov T., Paul W. Folded alkane chains and the emergence of the lamellar crystal // J. Chem. Phys. 2019. V. 150. P. 084903.
Teplukhin A.V. Monte Carlo calculation of thermodynamic and structural characteristics of liquid hydrocarbons // J. Struct. Chem. 2021. V. 62. P. 70.
Allen F.H., Kennard O., Watson D.G., Brammer L., Orpen A.G., Taylor R. Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds // J. Chem. Soc. Perkin Trans. 2. 1987. P. S1.
Cornell W.D., Cieplak P., Bayly C.I., Gould I.R., Merz K.M., Ferguson D.M., Spellmeyer D.C., Fox T., Cald-well J.W., Kollman P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules // J. Am. Chem. Soc. 1995. V. 117. P. 5179.
Jorgensen W.L., Maxwell D.S., Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids // J. Am. Chem. Soc. 1996. V. 118. P. 11225.
Kilpatrick J.E., Pitzer K.S., Spitzer R. The thermodynamics and molecular structure of cyclopentane // J. Am. Chem. Soc. 1947. V. 69. P. 2483.
Cremer D., Pople J.A. A general definition of ring puckering coordinates // J. Am. Chem. Soc. 1975. V. 97. P. 1354.
Essén H., Cremer D. On the relationship between the mean plane and the least-squares plane of an N-membered puckered ring // Acta Cryst. B. 1984. V. 40. P. 418.
Cremer D. On the correct usage of the Cremer-Pople puckering parameters as quantitative descriptors of ring shapes – a reply to recent criticism by Petit, Dillen and Geise // Acta Cryst. B. 1984. V. 40. P. 498.
Sega M., Autieri E., Pederiva F. Pickett angles and Cremer–Pople coordinates as collective variables for the enhanced sampling of six membered ring conformations // Mol. Phys. 2011. V. 109. P. 141.
Cremer D., Szabo K.J. Ab initio studies of six-membered rings: Present status and future developments // In: Conformational Behavior of Six-Membered Rings: Analysis, Dynamics, and Stereoelectronic Effects / Ed. E. Juaristi. New York: Wiley-VCH, 1995. Ch. 3. P. 59.
McDonald I.R., Singer K. Machine calculation of thermodynamic properties of a simple fluid at supercritical temperatures // J. Chem. Phys. 1967. V. 47. P. 4766.
Chung K.L. Markov chains: With Stationary Transition Probabilities. Berlin: Springer-Verlag, 1967.
Feller W. An Introduction to Probability Theory and its Applications. V. 1. New York: John Wiley & Sons Ltd, 1968.
Hastings W.K. Monte Carlo sampling methods using Markov chains and their applications // Biometrika. 1970. V. 57. P. 97.
Stirzaker D. Stochastic Processes and Models. New York: Oxford University Press, 2005.
Wood W.W., Parker F.R. Monte Carlo equation of state of molecules interacting with the Lennard-Jones potential. I. A supercritical isotherm at about twice the critical temperature // J. Chem. Phys. 1957. V. 27. P. 720.
Fisher I.Z. Applications of the Monte Carlo method in statistical physics // Sov. Phys. Usp. 1960. V. 2. P. 783.
Peskun P.H. Optimum Monte-Carlo sampling using Markov chains // Biometrika. 1973. V. 60. P. 607.
Wichmann B.A., Hill I.D. Generating good pseudo-random numbers // Comput. Statist. Data Anal. 2006. V. 51. P. 1614.
Nevel’son M.B., Has’minskiῐ R.Z. Stochastic Approximation and Recursive Estimation. Providence: American Mathematical Society, 1976.
Anet F.A.L., Haq M.Z. Ring inversion in cyclohexene // J. Am. Chem. Soc. 1965. V. 87. P. 3147.
Scharpen L.H., Wollrab J.E., Ames D.P. Microwave spectrum, structure, and dipole moment of cyclohexene // J. Chem. Phys. 1968. V. 49. P. 2368.
Chiang J.F., Bauer S.H. The molecular structure of cyclohexene // J. Am. Chem. Soc. 1969. V. 91. P. 1898.
Naumov V.A., Dashevskii V.G., Zaripov N.M. Refinement of the molecular structure of cyclohexene // J. Struct. Chem. 1970. V. 11. P. 736.
Rivera-Gaines V.E., Leibowitz S.J., Laane J. Far-infrared spectra, two-dimensional vibrational potential energy surface, and conformation of cyclohexene and its isotopomers // J. Am. Chem. Soc. 1991. V. 113. P. 9742.
Saebø S., Cordell F.R., Boggs J.E. Structures and conformations of cyclopentane, cyclopentene, and cyclopentadiene // J. Mol. Struct. (Theochem). 1983. V. 104. P. 221.
Anet F.A.L., Freedberg D.I., Storer J.W., Houk K.N. On the potential energy surface for ring inversion in cyclohexene and related molecules // J. Am. Chem. Soc. 1992. V. 114. P. 10969.
Shishkina S.V., Shishkin O.V., Leszczynski J. Three-stage character of ring inversion in cyclohexene // Chem. Phys. Lett. 2002. V. 354. P. 428.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики