ВВЕДЕНИЕ
Широкое применение в мировой практике микрофонных решеток для визуализации источников шума различного характера [1–3] обусловлено рядом причин. Одними из главных преимуществ использования многоканальных решеток является возможность проведения бесконтактной диагностики акустического излучения в широком диапазоне частот, простота постановки эксперимента в различных условиях его проведения (например, в открытом или ограниченном пространстве), а также вариативность интерпретации результатов измерений в зависимости от применяемых программных кодов пост-обработки, содержащих приоритетную информацию о модели излучения искомых звуковых источников и об их когерентности. Существует множество различных типов микрофонных решеток, предназначенных для решения конкретных акустических задач. Широко распространены складные лучевые плоские решетки, сочетающие в себе большую измерительную площадь и простоту транспортировки, которые применяются для измерения источников шума крупногабаритных объектов (например, воздухозаборника [4] или струи авиационного двигателя [5]).
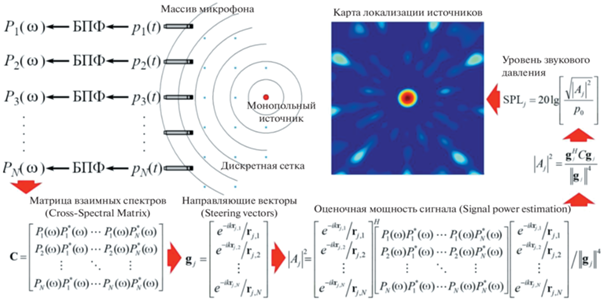
Пост-обработка матрицы сигналов звукового давления, синхронно регистрируемых микрофонами в решетке, выполняется с помощью различных процедур бимформинга [6–10], в результате работы которых становится возможным провести модельную реконструкцию звукового поля в плоскости сканирования, удаленной от решетки на заведомо известное расстояние. Классический алгоритм плоского бимформинга (Conventional Beamforming) решает данную задачу путем разбиения исследуемой области пространства дискретной сеткой, в узлах которой находятся некоррелированные точечные монопольные источники с неизвестной амплитудой, подлежащей дальнейшей оценке [6]. Путем выполнения ряда математических операций, минимизирующих невязку экспериментально полученной самосопряженной матрицы взаимных пар комплексных сигналов с ее модельным представлением, определяются значения амплитуд для каждой точки дискретной сетки, на основе которых формируется конечная карта визуализации. Схематическое представление данного алгоритма представлено на рис. 1.
Звуковое давление монополя в частотной области в общем виде можно записать как $p({\mathbf{x}},\omega ) = a(\omega )g({\mathbf{x}},\omega )$, где a(ω) – амплитуда давления; $g({\mathbf{x}},\omega )$ – передаточная функция, связывающая координаты узлов сетки с позициями микрофонов в решетке; ${\mathbf{x}}$ – вектор с координатами текущего узла сетки и позицией микрофона; ω – круговая частота. Далее формируется набор звуковых давлений в частотной области с помощью быстрого преобразования Фурье в виде N-мерного вектора ${\mathbf{p}} = {{\left( {\begin{array}{*{20}{c}} {{{p}_{1}}({{\omega }})}& \cdots &{{{p}_{N}}(\omega )} \end{array}} \right)}^{T}}$, где pn(ω) – сигнал в частотной области; n = 1…N – индекс микрофона в диапазоне общего числа микрофонов N в решетке; (…)T – операция транспонирования. Затем формируется матрица взаимных спектров ${\mathbf{C}} = {{{\mathbf{pp}}{\text{*}}} \mathord{\left/ {\vphantom {{{\mathbf{pp}}{\text{*}}} 2}} \right. \kern-0em} 2}$ и проводится минимизация методом наименьших квадратов невязки экспериментально полученной самосопряженной матрицы C с ее модельным представлением, что можно записать как $J = {{\left\| {{\mathbf{p}} - \bar {a}{\mathbf{g}}} \right\|}^{2}}$, где ${\mathbf{g}} = {{\left( {\begin{array}{*{20}{c}} {{{g}_{1}}(\omega )}& \cdots &{{{g}_{N}}({{\omega }})} \end{array}} \right)}^{T}}$. Аналитическое решение набора комплексных амплитуд выражается в виде $\bar {a} = {{{\mathbf{g}}{\text{*}}{\mathbf{p}}} \mathord{\left/ {\vphantom {{{\mathbf{g}}{\text{*}}{\mathbf{p}}} {{{{\left\| {\mathbf{g}} \right\|}}^{2}}}}} \right. \kern-0em} {{{{\left\| {\mathbf{g}} \right\|}}^{2}}}}$, на основе которого можно записать уравнение (1) для вычисления расчетной мощности сигналов в каждом узле дискретной сетки [11]:
(1)
$\begin{gathered} \bar {A} = \frac{1}{2}{{\left| {\bar {a}} \right|}^{2}} = \frac{1}{2}\bar {a}\bar {a}* = \frac{1}{2}\left( {\frac{{{\mathbf{g}}{\text{*}}{\mathbf{p}}}}{{{{{\left\| {\mathbf{g}} \right\|}}^{2}}}}} \right)\left( {\frac{{{\mathbf{g}}{\text{*}}{\mathbf{p}}}}{{{{{\left\| {\mathbf{g}} \right\|}}^{2}}}}} \right)* = \\ = \frac{1}{2}\frac{{{\mathbf{g}}{\text{*}}{\mathbf{pp}}{\text{*}}{\mathbf{g}}}}{{{{{\left\| {\mathbf{g}} \right\|}}^{4}}}} = \frac{{{\mathbf{g}}{\text{*}}{\mathbf{Cg}}}}{{{{{\left\| {\mathbf{g}} \right\|}}^{4}}}}. \\ \end{gathered} $Монопольной модели обработки зачастую бывает вполне достаточно для решения широкого круга задач. Однако в аэроакустике часто приходится встречаться с источниками немонопольного типа, например, шум обтекания имеет дипольный характер [12]. Существующие методы настройки микрофонных антенн также основаны на монопольном представлении источника звука. Очевидно, что для источников звука, имеющих другой характер, требуются специальные алгоритмы настройки, созданию которых и посвящена данная работа.
В мировой практике реализация алгоритмов локализации акустических диполей была проведена различными исследователями [13–16]. Существует два основных подхода, первый из которых заключается в коррекции непосредственно самих акустических сигналов, формирующих самосопряженную матрицу C, после чего обработка производится традиционным способом, согласно уравнению (1) [17]. Однако данный подход требует наличия существенных вычислительных ресурсов из-за неидеального совмещения фаз сигналов и ограничивается рассмотрением только одного фиксированного диполя. Второй подход заключается в коррекции самого алгоритма бимформинг путем модификации направляющих передаточных функций с учетом ориентации дипольного момента относительно плоскости размещения решетки [13, 15]. Именно данный способ был реализован в настоящей работе.
Ключевым моментом в реализации дипольного алгоритма обработки является выбор направляющих функций g. В отличие от монопольного источника, акустический диполь имеет свойство направленности – косинусоидальной зависимости величины амплитуды от угла падения звуковой волны относительно наблюдателя (в данном случае, относительно плоскости размещения решетки). С учетом данного факта, направляющие векторы для продольных и поперечных (x и у) диполей соответственно можно записать в виде системы уравнений [14, 18]:
(2)
$\begin{gathered} g_{{nj}}^{x}\left( {\omega ,{{{{\mathbf{\vec {r}}}}}_{n}},{{{{\mathbf{\vec {r}}}}}_{j}}} \right) = \frac{{{{e}^{{ - ik\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|}}}}}{{2k{{{\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|}}^{2}}}}\left( { - 1 + ik\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|} \right)\cos \phi = \\ = \frac{{{{e}^{{ - ik\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|}}}}}{{2k{{{\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|}}^{3}}}}\left( {{{x}_{n}} - {{x}_{j}}} \right)\left( { - 1 + ik\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|} \right)\,, \\ g_{{nj}}^{y}\left( {\omega ,{{{{\mathbf{\vec {r}}}}}_{n}},{{{{\mathbf{\vec {r}}}}}_{j}}} \right) = \frac{{{{e}^{{ - ik\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|}}}}}{{2k{{{\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|}}^{2}}}}\left( { - 1 + ik\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|} \right)\cos \theta = \\ = \frac{{{{e}^{{ - ik\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|}}}}}{{2k{{{\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|}}^{3}}}}\left( {{{y}_{n}} - {{y}_{j}}} \right)\left( { - 1 + ik\left\| {\overrightarrow {{{r}_{n}} - {{r}_{j}}} } \right\|} \right)\,, \\ \end{gathered} $На степень достоверности и подробности конечной карты визуализации напрямую влияют два фактора: выбор типа микрофонной решетки и параметров ее настройки, а также способа пост-обработки регистрируемых сигналов. С целью повышения общего качества локализации, активно развиваются методы настройки решеток путем поиска оптимального размещения микрофонов, формирующих двумерную координатную схему акустического массива [19–21]. Выбор позиций микрофонов при сохранении их общего числа напрямую влияет на детализированность финальной карты визуализации за счет их прямого воздействия на уровни пиков паразитных боковых лепестков, которые в определенных случаях могут проявляться в качестве псевдоисточников, ошибочно принимаемых за реальное акустическое излучение. Кроме того, необходимо обеспечить высокое разрешение системы локализации для качественного разделения близкорасположенных звуковых источников между собой. Таким образом, основная задача проведения оптимизации – добиться оптимального сочетания высоких значений динамического диапазона в совокупности с высокой разрешающей способностью решетки.
Для достижения данной цели применяются различные способы оптимизации, с учетом оптимальных затрат вычислительных мощностей, скорости сходимости, способности алгоритма к преодолению локальных минимумов целевой функции и т.д. Применяются такие методы, как минимаксная оптимизация [19], метод дифференциальной эволюции [21], являющийся одним из вариантов генетического алгоритма [22, 23], выпуклая оптимизация [24], численные методы глобальной оптимизации, например, алгоритм имитации отжига (Simulated Annealing) в комбинации с применением внутриблочного метода Монте-Карло (Intra-Block Monte Carlo) [25], а также многие другие [26, 27]. Однако в этих работах рассматриваются только методы настройки решеток на оптимальное качество локализации источников монопольного типа, и не уделяется внимание их адаптации к источникам дипольного характера.
В данной работе предлагается подход для адаптации решетки к дипольной модели излучения, в основе которого лежит модификация передаточных (направляющих) функций, учитывающих влияние направленности падения звуковых волн. Вторая часть работы посвящена проведению серии экспериментальных исследований, результаты которых демонстрируют повышение динамического диапазона решетки при использованном оптимальном размещении микрофонов.
НАСТРОЙКА РЕШЕТКИ НА ЗВУКОВЫЕ ИСТОЧНИКИ ДИПОЛЬНОГО ТИПА
Для адаптации микрофонной решетки к дипольному звуковому полю было решено использовать прямой расчет локализации точечного диполя, находящегося на известном конечном расстоянии относительно плоскости размещения решетки. Данное решение было принято исходя из следующих соображений: при рассмотрении радиального профиля максимального уровня боковых лепестков на различных частотах было выявлено, что при повышении частоты происходит сжатие профиля по оси абсцисс в сторону главного лепестка, однако форма профиля остается практически неизменной. Было установлено также, что с ростом частоты наблюдаются колебания лепестков по уровню звукового давления, что в дальнейшем необходимо исследовать более тщательно для минимизации возможных погрешностей. Таким образом, было принято решение оценивать радиальный профиль только на верхней граничной частоте оптимизации.
Для обеспечения высокой вычислительной скорости, вместо выполнения полного алгоритма локализации, включающего в себя вычисление матрицы взаимных спектров С, была использована функция рассеяния точки (Point Spread Function, или PSF). Данная функция описывает отклик микрофонной антенны на единичный точечный источник. Как было описано в предыдущих главах, аналитическое решение для нахождения неизвестных мощностей сигналов для каждой точки сетки j на определенной частоте ω можно записать в виде выражения (1). Матрицу взаимных спектров, индуцируемую точечным источником с единичной амплитудой в точке с индексом j, можно записать как ${{{\mathbf{C}}}_{j}} = {{{\mathbf{g}}}_{j}}{\mathbf{g}}_{j}^{*}$. Следовательно, аналитическое решение для нахождения амплитуд, основанное на применении PSF, запишется в виде:
Таким образом, в настоящей работе предлагается проводить оценку параметров настраиваемой микрофонной решетки на основе построения функции максимального уровня боковых лепестков, извлекаемой напрямую с карты локализации точечного диполя, сформированного с помощью функции рассеяния точки на верхней частоте интересующего частотного диапазона, путем оценки радиального профиля боковых лепестков в исследуемой области пространства.
При проведении настройки микрофонной решетки на оптимальное качество локализации диполей было решено использовать линейные размеры, аналогичные 54-канальной микрофонной антенне “Брюль и Къер”. Конструкция данной антенны состоит из 9 лучей равной длины, закрепленных на центральном теле диаметром около 0.3 м, размещенных по окружности с равномерным угловым шагом (40°) и формирующих виртуальную описанную окружность диаметром 2.5 м; на каждом луче располагается по 6 точек для установки микрофонов, положения которых идентичны на каждом луче. Данное решение было принято, во-первых, для обеспечения сопоставимой величины разрешения, напрямую зависящего от диаметра описанной наиболее удаленными от центра микрофонами окружности; во-вторых, для демонстрации достижения более эффективной локализации акустических диполей путем проведения настройки антенны при соблюдении прочих равных условий – общего числа микрофонов, линейных размеров лучевой антенны и соответствия ее основных геометрических параметров.
Постановка задачи условной оптимизации выполнялась в математическом пакете прикладных программ MATLAB. На значения аргументов накладывались следующие ограничения: отклонение координаты наиболее удаленного от центра микрофона: ±0.05 м для обеспечения вариативности получаемых координат при сохранении ширины полосы главного лепестка в точке половинной мощности примерно в одних и тех же пределах; верхняя частота излучения, используемая для проведения оптимизации: 5000 Гц; расстояние между каждой парой соседних микрофонов на луче: не менее 0.04 м для обеспечения достаточного пространства при фиксации микрофонов; расстояние от плоскости положения антенны до виртуального источника: 2.5 м, соответствующее одному диаметру воображаемой описанной окружности антенны; радиус области сканирования для построения сетки: 1.45 м, рассчитанный по соотношению L = 1.15z (где L – диаметр охватываемой области, z – расстояние до решетки), что соответствует радиусу охватываемой антенной области при угле раскрытия 30°. Значение данного угла определяется исходя из оценки величины разрешения R(θ) в общем виде в зависимости от угла падения волнового фронта относительно оси, направленной по нормали к плоскости размещения антенны, но на практике угол раскрытия часто ограничивается значением 30° [6].
Решение оптимизационной задачи производилось с помощью метода минимаксной оптимизации. Число наборов координат микрофонов, используемых в качестве начальных условий, составляло более 100 тыс. После вычисления каждой итерации, путем оценки целевой функции, определялся динамический диапазон, соответствующий текущему набору координат. Для обеспечения сопоставимого с решеткой “Брюль и Къер” разрешения, дополнительно контролировалась ширина полосы главного лепестка, определяемая в точке –3 дБ, для получения пространственной координаты которой применялась одномерная линейная интерполяция.
На каждой итерации оценивался радиальный профиль карты локализации для выявления максимального уровня боковых лепестков в заданной круговой области L. Шаг изменения радиуса был равен ширине одной ячейки сетки (0.01 м). Для выполнения процедуры полукольцевой выборки из координат точек прямоугольной сетки применялись операции округления до ближайших ячеек. Для нахождения первого минимума функции после главного лепестка, представляющего собой начало отсчета диапазона изменения уровней боковых лепестков, проводилось численное дифференцирование с применением метода правосторонней разности.
После проведения вычислительных операций была найдена оптимальная двумерная координатная схема установки микрофонов, удовлетворяющая заданным параметрам. При сопоставимом значении разрешения, прирост динамического диапазона данного набора составил около 2 дБ в ширине полосы до 5000 Гц. Найденное распределение координат представлено на рис. 2. Сравнение функций максимального уровня боковых лепестков, соответствующих оптимальному набору координат и набору координат “Брюль и Къер”, представлено на рис. 3.
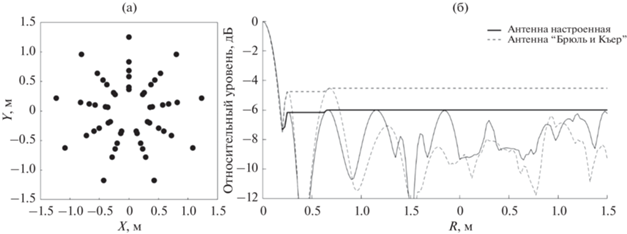
Рис. 2.
(а) – Набор координат микрофонов для локализации акустических диполей и (б) – сравнение функций максимального уровня боковых лепестков дипольно-настроенной микрофонной решетки с решеткой “Брюль и Къер”.
Для проведения последующих экспериментальных исследований были разработаны собственные программные и аппаратные средства визуализации источников шума, позволяющие обойти ограничения коммерческих систем локализации, не предусматривающих внесения требуемых изменений в конструкцию и в методы пост-обработки измерений. Для этих целей была выполнена разработка и изготовление регулируемой конструкции лучевой микрофонной антенны [28–30], необходимой для проведения дальнейших исследований по оценке зависимости качества локализации источников шума от позиций размещения микрофонов. Элементы разработанной антенны изготовлены из алюминиевых сплавов, стальных конструкций и полимерных материалов, вследствие чего обеспечивается оптимальная масса всей сборки, сопоставимая с массой антенны “Брюль и Къер”, в совокупности с необходимой жесткостью конструкции. Созданная конструкция имеет возможность изменения числа лучей и числа микрофонов на лучах, а также положения микрофонов с возможностью точного позиционирования по угловой (с шагом 1°) и по радиальной (с шагом 1 мм) координате.
Для обработки результатов было разработано программное обеспечение в математическом пакете прикладных программ MathWorks MATLAB. Была реализована тонкая настройка параметров последующей пост-обработки, в том числе: длины сигнала; частотного анализа (узкополосного или октавного и дробно-октавного); требуемой ширины полосы в герцах; числа линейных усреднений; типа оконной функции; настройки частотного диапазона; настройки параметров расчетной сетки; настройки положения фонового изображения.
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПО ЛОКАЛИЗАЦИИ ДИПОЛЬНЫХ ИСТОЧНИКОВ ШУМА
Экспериментальные исследования локализации источников шума дипольного типа проводились в акустической заглушенной камере Центра акустических исследований ПНИПУ. Для проведения последующего сравнительного анализа в измерениях были задействованы обе микрофонных антенны (собственная дипольно-настроенная и 54-канальная решетка “Брюль и Къер”). В качестве механизма для генерации акустических диполей рассматривалось взаимодействие воздушной турбулентной струи с твердым телом, в частности – обтекание тонкого металлического стержня цилиндрической формы, а также взаимодействие турбулентного потока с тонкой пластиной. Обе антенны располагались на расстоянии 2.5 м (одного диаметра своей описанной окружности) параллельно оси струи. В продольном направлении антенна устанавливалась таким образом, чтобы положение идентифицируемого акустического источника находилось как можно ближе к центру карты локализации.
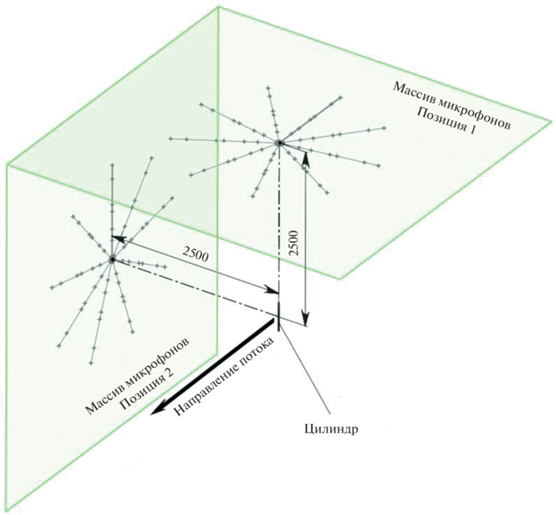
На первом этапе экспериментальных исследований проводилась локализация источников шума обтекания цилиндра. Данный эксперимент является классическим способом генерации аэродинамического шума обтекания, имеющего дипольно-ориентированный характер. Эксперимент был выполнен для двух случаев пространственной ориентации цилиндра: в первом случае продольная ось цилиндра пересекала центр микрофонной антенны, во втором случае была параллельна плоскости антенны и плоскости среза сопла. Если в первом случае рассматривалась классическая генерация поперечного y-диполя, то второй случай был выполнен для проверки корректности определения уровня звукового давления генерируемого диполя разработанным алгоритмом локализации: в данной пространственной ориентации область скачка фазы сигнала направлена прямо на антенну, и локализуемый монопольным алгоритмом уровень звукового давления в пике излучения сопоставим с уровнем звукового давления исходного акустического диполя [15]. Таким образом, с помощью монопольного метода Conventional Beamforming возможно провести отладку реализуемого алгоритма локализации диполей. Варианты расположения цилиндра относительно плоскости решетки показаны на схеме на рис. 3.
В системе генерации воздушной турбулентной струи [31] использовалось металлическое коническое сопло диаметром 50 мм. Диаметр тонкого металлического стержня был равен 5 мм, расстояние от среза сопла до цилиндра составляло 6.25 калибров (312.5 мм). Стержень был закреплен на металлической стойке. Запись акустических сигналов звукового давления производилась в проприетарном программном обеспечении “Брюль и Къер”, после чего выполнялась обработка в собственном приложении. Подготовленные к измерениям микрофонные решетки представлены на рис. 4.
Рис. 4.
Подготовленные к акустическим измерениям микрофонные антенны: (а) – “Брюль и Къер” и (б) – разработанная лучевая антенна.

Для построения частотного спектра компонент продольного и поперечного диполей с целью определения частоты пика излучения поперечного y-диполя было решено провести регистрацию звукового давления дополнительно еще в 6 точках (по 2 микрофона в 3 параллельных плоскостях) для применения упрощенного азимутального разложения звукового поля, по аналогии с работой [15]. Каждая пара микрофонов была удалена перпендикулярно оси потока на расстояние 0.75 м, первая плоскость находилась в плоскости расположения цилиндра, вторая и третья плоскости были удалены от первой на 0.5 и на 1 м соответственно. Схема установки микрофонов показана на рис. 5. Сигналы, соответствующие продольному (мода a0) и поперечному (мода a1) диполям, были вычислены по формулам [15]:
(3)
$\begin{gathered} {{a}_{0}}\left( {x,t} \right) \approx {{\left( {{{p}_{1}}\left( {x,t} \right) + {{p}_{2}}\left( {x,t} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{{p}_{1}}\left( {x,t} \right) + {{p}_{2}}\left( {x,t} \right)} \right)} 2}} \right. \kern-0em} 2}, \hfill \\ {{a}_{1}}\left( {x,t} \right) \approx {{\left( {{{p}_{1}}\left( {x,t} \right) - {{p}_{2}}\left( {x,t} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{{p}_{1}}\left( {x,t} \right) - {{p}_{2}}\left( {x,t} \right)} \right)} 2}} \right. \kern-0em} 2}, \hfill \\ \end{gathered} $Рис. 5.
Схема проведения измерений дипольных составляющих шума обтекания цилиндра с помощью 2-микрофонной решетки в трех плоскостях.
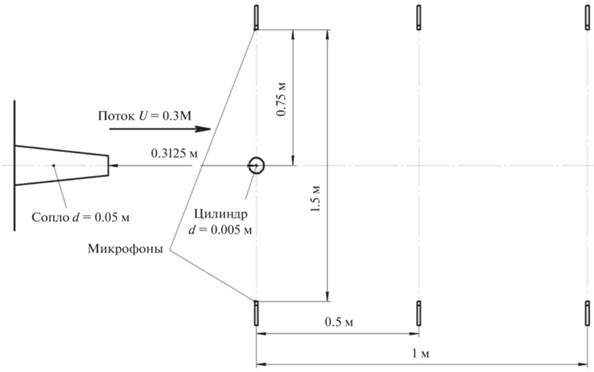
где p1(x, t) и p2(x, t) – сигналы, регистрируемые равноудаленной парой микрофонов во временной области. Вычисленные спектры сигналов a0 и a1 показаны на рис. 6.
Рис. 6.
Спектральные характеристики продольного (мода a0) и поперечного (мода a1) диполей, полученные с помощью азимутального разложения звукового поля в плоскости размещения цилиндра.
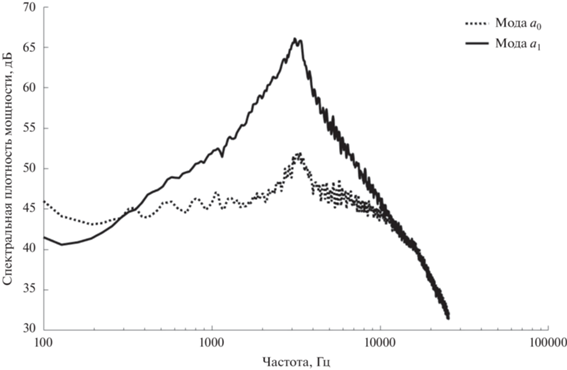
Максимальный уровень спектральной плотности мощности (СПМ) для поперечного y-диполя составил 66 дБ на частоте около 3200 Гц. Дополнительно была смоделирована кривая распределения СПМ модельного диполя, рассчитанная в зависимости от изменения параллельно оси струи продольной координаты, с целью проведения сравнительного анализа с экспериментальными точками для доминирующей в области размещения цилиндра моды a1. Модельная кривая описывается выражением [32]:
(4)
${\text{PSD}}(x) = \frac{{4 \times {{{10}}^{{L/10 - 10}}}}}{{\Delta f}}\frac{{R_{a}^{2}}}{{{{{\left( {R_{a}^{2} + \left( {x - x_{0}^{2}} \right)} \right)}}^{2}}}},$Уровень звукового давления, соответствующий представленной кривой СПМ, а также положение диполя по оси, параллельной оси струи, подбиралось путем наилучшего соответствия с экспериментальными точками. Радиус виртуальной окружности 2-микрофонной решетки составлял 1.5 м. Ширина полосы для вычисления СПМ составляла 256 Гц. В результате был получен модельный диполь, находящийся в точке x = = 0.1 м (относительно среза сопла в точке x = 0 м) и излучающий с уровнем звукового давления, эквивалентным 88 дБ. Результаты сравнительного анализа распределения СПМ модельного диполя с экспериментальными точками для моды a1 представлены на рис. 7. Визуализация шума обтекания цилиндра показана на рис. 8. Динамический диапазон дипольных карт 7 дБ, монопольных карт 5 дБ.
Рис. 7.
Результаты сравнительного анализа распределения СПМ модельного диполя с экспериментальными точками для антисимметричной моды a1.
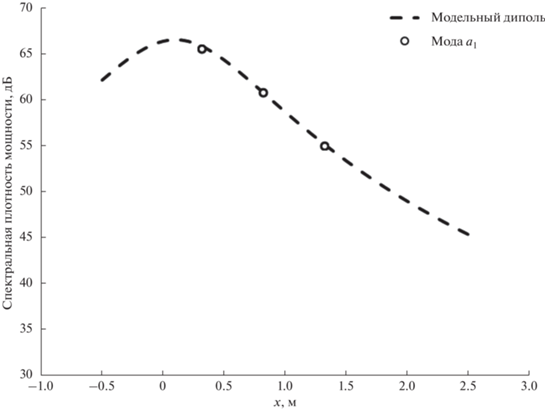
Рис. 8.
Локализация шума обтекания цилиндра с помощью двух микрофонных антенн: (а), (б) – монопольный алгоритм, антенны в позиции 1; (в), (г) – дипольный алгоритм, антенны в позиции 1; (д), (е) – монопольный алгоритм, антенны в позиции 2.

По результатам локализации шума обтекания стержня можно заключить, что дипольно-настроенная антенна дает менее зашумленную карту, чем антенна “Брюль и Къер”. На рис. 8а–8б представлен традиционный монопольный алгоритм локализации; пятна распределения источников практически идентичны в обоих случаях. На рис. 8в–8г представлена обработка реализованным дипольным алгоритмом. Как можно увидеть, настроенная антенна дает повышение динамического диапазона до 2 дБ по сравнению со своим фирменным аналогом при сопоставимом разрешении – ширина основного пика практически идентична. На рис. 8д–8е представлена обработка монопольным алгоритмом при ориентации цилиндра в параллельной относительно размещения антенны плоскости. Данные карты были построены для контроля уровней звукового давления, определяемых после выполнения дипольного алгоритма: путем оценки уровней в области скачка фазы, направленного на антенну, выполняется сравнительный анализ с уровнями звукового давления локализуемого диполя. Максимальное расхождение по уровням во всех случаях не превышает 3 дБ. Среднее значение уровня звукового давления локализуемого диполя составляет около 88 дБ, что соответствует значению, полученному с помощью азимутального разложения; однако существует различие в определении положения модельного диполя (312.5 против 100 мм). Данный факт может объясняться недостаточным количеством экспериментальных измерительных точек, используемых в азимутальном разложении – для получения точного результата необходимо увеличение числа рассматриваемых сечений относительно положения стержня. В целом можно заключить, что эксперимент поставлен корректно и согласуется с данными, полученными другими исследователями.
В качестве еще одного случая генерации звукового поля, близкого к полю излучения акустического диполя, рассматривалось взаимодействие воздушной турбулентной струи и задней кромки тонкой пластины. Данное взаимодействие объясняется дипольным характером доминирующего в боковом направлении звукового источника, связанного с рассеянием пульсаций ближнего поля струи на задней кромке пластины [33]. Пластина была изготовлена из фанерного листа с размерами 450 × 900 × 6 мм. При генерации воздушной струи использовалось металлическое коническое сопло диаметром 50 мм. Скорость истечения струи составляла 0.4М. Пластина устанавливалась на каркасную металлическую систему. Расстояние от среза сопла до кромки пластины в продольном направлении составляло 3.15 калибра (157.5 мм). Расстояние от оси струи до кромки пластины в поперечном направлении было равным 1 калибру (50 мм).
Для проведения сравнительного анализа распределения СПМ антисимметричной моды с распределением СПМ излучения модельного диполя (4), как и в предыдущем случае, было реализовано применение упрощенного метода азимутального разложения путем установки 6 микрофонов по трем сечениям вдоль оси струи, соответствующим координатам {x = 0.1575; x = 1.1575; x = = 2.1575} м относительно плоскости среза сопла в точке x = 0. Схема установки пластины относительно сопла и микрофонов представлена на рис. 9. Фотографии проведения эксперимента в заглушенной камере показаны на рис. 10. Спектры продольного и поперечного диполей, полученные с помощью выражения (3) в плоскости задней кромки пластины, представлены на рис. 11.
Рис. 9.
Схема установки микрофонов относительно пластины для реализации упрощенного метода азимутального разложения звукового поля.
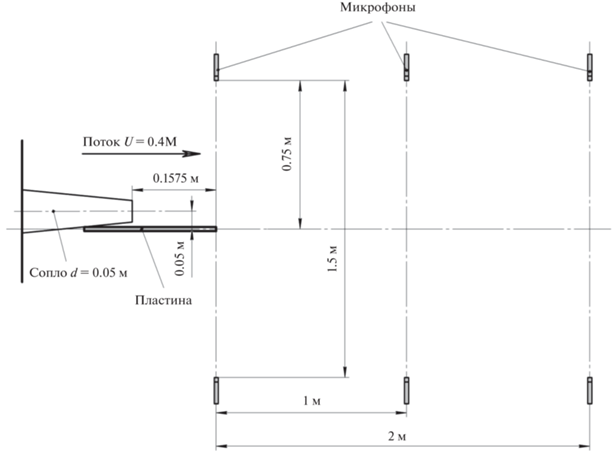
Рис. 11.
Спектры продольного (мода a0) и поперечного (мода a1) диполей, полученные с помощью азимутального разложения звукового поля в плоскости задней кромки пластины.
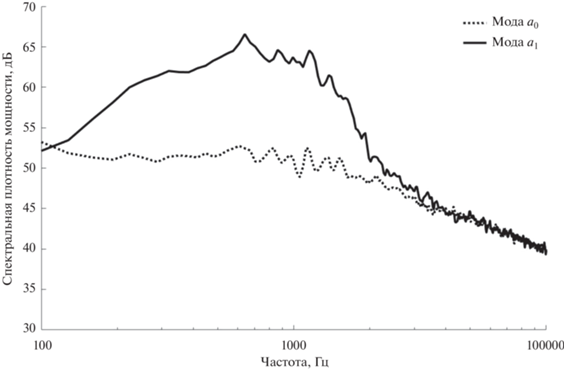
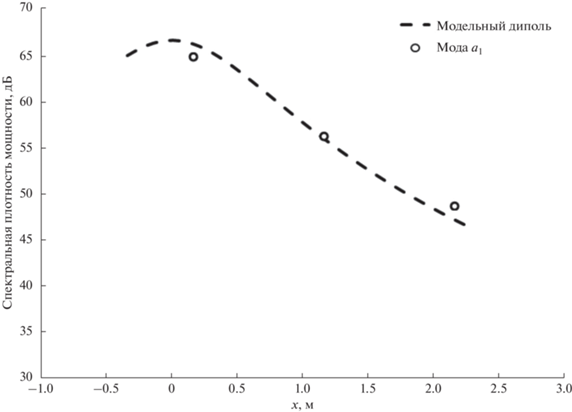
Путем сравнительного анализа, как и в предыдущем случае, был получен модельный диполь (4), находящийся в точке x = 0 м относительно положения среза сопла (с координатой x = 0) и излучающий с уровнем звукового давления, эквивалентным 88.2 дБ. Результаты сравнительного анализа распределения СПМ модельного диполя с экспериментальными точками для моды a1 представлены на рис. 12.
Рис. 12.
Результаты сравнительного анализа распределения СПМ модельного диполя с экспериментальными точками для антисимметричной моды a1.
Результаты локализации источников шума взаимодействия турбулентного потока и тонкой пластины, полученные с помощью двух микрофонных антенн, представлены на рис. 13. Ширина частотной полосы для расчета карт визуализации составила 256 Гц относительно центральной частоты 600 Гц, соответствующей частоте пика. На рис. 13а–13б представлен традиционный монопольный алгоритм локализации, на рис. 13в–13г – модифицированный дипольный алгоритм.
Рис. 13.
Локализация источников шума взаимодействия потока и задней кромки тонкой пластины с помощью двух микрофонных антенн: (а), (б) – монопольный алгоритм; (в), (г) – дипольный алгоритм.

По результатам акустических измерений шума взаимодействия струи и пластины можно заключить, что результаты локализации хорошо сопоставимы. На низких частотах, в диапазоне которых находится пик доминирующего источника (около 600 Гц), пятна локализации, как и ожидалось, довольно большие, и на таких частотах, как правило, не проявляются ярко выраженные боковые лепестки, как это было в предыдущем случае с металлическим стержнем, что обычно связано с замещением значительной области плоскости наблюдения одним главным лепестком.
Максимальное расхождение по уровням между локализуемыми обеими антеннами диполями не превышает 1.5 дБ. Среднее значение определяемого уровня звукового давления диполей составляет около 88.9 дБ, что хорошо соответствует значениям, полученным с помощью азимутального разложения звукового поля (88.2 дБ). Максимум пика излучения модельного диполя соответствует координате среза сопла (x = 0), что соответствует картам локализации, показанным на рис. 13. В целом также можно заключить, что эксперимент поставлен корректно и согласуется с данными, полученными другими исследователями.
ЗАКЛЮЧЕНИЕ
Усовершенствована математическая модель для поиска оптимальных схем установки микрофонов в антенну для высокоэффективной локализации акустических диполей. Лежащее в основе модели использование функции рассеяния точки (PSF) для оценки боковых лепестков, полученных напрямую с карты локализации точечного диполя, позволяет производить оптимальную дипольную настройку микрофонной антенны с минимальным количеством необходимых вычислений, что обеспечивается за счет свойства продольного масштабирования радиального профиля PSF при изменении частоты в фиксированной области. Проведенный в лабораторных условиях сравнительный анализ карт локализации диполей, полученных с помощью антенны “Брюль и Къер” и новой антенны, настроенной для этих целей специальным образом, подтверждает прирост динамического диапазона около 2 дБ. В качестве механизма для генерации диполей рассматривалось взаимодействие воздушной турбулентной струи с твердым телом, в частности – обтекание тонкого металлического стержня цилиндрической формы, а также взаимодействие турбулентного потока с тонкой пластиной. В результате было получено визуальное подтверждение эквивалентности областей распределения источников на картах локализации, что свидетельствует об обеспечении сопоставимого разрешения с фирменной антенной подобного класса.
Исследование проведено при финансовой поддержке Минобрнауки России в рамках реализации программы деятельности научно-образовательного центра мирового уровня “Рациональное недропользование”. Исследования выполнены на уникальной научной установке “Акустическая заглушенная камера с аэродинамическими источниками шума”, регистрационный номер 500617. Часть работы, связанная с настройкой традиционной решетки на извлечение диполей, выполнена на базе УНУ “Заглушенная камера с потоком АК-2” ФАУ “ЦАГИ”, модернизируемой при финансовой поддержке Министерства науки и высшего образования Российской Федерации по соглашению № 075-11-2021-066.