АСТРОНОМИЧЕСКИЙ ЖУРНАЛ, 2019, том 96, № 2, с. 120-143

УДК 521.9; 524.3

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

М. С. Пширков^2,3*, А. Е. Родин², М. В. Сажин³

¹Московский государственный университет им. М.В. Ломоносова,

Физический факультет, Mосква, Россия

²Физический институт им. П.Н. Лебедева РАН, Пущинская радиоастрономическая

обсерватория АКЦ ФИАН, Пущино, Россия

³Московский государственный университет им. М.В. Ломоносова,

Государственный астрономический институт им. П.К. Штернберга, Москва, Россия

Поступила в редакцию 10.05.2018 г.; принята в печать 13.09.2018 г.

Рассматривается пульсарная шкала времени, возможности ее реализации, а также возможные

приложения к фундаментальной астрономии и физике.

DOI: 10.1134/S0004629919020099

1. ВВЕДЕНИЕ

и массово используемые в лабораториях и обсер-

ваториях, имеют точность порядка 10-14 (опреде-

Во Введении мы кратко рассмотрим хрономет-

ление точности часов будет дано ниже). Вскоре

рию — науку об измерении времени или временных

могут быть созданы часы, которые на интервале в

интервалов. Для изучения многих астрономических

несколько часов имеют точность вплоть до 10-18.

и физических процессов необходимо знать момент

времени наблюдения (его эпоху), а также длитель-

Лабораторные часы основаны на осцилляторах

ность события. Самые ценные и дорогостоящие

различной природы, которые являются динамиче-

наблюдения могут оказаться бесполезными, если

скими системами с колебаниями. В таких системах

не будет известно, к какому моменту времени их

по крайней мере один из параметров является пе-

отнести.

риодической функцией, период которой мы обозна-

Определение момента и промежутка времени

чим P . Сопоставим этому периоду частоту осцил-

требует введения шкалы времени, т.е. выбора неко-

лятора f = 1/P. В каждом осцилляторе существу-

торого физического или астрономического процес-

ют диссипативные процессы, которые уменьша-

са, а также задание единицы измерения време-

ют энергию колебаний. Диссипативные процессы

ни. Промежуток между событиями определяется

можно определить одним параметром — добротно-

разностью эпох, которая измеряется в принятых

стью системы Q.

единицах времени. Единица времени назначается

Осциллятор может колебаться только с часто-

по соглашению как некоторое число периодов фи-

той, которая близка к собственной частоте осцил-

зического или астрономического процесса.

лятора f₀, значение которой определяется физи-

В современной астрономии определены и ис-

ческой природой осциллятора. Осциллятор можно

пользуются следующие шкалы времени [1]: 1) сол-

раскачать вынуждающей силой, причем максимум

нечного времени; 2) звездного времени; 3) эфе-

запасенной энергии достигается, когда частота вы-

меридного (динамического) времени; 4) атомного

нуждающей силы в точности равна собственной

времени. В последнее время активно обсуждаются

частоте осциллятора, которая называется также

возможности использования радиопульсаров для

резонансной частотой. Для других частот f = f₀ +

установления новой динамической шкалы времени.

+ Δfамплитуда вынужденных колебаний меньше,

меньше также и запасенная энергия. Амплитуда

Время — физическая величина, которая может

быть очень точно измерена современными часами.

осциллятора как функция частоты вынуждающей

Вначале кратко рассмотрим самые общие свойства

силы описывается, как правило, гауссовой кривой,

процесса измерения времени. Лучшие часы, со-

центрированной вокруг собственной частоты f₀.

зданные на основе современных квантовых законов

Добротность осциллятора определяется как Q =

= f₀/Δf. Если мы возбудим осциллятор и отклю-

^*E-mail: pshirkov@gmail.com

чим возбуждающую силу, то из-за диссипативных

120

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

121

процессов колебания начнут затухать с характер-

Это определение в настоящее время формулирует-

ся как промежуток времени, в течение которого со-

ной зависимостью e^-t/τ , где величина τ называется

вершается 9 192 631 770 колебаний, соответствую-

временем затухания и равна τ = f₀/Q = 1/Δf.

щих частоте излучения атома цезия¹³³Cs при ре-

Со случайными и систематическими вариация-

зонансном переходе между уровнями сверхтонкой

ми частоты осциллятора связаны две важнейшие

структуры основного состоянии атома цезия при

характеристики:

отсутствии внешних магнитных полей на уровне

моря [3]. Возможно, что в будущем это определение

1) Нестабильность осциллятора, которая ха-

секунды может быть заменено другим определе-

рактеризуется наличием случайных вариаций соб-

нием. Хотя любое новое определение обязательно

ственной частоты f₀. Это приводит к тому, что

будет тесно связано с предполагаемой неизменно-

показания часов, реализованных с помощью этого

стью фундаментальных констант [4].

осциллятора, с ходом времени все более расходят-

ся с показаниями идеальных часов.

Астрономические часы представляют собой пе-

риодические процессы в космосе. В отличие от

2) Точность, которая характеризуется погреш-

лабораторных часов они не могут контролировать-

ностью частоты Δf из-за настройки осциллятора.

ся исследователями, поэтому для использования

То есть его истинная частота f′0 отличается от

астрономических часов необходимы теория соот-

номинальной f₀ и равна f′0 = f₀ + Δf. Это вызыва-

ветствующего периодического процесса и выбор

ет равномерно нарастающее отличие от показаний

единицы времени (как правило, единицей времени

идеальных часов.

является период соответствующего процесса). В

астрономии исчисление времени чаще всего на-

Для реализации обоих свойств требуется высо-

зывается шкалой времени. Как уже говорилось,

кая добротность осциллятора.

в современной астрономии используют несколько

В качестве лабораторных высокоточных часов

астрономических шкал времени: солнечное время,

иногда используются кварцевые часы (точность

звездное время и динамическое или эфемеридное

таких часов в настоящее время не является удо-

время. В последнее время активно обсуждаются

влетворительной, и они выходят из использова-

возможности использования радиопульсаров для

ния), широко используются рубидиевые, цезиевые

установления новой динамической шкалы времени.

атомные стандарты частоты, а также водородные

В 2017 г. мы отметили 50-летие открытия пер-

часы. Последние обладают точностью ∼10-14 и

вого пульсара, а в 2018 г. отмечаем юбилей пуб-

нестабильностью ∼5 × 10-15 в сутки и сейчас мас-

ликации статьи о первом пульсаре [5]. Вскоре

сово используются в большинстве астрономиче-

после этого были обнаружены другие пульсары,

ских обсерваторий. Создано несколько атомных

было также обнаружено удивительное свойство их

стандартов частоты с лазерным охлаждением. Счи-

импульсов, которое является очень важным для

тается, что в таких стандартах частоты и време-

нашей задачи, — расхождение в периоде повторе-

ни можно достигнуть точности и нестабильности

ния между импульсами было не более 5-10% [6].

вплоть до 10-17. Недавно создан ультрастабиль-

Пульсары оказались источниками с удивительно

ный лазер, который стабилизирован кремниевым

стабильными характеристиками периода следова-

резонатором Фабри-Перо, охлажденным до 124 К.

ния импульсов. Сейчас известно более двух ты-

Частотная стабильность лазера полностью опре-

сяч пульсаров, расположенных в нашей Галактике.

деляется фундаментальным броуновским шумом

280 пульсаров входят в двойные звездные систе-

зеркальных покрытий. Достигнута нестабильность

мы [7]. Из них около двадцати пульсаров входят в

∼4 × 10-17 на интервале времени интегрирования

двойные системы, состоящие из двух нейтронных

звезд.

от 0.8 с и до нескольких десятков секунд [2].

Все пульсары обладают рядом одинаковых ха-

Можно ожидать, что в течение ближайшего

рактеристик, основной из которых является радио-

десятилетия технологически достижимыми вели-

излучение в виде периодической последовательно-

чинми станут нестабильность и точность часов на

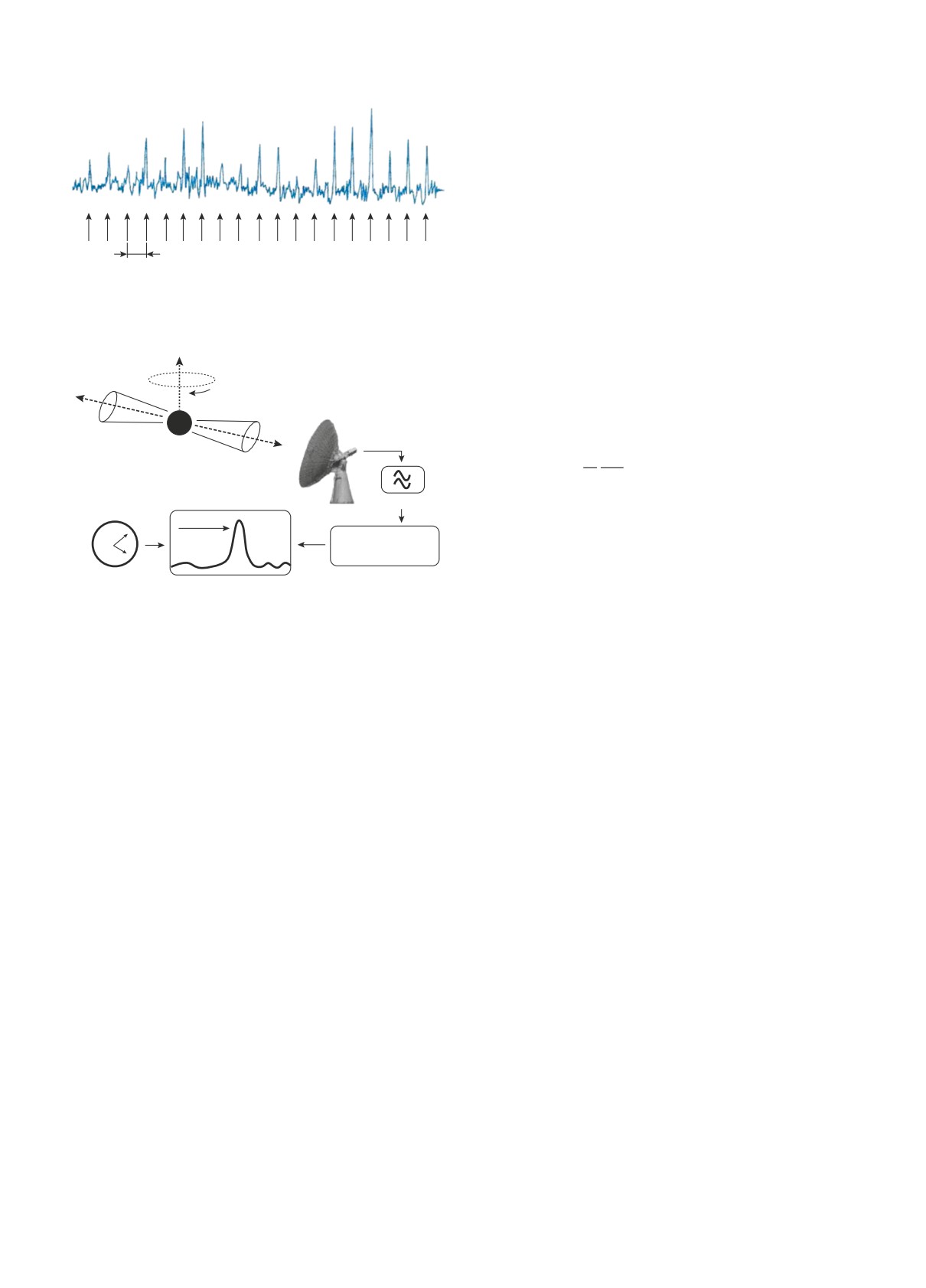
сти импульсов (рис. 1).

уровне 10-17 на интервале времени интегрирования

Интенсивность импульсов меняется, иногда на-

от десятков секунд или даже часов.

блюдается их полное отсутствие. Тем не менее мо-

Следует также обсудить определение секунды

менты прихода импульсов подчиняются периоди-

(единицы измерения времени) в системе СИ. Надо

ческому закону с высокой стабильностью периода,

различать понятия точности и стабильности часов,

несмотря на изменение амплитуды импульсов. При

а также эталон времени. Слово “точность” приме-

сложении многих импульсов синхронно с периодом

нительно к стандарту частоты означает, что частота

пульсара формируется средний профиль импульса

генератора связана с определением секунды СИ.

пульсара, который является очень стабильным и

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

122

ЖАРОВ и др.

известен приближенно и в различных моделях

меняется от 10 км до 20 км [6].

Современная модель пульсара представляет со-

бой вращающуюся нейтронную звезду, которая

обладает сильным магнитным полем (вплоть до

10¹⁴ гаусс), причем ось магнитного поля не сов-

падает с осью вращения. При этом радиоизлуче-

Импульсы пульсара

P ≈ 1.5 c

ние генерируется в пределах узкого конуса. При

вращении звезды наблюдатель периодически бу-

Рис. 1. Пример записи импульсов пульсара. Период

дет фиксировать излучение с периодом враще-

между импульсами 1.5 с.

ния пульсара. У осциллятора, которым является

пульсар, будут потери энергии на излучение. Эта

диссипация энергии приводит к тому, что период

пульсара уменьшается. Из-за гигантской энергии,

запасенной во вращении нейтронной звезды, на-

Телескоп

блюдаемая скорость изменения периода импульсов

очень мала и составляет

Пульсар

1 dP

∝ 10-15-10-21,

P dt

Приемник

что указывает на высокую добротность пульсара

Время

как физического осциллятора.

ТОА

Коррекция дисперсии и

движения барицентра,

когерентное сложение

Высокая стабильность суммарного импульса

Атомные

пульсара, а также большая добротность пульсаров

часы

Ср. профиль импульса

как осцилляторов указывают, что пульсары удо-

влетворяют всем требованиям, предъявляемым к

Рис. 2. Схематически показан процесс наблюдения

временным стандартам или к шкалам времени. Для

пульсара и формирование среднего импульса.

объективности отметим, что на пути к обоснованию

и установлению пульсарной шкалы времени суще-

ствует достаточно много трудностей.

имеет характерную для данного пульсара форму

(рис. 2).

Например, в отличие от лабораторного источ-

ника точной частоты, частота природного астрофи-

Пульсары обозначаются буквами PSR (сокра-

зического источника определяется некоторым сто-

щение слова pulsar, Pulsating Source of Radio), за

хастически распределенным начальным периодом,

которыми следует иногда еще одна буква: латин-

который вместе с некоторыми дополнительными

ская буква “B” означает, что координаты берутся

процессами сформировался в процессе эволюции

на эпоху 1950 г.; латинская буква “J” означает, что

звезды в ее нынешнем состоянии. Кроме того, как

координаты берутся на эпоху 2000 г. За ними сле-

мы увидим ниже, требуется проводить тщательный

дуют цифры, обозначающие координаты пульсара

контроль земных часов, чтобы определить все по-

(прямое восхождение и склонение) и состоящие из

тенциальные источники систематических неопре-

двух или более цифр, например, PSR B1937+21.

деленностей. Это невозможно сделать с астроно-

Периоды пульсаров P варьируются от 8.51 с для

мическими источниками.

пульсара PSR J2144-3933 до 1.4 мс для пульсара

Несмотря на эти трудности и внутреннюю

PSR J1748+244.

нестабильность пульсаров, наблюдения, получен-

Согласно общепринятой модели пульсары

ные от согласованного ансамбля пульсаров, могут

представляют собой нейтронные звезды, одиноч-

оказаться очень полезными, чтобы обеспечить

ные или входящие в двойные звездные системы.

доступную и очень стабильную шкалу времени

Для пульсаров, которые входят в двойные звездные

на длительном интервале — более десяти лет, а

системы, возможно измерение массы. Массы

возможно и несколько сотен лет. В свете этой

нейтронных звезд, которые входят в двойные си-

возможности, безусловно, следует изучать по-

стемы типа “нейтронная звезда — белый карлик”,

тенциальную стабильность этих астрофизических

варьируются в пределах от 1.2 до 2 масс Солнца.

источников. Массивы хронометрических наблю-

В двойных звездных системах, состоящих из двух

дений пульсаров могут потенциально обеспечить

нейтронных звезд, интервал масс составляет 1.1-

экстремально стабильную долговременную шкалу

1.6

масс Солнца [8]. Радиус нейтронных звезд

времени.

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

123

2. ШКАЛА ВРЕМЕНИ,

Первые модели имели феноменологический харак-

ОСНОВАННАЯ НА ПУЛЬСАРАХ

тер и не учитывали многие эффекты, что не поз-

воляло производить точную экстраполяцию МПИ

Сразу после обнаружения периодических сиг-

пульсаров в точку наблюдения на достаточно дли-

налов от пульсаров появились предложения ис-

тельных временах. С развитием техники хрономет-

пользовать их как космические часы [9]. В какой-

рирования был разработан ряд реалистичных мо-

то мере в качестве стандарта времени пульсары

делей, которые опирались на все более высокоточ-

предлагались вместо процессов вращения Земли

ные эфемериды движения тел Солнечной системы

вокруг своей оси и обращения Земли вокруг Солн-

и теории движения Земли, а также теории дви-

ца — именно в это десятилетие данные процессы

жения пульсара в двойной системе. К 1980-м го-

уступали свое место атомным стандартам частоты

дам хронометрирование пульсаров достигло того

и времени.

уровня точности, когда возникла необходимость

в использовании релятивистских формул, описы-

Конечно, первые полуинтуитивные подходы, на-

вающих движение пульсара и тел Солнечной си-

правленные на использование пульсаров в каче-

стемы, оперативных данных о вращении Земли,

стве первичных стандартов частоты и времени, не

а также релятивистских формул преобразования

имели под собой на конец 1960-х ни техноло-

шкал времени.

гического, ни научного обоснования и были ис-

ключительно спекулятивными. Однако в течение

Тем не менее сравнительно низкая стабильность

известных на начало того десятилетия пульсаров

нескольких лет они были подкреплены результата-

не позволяла использовать пульсары в качестве

ми наблюдений радиопульсаров, которые подтвер-

хранителей времени с качеством, приближающим-

дили предположение о высокой стабильности сле-

ся к атомным стандартам. В 1982 г. был открыт

дования импульсов пульсара, основанное на моде-

пульсар B1937+21 — первый представитель ново-

ли пульсара как быстровращающейся нейтронной

го класса миллисекундных пульсаров с периодом

звезды с огромным моментом инерции. Наблюде-

собственного вращения порядка нескольких мил-

ния пульсаров начали активно проводиться в ряде

лисекунд [10], которые обладают более чем на два

обсерваторий, обладающих крупными радиоастро-

порядка более высокой стабильностью следования

номическими инструментами, в частности, одни из

МПИ, чем секундные пульсары. Это позволило

первых в мире наблюдений индивидуальных им-

говорить о микросекундных точностях определе-

пульсов пульсара B1919+21 были проведены на

ния и экстраполяции МПИ пульсаров, а также о

Радиоастрономической станции ФИАН в Пущино

возможности достижения на длительных временах

(в настоящее время Пущинская радиоастрономи-

относительной нестабильности пульсарного вре-

ческая обсерватория АКЦ ФИАН) с использова-

мени, сравнимой с нестабильностью атомных шкал

нием диапазонного крестообразного радиотелеско-

(о численных характеристиках нестабильности см.

па ДКР-1000.

ниже в разделе 4).

В первые несколько лет число наблюдаемых

Необходимо отметить фундаментальное разли-

пульсаров было сильно ограничено из-за слабости

чие идей, лежащих в основе построения пульсар-

их излучения, а также из-за неразвитости при-

ного и атомного времен. Атомное время являет-

емной аппаратуры и техники обработки наблюде-

ся реализацией идеального земного координатного

ний. Затем была быстро развита техника наблюде-

времени TT (Terrestrial Time), которая строится из

ний, использующая особенности излучения пуль-

показаний часов в различных лабораториях. Атом-

саров, — высокую временную стабильность следо-

ное время, таким образом, реализуется набором

вания импульсов и стабильность их формы. Син-

стандартов, находящихся в неинерциальной систе-

хронное с периодом накопление сигнала стало ос-

ме отсчета, показания которых регистрируются в

новой метода хронометрирования (timing в англо-

ней же. Качество стандартов оценивается по со-

язычной литературе) пульсаров. Суть метода хро-

гласованности их со всеми остальными, построение

нометрирования заключается в точной регистрации

групповой шкалы происходит путем усреднения по

моментов прихода импульсов (МПИ) пульсара в

ансамблю. Наилучшая с точки зрения достиже-

точку наблюдения. Для проведения подобных на-

ния минимальной относительной нестабильности

блюдений было необходимо разработать модели

на длительных временах реализация времени —

временного поведения МПИ, вызванного вековым

шкала TT(BIPM) (Bureau International des Poids

замедлением вращения пульсара из-за потерь на

et Mesures) — ежегодно создается путем апостери-

излучение электромагнитных волн и релятивист-

орного анализа данных, полученных рядом наци-

ских частиц математических моделей, описываю-

ональных эталонов. Расхождение текущего меж-

щих вариации МПИ, вызванные относительным

дународного атомного времени TAI и TT(BIPM)

движением пульсара и наблюдателя, а также от-

служит мерой нестабильности шкалы TAI (Temps

носительным движением пульсара и наблюдатель.

Atomique International).

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

124

ЖАРОВ и др.

Опорные источники пульсарного времени

Обычно в этом качестве выбирается момент

расположены далеко от Земли — пульсарное

начала накопления импульсов. Для детального

время является реализацией барицентрического

изучения временного процесса следует использо-

координатного времени (TCB Time Coordinate

вать атомные стандарты времени. На интервале

Barycentric) в барицентре Солнечной системы,

наблюдений, соответствующем времени накоп-

реализуемой на основе галактических источни-

ления (от нескольких секунд до нескольких ча-

ков электромагнитного излучения, используемых

сов) такие стандарты обеспечивают необходимую

в качестве первичных стандартов. Пульсарное

временную точность. Преобразование времени

хронометрирование использует опорную шка-

прихода импульса от местного стандарта частоты в

лу атомного времени и сейчас мерой качества

шкалу TAI выполняется по стандартным правилам,

реализации пульсарного времени (PT — Pulsar

описанным, например, в книге [1]. Далее время

Time) является относительная нестабильность,

прихода требуется преобразовать в шкалу бари-

рассчитываемая по вариациям рядов остаточных

центрического времени TDB (Barycentric Dynamic

уклонений (ОУ) МПИ пульсаров. Опорной шкалой

Time) нашей Солнечной системы.

для определения МПИ служит земная шкала

Наблюдатель в барицентре Солнечной системы

атомного времени, реализованная на поверхности

по времени прихода импульса может вычислить его

геоида, это означает, что реализация PT требует

номер:

включения в модель, кроме параметров пульсаров,

N (t) = N₀ + f₀(t - t₀) +

(1)

также параметров, связанных с движением тел

Солнечной системы и вращением Земли.

+ 1/2df₀/dt(t - t₀)² + 1/6d²f₀/dt²(t - t₀)³ . . . ,

Таким образом, пульсарное время можно рас-

Здесь N₀ — номер импульса в начальную эпоху t₀,

сматривать как дополнительное к земному атом-

f₀ = 1/P₀, df₀/dt, d²f₀/dt² — частота, первая про-

ному времени TAI астрономическое время, которое

изводная частоты и вторая производная частоты

может служить для независимой оценки хода TAI

пульсара в эту эпоху. В идеальном случае, когда t₀

на длительных интервалах времени, а также для

совпадает с временем прибытия импульса, а часто-

тестирования аналитических и численных теорий

та, производная от частоты и вторая производная

движения Земли, тел Солнечной системы и формул

от частоты точно известны, N(t) и N₀ являются

преобразования релятивистских шкал времени.

целыми числами.

С практической точки зрения привлекательным

Однако наблюдатель находится в системе, ко-

качеством пульсарного времени, как и всех аст-

торая не является инерциальной. Поскольку те-

рономических времен, является его независимость

лескопы находятся на Земле, которая вращает-

от земных стандартов, что позволяет в течение

ся вокруг своей оси и движется вокруг Солнца,

длительного времени использовать его автономно,

необходимо сделать преобразования в инерциаль-

что особенно интересно при эксплуатации кос-

ную систему координат Солнечной системы. Кроме

мических аппаратов (КА), в частности, пульсар-

того, необходимо провести редукции, связанные с

ное время может применяться для решения задач

распространением импульса от пульсара в меж-

космической навигации, особенно на значительном

удалении от Земли.

звездной плазме. Очень точное измерение времени

прихода импульсов предполагает, что мы знаем за-

Обычно моменты прихода импульсов опреде-

коны распространения импульсов электромагнит-

ляют, вписывая принимаемый средний импульс в

ного излучения в 4-мерном пространстве-времени.

стандартный средний (или шаблонный) профиль

Момент прихода импульса t в барицентр Сол-

по определенному алгоритму. Для высокой точ-

нечной системы связан с моментом прихода им-

ности измерения времени прихода важно, чтобы

пульса t_obs в точку r_obs, в которой находится на-

форма среднего импульса была стабильной. Этого

блюдатель, уравнением

добиваются суммированием нескольких сотен или

тысяч импульсов (для ярких пульсаров), а в случае

t - t_obs = (kr_obs)/c - |kr_obs|²/2cR +

(2)

слабых пульсаров — нескольких миллионов им-

+ δt_rel + δt_disp + δt_ion + δt_trop.

пульсов. Находя корреляцию между шаблонным

импульсом и текущим средним импульсом, можно

Первый член в правой части уравнения называ-

определить фазу импульса с точностью до 10-5, по

ется задержкой Ремера и связан с конечной ско-

крайней мере, для ярких пульсаров. Это, в свою

ростью распространения света, второй член возни-

очередь, означает, что положение текущего сред-

кает из-за сферичности фронта электромагнитной

него импульса можно измерить с точностью вплоть

волны пульсара, который расположен на рассто-

до P × 10-5. В случае миллисекундных пульсаров

янии R от наблюдателя. Третье слагаемое возни-

такая точность соответствует долям микросекунд.

кает из-за действия релятивистских поправок в

Для вычисления моментов прихода импульсов

распространении света (гравитационная задержка

по фазе необходимо задать начальную эпоху.

или задержка Шапиро), δt_disp, δt_ion — задержки

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

125

импульса при распространении его в межзвездной

3. ГРУППОВАЯ ШКАЛА

плазме и ионосфере Земли, δt_trop возникает из-за

ПУЛЬСАРНОГО ВРЕМЕНИ

распространения импульса в тропосфере Земли.

В природе не существует идеального пульсара.

Пульсар как сложный физический объект обладает

Уравнение (1) устанавливает взаимную и одно-

собственными нерегулярностями вращения. Это

значную связь между номером импульса и време-

приводит к тому, что во временном ряде попра-

нем его прихода в барицентр Солнечной системы.

вок хода земных часов относительно пульсарной

Поэтому уравнение (1) может считаться определе-

шкалы на вариации хода часов накладываются

нием пульсарной шкалы времени [1].

собственные шумы вращения пульсара, что значи-

тельно усложняет анализ поправок.

Это уравнение можно переписать в виде

Для уменьшения влияния нерегулярностей вра-

щения индивидуального пульсара на шкалу вре-

t_N = t₀ + P₀(N - N₀) +

(3)

мени используют классический подход усредне-

+ 1/2P₀dP₀/dt(N - N₀)² + 1/6(P₀(dP₀/dt)² +

ния возможно большего количества шкал времени.

При этом по умолчанию принимается, что вариа-

+ P²⁰d²P₀/dt²)(N - N₀)³ + R(t).

ции вращения разных пульсаров не коррелированы

между собой. Алгоритм формирования групповой

шкалы вк∑ючает в себя вычисление взвешенного

Так, пульсарная шкала времени была определе-

среднего w_iΔt_i ≈ s(t), где w_i — относительный

на в работах [11-13]. В работе [13] впервые бы-

ло введено понятие “пульсарная шкала времени”

вес, приписываемый i-му пульсару.

(в дальнейшем будем использовать аббревиатуру

В простейшем случае, когда вариации враще-

ПШВ). Здесь P₀, dP₀/dt — период пульсара и его

ния пульсаров и стандарта частоты представляют

производная в начальный момент времени. N -

собой белый шум, веса выбираются в соответ-

- N₀ есть разница между текущим номером им-

ствии с теорией усреднения неравноточных дан-

пульса и первым наблюденным импульсом. В от-

ных пропорциональными w_i ∼

, где σ_i — сред-

личие от уравнения (1) здесь добавлен еще один

σ²

член. Это так называемые остаточные уклонения

неквадратичное отклонение измеряемой величины

МПИ — разность между зарегистрированным мо-

от среднего значения. В случае длительных рядов

ментом прихода импульса и моментом прихода,

наблюдений шум не всегда можно считать белым,

предсказанным на основании полинома третьей

что дает возможность применять различные мето-

степени. Эта разность обычно обозначается R(t),

ды взвешивания данных.

она зависит от влияния эффектов, которые не

Можно пойти еще дальше и применить для

входят в модель полинома, в том числе от уров-

выделения сигнала s(t) методы цифровой обра-

ня нестабильности вращения пульсара (следует

ботки. Например, в работах [16-18] предложен

упомянуть, что кубичный член является значимым

метод построения групповой пульсарной шкалы,

лишь для нескольких пульсаров, для большинства

основанный на применении винеровского фильтра.

пульсаров в разложение включается лишь квадра-

Метод винеровской фильтрации заключается в

тичный член).

оценивании сигнала s(t), если даны измерения Δt

и ковариационная функция сигнала. В развитом

Ход пульсарной шкалы времени относительно

в работах [16, 18] подходе задача восстановления

местного стандарта времени может быть определен

случайного сигнала решается в условиях недостат-

по формуле (3). В статье [13] также было отмечено,

ка априорной информации, так как ковариацион-

что для целей практического использования шкалы

ная функция сигнала априори неизвестна и оце-

пульсарного времени необходимо ввести “пульсар-

нивается из самих наблюдательных данных путем

ную секунду”, которая может быть определена как

кросс-корреляции всех данных между собой. При-

нимается естественное предположение, что вариа-

Пульсарная секунда = mP₀,

(4)

ции хода часов (оцениваемый сигнал) и вариации

вращательной фазы пульсара (аддитивный шум) не

причем коэффициент m выбирается таким обра-

коррелированы между собой.

зом, чтобы длительность “пульсарной секунды”

Групповая пульсарная шкала (оцениваемый

была как можно ближе к длительности секунды

сигнал) s(t) вычисляется по следующей формуле

TAI.

M (M-1)

Следует заметить, что идея создания пульсар-

∑

ной шкалы времени высказывалась независимо

s(t) =

^mQ_ss ×ⁱwⁱQ-1rr ·ⁱΔt,

M (M - 1)

несколько раз (см., например, [14, 15]).

m=1

i=1

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

126

ЖАРОВ и др.

-20

-40

-20

-40

Рис. 3. Барицентрическиеостаточные уклонения моментов приходов импульсов шести миллисекундныхпульсаров в мкс.

По горизонтальной оси время в годах от момента 1998.5. Нижний график: усреднение методом взвешенного среднего,

верхний график: перед усреднением данные пропущены через винеровский фильтр.

где M — число пульсаров,^mQ_ss — автоковари-

ненияⁱΔt и приводящий их к виду белого шу-

ационная матрица сигнала,ⁱQ_rr — автоковари-

ма (т.н. выбеливающий фильтр). Далее весаⁱw =

ационная матрица остаточных уклоненийⁱΔt,

= k/σ2i вычисляются уже в соответствии с дис-

ⁱw = k/σ2i — относительный вес i-го пульсара,

персией величиныⁱQ-1rr ·ⁱΔt (i = 1, 2, . . . , M). Ве-

σ_i — среднеквадратичное отклонение величины

M (M-1)

ⁱQ-1rr ·ⁱΔt (i = 1,2,... , M,m = 1,2,... ,M (M -

∑

личина

^mQ_ss, (m = 1,2,... ,M

- 1)/2). Матрицы^mQ_ss иⁱQ_rr строятся как

M (M - 1)m=1

теплицевы матрицы из соответствующих ковари-

(M - 1)/2) представляет собой среднюю по всем

ационных функций.

парам пульсаров кросс-корреляционную функцию

Обратную матрицуⁱQ-1rr можно рассматривать

сигнала s(t). Таким образом, главное отличие мето-

как оператор, действующий на остаточные укло- да винеровской фильтрации от взвешенного сред-

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

127

σ_z

J0613-0200

J1640+2224

J1643-1224

5×10^-12

1×10^-12

5×10^-13

1×10^-13

5×10^-14

1×10^-14

0.5

1.0

2.0

5.0

0.5

1.0

2.0

5.0

0.5

1.0

2.0

5.0

σ_z

J1713+0747

J1939+2134

J2145-0750

5×10^-12

1×10^-12

5×10^-13

1×10^-13

5×10^-14

1×10^-14

0.5

1.0

2.0

5.0

0.5

1.0

2.0

5.0

0.5

1.0

2.0

5.0

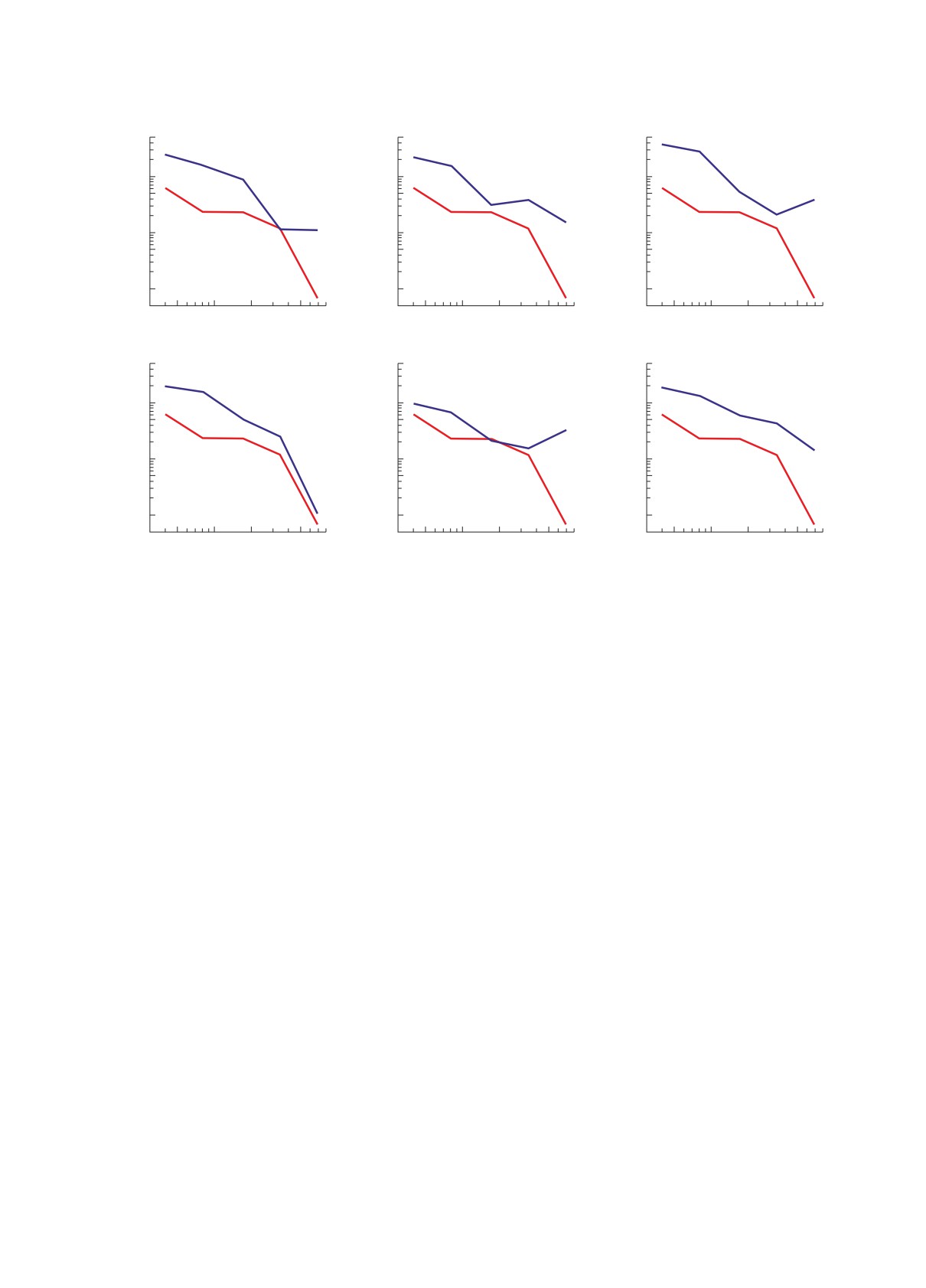
Рис. 4. Относительная нестабильность вращения шести миллисекундных пульсаров. Нижняя кривая — относительная

нестабильность групповой шкалы. По горизонтальной оси отложен интервал времени в годах.

него заключается в том, что в первом перед взве-

порядок для всех пульсаров, кроме PSR J1713+

шиванием ряды пропускаются через винеровский

+0747, обладающего уникальной стабильностью

фильтр, который выделяет общий сигнал, т.е. вари-

вращения. Если проэкстраполировать данный

ации опорной шкалы времени.

результат на несколько пульсаров, которые имеют

В работах [16-18] показано, что использование

индивидуальную нестабильность вращения σ_z <

винеровского фильтра перед операцией усреднения

< 10-15, то мы придем к групповой шкале с σ_z ∼

в несколько раз улучшает точность восстановления

∼ 10-16 или даже лучше.

сигнала и относительную нестабильность по срав-

нению с простым методом взвешенного среднего.

4. ХАРАКТЕРИСТИКИ СТАНДАРТОВ

Рассмотрим, например, наблюдения шести милли-

ХРАНЕНИЯ ВРЕМЕНИ

секундных пульсаров, проведенные в 1997-2005 гг.

Часы содержат в качестве основного элемента

в Калязинской радиоастрономической обсервато-

стандарт частоты. Дополнение его интегратором

рии, и применим к ним для построения групповой

и счетчиком импульсов (или фазы) превращает

пульсарной шкалы метод взвешенного среднего и

стандарт частоты в часы. Стандарт частоты —

метод винеровской фильтрации.

это высокостабильный по частоте генератор элек-

На рис. 3 показаны остаточные уклонения бари-

тромагнитных сигналов в радио или оптическом

центрических моментов прихода импульсов шести

диапазоне. Одной из самых важных характери-

миллисекундных пульсаров, усредненные методом

стик является нестабильность частоты генератора.

взвешенного среднего (нижний рисунок) и методом

Нестабильность частоты определяется дисперсией

винеровской фильтрации. Видно, что точность вос-

Аллана, определение которой будет дано ниже.

становления даже индивидуальных сигналов, про-

В идеальном случае на выходе генератора ча-

пущенных через фильтр, улучшилась в несколько

стоты имеется синусоидальный сигнал вида

раз.

V (t) = V₀ cos2πν₀t,

(5)

На рис. 4 показана относительная нестабиль-

где ν₀ — номинальная частота генератора. Однако

ность вращения шести пульсаров и групповой

пульсарной шкалы, построенной на их основе.

в действительности сигнал представляется выра-

жением

Видно, что относительная нестабильность на

семилетнем интервале улучшилась более чем на

V (t) = V₀ cos [2πν₀t + ϕ (t)] ,

(6)

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

128

ЖАРОВ и др.

где ϕ (t) — фаза, меняющаяся со временем случай-

с конечным временем наблюдения процесса. На-

ным образом. Здесь для простоты мы не рассмат-

личие в модели (9) слагаемых со степенями n =

риваем флуктуации амплитуды сигнала. Мгновен-

= -2 (шум случайных блужданий частоты) и n =

ная частота генератора определяется производной

= -1 (фликкерный частотный шум) приводит к

по времени от аргумента Φ (t) = 2πν₀t + ϕ (t) в

тому, что случайный процесс отсчетов разностей

выражении

частот ý_k (τ) (8) будет являться нестационарным.

Оценка дисперсии разности частот сравниваемых

1 dΦ

1 dϕ

ν (t) =

=ν₀ +

генераторов будет стремиться к бесконечности при

2π dt

стремлении к бесконечности времени наблюдения

Определим относительное отклонение частоты ге-

(или f₁ → 0). Поэтому в качестве характеристики

нератора от его номинальной частоты следующим

нестабильности частоты вместо “истинной” дис-

образом

персии используют так называемую дисперсию

Аллана, характеризующую дисперсию вариаций

ν (t) - ν₀

dϕ

частоты.

y (t) =

(7)

ν₀

2πν₀ dt

На практике, используя N фазовых отсчетов

с интервалом τ, оценку дисперсии Аллана можно

Для современных стандартов частоты справедливо

соотношение:

вычислить по следующей формуле [21]:



dϕ

∑



^≪

σ2y (τ) =

σ2n (τ),

(10)

^ 2πν₀ dt

2(N - 2)

n=1

т.е. относительное изменение частоты мало.

Так как время находится интегрированием ча-

σ2n (τ) = ýn+1 - ý_n =

(xn+2 - 2xn+1 + x_n) .

стоты, добавление к генератору счетчика (интегра-

тора) количества периодов сигнала (6) превращает

Отсчеты вариации частоты σ2n представляют со-

это устройство в часы. Это означает, что интеграл

бой стационарный случайный процесс для моде-

ли (9), и соответствующая дисперсия является

∫

(

)

ограниченной. Дисперсию Аллана в русскоязыч-

x_k (t) =

t^′

)dt^′

ной литературе часто обозначают аббревиатурой

СКДО (среднеквадратическое двухвыборочное от-

клонение результата измерения частоты). Назва-

представляет собой величину, на которую уходят

ние СКДО отражает смысл дисперсии Аллана,

или отстают часы на промежутке времени от t_k до

значение которой для интервала времени измере-

t_k + τ, относительно идеального стандарта време-

ния τ характеризует погрешность измерения часто-

ни, в основе которого лежит генератор сигнала (5).

ты (разности частот) на интервале τ.

Среднее относительное отклонение частоты ге-

При увеличении τ до определенной величи-

нератора на k-ом интервале, продолжительность

ны случайные флуктуации частоты усредняются, и

которого равна τ, есть

дисперсия Аллана уменьшается; однако при даль-

нейшем увеличении τ начинается систематическое

xk+1 - x_k

ýk (τ) =

(8)

увеличение шумов, приводящее к увеличению дис-

персии Аллана.

Для описания шумов генераторов и квантовых

В табл. 1 представлена зависимость дисперсии

стандартов частоты применяется следующая мо-

Аллана от длины интервала τ для шумов с раз-

дель (односторонней) спектральной плотности

личным показателем спектра. На рис. 5 показана

мощности S_y (f) относительных флуктуаций часто-

дисперсия Аллана (или нестабильность) наиболее

ты y (t) (7) [19, 20]:

распространенных стандартов частоты, а также

{∑α=2

астрономических шкал времени UT (Всемирное

α=-2

h_αf^α, f₁ ≤ f ≤ f_h

время), TAI (атомная шкала времени) и пульсарной

S_y (f) =

(9)

S_y (f) = 0, f > f_h, f < f₁,

шкалы времени (ПШВ). Нестабильность лучших

цезиевых стандартов достигает 10-14 при времени

где α — целое число в диапазоне от -2 до +2.

усреднения порядка нескольких суток. Водородные

Значения констант h_α зависят от источника шума.

стандарты имеют лучшую из всех кратковремен-

Ограничение спектра флуктуаций частотой f_h

ную нестабильность (до 10-15) на интервале 100-

вызвано тем, что реальные измерения всегда про-

1000 с. В настоящее время несколько лабораторий

исходят в некоторой полосе частот. Верхняя ча-

разработали и используют новые цезиевые и руби-

стота f_h определяет минимальный интервал вре-

диевые часы, принцип действия которых основан

мени измерения τ. Нижняя частота f₁ связана

на использовании атомного фонтана. Ожидается,

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

129

Таблица 1. Связь дисперсии Аллана со спектральной плотностью мощности S_y (f) относительных флуктуаций

частоты

Тип шума

S_y(f), f > 0

σ2y (τ)

Белый шум фазы

h₂f²

∼τ-2

Фликкерный шум фазы

h₁f

∼τ-2

Белый шум частоты

h₀

∼τ-1

Фликкерный шум частоты

h-1f-1

∼τ⁰

Шум случайных блужданий частоты

h-2f-2

∼τ

что нестабильность этих часов достигнет 10-16 на

вать односторонний спектр шума фазы L (f):

интервале усреднения порядка нескольких суток.

f²⁰

Из рисунка видно, что нестабильность дисперсии

L (f) =

S_y (f).

f²

Аллана для пульсара PSR 1937+21 уже сейчас

меньше нестабильности всех стандартов времени

Размерность спектра — рад²/Гц; f₀ — некая ха-

(Rb, Cs, H), включая шкалу времени (TAI). Здесь

рактерная частота.

следует отметить, что вариация Аллана для пуль-

сарной шкалы времени вычислялась не по форму-

5. СТАБИЛЬНОСТЬ ПУЛЬСАРНОЙ

ле (10), а по формуле (11). Эта формула исключает

ШКАЛЫ ВРЕМЕНИ

вековой тренд пульсара.

Стабильность пульсарной шкалы времени сле-

Кроме спектральной плотности мощности S_y (f)

дует оценивать по тем же критериям, что и зем-

относительных флуктуаций частоты в качестве ха-

ные шкалы времени. Другими словами, для ха-

рактеристики стандарта частоты можно использо-

рактеристик пульсарной шкалы времени мы будем

использовать спектральную плотность мощности

S_y (f) относительных флуктуаций частоты, а также

σ_y(τ)

дисперсию Аллана.

10^-8

Впервые оценка стабильности пульсарной шка-

лы времени была сделана в [22] для набора из

29 пульсаров. Надо отметить, что это были не са-

мые стабильные пульсары, но оценки показали, что

10^-10

PSR 1937+21

максимум стабильности в случае пульсарной шка-

лы времени соответствует интервалу в несколько

десятков и даже сотен лет, а нестабильность может

достигать величины 10-16 на таком продолжитель-

ном интервале времени. Был сделан также вывод о

10^-12

том, что для шкалы времени надо выбирать пульса-

ры с наименьшим значением производной периода

пульсара. После почти 30 лет исследований ста-

бильности пульсаров эти заключения остаются в

силе.

10^-14

Вопросы описания (частотной) стабильности

TAI

частотных генераторов и стабильности временных

шкал являются очень важными для метрологии. С

1960-х годов в этой области широкое применение

10^-16

получила дисперсия Аллана, которую также иногда

10¹

10²

10³

10⁴

10⁵

10⁶

10⁷

10⁸ τ, c

называют вариацией двойной выборки (10).

К сожалению, простое применение этой величи-

1 мин

1 час

1 сутки 1 месяц1 год10 лет

ны к пульсарным наблюдениям невозможно. Пуль-

Рис. 5. Нестабильность шкал времени и стандартов

сары по своей природе постоянно замедляются,

частоты как функция времени (UT — Всемирное вре-

теряя энергию вращения на излучение электро-

мя, TAI — атомное время, Rb, Cs, H — рубидиевый,

магнитных волн и ускорение релятивистских заря-

цезиевый, водородный стандарт частоты, PSR 1937+

женных частиц. Вращательное поведение подав-

+21 — пульсар).

ляющего большинства пульсаров, за исключением

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

130

ЖАРОВ и др.

самых молодых, описывается значениями частоты

хронометрирования в случае шума в рядах ОУ

вращения f₀ и ее первой производной f₁ на какую-

МПИ). Если спектр представляется степенной за-

то заданную эпоху T₀, т.е. частота вращения пуль-

висимостью S_x(f) ∝ f^α, то σ2z также следует сте-

саров обладает неустранимым линейным дрейфом.

пенному закону σ2z(τ) ∝ τ^μ, а показатели α и μ

Если подставить выражение y (t) = f₁ (t - T₀) /f₀

связаны следующим образом:

в формулу для вычисления дисперсии Аллана, по-

лучится следующее выражение:

μ = -(α + 3), если α < 1

f²¹τ

σ2y (τ) =

(11)

-4

в остальных случаях.

2f²

D₃(t,τ) =

На рис. 6 схематически показана эволюция

(

)

(

)

(

)

σ_z(τ) с ростом τ в присутствии красного шума.

- 3x

t+τ6

+ 3x

t-τ6

- x(t - τ2 )

В [24] приведена σ_z-статистика для 20 пульсаров

√

5τ

РРТА, причем там показаны уровни белого шума

амплитудой 0.1 и 10 мкс с продолжительностью

Для ее оценки в [23] был предложен следующий

алгоритм:

наблюдений, в некоторых случаях превышающей

10 лет.

1) Исходные данные — временной ряд остаточ-

ных уклонений x_i(t_i) и их ошибок σ_i, i = 1, . . . , N (в

К сожалению, для расчета σ_z(t) необходимо

хронологическом порядке). Длина всего временно-

знание всего ряда ОУ МПИ, что осложняется

го интервала t_N — t_i = T .

тем, что в большинстве случаев эти данные не

являются общедоступной информацией. Исключе-

2) Весь интервал наблюдений делится на непе-

нием служат ряды МПИ РРТА, из которых могут

рекрывающиеся промежутки длиной τ. τ выбира-

быть получены остаточные уклонения МПИ, но

ется равным T , T/2, T/4, T/8 и т.д. В каждом

они представляют чуть меньший интерес, так как

из промежутков производится аппроксимация ОУ

на радиотелескопе в Парксе наблюдается меньше

МПИ кубическим полиномом:

всего пульсаров [24] и, что важнее, он нацелен на

X (t) = c₀ + c₁ (t - t₀) + c₂(t - t₀)² + c₃(t - t₀)³,

обзор южного неба. Для построения ПШВ важ-

нее всего стабильность пульсаров на наибольших

где t₀ — произвольный отсчет. (Его удобно взять

интервалах времени, сравнимых с полной длиной

посередине интервала, либо равным начальному

ряда наблюдений, поэтому хорошей оценкой этой

отсчету интервала). Аппроксимация делается ме-

величины может служить безразмерное отношение

тодом наименьших квадратов с учетом весов (весо-

σ/T , где σ

— среднеквадратические остаточные

вые коэффициенты — σ_i):

уклонения МПИ для всего ряда, T — продолжи-

тельность этого ряда. На рис. 7 показано распре-

σ_z(τ) =

√

c²³

1/2.

(12)

деление пульсаров РРТА, ЕРТА, NANOGrav по

величине этого отношения.

Угловые скобки обозначают средневзвешенное

Как было показано при обработке данных на-

значение c²³ по всем промежуткам. Веса считаются

блюдений на РТ-64 в Калязине, исключение наи-

обратно пропорциональными квадратам абсолют-

более шумных пульсаров и пульсаров с сильным

ных ошибок при расчете c₃.

красным шумом позволяет улучшить качество ан-

Также необходимо учесть некоторые статистики

самблевой шкалы (см. рис. 8). Наименьшее зна-

σ_z(τ) для пульсаров:

чение σ_z для PT приблизительно в 1.5 раза мень-

1) Для расчета c₃ в каждом промежутке должно

ше, чем для любого из использованных для ее

быть по крайней мере 4 измерения, а интервал

построения пульсаров, что хорошо соответствует

между первым и последним измерением в каждом

теоретическим ожиданиям σ_z ≈ σ_{z_av} (N - 1)-1/2,

√

промежутке должен быть не менее τ/

где N ≥ 3 — число пульсаров ансамбля, σ_{z_av} —

2) Если число точек в некотором промежутке

среднее значение σ_z для пульсаров ансамбля.

длины τ равно 4, то значение веса для c₃ данного

Таким образом, наиболее выигрышной страте-

промежутка принимается равным максимальному

гией отбора для построения ПШВ является вы-

значению веса среди всех промежутков этой длины.

бор меньшего количества наилучших пульсаров,

Если все промежутки длины τ содержат по 4 точки,

а не прямое увеличение количества наблюдаемых

веса для них считаются равными.

пульсаров, которое может ухудшить качество шка-

Как и обычная, и модифицированная диспер-

лы. C другой стороны, слишком малое количество

сия Аллана, широко используемая в частотных

пульсаров может привести к значительным ста-

генераторах, σ_z-статистика также чувствительна к

тистическим флуктуациям построенной шкалы и

спектральным показателям красного шума (шума

неудобной наблюдательной конфигурации. Также

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

131

logσ(τ)

σ_V(τ)

10^-9

σ_Z(τ)

τ^-3/2

10^-11

τ^-3/2

τ^3/2

τ^-1

10^-13

τ^-1/2

τ^1/2

const

10^-15

τ^-1

const

τ^1/2

τ^-1/2

τ₀

τ₁

τ₂

τ₃

τ₄

τ₅

τ₆

logτ

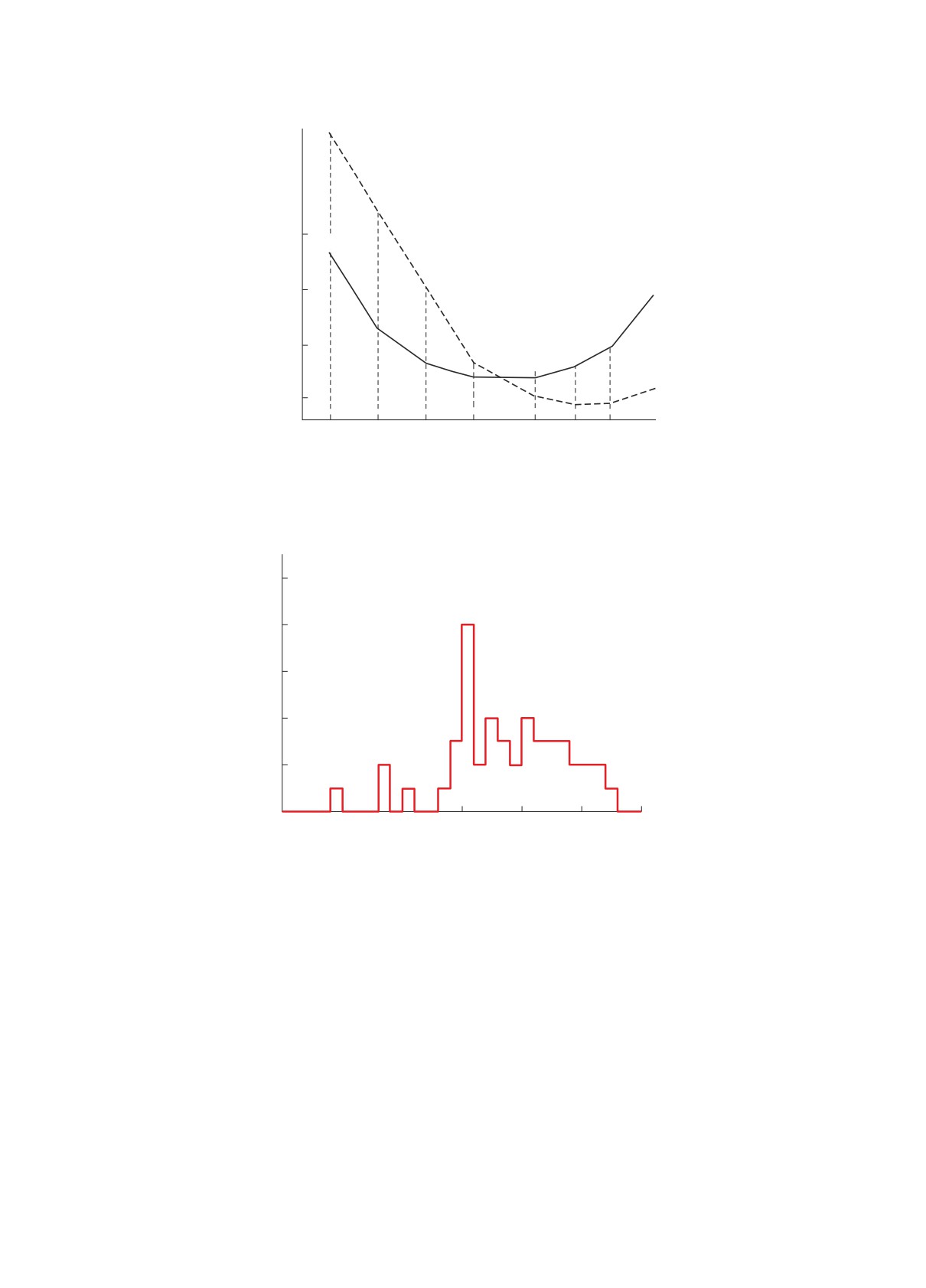
Рис. 6. Схематическое изображение влияния “красных” шумов на ход PT (теоретическая оценка для “среднего”

миллисекундного пульсара). По оси абсцисс отложен логарифм временного интервала (в условных единицах), по оси

ординат — логарифм соответствующей статистики (Z или V).

Число пульсаров

-16.0

-15.5

-15.0

-14.5

-14.0

-13.5

-13.0

log(σ/T)

Рис. 7. Распределение пульсаров РРТА, ЕРТА и NANOGrav по отношению СКО остаточные уклонения МПИ к

продолжительности ряда наблюдений.

количество отобранных пульсаров зависит от са-

распределение выбранных пульсаров по небесной

мой программы: будут ли пульсары наблюдаться на

сфере.

выделенном радиотелескопе или они будут включе-

Величина относительной нестабильности слу-

ны в наблюдательные программы на других радио-

жит для количественной характеристики пригодно-

телескопах, что приведет к уменьшению доступного

сти того или иного пульсара в качестве кандидата

наблюдательного времени. В табл. 2 приведены и

для включения в пульсарную шкалу времени. На

отсортированы 20 пульсаров с наибольшей ста-

практике, однако, необходимы величины взаимного

бильностью (порог σ/T < 5.7 × 10-15). Эти пуль-

хода шкал относительно друг друга для внесения,

сары являются наилучшими кандидатами для на-

если необходимо, поправок в ход шкалы. Впервые

блюдений с целью формирования шкалы. 7 пуль-

поправки хода земной атомной шкалы относитель-

саров из этого списка и 5 из первых 10 недоступны

но групповой пульсарной шкалы были получены

для наблюдения с территории РФ, так как их

в работах [16-18]. Был использован подход, ос-

склонение меньше -30^◦. На рис. 9 представлено

нованный на оптимальных фильтрах. Было пока-

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

132

ЖАРОВ и др.

σ_z

J0437-4715

J1024-0719

10^-13

J1603-7202

J1713+0747

J1730-2304

10^-14

J1744-1134

J2145-0750

10^-15

-16

0.5

τ, year

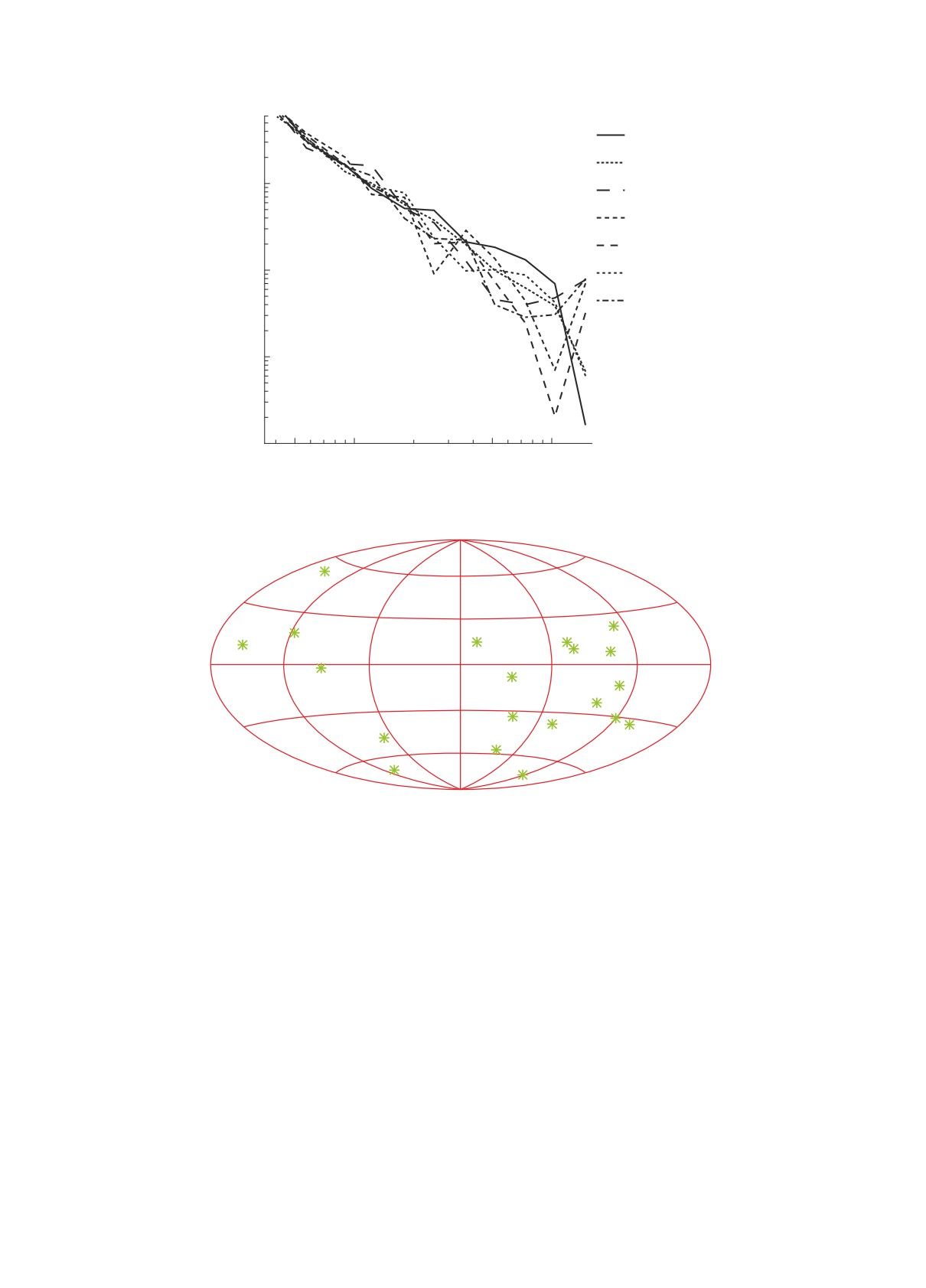
Рис. 8. Ход σz для ПШВ, построено по 7 пульсарам, наблюдавшимся на РТ-64 [25].

12 h

Рис. 9. Распределение выбранных пульсаров по небесной сфере.

зано, что применение оптимальных винеровских

секундных пульсаров в качестве стандарта време-

фильтров позволяет разделить вклад в остаточные

ни. Статистика σ_z, изученная на интервале 10 лет

уклонения МПИ пульсаров собственных вариа-

для подавляющего большинства таких пульсаров,

ций вращения пульсара и вариаций хода опорной

лежит в диапазоне 10-12-10-8 [27].

шкалы на более высоком, в сравнении с методом

взвешенного среднего, уровне точности. Впослед-

6. ДИНАМИЧЕСКАЯ ШКАЛА ВРЕМЕНИ,

ствии поправки земной шкалы TT относительно

групповой пульсарной шкалы были получены в ра-

ОСНОВАННАЯ НА ДВОЙНЫХ

боте [26]. Величина относительной нестабильности

ПУЛЬСАРАХ

σ_z разности шкал TT - PT получилась на уровне

Впервые астрономы начали использовать дина-

6 × 10-15.

мическую шкалу времени после того, как попытки

Следует отдельно сказать о секундных пуль-

построения равномерной шкалы времени, основан-

сарах. Ряды их ОУ МПИ также демонстрируют

ной на вращении Земли, оказалась неудачной. То-

красный шум, единственное отличие в том, что

гда в качестве новой более точной шкалы времени

амплитуды отклонений на 2-3 порядка превос-

было предложено использовать шкалу, определя-

ходит амплитуды для миллисекундных пульсаров.

емую периодическим движением тел в Солнечной

Это приводит к гораздо более низкой стабильности

системе [1].

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

133

Таблица 2. Список кандидатов на включение в ансамбль для формирования ПШВ. Обозначения в колонках: (1)

имя пульсара в эпохе 2000 г. соответственно, (2) минимальное значение достигнутого СКО остаточных уклонений в

мкс для данного пульсара на всем промежутке наблюдений, (3) продолжительность наблюдений, (4) относительная

стабильность (σ/T ), (5,6) σ_z и интервал усреднения T_z, на котором она была получена для пульсаров из РРТА

(из анализа графиков относительной нестабильности, приведенных в статье [25]. Жирным шрифтом выделены

пульсары со склонением больше -30^◦)

Пульсар

σ, мкс

T, лет

σ/T

σ_z

T_z, лет

J1909-3744

0.08

9.1

2.9 × 10-16

9.0 × 10-16

J0437-4715

0.3

14.9

6.8 × 10-16

5.0 × 10-16

J1713+0747

0.4

7.8 × 10−16

1.0 × 10-16

J1744-1134

0.5

16.3

1.0 × 10−15

2.5 × 10−16

J1843-1113

0.7

10.1

2.3 × 10−15

J1455-3330

0.7

9.2

2.5 × 10-15

J1600-3053

0.8

3.0 × 10-15

J2129-5721

1.4

15.4

3.0 × 10-15

J1730-2304

1.6

16.7

3.2 × 10−15

1.2 × 10−15

J1012+5307

1.6

16.8

3.2 × 10−15

J1857+0943

1.7

17.3

3.3 × 10−15

2.0 × 10−15

J1643-1224

1.7

17.3

3.3 × 10−15

J2145-0750

1.8

17.5

3.4 × 10−15

3.0 × 10−15

J1640+2224

1.8

17.3

3.5 × 10−15

J0613-0200

1.8

16.1

3.7 × 10−15

J0711-6830

17.1

3.9 × 10-15

2.0 × 10-15

J2317+1439

2.4

17.3

4.6 × 10−15

J1022+1001

2.5

17.5

4.8 × 10−15

J0751+1807

17.6

5.7 × 10−15

J2124-3358

2.9

16.8

5.7 × 10-15

√

Основная идея этой шкалы времени основана

1+e

на использовании уравнений Ньютона. В класси-

1-e

ческой физике время считается абсолютным и яв-

E - esinE = n(t - t₀) + M₀,

ляется аргументом в уравнениях движения планет

√

и других тел Солнечной системы. В задаче двух тел

(скажем Солнце и какая-либо планета) положение

a³

тела описывается уравнениями:

2π

P =

x = r(cosucosΩ - sinusinΩcosι),

(

)

1-e²

y = r(cosusinΩ + sinucosΩcosι),

1 + ecosϑ

z = rsinusinι.

Здесь t — абсолютное время, t₀ — начальный мо-

Здесь Ω, ι — два элемента орбиты (наклон орбиты

мент времени (эпоха), а также остальные элементы

и долгота восходящего узла), а аргумент u выража-

орбиты: эксцентриситет (e), среднее движение (n),

ется через время согласно формулам вида:

угловое расстояние перицентра от узла (ω), сред-

u=ϑ+ω,

няя аномалия на эпоху (M₀).

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

134

ЖАРОВ и др.

Из этих формул видно, что координаты планеты

Пусть слабая гравитационная волна, которая

(x, y, z) являются функциями времени t. Если в

проходит через Солнечную систему, описывается

качестве аргумента при проведении наблюдений

метрикой

планеты используется Всемирное время UT, то

ds² = c²dt² -

(13)

разницу между вычисленными и наблюденными

координатами планеты можно интерпретировать

− (1 + h₊(ct - z)) dx² - (1 - h₊(ct - z)) dy² +

как разницу между шкалами времени t и UT: ⊗

+ 2h_×(ct - z)dxdy - dz².

⊗T = t - UT. В этом заключается основная идея

использования наблюдений положений планет для

Пусть {ct, x, y, z} образуют систему координат с

установления динамической шкалы времени, так

центром в барицентре Солнца. Безразмерные ве-

называемой шкалы эфемеридного времени ET (в

личины h₊ и h_x, как предполагается, значительно

нашем случае t = ET).

меньше 1 и являются функциями (ct - z). Таким

Аналогичный метод можно использовать при

образом, волна представляет собой плоскую волну,

наблюдении двойных пульсаров. При этом ошиб-

перемещающуюся в положительном направлении

ка в определении шкалы времени зависит как от

z с двумя поляризациями. Поскольку источники

ошибок в определении положения, так и от ошибок

гравитационных волн находятся далеко от Земли,

определения параметров орбиты. В случае двойных

форму гравитационных волн можно считать плос-

пульсаров параметры определяются недостаточно

кой.

точно, поэтому лишь несколько двойных пульсаров

могут использоваться для создания шкалы време-

Для простоты мы предполагаем, что существует

ни, основанной на двойных пульсарах [28]. Так как

идеальный пульсар с постоянной частотой посылки

аргументом при проведении наблюдений является

импульсов f₀ =1/P , в направлении, определяемом

атомное время TAI, то пульсарное время реализу-

единичным вектором n = (n₁, n₂, n₃). Свет распро-

ется в виде PT = TAI + ΔT, где ΔT — поправка,

страняется так, что ds = 0. Решать это уравнение

требуемая для согласования теории и наблюдений

будем методом последовательного приближения

двойных пульсаров.

по малому параметру — амплитуде гравитацион-

ной волны (будем считать, что h₊ и h_x имеют

7. ПРИМЕНЕНИЕ ПУЛЬСАРНОЙ ШКАЛЫ

одинаковый порядок малости). В нулевом порядке

ВРЕМЕНИ

по h имеем:

Из рис. 6 и 8 видно, что для большинства

r = r₀ -nl,

стабильных пульсаров минимум дисперсии Алла-

ct = ct₀ + l,

на еще не достигнут, хотя пульсары наблюдают-

ся уже более десяти лет. Отсюда можно сделать

ct = ct₀ + (nr₀) - (nr) .

предварительный вывод, что пульсарная шкала

Здесь r₀ и t₀ — положение пульсара и момент вы-

времени обладает наилучшей стабильностью на

хода импульса из пульсара, знак минус у вектора n

интервалах времени порядка нескольких лет или

показывает, что направление на пульсар и направ-

даже десятилетий. Поэтому ее следует применять

ление волнового вектора импульса противополож-

для исследований физических процессов, которые

ны, l есть аффинный параметр вдоль траектории.

длятся несколько лет. ПШВ можно применять

для исследования долговременной стабильности

Сумма нулевого и первого порядка по h имеет

лабораторных часов или для исследования веко-

вид:

вых трендов в Солнечной системе, скажем, для

(

)

ct = l +

n²¹ - n²²

исследования трения внутри Земли и замедления

системы Земля-Луна.

∫

(

()

( ))

Одно из главных применений ПШВ — детекти-

× h₊ ct

-z

l dl-

рование гравитационных волн космического про-

исхождения в частотном диапазоне 10-7-10-9 Гц.

∫l

(

()

( ))

8. ДЕЙСТВИЕ ГРАВИТАЦИОННЫХ ВОЛН

−n₁n₂

h_x ct

-z

l dl.

НА ХРОНОМЕТРИРОВАНИЕ ПУЛЬСАРОВ

Предложение детектирования гравитационных

волн при помощи тайминга пульсаров было сде-

Произвольный набор гравитационных волн можно

лано еще до открытия миллисекундных пульса-

разложить в ряд Фурье по гармоникам. Поэтому

ров [29-32]. Гравитационные волны влияют на из-

ниже мы будем обсуждать только действие плоской

меренное время прихода импульса пульсара. Ниже

монохроматической гравитационной волны на тай-

мы обсудим результат этого влияния.

минг пульсаров. Если нам понадобятся оценки для

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

135

линейчатого или непрерывного спектра гравитаци-

малошумящих. Среднеквадратичное уклонение для

онных волн, мы проинтегрируем по спектральной

него составляет примерно 100 наносекунд за время

плотности.

примерно 10 лет. Отсюда можно оценить чувстви-

В случае монохроматической волны амплитуды

тельность его как детектора на уровне H ≈ 10-15 в

ГВ имеют вид

терминах безразмерной амплитуды ГВ.

Помимо монохроматического излучения, во

h₊ = H₁ exp (iΩ (ct - z)),

(14)

Вселенной должно существовать стохастическое

h_× = H₂ exp (iΩ (ct - z)).

гравитационное излучение. Такое излучение может

порождаться либо совокупностью монохромати-

Здесь H₁ и H₂ — постоянные комплексные ампли-

ческих источников, расположенных в случайном

туды, соответствующие двум поляризациям. Под-

ставив траекторию движения импульса в нулевом

порядке вблизи нас (т.е. на расстояниях, соответ-

порядке, получаем зависимость эйконала ГВ от

ствующих красному смещению z ∼ 0.1-10), либо в

ранней Вселенной на расстояниях, соответствую-

аффинного параметра:

щих красному смещению z > 1500.

Ω(ct - z) = Ω(ct₀ - z₀) + Ωl(1 + n₃).

Плотность энергии в гравитационных волнах

определяется нулевым компонентом псевдотензора

Пусть расстояние от пульсара до наблюдателя

энергии-импульса [33]:

есть L. Тогда время распространения импульса

от источника к наблюдателю из-за действия ГВ

c⁴

∂h_ij ∂h_ij

ε=

меняется и становится равным:

32πG c∂t c∂t

cT = L + R(L).

Здесь 〈〉 означает усреднение (по времени или по

Время импульса в пути есть сумма времени, потра-

реализациям), а по повторяющимся индексам про-

ченного на движение в эвклидовом пространстве

изводится суммирование (i, j пробегают значения

(L), и добавки, которая возникает из-за действия

1, 2, 3). Для стохастического спектра поправки к

гравитационной волны R(L):

метрике (14) будут иметь вид:

∫

(

)

[

(

)

Re{H₁ exp (iψ)}

n²¹ - n²

h₊(t,r) =

d³kH₁(^k)exp i(Ωt -kr) ,

3/2

R(L) =

(15)

(2π)

(1 + n₃)

∫

(

)

]

h_×(t,r) =

d³kH₂(^k)exp i(Ωt -kr)

Re{H₂ exp (iψ)}

2n₁n₂

3/2

sin σ,

(2π)

(1 + n₃)

Для простоты положим, что спектр гравитацион-

σ=

ΩL(1 + n₃), ψ = Ω(ct₀ - z₀) + σ.

ных волн сосредоточен в интервале частот Δf ≈ f

вокруг центральной частоты f. Тогда усредненный

Здесь R(L) — неравномерность прихода импуль-

квадрат остаточного уклонения импульсов пульса-

са пульсара к наблюдателю из-за действия ГВ.

ра будет определяться простой формулой [32]:

Неравномерность прихода импульса пульсара к

208

Gε

R2 =

наблюдателю обозначена R(L), поскольку в аст-

243 π³c²f⁴

рономии пульсаров остаточные уклонения обозна-

Введем стандартное обозначение для плотности

чаются этой буквой. Эта величина зависит как от

энергии ГВ в терминах омега-параметра Ω_gw =

амплитуды ГВ, так и от направления на пульсар. В

3c²

выражение для R(L) входят также величины sin σ

= εε

, где ε_cr =

H², H = 69^кмсМпк — современ-

8πG

и exp (iψ). Они зависят от фазовых величин и по

ное значение параметра Хаббла. Квадрат оста-

модулю не превосходят единицы. Поэтому модуль

точного уклонения тогда можно выразить простой

величины R(L) определяется только величиной

формулой:

амплитуды и периодом ГВ (P = 2π/Ω), а также

⁽f_yr)⁴

направлением на пульсар относительно волнового

= 1.6

Ω_gw.

100 μs

вектора гравитационной волны.

Оценим остаточное уклонение R(L) для ГВ с

Здесь f_yr = 3.17 × 10-8 Гц.

(

)

амплитудой H и периодом P . Пусть

n²¹ - n²²

≈ 1,

n₃ ≈ 0. Тогда

9. КРОСС-КОРРЕЛЯЦИЯ

ХРОНОМЕТРИРОВАНИЯ ПУЛЬСАРОВ

R≈

HP.

КАК МЕТОД ПОВЫШЕНИЯ

ЧУВСТВИТЕЛЬНОСТИ

Оценим чувствительность к детектированию ГВ,

Детектирование гравитационно-волнового сиг-

например, пульсара J1909-3744, одного из самых

нала по одному пульсару ограничено стабильно-

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

136

ЖАРОВ и др.

стью периода пульсара. Даже самые стабильные

n₂(t₀), которые определяются внутренними свой-

пульсары не позволяют детектировать сигнал луч-

ствами каждого пульсара.

ше, чем на уровне

После знака равенства мы переписали это вы-

ражение в виде суммы двух членов. Первое слага-

h= 10-15

емое в хронометрировании каждого из пульсаров

по амплитуде гравитационной волны.

зависит от гравитационной волны и направления

на каждый пульсар RGW1,2 и является детерми-

Поскольку пульсары — небесные тела, то на-

блюдатели не имеют возможности улучшить их ха-

нированной величиной, а второе слагаемое n(t₀)_1,2

рактеристики и, следовательно, повысить чувстви-

зависит только от шума в каждом из пульсаров и

тельность обнаружения сигнала по одному пуль-

является стохастической величиной.

сару. Однако повысить чувствительность можно,

Естественно полагать, что шум тайминга в каж-

наблюдая несколько пульсаров.

дом из пульсаров является некоррелированным.

Кросс-корреляция между таймингом первого и

Повысить чувствительность можно, используя

второго пульсаров есть:

кросс-корреляцию рядов остаточных уклонений

нескольких пульсаров [34]. Поясним на примере

C(τ, t₀) = R₁(t₀ + τ)R₂(t₀) =

алгоритма наблюдения двух пульсаров.

= RGW1(t₀ + τ)RGW2(t₀) +

Гравитационная волна распространяется вдоль

+ RGW1(t₀ + τ)n₂(t₀) +

оси Oz. Пусть направление на первый пульсар

определяется сферическими углами θ₁ и φ₁, а

+ RGW2(t₀)n₁(t₀ + τ) + n₁(t₀ + τ)n₂(t₀).

направление на второй пульсар — соответственно

Первый член зависит только от гравитационной

углами θ₂ и φ₂ .

плоской монохроматической волны, второй, третий

Неравномерность времени прихода импульсов

и четвертый содержат произведения стохастиче-

от первого и второго пульсаров можно обозначить

ских величин. При усреднении все члены, кроме

как:

первого, стремятся к нулю, поскольку средние ве-

H+(t0)

личины от n(t₀)_1,2 полагаются равными нулю, и

R₁(t₀) =

cos 2ϕ₁ (1 - cos θ₁) -

последний член также стремится к нулю, поскольку

H_×(t₀)

шумы двух различных пульсаров являются некор-

sin 2ϕ₁ (1 - cos θ₁) + n₁(t₀) =

релированными.

Поэтому среднее значение коррелятора равно

= RGW1(t₀) + n₁(t₀),

C(τ, t₀) = 〈RGW1(t₀ + τ)RGW2(t₀)〉 =

H+(t0)

R₂(t₀) =

cos 2ϕ₂ (1 - cos θ₂) -

= R2GW(t₀,τ) .

H_×(t₀)

Здесь треугольные скобки означают усреднение

−

sin 2ϕ₂ (1 - cos θ₂) + n₂(t₀) =

(по времени или по реализациям). Дисперсия кор-

= RGW2(t₀) + n₂(t₀).

реляционной функции стремится к нулю при уве-

личении интервала усреднения обратно пропорци-

Здесь неравномерность уже является функцией от

онально длительности интервала усреднения T-1,

времени наблюдения t₀, а величины H₊(t₀) и H_x(t₀)

или обратно пропорционально количеству сеансов

есть действительные части комплексных амплитуд

N измерений времени прихода импульсов. Таким

H₁ exp (iψ) , H₂ exp (iψ).

образом, можно достичь значительно более высо-

кой чувствительности.

Отметим, что величины R(t₀) от каждого из пуль-

При конечном интервале времени усреднения

саров имеют общую часть, которая определяет-

всегда остается остаточный член корреляционной

ся монохроматической волной H₊(t₀) и H_x(t₀),

функции^TM C, который определяет ее шум и опре-

а также множители, которые индивидуальны для

деляет чувствительность метода.

каждого пульсара и зависят от углов θ₁ и φ₁, а

При большом интервале усреднения корреляци-

также θ₂ и φ₂. Кроме того, появляются слагае-

онная функция C не зависит от времени наблюде-

мые n₁(t₀), n₂(t₀), которые также меняют время

ния t₀, а является только от временного сдвига τ.

прихода. Эти слагаемые возникают из-за шума

Кроме того, корреляционная функция C является

тайминга в каждом из пульсаров. Если первые

четной функцией временного сдвига. Остаточный

два слагаемых в выражении для неравномерности

шум^TM C, не обладает такой симметрией, поэтому

прихода импульсов определяются детермирован-

ными величинами — параметрами плоской моно-

можно уменьшить шум еще в 2-1/2, рассматривая

хроматической гравитационной волны, а также на-

четную корреляционную функцию [34]:

правлением на пульсары, — то третьи слагаемые

(C(τ) - C(-τ)) .

определяются стохастическими величинами n₁(t₀),

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

137

Таким образом, при использовании, скажем,

Предположим, что мы хотим зарегистрировать гра-

100

сеансов измерений времени прихода им-

витационное излучение от сверхмассивных двой-

пульсов с помощью кросс-корреляции тайминга

ных черных дыр. Одним из таких гипотетических

двух равноточных пульсаров, можно повысить

объектов является OJ 287. Предполагают, что ме-

чувствительность в 10 раз.

ханизм активности OJ 287 — двойная черная дыра

с массами 18 миллиардов солнечных масс, а второй

компонент — черная дыра с массой 150 миллионов

10. ИСТОЧНИКИ

солнечных масс. Красное смещение этого объекта

ГРАВИТАЦИОННЫХ ВОЛН

составляет 0.3, что соответствует болометрическо-

Теперь рассмотрим процесс излучения гравита-

му расстоянию 1.56 Гпк.

ционных волн как монохроматическими источни-

Для сверхмассивных двойных черных дыр вели-

ками, так и источниками с широким спектром и

чина h₀ есть:

стохастическими характеристиками.

Вначале в качестве источника рассмотрим двой-

⁽m_ch)5/3 (f_GW )2/3 1 Гпк

h₀ = 1.22 × 10-30

ную звездную систему. Такая система может со-

m_⊙

f1y

стоять из обычных звезд или вырожденных звезд:

белых карликов, нейтронных звезд или черных дыр,

“Chirp mass” для объекта подобного OJ 287 есть

в частности сверхмассивных черных дыр.

1 миллиард солнечных масс. Предположим, что

период такого двойного объекта есть 2 года, тогда

10.1. Гравитационные волны от двойных звезд

h₀ = 4.9 × 10-16.

Частота гравитационной волны, излучаемой

Даже если полагать, что амплитуды двух поляри-

двойной звездной системой, вдвое больше частоты

заций совпадают с оценкой для h₀, обнаружить

самой системы:

такую гравитационную волну с помощью тайминга

√

только по одному из пульсаров невозможно. Од-

f_GW =

нако, применяя кросс-корреляционный метод по

π a³

нескольким малошумящим пульсарам, это сделать

Здесь m — сумма масс звезд, a — большая полу-

можно.

ось системы. Частота гравитационной волны яв-

ляется функцией времени, поскольку из-за потери

энергии на гравитационное излучение двойная си-

10.2. Космологические гравитационные волны

стема уменьшает свой период. Предположим, что

эксцентриситет системы равен нулю, тогда ампли-

Наша Вселенная расширяется. В расширяю-

туды двух поляризаций гравитационных волн от

щейся Вселенной гравитационные волны претер-

двойной системы определяются как [35]:

певают эволюцию, которую сейчас мы кратко опи-

шем. Так же, как и у электромагнитной волны, у

1 + cos2 ι

гравитационной волны меняется частота, она уве-

h₊ = h₀

cos Φ (t - R/c) ,

(16)

личивается, испытывает красное смещение. Ам-

h_× = h₀ cos ιcos Φ (t - R/c),

плитуда гравитационной волны, соответственно,

(

)

будет адиабатически убывать.

2π²

h₀ =

^GW .

Любая волна, не исключая гравитационную, это

c³ R

колебательный процесс, который характеризует-

ся периодом. Если с момента Большого Взрыва

Здесь ι — угол наклона плоскости орбиты двой-

времени прошло меньше, чем период волны, то

ной системы, Φ — фаза системы, которая является

гравитационная волна еще не успела совершить

функцией времени:

однократное колебание и, следовательно, для на-

∫^t

блюдателя такая волна будет выглядеть “застыв-

(

)

Φ (t) = 2π f_GW

t^′′

шей неравномерностью” пространства-времени.

В космологии выделяется момент времени, ко-

гда гравитационная волна приобретает свойства

m_ch — “chirp mass”, R — расстояние до системы.

волнового процесса. Этот момент времени называ-

По определению “chirp mass”, выраженная в гео-

ется моментом выхода волны из-под горизонта ча-

метрических единицах, есть

стиц и, очевидно, определяется равенством длины

волны размеру горизонта частиц (т.е. длине свето-

2G (m₁m₂)

m_ch =

вого пути с момента начала расширения Вселенной

c² (m₁ + m₂)

после Большого взрыва).

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

2019

№2

138

ЖАРОВ и др.

В ранней Вселенной предсказывается суще-

Плотность энергии ε_g гравитационного излуче-

ствование двух видов стохастического гравитаци-

нии будет меньше плотности энергии ε_γ = 4 ×

онного излучения. Первый вид порождается нуле-

× 10-13 эрг см-3 реликтового электромагнитного

выми колебаниями гравитационного поля на ста-

излучения, если амплитуда волн в момент излуче-

дии инфляции [36, 37]. В результате порождаются

ния меньше единицы: ε_g

≈ h^2gε_γ. Из указанных

космологические гравитационные волны с очень

выше формул очевидно следует, что когда темпе-

широким спектром от 10-18 Гц до 100 МГц. В

ратура во Вселенной составляла величину в интер-

каждом бине со средней частотой f и полосой Δf ∼

вале от 10³ до 10⁴ ГэВ, генерируемые в ту эпоху

∼ f содержится одинаковое количество энергии.

гравитационные волны сегодня как раз попали бы

Амплитуда гравитационной волны на длине, равной

в диапазон детектора LISA, от 10-4 до 10-5 Гц.

размеру горизонта, в момент выхода из-под гори-

Другими словами, следы каждой космологической

зонта есть

эпохи сохраняются в виде гравитационного излу-

H_inf

h∼

чения определенной частоты.

m_pl

Для такого чудовищно широкого диапазона ча-

Здесь H_inf — величина параметра Хаббла на ин-

стот — от 10⁴³ Гц до 10-18 Гц — необходимы, оче-

фляционной стадии, m_pl = 1.2 × 10¹⁹ ГэВ — масса

видно, разные детекторы.

Планка. Из этой формулы видно, что, измеряя ам-

Детекторы типа LIGO — лазерные интерферо-

плитуду гравитационных волн на различных длинах

метры — эффективны для регистрации волн с дли-

волн, можно измерять параметр Хаббла в течение

ной порядка размеров своего “плеча”, т.е. расстоя-

инфляционной стадии эволюции Вселенной.

ния между антеннами. Если такой размер должен

быть порядка нескольких световых лет или даже

Рассмотрим теперь второй вид стохастического

больше, то необходимы соответствующие космиче-

гравитационного излучения, которое может гене-

ские конструкции.

рироваться в ранней Вселенной. Во время эво-

люции вещество может образовывать нестацио-

Проекты LISA (Laser Interferometer Space

нарный контраст плотности. В том случае, когда

Antenna) и TIANQIN

[41] (китайский проект

локально появляется переменный квадрупольный

“Небесная лира”) сходны с проектами LIGO.

момент в распределении контраста плотности, бу-

В них также используются свободные массы,

дут излучаться гравитационные волны [38-40].

удаленные на большое расстояние, и лазерный

интерферометр для измерения малых вариаций

Обозначив амплитуду излученной волны h_g, бу-

расстояния, вызванных гравитационными волнами.

дем считать, что эта амплитуда соответствует мо-

менту, когда длина гравитационной волны срав-

Различие этих проектов — в величине расстоя-

нивается с текущим горизонтом частиц Вселенной

ния между антеннами (10⁵ км для TIANQIN, что

(λ_g = H_g). Будем также полагать, что температура

на 5 порядков больше, чем у наземных антенн), и

окружающей плазмы в этот момент есть T_g.

в различии в рабочем диапазоне частот: от 10-5 до

В современную эпоху амплитуда излучения h₀

10-2 Гц, что много ниже соответствующих величин

связана с амплитудой h_g и температурой T_g из-

для LIGO. Таким образом, эти проекты рассчитаны

лучения плазмы в ранней Вселенной следующим

на совершенно другие типы источников. Пробные

массы — это три спутника, которые находятся на

образом:

орбите вокруг Земли (TIANQIN) или вокруг Солн-

h₀ = (5 × 10-13)h_g1 ГэВ/T_g.

ца (LISA).

С другой стороны, очень длинные гравитаци-

Энергетическая величина 1 ГэВ примерно соответ-

онные волны, с длиной волны в несколько све-

ствует 10¹³ К. В современную эпоху частота f₀

товых лет, тоже можно детектировать с помощью

(в Гц) есть:

интерферометров. Так, если в качестве источника

f₀ = (10-8)T_g/1 ГэВ.

радиоизлучения принять пульсар, то размер плеча

полученного интерферометра будет равен расстоя-

Так, процессы в ранней Вселенной, происходив-

нию до пульсара. Пульсар — это нейтронная звез-

шие, к примеру, при температурах T_g = 10¹¹ ГэВ,

да в нашей Галактике, которая является источни-

будут доступны на частотах 1000 Гц. Такие часто-

ком радиоимпульсов. Период следования импуль-

ты могут быть зарегистрированы интерферометром

сов обладает очень большой стабильностью: ста-

LIGO. Связь частоты f₀ и амплитуды h₀ излучения,

бильность периода некоторых пульсаров сравнима

регистрируемого в современную эпоху, и амплиту-

со стабильностью лучших земных часов, а стабиль-

ды h_g излучения плазмы в ранней Вселенной:

ность так называемых миллисекундных пульсаров

даже превосходит земные часы. Поэтому вместо

h₀ = (5 × 10-21)h_g1 Гц/f₀.

излучения лазера можно использовать излучение

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

139

пульсара. Эта схема детектирования гравитацион-

PPTA, EPTA и NANOGrav, целью которых бы-

ных волн была предложена М.В. Сажиным. Совре-

ло не только прямое обнаружение гравитационно-

менная точность наблюдений пульсаров позволяет

волнового фона, но и построение пульсарной шка-

достичь точности измерений амплитуды возмуще-

лы времени и уточнение планетных эфемерид.

ний метрики порядка 3 × 10-16 в интервале перио-

На момент выхода работы [42] в России уже

дов от 1 года до 3 лет. При условии использования

были накоплены долговременные ряды тайминга

корреляционных схем можно повысить чувстви-

нескольких миллисекундных пульсаров [43]. Пред-

тельность на два порядка.

ложенный метод с модификациями был применен

Наконец, рассмотрим способы детектирования

к имеющимся рядам остаточных уклонений ше-

гравитационных волн с периодом порядка возраста

сти миллисекундных пульсаров и действительно

нашей Вселенной. Для этого нам надо выбрать

позволил обнаружить искомую корреляционную

излучатель, расположенный на расстоянии, равном

функцию на статистически значимом уровне [44,

произведению скорости света на возраст Вселен-

45].

ной. Это поверхность последнего рассеяния (о ко-

Полученный результат имеет множественную

торой мы упоминали выше). Правда, в отличие от

интерпретацию. Первая, наиболее интересная,

других способов детектирования гравитационных

заключается в том, что гравитационно-волновой

волн, здесь мы не можем наблюдать переменно-

сти сигнала во времени — слишком уж длительный

фон действительно был обнаружен в диапазоне 3 ×

период. Но мы можем наблюдать “застывшую”

× 10-9 Гц. Полученная коррелированная амплиту-

картинку на небесной сфере. Для такой задачи

да вариаций ∼0.5 мкс на частоте 3 × 10-9 Гц соот-

астрономы должны исследовать анизотропию и

ветствует безразмерной амплитуде гравитационной

поляризацию реликтовых фотонов.

волны 2 × 10-15 и при пересчете в относитель-

Вместо заключительных слов еще раз отметим,

ную плотность стохастического гравитационно-

что из-за чрезвычайно слабого взаимодействия

волнового фона дает величину Ω_gh² = 3 × 10-9,

гравитационных волн с веществом, этот вид из-

что превышает ожидаемые теоретические оценки,

лучения может служить как новый телескоп для

поэтому такие данные стоит воспринимать только

изучения глубинных свойств материи и нашей Все-

как верхний предел на гравитационно-волновой

ленной. От первых мгновений новорожденной Все-

фон.

ленной до нас могут доходить только гравитаци-

Второе возможное объяснение состоит в том,

онные волны. Любые другие виды излучения будут

что характерная форма угловой корреляционной

поглощены чудовищной толщей горячего вещества.

функции математически получается из квадру-

Только гравитационные волны могут донести до

польной зависимости принимаемого с неба сиг-

нас свойства Вселенной в эти первые мгновения ее

нала. Квадрупольную же зависимость имеет не

жизни.

только гравитационно-волновой сигнал, но и ряд

Дальнейшее развитие идея использования

других эффектов. В первую очередь на такую

пульсаров для детектирования гравитационных

роль подходит задержка пульсарного сигнала при

волн получила в работе [42]. В этой работе авторы

прохождении гелиосферной мантии, которая имеет

предложили экспериментально измерить угловую

каплевидную форму, определяемую обтеканием

корреляционную функцию, выведенную теорети-

гелиосферы звездным ветром. Из-за отличия

чески в статье [34] путем кросс-корреляции рядов

формы гелиосферной мантии от сферической в

остаточных уклонений пульсаров от примерно два-

задержке радиосигнала от источника возникает

дцати пульсаров. Если экспериментальные данные

квадрупольный член, который проявляется при

совпадут с наперед заданной точностью и уровнем

кросс-корреляционном анализе данных. Этот член

достоверности с предвычисленной теоретической

может симулировать сигнал от гравитационно-

кривой, то это, по мнению авторов, будет означать

волнового шума.

прямое обнаружение гравитационных волн. Этот

метод позиционировался как предназначенный, в

В работе [46] рассматривалось излучение грави-

первую очередь, для детектирования стохастиче-

тационных волн сверхмассивными двойными чер-

ского гравитационно-волнового фона, вызванно-

ными дырами, которое формируется во время слия-

го реликтовым волнами или же суперпозицией

ния галактик. Это источники гравитационных волн

гравитационно-волновых всплесков, вызванных

в ближней (z < 10) Вселенной. Стохастическая

слияниями массивных объектов (черных дыр,

суперпозиция гравитационных волн от всех таких

нейтронных звезд) во Вселенной.

двойных систем модулирует время прихода им-

Основываясь на этой идее, в мире были нача-

пульсов от пульсаров. Использование данных на-

ты программы одновременного хронометрирования

блюдений миллисекундных пульсаров, полученных

миллисекундных пульсаров, среди которых следует

на радиотелескопе Паркса, позволило получить

отметить уже упоминавшиеся в статье проекты

верхнее ограничение на амплитуду этого фона, A <

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

140

ЖАРОВ и др.

1.0 × 10-15, с достоверностью 95%. Это ограни-

не только для построения новой шкалы време-

чение исключает предсказанные модели для эво-

ни, для детектирования гравитационных волн в

люции двойных черных дыр в центрах галактик с

наногерцовом диапазоне частот, но также и для

вероятностью 91-99.7%.

детектирования темной материи, которая должна

содержаться в нашей Галактике.

Хотя в результате этого эксперимента не были

детектированы гравитационные волны, исследова-

В работе Сажина [53] впервые было предложено

тели разрабатывают новые проекты, направлен-

детектировать темные тела нашей Галактики по

ные на детектирование гравитационных волн мето-

влиянию возникающего эффекта слабого грави-

дом пульсарного хронометрирования [47]. Астро-

тационного микролинзирования на хронометриро-

номы полагают, что объединение проектов IPTA,

вание пульсаров. Массивное тело (звезда, черная

NANOGrav, EPTA и PPTA позволит значительно

дыра или облако темной материи), которое про-

повысить чувствительность метода, что позволит

летает недалеко от линии пульсар-наблюдатель,

зарегистрировать гравитационные волны в этом

создает задержку во времени прихода сигналов

диапазоне частот. В частности, обсуждаются дан-

пульсара к наблюдателю. Более подробное иссле-

ные трех обзоров PPTA, EPTA и NANOGrav для

дование эффекта микролинзирования было про-

детектирования гравитационных волн [48].

ведено в 1995 г. в работе [54]. Было показано,

Помимо детектирования “почти” монохромати-

что влияние эффекта микролинзирования вызовет

ческих гравитационных волн от двойных систем и

быстрый рост ОУ МПИ и последующую релак-

накопления сигнала от стохастических гравитаци-

сацию к невозмущенному значению. Влияние эф-

онных волн, было предложено много других приме-

фекта будет значительным на протяжении несколь-

нений использования хронометрирования пульса-

ких лет, и максимальная амплитуда отклонений

ров для детектирования транзиентных источников

МПИ составит ∼20-30 мкс, при условии, что

типа всплесков. В статье [49] был предложен новый

гравитационная линза обладает значительной мас-

метод наблюдения сигнатуры слияний сверхмас-

сой и пролетает на небольшом расстоянии от ли-

сивных черных дыр. Этот метод основан на обна-

нии пульсар-наблюдатель (∼10 мс дуги). События

ружении определенного типа гравитационных волн,

микролинзирования, вызываемые пролетами линз

а именно гравитационного всплеска волны с памя-

на небольшом расстоянии, очень редки, но очевид-

тью, с использованием синхронизации хрономет-

но, что в той или иной степени пульсары подвер-

рирования пульсаров. Показано, что современная

жены влиянию эффекта слабого микролинзирова-

точность синхронизации пульсаров позволяет об-

ния, вызванного пролетом линз на значительном

наруживать “всплески с памятью” за счет слияний

расстоянии от линии пульсар-наблюдатель. Было

сверхмассивных черных дыр с расстояний до 1 Гпк.

также предложено использовать влияние эффекта

Был также предложен метод исследования гра-

при хронометрировании миллисекундных пульса-

витационного волнового фона в диапазоне частот

ров для детектирования MACHO [55]. Увеличение

10-12-10-8 Гц [50]. Этот метод основан на точных

числа наблюдаемых пульсаров и временной про-

измерениях параметров вращения пульсара. Гра-

должительности серий наблюдений позволит на-

витационные волны влияют на эти параметры, и,

деяться на обнаружение МАСНО. Были сделаны

следовательно, можно сделать выводы о плотности

численные оценки: для пульсара на расстоянии

энергии этих волн. Получены ограничения на плот-

несколько кпк, наблюдающегося на протяжении

ность гравитационного волнового фона: Ω_gw < 2 ×

10 лет с точностью 10 нс оптическая толща по мик-

ролинзированию будет достигать величины 0.1 [56].

× 10-6.

В некоторых расширенных теориях гравита-

Влияние эффекта слабого гравитационного

ции появляется узкополосный гравитационно-

микролинзирования на хронометрирование пуль-

саров было рассмотрено при более реальных

волновой шум. Гравитон в таких моделях явля-

ется массивной частицей. Из хронометрирования

предположениях в [57]. Было показано, что оста-

точные уклонения моментов прихода импульса,

пульсаров можно установить сильные ограничения

на такие теории гравитации [51]. Кроме того,

вызванные влиянием эффекта, для пульсара

по хронометрированию пульсаров можно сделать

В1937+21

составят величину порядка

нс,

сильное ограничение на скорость распространения

если продолжительность наблюдений будет около

гравитационных волн [52].

20 лет. Также было показано, что при будущих

наблюдениях на SKA (Square Kilometer Array)

пульсаров, расположенных за балджем, величина

11. ДЕТЕКТИРОВАНИЕ ТЕМНОЙ

из-за эффекта составит несколько микросекунд за

МАТЕРИИ С ПОМОЩЬЮ ПУЛЬСАРОВ

те же 20 лет.

Тайминг пульсаров обладает высокой точно-

По хронометрированию пульсаров можно также

стью определения времени прихода импульсов, та-

ограничить космологическую плотность таких

кой физический механизм может использоваться

экзотических объектов, как космические струны

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

ПУЛЬСАРНАЯ ШКАЛА ВРЕМЕНИ

141

в виде петель, используя два наблюдательных

деленный на сто дней, σ₁₅₀ — дисперсия скоростей

признака — гравитационное микролинзирование и

частиц темной материи, деленная на 150 км/с.

эффект Кайзера-Стеббинса. Данные пульсарной

Сравнивая эти предсказания с измерениями,

хронометрии обеспечивают наиболее строгие огра-

можно вывести модельно независимые пределы

ничения на обилие легких струн [58].

плотности темной материи на разных расстояниях

Теперь мы рассмотрим предположение Хмель-

D от центра Галактики. Например, наблюдения

ницкого и Рубакова о темной материи в виде ска-

пульсара J1713+0747 накладывают верхний пре-

лярного поля [59]. Такая модель помогает решить

дел ρ_DM ≲ 10⁵ Гэв/см³ при D ≈ 7 кпк. Обнару-

многие задачи на масштабе меньше, чем галакти-

жение двойного пульсара, который находится на

ческие масштабы. Поле состоит из ультра-легких

расстоянии в D ≲ 10 пк от центра Галактики, поз-

частиц с массой в диапазоне 10-22-10-23 эВ. Ко-

волит вывести профиль темной материи в центре

лебания такого поля вызывает переменный грави-

и наложить сильные ограничения на модели роста

тационный потенциал, который, в частности, воз-

центральной черной дыры.

действует на тайминг пульсаров. Авторы полагают,

Современные модели темной материи в нашей

что вызываемые амплитуды переменности метрики

Галактике предсказывают значительно менее плот-

составляют порядка 10-15. В работе [60] проана-

ное распределение темной материи в нашей Галак-

лизирован тайминг пульсаров проекта NANOGrav,

тике. Так, DD модель темной материи, выведенная

который выложен в интернет и доступен для ана-

по звездной кинематике, в случае толстого диска

лиза. Н. Порайко и К. Постнов получили значимые

предсказывает плотность темной материи и дис-

верхние пределы на величину метрики h_c < 4 ×

персию скоростей частиц:

× 10-15 на частоте монохроматических колебаний

ρDM0 ≤ 3 ГэВ/см³,

поля f = 1.75 × 10-8 Гц.

σ ≤ 9 км/с.

В работе [25] получены сходные по амплитуде

оценки вариаций гравитационного потенциала, ос-

Здесь верхний индекс DM означает сокращение от

нованные на величине относительной нестабиль-

Dark Matter (темная материя).

ности σ_z рядов хронометрирования пульсаров, на-

В случае тонкого диска

блюдавшихся в Парксе (Австралия).

Другие идеи детектирования темной материи в

ρDM0 ≤ 12 ГэВ/см³,

нашей Галактике связаны с наблюдениями двойных

σ ≤ 2 км/с.

пульсаров [60, 61]. Во время движения двойного

пульсара в Галактике на него могут влиять частицы

При этом дисперсия скоростей также значительно

темной материи посредством динамического тре-

меньше, что позволяет надеяться на проверку DD

ния. Можно показать, что этот эффект производит

модели темной материи на двойных пульсарах в

характерную модуляцию орбиты и вызывает ве-

ближайшем будущем.

ковое изменение орбиты. Изменения орбитального

периода находятся в пределах точности наблюде-

12. ЗАКЛЮЧЕНИЕ

ний. Для двойных систем с орбитальным периодом

более суток найдены соответствующие зависимо-

После краткого обзора методов построения

сти основных орбитальных параметров. Изменение

ПШВ и применения этой шкалы для решения

периода двойной системы зависит от многих па-

астрономических и физических задач, резюмируем

раметров задачи: сечения взаимодействия частиц

основные цели и приложения этой проблемы

темной материи с барионным веществом, диспер-

для решения астрономических задач, а также

сии скоростей частиц темной материи, периода

астрофизических, космологических и задач фунда-

двойной системы, галактической скорости двойной

ментальной физики.

системы, масс звезд в системе, плотности частиц

Одно из главных преимуществ хронометриро-

темной материи вокруг двойного пульсара и т.п. В

вания пульсаров для классической астрономии

достаточно простом случае изменение периода из-

заключается в возможности точного определения

за динамического трения определяется формулой:

ориентации осей динамических систем отсчета от-

носительно друг друга и относительно кинемати-

μ₁λ₂₀ρGCDMP100b

ческой системы отсчета. Эта ориентация плохо

≈ -3 × 10-14

σ³

определяется традиционными методами астроно-

150

m₁m₂

мии. Пульсарные измерения имеют потенциальную

здесь μ₁ =

— приведенная масса в

(m₁+m₂) M_⊙

точность 0.1 мс дуги.

солнечных единицах, λ₂₀ — кулоновский лога-

Детектирование сверхмассивных двойных чер-

рифм, ρ^GCDM — плотность темной материи в галак-

ных дыр в центрах галактик посредством детек-

тическом центре, P100b — период двойной системы,

тирования гравитационных волн от них открывает

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019

142

ЖАРОВ и др.

для астрофизики возможности изучения эволюции

21.

К. Одуан, Б. Гино, Измерение времени. Основы

таких объектов, частоты и механизмов слияния

GPS (Москва, Техносфера, 2002).

галактик.

22.

М. В. Сажин, Измерительная техника № 1, 27

(1989).

Детектирование стохастического гравитацион-

ного излучения от ранних стадий эволюции нашей

23.

D. N. Matsakis, J. H. Taylor, and T. M. Eubanks,

Astron. and Astrophys. 326, 924 (1997).

Вселенной, несомненно, принесет важную инфор-

24.

J. P. W. Verbiest, M. Bailes, W. A. Coles, G. B. Hobbs,

мацию об эволюции ранней Вселенной.

et al., Monthly Not. Roy. Astron. Soc. 400, 951

Наконец, хронометрирование пульсаров позво-

(2009).

ляет изучать темную материю внутри нашей Га-

25.

А. Е. Родин, В. А. Федорова, Aстрон. журн. 95, 401

лактики. При повышении точности хронометриро-

(2018).

вания в несколько раз, можно будет обнаружить

26.

G. B. Hobbs, W. Coles, R. N. Manchester, et al.

влияние темной материи, а для некоторых моделей

Monthly Not. Roy. Astron. Soc. 427, 2780 (2012).

темной материи определить также ее природу.

27.

G. Hobbs, A. G. Lyne, and M. Kramer, Monthly Not.

В работе использовались материалы исследо-

Roy. Astron. Soc. 402, 1027 (2010).

ваний, полученные на радиотелескопах ДКР-1000

28.

Ю. П. Илясов, С. М. Копейкин, А. Е. Родин,

Письма в Aстрон. журн. 24, 275 (1998).

и БСА ФИАН.

29.

М. В. Сажин, Aстрон. журн. 55, 65 (1978).

30.

М. В. Сажин, Астрон. цирк. № 1002, 1 (1978).

СПИСОК ЛИТЕРАТУРЫ

31.

M. V. Sazhin, Sov. Astron. 22, 36 (1978).

В. Е. Жаров Сферическая астрономия (Фрязи-

32.

S. Detweiller, Astrophys. J. 234, 1100 (1979).

но, Век-2, 2006).

33.

Л. Д. Ландау, Е. М. Лифшиц Теория поля (М.,

D. G. Matei, T. Legero, S. H ¨afner et al. Phys. Rev.

Наука, 1988).

Lett. 118, id.263202 (2017).

34.

R. W. Hellings and G. S. Downs, Astrophys. J. 265,

L39 (1983).

13th CGPM

1967/68, Resolution

1, URL

https://www.bipm.org/en/publications/si-

35.

http://www.tapir.caltech.edu/∼teviet/Waves/gwave

_details.html

brochure/ second.html

36.

А. А. Старобинский, Письма в ЖЭТФ 30, 719

B. N. Taylor and P. J. Mohr, EEE Trans. Instr. Meas.

(1979).

50, 563 (2001).

A. Hewish, S. J. Bell, and J. D. H. Pilkington, Nature

37.

V. A. Rubakov, M. V. Sazhin, and A. V. Veryskin,

217, 709 (1968).

Phys. Lett. B. 115, 189 (1982).

Р. Манчестер, Дж. Тэйлор, Пульсары (М.: Мир,

38.

D. V. Deryagin, D. Yu. Grigoriev, V. A. Rubakov, and

1980).

M. V. Sazhin, Modern Phys. Lett. A 1, 593 (1986).

The

ATNF pulsar

database.

URL.

39.

D. V. Deriagin, D. Iu. Grigor’ev, V. A. Rubakov, and

http://www.atnf.csiro.au/people/pulsar/psrcat/

M. V. Sazhin, Monthly Not. Roy. Astron. Soc. 229,

357 (1987).

B. Kiziltan, A. Kottas, M. DeYoureo et al., Astrophys.

J. 778, id. 66 (2013).

40.

M. V. Sazhin, in Proceedings of the Friedmann

A. Shostak, Pulsar Communication System. Пат.

Centenary Conference, held in Leningrad, USSR,

№ 3550002 США. 1970.

June 22-26, 1988. Ed., M. A. Markov, V. A. Berezin,

10.

D. C. Backer, S. R. Kulkarni, C. Heiles et al., Nature

V. F. Mukhanov; Publisher, World Scientific Pub. Co.

300, 615 (1982).

1990. P. 147.

11.

В. Г. Ильин, Ю. П. Илясов, А. Д. Кузмин и др.,

41.

L. Jun, Ch. Li-Sheng, D. Hui-Zong, et al., Class.

Измерительная техника № 12, 34 (1983).

Quantum Grav. 33, 035010 (2016).

12.

В. Г. Ильин, Ю. П. Илясов, А. Д. Кузмин и др.,

42.

F. A. Jenet, G. B. Hobbs, K. J. Lee, and

Докл. АН 275, 835 (1985).

R. N. Manchester, Astrophys. J. 625, L123 (2005).

13.

Ю. П. Илясов, А. Д. Кузьмин, Т. В. Шабанова,

43.

Yu. P. Ilyasov, V. V. Oreshko, V. A. Potapov, and

Ю. П. Шитов, Труды ФИАН 199, 149 (1988).

A. E. Rodin, in Young Neutron Stars and Their

14.

G. S. Bisnovatyi-Kogan, J. Phys. Stud. 11, 450

Environments, IAU Symposium no. 218, held as

(2007).

part of the IAU General Assembly, 14-17 July,

15.

G. S. Bisnovatyi-Kogan, Mem. S. A. It. 81, 258

2003

in Sydney, Australia. Edited by Fernando

(2010).

Camilo and Bryan M. Gaensler. San Francisco, CA:

16.

A. E. Rodin, Chinese J. of Astron. and Astrophys.

Astronomical Society of the Pacific, 2004, p. 433

Suppl. 6, 157 (2006).

44.

A. E. Rodin, AIP Conf. Proc. 1357, 81 (2011).

17.

A. E. Rodin, Monthly Not. Roy. Astron. Soc. 387,

45.

А. Е. Родин, Астрон. журн. 88, 152 (2011).

1583 (2008).

46.

R. M. Shannon, V. Ravi, L. T. Lentati, et al., Science

18.

А. Е. Родин, Д. Чен, Aстрон. журн. 88, 677 (2011).

349, 1522 (2015).

19.

Ж. Рютман, ТИИЭР 66 (9), 70 (1978).

47.

G. H. Hobbs and S. Dai, National Science Review 4,

20.

D. N. Matsakis and F. J. Josties, Proc. of the Precise

707 (2017).

Time and Time Interval Meeting (PTTI) 9 (28), 225

48.

X. Zhu, L. Wen, G. Hobbs, R. N. Manchester,

(1996).

R. M. Shannon, препринт arXiv:1509.06438v1, 2015.

АСТРОНОМИЧЕСКИЙ ЖУРНАЛ том 96

№2

2019