Автоматика и телемеханика, № 1, 2019

Нелинейные системы

П.В. ЛЫСЕНКО (pashlys@yandex.ru),

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ОПТИМАЛЬНОЕ ПО ЭНЕРГИИ УПРАВЛЕНИЕ

ГАРМОНИЧЕСКИМ ОСЦИЛЛЯТОРОМ¹

Решается задача оптимального управления гармоническим осциллято-

ром. В качестве критерия оптимизации выбрано значение энергии осцил-

лятора в конечный момент времени. Находятся оптимальное управление

и оптимальное значение энергии как функции этого момента времени. По-

лученный результат сравнивается с решением задачи оптимального быст-

родействия при приведении осциллятора в состояние покоя.

Ключевые слова: оптимальное управление, принцип максимума Понтря-

гина, гармонический осциллятор.

DOI: 10.1134/S0005231019010021

1. Введение

Решение задачи оптимального управления гармоническим осциллятором

является одним из важнейших и показательных результатов, полученных в

теории оптимального управления. В данной статье исследуются задачи оп-

тимального управления осциллятором, изначально находящимся в состоянии

покоя, по критерию, максимизирующему конечную энергию системы в фик-

сированный момент времени T . Критерий может быть записан в интеграль-

ном виде

∫T

(1.1)

J = E(T) =

dt -→ max .

Известно, что эта задача схожа с задачей быстродействия D.W. Bushaw, опи-

санной в [1], однако до сих пор не рассматривалась, хотя ее решение может

представлять научный и практический интерес. Кроме того, в статье будет

произведено сравнение оптимальных решений в обеих указанных задачах.

До открытия принципа максимума Понтрягина задача быстродействия

для приведения гармонического осциллятора в нулевую точку представля-

ла собой серьезное испытание для математиков того времени. Полученное в

диссертации D.W. Bushaw 1952 г. решение этой задачи было настолько гро-

моздким, что Р.В. Гамкрелидзе в [2] написал: “Результат, без доказательства,

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фунда-

ментальных исследований (проект № 16-08-01285 а).

достиг Москвы в 1953 г., и два ведущих специалиста в области (управления),

в Научно-исследовательском институте системных исследований АН СССР,

не смогли восстановить (получить) доказательство”.

Задачи управления как одиночным осциллятором, так и группой осцилля-

торов привлекали внимание исследователей по причине простоты постановок

и сложности получаемых решений.

В [1] приведено одно из первых решений задачи быстродействия для при-

ведения осциллятора в нулевую точку при симметричном двустороннем огра-

ничении на управление с помощью принципа максимума Понтрягина, осно-

ванное на анализе фазовых траекторий системы. В [3] на фазовой плоскости

приводится вид всех оптимальных траекторий, они имеют форму спирали с

конечным числом переключений. Однако значение функционала как функ-

ции начального положения осциллятора не приводится. Аналитическое реше-

ние для программного управления задачи быстродействия одиночным осцил-

лятором получено в [4], где был исследован случай воздействия ограничен-

ного одностороннего управления и решена задача оптимального управления

осциллятором с целью его полной остановки по двум критериям качества: по

критерию минимального времени и критерию минимума импульса, передан-

ного системе управляющим устройством.

Задача управления несколькими осцилляторами описана академиком

Ф.Л. Черноусько в [5]. Там же доказана управляемость системы, состоящей

из n осцилляторов, и приведен алгоритм решения для задачи симметричного

разгона двух маятников. Аналитического решения в общем виде получить

не удалось. Для системы несинхронных маятников в [6] получен алгоритм

решения задачи оптимального быстродействия.

Помимо критерия быстродействия, наиболее популярными критериями

являются

∫T

J_k =

|u(t)|^kdt, k = 1, 2.

Критерий J₁ отвечает минимуму переданного системе импульса, а J₂ - ми-

нимальному расходу энергии при управлении.

Отдельный класс задач составляют задачи построения областей достижи-

мости для управляемых систем [7]. Граничные точки множества достижимо-

сти для одиночного осциллятора могут быть получены вследствие решения

задачи оптимального управления с фиксированными временем и одной из

обобщенных координат по критерию максимума другой координаты.

2. Постановка задачи оптимального управления

Рассматривается линейный осциллятор, управляемый с помощью ограни-

ченной по величине силы. Уравнения динамики системы имеют вид

{

˙q(t) = p(t),

(2.1)

p(t) = -ω²q(t) + u(t),

где q - положение маятника, а p - его импульс, ω - частота колебаний.

Считаем, что на скалярное управление (силу) наложено симметричное

ограничение

|u| ≤ ε.

Поскольку в начальный момент осциллятор покоится, то начальные усло-

вия для (2.1) нулевые:

q(0) = 0,

(2.2)

p(0) = 0.

Требуется найти оптимальный закон управления u^∗(t) такой, что по ре-

шению системы (2.1) с начальными условиями (2.2) достигается максимум

критерия (1.1).

3. Решение задачи

3.1. Принцип максимума

Известно, что энергия осциллятора равна

ω²q(t)

p(t)²

E(t) =

Преобразуем выражение для критерия (1.1) с использованием уравнений ди-

намики (2.1) и получим, что критерий принимает вид

∫T

∫

J =

dt = (ω²q

˙q + pp)dt = (ω²qp + p(-ω²q + u))dt =

∫T

= pudt -→ max .

Для каноничности переобозначим выражение, устремив критерий к миниму-

му, а именно:

∫T

(3.1)

J = - pudt -→ min.

Далее для решения задачи оптимального управления (2.1)-(3.1) используем

принцип максимума Понтрягина. Функция Понтрягина записывается как

(3.2)

H(q, p, Ψ₁, Ψ₂, u) = Ψ₁p - Ψ₂ω²q + Ψ₂

u + pu.

Поскольку искомое u^∗(t) должно максимизировать H, следовательно за-

кон оптимального управления имеет вид

(3.3)

u^∗(t) = ε sign(Ψ₂

(t) + p(t)).

Уравнения для сопряженных переменных записываются как

{

Ψ₁ = ω²Ψ₂,

(3.4)

Ψ₂ = -Ψ₁ - u.

Теперь обратим внимание, что поскольку решаемая задача с фиксирован-

ным временем и свободным правым концом, то имеют место такие условия

трансверсальности:

^{ Ψ₁(T) = 0,

(3.5)

Ψ₂(T) = 0.

Далее совершим линейную замену переменных

^{ Ψ₁ =Ψ_I -ω²q,

(3.6)

Ψ₂ = Ψ_II - p

и п одставим в (3.4). Получим новую систему для сопряженных переменных

{

Ψ_I - ω²

˙q = ω²(Ψ_II - p),

Ψ_II - p = -Ψ_I + ω²q - u.

Учет (2.1) приводит последнюю систему к виду, в котором нет зависимости

от обобщенных координат и управления, а именно:

{

Ψ_I = ω²Ψ_II,

(3.7)

Ψ_II = -Ψ_I.

Общим решением системы (3.7) являются гармонические функции с неиз-

вестными амплитудой A > 0 и фазой φ:

^{ Ψ_I = ωAsin(ωt + φ),

(3.8)

Ψ_II = Acos(ωt + φ).

С учетом (3.8) закон оптимального управления (3.3) принимает вид

(3.9)

u^∗(t) = ε signΨ_II

(t) = ε sign cos(ωt + φ).

Это означает, что управление переключается между своими крайними зна-

чениями в моменты времени

(3.10)

ωt_k =

− φ + π(k - 1), k = 1,...,K,

где K - количество переключений управления, равное

]

^[ω(T - t₁)

(3.11)

K =1+

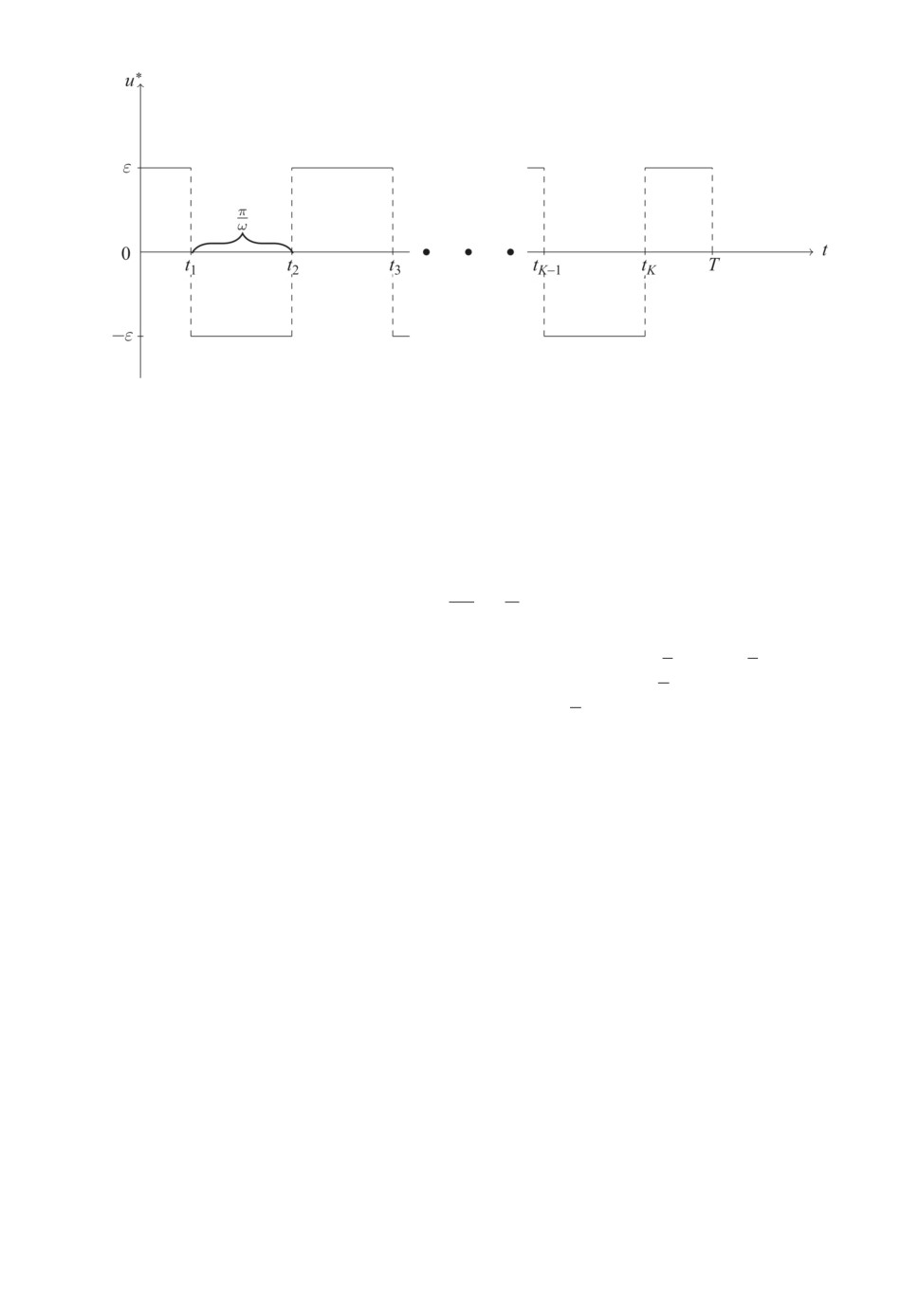
Рис. 1. Вид оптимального управления.

Квадратные скобки здесь означают целую часть числа. Из (3.11) сразу следу-

ет, что K ≥ 1 при любом T > t₁ в задаче максимизации энергии осциллятора.

Случай с K = 0 будет рассмотрен и проанализирован после леммы 2. Момент

первого переключения

(3.12)

t₁ =

2ω

должен удовлетворять условию 0 < ωt₁ < π, а значит, -π2 < φ <π2 . Таким

образом, переключение управления происходит каждые^πω секунд. Первый

и последний интервалы управления отличны от^πω . Так как в данной поста-

новке начальное значение управления не влияет на решение задачи, выберем

u^∗(0) = ε. На рис. 1 показана зависимость оптимального управления от вре-

мени.

Поскольку данный закон решения допускает особые экстремали, возмож-

ные в случае

^{ Ψ_I(t) ≡ 0,

(3.13)

Ψ_II(t) ≡ 0,

покажем, что они не могут содержаться в искомом решении. Из условий

трансверсальности (3.5) и (3.13) следует, что

^{ q(T) = 0,

(3.14)

p(T ) = 0.

Однако последнего не может быть, так как E(T ) > 0. Если же на некотором

интервале времени t ∈ [t^′, t^′′] выполнено (3.13), то из справедливости этих

равенств в момент времени t^′′ и из (3.8) следует, что A = 0. Тогда верно (3.13)

в момент времени T , и поэтому справедливо (3.14), а это невозможно, как

показано ранее. Таким образом, доказано, что особые экстремали не могут

содержаться в исходном решении.

Для решения задачи достаточно найти момент первого переключения t₁.

Перепишем (3.5) с учетом полученных для сопряженных переменных формул

и получим, что

^{ Asin(ωT + φ) = ωq(T),

(3.15)

A cos(ωT + φ) = p(T ).

Видно, что если найти p(T ) и q(T ) как функции t₁, то, учитывая (3.12), из

системы (3.15) можно получить искомый момент t₁.

3.2. Замечания о фазовом портрете

Для нахождения фазовых координат системы в конечный момент времени

обратимся к фазовому портрету.

Рассмотрим фазовые кривые одного осциллятора, описываемого уравне-

ниями динамики (2.1) на фазовой плоскости (q, p) при прикладывании к нему

конкретного управления u. Пусть u = ε:

{

˙q(t) = p(t),

p(t) = -ω²q(t) + ε.

Второе уравнение записывается в виде (зависимость от t здесь и далее опус-

каем для удобства)

(

ε )

q+ω²

= 0.

ω²

Его решение имеет вид

{

q = Rcos(-ωt + γ₀) +

ω²

p = Rω sin(-ωt + γ₀),

где R - константа, алгебраический и геометрический смыслы которой будут

раскрыты далее по тексту, γ₀ - некоторая фаза, а знак минус перед частотой

показывает на фазовой плоскости движение по часовой стрелке.

Аналогичные рассуждения можно провести для случая u = -ε. Результат

будет идентичен предыдущему с разницей лишь в знаке перед вторым сла-

гаемым первого уравнения системы. Итак, фазовыми траекториями системы

являются окружности

(

)₂

⁽p

q∓

=R²

ω²

(

)

с центром в точке с координатами e

± εω2,0 . По этим окружностям фазовая

точка движется по часовой стрелке c угловой скоростью ω.

3.3. Исследование структуры решения

Используя выводы из подраздела 3.2, можно представить вид фазовой

траектории, приведенный на рис. 2 для исследуемой задачи с законом опти-

мального управления, показанным на рис. 1.

Здесь точками показаны состояния осциллятора на фазовой плоскости в

начальный, конечный моменты и моменты переключения управления. Видно,

что координаты первой точки переключения определяются соотношениями

⎧

⎨ q₁ =^ε

(1 - cos(ωt₁)),

ω²

^⎩ p₁ =^ε

sin(ωt₁)

γ₀ = π,

ω²

а общий вид координат точек переключения -

⎧

(

ε )

^⎨ q_k

= (-1)(k-1) q₁ + 2(k - 1)

(3.16)

ω²

^⎩ p_k = (-1)(k-1)p₁.

Знак в системе (3.16) определяется четностью k и соответствует описанию

движения осциллятора между k - 1 и k переключениями управления, т.е. ин-

тервалу движения с номером k. Последнее переключение имеет номер k = K,

Рис. 2. Фазовый портрет осциллятора с ω = 1, ε = 1 с переключениями со-

гласно закону (3.10) и произвольным моментом t₁.

определяемый (3.11), поэтому интервал времени, отвечающий заключитель-

ному участку движения, равен

(K - 1)π

(3.17)

Δt_L = T - t₁ -

Рассмотрим движение фазовой точки на заключительном интервале дви-

жения от положения (q_K , p_K ) до (q(T ), p(T )). Поскольку интервал движения

имеет номер K + 1, то для соответствующих координат справедливы соотно-

шения

⎧

⎪

q_K = (-1)^K

+ Rcosγ,

⎪

ω²

⎪

⎨

p_K = ωRsin γ,

(3.18)

⎪

q(T ) = (-1)^K

+ Rcos(-ωΔt_L + γ),

⎪

ω²

⎩

p(T ) = ωR sin(-ωΔt_L + γ),

где |R| - радиус окружности движения, γ - начальный угол, (-1)^Kε

- опре-

ω²

деляет сдвиг центра окружности по оси q на фазовой плоскости. Далее, из

уравнений (3.16) и первого момента переключения управления для систе-

мы (3.8) следует, что

⎧

(

)

sin(ωt₁)

⎪

⎨ γ = arctg

2K - cos(ωt₁)

(3.19)

⎪

εsin(ωt₁)

⎩R=

(-1)(K-1).

ω² sinγ

Поделив второе и первое уравнения (3.15) друг на друга и использовав (3.18),

получаем

(

)

(-1)^K ε + Rω² cos(-ωΔt_L + γ)

(3.20)

tg ωT +

- ωt₁

Rω² sin(-ωΔt_L + γ)

Решение уравнения (3.20) даeт искомое t₁. Аналитическое решение (3.20)

определяется следующей леммой.

Лемма 1. Пусть Δt_L определяется выражением (3.17), а γ и R - выра-

жениями (3.19). Тогда момент времени t₁ определяется из решения урав-

нения (3.20) как

(K - 1)π

(3.21)

t₁ =

2ω

Доказательство леммы 1. Обозначим ξ = ω(T - t₁) и ϕ = ωt₁. То-

гда (3.20) принимает вид

sinϕ

(-1)^K + (-1)K-1(-1)K-1

cos(γ - ξ)

sinγ

- ctg ξ =

(-1)K-1(-1)K-1sinϕsinγ sin(γ - ξ)

Рис. 3. Зависимость энергии E(t₁) при фиксированных T : 1 - T = π + 0,1; 2 -

T = π + 1; 3 - T = π + 2; 4 - T = π + 3.

Перепишем последнее выражение, раскрыв ctg ξ и избавившись от знамена-

теля

cos ξ sin ϕ sin(γ - ξ) + sin ξ sin ϕ cos(γ - ξ) = (-1)K-1 sin ξ sin γ.

Сгруппировав слагаемые в левой части последнего равенства, получим

sin ϕ sin γ = (-1)K-1 sin ξ sin γ.

Поскольку из (3.19) видно, что sin γ = 0 при t₁ = 0, то имеем равенство

sin ϕ = (-1)K-1 sin ξ,

из которого получаем, что для всех K ∈ Z выполнено

ϕ = ξ - (K - 1)π или ωt₁ = ω(T - t₁) - (K - 1)π,

откуда следует утверждение леммы 1. Лемма 1 доказана.

Следствие 1. Из леммы 1 и (3.17) следует, что когда t₁ оптимально

и удовлетворяет (3.21),

(K - 1)π

Δt_L = T - t₁ -

=T -

2ω

(3.22)

(K - 1)π

=t₁.

2ω

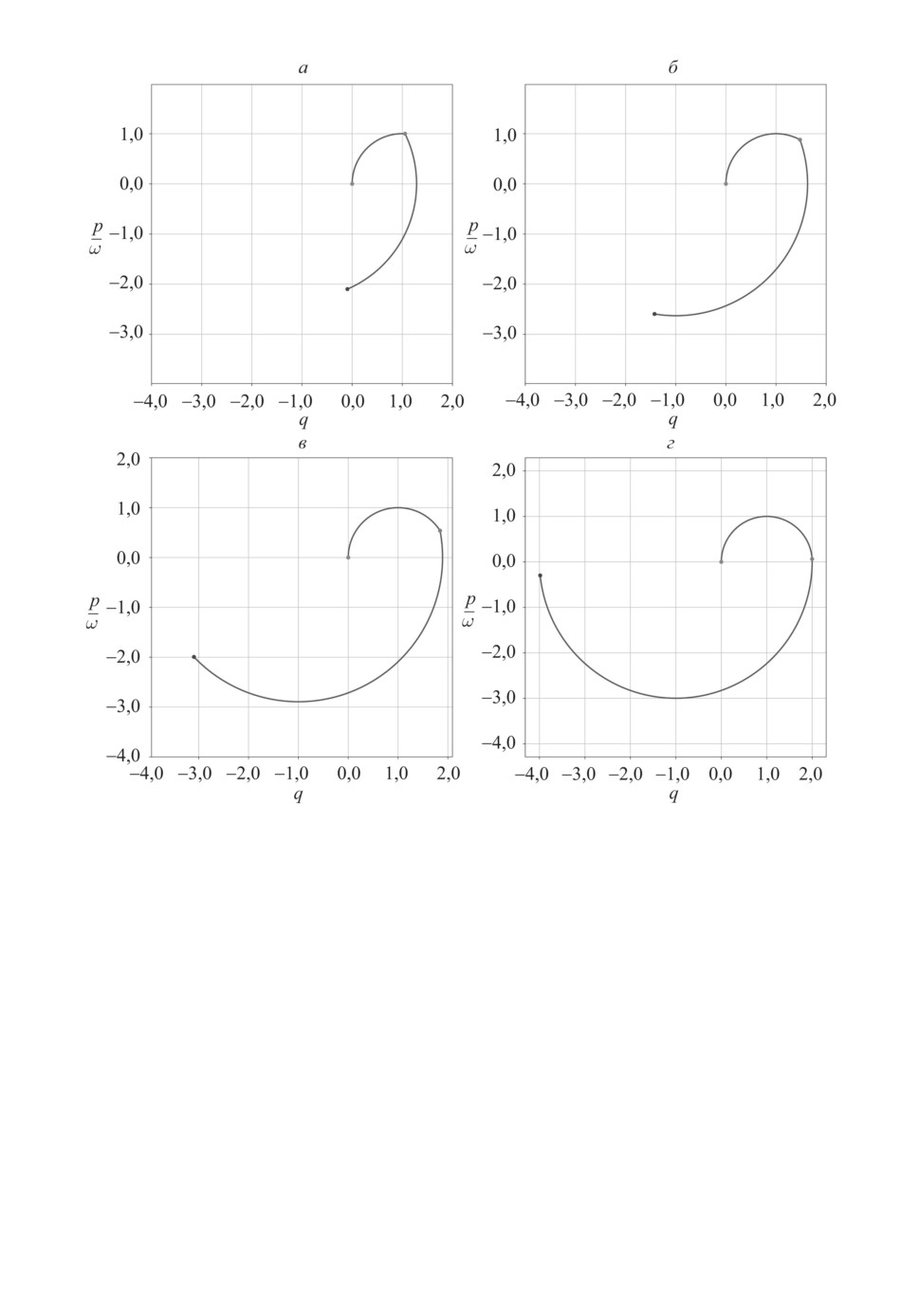
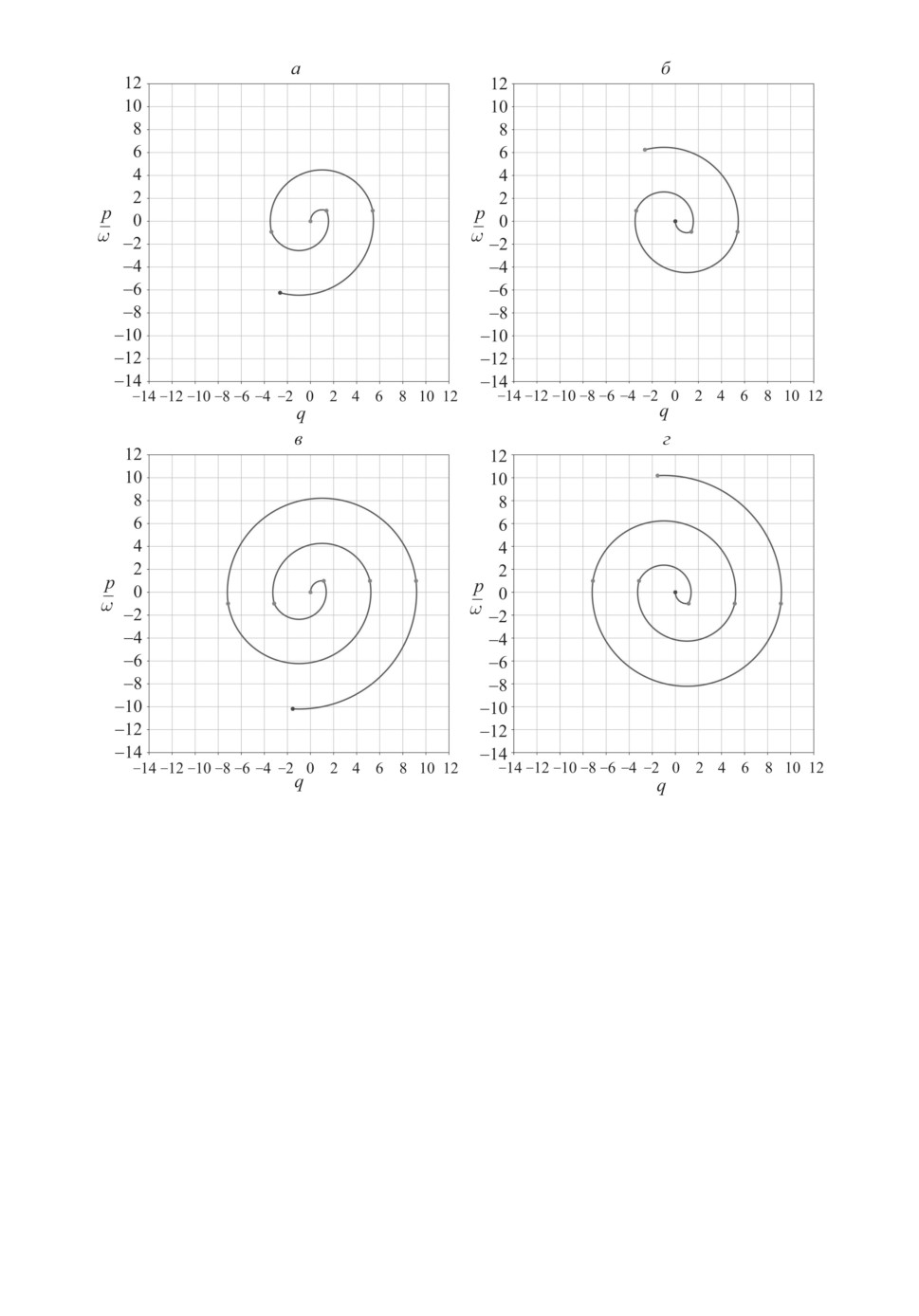
Рис. 4. Фазовые портреты для четырех пар значений (T, t₁): a) T = π + 0,1;

б) T = π + 1; в) T = π + 2; г) T = π + 3.

Выражение (3.22) означает, что для максимальности энергии длительно-

сти первого и последнего интервалов управления должны быть равны.

Положим ω = 1 и рассмотрим различные значения T из отрезка [π, 2π].

С помощью моделирования методом перебора были найдены значения t₁, при

которых значения E(T ) максимальны. Результат эксперимента представлен

на рис. 3.

Значения моментов первого переключения, максимизирующие энергию:

T = 3,24159265359, t₁ = 1,62609871015;

T = 4,14159265359, t₁ = 2,06811777699;

T = 5,14159265359, t₁ = 2,5732824248;

T = 6,14159265359, t₁ = 3,07844707261.

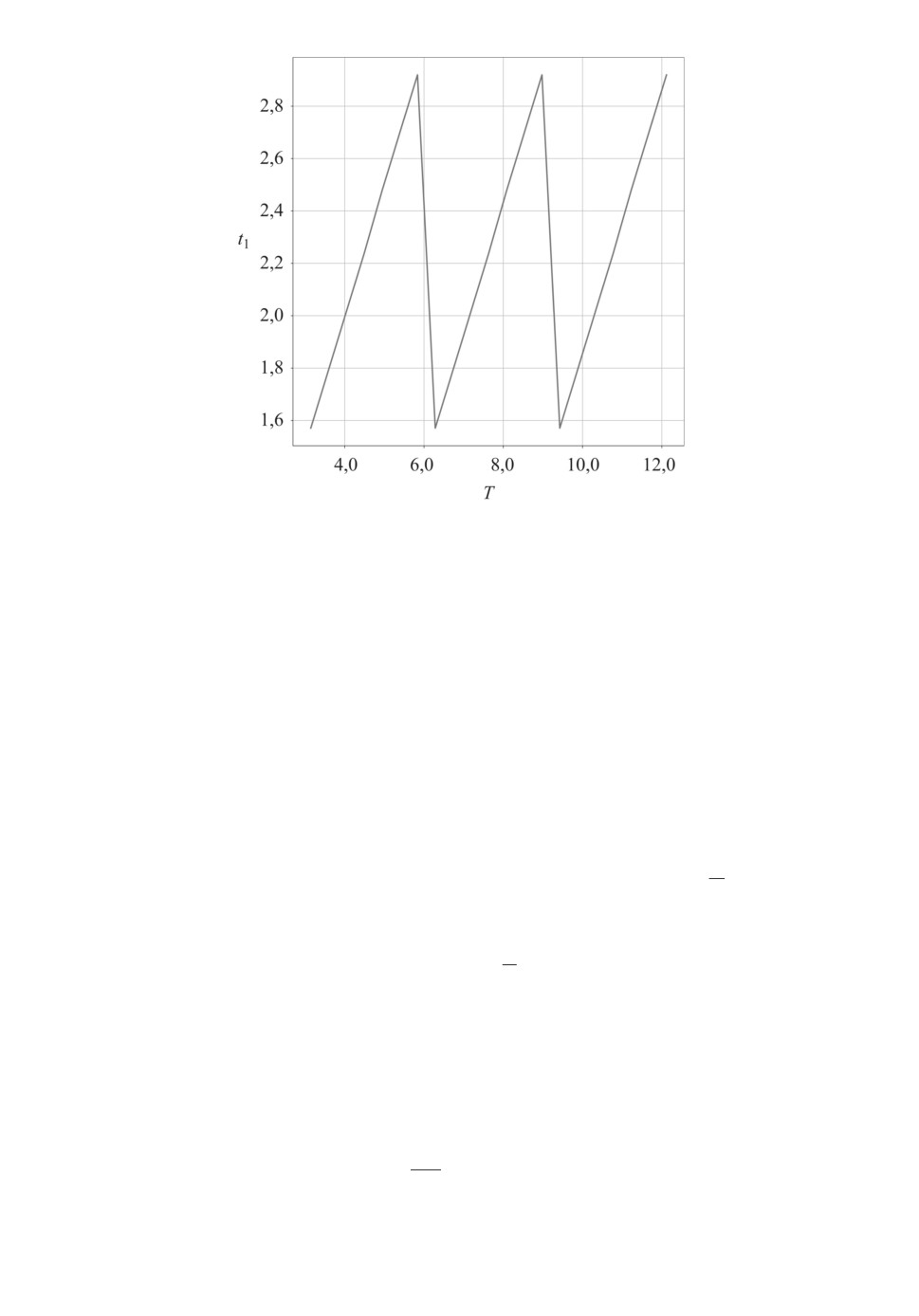
Рис. 5. Зависимость оптимального t₁ от T .

Фазовые портреты для различных значений T представлены на рис. 4,

а зависимость t₁(T ) - на рис. 5.

Численное решение уравнения (3.20) готовыми программными средствами

языка Python дает следующий результат:

T = 3,24159265359, t₁ = 1,62079632679;

T = 4,14159265359, t₁ = 2,07079632679;

T = 5,14159265359, t₁ = 2,57079632679;

T = 6,14159265359, t₁ = 3,07682946837.

Видно, что в случае одного переключения управления t₁ =

. Этот сим-

метричный результат следует из формул аналитического решения с помощью

принципа максимума и следствия из леммы 1. Что касается других T , то по

лемме 1 решения периодичны с периодом

После того как момент времени t₁ определен, можно найти значение энер-

гии в финальный момент T .

Лемма 2. Максимальное значение энергии в момент времени T, дости-

жимое из состояния покоя осциллятора при ограниченном скалярном управ-

лении, удовлетворяющем ограничению |u| ≤ ε, равно:

2ε

E(T ) =

(K - cos ωt₁)² ,

ω²

где значение t₁ получено в лемме 1.

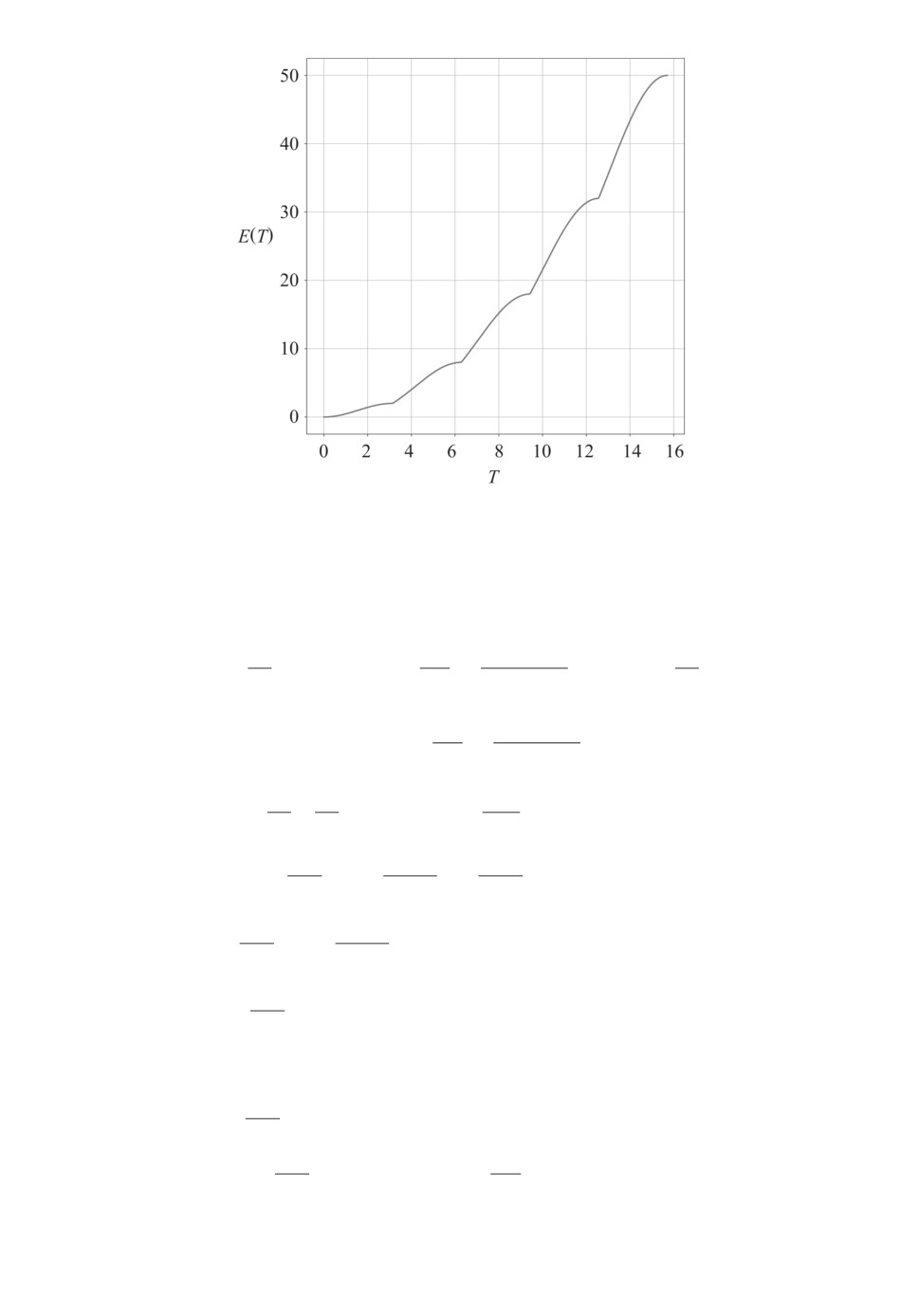
Рис. 6. Зависимость максимального значения E(T ).

Доказательство леммы 2. Выразим q(T) и p(T) через t₁ и подста-

вим в выражение для энергии осциллятора. Справедлива цепочка равенств

((

(

)

)₂

ωT

(K - 1)π

E(T ) =

R cos γ -

+ (-1)^K

ω²

(

))

ωT

(K - 1)π

+ R2 sin²

γ-

)

⁽ε²

2Rε

+ R² + (-1)^K

cos(γ - ωt₁)

ω⁴

ω²

(

)

sin² ϕ

sin ϕ

-2

cos(γ - ϕ)

2ω²

sin² γ

sin γ

(

)

sin²

- 2sin2 ϕ - 2sinϕcosϕctgγ

2ω²

sin² γ

(

)

cos² ϕ + sin² ϕ ctg² γ - 2 sin ϕ cos ϕ ctg γ

2ω²

Подставим выражение для γ из (3.19) и получим:

(

)

E(T ) =

cos² ϕ + (2K - cos ϕ)² - 2 cos ϕ (2K - cos ϕ)

2ω²

(2K - 2 cos ϕ)² =2ε2

(K - cos ωt₁)² .

2ω²

ω²

Лемма 2 доказана.

Проиллюстрируем полученную зависимость графиком, представленным

на рис. 6. Из рис. 6 видно, что рост энергии E(T ) с возрастанием значений T

существенно нелинейный.

Поскольку получено значение энергии осциллятора при K ≥ 1, то необхо-

димо сравнить значение энергии при K = 1 с значением энергии при K = 0

и фиксированном T < π. Эти значения равны:

(

)₂

2ε²

ωT

EK=0 =

(1 - cos ωT ), EK=1 =

1 - cos

ω²

Сравнивая EK=0 и EK=1, получаем, что EK=0 ≥ EK=1 при всех ωT ∈ [0, π].

Лемма 3. Значение энергии в момент времени T, достижимое из со-

стояния покоя осциллятора при ограниченном скалярном управлении, удо-

влетворяющем (3.9), при T =^nπω , n ∈ N, не зависит от t₁ и равно:

2ε²K

E(T ) =

ω²

Доказательство леммы 3.

[(

(

)

)₂

(K - 1) π

E(T ) =

R cos

-ω T - t₁ -

+γ

+ (-1)^K

ω²

]

(

)

))₂

(K - 1) π

+R²

sin

-ω T - t₁ -

+γ

Заметим, что если T =^nπω , то K = n. Поэтому выражение принимает вид

[(

)₂

E(T ) =

R cos (-ω (-t₁) + π + γ) + (-1)^K

ω²

]

+R² (sin (-ω (-t₁) + π + γ))²

]

[(

)₂

-R cos (ωt₁ + γ) + (-1)^K

+ R2 (sin(ωt₁

+ γ))²

ω²

)

⁽ε²

2Rε

+ R² - (-1)^K

cos (ωt₁ + γ)

ω⁴

ω²

Используя (3.19) и сделав замену ϕ = ωt₁, получаем:

(

)

sin²

E(T ) =

- 2sin2 ϕ + 2sinϕcosϕctgγ

2ω²

sin² γ

(

)

1 + sin2 ϕ

1 + ctg2 γ

- 2sin2 ϕ + 2sinϕcosϕctgγ

2ω²

(

)

2ε²K²

cos² ϕ + (2K - cos ϕ)² + 2 cos ϕ (2K - cos ϕ)

2ω²

ω²

Лемма 3 доказана.

Выражение для энергии в лемме 3 совпадает с асимптотической формулой

для энергии осциллятора в задаче гашения колебаний на больших временах,

приведенной в [8].

4. Сравнение с задачей быстродействия

Напомним задачу быстродействия для одного осциллятора. Для системы,

описываемой (2.1) с ограничением на управление вида |u| ≤ ε и краевыми

условиями

⎧

⎪

q(0) = a,

⎨

p(0) = b,

(4.1)

⎪

q(T ) = 0,

⎩

p(T ) = 0,

найти оптимальное управление u(t), минимизирующее критерий

∫T

(4.2)

J =

dt -→ min .

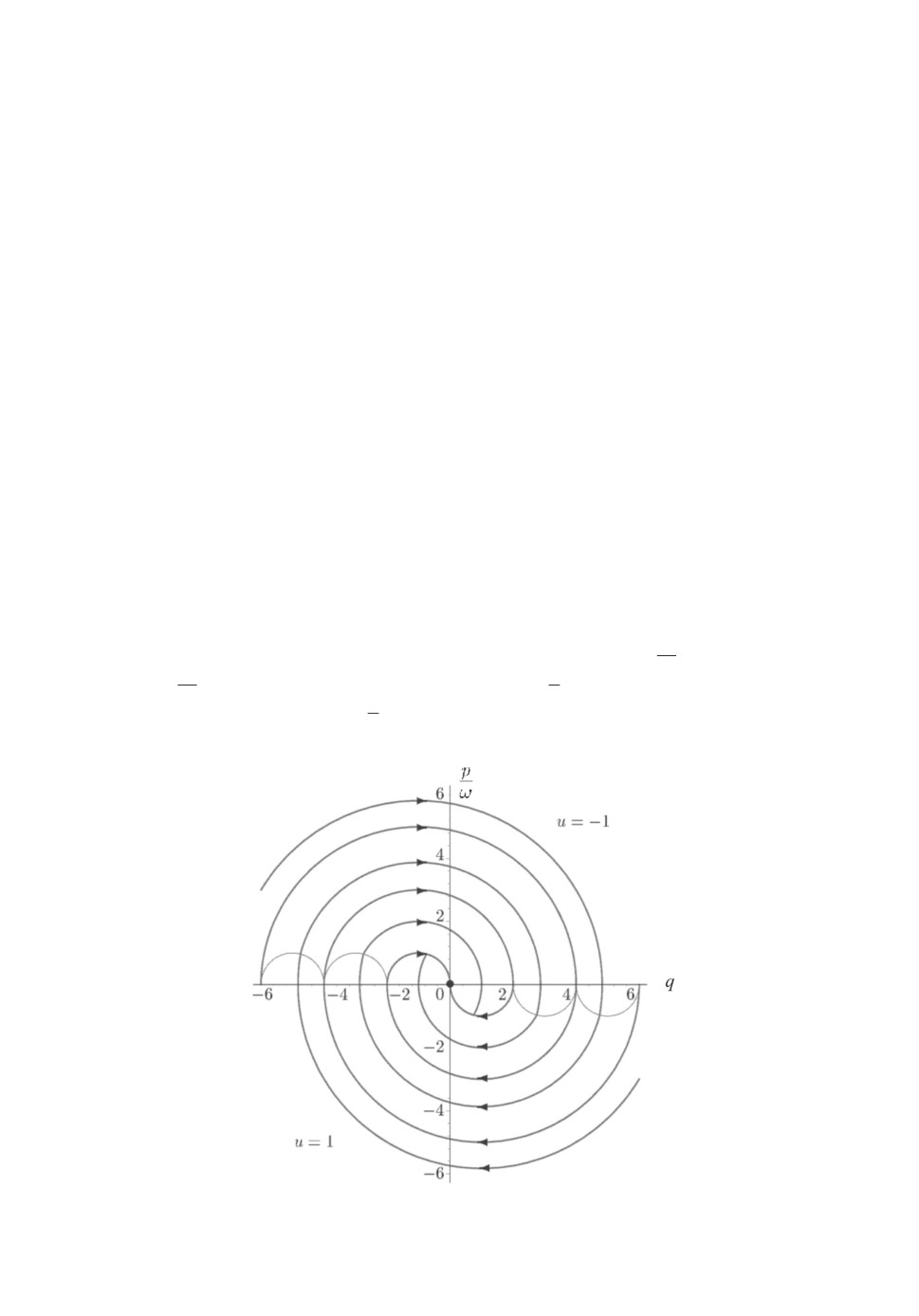
Как показал Болтянский в [1], решением этой задачи является оптималь-

ное кусочно-непрерывное управление, переключающееся в фазовых точках

пересечения дуг фазовой траектории и полудуг радиусаεω2 , проведенных в

точках ±kεω2 , k = 2n - 1, n ∈ N, через каждые^πω секунд. Фазовая плоскость

(

)

построена в координатах

q,^pω

(см. рис. 7).

Рис. 7. Фазовые траектории в задаче быстродействия.

В [4] приведено аналитическое решение схожей задачи с частными началь-

ными условиями с указанием полного времени и времени первого переклю-

чения. Они полностью определяют решение. Следуя той же логике и гра-

фическому представлению решения, приведенному в [1, 3], можно выписать

аналитическое значение критерия в задаче быстродействия, которое в явном

виде приводится впервые, а именно:

⎧

(

)

⎪

T^∗ =

K-

+ Δt_L,

⎪

⁽Rω² cos(φ + γ₀)⁾

⎪

Δt_L =

arcsin

⎪

⎨

(

)

ε²

(4K² - 1) + ω²R²

(4.3)

φ = arcsinω2

-γ₀,

⎪

4KεR

⎪

√(

)₂

⎪

⁽b)2

⎪

R= a+

⎪

ω²

⎪

^⎩ γ₀ = arctg^bω

ω²a + ε

где K - число переключений управления, а T^∗ - величина оптимального пол-

ного времени быстродействия. K может принимать одно из значений:

]

}

^{[ω²R

^[ω²R^]

K =

- 1;

;

2ε

Здесь квадратные скобки обозначают целую часть числа, а решение приве-

дено для начального положения, которому соответствует u(0) = -ε.

Решение задачи максимизации энергии осциллятора за фиксированное

время дает оптимальные значения обобщенных координат осциллятора в мо-

мент времени T . Если теперь выбрать любую другую точку на окружно-

сти, соответствующей максимальному значению энергии, то очевидно, что

значение критерия T^∗, полученного из решения задачи быстродействия, бу-

дет больше T - фиксированного времени в исходной задаче. Однако также

очевидно, что при перемене знака скорости существует оптимальное реше-

ние задачи быстродействия (те же самые моменты переключения управления

только в обратном времени и уровни переключения на фазовой плоскости),

дающее решение этой задачи с T^∗ = T .

На рис. 8,а и 8,в показаны фазовые портреты для задачи максимизации

энергии, на рис. 8,б и 8,г - для соответствующей задачи быстродействия.

Начальное значение фазовых координат для задачи быстродействия выбра-

но a = q(T ), b = -p(T ) равным оптимальным значениям, полученным при

решении задачи максимизации энергии.

Множество точек (a, b) фазовой плоскости осциллятора с равной энерги-

ей представляет собой окружность ω²a² + b² = const, являющуюся ограни-

ченным замкнутым множеством. Значение T^∗ как функция начальных усло-

вий (a, b) достигает на этом множестве своих верхней и нижней граней. Ниж-

няя грань T_l, как сказано ранее, есть T_l = T . Верхняя грань T_h может быть

Рис. 8. Разгон маятника до максимальной энергии и приведение его в состоя-

ние покоя из точки с полученной энергией за минимальное время.

найдена как решение задачи T^∗ → max(a,b) при условии ω²a² + b² = const, а

численно - например, перебором по всем точкам окружности соответствую-

щей энергии. Приведем значения T_h для некоторых значений T_l.

T_l = 9,92477796077, T_h = 10,5273991806;

T_l = 4,44159265359, T_h = 5,1503994477;

T_l = 17,407963268, T_h = 17,8359447879.

5. Заключение

В статье исследована и решена задача управления осциллятором по крите-

рию максимизации его энергии в заданный фиксированный момент времени.

Аналитически получены вид оптимального управления и значения времен пе-

реключения управления, а также формулы конечного оптимального значения

энергии как функции времени T , отведенного на решение задачи. Разработа-

ны программные модули на языке Python для решения задачи оптимального

управления при максимизации энергии, задачи быстродействия и для экспе-

риментальной проверки лемм 1, 2 и 3. Полученное решение расширяет набор

классических решений для задачи оптимального ограниченного скалярного

управления одиночным осциллятором, дает понимание структуры получен-

ных законов управления и дополняет решение задачи быстродействия.

В будущем планируется применить разработанный подход для решения

задачи максимизации энергии системы осцилляторов.

СПИСОК ЛИТЕРАТУРЫ

1. Болтянский В.Г. Математические методы оптимального управления. М.: Наука,

1969.

2. Гамкрелидзе Р.В. Открытие Принципа Максимума Понтрягина (ПМП). 2013.

9-10 апреля. Докл. в Тулонском университете. Франция.

3. Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.: Физматлит,

2005.

4. Галяев А.А. Задача оптимального управления осциллятором с целью обнуления

его энергии при ограничении на управляющее воздействие // АиТ. 2009. № 3.

C. 24-33.

Galyaev A.A. Problem of Optimal Oscillator Control for Nulling its Energy under

Bounded Control Action // Autom. Remote Control. 2009. V. 70. No. 3. P. 366-374.

5. Черноусько Ф.Л. Управление колебаниями. М.: Наука, 1980.

6. Галяев А.А. Скалярное управление группой несинхронных осцилляторов //

АиТ. 2016. № 9. С. 3-18.

Galyaev A.A. Scalar Control of a Group of Free-running Oscillators // Autom.

Remote Control. 2016. V. 77. No. 9. P. 1511-1523.

7. Fedorov A., Ovseevich A.I. Asymptotic Control Theory for a System of Linear

Oscillators // Moscow Math. J. 16. 2016. P. 561-598.

8. Ovseevich A.I. Complexity of the Minimum-time Damping of a Physical Pendulum //

SIAM J. Control Optim. 2014. V. 52. No. 1. P. 82-96.

Статья представлена к публикации членом редколлегии Е.Я. Рубиновичем.

Поступила в редакцию 18.01.2018

После доработки 25.05.2018

Принята к публикации 08.11.2018