Автоматика и телемеханика, № 1, 2019
Стохастические системы
© 2019 г. В.М. АЗАНОВ (azanov59@gmail.com),
Ю.С. КАН, д-р физ.-мат. наук (yu_kan@mail.ru)
(Московский авиационный институт)
ОБ ОПТИМАЛЬНОМ УДЕРЖАНИИ ТРАЕКТОРИИ ДИСКРЕТНОЙ
СТОХАСТИЧЕСКОЙ СИСТЕМЫ В ТРУБКЕ1
Рассматривается задача синтеза оптимального управления дискретной
стохастической системой общего вида с критерием в форме вероятности
пребывания вектора состояния в каждый момент времени на заданных
множествах. Выводятся соотношения метода динамического программи-
рования, позволяющие найти оптимальное решение в классе марковских
стратегий без расширения вектора состояния с последующим сведением
к эквивалентной задаче с вероятностным терминальным критерием. Рас-
смотрена задача однопараметрической коррекции траектории движения
летательного аппарата. Получено аналитическое решение.
Ключевые слова: дискретные системы, стохастическое оптимальное
управление, вероятностный критерий, метод динамического программи-
рования, однопараметрическая импульсная коррекция, управление дви-
жением летательного аппарата.
DOI: 10.1134/S0005231019010033
1. Введение
Дискретные стохастические системы обсуждаются во многих прикладных
задачах синтеза оптимального управления, например, в аэрокосмической об-
ласти при импульсной коррекции положения летательного аппарата [1-7],
в экономической области в проблеме оптимального управления портфелем
ценных бумаг [8-10], в области робототехники в задачах автоматизирован-
ного управления [11-13], в информатике в задачах оптимизации распределе-
ния внешних и внутренних вычислительных ресурсов программных систем
[14-16].
Критерий в форме функционала вероятности характерен больше для аэро-
космических [1-4], экономических [8-10] и робототехнических [11-13] задач, в
которых требуется оптимизировать вероятность обеспечения желаемой точ-
ности системы при ограничении на ресурс управления, при этом точност-
ной функционал задан на траекториях системы в терминальный момент вре-
мени. Альтернативой вероятностному критерию служит среднеквадратиче-
ский критерий, нацеленный на выполнение точностного ограничения с уче-
том неравенства Чебышева. Недостатки такого подхода, связанные с грубо-
стью неравенства Чебышева, подробно освещены в [1].
1 Работа, за исключением раздела 4, выполнена при поддержке Российского научного
фонда (проект № 16-11-00062). Результаты раздела 4 получены при поддержке Российского
фонда фундаментальных исследований (проект № 18-08-00595).
38
Во многих задачах в качестве критерия рассматривается точностной
функционал, зависящий не только от терминального состояния, но и от со-
стояний во все моменты дискретного времени. Критерий такого вида играет
важную роль в приложениях как с точки зрения задач оптимизации точ-
ности (см., например, [17, 18]), так и оптимизации ресурса управления (см.,
например [14-16]).
В настоящей статье исследуется задача оптимального управления дискрет-
ной стохастической системой по критерию максимума вероятности попадания
траектории системы в заданную трубку. Доказывается теорема о существо-
вании оптимальной стратегии в классе марковских и выводится уравнение
Беллмана. На примере задачи однопараметрической коррекции сравнивают-
ся два подхода: первый — с использованием уравнения Беллмана и второй —
с использованием приема расширения пространства состояний и сведения
исходной задачи к эквивалентной в определенном смысле задаче с вероят-
ностным терминальным критерием.
2. Постановка задачи
Пусть динамика объекта управления описывается разностным уравнением
⎧
⎨xk+1 = fk (xk,uk,ξk) ,
(1)
k = 0,N,
⎩x0 = X,
где xk ∈ Rn — вектор состояния, uk ∈ Uk ⊂ Rm — вектор управления, Uk —
множество ограничений на управление, ξk — вектор случайных возмущений
с значениями на Rs, fk : Rn × Rm × Rs → Rn — функция перехода (функция
системы), N ∈ N — горизонт управления.
В отношении системы (1) введем ряд предположений:
1) известна полная информация о векторе состояния xk (данный факт поз-
воляет строить управление в классе функций uk = γk (xk), где γk (·) —
некоторая измеримая функция. В данном случае говорят, что “управле-
ние ищется в классе полной обратной связи по состоянию”;
2) начальное состояние x0 = X является в общем случае случайным вектором
с значениями в Rn и с известным распределением PX ;
3) функция системы fk (xk, uk, ξk) непрерывна для всех k;
4) вектор управления uk формируется следующим образом: uk = γk (xk),
где γk : Rn → Rm — измеримая функция с ограниченными значениями
uk ∈ Uk, причем Uk — компактное множество;
5) вектор состояния xk+1 формируется следующим образом: на шаге k реа-
лизуется вектор xk, далее формируется вектор управления uk = γk (xk) и
в последнюю очередь реализуется случайное возмущение ξk;
6) управлением называется набор функций u(·) = (γ0(·), . . . , γN (·)) ∈ U, клас-
сом допустимых управлений называется множество U = U0 × . . . × UN , где
Uk — множество борелевских функций γk (·) с ограниченными на Uk зна-
чениями;
39
7) случайный вектор ξk является непрерывным с значениями в Rs и извест-
ным распределением Pk, причем компоненты вектора ζ = (X, ξ0, . . . , ξN )
независимы.
Заметим, что система (1) является марковской, т.е. ее поведение в будущем
не зависит от прошлого и полностью определяется текущим состоянием.
На траекториях системы (1) определим функционал вероятности
(
)
⋂
Pϕ (u(·)) = P
{xk+1 ∈ Fk+1}
,
k=0
множества Fk имеют вид
Fk = {x ∈ Rn : Φk (x) ≤ ϕ} ,
где ϕ ∈ R — известный скаляр, Φk : Rn → R — непрерывные функции,
k = 1,...,N + 1, причем ΦN+1 (x) ограничена снизу.
Рассматривается задача
(2)
Pϕ (u(·)) → max ,
u(·)∈U
где U = U0 × . . . × UN .
Задача (2) является задачей синтеза оптимального управления в классе
позиционных стратегий. Отметим, что если принять
Fk = Rn, k = 1,N,
то получаем задачу синтеза оптимального управления с вероятностным тер-
минальным критерием в классической постановке [1, 3].
Для синтеза оптимальной стратегии может быть использован прием, при-
мененный, например, в [19], сведения задачи (2) к задаче оптимального управ-
ления с вероятностным терминальным критерием c расширенным простран-
ством состояний размерности n + 1 (сказанное поясняется в разделе 4 на
примере простейшей задачи импульсной коррекции траектории движения ле-
тательного аппарата). Такой подход влечет за собой усложнение как числен-
ного, так и аналитического синтеза оптимальной стратегии. Кроме того, в
некоторых случаях аналитическое решение “приведенной задачи” с вероят-
ностным терминальным критерием и вовсе затруднено, в то время как реше-
ние исходной задачи возможно.
В разделе 3 выводится уравнение Беллмана для задачи (2).
3. Условия оптимальности в форме уравнения Беллмана
Для удобства примем
F0 = Rn.
40
Определим функцию Беллмана Bk : Rn → [0, 1] в задаче (2) как
Bk (x) =
(
)
=
sup
P max Φi+1(xi+1(xk,γk(·),... ,γi(·),ξk,... ,ξi)) ≤ ϕxk = x
γk(·)∈Uk,...,γN (·)∈UN i=k,N
Принимая во внимание сделанные в разделе 2 предположения, cформулируем
теорему об уравнении Беллмана для задачи (2) в пространстве состояний
размерности n.
Теорема. Пусть выполнены условия:
1) функции fk (xk, uk, ξk)непрерывны для всех k = 0, N ;
2) функции Φk (xk) непрерывны для всех k = 1, N + 1;
3) функция ΦN+1 (xN+1) ограничена снизу;
4) случайные векторы X, ξ0, . . . , ξN независимы;
5) множества U0, . . . , UN компактны.
Тогда оптимальная стратегия в задаче (2) существует в классе изме-
римых функций u∗ (·) ∈ U и определяется в результате решения следующих
задач:
[
]
xk
(3)
u∗k = arg max M
IFk (xk)Bk+1 (fk (xk,uk,ξk))
,
uk∈Uk
[
]
(4)
Bk (x) = max M
IFk (xk) Bk+1 (fk (xk,uk,ξk))xk = x
,
k = 0,N,
uk∈Uk
(5)
BN+1 (x) = IFN+1
(x) .
Доказательство теоремы вынесено в Приложение.
Таким образом, получено уравнение Беллмана в пространстве состояний
размерности n. Оно отличается от уравнения Беллмана для задачи с вероят-
ностным терминальным критерием наличия в правой части сомножителя в
виде индикаторной функции IFk (xk) множества Fk.
4. Задача однопараметрической коррекции
траектории летательного аппарата
4.1. Постановка задачи с использованием разных подходов
На примере простой одномерной задачи сравнивается подход к решению
задачи (2), описанный в разделе 3 с другим подходом, основанным на сведе-
нии задачи (2) к эквивалентной (в определенном смысле) задаче оптимально-
го управления с вероятностным терминальным критерием и, как следствие,
на использовании метода динамического программирования в классической
форме [1].
Пусть n = m = s = 1 — размерности вектора состояния, вектора управле-
ния и вектора случайного возмущения ξk ∼ R [-ε, ε], ε ∈ (0, 1), {rk}N+1k=1 —
убывающая последовательность вещественных чисел, rk ≥ rk+1, rN+1 > 0.
41
Рассмотрим задачу
(
)
⋂
(6)
P
{|xk+1| ≤ rk+1}
→ max,
u(·)
k=0
{
xk+1 = xk + uk (1 + ξk) ,
(7)
k = 0,N,
x0 = X,
и задачу
(8)
P(yN+1 ≤ 1) → max,
u(·)
⎧
⎪xk+1 = xk + uk (1 + ξk) ,
⎨
yk+1 = max{yk,
|xk + uk (1 + ξk)| /rk+1} ,
(9)
k = 0,N,
⎪x0 = X,
⎩
y0 = |X + u0 (1 + ξ0)|/r1,
которые, очевидно, являются эквивалентными в смысле критериев
)
(
{
})(N⋂
|xk+1|
P(yN+1 ≤ 1) = P max
≤1
=P
{|xk+1| ≤ rk+1}
k=0,N
r
k+1
k=0
Задача (6) относится к классу задач, описанных в разделах 2 и 3 настоящей
статьи, а задача (8) — к классу задач оптимального управления с вероят-
ностным терминальным критерием [1]. Отметим, что в задаче (8) управление
ищется в более широком классе функций uk = γk (xk, yk), при этом для поиска
оптимальной стратегии применим метод динамического программирования в
классической форме [1], а также его модификации (см. [3, 20]).
Важно отметить, что задача (6) возникает естественным образом в аэро-
космических приложениях [1, 3] в рамках задач однопараметрической им-
пульсной коррекции траектории движения космических аппаратов. Прин-
ципиальным отличием от постановок с терминальным критерием каче-
ства P (|xN+1| ≤ ϕ) → maxu(·) является то, что корректирующие импуль-
сы должны обеспечивать “равномерную” во времени коррекцию парамет-
ра движения, что в постановке (6) формализуется в виде ограничения
xk+1 ≤ rk+1 в каждый момент времени, где убывающая положительная по-
следовательность чисел {rk+1}Nk=0 имеет смысл максимально допустимого
промаха состояния xk+1. Подобный смысл в среднеквадратической задаче[
]
M (xN+1)2 → minu(·) несут в себе изопериметрические ограничения на век-
[
]
тор состояния в каждый момент времени M (xk+1)2 ≤ rk+1. Отметим, что
задача с терминальным критерием в более общей постановке с векторной си-
стемой и ограниченным скалярным управлением аналитически решена в [2],
а одномерный случай без ограничений рассматривался в [1, 3].
42
4.2. Решение задачи (6)
Перейдем к решению задачи (6). В исходных обозначениях имеем
fk (xk,uk,ξk) = xk + uk (1 + ξk), Φk (x) = |x|, Fk = [-rk,rk].
В утверждении 1 с использованием теоремы найдено аналитическое решение
задачи (6) для случая, когда граница носителя распределения случайной ве-
личины ξk связана естественными ограничениями с границей множества Fk.
Утверждение 1. Пусть выполнено
rk+1
(10)
ε ≤ min
,
k=1,N rk
тогда функция Беллмана в задаче (6) имеет вид
⎧
⎨I[-rk,rk] (x) ,
k = 1,N,
Bk (x) =
{
}
r1
1+ε
⎩min
1,
,
k = 0,
r1+|x| ε
и оптимальное управление определяется выражением
{
любое из U∗
(xk) ,
|xk| ∈ [0,rk] ,
k
u∗k =
k = 1,N,
любое из R,
|xk| ∈ (rk,+∞),
⎧
[
]
⎨любое из U∗0 (X) ,
|X| ∈
0, r1ε-1
,
u∗
0
(
)
k = 0,
= ⎩-sign(X)r1 - X,
|X| ∈
r1ε-1,+∞
,
1+ε
где
{
U∗k (xk) = uk ∈ R : sign(uk) = -sign(xk) ,
}
{
}
-rk+1 + |xk|
rk+1 + |xk|
max
0,
≤ |uk| ≤
1-ε
1+ε
Доказательство утверждения 1 вынесено в Приложение.
Основным условием утверждения 1 является неравенство (10). Оно оче-
видно выполнено в случае, когда rk = const для всех k, так как из по-
становки задачи следует, что ε < 1. Как видно из утверждения 1, функ-
ция Беллмана является индикаторной (на шагах k = 1, N ) и выполнено
Fk = {x ∈ R : Bk (x) = 1}, что означает, что цели управления выполняются
с вероятностью единица на шагах k = 1, N , при этом оптимальным является
целое множество управлений на указанных шагах. Важно отметить, что оп-
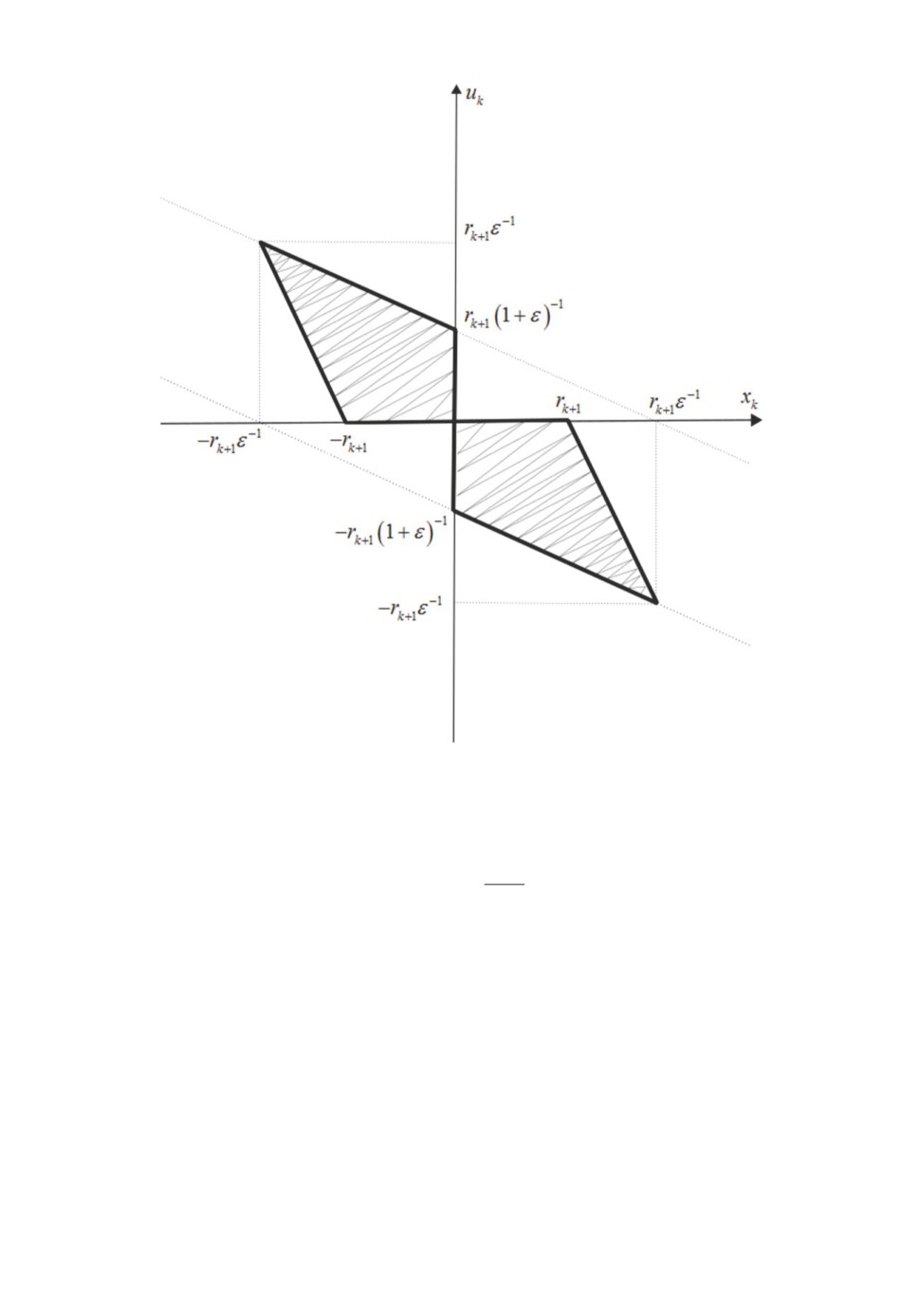
тимальным при xk ∈ [-rk, rk] является любой элемент из множества U∗k (xk).
Указанное множество изображено на рисунке.
Интересным является тот факт, что при k = 0 функция Беллмана пред-
ставляет собой максимальную вероятность попадания траекторией системы
43
Множество U∗k (xk).
на множество F1, т.е. B0 (x) = maxu0 P (f0 (x, u0, ξ0) ∈ F1), что означает, что
при фиксированном начальном состоянии максимальная вероятность пребы-
вания системы на множествах Fk+1, k = 0, N , равна максимальной вероятно-
сти попадания системы на множество F1. Упомянутый факт обусловлен тем,
что при выполнении неравенства (10) любым управлением из U∗k (xk) удается
с вероятностью единица перевести систему из Fk на множество Fk+1.
4.3. Решение задачи (8)
Перейдем теперь к решению задачи (8). В соответствии с [1] функция
БеллманаBk : Rn+1 → [0, 1] для (8) равна:
Bk (x,y) =
(
)
= sup P yN+1 (xk,yk,γk (·) ,... ,γN (·) ,ξk,... ,ξN ) ≤ 1xk = x, yk = y
,
γk(·),...,γN (·)
44
а уравнения метода динамического программирования имеют вид:
[
(
)
]
Bk+1
ũ∗k = arg max M
fk (xk,yk,uk,ξk)
xk, yk ,
k = 0,N,
uk
[
(
)
]
Bk+1
Bk (x,y) = maxM
fk (xk,yk,uk,ξk)
xk = x, yk = y
,
uk
BN+1 (x,y) = I(-∞,1] (y),
гд
fk : Rn+1 → Rn+1 — функция правой части “расширенной” системы управ-
ления
⎛
⎞
xk + uk (1 + ξk)
⎜
{
}⎟
fk (xk,yk,uk,ξk) =
⎝
|xk + uk (1 + ξk)|
⎠.
max yk,
rk+1
В следующем утверждении 2 найдено аналитическое решение задачи (8)
при условии (10): оптимальное управление и функция Беллмана.
Утверждение 2. Пусть для задачи (8) выполнено условие (10). Тогда
фукнция Беллмана имеет вид
⎧
{
}
⎪
rk+1
1+ε
⎨I(-∞,1] (y)min
1,
,
k = 1,N,
rk+1 + |x| ε
Bk (x,y) =
{
}
⎪
r1
1+ε
⎩min
1,
,
k = 0,
r1 + |x| ε
и оптимальное управление определяется выражением
⎧
⎪любое из U∗k (xk) ,
|xk| ≤ rk+1ε-1, yk ≤ 1,
⎪
⎨
-sign(xk) rk+1 - xk
ũ∗k =
,
|xk| > rk+1ε-1, yk ≤ 1,
k = 1,N,
⎪
1+ε
⎪
⎩любое из R,
yk > 1,
⎧
[
]
⎨любое из U∗0 (X) ,
|X| ∈
0, r1ε-1
,
u∗0 (X) =
k = 0,
(
)
⎩-sign(X)r1-X
,
|X| ∈
r1ε-1,+∞
,
1+ε
где множество U∗k (xk) определяется в соответствии с утверждением 1.
Доказательство утверждения 2 вынесено в Приложение.
Нетрудно видеть, что функция Беллмана в задаче (8) при k = 0 не зави-
сит от yk и совпадает с функцией Беллмана в задаче (6), что подтверждает
факт эквивалентности задач (6) и (8) в смысле оптимальных значений кри-
териев. Покажем теперь, что в силу специфики оптимальных управлений в
обеих задачах (а именно: для некоторых областей пространства состояний
оптимальным является целое множество стратегий) эквивалентность задач
(6) и (8) может быть усилена.
45
4.4. Сравнение подходов
Из утверждений 1 и 2 видно, что функция Беллмана в задаче (8) при
k = 0 не зависит от yk и совпадает с функцией Беллмана в задаче (6). Та-
ким образом, функции оптимальных значений вероятностных критериев в
этих задачах совпадают. Более того, эти функции зависят лишь от распре-
деления начального состояния X, параметра ε и r1. Покажем теперь, что
оптимальное управление в задаче (8) можно выбрать таким образом (в силу
того, что оптимальным является целое множество управлений при yk ≤ 1),
что оно совпадает с оптимальным управлением в задаче (6). Для этого вы-
берем управление (с учетом специфики множества U∗k (xk)) в задаче (6) в
следующем виде:
⎧
⎪0,
|xk| ∈ [0,rk] ,
⎪
⎨
sign(xk)rk+1 - xk
(
]
(11)
u∗k =
,
|xk| ∈
rk,rkε-1
,
k = 0,N.
⎪
1-ε
⎪
⎩-sign(xk) rk+1 - xk
(
)
,
|xk| ∈
rkε-1,+∞
,
1+ε
Нетрудно видеть, что в задаче (8) в области yk > 1, k = 1, N , оптимальным
является любое управление из R, и, следовательно, оно может быть выбрано
как
⎧
⎪0,
|xk| ∈ [0, rk+1] ,
⎪
⎨
sign (xk) rk+1 - xk
(
]
(12)
ũ∗k = u∗k =
,
|xk| ∈
rk+1,rk+1ε-1
,
k = 0,N.
⎪
1-ε
⎪
⎩-sign(xk) rk+1 - xk
(
)
,
|xk| ∈
rk+1ε-1,+∞
,
1+ε
Таким образом, оптимальным в задаче (8) может быть выбрано управле-
ние, оптимальное в задаче (6) и не зависящее явно от yk.
5. Заключение
В статье рассмотрена задача оптимального управления дискретной сто-
хастической системой с критерием в форме вероятности пребывания траек-
тории системы на заданных множествах. Найдены достаточные условия су-
ществования оптимального управления в классе измеримых функций, а так-
же выведены соотношения метода динамического программирования, отли-
чающиеся от “классических”, справедливых для задач с вероятностным тер-
минальным критерием. С помощью этих соотношений аналитически решена
задача однопараметрической коррекции траектории движения летательного
аппарата в постановке с ограничениями на траекторию системы. Показана
эквивалентность в смысле оптимальных стратегий и оптимальных значений
критериев указанной задачи и аналогичной задачи с вероятностным терми-
нальным критерием и расширенным пространством состояний.
46
ПРИЛОЖЕНИЕ
Доказательство теоремы. Покажем, что уравнения МДП есте-
ственным образом получаются из эквивалентной задачи с вероятностным тер-
минальным критерием и расширенным пространством состояний. Для этого
введем в рассмотрение переменную yk ∈ R:
yk = max Φi (xi) .
i=0,k
Рассмотрим расширенную систему управления
⎧
⎪xk+1 = fk (xk,uk,ξk) ,
⎨
yk+1 = max {yk, Φk (xk)} ,
k = 0,N,
⎪x0 = X,
⎩
y0 = Φ0 (X) ,
где Φ0 : Rn → (-∞, ϕ] — некоторая ограниченная сверху функция (отсюда
следует, что F0 = Rn). На траекториях расширенной системы рассмотрим
задачу
(Π.1)
P(max{yN+1, ΦN+1 (xN+1)} ≤ ϕ) → max ,
ũ(·)
U
где управление ищется в более широком классе функций ũk = ũk (xk, yk)
Uk,
U
U0 × ...
UN
Uk — множество борелевских функций с ограниченными
на Uk значениями. Запишем уравнения МДП для задачи (П.1):
[
(
)
]
(Π.2)
ũ∗k = arg max M
Bk+1
fk (xk,yk,uk,ξk)
xk, yk ,
uk∈Uk
[
(
)
]
Bk+1
(Π.3)
Bk (x,y) = max M
fk (xk,yk,uk,ξk)
xk = x, yk = y ,
uk∈Uk
(Π.4)
BN+1 (x,y) = I(-∞,ϕ] (max {y, ΦN+1
(x)}) .
В [8, теорема 3, с. 143] приведены достаточные условия, при которых оп-
тимальная стратегия существует в классе измеримых функций для зада-
чи оптимального управления с вероятностным терминальным критерием.
В соответствии с этими достаточными условиями функция правой части
системы должна быть непрерывной для всех k = 0, N , случайные векто-
ры X, ξ0, . . . , ξN независимы, функция терминального состояния (так на-
зываемый точностной функционал) полунепрерывен снизу, а множества
U0,... ,UN компактны. Применим эти условия к задаче (П.1). Получаем, что
если выполнены условия:
1) функции fk (xk, uk, ξk) непрерывны для всех k = 0, N ;
2) функции Φk (xk) непрерывны для всех k = 1, N + 1;
3) функция ΦN+1 (xN+1) ограничена снизу;
4) случайные векторы X, ξ0, . . . , ξN независимы;
5) множества U0, . . . , UN компактны,
47
то оптимальная стратегия существует в классе измеримых функций ũ∗ (·)
U
и определяется в результате решения уравнения Беллмана в форме (П.2).
Покажем теперь, что само уравнение Беллмана допускает упрощение. Пусть
k = N, тогда
BN (x,y) = max P(max{y, ΦN (x), ΦN+1 (fN (x,uN ,ξN))} ≤ ϕ) =
uN ∈UN
= max I(-∞,ϕ] (y)I(-∞,ϕ] (ΦN (x)) P(ΦN+1 (fN (x,uN ,ξN)) ≤ ϕ) =
uN ∈UN
= I(-∞,ϕ] (y)BN (x),
при этом
{
u∗N ,
yN ≤ ϕ,
ũ∗N =
любое из UN ,
yN > ϕ,
где u∗N определяется соотношением (3).
Пусть теперь k = N - 1, тогда имеем
[
BN-1 (x,y) = max M I(-∞,ϕ] (max{yN-1, ΦN-1 (xN-1)})×
uN-1∈UN-1
]
× BN (fN-1 (xN-1,uN-1,ξN-1))xN-1 = x, yN-1 = y =
[
= max I(-∞,ϕ] (y)M I(-∞,ϕ] (ΦN-1 (xN-1)) ×
uN-1∈UN-1
]
× BN (fN-1 (xN-1,uN-1,ξN-1))xN-1 = x, yN-1 = y =
= I(-∞,ϕ] (y)BN-1 (x).
Продолжая аналогичные размышления, получаем, что для всех k = 0, N вы-
полнено равенство
Bk (x,y) = I(-∞,ϕ] (y)Bk (x),
причем
[
]
Bk (x) = max M I(-∞,ϕ] (Φk (xk)) Bk+1 (fk (xk,uk,ξk))xk = x
uk∈Uk
и
{
u∗k,
yk ≤ ϕ,
ũ∗k =
любое из Uk,
yk > ϕ.
Таким образом, доказана справедливость соотношений (3). Заметим теперь,
что компонента yk не влияет на выбор оптимального управления и, более
48
того, в силу того, что при yk > ϕ оптимальным является любое управление
из Uk и выполненоBk (x, y) = 0, получаем, что управление u∗k (xk), k = 0, N,
является оптимальным в задаче (П.1).
Теорема доказана.
Доказательство утверждения 1. Применим метод динамическо-
го программирования из теоремы к решению задачи (6). На шаге k = N по-
лучаем задачу стохастического программирования
(
)
|x + uN (1 + ξN )|
BN (x) = max
I[-rN ,rN ] (x) P
≤1
,
uN
rN+1
решение которой (при |x| ≤ rN ) известно (см. [3, утверждение 1, с. 117]) с
точностью до параметров:
⎧
{
}
⎪любое из U∗N (xN ) ,
|xN | ≤ min
rN, rN+1ε-1
,
⎪
⎨
−sign(xN)rN+1 - xN
u∗N =
,
|xN | > rN+1ε-1, |xN | ≤ rN ,
⎪
1+ε
⎪
⎩любое из R,
|xN | > rN ,
{
}
rN+1
1+ε
BN (x) = I[-rN ,rN ] (x)min
1,
rN+1 + |x| ε
Последнее выражение допускает следующее представление
(
BN (x) = I[-rN ,rN ] (x) I[-rN+1ε-1,rN+1ε-1] (x) +
)
rN+1
1+ε
+ I(-∞,-rN+1ε-1)∪(rN+1ε-1,+∞) (x)
,
rN+1 + |x| ε
откуда с учетом неравенства (10) (из которого следует rN ≤ rN+1ε-1) полу-
чаем:
{
любое из U∗N (xN ) ,
|xN | ≤ rN ,
u∗N =
любое из R,
|xN | > rN ,
BN (x) = I[-rN ,rN ] (x) .
Перейдем теперь к шагу k = N - 1, на котором в соответствии с МДП полу-
чаем
(
)
|x + uN-1 (1 + ξN-1)|
BN-1 (x) = max
I[-rN-1,rN-1] (x) P
≤1
uN-1
rN
Нетрудно видеть, что правая часть уравнения МДП при k = N - 1 совпа-
дает с правой частью уравнения МДП при k = N с точностью до парамет-
ров rk, k = N - 1, N + 1, откуда с учетом (10) получаем аналогичное решение
49
и функцию Беллмана. Продолжая рассуждения по аналогии, заключаем, что
оптимальное управление и функция Беллмана на шагах k = 1, N имеют вид:
{
любое из U∗k (xk) ,
|xk| ∈ [0,rk] ,
u∗k =
любое из R,
|xk| ∈ (rk,+∞),
Bk (x) = I[-rk,rk] (x) .
Перейдем к шагу k = 0. Учитывая тот факт, что F0 = Rn = R (см. начало
раздела 3) получаем задачу стохастического программирования
(
)
|x + u0 (1 + ξ0)|
B0 (x) = maxP
≤1
,
u0
r1
откуда с учетом [3] получаем:
⎧
[
]
⎨любое из U∗0 (X) ,
|X| ∈
0, r1ε-1
,
u∗0 =
(
)
⎩-sign(X)r1-X
,
|X| ∈
r1ε-1,+∞
,
1+ε
{
}
r1
1+ε
B0 (x) = min
1,
r1 + |x| ε
Утверждение 1 доказано.
Доказательство утверждения 2. Применим метод динамическо-
го программирования к решению задачи (8). На шаге k = N получаем задачу
стохастического программирования
(
)
|x + uN (1 + ξN)|
BN (x,y) = maxI(-∞,1] (y)P
≤1
,
uN
rN+1
решение которой (в области y ≤ 1) известно [3] с точностью до параметров:
⎧
⎪любое из U∗N (xN ) ,
|xN| ≤ rN+1ε-1, yN ≤ 1,
⎪
⎨
-sign(xN) rN+1 - xN
ũϕN =
,
|xN| > rN+1ε-1, yN ≤ 1,
⎪
1+ε
⎪
⎩любое из R,
yN > 1,
{
}
rN+1
1+ε
BN (x,y) = I(-∞,1] (y)min
1,
rN+1 + |x| ε
Перейдем теперь к шагу k = N - 1. Получаем, что
[
)
( |x + uN-1 (1 + ξN-1)|
BN-1 (x,y) = max
I(-∞,1] (y)M I(-∞,1]
×
uN-1
rN
{
}]
rN+1
1+ε
× min
1,
rN+1 + |x + uN-1 (1 + ξN-1)| ε
50
Последнее выражение может быть представлено в виде
[
BN-1 (x,y) = max
I(-∞,1] (y)M I(-∞,rN ] (|x + uN-1 (1 + ξN-1)|)×
uN-1
(
× I(-∞,rN+1ε-1] (|x + uN-1 (1 + ξN-1)|) +
)]
rN+1
1+ε
+I(rN+1ε-1, +∞) (|x + uN-1 (1 + ξN-1)|)
,
rN+1 + |x + uN-1 (1 + ξN-1)| ε
откуда с учетом неравенства (10), из которого получаем, что rN ≤ rN+1ε-1,
[
]
BN-1 (x,y) = max
I(-∞,1] (y)M I(-∞,rN ] (|x + uN-1 (1 + ξN-1)|)
=
uN-1
(
)
|x + uN-1 (1 + ξN-1)|
= max
I(-∞,1] (y)P
≤1
uN-1
rN
Видно, что полученное выражение совпадает с выражением для функции
Беллмана для k = N c точностью до параметров rN и rN+1. Продолжая ана-
логичные рассуждения для k = 1, N , получаем выражения для оптимального
управления и функции Беллмана на указанных шагах:
⎧
⎪любое из U∗k (xk) ,
|xk| ≤ rk+1ε-1, yk ≤ 1,
⎪
⎨
-sign(xk)rk+1 - xk
ũϕk =
,
|xk| > rk+1ε-1, yk ≤ 1,
⎪
1+ε
⎪
⎩любое из R,
yk > 1,
{
}
rk+1
1+ε
Bk (x,y) = I(-∞,1] (y)min
1,
k = 1,N.
rk+1 + |x| ε
Рассмотрим теперь шаг k = 0. С учетом y0 = x1 = |X + u0 (1 + ξ0)| справед-
ливо
[
B0 (x,y) = maxM I(-∞,r1] (|x + u0 (1 + ξ0)|) I(-∞, r1] (|x + u0 (1 + ξ0)|)×
u0
(
× I(-∞, r2ε-1] (|x + u0 (1 + ξ0)|)+
)]
r2
1+ε
+I(r2ε-1, +∞) (|x + u0 (1 + ξ0)|)
=
r2 + |x + u0 (1 + ξ0)| ε
[
]
= maxM
= max P(|x + u0 (1 + ξ0) ≤ r1|) =
I(-∞,r1] (|x + u0 (1 + ξ0)|)
u0
u0
{
}
r1
1+ε
= min
1,
r1 + |x| ε
Утверждение 2 доказано.
51
СПИСОК ЛИТЕРАТУРЫ
1.
Малышев В.В., Кибзун А.И. Анализ и синтез высокоточного управления лета-
тельными аппаратами. М.: Машиностроение, 1987.
2.
Азанов В.М., Кан Ю.С. Синтез оптимальных стратегий в задачах управле-
ния стохастическими дискретными системами по критерию вероятности // АиТ.
2017. № 6. C. 57-83.
Azanov V.M., Kan Yu.S. Design of Optimal Strategies in the Problems of Discrete
System Control by the Probabilistic Criterion // Autom. Remote Control. 2017.
V. 78. No. 6. P. 1006-1027.
3.
Азанов В.М., Кан Ю.С. Однопараметрчиеская задача оптимальной коррек-
ции траектории летательного аппарата по критерию вероятности // Изв. РАН.
ТиСУ. 2016. № 2. С. 1-13.
4.
Азанов В.М., Кан Ю.С. Оптимизация коррекции околокруговой орбиты искус-
ственного спутника Земли по вероятностному критерию // Тр. ИСА РАН. 2015.
№ 2. С. 18-26.
5.
Красильщиков М.Н., Малышев В.В., Федоров А.В. Автономная реализация ди-
намических операций на геостационарной орбите. I // Изв. РАН. ТиСУ. 2015.
№ 6. С. 82-95.
6.
Малышев В.В., Старков А.В., Федоров А.В. Cинтез оптимального управления
при решении задачи удержания космического аппарата в орбитальной группи-
ровке // Космонавтика и ракетостроение. 2012. № 4. С. 150-158.
7.
Малышев В.В., Старков А.В., Федоров А.В. Совмещение задач удержания и
уклонения в окрестности опорной геостационарной орбиты // Вестн. Москов.
город. пед. ун-та. Сер. Экономика. 2013. № 1. С. 68-74.
8.
Кибзун А.И., Игнатов А.Н. О существовании оптимальных стратегий в задаче
управления стохастической системой с дискретным временем по вероятностному
критерию // АиТ. 2017. № 10. С. 139-154.
Kibzun A.I., Ignatov A.N. On the Existence of Optimal Strategies in the Control
Problem for a Stochastic Discrete Time System with Respect to the Probability
Criterion // Autom. Remote Control. 2017. V. 78. No. 10. P. 1845-1856.
9.
Кибзун А.И., Игнатов А.Н. Сведение двухшаговой задачи стохастического оп-
тимального управления с билинейной моделью к задаче смешанного целочис-
ленного линейного программирования. // АиТ. 2016. № 12. С. 89-111.
Kibzun A.I., Ignatov A.N. Reduction of the Two-Step Problem of Stochastic Optimal
Control with Bilinear Model to the Problem of Mixed Integer Linear Programming //
Autom. Remote Control. 2016. V. 77. No. 12. P. 2175-2192.
10.
Кибзун А.И., Игнатов А.Н. Двухшаговая задача формирования портфеля цен-
ных бумаг из двух рисковых активов по вероятностному критерию. // АиТ.
2015. № 7. С. 78-100.
Kibzun A.I., Ignatov A.N. The Two-Step Problem of Investment Portfolio Selection
from two Risk Assets via the Probability Criterion // Autom. Remote Control. 2015.
V. 76. No. 7. P. 1201-1220.
11.
Jasour A.M., Aybat N.S., Lagoa C.M. Semidefinite Programming For Chance
Constrained Optimization Over Semialgebraic Sets // SIAM J. Optim. 2015.
№ 25 (3). P. 1411-1440.
12.
Jasour A.M., Lagoa C.M. Convex Chance Constrained Model Predictive Control //
2016. arXiv preprint arXiv:1603.07413.
13.
Jasour A.M., Lagoa C.M. Convex Relaxations of a Probabilistically Robust Control
Design Problem // 52nd IEEE Conf. on Decision and Control. 2013. P. 1892-1897.
52
14. Босов А.В. Обобщенная задача распределения ресурсов программной систе-
мы // Информ. и ее применение. 2014. Т. 8. Вып. 2. С. 39-47.
15. Босов А.В. Задачи анализа и оптимизации для модели пользовательской актив-
ности. Ч. 3. Оптимизация внешних ресурсов // Информ. и ее применение. 2012.
Т. 6. Вып. 2. С. 14-21.
16. Босов А.В. Задачи анализа и оптимизации для модели пользовательской актив-
ности. Ч. 2. Оптимизация внутренних ресурсов // Информ. и ее применение.
2012. Т. 6. Вып. 1. С. 19-26.
17. Ярошевский В.А., Петухов С.В. Оптимальная однопараметрическая коррекция
траекторий космических аппаратов // Космич. исследования. 1970. Вып. 8. № 4.
С. 515-525.
18. Ярошевский В.А., Парышева Г.В. Оптимальное распределение корректирующих
импульсов при однопараметрической коррекции // Космич. исследования. 1965.
Т. III. Вып. 6; 1966. Т. IV. Вып. 1.
19. Азанов В.М. Оптимальное управление линейной дискретной системой по кри-
терию вероятности // АиТ. 2014. № 10. С. 39-51.
Azanov V.M., Kan Yu.S. Optimal Control for Linear Discrete Systems with
Respect to Probabilistic Criteria // Autom. Remote Control. 2014. V. 75. No. 10.
P. 1743-1753.
20. Азанов В.М., Кан Ю.С. Двухсторонняя оценка функции Беллмана в задачах
стохастического оптимального управления дискретными системами по вероят-
ностному критерию качества // АиТ. 2018. № 2. С. 3-18.
Azanov V.M., Kan Yu.S. Bilateral Estimation of the Bellman Function in the
Problems of Optimal Stochastic Control of Discrete Systems by the Probabilistic
Performance Criterion // Autom. Remote Control. 2018. V. 79. No. 2. P. 203-215.
Статья представлена к публикации членом редколлегии Б.М. Миллером.
Поступила в редакцию 29.01.2018
После доработки 26.06.2018
Принята к публикации 08.11.2018
53