Автоматика и телемеханика, № 1, 2019

(agassi.melikov@gmail.com)

(Институт систем управления НАН Азербайджана, Баку),

М.О. ШАХМАЛЫЕВ (mamed.shahmaliyev@gmail.com)

(Национальная академия авиации, Баку)

СИСТЕМА ОБСЛУЖИВАНИЯ M/M/1/∞ С ПОРТЯЩИМИСЯ

ЗАПАСАМИ И ПОВТОРНЫМИ ЗАЯВКАМИ

Предложена модель системы обслуживания с одним сервером, портя-

щимися запасами и повторными заявками, которые могут образовывать

орбиту бесконечного размера. При отсутствии запасов в системе первич-

ные заявки согласно схеме Бернулли либо становятся в очередь, либо

уходят в орбиту. В системе используется (s, S)-политика пополнения запа-

сов. Разработан метод расчета характеристик системы и решается задача

минимизации суммарных штрафов за счет выбора критического уровня

запасов.

Ключевые слова: система обслуживания-запасания, портящиеся запасы,

повторные заявки, алгоритм расчета, оптимизация.

DOI: 10.1134/S0005231019010057

1. Введение

Первыми публикациями, посвященными изучению систем обслуживания-

запасания (Queuing-Inventory Systems, QIS) с долговечными запасами при

наличии повторных заявок, являются [1, 2]. В них авторы независимо друг

от друга различными методами изучили марковскую модель QIS с мгновен-

ным обслуживанием и (s, S)-политикой пополнения запасов. В этой модели

считается, что если в момент поступления первичной заявки (p-заявки) в си-

стеме отсутствуют запасы, то она поступает в орбиту бесконечного размера;

с орбиты повторные заявки (r-заявки) повторяют попытку быть обслужен-

ными после некоторого случайного времени, которое имеет показательную

функцию распределения (ф.р.). В качестве математической модели изучае-

мой системы используется двумерная цепь Маркова (ЦМ), при этом в [1] для

нахождения характеристик системы применяется метод производящих функ-

ций, а в [2] используется метод преобразования Лапласа. Подобные модели с

конечным размером орбиты для настойчивых r-заявок и при использовании

(S - 1, S)-политики изучены в [3, 4].

Модели QIS с долговечными запасами и положительным временем обслу-

живания заявок (т.е. время обслуживания заявок больше нуля) при наличии

повторных заявок изучены в [5-9]. Так, в [5] изучены три класса Марковских

моделей QIS с одним сервером, r-заявками и (s, S)-политикой пополнения

запасов. Для каждого типа моделей построены соответствующие трехмер-

ные ЦМ и показано, что они имеют трехдиагональную производящую мат-

рицу (ПМ); с использованием матрично-геометрического метода [10] найде-

ны стационарные распределения и характеристики изучаемых моделей QIS.

В [6] изучается марковская модель QIS с (s, S)-политикой, где серверы систе-

мы рассматриваются как запасы, при этом запасы пополняются мгновенно.

Если в момент поступления заявки все серверы системы заняты, то заяв-

ка уходит в орбиту бесконечного размера. В [6] построена соответствующая

трехмерная ЦМ и вычислены характеристики системы. В [7] изучена мар-

ковская модель QIS с конечной очередью высокоприоритетных p-заявок. Об-

служивание низкоприоритетных заявок не приводит к уменьшению уровня

запасов системы, при этом они обслуживаются лишь тогда, когда в момен-

ты их поступления сервер системы свободен; иначе они уходят в орбиту ко-

нечного размера, при этом в орбите они становятся нетерпеливыми. В [7]

построена четырехмерная ЦМ для нахождения совместного распределения

числа p-заявок в очереди, числа r-заявок в орбите и уровня запасов системы.

Искомое распределение находится в результате решения матричных урав-

нений. В [8] рассмотрена марковская модель QIS с ограниченной очередью

p-заявок, в которой после завершения обслуживания согласно схеме Бернул-

ли заявка либо уходит в орбиту, либо покидает систему. Орбита имеет ко-

нечную емкость и сервер обслуживает r-заявки лишь тогда, когда в момент

ее генерации в системе нет p-заявок и/или нет запасов, при этом r-заявки не

требуют запасы. Построена трехмерная ЦМ и с применением матричного ме-

тода [10] предложен алгоритм расчета ее стационарного распределения. В [9]

рассмотрена марковская модель QIS с одним сервером и без мест для ожида-

ния p-заявок. Если в момент поступления p-заявки сервер свободен и уровень

запасов больше нуля, то эта заявка принимается на обслуживание; если в мо-

мент поступления p-заявки сервер свободен, но уровень запасов равно нулю,

то эта заявка окончательно покидает систему. Поступившая p-заявка уходит

в орбиту бесконечного размера, если в этот момент сервер занят; если в мо-

мент поступления r-заявки уровень запасов равен нулю или сервер занят, то

она возвращается в орбиту. В [9] построена соответствующая трехмерная ЦМ

и с применением матричного метода [10] предложен алгоритм расчета ее ста-

ционарного распределения.

Модели QIS с портящимися запасами (Perishable QIS, PQIS) и повторными

заявками мало изучены. Авторам известны лишь публикации [11, 12]. В [11]

изучена модель с одним сервером и MAP-потоком, в которой время обслужи-

вания заявок имеет ф.р. фазового типа. В [12] предполагается, что времена

выполнения заказов, пребывания заявок в орбите и жизни запасов имеют

показательные ф.р. В системе используется (s, S)-политика, и заявки уходят

в орбиту, если в момент их поступления все места в ограниченной очереди

заняты. Математической моделью системы является пятимерная ЦМ. С по-

мощью матричного метода [10] разработан алгоритм расчета характеристик

системы. В [12] изучена модель PQIS с отдыхающим сервером, простейшим

потоком и мгновенным обслуживанием. Как и в [11] предполагается, что в

системе используется (s, S)-политика и времена выполнения заказов, пребы-

вания заявок в орбите и жизни запасов имеют показательные ф.р. Сервер

уходит в многократный отдых, если уровень запасов равно нулю. Если в мо-

мент поступления заявки уровень запасов равен нулю или сервер находится

в отдыхе, то она уходит в орбиту бесконечного размера. Математической

моделью системы является трехмерная ЦМ и с помощью матричного метода

разработан алгоритм расчета характеристик системы. Отметим, что в [11, 12]

с целью обеспечения возможности применения матричного метода принима-

ется не реальное допущение о том, что интенсивность поступления заявок

с орбиты является постоянной величиной и не зависит от числа заявок в

орбите.

Модель PQIS с мгновенным обслуживанием и повторными заявками изу-

чена в [13], где можно найти подробный обзор публикаций, посвященных

изучению моделей PQIS.

На русском языке непрерывные модели систем управления с портящими-

ся запасами были исследованы в [14, 15]. Так, в [15] изучена модель системы

управления c непрерывно портящимися запасами, в которой пополнение за-

пасов происходит также непрерывно. Считается, что моменты поступления

заявок образуют простейший поток с интенсивностью, зависящей от цены

продажи запасов, при этом размер покупок является непрерывной случай-

ной величиной. В [15] при релейном управлении интенсивностью потока и

определенных асимптотических условиях, налагаемых на скорости пополне-

ния запасов, найдена плотность распределения уровня запасов системы.

В настоящей статье изучается модель PQIS с одним сервером, простей-

шим потоком, положительным временем обслуживания заявок, неограничен-

ной очередью первичных заявок и повторными заявками. Считается, что при

отсутствии запасов поступившая p-заявка согласно схеме Бернулли либо ста-

новится в очередь, либо уходит в орбиту бесконечного размера. При отсут-

ствии запасов заявки в очереди проявляют нетерпеливость, а r-заявки в орби-

те являются весьма настойчивыми. После завершения обслуживания заявка

согласно схеме Бернулли либо получает запас, либо отказывается получить

запас. Такая схема обслуживания впервые независимо друг от друга была

введена в [7, 16] и далее она применена в [17]. В статье предложена мате-

матическая модель системы в виде трехмерной ЦМ, для изучения которой

применяется метод иерархического фазового укрупнения состояний систе-

мы [18].

Статья организована следующим образом. В разделе 2 приводится описа-

ние модели и дана постановка задачи исследования. В разделе 3 построена

математическая модель изучаемой системы в виде трехмерной цепи Маркова,

разработан алгоритм построения ее производящей матрицы и получены фор-

мулы для расчета точных значений характеристик системы. Приближенный

метод расчета характеристик системы разработан в разделе 4. Результаты

численных экспериментов по расчету и оптимизации модели приводятся в

разделе 5. В разделе 6 даны заключительные замечания.

2. Описание модели и постановка задачи

Рассмотрим модель M/M/1/∞/PQIS/RQ. В систему извне поступает про-

стейший поток идентичных (по размеру) p-заявок, т.е. после обслуживания

каждой заявки уровень запасов на складе уменьшается на единицу. Кроме

того, запасы системы независимо друг от друга становятся непригодными

после случайного времени, которые имеют показательные ф.р. с конечным

средним значением. Считается, что запас, который уже находится на этапе

отпуска по заявке, не может портиться.

Если в момент поступления p-заявки уровень запасов положительный, то

она с вероятностью единица принимается на обслуживание при условии, что

в этот момент сервер является свободным; иначе p-заявка становится в оче-

редь бесконечной длины. Заявки присоединяются к очереди согласно схеме

Бернулли даже тогда, когда уровень запасов равен нулю, т.е. если в момент

поступления очередной p-заявки в системе отсутствуют запасы. В этом слу-

чае p-заявка либо с определенной (положительной) вероятностью становится

в очередь, либо с дополнительной вероятностью уходит в орбиту бесконечно-

го размера для “обдумывания” и повторения своего запроса через некоторое

время.

Считается, что заявки (первичные и повторные) в очереди становятся

нетерпеливыми при отсутствии запасов системы. Интервалы времени между

уходами заявок из очереди имеют показательную ф.р. Уходящая из очереди

нетерпеливая заявка согласно схеме Бернулли либо с определенной (поло-

жительной) вероятностью окончательно уходит из системы, либо с дополни-

тельной вероятностью уходит в орбиту, при этом имеется возможность мно-

гократного ухода в орбиту.

Заявки в орбите не имеют информации как об уровне запасов системы,

так и о состоянии очереди. Если в орбите имеются заявки, то интервалы вре-

мени между их поступлениями имеют показательную ф.р. Повторные заявки

(r-заявки) являются настойчивыми, т.е. если в момент поступления r-заявки

уровень запасов системы равен нулю, то она опять мгновенно возвращается

в орбиту с вероятностью единица. После завершения обслуживания заявки

возможны два решения: (1) заявка отказывается получить запас и уходит из

системы; (2) заявка получает запас и уходит из системы.

Время обслуживания как первичных, так и повторных заявок является

одинаковым, при этом длительность обслуживания зависит от того, получила

ли заявка запас или нет; считается, что в обоих случаях это время имеет

показательную ф.р., но с различными средними значениями.

В системе используется (s, S)-политика пополнения запасов, т.е. предпо-

лагается, что когда уровень запасов опускается до некоторой пороговой ве-

личины s, то отправляется заказ на поставку запасов объема S - s. При этом

для предотвращения случаев многократных заказов необходимо выполнение

соотношения s < S/2. Считается, что заказы выполняются с некоторыми за-

держками, при этом эти задержки являются независимыми друг от друга

положительными случайными величинами, которые имеют общую показа-

тельную ф.р. с конечным средним значением.

Задача состоит в нахождении совместного распределения уровня запасов

системы, суммарного числа заявок в системе и числа r-заявок в орбите. Кро-

ме того, требуется определить усредненные характеристики изучаемой PQIS

и минимизировать суммарные штрафы, связанные с ее функционированием.

3. Точный метод расчета характеристик системы

Введем обозначения:

S — максимальный объем склада системы;

s — точка заказа запасов, s < S/2;

γ-1 — средняя длительность жизни единицы запаса;

λ-1 — среднее время между поступлениями p-заявок;

τ-1 — среднее время пребывания заявок в системе при отсутствии запасов;

φ₁ — вероятность того, что поступившая p-заявка становится в очередь,

если в этот момент в системе отсутствуют запасы;

φ₂ — вероятность того, что поступившая p-заявка уходит в орбиту, если в

этот момент в системе отсутствуют запасы;

ψ₁ - вероятность того, что покидающая очередь из-за нетерпеливости за-

явка уходит из системы;

ψ₂ — вероятность того, что покидающая очередь из-за нетерпеливости за-

явка уходит в орбиту;

σ₁ — вероятность того, что заявка не получает запас и уходит из системы;

σ₂ — вероятность того, что заявка получает запас и уходит из системы;

μ-11 — среднее время обслуживания заявок, которые не получают запас;

μ-12 — среднее время обслуживания заявок, которые получают запас;

ν-1 — среднее время задержки выполнения заказа;

η-1 — среднее время пребывания заявки в орбите.

Работа системы описывается трехмерной ЦМ с состояниями вида (m, n, k),

где m — уровень запасов на складе, n — число заявок в очереди и k — число

r-заявок в орбите. Пространство состояний (ПС) этой цепи определяется так:

⋃

⋂

(3.1)

E= E_k, E_k

E_k′ = ∅, k = k^′,

k=0

где

E_k = {(m,n,k) : m = 0,1,... ,S,n = 0,1,... }, k = 0,1,2,...

Переходы между состояниями внутри класса ПС (3.1) происходят при по-

ступлении p-заявок и пополнении запасов системы, а также после завершения

обслуживания заявок, времени жизни запасов и ухода заявок из очереди из-

за их нетерпеливости. Переходы между состояниями из различных классов

E_k и E_k′, k = k^′ ПС (3.1) связаны с уходами заявок в орбиту и поступлением

r-заявок с орбиты.

Интенсивность перехода из состояния (m₁, n₁, k₁) в состояние (m₂, n₂, k₂)

обозначим через q((m₁, n₁, k₁), (m₂, n₂, k₂)). Совокупность этих величин опре-

деляет ПМ данной цепи. Представим предложенный авторами псевдо-код ал-

горитма генерации элементов ПМ изучаемой цепи Маркова.

function QElem(m₁, n₁, k₁, m₂, n₂, k₂)

define q := 0

if k₂ = k₁ and m₁ > 0 then

if m₂ = m₁ and n₂ = n₁ + 1 then q := λ

else if m₂ = m₁ and n₂ = n₁ - 1 then q := μ₁σ₁

else if m₂ = m₁ - 1 and n₂ = n₁ - 1 then q := μ₂σ₂

else if m₂ = m₁ - 1 and n₂ = n₁ = 0 then q := m₁γ

else if m₂ = m₁ - 1 and n₂ = n₁ > 0 then q := (m₁ - 1)γ

else if m₁ <= s and m₂ = m₁ + S - s and n₂ = n₁ then q := ν

end if

else if k₂ = k₁ and m₁ = 0 then

if m₂ = 0 and n₂ = n₁ + 1 then q := λφ₁

else if m₂ = 0 and n₂ = n₁ - 1 then q := n₁τψ₁

else if m₂ = S - s and n₂ = n₁ then q := ν

end if

else if k₂ = k₁ then

if n₂ = n₁ and k₂ = k₁ + 1 and m₁ = m₂ = 0 then q := λφ₂

else if n₂ = n₁ - 1 and k₂ = k₁ + 1 and m₁ = m₂ = 0 then q := n₁τψ₂

else if n₂ = n₁ + 1 and k₂ = k₁ - 1 and m₁ = m₂ > 0 then q := k₁η

end if

return q

end function

Стационарную вероятность состояния (m, n, k) обозначим через p(m, n, k).

Условие существования стационарного режима определяется далее.

Основными характеристиками системы являются следующие величины:

средний уровень запасов на складе (S_av), средняя интенсивность порчи за-

пасов системы (Γ_av), средняя интенсивность заказов (RR); средняя длина

очереди заявок в системе (L_s); среднее число r-заявок в орбите L_o, интенсив-

ности потери заявок из очереди из-за их нетерпеливости (RL_q). Они находят-

ся через стационарные вероятности состояний. Так, средний уровень запасов,

среднее число заявок в системе и в орбите определяются как математические

ожидания соответствующих с.в.:

∑

(3.2)

S_av =

mp(m,n,k);

(m,n,k)∈E

∑

(3.3)

L_s =

np(m,n,k);

(m,n,k)∈E

∑

(3.4)

L_o =

kp(m,n,k).

(m,n,k)∈E

Средняя интенсивность порчи запасов вычисляется как

⎛

∑

(3.5) Γ_av = γ^⎝

p(m, 0, k)+

m=1

(m,0,k)∈E

⎞

∑

+ (m - 1)

p(m, n, k)I(n > 0)^⎠ ,

m=2

(m,n,k)∈E

где I(A) - индикаторная функция события A.

Заказы запасов осуществляются тогда, когда их уровень опускается до

значения s независимо от состояния очереди и числа заявок в орбите, т.е.:

∑

(3.6) RR = γ(s + 1)

p(s + 1, 0, k)+

(s+1,0,k)∈E

∑

+ (μ₂σ₂ + sγ)

p(s + 1, n, k)I(n > 0).

(s+1,n,k)∈E

Интенсивность ухода заявок из очереди из-за их нетерпеливости опреде-

ляется так:

∑

(3.7)

RL_q = τψ₁

np(0,n,k).

(0,n,k)∈E

Нахождение характеристик (3.2)-(3.7) требует определения вероятностей

состояний, которые удовлетворяют системе уравнений равновесия (СУР).

Она составляется на основе ПМ и представляет собой бесконечную систему

линейных уравнений.

Вычисление вероятностей состояний с помощью метода многомерных про-

изводящих функций связано с известными методологическими и вычисли-

тельными трудностями. Применение популярных матрично-геометрического

метода [10] или метода спектрального расширения [19] потребует введения

некоторых условий относительно элементов производящей матрицы, изучае-

мой трехмерной ЦМ с целью ее унификации. Часто эти допущения не соот-

ветствуют реальным условиям работы системы. Так, в данной модели для их

применения необходимо принимать нереальные допущения о постоянстве ин-

тенсивностей поступления r-заявок с орбиты, а также интенсивностей ухода

p-заявок из очереди из-за их нетерпеливости. Кроме того, указанные методы

часто страдают вычислительной неустойчивостью из-за плохой обусловлен-

ности используемых матриц большой размерности. Поэтому здесь для ре-

шения указанной проблемы используется альтернативный (приближенный)

метод.

4. Приближенный метод расчета характеристик системы

Этот метод корректно можно применить для систем, в которых интен-

сивности переходов между состояниями, входящими в различные классы E_k

и E_k′, k = k^′, оказываются малыми по сравнению с интенсивностями перехо-

дов между состояниями внутри классов. Это допущение, в частности, выпол-

няется в системах, в которых интенсивность p-заявок существенно больше

интенсивности r-заявок, т.е. когда выполняется условие η ≪ λ.

На основе расщепления (3.1) строится функция укрупнения U₁(m, n, k) =

= 〈k〉, где 〈k〉 означает укрупненное состояние, которое включает в себя все

состояния из класса E_k. Множество укрупненных состояний обозначается че-

рез Ω₁ = {〈k〉 : k = 0, 1, . . . }. Тогда имеем:

(4.1)

p(m, n, k) ≈ ρ^k(m, n)π₁

(〈k〉),

где ρ^k(m, n) — вероятность состояния (m, n) внутри расщепленной модели с

ПС E_k и π₁(〈k〉) — вероятность укрупненного состояния 〈k〉, 〈k〉 ∈ Ω₁.

Из (4.1) заключаем, что для решения поставленной задачи потребуется

нахождение вероятностей состояний бесконечного числа двумерных и одной

одномерной цепи Маркова, при этом все эти цепи имеют бесконечное про-

странство состояний.

Для нахождения вероятностей состояний ρ^k(m, n) предлагается к указан-

ным двумерным цепям Маркова с ПС E_k, k = 0, 1, . . . , еще раз применить

алгоритм фазового укрупнения состояний. Расщепленные модели с ПС E_k,

k = 0,1,..., являются идентичными двумерными ЦМ, поэтому далее фикси-

руется индекс k и рассматривается следующее расщепление:

⋃

⋂

(4.2)

E = E^mk, Em1k

Em2k=∅,m1=m2^,

m=0

где

E^mk = {(m,n,k) ∈ E_k : n = 0,1,... } , m = 0,... ,S.

На основе расщепления (4.2) строится функция укрупнения U₂(m, n, k) =

= 〈m〉, где 〈m〉 означает укрупненное состояние, которое включает в себя

все состояния из класса E^mk. Обозначим Ω₂ = {〈m〉 : m = 0, 1, . . . , S}. Тогда

имеем:

(4.3)

ρ^k(m,n) ≈ ρ^km(n)πk2

(〈m〉),

где ρ^km(n) — вероятность состояния (m, n) внутри расщепленной модели с

пространством состояний E^mk и πk2(〈m〉) — вероятность укрупненного состоя-

ния 〈m〉, 〈m〉 ∈ Ω₂.

Интенсивности переходов между состояниями расщепленной модели

с ПС E^mk не зависят от индекса k, поэтому далее в обозначениях вероятностей

состояний расщепленных моделей ρ^km(n) и укрупненных состояний πk2(〈m〉)

верхний индекс k опускается. Из алгоритма построения ПМ исходной модели

(см. псевдо-код) заключаем, что вероятности состояний внутри всех расщеп-

ленных моделей с ПС E^mk, m = 1, . . . , S, совпадают с вероятностями состоя-

ний модели M/M/1/∞ с загрузкой a = λ/(μ₁σ₁) Эрланг (Эрл), т.е.

(4.4)

ρ_m(n) = aⁿ

(1 - a), m = 1, . . . , S.

Замечание 1. Здесь предполагается, что выполняется условие эргодич-

ности модели, т.е. a < 1.

Замечание 2. Поскольку величины ρ_m(n), m = 1,...,S, не зависят от

индекса m, то далее этот индекс опускается.

Также из алгоритма построения ПМ исходной модели (см. псевдо-код) за-

ключаем, что вероятности состояний внутри расщепленной модели с ПС E0k

совпадают с вероятностями состояний модели M/M/∞ с загрузкой b =

= λφ₁/τψ₁ Эрл, т.е.

(4.5)

ρ₀(n) = θ_n(b), n = 0, 1, . . .

Здесь и в дальнейшем

θ_n(b) =

e^-b,

,n = 0,1,...

Интенсивности переходов между укрупненными состояниями 〈m₁〉, 〈m₂〉 ∈

∈ Ω₂ обозначаются через q₁(〈m₁〉,〈m₂〉). Эти величины вычисляются так:

∑

(4.6)

q₁(〈m₁〉,〈m₂〉) =

q((m₁, n₁, k), (m₂, n₂, k))ρm1 (n₁

(m₁,n₁,k)∈Em1

С учетом приведенного псевдо-кода, выражений (4.4) и (4.5) из (4.6) после

определенных преобразований находим, что q₁(〈m₁〉, 〈m₂〉) определяются из

соотношений:

⎧

⎨Λ1(m1), если m2 = m1 - 1,

q₁(〈m₁〉,〈m₂〉) =

ν,

если m₁ ≤ s, m₂ = m₁ + S - s,

⎩

в остальных случаях,

где

Λ₁(m₁) = m₁γ(1 - a) + a(μ₂σ₂ + (m₁ - 1)γ), m₁ = 1,2,... ,S.

Отсюда имеем (см. [13]):

⎧

⎨αmπ2(〈s + 1〉), если 0 ≤ m ≤ s,

(4.7)

π₂(〈m〉) =

β_mπ₂(〈s + 1〉), если s + 1 ≤ m ≤ S - s,

⎩

χ_mπ₂(〈s + 1〉), если S - s + 1 ≤ m ≤ S,

где

∏

Λ₁(i)

Λ₁(s + 1)

α_m =

β_m =

ν + Λ₁(i - 1)

Λ₁(m)

i=m+1

∑

χ_m =

α_i, Λ₁(0) = 0;

Λ₁(m)

i=m-S+s

(

)-1

∑

π₂(〈s + 1〉) =

α_m +

β_m +

χ_m

m=0

m=s+1

m=S-s+1

Интенсивности переходов между укрупненными состояниями 〈k₁〉, 〈k₂〉 ∈

∈ Ω₁, обозначаются через q₂(〈k₁〉,〈k₂〉). Они вычисляются следующим обра-

зом:

∑

(4.8)

q₂(〈k₁〉,〈k₂〉) =

q((m, n, k), (m^′, n^′, k^′))ρ^k

(m, n).

(m,n,k)∈E_k

С учетом псевдо-кода, выражений (4.3)-(4.5) и (4.7) из (4.8) после опреде-

ленных преобразований находим, что

⎧

⎨Λ2,

если k₂ = k₁ + 1 ,

(4.9)

q₂(〈k₁〉,〈k₂〉) =

k₁M₂,

если k₂ = k₁ - 1 ,

⎩

в остальных случаях ,

где

(

)

ψ₂

Λ₂ = λ φ₂ + φ₁

M₂ = η(1 - π₂(〈0〉)).

ψ₁

Следовательно, из (4.9) заключаем, что вероятности укрупненных состоя-

ний π₁(〈k〉), 〈k〉 ∈ Ω₁, совпадают с вероятностями состояний модели M/M/∞

с загрузкой c = Λ₂/M₂ Эрл, т.е

(4.10)

π₁(〈k〉) = θ_k

(c), k = 0, 1, . . .

Окончательно, с учетом (4.1), (4.4), (4.5), (4.7) и (4.10) находим, что иско-

мые вероятности состояний изучаемой трехмерной ЦМ определяются так:

(4.11)

p(m, n, k) ≈ ρ_m(n)π₂(〈m〉)π₁

(〈k〉).

Далее с учетом (4.11) после определенных преобразований из (3.2)-(3.7)

получим формулы для приближенного расчета характеристик изучаемой си-

стемы:

∑

(4.12)

S_av ≈

mπ₂

(〈m〉);

m=1

∑

(4.13)

Γ_av ≈ γ

(m - a)π₂

(〈m〉);

m=1

(4.14)

RR ≈ π₂(〈s + 1〉)[(s + 1)γ(1 - a) + (sγ + μ₂σ₂

)a];

(4.15)

L_s ≈ π₂(〈0〉)b + (1 - π₂(〈0〉))

;

1-a

(4.16)

L_o

≈ c;

(4.17)

RL_q ≈ λφ₁π₂

(〈0〉).

5. Численные результаты

Сначала рассмотрим задачу минимизации суммарных штрафов (Total

Cost, TC), связанных с функционированием системы. Эти штрафы включают

расходы, связанные с заказом, хранением и порчей запасов, а также штрафы

из-за ожидания заявок в очереди и их потери. Иными словами, указанные

штрафы определяются так:

(5.1)

TC(s) = (K + c_r(S - s))RR + c_hS_av + c_pΓ_av + c_lRL_q + c_w(L_s + L_o

где K — фиксированная цена одного заказа, c_r — цена единицы объема запаса;

c_h — цена хранения единицы объема запасов за единицу времени; c_p — цена

порчи единицы запаса; c_l — штрафы за потери одной заявки; c_w — цена за

единицу времени пребывания в системе (или в орбите) одной заявки.

Замечание 3. Считаем, что все параметры системы, кроме критическо-

го уровня запасов (т.е. s), являются фиксированными величинами. Для ком-

пактности записи в (5.1) лишь в левой части (в выражении функционала T C)

в скобках указан оптимизируемый параметр s. Очевидно, что все функции

в правой части (5.1), которые обозначают характеристики системы, также

зависят от этого параметра.

Задача оптимизации записывается так:

{

}

(5.2)

s^∗ = argmin

TC(s) : 0 ≤ s ≤ s^′

где

⎧

⎪⌈S⌉

⎨

если S - нечетное число,

s^′ =

⌈x⌉— целая часть x.

⎪

⎩^S

- 1, если S - четное число,

При любых значениях входных параметров задача (5.2) имеет решение,

так как множество возможных решений является дискретным и конечным.

Вместе с тем из-за многочисленности параметров, от которых зависят функ-

ции, входящие в правую часть (5.1), не удается делать общее заключение о

выпуклости (или вогнутости) функционала T C, поэтому для решения (5.2)

далее использован метод полного перебора.

Предположим, что система может заказывать запасы у нескольких постав-

щиков, при этом времена выполнения заказов и стоимости за единицу заказов

у различных поставщиков отличаются друг от друга. При этом считается,

что с ростом скорости выполнения заказа растет и стоимость за единицу

заказов.

Постоянные значения исходных данных системы и коэффициентов в вы-

ражении функционала (5.1) выбирались так:

S = 15, λ = 20, μ₁ = 60, μ₂ = 10, η = 5, γ = 2,

τ = 1,5, σ₁ = 0,4, φ₁ = 0,3, ψ₁ = 0,8;

c_h = 0,5, c_p = 0,2, c_l = 2,0, c_w = 1.

Результаты решения задачи (5.2) показаны в таблице, где T C^∗ — ми-

нимальное значение функционала (5.2). Из таблицы видно, что для дан-

ной системы целесообразно пользоваться услугами второго поставщика. Ана-

лиз результатов оптимизационной задачи (5.2) показывает, что с ростом

интенсивности пополнения запасов значение критического уровня запасов

не увеличивается. Иными словами, использование услуг “быстрых” постав-

щиков позволяет поддерживать достаточно низкий критический уровень

запасов.

Результаты решения задачи (5.2)

Номер

(k, c_r)

s^∗

TC^∗

поставщика

0,5

(2; 0,1)

22,92385

(3; 0,1)

20,26252

1,5

(4,5; 0,15)

21,09278

(5; 0,2)

21,83515

2,5

(5,5; 0,2)

21,95194

(7; 0,35)

25,28343

Теперь рассмотрим вопросы точности формул (4.12)-(4.17), при этом их

точность оценивается с помощью имитационного моделирования (при разра-

ботке программы имитационного моделирования использованы алгоритмы,

предложенные в [20]).

Характеристики системы разделены на две группы: первая группа оцени-

вает работу части “системы управления запасами” (формулы (4.12)-(4.14)),

а вторая группа — “системы обслуживания заявок” (формулы (4.15)-(4.17)).

На рис. 1 и 2 приводятся результаты сравнения значений характеристик си-

стемы при использовании различных подходов для указанных выше значений

параметров системы.

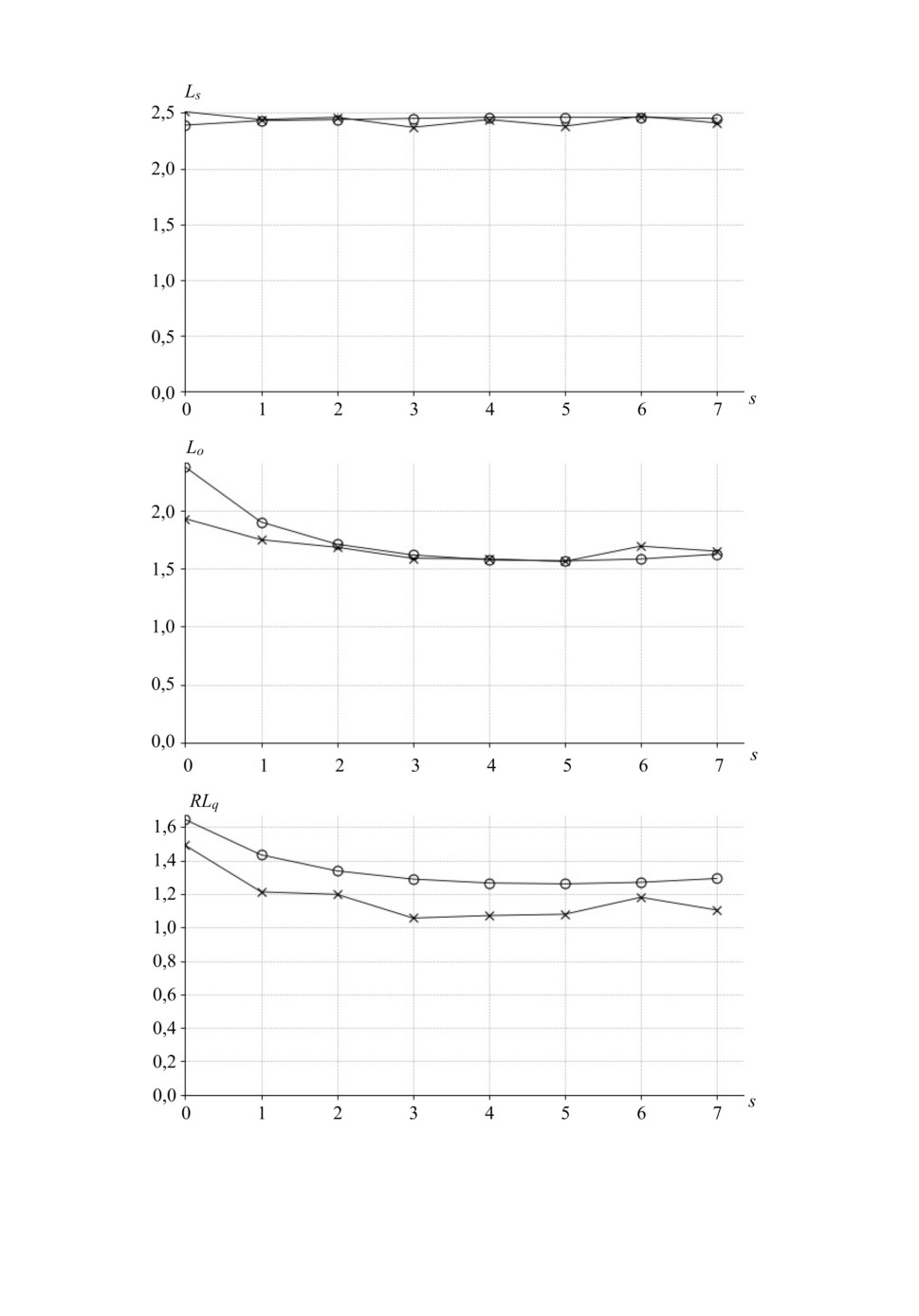
На рис. 1 и 2 символы o и × означают результаты, полученные с по-

мощью разработанных приближенных формул (4.12)-(4.17) и имитационно-

го моделирования соответственно. Отметим, что эти формулы имеют очень

высокую точность для первой группы (см. рис. 1), так как здесь результа-

ты обоих подходов почти совпадают. Иными словами, максимальная отно-

сительная погрешность для характеристик (4.12)-(4.14) при использовании

предложенных приближенных формул и имитационного моделирования со-

ставляет 0,007, 0,012 и 0,023 соответственно. Для второй группы предложен-

ные приближенные формулы также имеют достаточно высокую точность,

при этом небольшая погрешность наблюдается для характеристики (4.16)

(см. рис. 2). Для этой группы максимальная относительная погрешность для

характеристик (4.15)-(4.17) при использовании предложенных приближен-

ных формул и имитационного моделирования составляет 0,048, 0,193 и 0,182

соответственно.

6. Заключение

Предложена марковская модель системы обслуживания-запасания с пор-

тящимися запасами и положительным временем обслуживания заявок с по-

мощью одного сервера. При отсутствии запасов первичные заявки согласно

схеме Бернулли либо уходят в орбиту бесконечного размера, либо присоеди-

няются к очереди бесконечной длины. Заявки являются нетерпеливыми лишь

тогда, когда уровень запасов системы равен нулю, при этом интенсивность

ухода заявок из очереди, а также интенсивность поступления повторных

заявок с орбиты зависят от числа заявок в очереди и в орбите соответствен-

но. В системе принята (s, S)-политика пополнения запасов, при этом время

выполнения заказа является положительной случайной величиной.

Предложена трехмерная цепь Маркова, которая является математической

моделью изучаемой системы, и разработан алгоритм построения ее произво-

дящей матрицы. Разработан приближенный метод вычисления вероятностей

состояний этой цепи и найдены явные формулы вычисления ее характери-

стик. Решена задача минимизации суммарных штрафов системы, связанных

с заказом, хранением и порчей запасов, а также с ожиданием и потерей

заявок.

В качестве направлений дальнейших исследований следует указать изуче-

ние подобных моделей при наличии MAP потока заявок, произвольной ф.р.

времени их обслуживания, а также при использовании других политик по-

полнения запасов, в частности, рандомизированной политики, политики пе-

ременного объема заказов и т.д. Большой научный и практический интерес

представляют также вопросы решения задач минимизации суммарных штра-

фов при наличии определенных ограничений на характеристики системы, а

также изучение инвариантности оптимальных решений относительно изме-

нения нагрузочных параметров системы.

СПИСОК ЛИТЕРАТУРЫ

Artalejo J.R., Krishnamoorthy A., Lopez-Herrero M.J. Numerical Analysis of (s, S)

Inventory System with Repeated Attempts // Ann. Oper. Res. 2006. V. 141. P. 67-83.

Ushakumari P.V. On (s, S) Inventory System with Random Lead Time and Repeated

Demands // J. Appl. Math. Stoch. Anal. 2006. Article ID 81508.

Lopez-Herrero M.J. Waiting Time and Other First-Pasage Time Measures in an (s, S)

Inventory System with Repeated Attempts and Finite Retrial Group // Comput.

Oper. Res. 2010. V. 37. P. 1256-1261.

Anbazhagan N., Wang J., Gomathi D. Base Stock Policy with Retrial Demands //

Appl. Math. Model. 2013. V. 37. P. 4464-4473.

Krishnamoorthy A., Jose K.P. Comparision of Inventory Systems with Service,

Positive Lead-Time, Loss, and Retrial of Customers // J. Appl. Math. Stoch. Anal.

(Hindawi Publishing Corparation). V. 2007. Article ID 37848.

Nair A.N., Jacob M.J. (s, S) Inventory System with Positive Service Time and

Retrial of Demands: an Approach Through Multi-Server Queues // ISRN Oper.

Res. (Hindawi Publishing Corparation). V. 2014. Article ID 596031.

Yadavalli V.S.S., Anbazhagan N., Jeganathan K. A Retrial Inventory System with

Impatient Customers // Appl. Math. Inform. Sci. 2015. V. 9. No. 2. P. 637-650.

Amirthakodi M., Sivakumar B. An Inventory System with Service Facility and Finite

Orbit for Feedback Customers // OPSEARCH. 2015. V. 52. No. 2. P. 225-255.

Manikandan R., Nair S.S. M/M/1/1 Queuing-Inventory System with Retrial of

Unsatisfied Customers // Comm. Appl. Anal. 2017. V. 21. No. 2. P. 217-236.

10.

Neuts M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic

Approach. Baltimore: John Hopkins Univ. Press, 1981.

11.

Manuel P., Sivakumar B., Arivarignan G. A Perishable Inventory System with

Service Facilities and Retrial Customers // Comput. Ind. Eng. 2008. V.

54.

P. 484-501.

12.

Sivakumar B. An Inventory System with Retrial Demands and Multiple Server

Vacation // Quality Technol. Quantit. Management. 2011. V. 8. No. 2. P. 125-146.

13. Melikov A.Z., Ponomarenko L.A., Shahmaliyev M.O. Models of Perishable Queuing-

Inventory Systems with Repeated Customers // J. Autom. Inform. Sci. 2016. V. 48.

No. 6. P. 22-38.

14. Новицкая Е.В., Терпугов А.Ф. Оптимизация розничной продажи скоропортя-

щейся продукции. Томск: Изд-во Том. ун-та, 2004.

15. Лившиц К.И., Ульянова Е.С. Диффузионная аппроксимация процесса произ-

водства и сбыта скоропортящейся продукции // Изв. вузов. Физика. 2015. Т. 58.

№ 11/2. С. 281-285.

16. Krishnamoorthy A., Manikandan R., Lakshmy B. Revisit to Queuing-Inventory

System with Positive Service Time // Ann. Oper. Res. 2015. V. 233. P. 221-236.

17. Melikov A.Z., Ponomarenko L.A., Shahmaliyev M.O. Analysis of Perishable

Queuing-Inventory Systems with Different Types of Requests // J. Autom. Inform.

Sci. 2017. V. 49. No. 9. P. 42-60.

18. Melikov A.Z., Ponomarenko L.A., Rustamov A.M. Approximate Analysis of

Queuing-Inventory System with Earlier and Delayed Vacations // Autom. Remote

Control. 2017. V. 78. No. 11. P. 1991-2003.

Меликов А.З., Пономаренко Л.А., Рустамов А.М. Приближенный анализ систе-

мы обслуживания-запасания с ранним и запаздывающими отдыхами сервера //

АиТ. 2017. № 11. С. 64-78.

19. Mitrani I., Chakka R. Spectral Expansion Solution for a Class of Markov Models:

Application and Comparison with the Matrix-Geometric Method // Performance

Evaluat. 1995. V. 23. P. 241-260.

20. Gillespie D.T. A General Method for Numerically Simulating the Stochastic Time

Evolution of Coupled Chemical Reactions // J. Comput. Phys. 1976. V.

22.

P. 403-434.

Статья представлена к публикации членом редколлегии В.М. Вишневским.

Поступила в редакцию 09.04.2018

После доработки 23.07.2018

Принята к публикации 08.11.2018