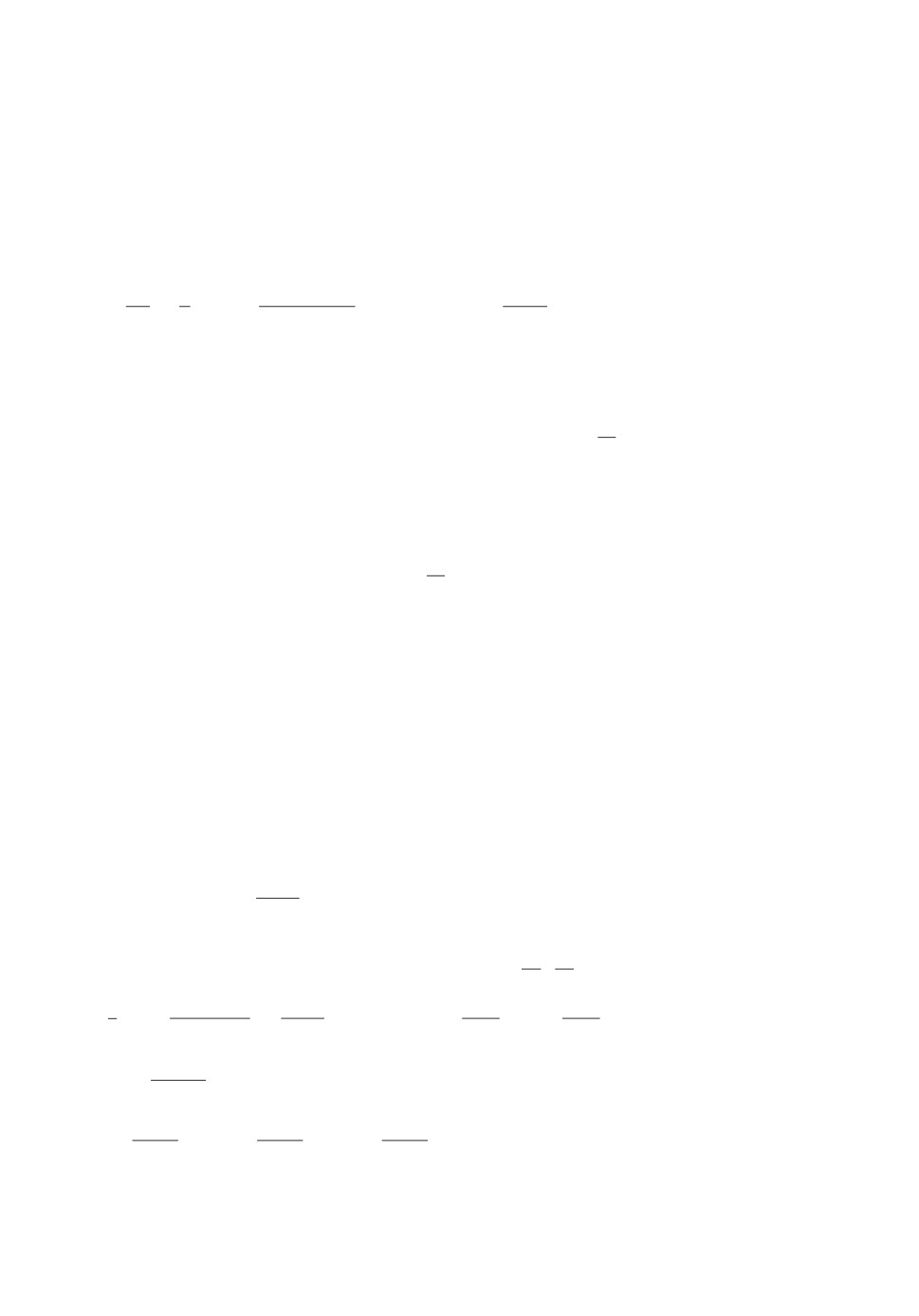Автоматика и телемеханика, № 1, 2019
Управление в технических системах
© 2019 г. И.С. ПОЛЯНСКИЙ, канд. техн. наук (van341@mail.ru)
(Академия ФСО России, Орёл),
Н.С. АРХИПОВ, д-р техн. наук (arhns97@mail.ru)
(ЗАО «Эврика», Санкт-Петербург),
С.Ю. МИСЮРИН, д-р физ.-мат. наук (ssmmrr@mail.ru)
(Национальный исследовательский ядерный университет «МИФИ», Москва)
О РЕШЕНИИ ПРОБЛЕМЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
АДАПТИВНОЙ МНОГОЛУЧЕВОЙ ЗЕРКАЛЬНОЙ АНТЕННОЙ
Рассмотрено решение задачи оптимального управления адаптивной
многолучевой зеркальной антенной. Задача с применением принципа мак-
симума Понтрягина сведена к решению системы обыкновенных диффе-
ренциальных уравнений. Решение полученной системы предполагается
выполнять численно с использованием современных методов типа Рунге-
Кутты и гибридных эволюционных алгоритмов. Оценка вектора состоя-
ния выполнена по критерию максимума правдоподобия при решении
порожденного стохастического дифференциального уравнения Фоккера-
Планка-Колмогорова. При этом функция апостериорной плотности ве-
роятности сопоставлена с нормированным значением плотности потока
энергии в раскрыве облучателей. Определена способность подавления по-
мех адаптивной многолучевой зеркальной антенной. Приведен пример ре-
шения задачи управления.
Ключевые слова: адаптивная многолучевая зеркальная антенна, подав-
ление помех, уравнение Фоккера-Планка-Колмогорова, принцип макси-
мума Понтрягина.
DOI: 10.1134/S0005231019010069
1. Введение
Теория оптимального приема сигналов средствами многоканальной ра-
диосвязи на фоне помех получила широкое развитие в работах отечествен-
ных и зарубежных ученых (таких как О.Е. Антонов, В.Г. Валеев, Г. Ван-
Трис, С. Кассама, Д.Д. Кловский, А.П. Лукошкин, Дж. Мелс, Э. Сейдж,
В.И. Тихонов, Б. Уидроу, С.Е. Фалькович, Я.Д. Ширман, М.С. Ярлыков и
др.) и связана с достижениями антенной техники - появлением антенных
решеток (АР). Эти результаты положены в основу корреляционной теории
пространственно-временной обработки сигналов (ПВОС), развитой Т. Кай-
латцевым, В.Ф. Комаровичем, М.П. Поповым, Ю.Г. Сосулиным, С.С. Щес-
няком и др. [1], и по сути сориентированы на решение проблемы синтеза адап-
тивных АР (ААР), инвариантных к воздействию преднамеренных и непред-
намеренных помех [2-4]. Наиболее часто во всех определениях в антенной
технике упоминается факт априорной известности о направлении на источ-
ник полезного сигнала и различие в направлении прихода полезного сигнала
83
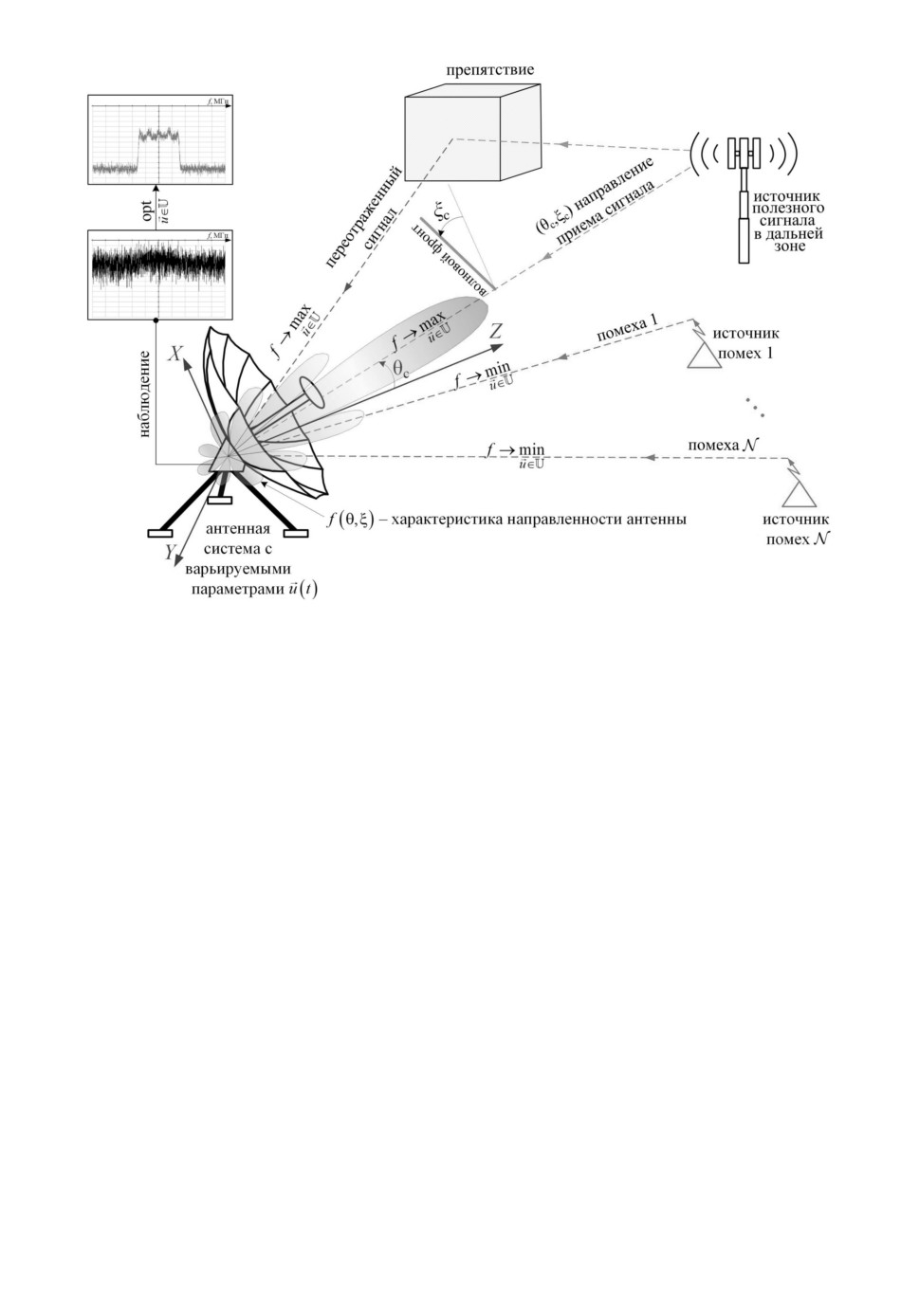
Рис. 1. Адаптация антенной системы к условиям сигнально-помеховой обстановки.
и подавляемых помех. Адаптация антенны сводится к формированию харак-
теристики направленности с провалами (минимумами) в направлениях на ис-
точники помех при максимизации уровня полезного сигнала (рис. 1). Энерге-
тические и конструктивно-технологические ограничения антенных решеток
для M степеней свободы [3, 5, 6] (M - число элементов ААР) затрудняют
эффективное решение указанной проблемы, в частности, и практическое во-
площение инвариантной к помеховым сигналам ААР в целом.
Попытки разработки инвариантной к помеховым сигналам антенной си-
стемы с учетом достижений адаптивной оптики [7] привели к разработке
адаптивных многолучевых зеркальных антенн (АМЛЗА) с деформируемым
рефлектором. Зависимость свойств АМЛЗА от особенностей конструкции,
взаимного размещения облучающих элементов [8] и формы деформируемого
рефлектора [9] приводит к выявлению дополнительных возможностей антен-
ны при реализации ПВОС [10].
В статье рассмотрено решение указанной проблемы с применением раз-
работанных авторами методов анализа и синтеза многолучевых зеркальных
антенн [9, 11-14].
2. Содержательная постановка задачи
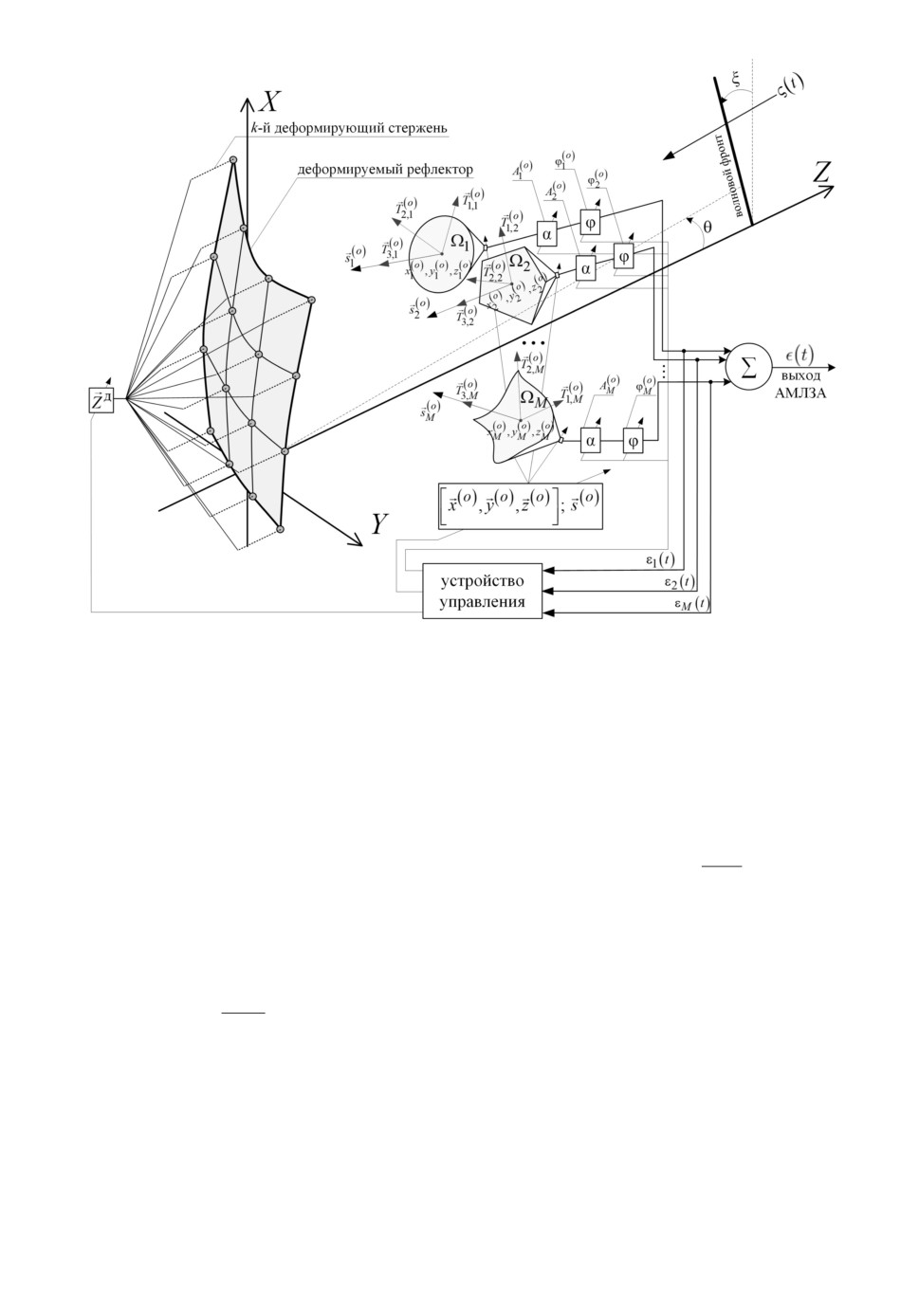
АМЛЗА представим деформируемым рефлектором и M облучателями
(рис. 2). В качестве управляемых параметров выберем [11]: амплитуду Amo)
84
Рис. 2. Обобщенная схема адаптивной многолучевой зеркальной антенны.
и фазу ϕmo) тока возбуждения m-го облучателя; угол νmo) поворота плос-
кости Ωm в системе координат рефлектора; координаты центра раскрыва
m-го облучателя - xmo), ymo), zmo); орт нормали smo) к плоскости Ωm, харак-
теризующий ориентацию m-го облучателя; форму отражающей поверхности,
формируемую K-мерной системой приводов, которые воздействуют на упру-
гую поверхность отражателя при параметризации переменной Zдk положения
k-го деформирующего стержня относительно оси OZ, где k = 1, K.
(
)
Пусть АМЛЗА принимает из дальней зоны с направления
θ,ξ
неко-
{
(
)
(
)
(
)}
E(ς)
H(ς)
торый сигнал ς
t
, заданный электромагнитной волной
t
,
t
с
плоским(ф)азовым фронтом, а с выхода АМЛ(З)А наблюдается суммарный
сигнал ϵ
t
, сформированный из сигналов ςm
t
с выходов m-х облучате-
(
)
лей, где m = 1, M. В физическом смысле ςm
t
характеризуется величиной
(
)
∮
(
Em
ЭДС Xm
t
=
t) dl, которая определяется мгновенным значением на-
Lm
(
)
пряженности электрического поляEm
t
, наводимого в режиме приема на
некотором замкнутом контуре Lm внутри m-го облучателя. Для определе-
(
)
(
)
(
( ))
ния зависимости между входным ς
t
и выходнымиX
t
=
Xm
{
} Mзначе-
ниями рассмотрим задачу дифракции внешнего поля
E(ς),H(ς) с учетом
следующих допущений: 1) деформируемый рефлектор представляет собой
85
бесконечно тонкую идеально проводящую гладкую поверхность S′; 2) m-й об-
лучатель представляется объемом Vm, который ограничен раскрывом Ωm и
бесконечно тонкой идеально проводящей поверхностью Sm; 3) Vm задается
однородной изотропной средой с диэлектрической и магнитной проницаемо-
стями εam и μam; 4) область V0 распространения ЭМП между рефлектором и
облучателями является однородной изотропной средой с диэлектрической и
магнитной проницаемостями εa0 и μa0. Тогда математическая постановка за-
{
(
)
(
)}
E(ς)
H(ς)
дачи дифракции
t
,
t
примет вид:
(1а) ∇×Hm0 = -iκm0 Em0 ,
∇× Em0 = iκm0 Hm0 в Vm0, m0 ∈ {0,1,M};
(1б)
n0 ×E0 = 0, n0 H0 = 0 на S′;
(1в)
nm ×Em = 0, nm Hm = 0 на Sm;
⎧
(
)
⎨smo) ×
Em -Em)
=smo) ×E(ς),
(1г)
(
)
на Ωm,
⎩smo) ×
Hm -Hm)
=smo) ×H(ς)
{
}
(
)
Em
Hm
с условиями излучения на бесконечности [15]:
,
=o
R-1
,R→∞
0
0
(
)
при Im κm0 > 0 (Зоммерфельда);Hm0 ×eR -Em0 = o
R-1
,
Em
×eR+Hm0 =
0
{
}
(
)
(
)
Em
=o
R-1
,
,
H
=O
R-1
, R → ∞ при Imκ0 = 0, κ0 = 0 на S′ и Sm
0
m0
√
(
)
(
)
(Сильвера-Мюллера);
Em × eR +
μam/εam Hm = o
R-1
,
Hm = O
R-1
,
R → ∞ при Imκm = 0, κm = 0 на Ωm (Сильвера-Мюллера в слабой фор-
ме [16]). Здесь n0 и nm - орты векторов нормалей к S′ и Sm соответственно;
{
}
∕
E(o)
m ,Hm)
- ЭМП в Ωm; κm0 = ω
√εam
μa
- волновое число; ω = 2π
λ -
0
m0
круговая частота; R = |r|; eR = r /|r|; r ∈ R3.
С целью снижения вычислительных затрат для решения задачи (1) в мас-
штабе времени, близком к реальному, примем дополнительное допущение на
то, что ЭМП, приходящее в Ωm\∂Ωm, полностью передается в соответствую-
щую фидерную линию (т. е. |Γm| → 0, где |Γm| - коэффициент отражения для
m-го облучателя) [11]. Введенное допущение позволяет декомпозировать об-
щую задачу (1) на последовательное решение задач (1а), (1б), (1г) и (1а), (1в),
(1г) - задач электродинамики в неограниченной и ограниченной расчетных
(
)
(
)
областях при задании соответствующих функций P〈m〉2 :E(ς)
t
→ Emo)
t
и
(
)
(
)
(
)
Em
P〈m〉1 :Emo)
t
→ Em
t
. Функцию P〈m〉1 определения
t
предполагается
задавать векторным барицентрическим методом [13] по заданному распре-
(
)
делению ЭМПEmo)
t
в раскрыве Ωm, которое формируется рефлектором в
(
)
режиме приема. Функцию P〈m〉2 определенияEmo)
t
предполагается задавать
модифицированным токовым методом [12] или барицентрическим методом
при численном решении сингулярных интегральных уравнений [14] с учетом
заданных постановок задач дифракции на ограниченном экране и отверстии
в плоском экране [15].
Для заданной электродинамической постановки, рассматривая величи-
ну ЭДС с выходов m-х облучателей марковским векторным процессом
86
Рис. 3. Пространственно-распределенное множество сигналов для АМЛЗА.
(
)
(
( ))
X
t
=
Xm
t M,вобщейформеприпредставлениипространственно-рас-
пределенного множества сигналов (рис. 3) и задании зависимости от управ-
(
)
= u
t
[18] априорные сведения о АМЛЗА определим из уравнений
состояния
(
)
(
)
Xt
(2)
Xt =D〈μ〉
Xt,ut,t
+D〈σ〉
Xt,ut,t
Vt при
= X0
0
и наблюдения
(
)
(3)
ς
Xt,ut,t
+ Wt,
t =h
(
)
(
)
(
(
)∕
)
(
)
(
)
D〈μ〉
где
= X
t
;
Xt =
dXm
t
= ς
t
;
Xt,ut,t =
Dmμ〉M
(
)
(
)
и D〈σ〉
Xt,ut,t
= D〈σ〉
=
mm′ M×M
def= V(t) - белый гауссовский нормированный вектор-шум, наблюдаемый при
помощи векторного нелинейного наблюдателя (3); t0 - начальный момент вре-
(
)
(
)
мени;X0 - начальное распределение векторного процессаX
t
;h
Xt,ut,t -
нелинейная векторная функция наблюдателя, задающая выходную характе-
(
)
= W
t
- гауссовский белый шум с ну-
[
]
(
)
(
)
Wt WT
левым средним и матрицей интенсивностей E
τ
=D〈W〉
t
δ
t-τ
Решение стохастического дифференциального уравнения (2) предполага-
ется выполнять при его понимании в смысле Ито (см. с. 148 в [17]).
Оптимальное управление предполагает получение для заданного момента
⃗
времени t наилучшей оценки
Xt векторного процессаX
t.
87
3. Оптимальная фильтрация вектора наблюдений
адаптивной многолучевой зеркальной антенны
⃗
Оценку
Xt векторного процессаX
t предполагается получить по критерию
максимум(а пр)доп(обия функции а)остериорной плотности вероятности
(АПВ) ρ
Xt,t =ρ
Xt,tς
τ, τ ∈ [t0,t] , которая удовлетворяет уравнению
Фоккера - Планка - Колмогорова (ФПК) [20]:
∑
[
∑
[
]
(
)
∂ρ
1
∂2
∂
(4)
=
ρG〈2〉
-
ρG〈1〉
при ρ
Xt
,t0
=ρ0,
mm′
m
0
∂t
2
∂Xm∂Xm′
∂Xm
m,m′=1
m=1
где
(
)
:[
;}
(
)
{1
]
G〈1〉
ς
Xt,ut,t =
G〈1〉
при G〈1〉m = D〈μ〉m = lim
X〈m〉t+Δ -X〈m〉t
τ
;
m M
Δ→0
Δ
(
)
(
)
∑
G〈2〉
Xt,ut,t =
D〈σ〉mjD〈σ〉jm′
G〈2〉mm′ M×MприGm2m′=
j=1
}
[
][
{1
<
]
=
ς
и D〈σ〉mm′ = lim
X〈m〉t+Δ - X〈m〉
X〈m′〉t+Δ - X〈m′〉t
τ
t
Δ→0
Δ
⃗
Сведем оценку
Xt при согласовании решений внешней и внутренней задач
электродинамики [11] к определению плотности потока энергии Jm (x, y, t),
формируемого в Ωm в режиме приема.
Теорема 1. Пусть наблюдаетсяςt по правилу (3), тогда нормирован-∕
∫
˜
ное значение
J
m (x, y, t) = Jm (x, y, t)
Jm (x,y,t) dΩ плотности потока
(
)
Ωm
энергии Jm (x,y,t) ЭМП в точке
x,y
∈ Ωm АМЛЗА удовлетворяет урав-
нению
∂J˜m
(
)
˜
(5)
=AmJ˜m +Bm
Jm +
∇Cm∇T
J
m.
∂t
{
}
∂
∂
В выражении (5
Jm
Jm (x,y,t); ∇ =
,
— оператор набла; Am =
∂x
∂y
}
)-1
∑
∂2G〈2〉
{(∂
mm′
Xm
=12
;
Bm = bm
)-1 ,(∂Xm∂y
при bm = -Gm1〉+
∂Xm∂Xm′
Xm
∂x
m′=1
)
( (
∕
)-1
(
∕
)-1
∑
∂G〈2〉
∂2Xm
∂x2
∂2Xm
∂x∂y
mm′
+
;
Cm = cm
(
∕
)-1
(
∕
)-1
при cm =
∂Xm′
m′=1
∂2Xm
∂y∂x
∂2Xm
∂y2
]
[(
)-1
(
)-1
(
)-1
=
2
+
+
x∂y
∂2ym∂2
Доказательство. Отно(ительно выхода)m-го облучателя АМЛЗА
ς
m-я функция АПВ ρm = ρm
Xt,t
τ, τ ∈ [t0,t] векторного процесса
Xt с
88
учетом (4) будет удовлетворять уравнению
∑
[
]
[
]
∂ρm
1
∂2
∂
(6)
=
ρmG〈2〉
-
ρmG〈1〉
mm′
m
∂t
2
∂Xm∂Xm′
∂Xm
m′=1
Применив формулу дифференцирования произведения функций уравне-
ние (6) представим в виде
∑
∂ρm
∂ρm
1
∂2ρm
(7)
=Amρm + bm
+
G〈2〉
mm′
∂t
∂Xm
2
∂Xm∂Xm′
m′=1
∮
Учитывая функции P〈m〉1 :Emo) →Em, P〈m〉2 :E(ς) →Emo) и Xm =
Em dl,
Lm
установим зависимость составляющих Xm от (x, y) ∈ Ωm, заданных в со-
ответствующих системах координат в раскрывах m-х облучателей. Для
установленной зависимости Xm = Xm(x, y) проведем преобразование ко-
ординат фазового пространства с плотностью вероятности
ρm (x, y, t) =
)-2
√(∂
Xm
= ρm (Xm,t)
)-2 +(∂Xm∂y
[17] в стохастическом дифференциальном
∂x
уравнении (7) с применением правил дифференцирования сложных функций
и с учетом Cm = CTm представим его в квадратичной форме:
∂ρm
(
)
(8)
=Amρm +Bm∇ρm +
∇Cm∇T
ρm.
∂t
∫
Для условий:
ρm (x, y, t) dΩ = 1; ρm (x, y, t) = 0, ∀ (x, y) ∈ Ωm′ , m′ = m;
Ωm
ρm (x, y, t) ≥ 0, ∀ (x, y) ∈ Ωm и определения значений функций АПВ ρm от-
носительно величины ЭДС, снимаемой с выходов m-х облучающих элемен-
тов, справедлива характеристика ρm нормированным значением плотности
˜
потока энергии ЭМП в раскрывах m-х облучателей Ωm, т.е.
J
m (x,y,t) =
= ρm (x,y,t).
Полученные представления позволяют задать уравнение (8) относительно
˜
J
m = ρm
Jm (x,y,t) в матричной форме (5), что и требовалось доказать.
Решение краевой задачи (5) предполагается выполнять численно в при-
ближении барицентрического метода при определении аппроксимации Рит-
∑
˜
˜
ца функции
J
m соотношением
J
m (x,y,t) =
I〈m〉j (t)α〈m〉j (x,y), в кото-
j∈Mr
ром [19]:
∏
∏
[(
)∕ ]
〈m〉
α
(x, y) =
β〈m〉j(x, y); β〈m〉(x, y) =j
rζ〈m〉n(x,y) - k + 1 k
,
j
n
n
(9)
n=1
k=1
jn > 0, β〈m〉0 (x,y) = 1, (x,y) ∈ Ωm,
где I〈m〉j(t) - величина нормированного значения плотности потока энергии
в j-х узловых точках раскрыва Ωm m-го облучателя в момент времени t;
89
ζnm〉(x,y) - барицентрические координаты, определяемые в Ωm по прави-
лам [21] при представлении Ωm произвольным многоугольником из Nm вер-
шин; r - порядок аппроксимации полиномом α〈m〉j(x, y); j - мультииндекс из
множества Mr:
⎧
⎫
⎨
∑
⎬
(10)
Mr =
j = (j1,j2,...,jn,...,jNm) : jn ∈ Z, jn ≥ 0,
jn = r
⎩
⎭
n∈[1;Nm]
Для заданной аппроксимации в приближении вариационных методов Га-
леркина и Ритца при определении зависимости от времени и управления све-
дем задачу (5) к решению системы обыкновенных дифференциальных урав-
нений (ОДУ), представленной в матричном виде:
˙
(11)
I
〈m〉 (t) - Qm (ut, t)I〈m〉
(t) = 0,
где
(
)
(
)
∕
˙
I〈m〉 (t) = I〈m〉j (t)
;
I
〈m〉 (t) = dI〈m〉j (t)
dt
;
|Mr |
|Mr |
(
)
Qm (ut,t) = Q〈m〉jj′ (ut,t)
при Q〈m〉jj′ (ut, t) =
|Mr |×|Mr|
∫
{[
]
}
(
)
=
Am (ut,t) α〈m〉j +Bm (ut,t) · ∇α〈m〉j +
∇Cm (t)∇Т
α〈m〉
α〈m〉
dΩ.
j
j′
Ωm
4. Оптимальное управление адаптивной многолучевой зеркальной антенной
Полученные результаты позволяют несколько упростить известные ре-
шения, применяемые при синтезе стохастических оптимальных систем [18].
С учетом (11) и связью максимума правдоподобия с минимумом эмпирическо-
го риска (средние потери) [22] сформулируем задачу оптимального в среднем
управления АМЛЗА при минимизации квадратичной функции потерь
t1
∫
(
)
I 〈1〉
(12)
F
,...,I〈M〉τ,uτ,τ dτ → min
τ
u(·)∈U
t0
для заданного уравнения динамики
〈m〉
˙
(13)
I
= Qm (ut,t) I〈m〉t,
t
и начального условия
I〈m〉
(14)
=I〈m〉0,
t0
где
)
I〈m〉
I〈1〉
def= I〈m〉(t); F(
,...,I〈M〉t,ut,t
=
t
t
∑
∑
(
)2
(
)
1
=
I〈m〉j (t) - J〈m〉j (ut,t)
;
J〈m〉 (ut,t) = J〈m〉j (ut,t)
2
|Mr|
m=1 j∈Mr
90
— рассчитываемое по методам [12, 13] распределение нормированных значе-
ний плотности потока энергии в j-х узловых точках раскрыва Ωm m-го об-
лучателя в момент времени t для заданных значений вектора управления ut;
t ∈ [t0,t1]; [t0,t1] - отрезок времени управления; U - множество допустимых
управлений.
Значения вектор
J 〈m〉 (ut,t) для аппроксимационных полиномов (9) при
∑
J m (ut,x,y,t) =
J〈m〉j (ut,t) α〈m〉j (x,y) определяется из решения задачи
j∈Mr
∫
Jm (ut,x,y,t)
J m (ut,x,y,t)2 dΩ → min соотношением
Ωm
(15)
J〈m〉(ut,t)=T
Jαm (ut
,t) ,
где(
)
∫
Tm = T〈m〉
- метрическая матрица Ωm при T〈m〉jj′ = α〈m〉jα〈m〉j′dΩ [13];
jj′
|Mr |×|Mr|
Ωm
(
)
∫
Jαm (ut,t) = Jαm,j (ut,t)
при Jαm,j (ut, t) =
Jm (ut,t)α〈m〉jdΩ;
Jm (ut,t) =
|Mr |
Ωm
=
Jm (ut,x,y,t), а
Jm (ut,x,y,t) задается соотношением [11]
(o)
(o)
Em (ut, x, y, t) ×Hm (ut, x, y, t)
(16)
Jm (ut,x,y,t) =
,
∫
(o)
(o)
Em (ut, x, y, t) ×Hm (ut, x, y, t) dΩ
Ωm
при оценке мгновенных значений напряженностей электрического
E(o)
H(o)
в
m (ut, x, y, t) и магнитного
m (ut, x, y, t) полей функциями
2
раскрывах m-х облучателей (x, y) ∈ Ωm - задача (1а), (1б), (1г).
Решение задачи (12)-(14) выполним с применением принципа максимума
Понтрягина [23]. Функцию Гамильтона определим в виде:
(
)
I〈1〉
H
,...,I〈M〉t,ψ〈1〉t,...,ψ〈M〉t,ut,t =
t
]
(17)
(
∑
[(
)T
I〈1〉
ψ〈m〉
=F
,...,I〈M〉t,ut,t -
Qm (ut,t)I〈m〉
,
t
t
t
m=1
(
)
(
)
= ψ〈m〉
t
;
ψ〈m〉 (t) = ψ〈m〉j (t)
- вспомогательный вектор им-
|Mr|
пульсов управления.
Таким образом, итоговую задачу управления АМЛЗА для (17) сведем к
решению системы ОДУ, включающей с учетом (13) и начального условия (14)
91
для m = 1, M, j ∈ Mr следующие уравнения:
⎧
(
)
∑∑
⎨∂J〈m〉j(ut,t)
I〈m〉j (t) - J〈m〉j (ut,t)
+
⎩
∂ut
m=1 j∈Mr
(18)
⎫
∑
∂Q〈m〉jj′ (ut,t)
⎬
+ ψ〈m〉j(t)
I〈m〉j′ (t)
= 0;
∂ut
⎭
j′∈Mr
⎧
⎫
⎨(
)
⎬
dψ〈m〉j (t)
∑
∑
(19)
=
I〈m〉j (t) - J〈m〉j (ut,t) -
ψ〈m〉j′ (t)Q〈m〉j′j(ut,t)⎭.
dt
⎩
m=1
j′∈Mr
Общее решение задачи (13),(14),(18),(19) предлагается осуществлять чис-
ленно при построении алгоритма адаптации АМЛЗА по рекуррентно-
итерационной модели [24]. Алгоритм формируется для следующих обозначе-
ний и условий: τ ∈ [t0, t1]; непрерывные значения элементов вектора наблюде-
ния (3) оцифровываются на интервале управления (N отсчетов, n = 0, N - 1)
1
с учетом теоремы Котельникова при Δ = (τn+1 - τn) ≤
, где fc - ширина
2fc
полосы принимаемого сигнала; каждый интервал [τn, τn+1] дискретизируется
отсчетами v = 0, 1, 2, . . . , (число отсчетов определяет степень точности чис-
ленного решения). Основные этапы работы алгоритма:
1) максимально-правдоподобная оценка плотности потока энергииI〈m〉 (τn+1)
в раскрывах облучателей в дискретный момент времени τn+1:
- в дискретные моменты времени τnv ∈ [τn,τn+1] учет наблюдения ςτn
(3);
v
– для принятых значений отсчетов (v = 0, 1, 2, . . . , ) вектора сигналов ςτn
(
)
(
)
v
ς
ς
вычислить элементы, составляющиеG〈1〉
τ,un,τ и G〈2〉
τ,un,τ
(un =
= u(τn)) в (6) относительно вектора сноса и матрицы диффузии соответствен-
но с учетом правил из [25];
- в анализируемый момент времени τn+1 функциями P〈m〉1 и P〈m〉2, задавае-
мыми методами [12, 14] и [13] соответственно, рассчитать элементы матрицы
Qm (un,τn+1);
- вычислить приближенные значенияI〈m〉 (τn+1) иψ〈m〉 (τn+1) при реше-
нии уравнений (13),(19) для момента времени τn+1 с использованием эконо-
мичных явных схем типа Рунге-Кутты [26, 27] с учетом выбранного числа
отсчетов v = 0, 1, 2, . . . , на [τn, τn+1];
2) вычисление вектора управляющих воздействий un+1 для момента времени
τn+1 при решении уравнения (18) для m = 1,M с применением комбиниро-
ванных эволюционных методов [28] и учетом заданной оценкиI〈m〉 (τn+1) и
ψ〈m〉 (τn+1) на [τn, τn+1].
Вычисление частных производных в (18) по вектору управления для
J〈m〉 (ut,t) выполнено аналитически с учетом (15), (16) и функций P〈m〉1
и P〈m〉2, задаваемых методами [12, 14] и [13] соответственно, а для Qm (ut,t) -
численно с учетом указанных правил дискретизации интервалов и подынтер-
92
валов управления. Отметим, что применение принципа максимума при по-
добном решении (разделение общей задачи управления на (13), (19) и (18) на
интервале дискретизации [τn, τn+1]) необходимо ввиду невозможности удовле-
творить условию стационарности (требуется при решении задачи управления
(12)-(14) при раздельном решении (13) и (18) на интервале дискретизации
[τn, τn+1] без введения вспомогательных векторов импульсов управления).
5. Подавление помех адаптивной многолучевой зеркальной антенной
Заданные соотношения (13), (18), (19) с учетом критерия (12) согласно ре-
зультатам, полученным в корреляционной теории ПВОС [2, 3], соответствуют
стандартному критерию качества ААР - максимум отношения правдоподо-
бия. Целесообразность его использования заключается в том, что в большин-
стве возможных случаев единственная априорная информация о полезном
сигнале состоит в известности направления его возможного прихода. Для
полученных результатов в сравнении с теорией ААР [3, 5, 6] возникает до-
полнительный интерес в оценке числа степеней свободы АМЛЗА.
Утверждение 1. Пусть задана АМЛЗА, включающая M облучателей
и деформируемый рефле()ор с K устройс(ва )и деформации, тогда, прини-
мая полезный сигнал ς
t
с направления
θ,ξ
, АМЛЗА максимально спо-
собна подавит(N =)MK(- 1)помеховых сигналов ηn (t), которые приходят
с направлений
θn,ξn
=
θ,ξ
, где n = 1, N .
Доказательство. С учетом принципа обратимости процессов приема
и передачи для заданной модели приемной АМЛЗА (рис. 2, 3) изначально
отметим, что для доказательства справедливо рассматривать антенну и как
передающую. Из теории ААР известно [3], что изменением амплитуды Amo) и
фазы ϕmo) токов возбуждения m-х реальных источников ЭМП (облучателей)
можно добиться подавления M - 1 помеховых сигналов при формировании
M - 1 нулей диаграммы направленности (ДН) весовыми коэффициентами
wmo) = Amo)eiϕmo), где i =√-1. При этом ноль ДН в некотором направлении
задается интерференцией когерентных волн антенны, равных по амплитуде
и противоположных по фазе. Число M весовых коэффициентов wmo) опреде-
ляет число степеней свободы ААР. Исходя из принципа Гюйгенса-Френеля
АМЛЗА содержит M весовых коэффициентов wmo), параметризующих сово-
купность реальных источников (облучателей), и весовой коэффициент w(p),
параметризующий комплексную амплитуду совокупности фиктивных вто-
ричных источников (рефлекторов). Рассмотрим w(p) в качестве скалярного
потенциала в точке Θ. Из интегральной теоремы Кирхгофа - Гельмгольца из-
вестно, что мгновенное значение w(p) (t, Θ) определяется соотношениями [16]
∞
∫
1
w(p) (t,Θ) =
√
v(p) (ω,Θ)e-iωtdω;
2π
-∞
(20)
{
∮
1
∂v(p) e-iκR
∂
(e-iκR)}
v(p) (ω,Θ) =
-v(p)
dS,
4π
∂n0
R
∂n0
R
S
93
где κ = ω
√εaμa; εa и μa - электрический и магнитный параметры среды;
ω - угловая частота; R - расстояние между Θ и точкой интегрирования на
поверхности S; n0 - орт вектора нормали к S в точке интегрирования.
∑
Задав аппроксимацию функции v(p) = vдkαдk (x, y) под знаком второго
k=1
интеграла (20) в некоторой K-мерной системе ортогональных функций де-
формации формы αдk (x, y), введенных, например, в [19], приведем (20) к виду
∑
(21)
w(p) (t,Θ) =
A(p)k (t,Θ)eiϕkp)(t,Θ),
k=1
где A(p)k и ϕ(p)k характеризуются амплитудой и фазой соответствующего ком-
плексного числа
∞
∫
∮
1
{∂αдk e-iκR
(e-iκR)}
(22)
w(p)k =
√
vдke-iωt
-αд ∂
dSdω.
4π
2π
∂n0
R
k ∂n0
R
−∞
S
Полученные соотношения (21), (22) определяют то, что при параметри-
зации поверхности рефлектора [19] положением Xдk, Yдk, Zдk деформирующих
∑
(
)
(
)
стержней (приводов [29]) z (x, y) =
Zдkδ
x-Xдk
δ
y-Yдk
число степеней
k=1
свободы рефлектора равно K.
Поскольку k-е весовые функции w(p)k являются фиктивными вторичными
(
)
источниками излучения m-х облучателей
m = 1,M
, общее число степеней
свободы АМЛЗА равно MK. Таким образом, принимая смесь, включающую
один полезный и N помеховых сигналов, АМЛЗА способна подавить MK - 1
помех, что и требовалось доказать.
С учетом полученных результатов, закона необходимого разнообразия при
K → ∞ возможно доказать следующее утверждение.
Следствие 1. Существует конструкция адаптивной многолучевой
зеркальной антенны, инвариантной к воздействию помех.
6. Результаты моделирования и их обсуждение
Для верификации полученных решений в Matlab проведено математиче-
ское моделирование задачи оптимального управления АМЛЗА, состоящей
из трех рупорных облучателей с треугольным, прямоугольным и круглым
раскрывами. Поверхность деформируемого рефлектора исходно задана па-
раболическим цилиндром. Параметры синтезируемой антенной системы сле-
дующие: средняя длина волны λ = 0,05 м из спектра принимаемого сигна-
ла, радиус вписанной в раскрывы облучателей окружности 1,25λ (раскры-
вы заданы правильными многоугольниками), ширина раскрыва рефлекто-
ра по оси OX 20λ, длина раскрыва рефлектора по оси OY
30λ, фокус-
ное расстояние f(= 40λ, )∕ходная поверхность деформируем(г) рефлекто-
ра Z (x, y) = 0,25
x2 + y2
f, направление приема сигнала ς
t
выбрано в
94
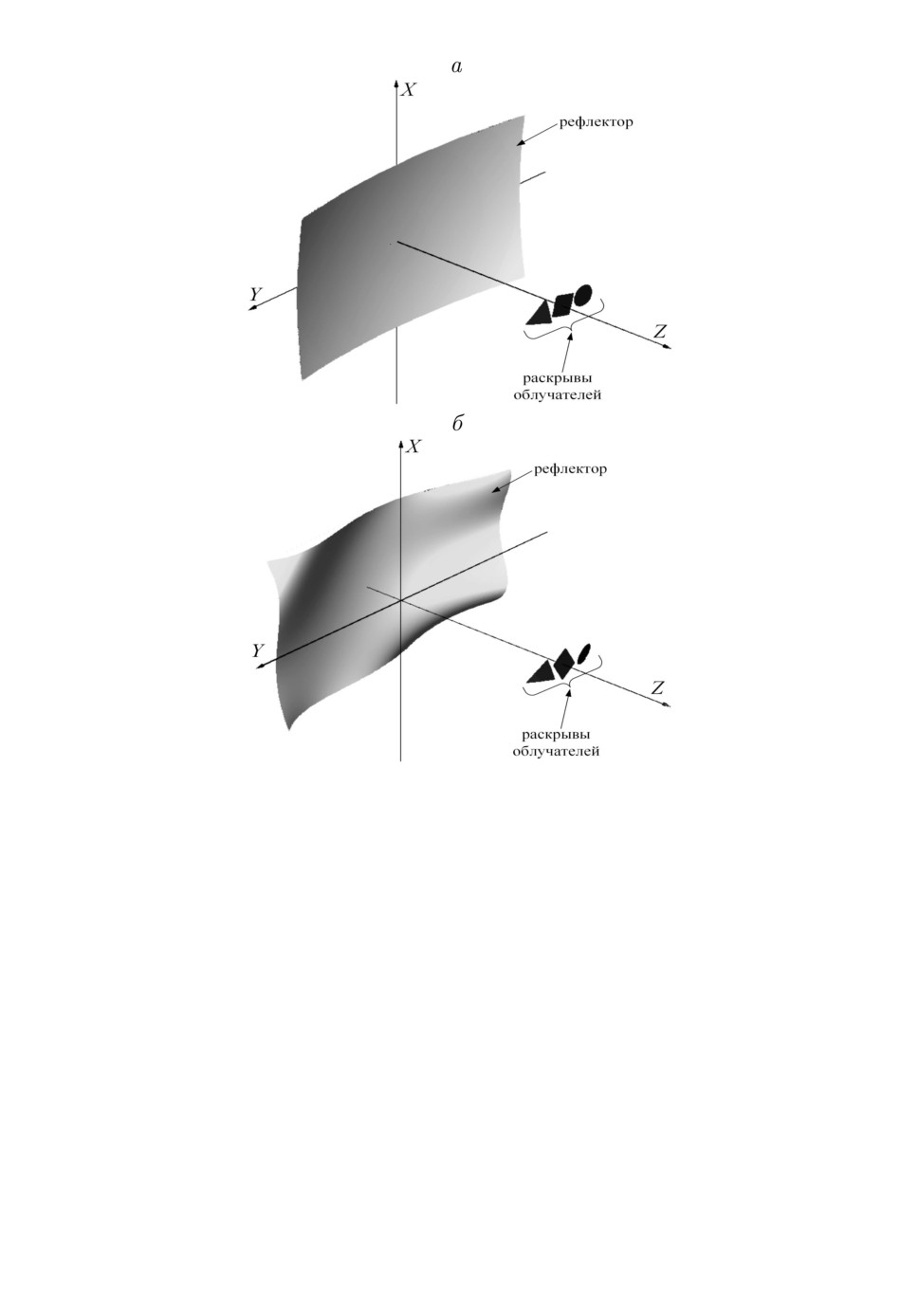
Рис. 4. Геометрия АМЛЗА до (а) и после (б ) адаптации.
H-плоскости для угла отклонения θ = 0◦. Адаптивная антенна принимает
(
)
сигнал ς
t
с информационной скоростью 512 кБит/с и модуляцией QPSK
пр(и)озд(й)стви(и)в H-плоскости трех некоррелированных помеховых сигналов
η1
t
, η2
t
, η3
t
в соответствующих углах отклонения θ1 = -10◦, θ2 = -5◦,
θ3 = 8◦. Предполагается, что облучатели подключены к прямоугольным вол-
новодам с шириной 0,7λ и высотой 0,4λ (для моделируемой задачи граница
раскрыва волновода - Lm). Исходное положение координат центров раскры-
вов облучателей выбрано по критерию максимальной концентрации геомет-
рооптических лучей [8] с подбором соответствующих амплитудно-фазовых
распределени( )токов возбуждения [30] для заданного направления прихо-
да сигнала ς
t
. Число деформирующих стержней K выбрано равным 25
при определении положения их воздействия на отражающую поверхность
рефлектора по правилам из [19].
На рис. 4 представлены геометрии АМЛЗА: исходная и реализованная по-
сле решения задачи адаптивного приема. На рис. 5 отражены реализуемая
95
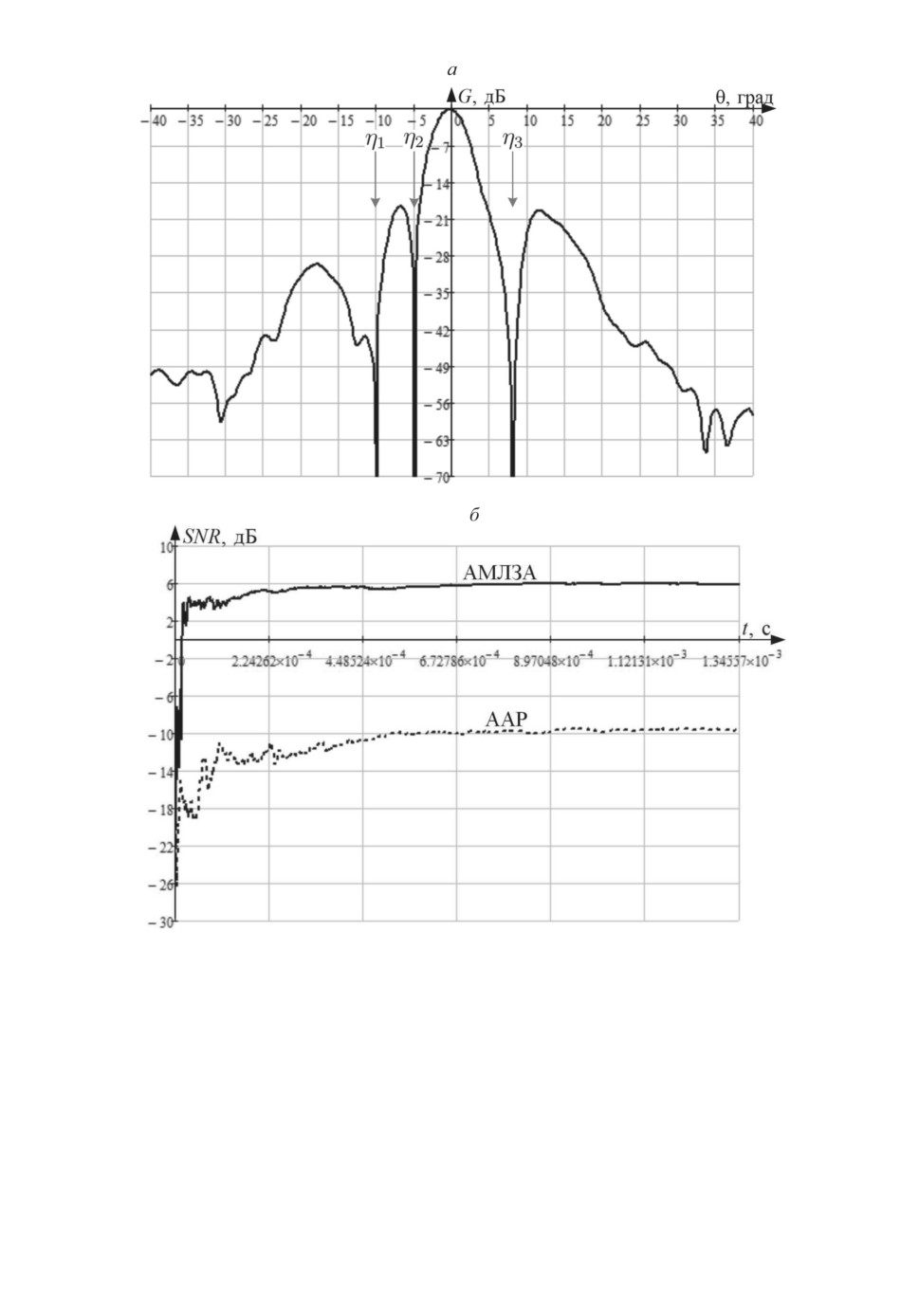
Рис. 5. ДН АМЛЗА после адаптации (а) и временная зависимость SNR (б ).
средняя ДН [31] при адаптивном приеме и временная зависимость отноше-
ния сигнал/(шум плюс помеха) SNR при адаптации. Для определения пред-
почтительности применения АМЛЗА график временной зависимости SNR
(рис. 5,б ) построен в сравнении с ААР, сост(я)щей из трех элементов и фор-
мирующей в направлении приема сигнала ς
t
аналогичный АМЛЗА коэф-
фициент усиления. Адаптивный прием сигнала ААР (рис. 5,б ) реализован
рекурсивным алгоритмом адаптации [32] при оценке ковариационной матри-
цы посредством калмановской фильтрации по критерию максимума SNR [6].
96
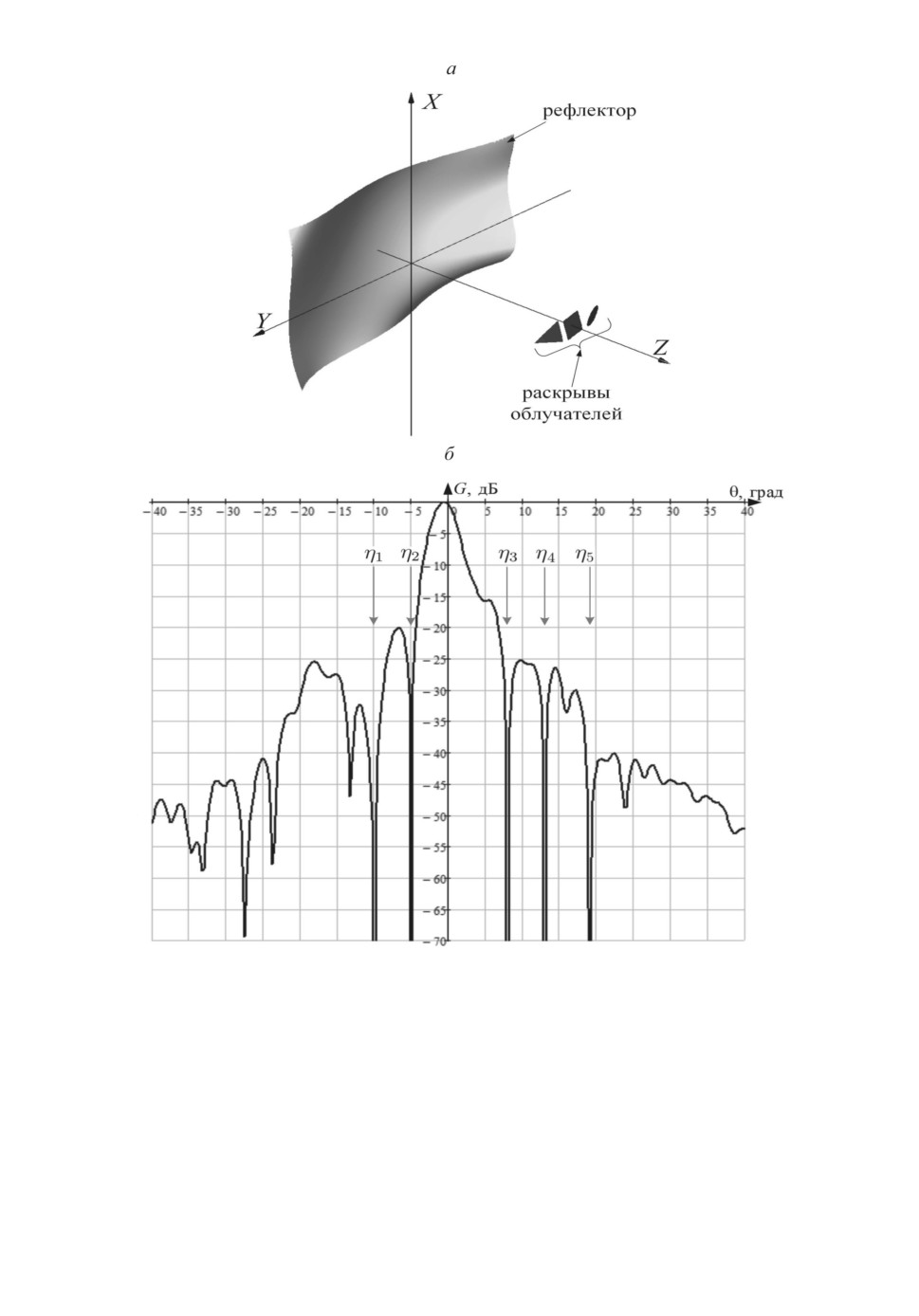
Рис. 6. Геометрия АМЛЗА (а) и реализуемая средняя ДН (б ) после адаптации.
Для заданной конструкции АМЛЗА оптимальное соотношение SNR фор-
мируется на 150-200-м такте работы рекурсивного алгоритма (t≈1, 21·10-4 с,
см. рис. (,)), р(а)лизу(я)в направлениях θ1 = -10◦, θ2 = -5◦, θ3 = 8◦ прихода
помех η1
t
, η2
t
, η3
t
нули ДН (рис. 5,а). В случае включения в адаптив-
ну(ю)мод(е)ь дополнительных двух некоррелированных помеховых сигналов
η4
t
,η5
t
в соответствующих углах отклонения θ4 = 13◦, θ5 = 19◦ геометрия
АМЛЗА после адаптации и реализуемая средняя ДН примут вид, представ-
ленный на рис. 6.
97
Полученные результаты моделирования (рис. 4-6) на наглядном примере
определяют предпочтительность использования АМЛЗА в сравнении с ААР
по потенциальной возможности адаптации к условиям сигнально-помеховой
обстановки при исходной эквивалентности интегральных характеристик на-
правленности сравниваемых антенн.
7. Заключение
Полученные в работе соотношения (13),(18),(19) с учетом принципа макси-
мума Понтрягина [23] задают обобщенную постановку задачи оптимального
управления АМЛЗА, определяя в качестве состояния антенной системы рас-
пределение нормированного значения плотности потока энергии в раскрывах
облучателей (13). Уравнение состояния (13) определено в приближении бари-
центрического метода [13, 19] аппроксимацией (9) при сведении стохастиче-
ского дифференциального уравнения ФПК (4) к начально-краевой задаче (5).
Для сформированной постановки задачи оптимального управления опреде-
лена способность подавления помеховых сигналов АМЛЗА, равная MK - 1,
где M - число облучателей, K - число деформирующих отражающую поверх-
ность рефлектора устройств деформации. Полученные решения, подкреплен-
ные результатами математического моделирования (рис. 4-6), определяют
предпочтительность применения в современных системах беспроводной связи
АМЛЗА. Для реализации эффективных алгоритмов оптимального управле-
ния АМЛЗА предлагается использовать аналитические и численные методы
решения внешней и внутренней задач электродинамики для многолучевых
зеркальных антенн, разработанные авторами [9, 11-14, 19, 28] с последующим
возможным развитием предложенного решения в направлении применения
тестовых сигналов второго типа [6] (априорной известности структуры пере-
даваемого сигнала) при соответствующем выборе вместо критерия МОП (12)
других критериев адаптивных антенн (МСКО, МСШП, ММВС, МСПП [3]).
СПИСОК ЛИТЕРАТУРЫ
1. Сосулин Ю.Г., Костров В.В. Оценочно-корреляционно-компенсационная обра-
ботка сигналов на фоне помех // Радиотехника. 2006. № 9(51). С. 1027-1065.
2. Сосулин Ю.Г., Костров В.В., Паршин Ю.Н. Оценочно-корреляционная обра-
ботка сигналов и компенсация помех. М.: Радиотехника, 2014.
3. Щесняк С.С., Попов М.П. Адаптивные антенны. СПб.: Изд-во ВКИКА им.
А.Ф. Можайского, 1995.
4. Weiner M.M. Adaptive antennas and receivers. Boca Raton; London: CRC Taylor
& Francis, 2006.
5. Ada Poon, Robert W. Brodersen, David Tse. Degrees of Freedom in Multiple-
Antenna Channels: A Signal Space Approach // IEEE Transact. Inform. Theory.
V. 51(2). March 2005. P. 523-536.
6. Пистолькорс А.А., Литвинов О.С. Введение в теорию адаптивных антенн. М.:
Наука, 1991.
7. Madec P-Y. Overview of deformable mirror technologies for adaptive optics and
astronomy // Adaptiv. Optics Syst. III, Ellerbroek, Marchetti, Veran Eds, Proc.
SPIE V. 8447. 2012.
98
8.
Arkhipov N.S., Velikikh A.S., Karpov A.V., Polyanskii I.S. An Algorithm for
Generating the Cluster Groups of Hybrid Mirror Antenna Radiators // Telecommun.
Radio Engineer. 2013. No. 72(2). P. 147-160.
9.
Сомов А.М., Полянский И.С., Степанов Д.Е. Синтез отражающих поверхно-
стей антенной системы зеркального типа с использованием барицентрического
подхода при параметризации рефлектора // Антенны. 2015. № 8. С. 11-19.
10.
Архипов Н.С., Захаров И.С., Чаплыгин И.А. Представление гибридных зер-
кальных антенн в виде пространственных и угловых фильтров // Телекомму-
никации. 2000. № 3. С. 29-37.
11.
Архипов Н.С., Полянский И.С., Сомов А.М. Анализ и структурно-параметри-
ческий синтез зеркальных антенн: под ред. А.М. Сомова. М.: Горячая линия -
Телеком, 2017.
12.
Сомов А.М., Архипов Н.С., Полянский И.С., Степанов Д.Е. Расчет диаграммы
направленности зеркальных антенн в приближении методов физической оптики
и физической теории дифракции // Тр. НИИР. 2015. № 2. С. 43-53.
13.
Полянский И.С. Векторный барицентрический метод в вычислительной элек-
тродинамике // Тр. СПИИРАН. 2017. № 2(51). С. 206-222.
14.
Полянский И.С., Пехов Ю.С. Барицентрический метод в решении сингулярных
интегральных уравнений электродинамической теории зеркальных антенн //
Тр. СПИИРАН. 2017. № 5(54). С. 244-262.
15.
Ильинский А.С., Смирнов Ю.Г. Дифракция электромагнитных волн на прово-
дящих тонких экранах. М.: ИПРЖР, 1996.
16.
Colton D., Kress R. Integral equation methods in scattering theory. Philadelphia:
SIAM, 2013.
17.
Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических
устройств и систем: Уч. пос. для вузов. М.: Радио и связь, 2004.
18.
Пантелеев А.В., Рыбаков К.А. Методы и алгоритмы синтеза оптимальных сто-
хастических систем управления при неполной информации. М.: Изд-во МАИ,
2012.
19.
Полянский И.С. Барицентрический метод в задаче оптимального управления
формой отражающей поверхности зеркальной антенны // Мат. моделирование.
2017. Т. 29. № 11. С. 140-150.
20.
Кузнецов Д.Ф. Стохастические дифференциальные уравнения: теория и прак-
тика численного решения. 4-е изд., испр. и доп. СПб.: Изд-во политехн. ун-та,
2010.
21.
Полянский И.С. Барицентрические координаты Пуассона-Римана
// Тр.
СПИИРАН. 2016. № 6(49). С. 32-48.
22.
Klebanov L., Rachev S.T., Fabozzi F. Robust and Non-Robust Models in Statistics.
N.Y.: Nova Scientific Publishers, 2009.
23.
Болтянский В.Г. Математические методы оптимального управления. М.: Наука,
1968.
24.
Блюмин C.Л., Погодаев А.К. Рекуррентно-итерационные алгоритмы адаптив-
ной идентификации нелинейных динамических сосредоточенных систем // АиТ.
2003. № 10. C. 80-87.
Blumin S.L., Pogodaev A.K. Recursive Iterative Algorithms for Adaptive
Identification of Nonlinear Concentrated Dynamic Systems // Autom. Remote
Control. 2003. V. 64. No. 10. P. 1583-1588.
25.
Полянский И.С., Патронов Д.Ю. Максимально правдоподобная оценка
дисперсионно-ковариационной матрицы // Современные проблемы науки и об-
99
26. Olemskoy I.V., Eremin A.S., Kovrizhnykh N.A. Embedded methods of order six for
special systems of ordinary differential equations // Appl. Math. Sci. 2017. V. 11.
No. 1. P. 31-38.
27. Kreinin G.N., Misyurin S.Yu. Choice of the law for a position control system //
J. Machin. Manufact. Reliabilit. 2012. V. 41. No. 4. P. 331-336.
28. Полянский И.С., Степнов Д.Е., Фролов М.М. Гибридный генетический метод
с градиентным обучением и прогнозированием для решения задач глобальной
оптимизации многоэкстремальных функций // Вестн. БГТУ. 2014. № 3(43).
С. 138-146.
29. Kreinin G.V., Misyurin S.Yu. A systematic approach to synthesis of a drive
system // J. Machin. Manufactur. Reliabilit. 2011. V. 40. No. 6. P. 507-511.
30. Архипов Н.С., Полянский И.С., Сахончик В.Д. Алгоритм формирования ха-
рактеристики излучения многолучевой гибридной зеркальной антенны // Тр.
НИИР. 2012. С. 68-78.
31. Шифрин Я.С. Вопросы статистической теории антенн. М.: Сов. радио, 1970.
32. Джиган В.И. Адаптивная фильтрация сигналов: теория и алгоритмы. М.: Тех-
носфера, 2013.
Статья представлена к публикации членом редколлегии Е.Я. Рубиновичем.
Поступила в редакцию 28.03.2018
После доработки 04.06.2018
Принята к публикации 08.11.2018
100