Автоматика и телемеханика, № 1, 2019
Управление в социально-экономических
системах
© 2019 г. Д.В. УЖЕГОВ (denis.uzhegov@phystech.edu),
А.А. АНАНЬЕВ (ananev.andrey@phystech.edu),
П.В. ЛОМОВИЦКИЙ (pavel.lomovitskiy@phystech.edu),
А.Н. ХЛЮПИН (khlyupin@phystech.edu)
(Инжиниринговый центр МФТИ по трудноизвлекаемым полезным ископаемым,
Московский физико-технический институт (государственный университет))
НОВЫЙ АЛГОРИТМ ДЛЯ РЕШЕНИЯ СПЕЦИАЛЬНОЙ ЗАДАЧИ
О НАЗНАЧЕНИЯХ С ФУНКЦИЕЙ СТОИМОСТИ ОБЩЕГО ВИДА
ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
Рассматривается задача о назначениях специальной структуры с функ-
цией стоимости общего вида и запретами на некоторые паросочетания.
В этом случае стоимость назначения может быть не определена, пока не
будет найдена какая-либо подстановка. Задача формулируется в терми-
нах теории графов и сводится к поиску пути минимальной стоимости в
графе с нелокальными весами ребер. Предлагаемый метод решения яв-
ляется модификацией алгоритма Дейкстры поиска кратчайшего пути во
взвешенном ориентированном графе. Исследования мотивированы прило-
жениями к бурению скважин. Приведен анализ численных эксперимен-
тов.
Ключевые слова: квадратичная задача о назначениях, недопустимые па-
росочетания, кратчайший путь в графе, алгоритм Дейкстры.
DOI: 10.1134/S0005231019010070
1. Введение
Задача о назначениях является одной из фундаментальных задач в об-
ласти исследований операций, которая на практике возникает при решении
проблем снабжения предприятий, строительства магистралей, медицинского
обслуживания, создания радиоэлектронной аппаратуры и т.п. [1]. В общем
случае ее можно сформулировать следующим образом:
Даны два множества A и B одинаковой мощности и задана функция
C: A × B → R. Необходимо найти биекцию π: A → B такую, чтобы была ми-
нимальной целевая функция
∑
C(a, π(a)).
a∈A
Если функция стоимости задана матрицей, то целевую функцию можно за-
писать в виде
∑
Caπ(a).
a∈A
101
Другими словами, имеется некоторое одинаковое количество работ и испол-
нителей. Каждый исполнитель может быть назначен на выполнение только
одной работы, но с различными затратами. Необходимо распределить работы
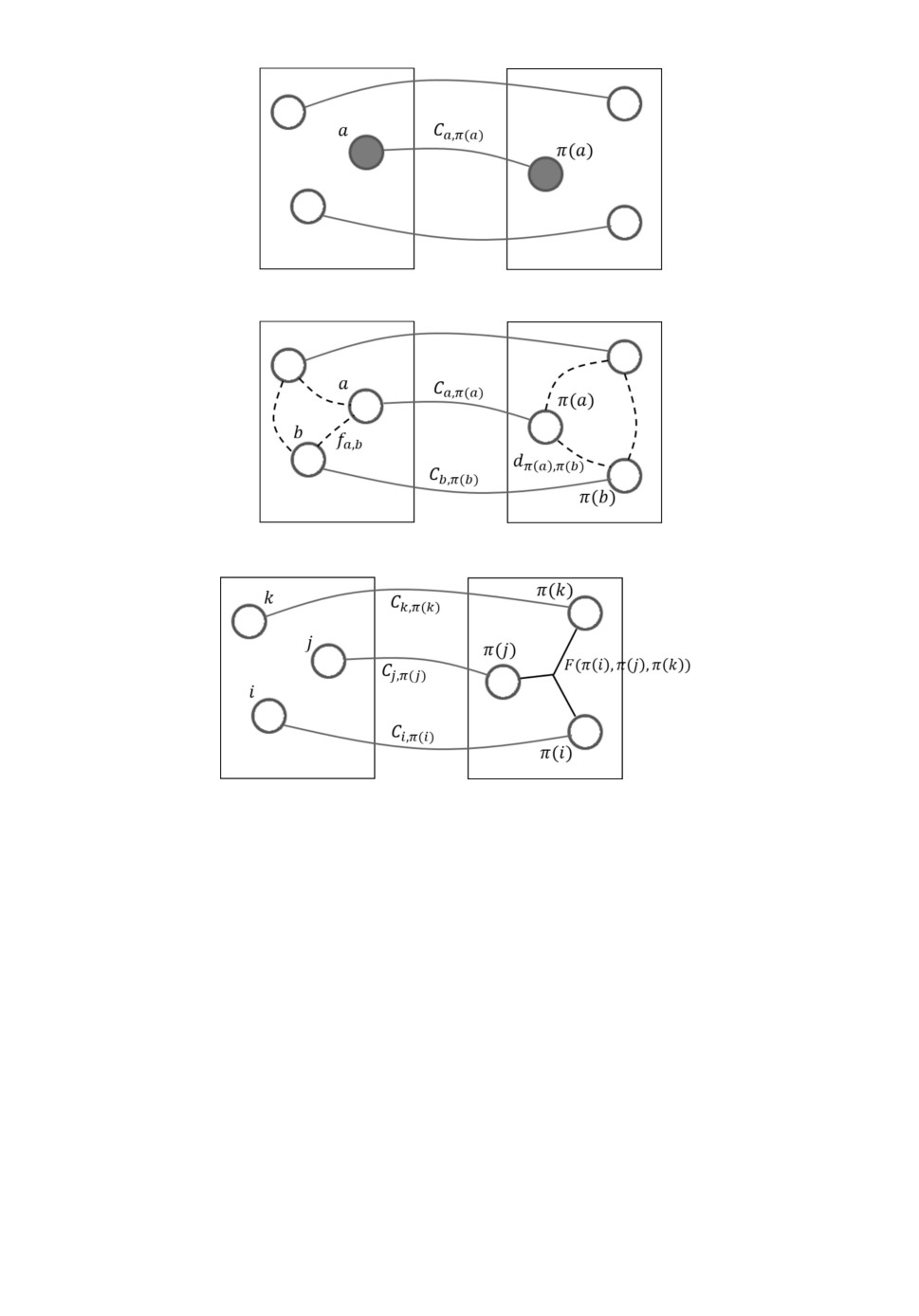
по исполнителям, минимизируя суммарные затраты (рис. 1,a).
В данной постановке задача является линейной (linear assignment problem,
LAP). Известно множество методов ее решения, которое можно поделить на
две части: симплекс-методы (см. [2, 3]) и прямодвойственные (primal-dual)
методы (см. [4, 5]). В основе первых лежит тот факт, что задача о назна-
чениях является разновидностью транспортной задачи, которая может быть
представлена как задача линейного программирования [6]:
∑∑
min
Cijxij
i=1 j=1
при условии
∑
xij = 1, i = 1,... ,n,
j=1
∑
xij = 1, j = 1,... ,n,
i=1
xij ∈ {0,1} , i,j = 1,... ,n,
где
Cij - стоимость назначения исполнителя i на работу j, i ∈ A, j ∈ B;
xij = 1, если исполнитель i назначен на работу j;
xij = 0 в противном случае.
К прямодвойственным методам относится широко используемый венгерский
алгоритм [4] и схожие с ним, например аукционный алгоритм [5]. Основная
идея методов заключается в приведении матрицы стоимости к определенно-
му виду. Большинство методов решения LAP подробным образом разобраны
в [7].
В случае, когда целевая функция квадратична, говорят о квадратичной
задаче о назначениях (Quadratic assignment problem, QAP). В формулиров-
ке Купманса-Бекмана [8] она звучит следующим образом (рис. 1,б ). Заданы
два множества одинаковой мощности: A — предприятия и B — города, а так-
же функция f : A × A → R, характеризующая поток между предприятиями,
расстояние между городами d: B × B → R и стоимость размещения пред-
приятия в городе C : A × B → R. Обычно все функции стоимостей задаются
в виде матриц (fij ), (dkl), (Cik). Необходимо найти подстановку (трактуется
как биекция) π : A → B такую, чтобы была минимальной целевая функция
∑∑
∑
(1)
fabdπ(a)π(b) +
Caπ(a).
a∈A b∈A
a∈A
102
а
б
в
Рис. 1. Иллюстрация задач о назначениях: а - линейная задача о назначениях;
б - квадратичная задача о назначениях; в - специальная задача о назначениях
с функцией стоимости общего вида.
Будучи NP-сложной, квадратичная задача о назначениях не может быть
решена за полиномиальное время [9]. Однако при выполнении специальных
условий на матрицы задача является полиномиально разрешимой на подста-
новке заданного вида. Так называемые условия сильной разрешимости впер-
вые были сформулированы в [10] и исследованы затем в [11, 12]. Тем не менее,
для задач размерности более 25 нахождение точного решения не гарантирова-
но [13]. Существуют эвристические алгоритмы, такие как генетический [14],
муравьиный [15], имитирующие природные процессы, или алгоритм поиска с
запретами [16]. Применение эвристических алгоритмов позволяет найти близ-
кое к оптимальному решение задач большой размерности за разумное время.
В работе рассматривается некоторое обобщение квадратичной задачи.
Можно представить ситуацию, когда необходимо учесть не расстояния меж-
ду каждыми предприятиями, а их совокупное расположение, которое может
103
быть задано условием на все предприятия сразу (рис. 1,в). В таком случае
получить значение целевой функции невозможно без предположения о под-
становке. Еще одно обобщение связано с существованием недопустимых па-
росочетаний, если размещение предприятия в каком-либо городе запрещено.
В статье предлагается решение данной проблемы для случая равенства по-
токов между предприятиями fij = δij . Метод основан на представлении за-
дачи о назначениях в терминах теории графов, который описан в [17]. Также
показывается, что предлагаемый алгоритм позволяет решить квадратичную
задачу о назначениях для симметричных матриц стоимостей. В первой гла-
ве приводится математическая формулировка задачи. Вторая глава содер-
жит описание алгоритма решения. В третьей главе представлены результаты
практического применения алгоритма.
2. Математическая формулировка задачи
С математической точки зрения задача отличается от классической более
общим видом функции стоимости,
∑{
}
(2)
Zπ =
Ciπ(i) + F(π(1),... ,π(i))
,
i
где F — произвольная функция, зависящая от подстановки π. Если речь идет
о квадратичной задаче о назначениях, данная функция имеет следующий
вид:
∑
(3)
F (π(1), . . . , π(i)) = dπ(i)π(1) + dπ(i)π(2) + · · · + dπ(i)π(i) =
dπ(i)π(j).
j≤i
Тогда в случае равенства потоков между предприятиями fij = δij и симмет-
рии матрицы dij = dji задача о назначениях (1) эквивалентна (2) с функци-
ей F вида (3). Решение задачи представимо в виде матрицы
{
1, если j = π(i),
Xπ = (xij), где xij =
0, если j = π(i).
Это матрица, в которой каждая строка и столбец содержат ровно один от-
личный от нуля элемент, а его положение задает искомую биекцию
(
)
i
1
i2
in
Π =
π(i1) π(i2) . . . π(in)
Например, решению Xφ соответствует биекция φ
⎞
⎛0 0 0 1
(
)
⎜1
0
0
0⎟
1
2
3
4
Xφ =
⎝
⎠, φ=
0
1
0
0
4
1
2
3
0
0
1
0
104
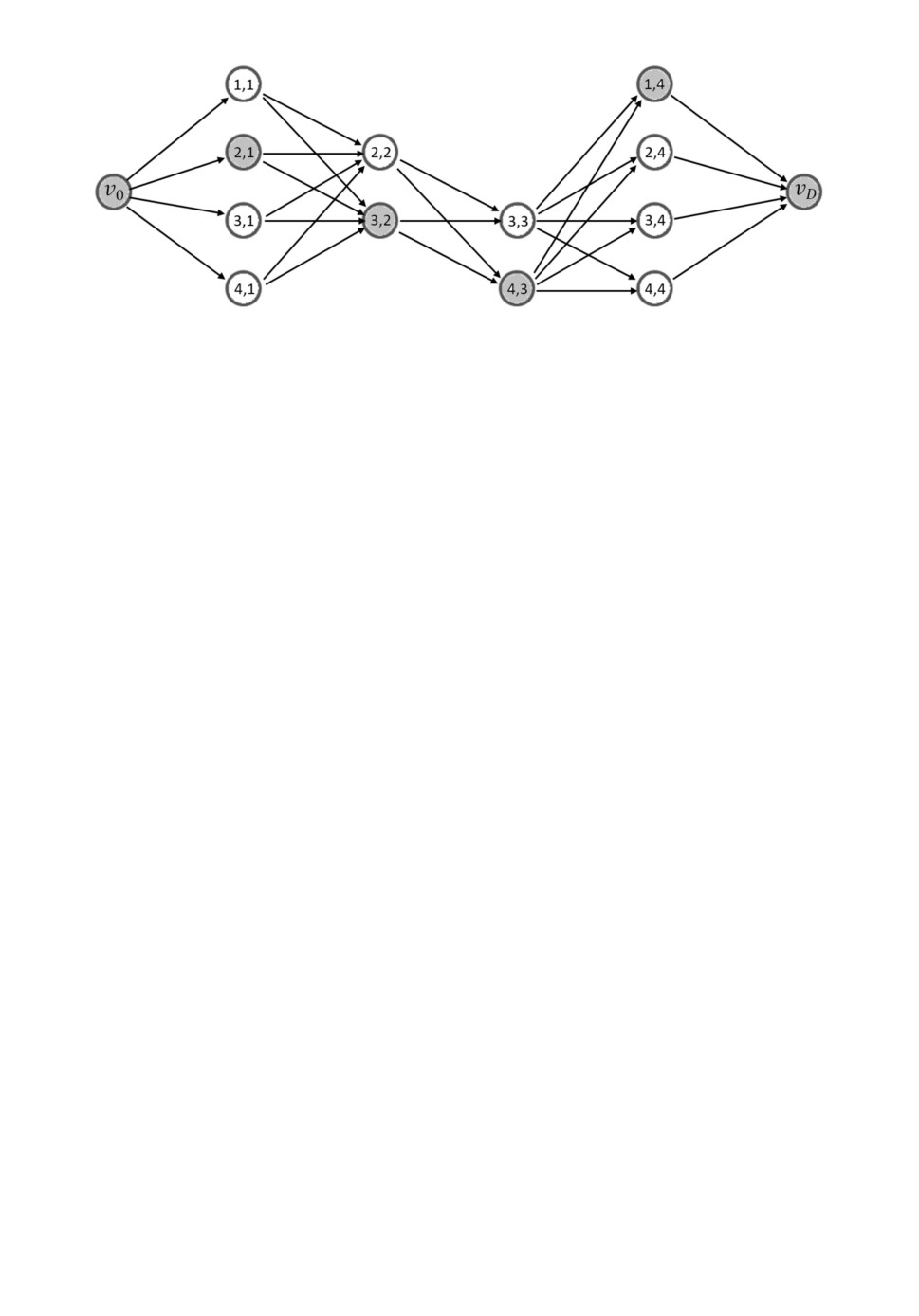
Рис. 2. Граф возможных назначений. Выделенный путь соответствует биекции
φ, задающей матрицу Xφ.
Для дальнейшего изложения необходимо ввести матрицу Φ, которая отража-
ет информацию о том, возможно ли размещение предприятия в городе:
{
1, если Cij < ∞,
Φ = (fij), где fij =
0, если Cij = ∞.
Таким образом, матрица Xφ получается из матрицы Φ выбором элементов,
соответствующих биекции φ.
Все возможные назначения в соответствии с матрицей Φ можно предста-
вить в качестве множества вершин некоторого графаG
V
E):
{
}
V =
v(i,j) : 1 ≤ i,j ≤ n
,
{
}
E=
[v(i,j), v(k,l)]: i = k, j = l
Если в матрице есть нули, то соответствующие вершины в графе отсутствуют.
Как и квадратичную задачу о назначениях, (2) можно рассматривать как
задачу поиска максимальной клики в графеG
V
E) с минимальным общим
весом вершин и ребер [17]. В качестве веса вершины ω(v(i,j)) принимается
значение стоимости Cij ; вес ребра ω[v(i,j), v(k,l)] равен в общем виде F (j, l), а
в эквивалентной квадратичной задаче — djl.
Пусть теперь есть несколько иной граф G(V, E) с теми же вершинами V =
{
}
=
V , но с ребрами E =
[v(i,j), v(k,j+1)]: i = k
, соединяющими вершины, со-
ответствующие соседним столбцам матрицы Φ. Веса ребер априори неизвест-
ны, но могут быть вычислены в соответствии с (2) как значения известной
функции F (π(j)(i1), π(j)(i2), . . . , j, j + 1), где π(j) - некоторая подстановка, из-
вестная на момент вычисления веса. Если добавить к нему две вершины с
нулевым весом и нулевым весом смежных с ними ребер
v0 : {[v0, (i, 1)]: 1 ≤ i ≤ n} ⊂ E,
vD : {[(i,n),vD]: 1 ≤ i ≤ n} ⊂ E,
то подстановка π будет задавать матрицу Xπ, единичные элементы которой
соответствуют пути минимальной длины (с минимальным суммарным весом
105
ребер и вершин) из корневой вершины v0 в конечную вершину vD (рис. 2).
Матрица Φ, соответствующая данному графу, выглядит следующим образом:
⎞
⎛1 0 0 1
⎜1
1
0
1⎟
Φ=
⎝
⎠.
0
1
1
1
1
0
1
1
В таком случае задача поиска максимальной клики в графеG
V , E) сво-
дится к задаче нахождения кратчайшего пути в графе G(V, E). Дана мат-
рица Φ, которая задает граф G(V, E), где V — описанное выше множество
вершин, веса которых равны Cij , а E — ребра графа. Веса ребер, выходящих
из корневой вершины v0, и ребер, входящих в вершину vD, полагаются рав-
ными нулю. Веса остальных ребер априори не определены, но известна функ-
ция F . Необходимо найти кратчайший путь из v0 в vD, содержащий ровно
одну вершину, соответствующую каждому столбцу и строке матрицы Φ.
3. Алгоритм решения
G(V, E) является взвешенным ориентированным графом с неотрицатель-
ными весами ребер. Для поиска кратчайшего расстояния между двумя вер-
шинами v0 и vD модифицирован широко известный алгоритм Дейкстры.
Прежде чем приводить предлагаемую модификацию, стоит остановиться на
основных моментах алгоритма Дейкстры. Его цель — поиск кратчайшего рас-
стояния от одной вершины a до всех остальных во взвешенном ориентирован-
ном графе без дуг отрицательного веса. Каждой вершине графа сопоставля-
ется метка — минимальное расстояние от нее до заданной вершины. Изна-
чально значение меток всех вершин равно бесконечности, а метка начальной
вершины равна нулю. Все вершины помечаются как непосещенные. Шаг ал-
горитма состоит в выборе среди еще непосещенных вершины u с минималь-
ной меткой и посещении всех соседних с ней вершин. При этом вычисляются
расстояния до них как сумма метки вершины u и веса ребра, соединяюще-
го каждую соседнюю вершину с u. Если это значение меньше текущей метки
вершины, то новым значением метки становится полученное расстояние до a.
Вершина u помечается посещенной, и шаг алгоритма повторяется до тех пор,
пока все вершины не будут посещены.
В графе G(V, E) метка конечной вершины vD будет равна минимально-
му значению функции стоимости (2). Чтобы получить весь путь, необходимо
в каждой вершине хранить информацию о родительской вершине, из кото-
рой совершен шаг. Далее подробно рассматривается модификация алгоритма
Дейкстры.
На начальном этапе метка корневой вершины полагается равной 0, роди-
тельская вершина для нее отсутствует, метки остальных вершин равны беско-
нечности, а их родители не определены, множество непосещенных вершин U
совпадает с V . Шаг алгоритма начинается с выбора среди множества U вер-
шины u(k,l) с минимальной меткой (на первом шаге это вершина v0). Далее
среди всех соседних вершин определяется множество Q, в которые возможно
сделать шаг. Здесь есть две причины, по которым необходима эта проверка.
106
а
б
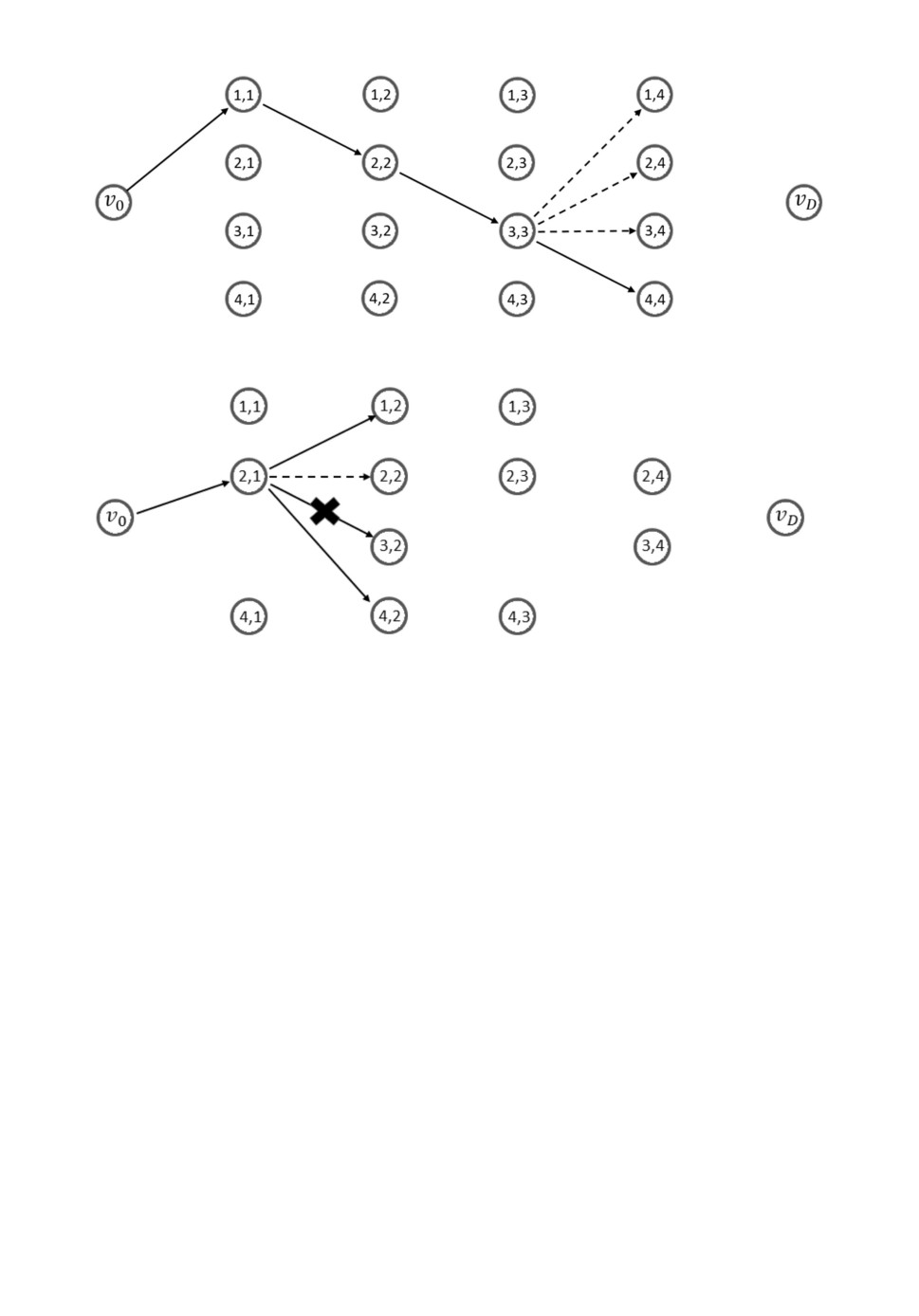
Рис. 3. а - Единственной допустимой вершиной, куда можно сделать шаг
из вершины v(3,3), является v(4,4). б - Выбор вершины v(3,2) на данном ша-
ге невозможен, так как из нее нельзя построить путь до vD в силу причин,
проиллюстрированных на рис. 3,а.
Каждой вершине, кроме корневой и конечной, сопоставлена пара (k, l), ко-
торая соответствует элементу φkl матрицы Φ, и она имеет вес ω(v(k,l)) = Ckl.
Чтобы добиться взаимной однозначности, вершина q(k,l) ∈ Q должна иметь
пару индексов, отличную по обоим значениями от всех уже посещенных вер-
шин (рис. 3,a). Поскольку в матрице возможных назначений Φ есть нулевые
элементы, которые не задают вершин графа (рис. 2), то существуют верши-
ны, из которых невозможно построить путь до конечной точки (рис. 3,б ).
Чтобы определить, принадлежит ли вершина q(k,l) множеству Q, из мат-
рицы Φ вычеркиваются строки и столбцы, соответствующие родительским
вершинам, т.е. которые составляют путь до q(k,l). Если в матрице Φ не по-
являются нулевые строки или столбцы, то производятся те же действия с
оставшейся матрицей и так далее, пока либо останется одна единица — q(k,l) ∈
∈ Q , либо обнаружится столбец или строка из одних нулей — q(k,l) признается
недопустимой.
Данная процедура проверки — крайне важная модификация алгоритма.
Нельзя не учитывать факт наличия недопустимых паросочетаний и отбро-
сить проверку — это приведет к неверным результатам. Далее разобран слу-
107
а
б
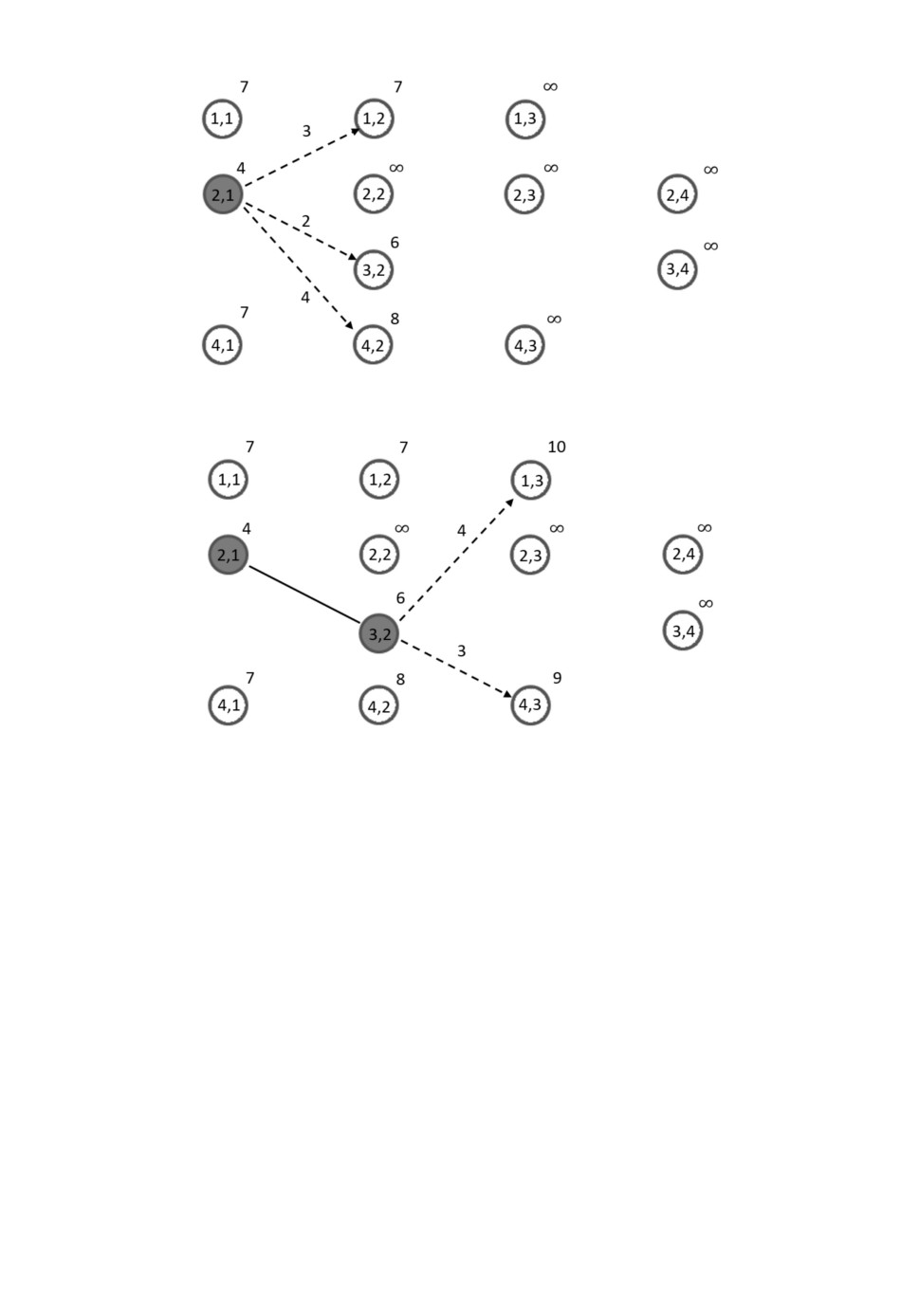
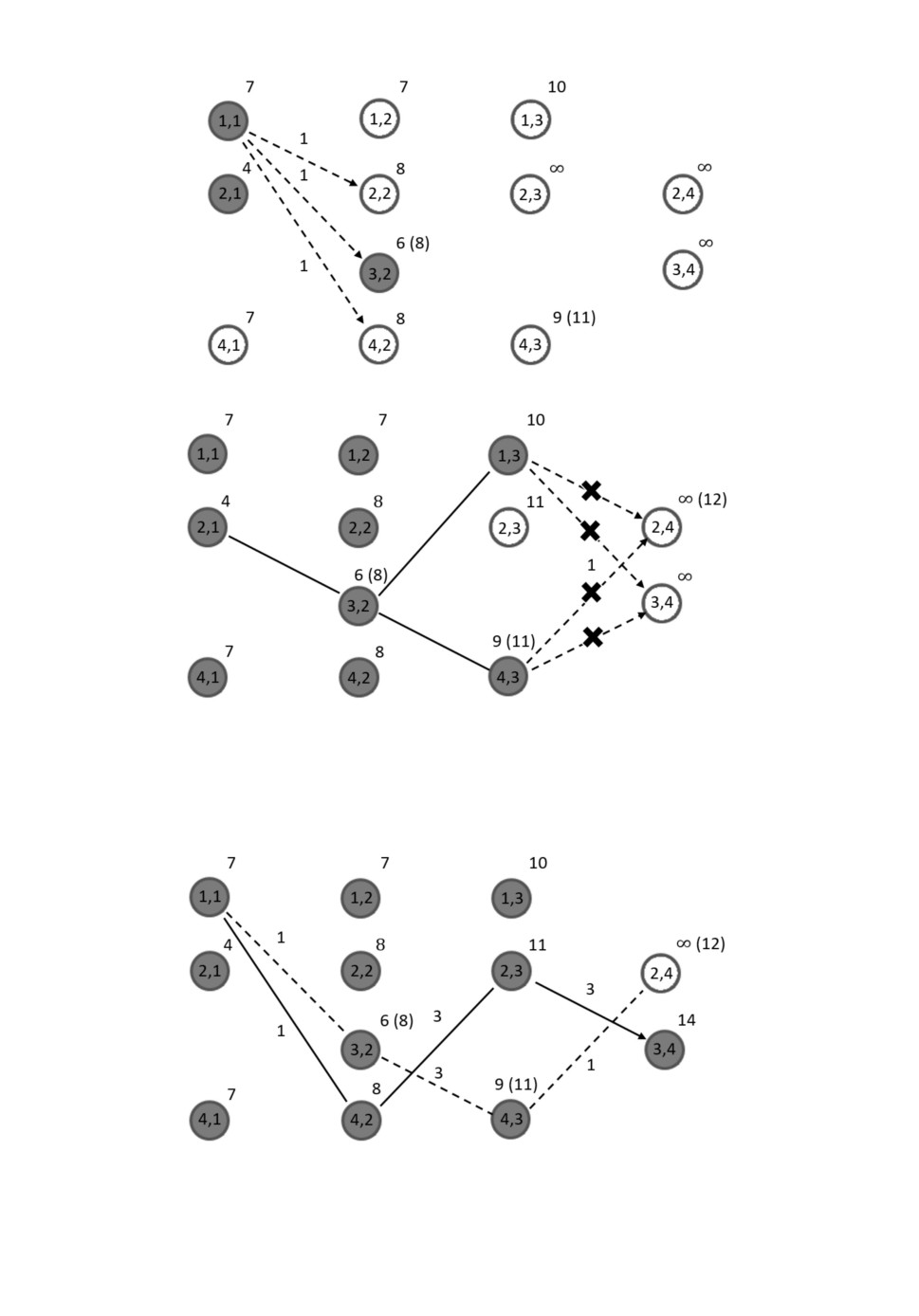
Рис. 4. Иллюстрация шага алгоритма. Закрашены посещенные вершины. Чис-
ла над стрелками соответствуют весам ребер. а - Изменение маркеров со-
седних вершин; б - вершина с маркером 6 посещена и изменяются маркеры
соседних для нее вершин
чай, когда отсутствие проверки допустимости вершины приводит к неверному
результату.
Если на шаге алгоритма не осуществлять проверку на возможность дойти
до конечной вершины, то вершине v(3,2) присвоится значение маркера, рав-
ное 6 (рис. 4,а). На следующем шаге она будет отмечена посещенной, так
как ее маркер будет минимальным среди всех непосещенных вершин (рис.
4,б ). Далее алгоритм не сможет изменить маркер этой вершины, посколь-
ку все остальные маркеры меньше 6, а веса ребер положительны (рис. 5,а).
Родительской вершиной для нее навсегда останется вершина v(2,1).
Спустя несколько шагов окажется, что из нее нельзя дойти до конечной
вершины (рис. 5,б ). Причина в том, что самый первый шаг (рис. 4,а) был
недопустим, из-за чего родителя этой вершины никак не изменить. При этом
оптимальным окажется путь, изображенный сплошной линией на рис. 6, что
108
а
б
Рис. 5. Иллюстрация шага алгоритма. а - Значение маркера вершины v(3,2)
не меняется. В скобках указаны возможные значения маркеров. б - Шаги,
обозначенные пунктиром, запрещены. Сплошными линиями выделены связи
с родительскими вершинами.
Рис. 6. Возможные пути в графе. Выбранный путь (сплошная линия) дороже.
109
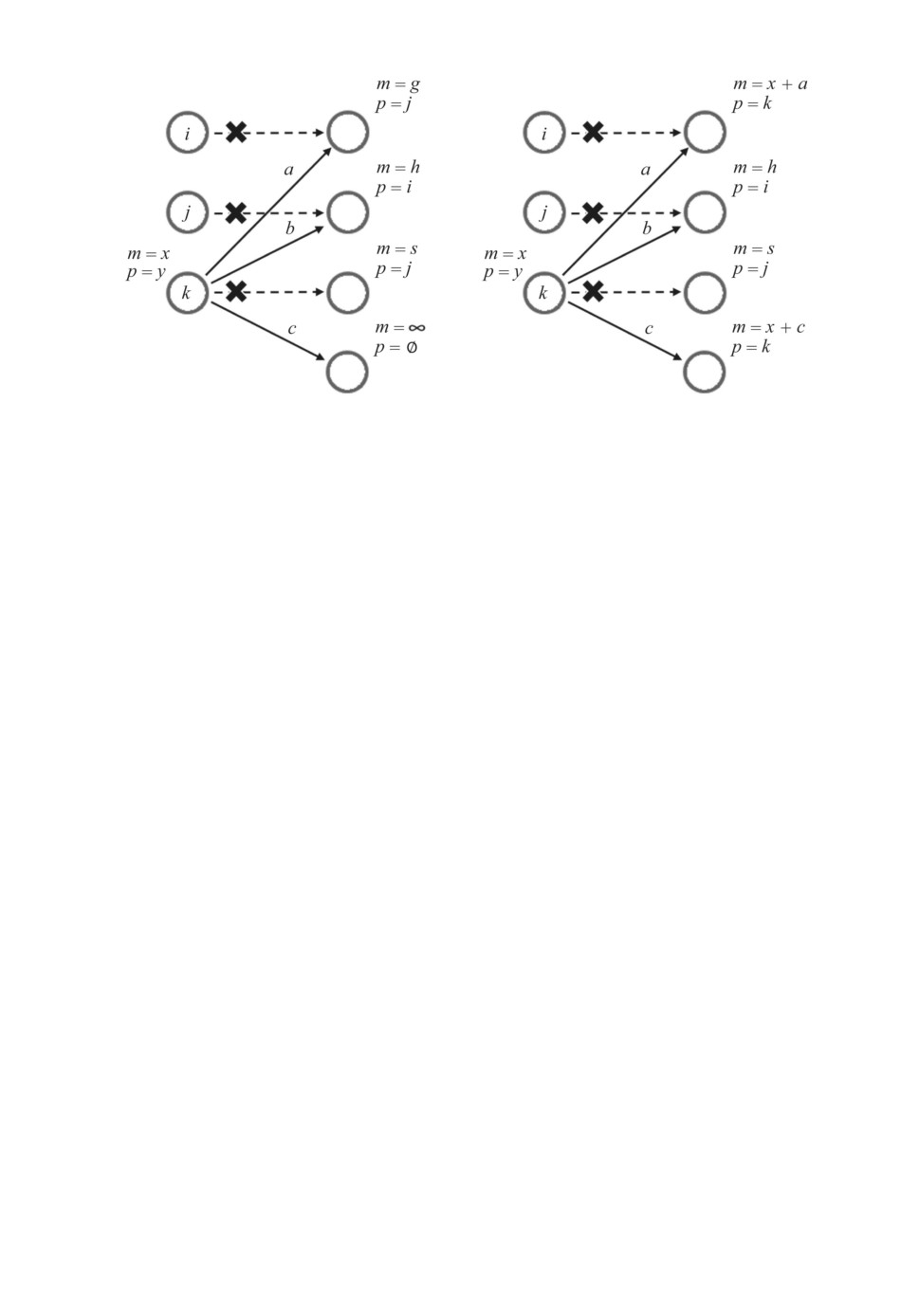
Рис. 7. Иллюстрация шага алгоритма; p - родительская вершина, m - метка
вершины, x + a > g; x + b > h; x + c < ∞.
неправильно. Если же предусмотреть все, то алгоритм найдет оптимальный
путь, изображенный штрихом на рис. 6 (в скобках указаны значения марке-
ров, которые бы имели вершины в таком случае).
После определения множества Q допустимых вершин вычисляется вес ω
для каждого ребра, соединяющего u и все q ∈ Q, а также метки m всех до-
пустимых вершин. Чтобы правильно вычислить стоимость назначений для
каждой вершины, необходимо хранить множество всех ее родительских вер-
шин P [u(i,j)] = {v(i(j),j), v(i(j-1),j-1), . . . , v(i(1),1)}. Это множество составляет те-
кущий путь до нее от корневой вершины и задает подстановку π(P) для вы-
числения веса ребра:
(
)
[
]
ω
u(i,j),q(k,j+1)
= F π(P)(i1),π(P)(i2),...,j,j + 1 ,
(4)
где k = 1, . . . , |Q|, j = π(P)(k),
(
)
(
)
(
)
(5)
m
q(k,j+1)
=m
u(i,j)
+Ckj+1 +ω
u(i,j),q(k,j+1)
Затем в соответствии с классическим шагом алгоритма Дейкстры про-
исходит сравнение с существующей меткой m∗(qk,j+1). Если значение новой
метки меньше существующей, то метка вершины изменяется, а родителем
помечается вершина, из которой произведен шаг (рис. 7).
Когда все допустимые вершины рассмотрены, u(i,j) помечается посещен-
ной и удаляется из множества U. После чего шаг алгоритма повторяется до
тех пор, пока вершиной с минимальной меткой не окажется u(i,n). В таком
случае единственной вершиной, куда возможно сделать шаг, является конеч-
ная вершина. Цепочка всех родителей составит кратчайший путь из v0 в vD.
Их индексы определят финальную подстановку (биекцию) π и соответствую-
щее решение задачи о назначении Xπ. Значение метки m(vD) (см. (4), (5))
110
определит минимальную стоимость в соответствии с функцией стоимости (2):
⎧
(
)
(
)
⎪m(vD) = m
v(π(n),n)
=m
v(π(n-1),n-1)
+Cn,π(n) +
⎪
[
]
⎪
+ω
v(π(n-1),n-1),v(π(n),n)
,
⎪
⎪
[
]
⎪ω
v(π(n-1),n-1),v(π(n),n)
= F(π(1),...,π(n)),
⎪
(
)
(
)
⎪
⎪m
v(π(n-1),n-1)
=m
v(π(n-2),n-2)
+Cn-1,π(n-1) +
⎪
[
]
⎪
+ω
v(π(n-2),n-2),v(π(n-1),n-1)
,
⎨
[
]
(6)
ω
v(π(n-2),n-2),v(π(n-1),n-1)
= F(π(1),...,π(n - 1)),
⎪
⎪
⎪
(
)
(
)
[
]
⎪
m
v(π(2),2)
=m
v(π(1),1)
+C2,π(2) +ω
v(π(1),1),v(π(2),2)
,
⎪
⎪
[
]
⎪ω
v(π(1),1),v(π(2),2)
= F(π(1),π(2)),
⎪
⎪
(
)
[
]
⎪m
v(π(1),1)
= m(v0) + C1,π(1) + ω
v0,v(π(1),1)
,
⎪
]
⎩ω[
v0,v(π(1),1)
= 0.
Таким образом, метка конечной вершины равна сумме всех весов ребер, со-
ставляющих путь из v0 в vD:
m(vD) = Cn,π(n) + Cn-1,π(n-1) + . . . + C2,π(2) + C1,π(1) +
(7)
+ F(π(1),π(2)) + ... + F(π(1),...,π(n - 1)) + F(π(1),...,π(n)).
Полученное выражение (7) совпадает с целевым функционалом (2), а значит,
значение метки m(vD) равно минимуму стоимости назначений, что иллю-
стрирует оптимальность решения π задачи о назначении.
4. Результаты и практическое применение алгоритма
В качестве демонстрации результатов работы предлагается рассмотреть
применение данного алгоритма для решения задачи о назначениях, возни-
кающей в нефтяной индустрии при планировании бурения на месторожде-
нии. Задача состоит в следующем: требуется пробурить скважины так, что-
бы каждая скважина вскрывала нефтяной пласт в определенном месте. При
этом есть множество устьев (начало скважин на поверхности) и множество
целей в пласте. Необходимо пробурить скважину из устья до цели так, что-
бы обеспечить минимальную суммарную стоимость бурения. Кроме того, на
геометрию скважин накладываются некоторые ограничения, из-за которых
существует риск пересечения траекторий. Поэтому необходимо не допустить
опасного сближения скважин.
В терминах задачи о назначениях необходимо установить взаимно одно-
значное соответствие между двумя данными множествами. Заданы стоимо-
сти Cij строительства скважины из j-го устья, вскрывающего пласт в i-й точ-
ке. Функция F выражает зависимость от расстояния между скважинами в
пространстве. Если эта функция зависит от положения только двух скважин
и нет разницы в выборе устья, то задача становится в точности квадратичной
задачей, описанной в главе 2.
111
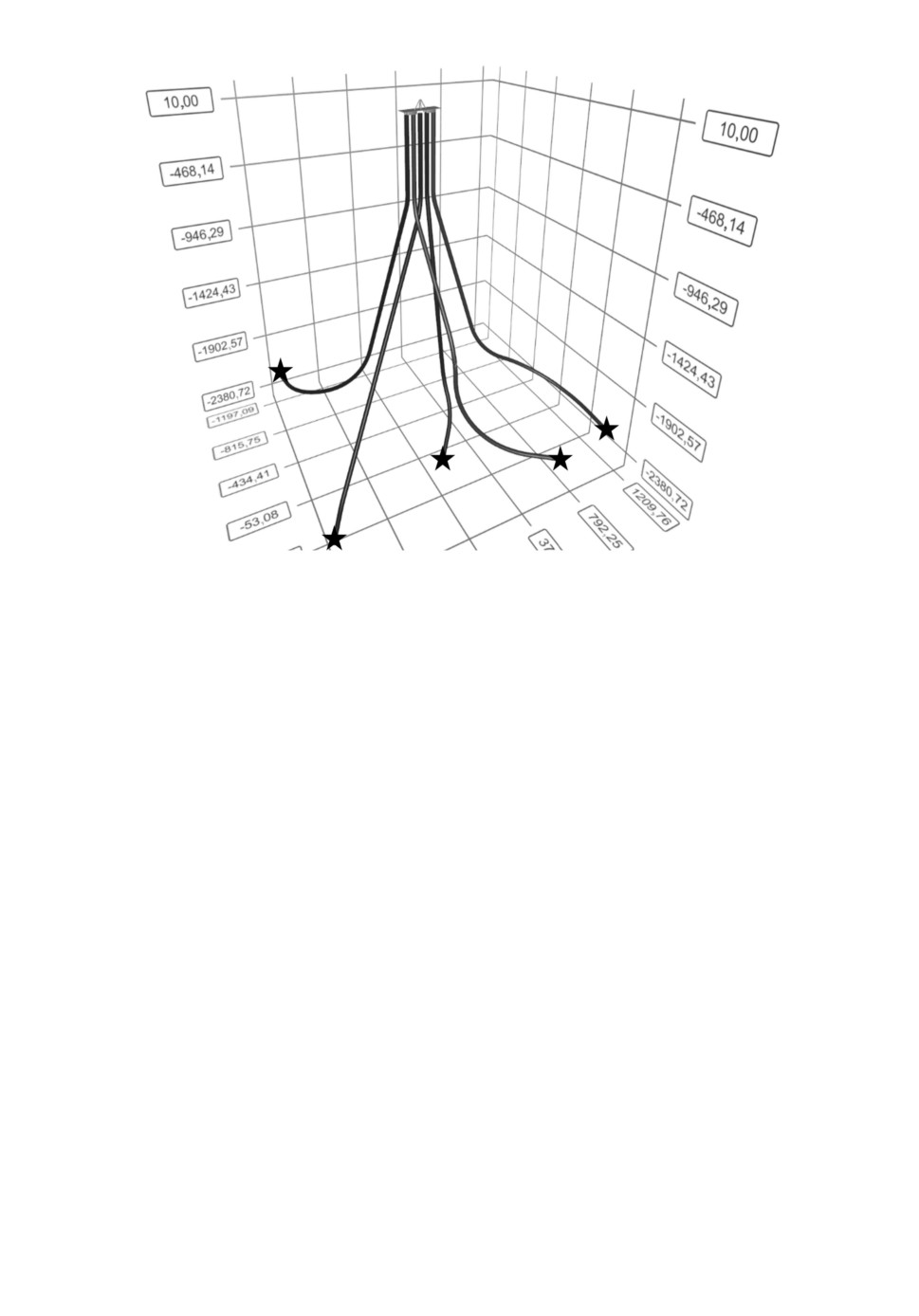
Рис. 8. Результат применения алгоритма при решении задачи бурения пяти
скважин.
Решение π задачи о назначениях с такими функциями стоимостей, полу-
ченное в результате работы рассматриваемого алгоритма, определит опти-
мальное множество скважин. На рис. 8 изображены траектории скважин,
соответствующие решению для пяти устьев и соответственно пяти целей.
В приведенном примере для каждой скважины дополнительно подбира-
лась ее геометрия, чтобы протяженность была минимальной. Также вычис-
ление веса ребра (функции F ) на каждом шаге алгоритма может быть крайне
ресурсозатратно в зависимости от специфики прикладной задачи и связано
с наличием недопустимых паросочетаний. В данном случае не все скважины
возможно пробурить из-за технологических ограничений на бурение. Поэто-
му необходимо провести анализ трудоемкости самого алгоритма.
Далее приведены зависимости временных затрат от размерности задачи.
На рис. 9 представлена зависимость времени работы алгоритма, реализован-
ного на языке MATLAB, от количества элементов в множествах n. Значе-
ния C(ij) заданы и не меняются в ходе решения. Элементами множеств яв-
ляются координаты точек на поверхности и в пласте. Функция F задана в
виде (3), где
(8)
dπ(i)π(j)
= |S(i, π(i)) - S(j, π(j))| ,
S - длина отрезка, соединяющего точки i и π(i).
Кривая «А» соответствует случаю, когда матрица Φ имеет нули. На каж-
дом шаге алгоритма необходимо производить проверку для определения мно-
112
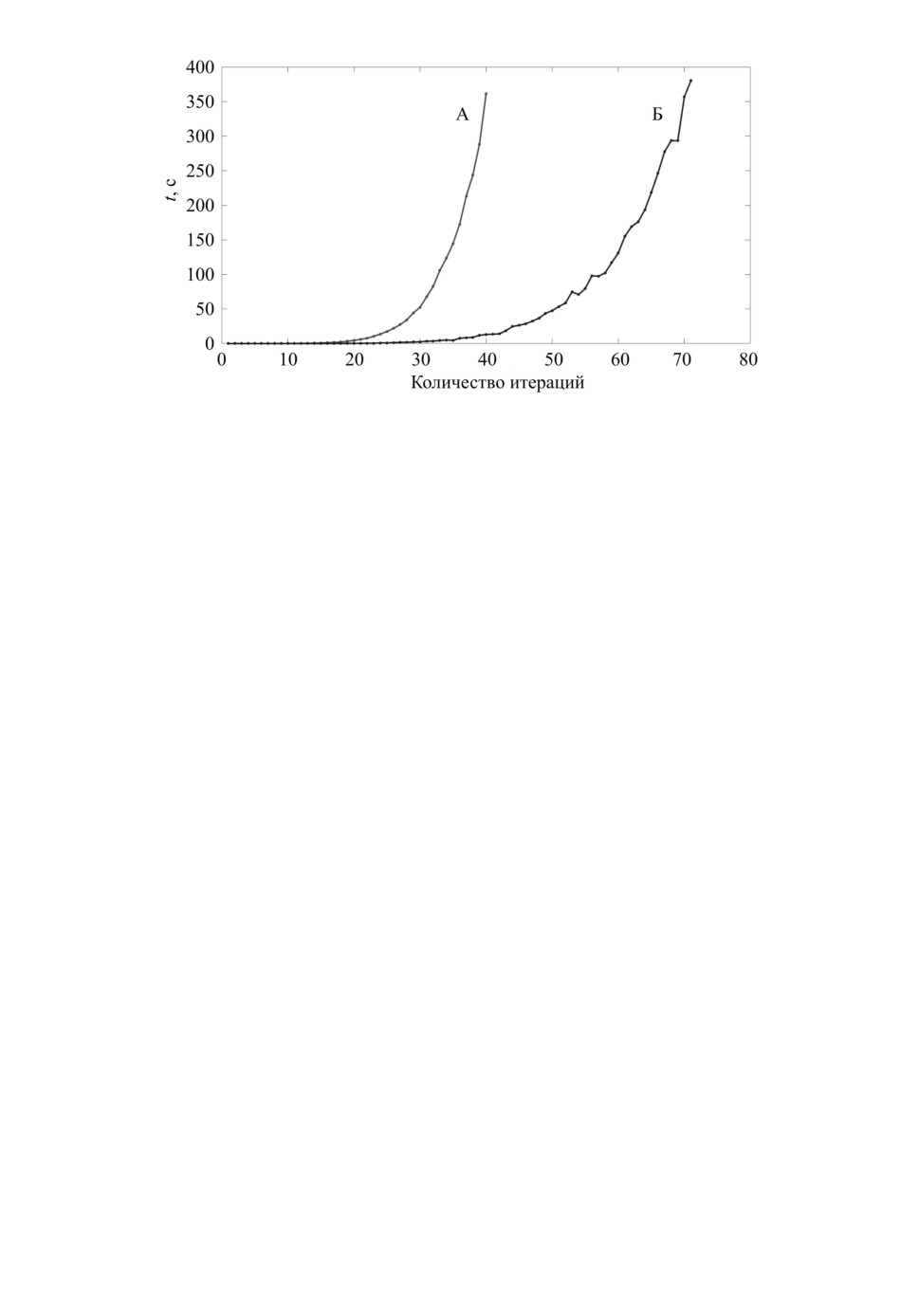
Рис. 9. Зависимость времени работы алгоритма от размерности задачи в слу-
чае наличия нулей в матрице Φ (кривая «А»), и их отсутствия (кривая «Б»).
жества допустимых вершин Q (см. главу 3). Временные затраты резко воз-
растают при размерности задачи более 25-30. Если же в матрице нет нулей,
что соответствует отсутствию каких-либо ограничений на назначения, то нет
необходимости в этой проверке (кривая «Б» на графике).
Полученный результат обосновывает применимость алгоритма в приклад-
ных задачах, в которых количество объектов невелико. В задаче бурения,
например, число скважин, которые бурят с одной площадки, редко превы-
шает 20-25. Кроме того, зависимость, полученная при отсутствии недопу-
стимых паросочетаний, иллюстрирует разрешимость за разумное время рас-
сматриваемой в главе 2 квадратичной задачи о назначениях при размерно-
сти 60-70. Отбрасывая условие равенства потоков fij = δij , задавшись вместо
этого симметричной матрицей bij = |βi - βj |, функцию F можно представить
в следующем виде:
(9) F (π(1), . . . , π(i)) =
∑
=dπ(i)π(1)bi,1 +dπ(i)π(2)bi,2 +···+dπ(i)π(i-1)bi,i-1 =
dπ(i)π(j) |βi - βj|.
j<i
Тогда задача (2) с функцией (9) представляет собой специальный случай
квадратичной задачи о назначении, описанный в [18], и может быть также ре-
шена с помощью предлагаемого алгоритма. Таким образом, подбирая функ-
цию F , возможно разрешить различные специальные случаи квадратичной
задачи о назначениях.
5. Заключение
Разработан алгоритм для решения задачи о назначениях специальной
структуры с функцией стоимости общего вида при наличии ограничений на
допустимые паросочетания. При таком обобщении затраты на назначения
невозможно определить без предположения о подстановке или задать их в
113
виде матрицы с известными коэффициентами. Кроме некоторых постоянных
коэффициентов стоимости, необходимо учесть зависимость затрат на одно
назначение от всех остальных назначений. В терминах теории графов дан-
ная проблема может быть сформулирована как задача поиска кратчайшего
пути в графе, построенном по всем возможным назначениям.
Предлагаемый метод решения основан на модификации алгоритма Дейкс-
тры для нахождения кратчайшего пути во взвешенном ориентированном гра-
фе и не требует задания определенного вида подстановки.
Разработанный метод является эмпирическим, поскольку авторы не каса-
лись вопроса строгого математического обоснования эффективности работы
алгоритма. Единственным обоснованием является хорошая работа на прак-
тике. Алгоритм был применен для решения прикладной задачи, связанной
с бурением скважин. В результате получены зависимости времени работы
от размерности задачи. Отмечено, что на время оказывает сильное влияние
наличие недопустимых паросочетаний. Однако для характерных задаче буре-
ния размерностей алгоритм эффективно находит оптимальные назначения.
Другим практическим применением алгоритма может быть его использова-
ние в задачах размещения радиолокационного оборудования различной мощ-
ности в определенном множестве позиций для покрытия области наибольшей
площади.
СПИСОК ЛИТЕРАТУРЫ
1.
Ловас Л., Пламмер М. Прикладные задачи теории графов. Теория паросочета-
ний в математике, физике, химии. М.: Мир, 1998.
2.
Dantzig G.B. Linear Programming and Extensions, Princeton UniversityPress,
Princeton, N.J. 1963 / Linear Programm. Extensions 1963. MLA.
3.
Barr R.S., Glover F., Klingman D. The alternating basis algorithm for assignment
problems // Math. Programm. 1977. Т. 13. No. 1. С. 1-13.
4.
Kuhn H.W. The Hungarian method for the assignment problem // Naval Res. Logist.
(NRL). 1955. Т. 2. No. 1-2. С. 83-97.
5.
Bertsekas D.P. A new algorithm for the assignment problem // Math. Programm.
1981. Т. 21. No. 1. С. 152-171.
6.
Хемди А. Таха Введение в исследование операций. 7-е изд М.: Вильямс, 2007.
7.
Burkard R.E., Cela E. Linear assignment problems and extensions / Handbook
Combinat. Optim. Springer US, 1999. С. 75-149.
8.
Koopmans T.C., Beckmann M. Assignment problems and the location of economic
activities // Econometrica: j. Econometric Soc. 1957. T. 25. No. 1. С. 53-76.
9.
Sahni S., Gonzalez T. P-complete approximation problems // J. ACM (JACM).
1976. Т. 23. No. 3. С. 555-565.
10.
Hardy G.H., Littlewood J.E., Polya G. The maximum of a certain bilinear form //
Proc. London Math. Soc. 1926. Т. 2. No. 1. С. 265-282.
11.
Burkard R.E., Cela E., Rote G., Woeginger G.J. The quadratic assignment problem
with a monotone anti-Monge and a symmetric Toeplitz matrix: Easy and hard
cases // Math. Programm. 1998. Т. 82. No. 1. С. 125-158.
114
12. Demidenko V.M., Finke G., Gordon V.S. Well solvable cases of the quadratic
assignment problem with monotone and bimonotone matrices // J. Math. Modell.
Algorithms. 2006. Т. 5. No. 2. С. 167-187.
13. Burkard R., Dell’Amico M., Martello S. Assignment problems: revised reprint. Siam,
2012. Т. 125.
14. Tate D.M., Smith A.E. A genetic approach to the quadratic assignment problem //
Comput. Oper. Res. 1995. Т. 22. No. 1. С. 73-83.
15. Maniezzo V., Colorni A. The ant system applied to the quadratic assignment
problem // IEEE Transact. Knowledge Data Engineer. 1999. Т. 11. No. 5. С. 769-778.
16. Taillard E. Robust taboo search for the quadratic assignment problem // Parallel
Comput. 1991. Т. 17. No. 4. С. 443-455.
17. Jünger M., Kaibel V. A basic study of the QAP polytope // Techincal Report 96.215.
Institut für Informatik, Universität zu Köln, Germany. 1996.
18.
Çela E., Schmuck N.S., Wimer S., Woeginger G.J. The Wiener maximum quadratic
assignment problem [Электронный ресурс] // arXiv.org. 2011. Дата обновления:
Статья представлена к публикации членом редколлегии А.А. Лазаревым.
Поступила в редакцию 10.03.2017
После доработки 11.01.2018
Принята к публикации 08.11.2018
115