Автоматика и телемеханика, № 1, 2019

(Национальный исследовательский университет

«Высшая школа экономики», Москва,

Институт проблем управления им. В.А. Трапезникова РАН, Москва)

АНАЛИЗ ПАТТЕРНОВ В СИСТЕМЕ ПАРАЛЛЕЛЬНЫХ КООРДИНАТ

НА БАЗЕ ПАРНОГО СРАВНЕНИЯ ПОКАЗАТЕЛЕЙ¹

Представлены основные свойства нового метода анализа паттернов в

системе параллельных координат, результат которого не зависит от после-

довательности данных в исходной выборке анализируемых объектов. До-

казано утверждение о том, что кластеры, полученные с использованием

данного метода, не пересекаются. Показана возможность представления

объектов одного кластера в виде монотонно возрастающих/убывающих

функций.

Ключевые слова: анализ паттернов, порядково-инвариантная паттерн-

кластеризация, кластерный анализ.

DOI: 10.1134/S0005231019010100

1. Введение

C развитием информационных технологий и накоплением больших объе-

мов данных все более значимым становится создание методов, позволяющих

автоматизировать процесс распознавания и выделения различных групп, об-

ладающих схожими свойствами. К первым подобным работам можно отне-

сти [1], предлагающую разбиение множества трех видов Ирисов по четырем

признакам c использованием линейного дискриминантного алгоритма. Опи-

санная в [1] база данных 150 Ирисов до сих пор является одной из наиболее

популярных в машинном обучении, а предложенная Р. Фишером методоло-

гия подробно рассматривается в ряде учебных пособий (например, [2, 3]).

Дальнейшее развитие данное направление получило в алгоритмах кластер-

ного анализа, основанных на использовании различных мер близости объ-

ектов [4, 5]. Однако потребности исследования все более сложных процессов

(экономических, финансовых, социальных и иных) привели к необходимости

учета не только близости значений, но и близости структуры самих данных,

что, в свою очередь, привело к развитию методов их визуального представ-

ления и анализа (в общем русле которых находится данная работа).

Из более современных исследований, учитывающих отмеченные тенден-

ции, укажем, в частности, на прикладные работы в банковской сфере [6, 7]

(анализ показателей CAMEL [8-10]), менеджменте [11], макроэкономике [12].

¹ Статья подготовлена в результате проведения исследования в рамках Программы

фундаментальных исследований Национального исследовательского университета «Выс-

шая школа экономики» (НИУ ВШЭ) и с использованием средств субсидии в рамках го-

сударственной поддержки ведущих университетов Российской Федерации “5-100”. Автор

выражает благодарность д-ру техн. наук, проф. Алескерову Ф.Т. за помощь в написании

данной статьи.

138

В основе данного направления лежит понятие «паттерн», которое в различ-

ных областях знаний определяется по-разному. Основные определения при-

ведены в [13]:

1) «как сущность явления, имеющего повторяющиеся черты»;

2) «как свойство повторяющихся компонентов, объединенных общей

структурой»;

3) «как процесс, фиксирующий модель взаимодействия изучаемых объек-

тов, включающего повторения».

В [2] под паттерном понимается «любые отношения, закономерности или

структура, присущая некоторому набору данных», а под анализом паттер-

нов — «процесс нахождения общих соотношений в наборе данных». Опира-

ясь на предложенные формулировки, под паттерном, в данной работе бу-

дем понимать комбинацию определенных, качественно похожих признаков.

В [2] отмечается, что для признания метода анализа паттернов эффектив-

ным, реализующий его алгоритм должен удовлетворять следующим усло-

виям: возможность обработки больших объемов данных (что подразумевает

относительно невысокую вычислительную сложность), робастность и стати-

стическую устойчивость. В данной работе будем учитывать еще один кри-

терий, затронутый в [14]: независимость конечных результатов от выбора

исходной последовательности показателей. В связи с этим рассматривают-

ся предложенные в [15] методы анализа паттернов: порядково-фиксирован-

ная и порядково-инвариантная паттерн-кластеризации. В работе обобщаются

реализующие их алгоритмы, предлагаются методы распознавания паттернов,

объединения схожих объектов в группы, а также исследуются ряд свойств

данных групп, в том числе описываются удобные способы их визуализации

и определения «средних/центральных» объектов кластера. Таким образом,

цель работы — обобщение и структурирование разработанных алгоритмов

анализа паттернов с не зависимым от последовательности входных данных

конечным результатом, а также исследование основных свойств как самих

алгоритмов, так и полученных на их основе групп объектов. Для удобства и

цельности изложения, доказательства всех сформулированных в работе пред-

ложений вынесены в Приложение.

2. Анализ паттернов: основные понятия

Исследуется некоторое множество, состоящее из m объектов, по n пока-

зателям. Элементы множества будем обозначать через x_i, набор показателей

конкретного объекта — x_i = (xi1, . . . , x_ij , . . . , x_in), где x_ij — j-й показатель

i-го объекта. Основной задачей являются выделение и объединение каче-

ственно схожих объектов. Для визуализации используется система парал-

лельных координат [14, 16, 17], которая состоит, как правило, из вертикаль-

ных линий (осей), отражающих значения показателей. На данных линиях

отмечаются их фактические значения, после чего значения соединяются от-

резками. В результате образуются кусочно-линейные функции, характеризу-

ющие анализируемые объекты.

Поясним идею метода объединения объектов в отдельные группы (класте-

ры) по виду кусочно-линейных функций на гипотетическом примере.

139

Рис. 1. Пример гипотетических объектов.

Пример. Исследуются пять объектов по четырем показателям (А, В, С

и D), значения которых приведены в табл. 1.

Визуально объекты 1-5 представлены на рис. 1.

Из рисунка наглядно видно, что объекты 1 и 2 имеют схожие структу-

ры. Данное утверждение верно и для объектов 4 и 5. Объект 3 рассмотрим

отдельно. Несмотря на тот факт, что абсолютные значения показателей дан-

ного объекта сильно отличаются от объектов 1 и 2, структуры их схожи:

показатели объекта 1 есть показатели объекта 3, умноженные на 5. Таким

образом, все три объекта описываются кусочно-линейными функциями еди-

ной структуры (единым паттерном), что дает основание для их объединения

по данному критерию.

Использование такого подхода оказалось удобным для решения широкого

круга прикладных задач. В частности, в [6] проведен динамический анализ

паттернов показателей 1018 банков России за 1999-2003 гг. Исходные дан-

ные базируются на фундаментальных характеристиках банков — показателях

СAMEL (C - достаточность капитала, A - качество активов, M - менеджмент,

E - прибыль, L - ликвидность) с учетом некоторых дополнений.

Таблица 1. Пример с гипотетическими объектами

Объекты

140

На базе квартальных данных за указанный период построено 19342 ку-

сочно-линейные функции, что позволило выделить 151 типовых паттернов,

причем первые 50 содержали 90,14% всех данных, а первые 13-52,19%. В [7]

применен аналогичный подход для исследования 55 банков Турции. Базовая

система показателей также основывалась на CAMEL, а результатом являлось

формирование 27 паттернов.

Использование метода анализа паттернов в системе параллельных коорди-

нат демонстрирует его эффективность для различных приложений [13, 16],

однако сам метод критичен к последовательности параметров. Ниже пред-

ставлены алгоритмы его реализации, основанные на парном сравнении по-

казателей порядково-фиксированной и порядково-инвариантной паттерн-

кластеризаций, позволившие устранить указанный недостаток.

3. Порядково-фиксированная и порядково-инвариантная

паттерн-кластеризация

Приведем краткое описание порядково-фиксированной и порядково-ин-

вариантной паттерн-кластеризаций, реализующих объединение объектов в

группы/кластеры по виду их кусочно-линейных функций в системе парал-

лельных координат (полное описание методов приведено в [15, 18]).

Как отмечено выше, исходные данные представлены множеством X,

состоящим из m объектов, каждый из которых характеризуется n показа-

телями. Образуем кодировки c_i каждого объекта x_i ∈ X путем парного срав-

нения его показателей согласно формуле

∑

(1)

c_i =

10s-1z^n-si,

s=1

где z^si определяется как

⎧

⎨1, если xis < xis+1,

(2)

z^si =

0, если x_is = xis+1,

⎩

2, если x_is > xis+1.

Если c_i = c_k, объекты x_i и x_k объединяются в единый кластер, если нет —

разделяются. Отметим, что значение z^si определяется выражением 2 путем

сравнения рядом стоящих показателей x_is и xis+1 в заданной их последо-

вательности. Поэтому в дальнейшем данный метод будем называть поряд-

ково-фиксированной паттерн-кластеризацией, а кластеры, полученные на ос-

нове данного метода, соответственно порядково-фиксированными паттерн-

кластерами.

Вычислительная сложность N_fix данного метода можно выразить форму-

лой

m²(m - 1)(n - 1)

N_fix =

141

Поскольку N_fix является относительно невысокой, данный метод удобно

применять для предварительного анализа данных.

Второй метод — порядково-инвариантная паттерн-кластеризация — раз-

работан для получения не зависимых от исходной последовательности пока-

зателей результатов. Потребность в создании такого метода обусловлена, как

отмечено выше, комментариями некоторых работ по параллельным коорди-

натам (в том числе [14]), указывающих на необходимость «крайне осторожно-

го выбора последовательности анализируемых показателей», поскольку она

влияет на вид формируемых паттернов и в общем случае другая последова-

тельность может приводить к альтернативному характеру кусочно-линейных

функций и, как следствие, к альтернативным результатам.

Алгоритм порядково-инвариантной паттерн-кластеризация аналогичен

порядково-фиксированной и основан на сравнении кодировок объектов. Сами

объекты в этом случае представлены в виде полных взвешенных ориентиро-

ванных графов, вершины которых соответствуют анализируемым показате-

лям, а значения соединяющих их ребер — результатам парных сравнений

(предполагается сравнения вида «больше», «равно» и «меньше»). С исполь-

зованием значений ребер, формируется дополнительная кодировка объекта:

∑

(3)

c^dopi =

10j-(s+2)e^sji,

s=1 j=s+2

где: e^sji — значение ребра графа, соединяющего s-ю и j-ю вершины, которое

аналогично (2) определяется по формуле

⎧

⎨1, если xis < xis+1,

(4)

e^sji =

0, если x_is = xis+1,

⎩

2, если x_is > xis+1.

Принцип формирования групп аналогичен порядково-фиксированной

паттерн-кластеризации: если c^dopi = c^dopk, объекты x_i и x_k объединяются в еди-

ный кластер, в противном случае разбиваются по разным.

В дальнейшем кластер, сформированный на основе порядко-инвариантной

паттерн-кластеризации, будем называть порядково-инвариантным паттерн-

кластером.

Вычислительная сложность N_inv данного метода определяется как

m²n(m - 1)(n - 1)

N_inv =

однако с использованием доказанного ниже утверждения 2 может быть сни-

жена до сложности алгоритма сортировки.

Далее, определим максимальное число порядково-фиксированных и

порядково-инвариантных паттерн-кластеров.

В рассматриваемых методах критерием объединения в единый кластер

служит совпадение кодов, формируемых при парных сравнениях соответ-

142

ствующих показателей объекта. Используя известное выражение теории ко-

дирования (при использовании алфавита кодирования, состоящего из β раз-

личных символов и длине кодовой последовательности γ, максимальное чис-

ло V различных кодовых комбинаций равно β^γ ), запишем:

V =R^N,

где R — число возможных значений, характеризующих результат парных

сравнений соответствующих показателей объекта (определяемых формула-

ми (2) и (4)).

Поскольку для порядково-фиксированной паттерн-кластеризации код

формируется путем n - 1 парных сравнений, число возможных порядко-

во-фиксированных паттерн-кластеров V_fix определяется как

V_fix = R(n-1) = 3(n-1),

а число кластеров, формируемых в результате порядково-инвариантной

паттерн-кластеризации, V_inv —

n(n-1)

V_inv = R

Взяв отношение этих величин, получим оценку соотношения между макси-

мально-возможными числами порядково-инвариантных и порядково-фикси-

рованных паттерн-кластеров:

n(n-1)

V_inv

n(n-1)

V_fix

R(n-1)

Замечание 1. Полученное выражение определяет максимально воз-

можное число подклаcтеров, которое можно выделить в рамках поряд-

ково-фиксированного паттерн-кластера. Реальное их количество может ока-

заться существенно меньше. В частности, если порядково-фиксированный

паттерн-кластер удовлетворяет условию утверждения 2 (см. раздел 4), то он

сам является порядково-инвариантным паттерн-кластером и в силу утвер-

ждения 1 (см. ниже), никаких иных подкластеров не содержит.

4. Порядково-инвариантная паттерн-кластеризация: основные свойства

Рассмотрим три утверждения, демонстрирующие важные свойства опи-

санного выше метода.

Утверждение 1. Кластеры, полученные с использованием порядково-

инвариантной паттерн-кластеризации, не пересекаются.

Доказательство приведено в Приложении.

Можно привести следующее замечание.

Замечание 2. Утверждение 1 весьма важно, поскольку декларирует од-

нозначность результатов рассматриваемого метода. Это означает, что произ-

вольное расположение объектов в исходном множестве, равно как и произ-

вольный порядок их показателей, а также использование порядково-инвари-

антной паттерн-кластеризации произвольное число раз на одних и тех же

данных не влияет на результат кластеризации.

143

Рис. 2. Гипотетический пример двух порядково-инвариантных паттерн-кластеров.

Отметим, что если порядок показателей строго фиксирован и не меняется,

то утверждение 1 верно и для порядково-фиксированных паттерн-кластеров.

Утверждение 2. Если существует последовательность расположе-

ния показателей, при которой их значения образуют строго монотонно

возрастающую/убывающую последовательность для каждого объекта ис-

ходного множества X, то это множество представляет собой порядково-

инвариантный паттерн-кластер.

Доказательство приведено в Приложении.

Можно привести замечание 3.

Замечание 3. Отмеченное свойство порядково-инвариантных паттерн-

кластеров, определяемое утверждением 2, удобно использовать для предва-

рительного сравнения различных групп объектов и визуального восприятия

их отличительных особенностей. В качестве примера, рассмотрим множество

из трех объектов, показатели которых и соответствующие кусочно-линейные

функции приведены на рис. 2. Использование описанных выше методов поз-

воляет выделить два порядково-инвариантных паттерн-кластера: Объект 1;

Объект 3, Объект 2.

Расположим показатели таким образом, чтобы их значения образовали мо-

нотонно возрастающую последовательность для первого и третьего объектов,

образующих порядково-инвариантный паттерн-кластер (см. рис. 3). Можно

видеть, что в этом случае более четко выражен характер их различия с объ-

ектом 2.

Утверждение 3. Для объектов порядково-инвариантного паттерн-

кластера, существует порядок расположения показателей, при котором их

значения образуют монотонную неубывающую/невозрастающую последова-

тельность для каждого объекта кластера.

144

Рис. 3. Гипотетический пример двух порядково-инвариантных паттерн-кластеров.

Доказательство приведено в Приложении.

Можно привести замечание 4.

Замечание 4. Важным следствием утверждений 2 и 3 является возмож-

ность их использования для снижения вычислительной сложности поряд-

ково-инвариантной паттерн-кластеризации до сложности алгоритма сорти-

ровки.

5. Использование порядково-инвариантной паттерн-кластеризации

при исследовании экономических, инновационных

и образовательных показателей в РФ

Для иллюстрации предложенных методов, а также некоторых основных

свойств рассмотрим пример реальных данных из [19], где исследуются по-

казатели науки, образования и инновационной активности регионов РФ за

2007-2010 гг. На базе российского регионального инновационного индекса [20]

были сформированы 6 блоков показателей: социально-экономические усло-

вия (A), образовательный потенциал (B), потенциал научно-технической дея-

тельности (X), результативность исследований и разработок (C), потенциал

инновационной деятельности (D) и результативность инновационной деятель-

ности (E). В результате корреляционного анализа блок, научно-технический

потенциал был исключен, и регионы РФ подразделялись на основании бло-

ков А-E.

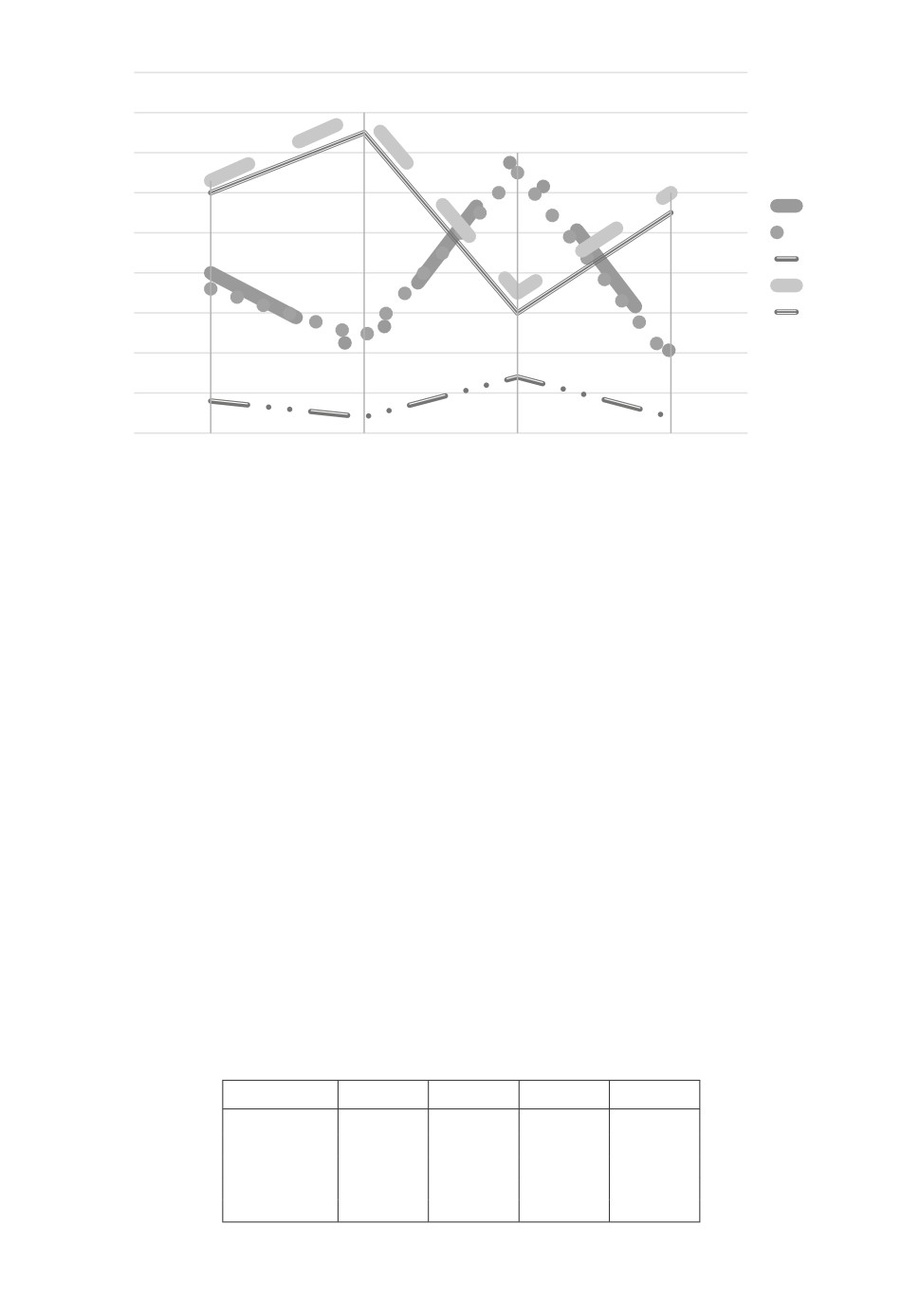
Для начала воспользуемся порядково-инвариантной паттерн-кластериза-

цией для разбиения регионов на кластеры. Результатом являются 22 кла-

стера, содержащих более 5 объектов, 12 кластеров — от 3 до 5 и 1 кластер,

в который вошли «уникальные объекты». Примеры полученных кластеров

представлены на рис. 4.

145

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

A B C D E A B C D E A B C D E

Рис. 4. Примеры кластеров, полученных при использовании порядково-инва-

риантной паттерн-кластеризации.

Далее, возьмем один из полученных в работе [20] кластеров и проверим,

можно ли его отнести к порядково-инвариантным паттерн-кластерам (дан-

ные приведены в табл. 2, значения округлены до второго знака после запя-

той).

Каждому региону табл. 2 соответствует единая кодировка, полученная

при помощи формул (1) и (3): «1122» и «222221» (дополнительная кодиров-

ка). Следовательно, полученный в [19] паттерн является порядково-инвари-

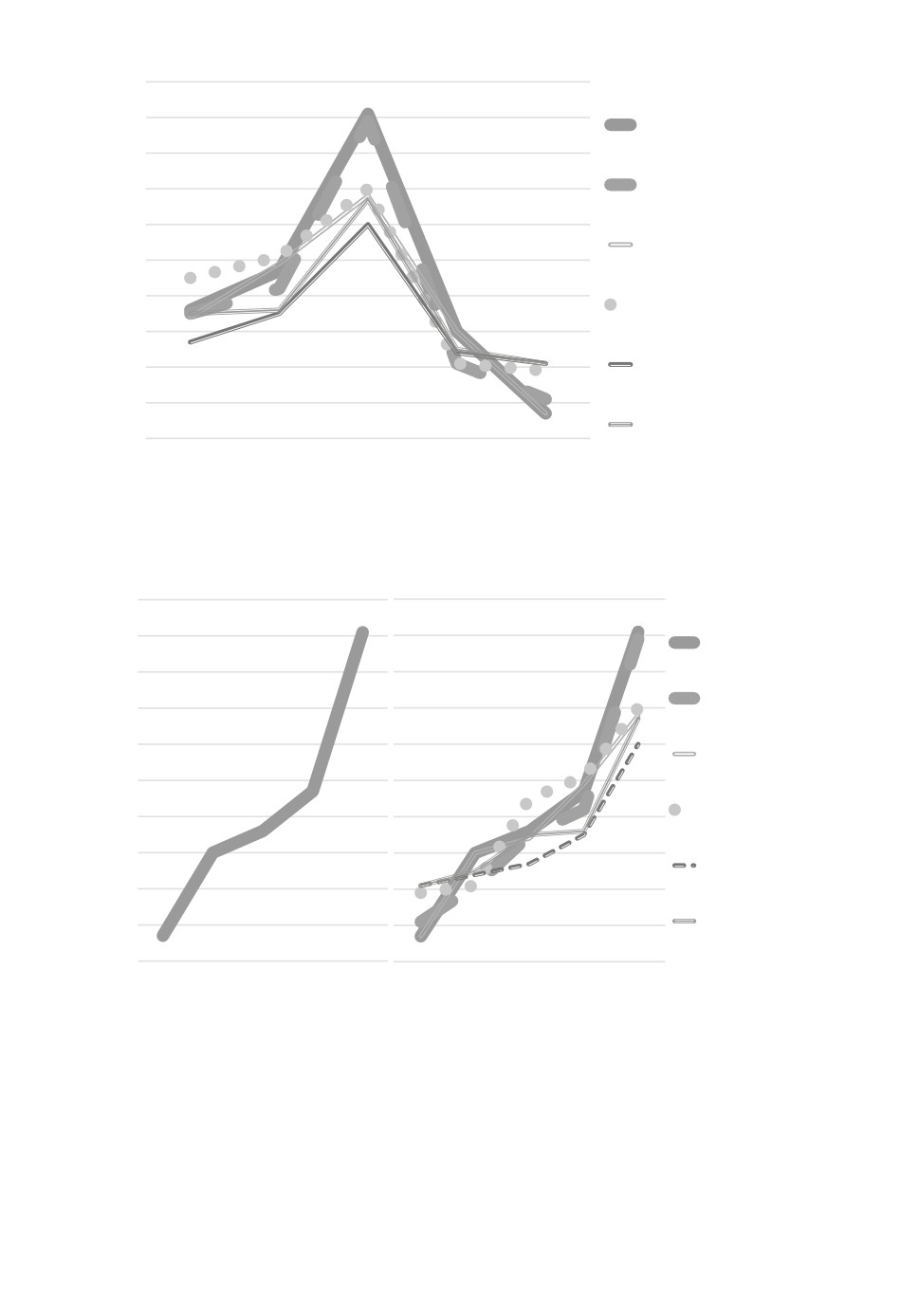
антным паттерн-кластером. Для данных регионов построим кусочно-линей-

ные функции, см. рис. 5.

Теперь проиллюстрируем справедливость утверждения

3. Выделим

первую строку табл. 2: (0,36; 0,47; 0,91; 0,3; 0,07). Данная строка описывает

выбранные показатели Москвы в 2009 г. Расположим значения показателей в

порядке возрастания (E, D, A, B, C). Такому порядку расположения показате-

лей соответствует паттерн, имеющий форму кусочно-линейной неубывающей

функции. При данном расположении показателей согласно утверждению 3

кусочно-линейные функции других объектов также будут иметь вид неубы-

вающей функции, что продемонстрировано на рис. 6. Несложно проверить

Таблица 2. Пример с гипотетическими объектами

Регион/года

Москва 2009

0,36

0,47

0,91

0,3

0,07

Москва 2010

0,35

0,42

0,89

0,21

0,11

Санкт-Петербург 2007

0,34

0,49

0,68

0,3

0,07

Санкт-Петербург 2009

0,45

0,51

0,7

0,21

0,19

Приморский край 2008

0,27

0,35

0,6

0,24

0,21

Приморский край 2009

0,35

0,36

0,67

0,25

0,21

146

0,9

Москва 2009

0,8

0,7

Москва 2010

0,6

Санкт- Петербург 2007

0,5

0,4

Санкт-Петербург 2009

0,3

0,2

Приморский край 2008

0,1

Приморский край 2009

Рис. 5. Кусочно-линейные функции объектов, соответствующие порядку по-

казателей A, B, C, D, E.

0,9

Москва 2009

0,8

Москва 2010

0,7

0,6

Санкт-

0,5

Петербург 2007

Санкт -

0,4

Петербург 2009

0,3

Приморский

0,2

край 2008

0,1

Приморский

край 2009

E D А В С

D А В С

Рис. 6. Кусочно-линейные функции объектов, соответствующие порядку по-

казателей A, B, C, D, E.

на данном примере и справедливость утверждения 2: для любого из трех

рассматриваемых регионов (за два года каждый) существует последователь-

ность расположения показателей (E, D, A, B, C), при которой формируется

строго возрастающая последовательность, и, следовательно, рассматривае-

мые регионы формируют единый порядково-инвариантный паттерн-кластер.

147

6. Операции над объектами кластеров и их свойства

Рассмотрим некоторые математические операции над объектами поряд-

ково-инвариантных паттерн-кластеров.

1. Операция суммирования. Под суммой двух объектов x₁ = (x₁₁,

...,x1j,...,x1n) и x₂ = (x₂₁,...,x2j,...,x2n) будем понимать новый объект

x_s = x₁ + x₂, значения показателей которого определяются как сумма соот-

ветствующих показателей объектов x₁ и x₂: x_s = (x₁₁ + x₂₁, . . . , x1j + x2j ,

...,x1n + x2n).

2. Произведение объекта на число. Под произведением объекта x₁ =

= (x₁₁, . . . , x1j , . . . , x1n) порядково-инвариантного паттерн-кластера на дей-

ствительное число α будем понимать новый объект x_α = αx₁, значения по-

казателей которого определяются как произведение показателей исходного

объектов x₁ на число α: x_α = (αx₁₁, . . . , αx1j , . . . , αx1n).

Утверждение 4. Если два объекта x₁ = (x₁₁,...,x1j,...,x1n) и x₂ =

= (x₂₁, . . . , x2j , . . . , x2n) принадлежат одному порядково-инвариантному

паттерн-кластеру, то и их сумма x_s = x₁ + x₂ = (x₁₁ + x₂₁, . . . , x1j +

+x2j,... ,x1n + x2n) также принадлежит этому кластеру.

Доказательство приведено в Приложении.

Утверждение 5. Если объект x₁ = (x₁₁,...,x1j,...,x1n) принадле-

жит некоторому порядково-инвариантному паттерн-кластеру v^inva, то для

любых положительных значений α (α > 0) объект x_α = αx₁ также принад-

лежит данному кластеру.

Доказательство данного утверждения аналогично доказательству утвер-

ждения 4.

Сформулируем важные следствия утверждений 4 и 5.

Следствие 1. Если объекты x₁,...,x_i,...,x_n принадлежат одному

порядково-инвариантному паттерн-кластеру, то и «средний» («централь-

ный») объект x_st вида

∑

x_st =

x_i

i=1

также принадлежит данному кластеру.

Следствие 2. Если объекты x₁,...,x_i,...,x_n принадлежат одному

порядково-инвариантному паттерн-кластеру, то и их линейная комбина-

ция x_lc вида

∑

x_lc =

λ_ix_i,

i=1

где λ_i > 0 | i = 1, . . . , n, также принадлежит данному кластеру.

148

7. Заключение

В работе приведено описание двух разновидностей перспективного метода

анализа данных — анализа паттернов и описаны некоторые их свойства. При-

ведена вычислительная сложность соответствующих методов. Сформулиро-

ваны и доказаны пять утверждений и два следствия, в том числе о непересе-

чении порядково-инвариантных паттерн-кластеров, о представлении объек-

тов данных кластеров в виде монотонно возрастающих/убывающих функций,

а также о нахождении «среднего» («центрального») объекта кластера.

ПРИЛОЖЕНИЕ

Доказательство утверждения 1. Предположим, что существуют

два различных (несовпадающих) кластера v^inva = v^invb, полученных в резуль-

тате порядково-инвариантной паттерн-кластеризации некоторого множества

объектов X. Согласно утверждению 1 v^inva ∩ v^invb = ∅.

Доказательство проведем от противного. Допустим, что данное утвержде-

ние не выполняется и v^inva ∩ v^invb = ∅. Это означает, что существует хотя бы

один объект x^∗i ∈ X : x^∗i ∈ v^inva ∩ v^invb.

Поскольку v^inva = v^invb, то существует и некоторая последовательность ис-

ходных показателей, при которой кусочно-линейные функции данных класте-

ров имеют различный вид. Данную последовательность обозначим через Y .

Согласно определению (алгоритму построения) порядково-инвариантных

паттерн-кластеров вид кусочно-линейных функций всех объектов класте-

ра v^inva должен совпадать при любой последовательности исходных показате-

лей (включая последовательность Y ). Поскольку x^∗i ∈ v^inva, то вид кусочно-

линейных функций всех объектов кластера v^inva аналогичен виду кусочно-

линейной функции объекта x^∗i. Повторив данное рассуждение для класте-

ра v^invb, приходим к заключению, что вид кусочно-линейных функций всех

объектов кластера v^invb также аналогичен виду кусочно-линейной функции

объекта x^∗i. Таким образом, приходим к заключению, что вид кусочно-

линейных функций всех объектов кластеров v^inva и v^invb совпадает (анало-

гичен виду кусочно-линейной функции объекта x^∗i). Однако в этом слу-

чае согласно определению (алгоритму построения) порядково-инвариантной

паттерн-кластеризации кластеры v^inva и v^invb должны быть объединены в еди-

ный порядково-инвариантный паттерн-кластер, что противоречит сделанно-

му предположению о том, что v^inva и v^invb — различные, несовпадающие кла-

стеры. Следовательно, v^inva ∩ v^invb = ∅. Утверждение 1 доказано.

Доказательство утверждения 2. Рассмотрим случай монотонно

возрастающей последовательности показателей (аналогичное доказательство

можно привести и для монотонно убывающей последовательности). Дока-

жем утверждение 2, используя метод математической индукции (для чего

проверим его справедливость для множества из двух и трех объектов и пред-

положив, что оно выполняется для случая k > 3 объектов, докажем его спра-

ведливость для случая k + 1).

1. Пусть множество X содержит только два объекта: x₁ = (x₁₁,

...,x1j,...,x1n) и x₂ = (x₂₁,...,x2j,...,x2n), причем x₁₁ < ... < x1j < ...

149

... < x1n, и x₂₁ < ... < x2j < ... < x2n. Исходя из метода порядково-инва-

риантной паттерн-кластеризации, описанного выше, для парного сравнения

всех показателей одного объекта требуется n(n - 1)/2 сравнений, результат

которых однозначно определяется выражением (2). Поскольку значения по-

казателей первого объекта расположены в порядке их возрастания (x₁₁ <

... < x1j < ... < x1n), получаем, что x1p < x1q ∀ p < q и x1r > x1s ∀ r > s.

Для объекта x₂ можно сделать такой же вывод: x2p < x2q ∀ p < q и

x2r > x2s ∀ r > s. Отмеченная идентичность неравенств для первого и второ-

го объектов определяет идентичность результатов сравнения, определяемых

выражением (4), и, как следствие, идентичность кодовых последовательно-

стей, определяемых выражением (3).

Поскольку для объектов x₁ и x₂ получены одинаковые кодировки, мож-

но сделать вывод, что данные объекты могут быть объединены в единый

порядково-инвариантный паттерн-кластер.

2. Дополним анализ объектом x₃ = (x₃₁, . . . , x3j , . . . , x3n), причем x₃₁ <

...<x3j <...<x3n.

Поскольку для показателей объекта x₃ выполняется условие x₃₁ <

... < x3j < ... < x3n, то, опираясь на п. 1 доказательства, можно сделать сле-

дующие выводы:

а) x₁ и x₃ принадлежат одному порядково-инвариантному паттерн-класте-

ру;

б) x₂ и x₃ принадлежат одному порядково-инвариантному паттерн-класте-

ру.

Согласно утверждению 1 кластеры, полученные с использованием поряд-

ково-инвариантной паттерн-кластеризации, не пересекаются. Таким образом,

все три объекта образуют единый порядково-инвариантный паттерн-кластер.

3. Предположив, что утверждение 2 справедливо для случая k объектов,

проверим его справедливость для случая k + 1. С этой целью дополним дан-

ное множество новым объектом x(k+1) = (x(k+1)1, . . . , x(k+1)j , . . . , x(k+1)n), где

x(k+1)1 < ... < x(k+1)j < ... < x(k+1)n. По аналогии с п. 1 данный объект обра-

зует единый порядково-инвариантный паттерн-кластер с любым из k преды-

дущих объектов. Опираясь на утверждение 1, сделаем вывод, что все k + 1

объектов принадлежат одному порядково-инвариантному паттерн-кластеру.

Утверждение 2 доказано.

Доказательство утверждения 3. Рассмотрим кластер v^inva, полу-

ченный в результате порядково-инвариантной паттерн-кластеризации. Выде-

лим в нем произвольный объект x^∗i и расположим его показатели в неубы-

вающем порядке: x∗i1 ≤ . . . ≤ x^∗ij ≤ . . . ≤ x^∗in. Графически это означает, что

объект представлен в системе параллельных координат в виде неубываю-

щей кусочно-линейной функции. Данную последовательность расположения

показателей (x∗i1, . . . , x^∗ij , . . . , x^∗in) обозначим через P^′ .

В силу порядковой инвариантности паттерн-кластера v^inva кусочно-линей-

ные функции всех входящих в него объектов имеют одинаковый вид для

любой последовательности показателей, в том числе последовательности P^′ .

Следовательно, при последовательности показателей P^′ все объекты пред-

150

ставлены в системе параллельных координат в виде неубывающих кусочно-

линейных функций.

Утверждение 3 доказано.

Доказательство утверждения 4. Воспользуемся теоремой, дока-

занной в [15]: «Два объекта x₁ и x₂, описанные векторами x₁ = (x₁₁,

...,x1j,...,x1n) и x₂ = (x₂₁,...,x2j,...,x2n) соответственно, принадлежат

одному порядково-инвариантному паттерн-кластеру тогда и только тогда, ко-

гда они могут быть представлены полными взвешенными орграфами G₁ и G₂

с идентичными весами ребер . . . , соединяющих их соответственные верши-

ны». При этом значения ребер определяются формулой (4), т.е. значениями

парных сравнений соответствующих вершин.

Для исходных объектов x₁ и x₂ построим соответствующие орграфы G₁

и G₂, а также орграф G_s суммарного объекта x_s = x₁ + x₂. Поскольку со-

гласно условию эти объекты принадлежат одному порядково-инвариантному

паттерн-кластеру, то значения соответствующих ребер (парных сравнений)

орграфов G₁ и G₂ совпадают. Необходимо показать, что с этими значения-

ми совпадают также и значения ребер орграфа G_s. Справедливость этого

утверждения следует из известных свойств:

^{x_ij >x_ik

⇒ (x_ij + x_zj) > (x_ik + x_zk),

x_zj > x_zk

^{x_ij =x_ik

⇒ (x_ij + x_zj) = (x_ik + x_zk),

x_zj = x_zk

^{x_ij <x_ik

⇒ (x_ij + x_zj) < (x_ik + x_zk),

x_zj < x_zk

где j, k = 1, . . . , n.

Из этого следует, что, во-первых, кодировка нового объекта x_s будет совпа-

дать с кодировками объектов x₁ и x₂ и, во-вторых, значения ребер орграфа G_s

будут совпадать со значениями ребер G₁ и G₂.

Утверждение 4 доказано.

СПИСОК ЛИТЕРАТУРЫ

1. Fisher R.A. The use of multiple measurements in taxonomic problems // Ann.

Eugenics. 1936. V. 7. P. 179-188.

2. Shawe-Taylor J., Cristianini N. Kernel methods for pattern analysis. Cambridge

Univer. press, UK. 2004.

3. Duda R.O., Hart P.E., Stork, D.G. Pattern classification. John Wiley & Sons, 2012.

4. Mirkin B.G. Clustering for Data Mining: A Data Recovery Approach, 2005.

5. Mirkin B.G. Summary and semi-average similarity criteria for individual clusters, in:

Models, Algorithms, and Technologies for Network Analysis. V. 59. N.Y: Springer,

2013. P. 101-126.

6. Алескеров Ф.Т., Солодков В.М., Челнокова Д.С. Динамический анализ паттер-

нов поведения коммерческих банков России // Эконом. журн. Высш. шк. эко-

номики. 2006. Т. 10. № 1. С. 48-62.

151

Aleskerov F., Ersel H., Yolalan R. Clustering Turkish Commercial Banks According

to Structural Similarities // Yapi Credit Bank. Discussion Paper Ser.

1997.

No. 97-02. 24 p.

Cole R., Gunther J. A CAMEL Rating’s Shelf Life. Federal Reserve Bank of Dallas.

December, 1995.

Gardner M., Mills D.L. Managing Financial Institutions: An Asset. Liability

Approach. The Dryden Press, 1994.

10.

Golin J. The Bank Credit Analysis Handbook: A Guide for Analysts, Bankers and

Investors John Wiley & Sons, 2001.

11.

Aleskerov F., Ersel H., Gundes C., Yolalan R. Multicriterial Method for Personnel

Allocation among Bank Branches // Yapi Kredi Discus. Paper Ser. Istanbul. 1998.

No. 98-01.

12.

Aleskerov F.T., Alper C.E. Inflation, Money, and Output Growths: Some

Observations // Bogazici Univer. Res. Paper. 1996. No. SBE 96-06.

13.

Алескеров Ф.Т., Белоусова В.Ю., Егорова Л.Г., Миркин Б.Г. Анализ паттернов

в статике и динамике, часть 1// Бизнес-информатика. 2013. Т. З. С. 3.18.

14.

Few S. Multivariate Analysis Using Parallel Coordinates.

2006.

9p. URL:

https://www.perceptualedge.com/articles/b-eye/parallel_coordinates.pdf (дата об-

ращения 28.03.2018).

15.

Мячин А.Л. Анализ паттернов: порядково-инвариантная паттерн-кластериза-

ция // Управление большими системами. 2016. № 61. С.41-59.

16.

Inselberg A. Parallel Coordinates: Visual Multidimensional Geometry and Its

Applications. Tokyo: Springer, 2009.

17.

Inselberg A. The Plane with Parallel Coordinates // Visual Comput. 1985. V. 1 (2).

P. 69-91.

18.

Myachin A.L. New methods of pattern analysis in the study of Iris Anderson-Fisher

Data // 6 Int. Conf. Comput. Commun. Control (ICCCC). 2016. P. 97-102.

19.

Aleskerov F.T., Egorova L.G., Gokhberg L.M. et al. Pattern Analysis in the Study of

Science, Education and Innovation Activity in Russian Regions // Procedia Comput.

Sci. 2013. V. 17. P. 687-694.

20.

Рейтинг инновационного развития субъектов Российской Федерации: аналити-

ческий доклад / под ред. Л.М. Гохберга. М.: Нац. исслед. универ. «Высшая

школа экономики», 2012.

Статья представлена к публикации членом редколлегии А.И. Михальским.

Поступила в редакцию 17.10.2017

После доработки 02.04.2018

Принята к публикации 08.11.2018

152