Автоматика и телемеханика, № 1, 2019
© 2019 г. В.И. МЕРКУЛОВ, д-р техн. наук (from_fn@mail.ru),
А.С. ПЛЯШЕЧНИК, канд. физ.-мат. наук (a_plyashechnik@mail.ru)
(АО “Концерн “Вега”, Москва)
СПОСОБ ОБХОДА ОПАСНЫХ ЗОН
В ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ1
Предложен способ обхода летательным аппаратом (ЛА) случайно рас-
положенных опасных зон, основанный на использовании теории графов,
и алгоритм управления ЛА, реализующий этот способ. Приведены вари-
анты реализации способа и алгоритма управления и результаты их иссле-
дования.
Ключевые слова: обход опасных зон, система управления, алгоритм
Дейкстры.
DOI: 10.1134/S0005231019010112
1. Введение
В практике полетов как гражданской, так и военной авиации достаточно
часто возможны ситуации, требующие обхода (облета) опасных зон. К таким
зонам относятся: зоны сложных метеоусловий, зоны катастроф, вызванных
различными причинами, и т.д. Для военной авиации это прежде всего зоны
объектовой противовоздушной обороны [1].
Существует несколько подходов к решению этой задачи. Например, в [2]
используется метод построения сетки в фазовом пространстве, после чего при
помощи теории графов строится дискретный путь, который затем приближа-
ется гладкими участками с определенной параметризацией при согласовании
в промежуточных точках, а также при возможных дополнительных ограни-
чениях. Этот метод позволяет решить задачу построения оптимального по
заданному критерию пути, удовлетворяющего заданным ограничениям, при
наличии препятствий, причем можно строить путь как на плоскости, так и
в пространстве. Однако этот метод довольно сложен в реализации и требует
значительных вычислительных ресурсов. В [3] рассматривается способ, при
котором сначала с помощью диаграмм Вороного строится кусочно-линейная
траектория полета, которая затем сглаживается при помощи спиралей Кор-
ню. В [4] путь обхода строится по седловым точкам потенциала с помощью
теории графов.
В работе предполагается известным расположение всех опасных зон, бла-
годаря чему возможно построить сразу весь путь оптимальным образом.
Если же известна лишь информация об опасных зонах в некоторой окрест-
ности ЛА, то возможно следует использовать другие способы обхода [5].
Следует отметить, что после построения траектории облета опасных зон
необходимо сформировать алгоритм управления ЛА, обеспечивающий его по-
1 Работа выполнена при финансовой поддержке Российского фонда фундаментальных
исследований (проект № 18-08-01083-а).
153
лет по этой траектории. Есть различные подходы к решению этой задачи: сле-
дование за виртуальным ЛА [6], полет по заданным контрольным точкам [7],
использование алгоритмов оптимального управления [8, 9]. В последнем слу-
чае наиболее часто вручную выделяют точки по периметру опасной зоны и
проводят через них требуемую траекторию.
Цель статьи - разработка простого алгоритма формирования пути обхода
летательным аппаратом опасных зон в плоскости, способного быстро постро-
ить требуемую траекторию без участия человека, и разработка способа сле-
дования этому пути при движении из заданной начальной точки в заданную
конечную.
Целесообразность решения плоской, а не пространственной задачи обхода
опасных зон обусловлена, как минимум, двумя причинами:
• существенно большей простотой построения траектории полета и форми-
рования сигнала траекторного управления летательным аппаратом;
• случайным характером и сложностью достоверного определения парамет-
ров реальных опасных зон в вертикальной плоскости.
2. Постановка задачи
Задачу обхода опасных зон будем решать при следующих условиях:
1) зоны обхода сохраняют свою конфигурацию в пространстве достаточно
продолжительное время;
2) зоны описываются эллипсами в горизонтальной плоскости. Это при-
ближение позволяет достаточно просто описать зоны различной физической
природы;
3) известны начальная точка A и конечная точка B полета ЛА, а так-
же направление движения в начальной точке и его минимально допустимый
радиус разворота R;
4) ЛА обладает достаточной маневренностью, чтобы двигаться по грани-
цам эллипсов, задающих опасные зоны. Как правило, это предположение
оправдано, поскольку размер опасных зон обычно значительно больше ра-
диуса разворота ЛА;
5) известен перечень эллипсов, определяющих опасные зоны. Эллипсы за-
даются параметрами (x, y, a, b, ϕ) (рис. 1), где (x, y) - координаты центра
эллипса, a, b - полуоси эллипса, ϕ - угол наклона оси a в системе коорди-
нат XOY .
Рис. 1. Параметры эллипса.
154
Необходимо обеспечить движение ЛА из начальной точки A в конечную
точку B без захода внутрь опасных зон.
Решение задачи проводится в два этапа. На первом этапе строится требуе-
мая траектория облета опасных зон. На втором этапе определяется способ
формирования сигнала управления ЛА, обеспечивающий его следование по-
строенной траектории.
3. Построение траектории обхода
На первом этапе построим кратчайшую траекторию облета опасных зон
из точки A в точку B. Эта траектория не должна заходить внутрь опас-
ных зон, должна иметь заданное направление движения в начальной точке и
удовлетворять ограничениям на величину допустимого ускорения ЛА. Легко
понять, что она будет состоять из дуги окружности с заданным радиусом
разворота R и последовательно чередующихся отрезков и дуг эллипсов. При
этом в точках пересечения отрезки будут касаться эллипсов. Тем самым от-
резки пути между эллипсами будут отрезками общих касательных. Так как
между двумя эллипсами может быть не более четырех общих касательных,
то имеется конечное число возможных промежуточных точек, и для реше-
ния задачи можно применить методы теории графов [10]. В соответствии
с изложенным, результатом работы алгоритма будет массив элементарных
участков: отрезков и дуг эллипсов.
Приведем общее описание алгоритма. Реализация его отдельных частей,
связанная с решением частных геометрических задач, будет рассмотрена
после.
К списку эллипсов, задающих опасные зоны, добавим две окружности,
радиус которых равен радиусу разворота R, проходящие через начальную
точку A так, чтобы начальное направление движения было касательным.
Также в этот список добавим конечную точку B. Перебираем все возмож-
ные пары объектов из этого списка. Для каждой пары строятся все возмож-
ные отрезки, соединяющие их, причем для эллипсов и окружностей отрезки
должны касаться их в точке пересечения (способ построения отрезков приве-
ден в пп. 2 и 5 далее). Далее строится граф путей. Его вершинами будут все
концы построенных отрезков. Для N опасных зон их число не превышает ве-
личины 4(N + 2)2. Добавим две дополнительные вершины, соответствующие
начальной точке на каждой из окружностей.
Ребра графа определяются следующим образом. Две точки на разных объ-
ектах соединяются ребром, если они являются концами одного из построен-
ных отрезков, причем этот отрезок не пересекается ни с какими реальными
опасными зонами, кроме двух рассматриваемых (алгоритм проверки пересе-
чения приведен в п. 4 далее). Длина ребра полагается равной длине соеди-
няющего эти точки отрезка. Две точки на одном объекте соединяются ребром,
если направления движения в этих точках согласованы. Направление в на-
чальной точке соответствует начальному направлению движения. Если точка
является концом отрезка касательной, то направление в точке определяется
этим отрезком. Направления в точках согласованы, если путь между двумя
этими точками согласован с этими направлениями. На рис. 2 направления
155
Рис. 2. Согласованность направлений.
в точках 1 и 3 согласованы. Это означает, что можно двигаться к эллипсу
по касательной к точке 1, затем плавно перейти на движение по эллипсу до
точки 3, далее плавно перейти на касательную к точке 3. Точно так же усло-
вия согласования выполнены для точек 2 и 3. Для точек 1 и 2 эти условия
не выполнены. Для пары согласованных точек имеется путь между ними по
границе эллипса, согласованный с направлениями в этих точках. Если этот
путь не пересекает другие реальные опасные зоны (алгоритм проверки пе-
ресечения приведен в п. 3 далее), то вершины графа соединяются ребром,
длина которого равна длине этого пути.
Для построенного графа используем алгоритм Дейкстры [10] поиска крат-
чайшего пути. Начальными данными в алгоритме будет нуль в двух верши-
нах, соответствующих начальной точке на двух проходящих через нее окруж-
ностях, и бесконечность во всех остальных вершинах. Перебор соседних вер-
шин в алгоритме производится следующим образом. При обновлении значе-
ния в точке сохраняется ссылка на вершину, из которой пришло обновление.
Если при рассмотрении текущей вершины указанная по ссылке предыдущая
вершина лежит на том же эллипсе, то в процессе обновления соседних вершин
просматривается только вершина на другом конце касательной, проходящей
через текущую точку. Если же предыдущая вершина лежит на другом эллип-
се, то в процессе обновления соседних вершин рассматриваются все вершины
на том же эллипсе, что и текущая.
В результате для каждой точки графа будет построен кратчайший путь
в нее из начальной точки. Путь в конечную точку и будет искомым путем.
Вычислительная сложность алгоритма при числе опасных зон N пропорцио-
нальна N3. Отметим, что если вместо двух окружностей добавить начальную
точку, то можно построить кратчайший путь без учета начального направ-
ления движения.
Для определения практической значимости предложенного алгоритма
проведем его сравнение с похожим подходом из [2]. Рассмотрим приводи-
мый в [2] в разделе V. A пример обхода двух окружностей на плоскости при
заданных начальных и конечных точках и направлениях. Для ее решения
в [2] строится граф из 4140 вершин и порядка 300000 ребер. Для сравне-
ния в предлагаемом авторами алгоритме будет порядка 4N2 = 144 вершин и
порядка 12N2 = 432 ребер, где N - число окружностей, равное шести (для
начальной и конечной точки строится по две дополнительные окружности с
заданным радиусом разворота). Видно, что в этом примере предлагаемый ав-
торами статьи специализированный алгоритм гораздо более экономичен, чем
универсальный алгоритм из [2]. Кроме того, предлагаемый алгоритм стро-
156
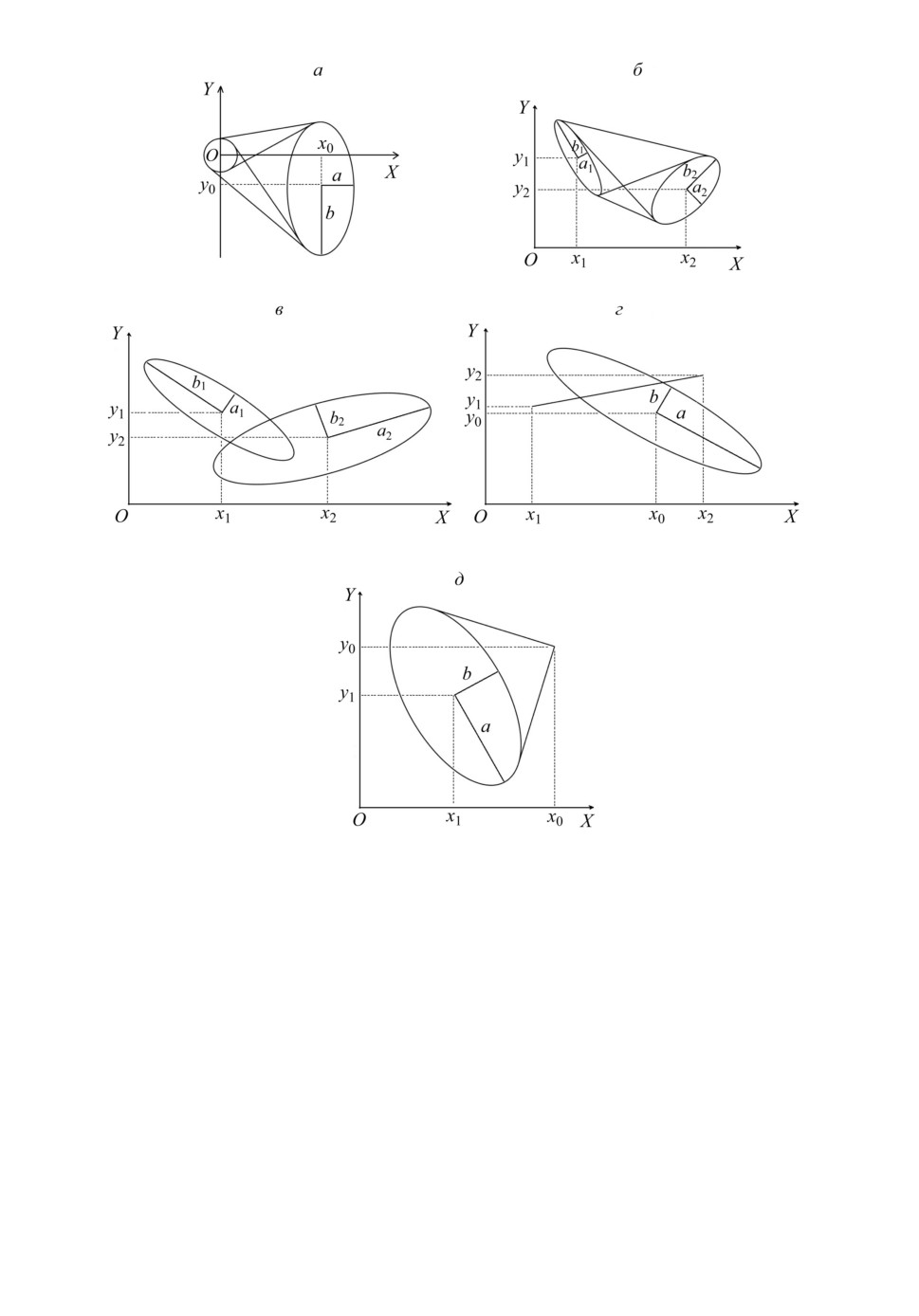
Рис. 3. Геометрические задачи: а - построение общих касательных к эллипсу
и окружности; б - построение общих касательных к двум эллипсам; в - поиск
точек пересечения эллипсов; г - поиск точек пересечения отрезка и эллипса;
д - построение касательных к эллипсу, проходящих через заданную точку.
ит действительно кратчайший путь, хотя при достаточном количестве точек
алгоритм [2] дает практически ту же самую длину траектории обхода.
Необходимо отметить, что для построения требуемой траектории необхо-
димо решить ряд частных геометрических задач (рис. 3), к которым отно-
сятся:
• нахождение общих касательных к окружностям и эллипсам,
• проверка пересечения эллипсов,
• определение пересечения отрезка с эллипсом,
• нахождение касательных к эллипсу, проходящих через заданную точку.
157
1. Нахождение общих касательных к единичной окружности с центром
в начале координат и к эллипсу, оси которого ориентированы по координат-
ным осям (рис. 3,а).
Эллипс задается координатами центра (x0, y0) и полуосями a и b. Уравне-
ние эллипса определяется соотношением
(1)
(x - x0)2/a2 + (y - y0)2/b2
= 1.
Точки касательной к окружности, проходящей через точку (cos ϕ, sin ϕ),
определяются в параметрическом виде через параметр t выражениями:
x = cosϕ - tsinϕ,
(2)
y = sinϕ + tcosϕ.
Условие касания эллипса записывается в виде
(3)
-(x - x0) sin ϕ/a2 + (y - y0) cos ϕ/b2
= 0.
Для нахождения касательной нужно решить систему (1)-(3).
Исключив t из уравнений (2), получим
(4)
x cos ϕ + y sin ϕ = 1,
откуда следует, что
(5)
(x - x0) cos ϕ + (y - y0) sin ϕ = 1 - x0 cos ϕ - y0
sin ϕ.
Решив систему (3), (5) относительно (x - x0) и (y - y0) и подставив ее
решение в (1), получим уравнение
a2 cos2 ϕ + b2 sin2 ϕ = (1 - x0 cos ϕ - y0 sin ϕ)2.
Заменой z = tg(ϕ/2) это уравнение приводится к уравнению четвертой сте-
пени
(
)
(
)
(1 + x0)2 - a2
z4 - 4y0(1 + x0)z3 + 2
1 - x20 + 2y20 + a2 - 2b2
z2-
(
)
− 4y0(1 - x0)z +
(1 - x0)2 - a2
= 0.
Каждое его действительное решение определяет общую касательную, иду-
щую от точки (cos ϕ, sin ϕ) окружности к точке (x, y) эллипса, определяемой
из системы линейных уравнений (3), (4) при найденном значении ϕ.
2. Нахождение общих касательных к двум эллипсам при условии, что
они заданы параметрами (x1, y1, a1, b1, ϕ1) и (x2, y2, a2, b2, ϕ2), иллюстрирует-
ся рис. 3,б. Приведем последовательность преобразований, сводящих задачу
к п. 1:
а) сдвигаем эллипсы на (-x1) по оси X и на (-y1) по оси Y так, чтобы
центр первого эллипса оказался в начале координат. При этом изменятся
координаты центра второго эллипса;
158
б) поворачиваем эллипсы на угол (-ϕ1) вокруг начала координат. Угол по-
ворота первого эллипса станет равным нулю, угол поворота второго эллипса
будет равен ϕ2 - ϕ1, вектор центра (x2, y2) тоже повернется;
в) используя преобразование x = x/a1; y = y/b1, изменяем масштаб осей
так, чтобы первый эллипс стал единичной окружностью. Преобразование
второго эллипса производится следующим образом. Оставляя для координат
его центра и угла поворота после преобразований а и б исходные обозначения
(x2, y2, ϕ2), запишем его уравнение в виде
(6)
a(x - x2)2 + b(x - x2)(y - y2) + c(y - y2)2
= 1,
где
a = cos2 ϕ2/a22 + sin2 ϕ2/b22,
b = 2cosϕ2 sinϕ2(1/a22 - 1/b22),
(7)
c = cos2 ϕ2/b22 + sin2 ϕ2/a22.
В новых координатах уравнение (6) примет вид
aa21(x - x2/a1)2 + ba1b1(x - x2/a1)(y - y2/b1) + cb21(y - y2/b1)2 = 1,
откуда следует, что координаты центра второго эллипса будут (x2/a1, y2/b1).
Для нахождения новых полуосей запишем матрицу, следующую из этого
уравнения,
(
)
aa21
ba1b1/2
ba1b1/2
cb2
1
и найдем ее собственные значения λ1, λ2 и собственный вектор, соответст-
вующий λ1. Тогда новые полуоси эллипса будут λ-1/21 и λ-1/22, а направление
собственного вектора определит новый угол ϕ2 поворота эллипса;
г) поворачиваем эллипсы на угол (-ϕ2) вокруг начала координат. Вектор
центра (x2, y2) повернется, а новое значение угла ϕ2 будет равным нулю.
Первый эллипс при этом не изменится, так как он является окружностью
с центром в начале координат.
В результате проделанных преобразований первый эллипс стал единичной
окружностью с центром в начале координат, а оси второго эллипса ориенти-
рованы по координатным осям. В соответствии с п. 1 найдем отрезки общих
касательных, соединяющие окружность с эллипсом. Эти отрезки задаются
декартовыми координатами двух точек, одна из которых лежит на окружно-
сти, а другая на эллипсе. После проведения над этими точками преобразова-
ний, обратных к преобразованиям п.п. г, в, б, а, получим координаты точек
отрезка касательной, соединяющей исходные эллипсы в первоначальной си-
стеме координат.
159
3. Проверка пересечения эллипсов (рис. 3,в).
Два эллипса заданы параметрами (x1, y1, a1, b1, ϕ1) и (x2, y2, a2, b2, ϕ2). На
первом эллипсе задана дуга, определяемая интервалом углов при задании
эллипса в параметрическом виде
x = a1 cosϕ,
(8)
y=b1
sin ϕ
в связанной с ним системе координат. Нужно определить, пересекается ли
эта дуга со вторым эллипсом или лежит внутри него.
Сдвигаем и поворачиваем эллипсы вокруг начала координат так, чтобы
центр первого эллипса попал в начало координат, а его оси были направлены
по координатным осям. Запишем уравнение второго эллипса в виде
(9)
ax2 + bxy + cy2
+ dx + ey + f = 0,
где первые три коэффициента определяются по формулам (7), а остальные
вычисляются по формулам
d = -2ax2 - by2; e = -2cy2 - bx2; f = ax22 + bx2y2 + cy22 - 1.
После подстановки (8) в (9) получим уравнение
(10)
a′ cos2 ϕ + b′ sin ϕcos ϕ + c′ sin2 ϕ + d′ cosϕ + e′ sin ϕ + f′
= 0,
где
a′ = a21a; b′ = a1b1b; c′ = b21c; d′ = a1d;e′ = b1e; f′ = f.
Заменой z = tg(ϕ/2) уравнение (10) приводится к виду
(
)
(
)
(
)
a′ - d′ + f′
t4 +
2e′ - 2b′
t3 +
2f′ + 4c′ - 2a′
t2+
(
)
(
)
+
2b′ + 2e′
t+
a′ + d′ + f′
= 0.
Найдем его действительные корни и соответствующие значения ϕ. Они опре-
деляют разбиение первого эллипса на участки, лежащие внутри или вне вто-
рого эллипса. Остается лишь проверить, пересекается ли заданный участок
с участками, лежащими внутри второго эллипса.
4. Определение пересечения отрезка с эллипсом (рис. 3,г).
Эллипс задан параметрами (x0, y0, a, b, ϕ), а координаты концов отрезка —
(x1, y1) и (x2, y2). Сдвигаем и поворачиваем эллипс и отрезок, так чтобы центр
эллипса попал в начало координат, а его оси были направлены по координат-
ным осям. Обозначим новые координаты концов отрезка (x′1, y′1) и (x′2, y′2).
Отрезок пересекается с эллипсом, если квадратное уравнение
(x′1 + t(x′2 - x′1))2
(y′1 + t(y′2 - y′1))2
+
=1
a2
b2
имеет корни, лежащие на отрезке [0, 1].
160
5. Нахождение касательных к эллипсу, проходящих через заданную точку
(рис. 3,д).
Эллипс задан параметрами (x1, y1, a, b, ϕ1), а координаты точки — (x0, y0).
Сдвигаем и поворачиваем эллипс и точку вокруг начала координат так, что-
бы центр эллипса попал в начало координат, а его оси были направлены по
координатным осям. Если координаты точки после преобразований равны
(x′0, y′0), то решения уравнения
(11)
ay′0 cos ϕ + bx0
sin ϕ - ab = 0
определяют искомые точки на эллипсе.
4. Формирование сигнала управления
Рассмотрим один из возможных вариантов формирования сигнала управ-
ления, обеспечивающих полет ЛА по требуемой траектории.
Пусть на плоскости XOY задана некоторая кривая P , по которой должен
следовать ЛА, находящийся в точке C (рис. 4).
Рис. 4. Облет требуемой траектории.
Найдем на кривой точку D, ближайшую к текущему положению ЛА. По-
--→
ложим r =
DC. В точке D вычислим единичный вектор τ, касательный к P
и направленный в сторону требуемого направления облета кривой. В точке D
вычислим вектор kn, где k - кривизна (по определению кривизна считается
положительной), а n - единичный вектор нормали, направленный в сторону
центра кривизны. При этом будем считать, что известен вектор V скоро-
сти ЛА, модуль которого V определяет требуемую скорость движения, а его
направление задается курсом ψ относительно какого-либо фиксированного
направления. Предлагаемый закон управления не меняет величины V , ко-
торая может быть заранее выбранной постоянной или может меняться по
независимому закону, исходя из каких-либо требований к скоростям прохож-
дения разных участков пути.
161
Используя методику, изложенную в [6], можно сформировать закон изме-
нения требуемого поперечного ускорения ЛА:
(12)
JT = μ2V [r,V ]z + 2μ[V ,τ]z + V2
[τ , kn],
где μ — числовой коэффициент, а [a, b]z - z компонента векторного произве-
дения векторов a и b, вычисляемая по формуле [a, b]z = axby - aybx.
Слагаемые в законе (12) имеют следующий смысл:
• слагаемое μ2V [r, V ]z отвечает за возврат ЛА на требуемую траекторию,
• слагаемое 2μ[V , τ ]z отвечает за уменьшение компоненты скорости, пер-
пендикулярной требуемой траектории,
• слагаемое V2[τ , kn] учитывает кривизну требуемой траектории.
Для иллюстрации физического смысла этих слагаемых рассмотрим мо-
дель ЛА, инерционностью которого пренебрегаем. Тогда закон управления
по курсу имеет вид
ψ=JT
(13)
/V,
где величина сигнала управления JT задается выражением (12).
Для иллюстрации смысла третьего слагаемого в (12) предположим, что в
начальный момент ЛА находится в точке кривой P и скорость направлена
по касательной к P . Тогда первые два слагаемых в правой части (12) будут
ψ=V[τ,kn].Еслиперейтиотвремениtк
равны нулю и (13) примет вид
длине пройденного пути s, то это уравнение примет вид dψ/ds = [τ , kn], т.е.
известное из дифференциальной геометрии натуральное уравнение кривой P .
Отсюда следует, что благодаря наличию третьего слагаемого в (12) ЛА будет
продолжать двигаться точно по кривой P .
Для иллюстрации смысла первых двух слагаемых в (12) рассмотрим част-
ный случай, когда кривая P представляет собой ось X, проходимую в поло-
жительном направлении. Скорость предполагаем постоянной, а угол ψ будем
отсчитывать от оси X. Тогда третье слагаемое в (12) будет равно нулю и
уравнение (13) примет вид
ψ=-μ2
(14)
y x - 2μy,
образуя вместе с уравнениями движения
x = V cosψ,
(15)
y = V sinψ
замкнутую систему дифференциальных уравнений.
Одним из решений системы (14), (15) является ψ = 0, y = 0, x = V t, опре-
деляющее движение по оси X в положительном направлении. Линеаризация
уравнений (14), (15) в окрестности этого решения дает уравнение
(16)
ÿ+ 2μV y + μ2V 2
y = 0.
162
Из (16) видно, что слагаемое со второй степенью μ представляет собой силу,
возвращающую ЛА на требуемую траекторию, а слагаемое с первой степе-
нью μ характеризует корректирующий сигнал, гасящий компоненту скорости,
направленную перпендикулярно требуемой траектории. Общее решение (16)
имеет вид
(17)
y(t) = (A + Bt)e-t/β ,
где β = (μV )-1 является характерным временем сходимости решения.
Движение по оси X в отрицательном направлении ψ = π, y = 0, x = -V t
также удовлетворяет системе (14), (15), но в окрестности этого решения ли-
неаризация системы (14), (15) дает уравнение ÿ - 2μV y + μ2V2y = 0, что со-
ответствует неустойчивому движению в обратную сторону.
Численное решение системы (14), (15) при различных начальных услови-
ях (за исключением движения в обратную сторону по оси X) показало, что
качественно ее решения имеют вид, аналогичный (17).
Рассмотрим более общую ситуацию, когда ЛА аппроксимируется моде-
лью [9]
ψ=ω,
(18)
ω = -ω/T + JT
/T V,
которая учитывает его инерционность, определяемую постоянной времени T ,
где величина сигнала управления JT определяется выражением (12). Вооб-
ще говоря, в этом случае движение по заданной кривой будет выполняться с
некоторыми ошибками. Тем не менее возможно точное движение по прямой и
по окружности с постоянной скоростью, так как угловая скорость движения
в этом случае постоянна. При движении по кривой, кривизна которой меня-
ется не слишком быстро, в частности при движении по эллипсу, близкому
по форме к окружности, летательный аппарат, определяемый моделью (18),
может обеспечивать движение с приемлемой точностью.
Для реализации (12) необходимо знание векторов τ и kn в ближайшей
точке требуемой траектории. В общем случае требуемая траектория облета
состоит из набора участков, каждый из которых является отрезком или дугой
эллипса. Для нахождения ближайшей точки требуемой траектории нужно
найти ближайшую точку каждого участка и выбрать самую близкую из них.
Если ближайшая точка находится на участке пути, который является от-
резком, заданным крайними точками (x1, y1) и (x2, y2), причем требуется дви-
гаться от первой точки до второй, то искомые векторы вычисляются по фор-
муле
(
)-1/2
τ =
(x2 - x1)2 + (y2 - y1)2
(x2 - x1, y2 - y1),
(19)
kn = 0.
Если ближайшая точка находится на участке пути, который является ду-
гой эллипса, заданного уравнениями x = a cos ϕ, y = b sin ϕ, и этой точке со-
163
ответствует значение параметра ϕ0, то искомые векторы вычисляются так:
(
)-1/2
τ =±
a2 sin2 ϕ0 + b2 cos2 ϕ0
(-asinϕ0,bcos ϕ0),
(
)-1/2
(20)
kn = -ab
a2 sin2 ϕ0 + b2 cos2 ϕ0
(b cos ϕ0, a sin ϕ0
).
В первом уравнении (20) знак плюс берется при движении в сторону возрас-
тания угла ϕ, а знак минус при движении в сторону убывания.
Величина требуемого сигнала управления вычисляется по (12), в которую
подставляются координаты местоположения и вектор скорости ЛА, а также
найденные с помощью (19) или (20) выражения для векторов τ и kn.
5. Исследование эффективности
Для моделирования использовалась среда Matlab на компьютере с про-
цессором Core I5-4670, 3,40 ГГц с 4 Гб оперативной памяти. Исследование
эффективности проводилось по результатам построения траектории между
заданными точками при наличии некоторого числа опасных зон по форму-
лам (1)-(11) и последующего следования ЛА по построенной траектории с
законом управления (12). При этом предполагалось, что известны:
• координаты начальной A и конечной B точек маршрута;
• число опасных зон, их координаты и параметры;
• начальное направление движения ЛА;
• радиус разворота ЛА;
• допустимые перегрузки.
Эффективность предложенного способа оценивалась по величине откло-
нения ЛА от требуемой траектории, по величине требуемых перегрузок, а
также временем построения требуемой траектории облета.
На первом этапе исследовался алгоритм построения требуемой траектории
облета. На рис. 5,а представлен результат построения кратчайшей траекто-
рии между точками A и B при наличии N = 7 опасных зон при заданном
начальном направлении движения в точке A. Для наглядности радиус пово-
рота выбран сравнимым с размерами некоторых опасных зон, несмотря на
то, что реализация полученной траектории может оказаться невозможной.
Другой вариант поиска кратчайшей траектории проводился при количе-
стве опасных зон N = 100, плотно расположенных на пути между начальной
и конечной точками. Один из вариантов построения кратчайшего пути меж-
ду точками A и B без учета начального направления движения приведен на
рис. 5,б . Время расчета пути при наличии ста зон составляет около одной
секунды.
На втором этапе исследовалась потенциальная возможность системы обхо-
да препятствий безынерционным ЛА, определяемым моделью (13), в которой
инерция управления пренебрежимо мала. При этом скорость движения пола-
галась постоянной величине 200 м/с, а максимальное поперечное ускорение
ограничено величиной 30 м/c2. Радиус разворота положен равным 2 км, что
при выбранной скорости соответствует поперечному ускорению 20 м/c2. Из-
мерения координат проводились с ошибками до 200 метров. В законе управ-
ления (12) был выбран коэффициент μ = 0,0006.
164
Рис. 5. Требуемая траектория обхода: а - семь опасных зон, б - сто опасных зон.
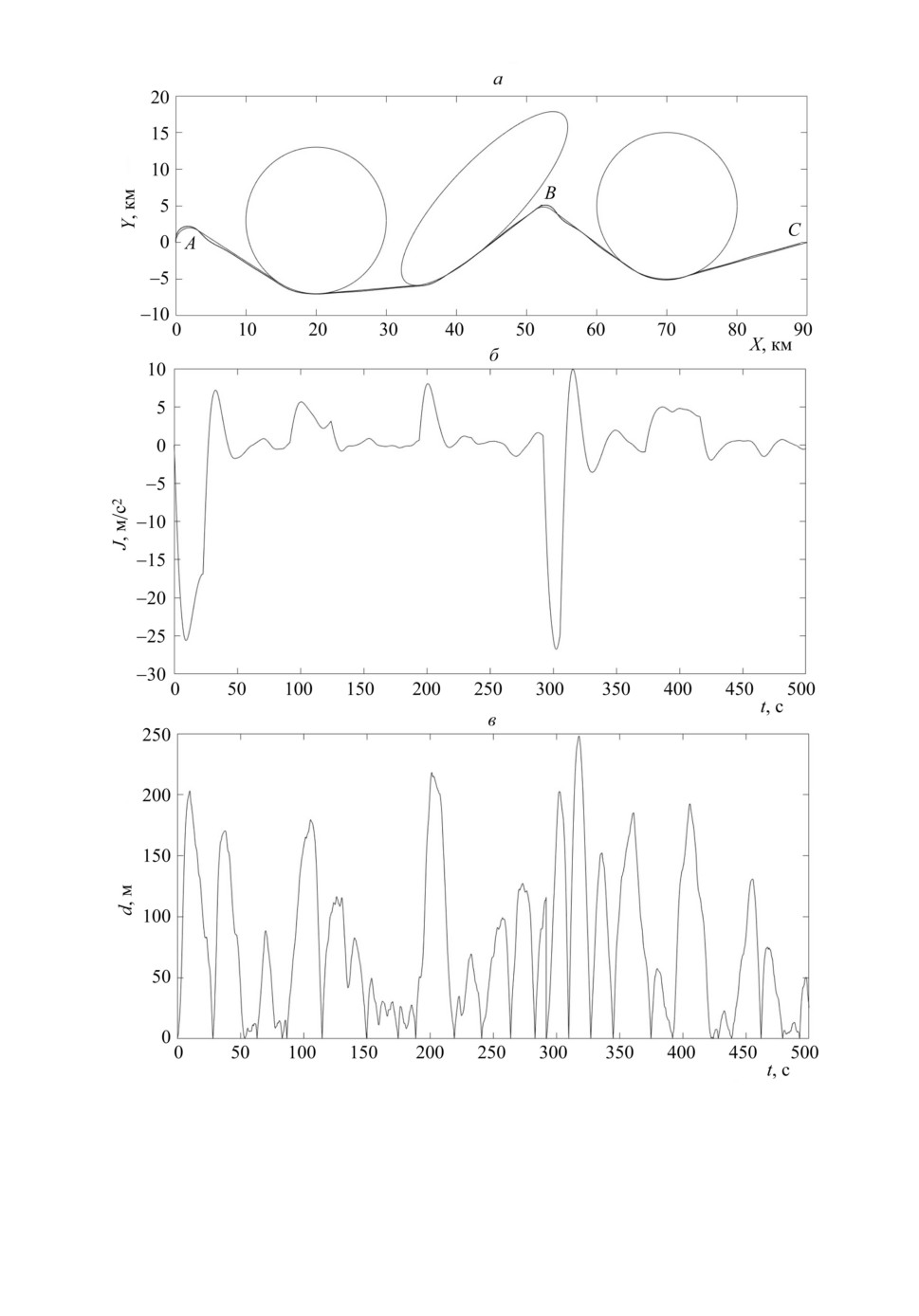
Рис. 6. Траектория обхода опасных зон безынерционным ЛА: а - вся траек-
тория, б - выделенный участок.
165
Рис. 7. Зависимость состояния ЛА от времени: а - поперечное ускорение, б -
отклонение от требуемой траектории.
Конфигурация задачи представлена на рис. 6,а. Заданы три опасные зо-
ны: две окружностями с радиусом 10 километров и эллипс с полуосями 5
и 16 километров. В начальный момент ЛА находится в точке A и скорость
направлена по оси Y . Ставится задача - прилететь сначала в промежуточную
точку B, а затем в конечную точку C.
На рис. 6,а приведены требуемая и реальная траектории облета. Посколь-
ку их сложно различить, на рис. 6,б отдельно приведен участок траектории
обхода последней окружности, выделенный на рис. 6,а рамкой. При этом сама
окружность изображена точечной линией 1, требуемая траектория изображе-
на сплошной линией 3, а реальная траектория изображена штриховой лини-
ей 2. Зависимость необходимого для реализации полета поперечного уско-
рения от времени показана на рис. 7,а, а на рис. 7,б приведена зависимость
от времени отклонения ЛА от требуемой траектории облета. Максимальная
величина отклонения 250 м, среднее квадратичное отклонение 66 м.
166
Рис. 8. Обход опасных зон инерционным ЛА: а - траектория облета, б - за-
висимость поперечного ускорения от времени, в - зависимость отклонения от
требуемой траектории от времени.
167
На третьем этапе решалась та же задача облета, что и выше инерционным
ЛА (18) с постоянной времени T = 4 секунды. Требуемая и реальная траекто-
рии движения для этого случая показаны на рис. 8,а. Зависимость необходи-
мого для реализации полета поперечного ускорения от времени отображена
на рис. 8,б , а на рис. 8,в приведена зависимость от времени отклонения ЛА
от требуемой траектории облета. Максимальное отклонение в этом случае
составляет 250 м, а среднее квадратичное отклонение 76 м.
Проведенный анализ показал, что при управлении инерционным ЛА про-
исходит незначительное ухудшение точности следования траектории при
незначительном увеличении перегрузок.
6. Заключение
Проведенный анализ позволяет сделать следующие выводы:
• предложенная система действительно решает задачу построения траекто-
рии обхода случайно расположенных опасных зон;
• построенная траектория представляет набор автоматически определяемых
отрезков и дуг эллипсов, а сформированный сигнал управления ЛА обес-
печивает следование траектории с достаточной точностью, не накладывая
ограничений на реализуемый диапазон перегрузок;
• для управления ЛА необходимо измерять координаты его местоположе-
ния, величину и направление скорости;
• алгоритм построения требуемой траектории не требует значительных вы-
числительных ресурсов и при умеренном количестве препятствий может
применяться в реальном масштабе времени, в том числе и при изменении
конфигурации и числа опасных зон;
• способ может быть использован для обхода опасных зон любой природы,
включая зоны природных катаклизмов.
СПИСОК ЛИТЕРАТУРЫ
1. Верба В.С. Авиационные комплексы радиолокационного дозора и наведения.
Принципы построения, проблемы разработки и особенности функционирования.
М.: Радиотехника, 2014.
2. Mattei M., Blasi L. Smooth Flight Trajectory Planning in the Presence of No-Fly
Zones and Obstacles // J. Guidance, Control, Dynam. 2010. V. 33. No. 2. P. 454-462.
3. Ran D., Cochran J.E. Path Planning and State Estimation for Unmanned Aerial
Vehicles in Hostile Environments // J. Guidance, Control, Dynam. 2010. V. 33.
No. 2. P. 595-601.
4. Hwang Y.K., Ahuja N. A Potential Field Approach to Path Planning // IEEE Trans.
Robot. Automat. 1992. V. 8. No. 1. P. 23-32.
5. Петров А.А., Сирота И.М. Формирование движений манипуляционного робота
при обходе препятствий в условиях ограниченной информации о среде // АиТ.
1983. № 4. С. 29-40.
Petrov A.A., Sirota I.M. Obstacle Avoidance by a Robot Manipulator under Limited
Information about the Environment // Autom. Remote Control. 1983. V. 44. No. 4.
P. 431-440.
6. Gates D.J. Nonlinear Path Following Method // J. Guidance, Control, Dynam. 2010.
V. 33. No. 2. P. 321-332.
168
7. Medagoga E.D.W., Gibbens P.W. Synthetic-Waypoint Guidance Algorithm for
Following a Desired Flight Trajectory // J. Guidance, Control, Dynam. 2010. V. 33.
No. 2. P. 601-606.
8. Kaminer I., Pascoal A., Xargay E., Hovakimyan N., Cao Ch., Dobrokhodov V.
Path Following for Unmanned Aerial Vehicles Using L1 Adaptive Augmentation of
Commercial Autopilots Trajectory // J. Guidance, Control, Dynam. 2010. V. 33.
No. 2. P. 550-564.
9. Меркулов В.И., Дрогалин В.В., Канащенков А.И. и др. Авиационные систе-
мы радиоуправления. Т. 2. Радиоэлектронные системы наведения / Под ред.
А.И. Канащенкова и В.И. Меркулова. М.: Радиотехника, 2003.
10. Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978.
Статья представлена к публикации членом редколлегии А.А. Лазаревым.
Поступила в редакцию 14.09.2017
После доработки 07.06.2018
Принята к публикации 08.11.2018
169