Автоматика и телемеханика, № 10, 2019

(Нижегородский государственный университет им. Н.И. Лобачевского),

Р.С. БИРЮКОВ, канд. физ.-мат. наук (biryukovrs@gmail.com),

М.М. КОГАН, д-р физ.-мат. наук (mkogan@nngasu.ru)

(Нижегородский государственный архитектурно-строительный университет)

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ МАКСИМАЛЬНЫМИ

УКЛОНЕНИЯМИ ВЫХОДОВ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ

СИСТЕМЫ НА КОНЕЧНОМ ИНТЕРВАЛЕ ВРЕМЕНИ¹

Вводится понятие максимального уклонения выхода линейной неста-

ционарной системы на конечном интервале времени как максимального

значения максимальной по времени евклидовой нормы выхода при усло-

вии, что сумма квадрата энергии внешнего возмущения и квадратич-

ной формы начального состояния системы равна единице. Максималь-

ное уклонение характеризуется в терминах решений дифференциальных

матричных уравнений или неравенств. Введено модифицированное поня-

тие ограниченности системы на конечном интервале при внешнем и на-

чальном возмущениях и установлена его связь с понятием максимального

уклонения. Получены необходимые и достаточные условия ограниченно-

сти системы на конечном интервале. Показано, что синтез оптимальных

управлений, в том числе и многокритериальных, минимизирующих мак-

симальные уклонения нескольких выходов, а также управлений, обеспе-

чивающих ограниченность системы, осуществляется в терминах линей-

ных матричных неравенств.

Ключевые слова: максимальное уклонение выхода, линейная нестацио-

нарная система, обобщенная H₂ норма, линейные матричные неравенства.

DOI: 10.1134/S0005231019100027

1. Введение

Одно из обязательных требований к системе управления заключается в

том, чтобы значения целевых переменных объекта и системы управления на-

ходились в определенных границах по отношению к их номинальным значе-

ниям несмотря на внешние возмущения и ненулевые начальные условия. Чем

уже эти границы, т.е. чем меньше максимальные отклонения, тем эффектив-

нее система управления.

Проблема больших отклонений, вызванных ненулевыми начальными усло-

виями, или, как ее иногда называют, проблема всплеска была рассмотрена

А.А. Фельдбаумом [1], а затем Р.Н. Измайловым [2]. В [3] была поставлена и

решена классическая задача Б.В. Булгакова о накоплении ограниченных воз-

мущений, и в [4] приведено ее обобщение на случай нескольких переменных.

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проекты №№ 18-41-520002, 19-01-00289).

В [5] находится наихудшее ограниченное скалярное возмущение, доставляю-

щее наибольшее значение отклонению выхода системы в конечный момент

времени. Различные способы вычисления матричной экспоненты и наличие

у ее нормы характерных максимумов демонстрируются в [6]. Верхние оценки

максимальных отклонений при всплеске были выведены в терминах решений

линейных матричных неравенств в [7, 8]. В последнее время активно занима-

ются проблемой всплеска в лаборатории им. Я.З. Цыпкина ИПУ РАН [9-11].

Понятие обобщенной H₂ нормы, отвечающее максимальному отклонению при

внешнем возмущении с известной энергией (L₂ нормой) и нулевых начальных

условиях, было введено D.A. Wilson [12, 13]. В [14] получены оценки обобщен-

ной H₂ нормы для непрерывно-дискретных систем.

Приведенные выше исследования в большей своей части касались анализа

максимальных отклонений и всплесков. Что касается задачи синтеза управ-

ления, то в [15] для непрерывных систем и в [16] для дискретных систем

был получен оптимальный регулятор по выходу на бесконечном горизонте,

реализация которого требует решений уравнения Риккати и задачи выпук-

лого программирования. В [17] для непрерывных систем и в [18] для дис-

кретных систем были синтезированы законы управления, минимизирующие

верхние оценки всплесков, вызванных неизвестным начальным возмущени-

ем, а в [19, 20] были получены законы управления, минимизирующие мак-

симальное отклонение выхода непрерывной системы при нулевом начальном

состоянии и внешнем возмущении с заданной энергией на бесконечном гори-

зонте. Заметим, что исследования максимальных отклонений при внешнем

ограниченном возмущении, т.е. из класса l_∞, развивающие в определенном

смысле задачу Б.В. Булгакова, проводились в рамках теории l₁-оптимального

управления в [21, 22] и в других работах, но здесь далее эта тема не рассмат-

ривается.

Особую трудность представляют задачи управления максимальными от-

клонениями при неопределенных начальных условиях и внешнем возмуще-

нии на конечном временном интервале. В рамках концепции так называемой

практической устойчивости, которая в западных публикациях получила на-

звание устойчивости на конечном интервале (“finite-time stability”), в [23, 24]

были получены условия, при выполнении которых состояние линейной неста-

ционарной системы на заданном конечном интервале при любом начальном

состоянии из некоторой ограниченной области в отсутствие внешних возму-

щений не покидает в каждый момент времени заданные, например, эллипсо-

идальные области. Эти условия выражаются в терминах решений матричных

дифференциальных уравнений или неравенств Ляпунова, численная дискре-

тизация которых позволяет синтезировать нестационарные обратные связи,

обеспечивающие указанную устойчивость замкнутой системы. В [25] в рам-

ках так называемой концепции устойчивости по входу и выходу на конечном

интервале (“input-output finite-time stability”) были синтезированы обратные

связи, при которых выход линейной нестационарной системы с нулевыми на-

чальными условиями находится в заданных пределах на конечном интерва-

ле при любых внешних возмущениях из определенного класса. Что касается

максимальных отклонений на конечном интервале при наличии обоих фак-

торов, т.е. при неопределенных начальных условиях и внешнем возмущении,

то в [26] приведены достаточные условия ограниченности системы на конеч-

ном интервале при ненулевых начальных условиях (“finite-time boundedness

with non-zero initial state”). В полной мере проблема оптимального управ-

ления, минимизирующего максимальные отклонения на конечном интервале

при наличии неопределенных начальных условий и внешнего возмущения, не

решена до сих пор.

В данной статье предпринимается попытка перейти от оценки максималь-

ного отклонения выхода линейной нестационарной системы на конечном ин-

тервале к точному значению так называемого максимального уклонения вы-

хода при внешнем и начальном возмущениях, понимаемому как максималь-

ное значение максимальной по времени евклидовой нормы выхода при усло-

вии, что сумма квадрата энергии внешнего возмущения и квадратичной фор-

мы начального состояния системы равна единице. Для этого здесь применя-

ется вариационный подход, подобно тому, как это делалось в [27, 28] в за-

даче H_∞ оптимального управления при ненулевых начальных условиях для

линейного нестационарного объекта на конечном горизонте и в [29, 30] для

линейного стационарного объекта на бесконечном горизонте. Максимальные

уклонения выхода при внешнем возмущении и нулевом начальном состоя-

нии, а также при неопределенном начальном состоянии в отсутствие внешне-

го возмущения тоже определяются соответствующим образом. Максималь-

ные уклонения характеризуются в терминах решений матричного диффе-

ренциального уравнения, а затем в терминах решений линейных матричных

неравенств. Показано, что условия устойчивости по входу и выходу и усло-

вия ограниченности линейной нестационарной системы на конечном интер-

вале могут быть сформулированы в терминах соответствующих максималь-

ных уклонений. Введено модифицированное понятие ограниченности систе-

мы на конечном интервале при внешнем и начальном возмущениях, для ко-

торого получены необходимые и достаточные условия. Синтезированы оп-

тимальные законы управления, минимизирующие максимальные уклонения,

в том числе многокритериальные, и законы управления, обеспечивающие

ограниченность системы на конечном интервале при внешнем и начальном

возмущениях.

2. Максимальное уклонение при внешнем и

начальном возмущениях

Рассмотрим динамический объект, описываемый неавтономной системой

линейных дифференциальных уравнений:

x = A(t)x + B(t)v, x(t₀) = x₀,

(2.1)

z = C(t)x,

где x ∈ Rnx - состояние объекта, v ∈ L₂ - возмущение, действующее на объ-

ект, принадлежащее классу интегрируемых с квадратом на отрезке [t₀, T₀]

функций времени, z ∈ Rnz - выход объекта. Под максимальным уклонением

выхода системы (2.1) при начальном и внешнем возмущениях на конечном

интервале [t₀, T₀] будем понимать величину

sup

|z(t)|

t∈[t₀,T₀]

(2.2)

J0,v

= sup

(

)1/2 ,

x₀, v∈L₂

x^T0R-1x₀ + ∥v∥²

[t₀,T₀]

где | · | обозначает евклидову норму вектора, а

t₁

∫

∥v∥2[t

|v(t)|²dt.

0,t1]

t₀

Весовая матрица R = R^T > 0 отражает относительную важность учета

неопределенностей начальных условий и внешнего возмущения: чем “боль-

ше” R, тем больший вес придается неопределенности в начальных усло-

виях. Величину (2.2) можно рассматривать как индуцированную норму ли-

нейного оператора, порожденного системой (2.1) и отображающего пару

(x₀, v(t)) ∈ Rnx × L₂[t₀, T₀] в z(t) ∈ L_∞[t₀, T₀].

Максимальное уклонение (2.2) может быть записано в виде

|z(T )|

(2.3)

J0,v = sup

sup

(

)1/2 .

T ∈[t₀,T₀] x0, v∈L2 x^T0R-1x₀ + ∥v∥²

[t₀,T]

Заметим, что в (2.3) величина |z(T )| для каждого T зависит от внешнего воз-

мущения на отрезке [t₀, T ], поэтому точная верхняя грань по возмущениям

берется, фактически, только по всем возмущениям на этом отрезке. Это ска-

жется на том, что, как будет показано далее, наихудшие начальное состояние

и возмущение, максимизирующие этот функционал, определяются неодно-

значно. Кроме того, ясно, что в силу линейности системы и однородности

функционала наихудшие начальное состояние и возмущение определяются с

точностью до постоянного множителя.

В частном случае, когда начальные условия в системе (2.1) нулевые, мак-

симальным уклонением выхода при внешнем возмущении назовем величину

sup

|z(t)|

t∈[t₀,T₀]

|z(T )|

(2.4)

J_v

= sup

= sup sup

v∈L₂

∥v∥[t0,T₀]

T ∈[t₀,T₀] v∈L2 ∥v∥[t0,T ]

По аналогии со случаем стационарной системы и бесконечного горизонта ве-

личина J_v может быть названа обобщенной H₂ нормой.

В другом частном случае, когда внешнее возмущение отсутствует, макси-

мальное уклонение выхода при начальном возмущении определим как

sup

|z(t)|

t∈[t₀,T₀]

|z(T )|

(2.5)

J₀

= sup

= sup sup

x₀=0 (x⁰R-1x0)1/2

T ∈[t₀,T₀] x0=0 (x⁰R-1x0)1/2

Теорема 2.1. Для системы (2.1) имеют место следующие утвержде-

ния:

1. Максимальное уклонение выхода при начальном и внешнем возмуще-

ниях на конечном отрезке [t₀,T₀] определяется формулой

[

]

(2.6)

J0,v = sup λ1/2max

C(t)Y0,v(t)C^T(t)

t∈[t₀,T₀]

где λ_max(·) - максимальное собственное значение соответствующей мат-

рицы, а Y0,v(t) есть решение дифференциального матричного уравнения

(2.7)

= A(t)Y + Y A^T(t) + B(t)B^T

(t)

с начальным условием Y (t₀) = R. Максимальное уклонение J₀ при начальном

возмущении определяется как

[

]

(2.8)

J₀ = sup λ1/2max

C(t)Y₀(t)C^T(t)

t∈[t₀,T₀]

где Y₀(t) - решение уравнения (2.7), B(t) ≡ 0 с начальным условием Y (t₀) =

= R. Максимальное уклонение J_v при внешнем возмущении определяется

как

[

]

(2.9)

J_v = sup λ1/2max

C(t)Y_v(t)C^T(t)

t∈[t₀,T₀]

где Y_v(t) - решение уравнения (2.7) с начальным условием Y (t₀) = 0;

2. Наихудшие внешнее возмущение v_∗(t) и вектор начальных условий x∗0

по отношению к максимальному уклонению (2.2) на конечном отрезке [t₀,T₀]

определяются так:

(2.10)

v_∗(t) = gB^T(t)Y-1(t)s(t), x∗0 = gs(t₀

где s(t) - решение задачи Коши для системы

[

]

(

)

(2.11)

A(t) + B(t)B^T(t)Y-1(t)

x, x(T_∗) = e_max

Y (T_∗)C^T(T_∗)C(T_∗)

Y (t) - решение уравнения (2.7), T_∗ - момент времени, в который

[

]

[

]

λ_max

C(T_∗)Y (T_∗)C^T(T_∗)

= sup λ_max

C(t)Y (t)C^T(t)

t∈[t₀,T₀]

e_max(·) - нормированный собственный вектор матрицы, отвечающий ее

максимальному собственному значению,

⎛

⎞-1/2

T∗

∫

(2.12) g =^⎝s^T(t₀)R-1s(t₀) + s^T(τ)Y-1(τ)B(τ)B^T(τ)Y-1(τ)s(τ)dτ ⎠

t₀

Замечание 1. Из доказательства теоремы 2.1, приведенного в Приложе-

нии, следует, что наихудшее возмущение по отношению к функционалу J0,v

определяется неоднозначно: на отрезке [t₀, T_∗] оно совпадает с наихудшим воз-

мущением v_∗(t), t ∈ [t₀, T_∗], по отношению к вспомогательному функционалу

J (v) = |z(T_∗)|², а на отрезке [T_∗, T₀] оно не влияет на максимальное укло-

нение выхода и, следовательно, может быть продолжено произвольным об-

разом. Действительно, пусть v_∗(t), t ∈ [t₀, T₀], - произвольное возмущение,

совпадающее с v_∗(t) на интервале [t₀, T_∗]. Тогда оно также будет наихудшим

по отношению к функционалу J0,v, так как

|z(T )|

|z(T_∗)|

J0,v ≥ sup

≥

T ∈[t₀,T₀] (x^0TR-1x⁰ + ∥v∗∥2[t

)1/2

0,T]

(x∗T0R-1x∗0 + ∥v_∗∥2[t0,T∗])1/2

|z(T_∗)|

=J0,v.

(x∗T0R-1x∗0 + ∥v_∗∥2[t0,T∗])1/2

При этом не исключается возможность того, что при разных наихудших воз-

мущениях момент T_∗ может быть разным, но в любом случае значение мак-

симального уклонения будет одно и то же. Ясно, что “большие” значения

возмущения на отрезке [T_∗, T₀] вызовут “большие” значения выхода, однако

максимальное уклонение выхода, понимаемое как отношение (2.2), не пре-

высит величину |z(T_∗)|, которая совпадает с максимальным уклонением, так

как

∫T∗

x∗T0R-1x∗0 +

|v_∗(t)|² dt = 1.

t₀

Один из возможных способов определения наихудшего внешнего возмущения

на всем отрезке [t₀, T₀] задается формулой (2.10), другой - определить v_∗(t),

t ∈ [t₀,T_∗], как в (2.10) и v_∗(t) = 0, t ∈ [T_∗,T₀].

Замечание 2. Из доказательства теоремы 2.1 следует, что решение Y (t)

уравнения (2.7) при Y (t₀) = 0 монотонно не убывает по времени. Отсюда сле-

дует, что для стационарной системы функция λ^m

ax[CY (t)C^T] также монотон-

но не убывает. Это означает, что

[

]

J_v = λ1/2max

CY_v(T₀)C^T

т.е. максимум по T из максимальных по всем допустимым возмущениям зна-

чений отношения евклидовой нормы выхода на конце интервала [t₀, T ] к

L₂ норме возмущения на этом интервале для стационарной системы при ну-

левых начальных условиях достигается на конце интервала, т.е. при T = T₀

(см. (2.4)). Стоит добавить, что при неограниченном увеличении T₀ макси-

мальное уклонение J_v выхода устойчивой стационарной системы стремится

(

)

к величине λ^m

CY_∗C^T

, где матрица Y_∗, называемая граммианом управ-

ляемости, является решением уравнения

AY + Y A^T + BB^T = 0.

В этом случае можно говорить о максимальном уклонении выхода на беско-

нечном горизонте, которое совпадает с одним из вариантов обобщенной H₂

нормы стационарной системы, введенной в [12].

Замечание 3. Доказательство теоремы 2.1 показывает, что по траекто-

рии системы выполняется равенство

(2.13)

x^T(t)Y-10,v(t)x(t) = x^T0R-1x₀ + ∥v∥2[t

- ∥v - B^TY -10,vx∥²².

0,t]

Это наводит на мысль о том, что множество достижимости системы (2.1)

в момент времени t, т.е. множество состояний, в которые может попасть

вектор ее решений x(t) при всевозможных начальных состояниях и возму-

щениях, удовлетворяющих совместному ограничению x^T0R-1x₀ + ∥v∥2[t0,t]≤1,

представляет собою эллипсоид E(Y0,v(t)) = {x : x^TY-10,v(t)x ≤ 1}, матрица ко-

торого является решением уравнения (2.7). Действительно, из (2.13) следует,

что для всех указанных начальных состояний и возмущений выполняется

неравенство x^T(t)Y-10,v(t)x(t) ≤ 1, т.е. x(t) ∈ E(Y0,v(t)). Как нетрудно видеть

из (2.13), каждая точка этого эллипсоида будет конечной для решения си-

стемы при возмущении v(σ) = B^TY-10,v(σ)x(σ), σ ∈ [t₀, t] и некотором началь-

ном состоянии x₀ ∈ E(R). Множеством достижимости системы (2.1) в момент

времени t в отсутствие возмущений при начальных состояниях из эллипсои-

да E(R) является эллипсоид E(Y₀(t)), а множеством достижимости при нуле-

вых начальных условиях и возмущениях, для которых ∥v∥2[t0,t]≤1,является

эллипсоид E(Y_v(t)). К этому добавим, что Y0,v(t) = Y₀(t) + Y_v(t) в силу того,

что решение неоднородного дифференциального уравнения (2.7) суть сумма

соответствующего решения однородного уравнения и решения неоднородного

уравнения с нулевыми начальными условиями.

3. Устойчивость и ограниченность системы

на конечном интервале времени

Напомним, что согласно [26] система называется ограниченной на конеч-

ном интервале [t₀, T₀] при ненулевых начальных условиях и внешнем воз-

мущении из класса L₂ при заданных положительных параметрах c₁, c₂, d

(c₁ < c₂) и положительно определенной матрице Γ(t), если

(3.1) x^T(t₀)Γ(t₀)x(t₀) ≤ c₁ ⇒ x^T(t)Γ(t)x(t) < c₂

∀t ∈ [t₀,T₀],

∀v : ∥v∥2[t

≤ d.

0,T0]

Если для максимального уклонения выхода z = Γ1/2(t)x при выборе

R = Γ-1(t₀) справедливо неравенство

sup

x^T(t)Γ(t)x(t)

t∈[t₀,T₀]

c₂

(3.2)

J20,v

= sup

x₀, v∈L₂ x⁰Γ(t0)x0 + ∥v∥2[t

c₁ + d

0,T0]

то система ограничена для заданных c₁, c₂, d и Γ(t). С учетом теоремы 2.1

это условие совпадает с достаточным условием ограниченности системы

на конечном интервале, полученным в [26]. Неравенство (3.2) не являет-

ся необходимым условием ограниченности системы, так как из неравенства

J20,v ≥ c₂/(c₁ + d) при x^T(t₀)Γ(t₀)x(t₀) ≤ c₁ и ∥v∥2[t0,T₀]≤dнеследует,вообще

говоря, неравенство x^T(t)Γ(t)x(t) ≥ c₂, т.е. система может оставаться ограни-

ченной в смысле определения (3.1).

Модифицируем определение (3.1) и дадим следующее определение ограни-

ченности системы на конечном интервале времени при заданных положитель-

ных параметрах s₁, s₂ (s₁ < s₂) и положительно определенной матрице Γ(t):

(3.3)

x^T(t₀)Γ(t₀)x(t₀) + ∥v∥²² ≤ s₁ ⇒ x^T(t)Γ(t)x(t) < s₂

∀t ∈ [t₀,T₀

Необходимые и достаточные условия ограниченности системы на конечном

интервалы в смысле определения (3.3) формулируются следующим образом.

Теорема 3.1. Система (2.1) является ограниченной на конечном ин-

тервале [t₀,T₀] при заданных s₁, s₂ (s₁ < s₂) и Γ(t) в смысле определения (3.3)

тогда и только тогда, когда максимальное уклонение выхода z = Γ1/2(t)x

при R = Γ-1(t₀) удовлетворяет неравенству J20,v < s₂/s₁ или, другими сло-

вами, когда выполнено условие

[

]

(3.4)

λ_max Γ1/2(t)Y (t)Γ1/2(t) < s2/s1

∀t ∈ [t₀,T₀

где Y (t) - решение уравнения (2.7) при Y (t₀) = Γ-1(t₀).

Замечание 4. Из теоремы 3.1 следует, что необходимые и достаточные

условия устойчивости на конечном интервале при заданных c₁, c₂ и Γ(t),

когда отсутствует внешнее возмущение, понимаемой как

x^T(t₀)Γ(t₀)x(t₀) ≤ c₁ ⇒ x^T(t)Γ(t)x(t) < c₂

∀t ∈ [t₀,T₀],

или устойчивости по входу и выходу на конечном интервале при заданных

c₂, d и Γ(t), когда начальное состояние нулевое, понимаемой как

∥v∥2[t

≤ d ⇒ x^T(t)Γ(t)x(t) < c₂

∀t ∈ [t₀,T₀],

0,T0]

выражаются неравенством

[

]

(3.5)

λ_max Γ1/2(t)Y (t)Γ1/2(t)

<γ²

∀t ∈ [t₀,T₀

где Y (t) - решение уравнения (2.7) при B(t) ≡ 0, Y (t₀) = Γ-1(t₀) и γ² = c₂/c₁

в первом случае и при Y (t₀) = 0 и γ² = c₂/d во втором случае. Эти усло-

вия при согласовании обозначений совпадают с результатами [23, 24] и [25]

соответственно.

4. Оптимальное управление максимальным уклонением

Рассмотрим теперь нестационарную систему с управлением:

x = A(t)x + B(t)v + B_u(t)u, x(t₀) = x₀,

(4.1)

z = C(t)x + D(t)u,

где u ∈ Rnu - управление. Поставим задачу построения оптимального управ-

ления в форме обратной связи u(t, x) = Θ(t)x, t ∈ [t₀, T₀], минимизирующего

максимальное уклонение выхода замкнутой системы

sup

|z(t)|

t∈[t₀,T₀]

(4.2)

J [Θ(t)] = sup

(

)1/2 .

x₀, v∈L₂

x^T0R-1x₀ + ∥v∥²

[t₀,T₀]

Иначе говоря, требуется найти переменные коэффициенты обратной свя-

зи Θ(t), минимизирующие функционал J[Θ(t)]. Уравнения замкнутой систе-

мы имеют вид:

x = A_c(t)x + B(t)v, x(t₀) = x₀,

(4.3)

z = C_c(t)x,

где A_c(t) = A(t) + B_u(t)Θ(t), C_c(t) = C(t) + D(t)Θ(t).

Применяя теорему 2.1, получим

[

]

(4.4)

J [Θ(t)] = sup λ1/2max

C_c(t)Y_∗(t)CTc(t)

t∈[t₀,T₀]

где матрица Y_∗(t) есть решение дифференциального матричного уравнения

(4.5)

= A_c(t)Y + Y ATc (t) + B(t)B^T(t), Y (t₀

)=R.

Для решения поставленной задачи введем матрицу Z(t) = Θ(t)Y (t) и перей-

дем от задачи (4.4), (4.5) к эквивалентной задаче оптимального управления,

которая с учетом леммы Шура сформулирована как задача полуопределен-

ного программирования.

Теорема 4.1. Оптимальное управление в задаче минимизации макси-

мального уклонения выхода системы (4.1) на конечном отрезке [t₀, T₀] име-

ет матрицу обратной связи Θ_∗(t) = Z_∗(t)Y-1∗(t), где Z_∗(t), Y_∗(t) - решение

задачи минимизации γ² при ограничениях:

Y (t) - A(t)Y (t) - Y (t)A^T(t) - B_u(t)Z(t) - Z^T(t)BTu (t) - B(t)B^T(t) = 0,

(

)

(4.6)

Y (t)

⋆

≥ 0, Y (t₀) = R

∀t ∈ [t₀,T₀].

C(t)Y (t) + D(t)Z(t) γ²I

Для вычисления искомых параметров обратной связи проведем дискре-

тизацию указанной задачи. Введем на отрезке [t₀, T₀] равномерную сетку

t_k = tk-1 + h, k = 1,... ,N, где h = (T₀ - t₀)/N, и запишем дискретный ана-

лог рассматриваемой задачи:

min γ² :

(

)

Yk+1 - Y_k - h

A_kY_k + Y_kATk + B_u,kZ_k + ZTkB^Tu,k + B_kBTk

= 0,

(4.7)

(

)

Y_k

⋆

≥ 0, Y₀ = R; k = 0, . . . , N - 1,

C_kY_k + D_kZ_k

γ²I

где индекс k указывает на значение в момент времени t_k. Решив эту зада-

чу полуопределенного программирования относительно неизвестных Y_k, Z_k,

k = 0,...,N - 1 и γ², найдем матрицы Θ_k = Z_kY -1k.

Если система (4.1) без управления не является ограниченной в смысле

определения (3.3) на конечном отрезке [t₀, T₀] при данных s₁, s₂ и Γ(t), то

возникает вопрос о существовании нестационарной линейной обратной свя-

зи, при которой замкнутая система обладает этим свойством. Принимая во

внимание теорему 3.1, приходим к следующему утверждению.

Теорема 4.2. Для существования закона управления вида u(t) =

= Θ(t)x(t), при котором система (4.1) является ограниченной на конечном

отрезке [t₀,T₀] при данных s₁, s₂ и Γ(t), необходимо и достаточно, чтобы

задача

Y (t) - A(t)Y (t) - Y (t)A^T(t) - B_u(t)Z(t) - Z^T(t)BTu (t) - B(t)B^T(t) = 0,

(

)

(4.8)

Y (t)

⋆

≥ 0, Y (t₀) = Γ-1(t₀)

∀t ∈ [t₀,T₀]

Γ1/2(t)Y (t) (s₂/s₁)I

была разрешима относительно неизвестных матричных функций Y (t)

и Z(t). Если это условие выполнено, то матрица искомой обратной связи

определяется как Θ(t) = Z(t)Y-1(t).

Проверка выполнения этого условия и нахождение матриц параметров со-

ответствующей обратной связи осуществляются путем дискретизации (4.8) и

проверки разрешимости соответствующих линейных матричных неравенств.

5. Многокритериальные управления максимальными уклонениями

При оптимизации максимального уклонения определенного выхода систе-

мы некоторые переменные и управление могут принимать достаточно боль-

шие значения. В связи с этим целесообразно рассмотреть многокритериаль-

ную задачу управления максимальными уклонениями нескольких выходов.

Для синтеза многокритериального управления, рассмотренного далее, потре-

буется расширить понятие максимального уклонения на случай, когда выход

системы составлен из нескольких векторов разных, вообще говоря, размер-

ностей.

Рассмотрим систему:

x = A(t)x + B(t)v, x(t₀) = x₀,

(5.1)

z = col(z₁,...,z_m), z_i = C(i)(t)x, i = 1,...,m,

выход которой состоит из m векторов z_i ∈ Rni . Введем некоторые обозна-

чения. Пусть вектор a ∈ Rna представлен в виде a = col (a₁, . . . , a_m), где

∑_m

a_i ∈ Rni,

n_i = n_a. Обозначим обобщенную ∞-норму вектора a через

i=1

|a|_g∞ = max1≤i≤m |a_i|, где |a_i| - евклидова норма вектора a_i. В частных слу-

чаях эта норма совпадает с обычной ∞-нормой: если m = 1, то |a|_g∞ = |a|,

а если m = n_a, то |a|_g∞ = |a|_∞ = max1≤i≤na |a_i|, где a_i - компоненты вектора a.

Максимальное уклонение комбинированного выхода z этой системы на ко-

нечном интервале [t₀, T₀] при начальном и внешнем возмущениях определим

как

sup

max

|z_i(t)|

i=1,...,m

t∈[t₀,T₀]

J0,v = sup

(

)1/2 =

x₀, v∈L₂

x^T0R-1x₀ + ∥v∥²

[t₀,T₀]

(5.2)

sup

|z(t)|_g∞

t∈[t₀,T₀]

= sup

(

)1/2 = max

J(i)0,v,

x₀, v∈L₂

i=1,...,m

x^T0R-1x₀ + ∥v∥²

[t₀,T₀]

где J(i)0,v - максимальное уклонение выхода z_i, определенное в (2.2). Условие

J0,v < γ отвечает теперь более общему понятию ограниченности системы (5.1)

на конечном интервале, когда для нескольких ее выходов выполняются нера-

венства |z_i(t)| < γ, i = 1, . . . , m, для всех t ∈ [t₀, T₀] при любых начальных

условиях и внешних возмущениях, для которых x^T0R-1x₀ + ∥v∥2[t0,T₀]≤1.

Из теоремы 2.1 непосредственно следует, что

[

]

(5.3)

J0,v = max

sup λ1/2max C(i)(t)Y (t)C(i)T(t) ,

i=1,...,m t∈[t₀,T₀]

где матрица Y (t) есть решение дифференциального матричного уравне-

ния (2.7). В частном случае z_i могут быть компонентами вектора z и тогда

[

]

J0,v = max

sup d1/2max C(i)(t)Y (t)C(i)T(t)

i=1,...,m t∈[t₀,T₀]

где d_max(·) обозначает максимальный диагональный элемент соответствую-

щей матрицы. Соответствующим образом определяются максимальное укло-

нение комбинированного выхода при начальном возмущении и максимальное

уклонение комбинированного выхода при внешнем возмущении. Заметим, что

для устойчивой линейной стационарной системы при внешнем возмущении на

бесконечном горизонте максимальное уклонение комбинированного выхода,

состоящего из нескольких векторов, совпадает с обобщенной H₂ нормой, по-

нимаемой как в [19].

Далее переходим к синтезу многокритериального управления для систе-

мы:

x = A(t)x + B(t)v + B_u(t)u, x(t₀) = x₀,

(5.4)

z_i = C(i)(t)x + D(i)(t)u, i = 1,... ,m,

в классе обратных связей u = Θ(t)x. Введем критерии

sup

|z_i(t)|

t∈[t₀,T₀]

(5.5)

J_i[Θ(t)] = sup

(

)1/2,

i = 1,...,m,

x₀, v∈L₂

x^T0R-1x₀ + ∥v∥²

[t₀,T₀]

и поставим задачу поиска оптимальных по Парето параметров регуляторов

{

}

(5.6)

Θ_P (t) = arg min

J_i[Θ(t)], i = 1,... ,m

Для ее решения применим свертку Гермейера [31]:

{

}

J_α[Θ(t)] = max

J_i[Θ(t)]/α_i, α_i > 0

i=1,...,m

В [19] установлено, что множество оптимальных по Парето решений содер-

жится в множестве оптимальных решений по отношению к данному функ-

ционалу при всех значениях α_i. Обращаясь к (5.2), нетрудно видеть, что в

рассматриваемой многокритериальной задаче свертка Гермейера представля-

ет собой не что иное, как максимальное уклонение комбинированного выхода

системы:

x = [A(t) + B_u(t)Θ(t)]x + B(t)v, x(t₀) = x₀,

(5.7)

z_α = col (z₁,... ,z_m), z_i = α-1i[C(i)(t) + D(i)(t)Θ(t)]x, i = 1,... ,m,

где вектор z_α состоит из параметризованных выходов исходной системы. Та-

ким образом, приходим к следующему утверждению.

Теорема 5.1. Оптимальные по Парето управления в многокритериаль-

ной задаче (5.6) минимизации максимальных уклонений выходов систе-

мы (5.4) суть оптимальные управления по отношению к максимально-

му уклонению комбинированного выхода системы (5.7) для всех α_i > 0, i =

= 1, . . . , m.

Для численного решения этой задачи проведем, как и выше, дискретиза-

цию и с учетом того, что нахождение минимального значения J2α[Θ(t)] эк-

вивалентно вычислению минимального значения γ², при котором для всех

t ∈ [t₀,T₀] выполнены неравенства

[

]

[

]_T

C(i)(t) + D(i)(t)Θ(t) Y (t)

C(i)(t) + D(i)(t)Θ(t)

≤ γ²α2iI, i = 1,... ,m,

придем к следующей задаче полуопределенного программирования:

min γ² :

(

)

Yk+1 - Y_k - h

A_kY_k + Y_kATk + B_u,kZ_k + ZTkB^Tu,k + B_kBTk

= 0,

(

)

(5.8)

Y_k

⋆

≥ 0, Y₀

= R,

C(i)kY_k + D(i)kZ_k γ²α2iI

i = 1,...,m; k = 0,...,N - 1.

Для каждого набора α_i, i = 1, . . . , m, матрицы параметров оптимальных по

Парето регуляторов находятся как Θ_k = Z_kY-1k, где Y_k, Z_k - решения (5.8).

6. Результаты численных экспериментов

С целью иллюстрации приведенных выше теоретических результатов рас-

смотрим задачу активной виброзащиты объекта, подвергаемого вибрацион-

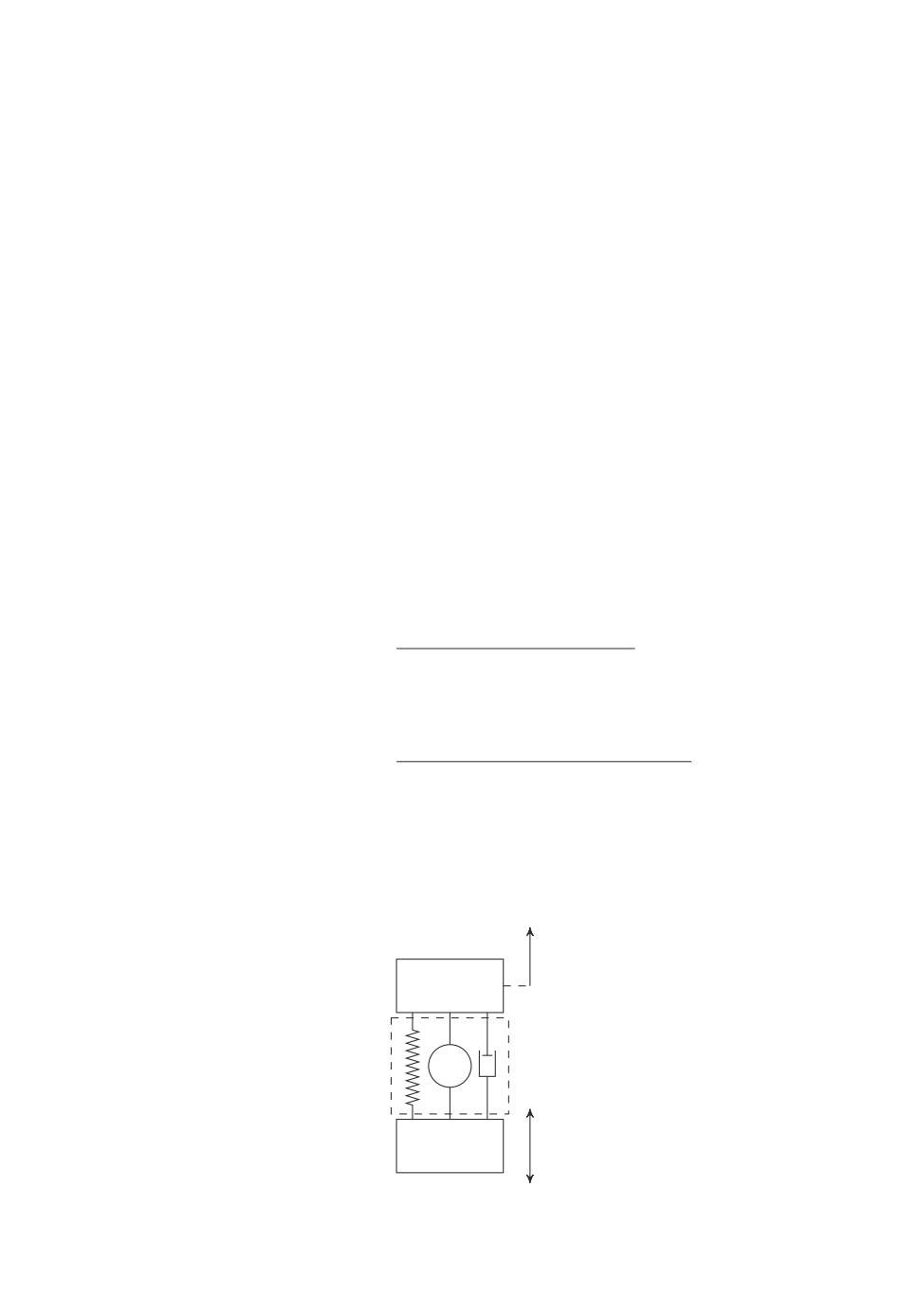
ным и ударным воздействиям. На рис. 1 показан защищаемый объект “2”,

связанный с подвижным основанием “1” посредством виброизолирующего

устройства “3”, включающего пассивную и активную части. Движения такой

системы описываются дифференциальными уравнениями:

x₁ = x₂,

x₂ = -x₁ - βx₂ + u + v,

(6.1)

x₁(0) = x₁₀, x₁(0) = x₂₀,

z₁ = x₁, z₂ = -x₁ - βx₂ + u,

где z1 — координата объекта защиты относительно подвижного основа-

ния, z2 — характеристика пассивной и активной частей виброизолирую-

щего устройства, v — внешнее воздействие, с точностью до знака совпа-

дающее с ускорением подвижного основания. Будем рассматривать задачу

оптимальной виброзащиты, состоящую в нахождении на конечном отрез-

ке времени t ∈ [0, T₀] управления в форме нестационарной обратной связи

u = θ₁(t)x₁ + θ₂(t)x₂, минимизирующего в смысле Парето следующие функ-

ционалы:

sup

|x₁(t)|

t∈[0,T₀]

J₁[Θ(t)] = sup

(

)1/2 ,

x₀, v∈L₂

xT0 R-1x₀ + ∥v∥²

[0,T₀]

(6.2)

sup

| - x₁(t) - βx₂(t) + u(t)|

t∈[0,T₀]

J₂[Θ(t)] = sup

(

)1/2

x₀, v∈L₂

xT0 R-1x₀ + ∥v∥²

[0,T₀]

где x₀ = (x₁₀ x₂₀)^T, Θ(t) = (θ₁(t) θ₂(t))^T. Первый функционал характеризует

максимальное смещение объекта защиты относительно подвижного основа-

ния, а второй функционал — максимальное абсолютное ускорение объекта

x₁

Рис. 1. Схематическое изображение системы активной виброзащиты.

3,5

J₂

3,0

2,5

2,0

1,5

1,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

J₁

Рис. 2. Парето оптимальный фронт.

защиты или максимальную действующую на него силу. Эти показатели каче-

ства виброзащиты являются “конфликтующими”: увеличение силы, противо-

действующей движению объекта защиты относительно основания, приводит

к уменьшению его смещения.

Для численного решения указанной задачи, положим β = 0,1, R-1 =

= diag (10,1) и T₀ = 20. С использованием теоремы 3.2 и соотношения (5.8)

были синтезированы оптимальные в смысле Парето регуляторы Θ_α(t) и

вычислены соответствующие им оптимальные значения функционалов. На

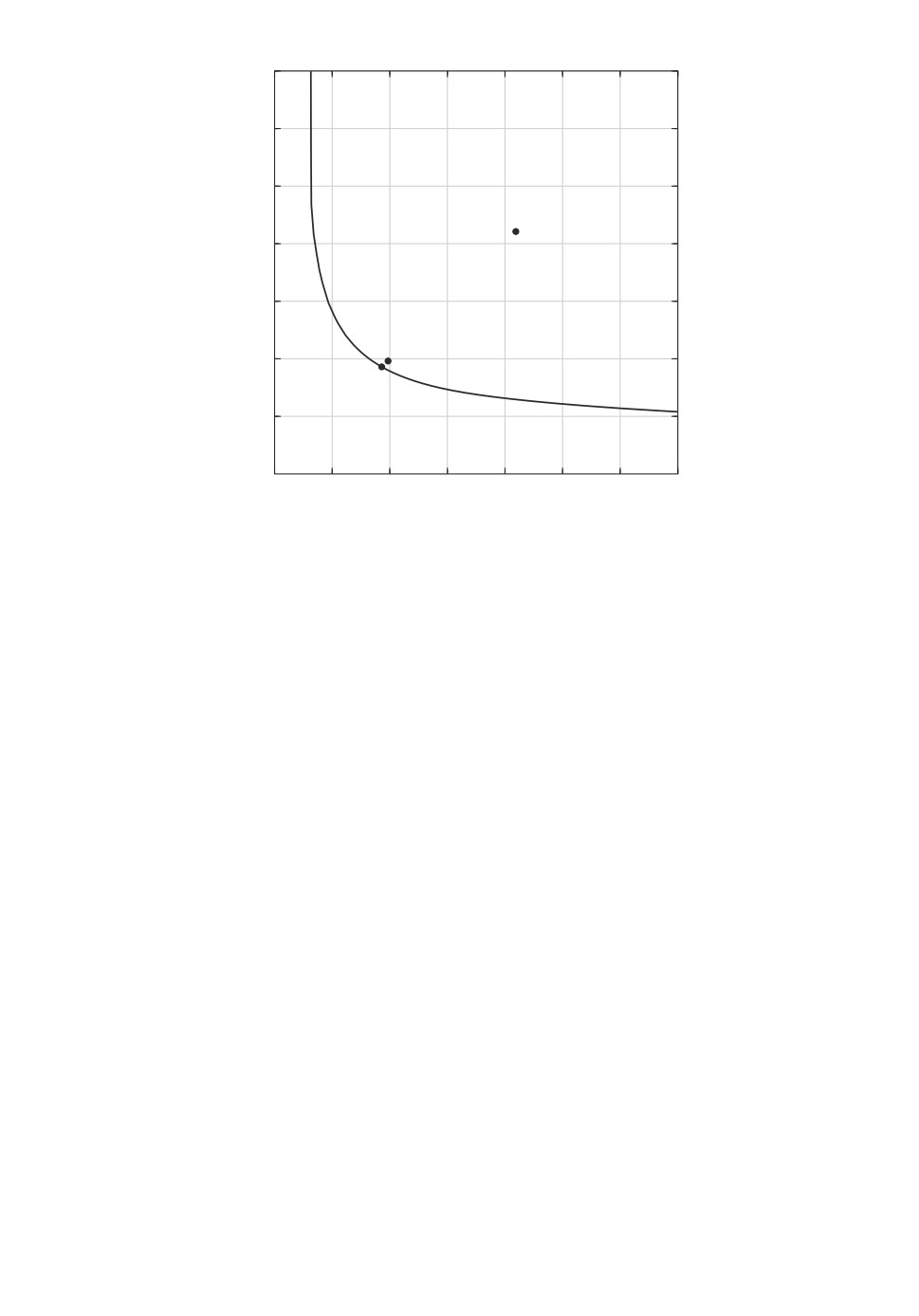
рис. 2 изображена оптимальная по Парето кривая (Парето оптимальный

фронт) на плоскости критериев (J₁, J₂), на которой указана точка B c коор-

динатами (0,930; 0,930). На этом же рисунке для сравнения указана точка A

с координатами (2,094; 2,106), отвечающая значениям функционалов в слу-

чае, когда в системе отсутствует активная составляющая виброзащиты, т.е. в

случае u = 0. Из представленных данных следует, что применение активной

виброзащиты позволяет улучшить показатели качества системы примерно в

два раза.

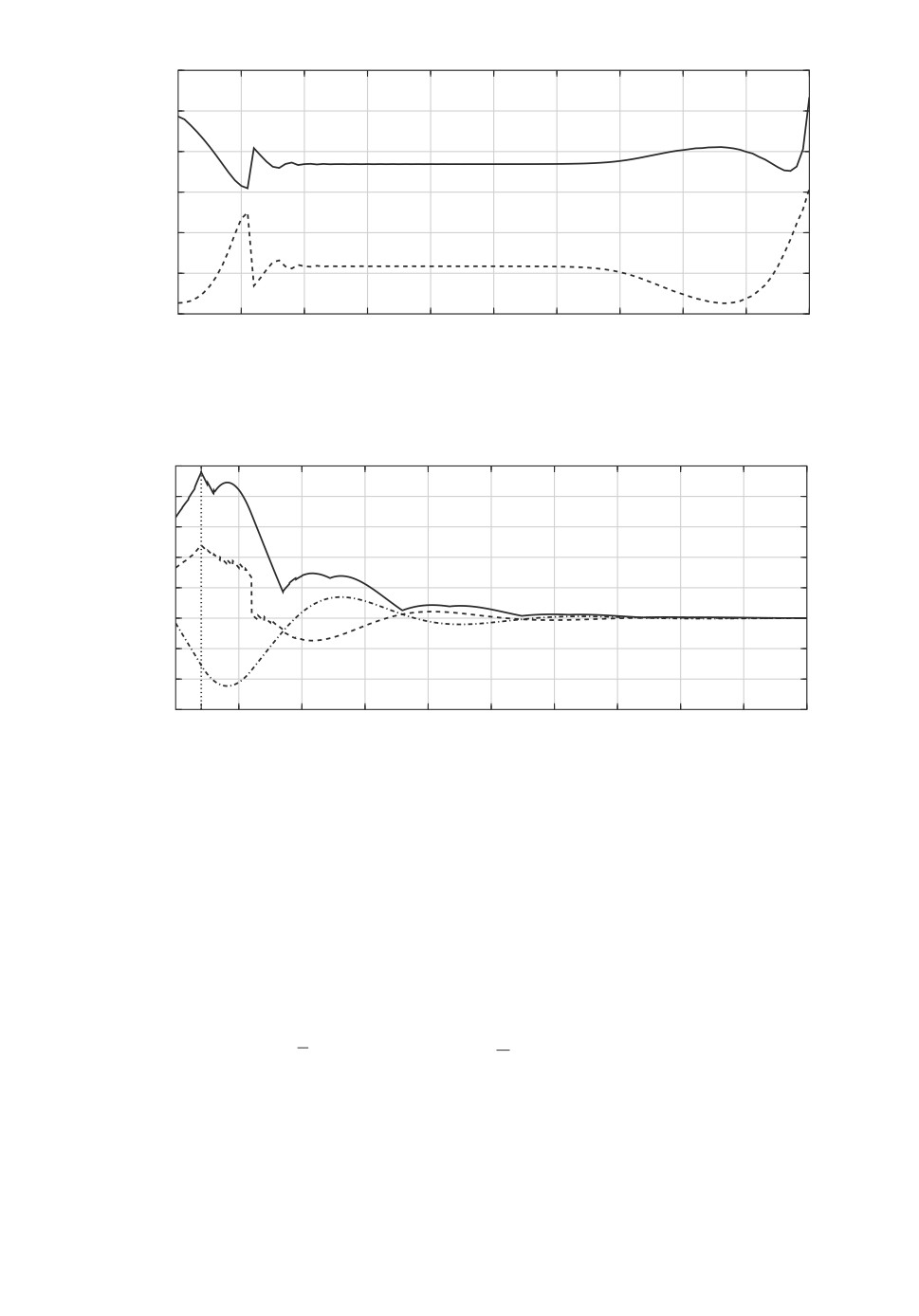
На рис. 3 приведены графики оптимальных по Парето коэффициентов

обратной связи Θ_α(t) в зависимости от времени (сплошная кривая соот-

ветствует коэффициенту θ₁(t), а штриховая — коэффициенту θ₂(t)) при

α = 0,5, отвечающие точке B. На рис. 4 показаны соответствующие графи-

ки изменения выходных переменных z₁ = x₁ (штрихпунктирная кривая) и

z₂ = -x₁ - βx₂ + u (штриховая кривая), а также обобщенной ∞-нормы ком-

бинированного выхода z_α при α₁ = α₂ = 1/2 (сплошная кривая), т.е.

|z_α(t)|_g∞ = 2 max{|z₁(t)|, |z₂(t)|},

0,9

0,6

0,3

0,6

0,9

Рис. 3. Графики зависимостей от времени оптимальных по Парето коэффи-

циентов обратной связи.

2,0

z₁, z₂

1,6

1,2

0,8

0,4

0,8

1,2

Рис. 4. Графики зависимостей от времени выходов и |z_α(t)|_g∞ в замкнутой

оптимальной по Парето системе при наихудших начальном и внешнем возму-

щениях.

для наихудших начальных условий x∗0 = (-0,066; -0,689) и внешнего возму-

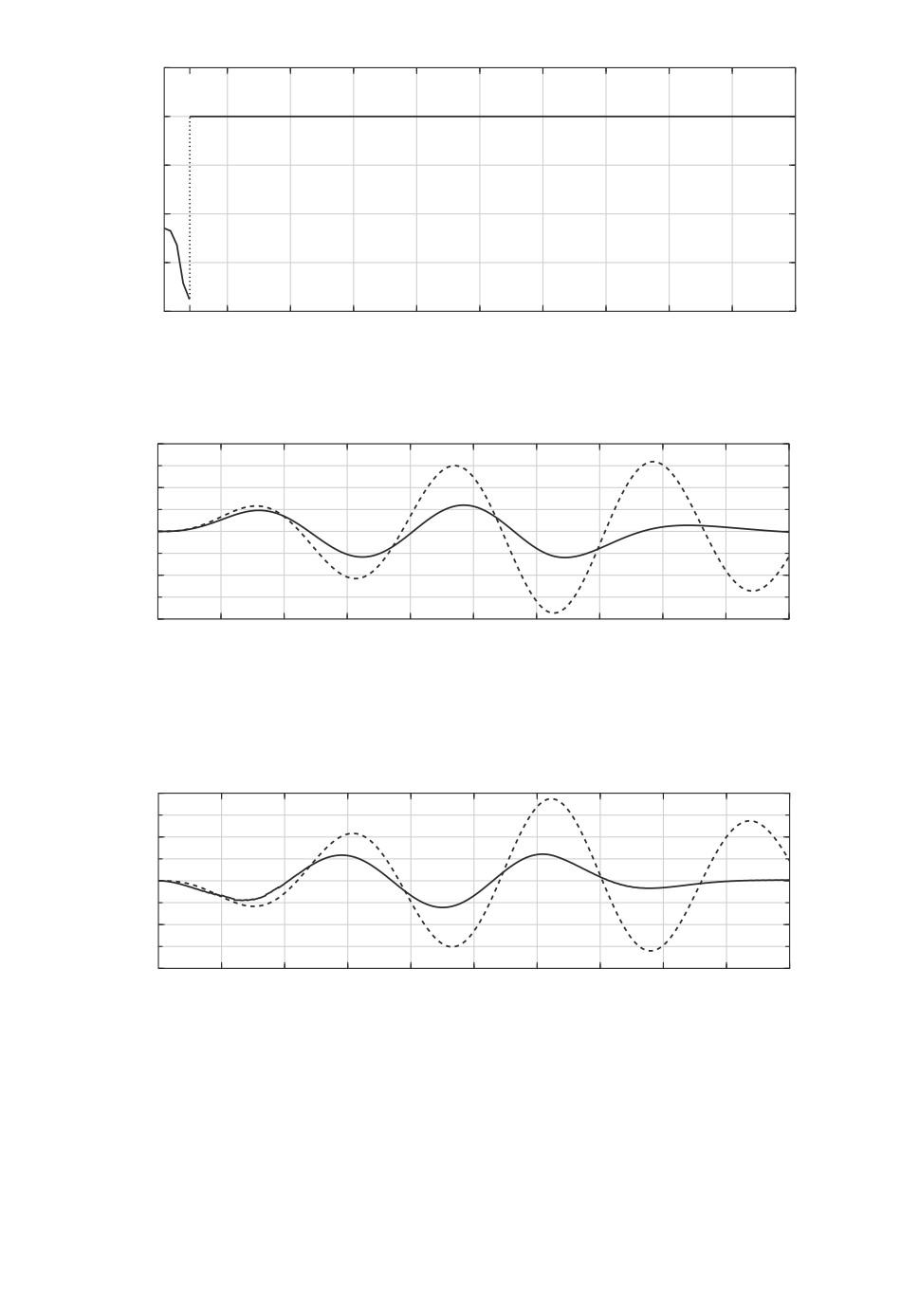
щения v^∗(t), а на рис. 5 - график выбираемого в этих расчетах наихудшего

возмущения v^∗(t) по отношению к максимальному уклонению этого комбини-

рованного выхода в замкнутой системе. На рис. 6 и 7 представлены графики

зависимостей выходов z₁ и z₂ системы с оптимальным управлением (сплош-

ные кривые), отвечающим точке B, и в отсутствие управления (штриховые

кривые) при одновременном действии ударного и гармонического возмуще-

√

ний: x₁₀ = 0, x₂₀ =

2/2, v(t) = sin t/(2√π), t ∈ [0,4π], v(t) ≡ 0, t ∈ (4π,20],

для которых

∫20

x²²⁰ +

|v(t)|² dt = 1.

Эти графики демонстрируют хорошее качество активной виброзащиты.

0,3

0,6

0,9

1,2

Рис. 5. График наихудшего возмущения.

Рис. 6. Графики зависимостей от времени выхода z₁ системы с оптимальным

по Парето управлением и в отсутствие управления при одновременном дей-

ствии ударного и гармонического возмущений.

Рис. 7. Графики зависимостей от времени выхода z₂ системы с оптимальным

по Парето управлением и в отсутствие управления при одновременном дей-

ствии ударного и гармонического возмущений.

Наконец, заметим, что примерно половину времени функционирования

системы коэффициенты обратной связи сохраняют “постоянные” значения

(рис. 3). Интересно сравнить значения функционалов при оптимальном регу-

ляторе и стационарном регуляторе, отвечающим этим “постоянным” значени-

ям θ₁(t) ≡ 0,2180 и θ₂(t) ≡ -0,5694, которым на рис. 2 соответствует точка C

с координатами (0,985; 0,981). Как следует из приведенных данных, потери в

качестве виброзащиты при использовании такого стационарного регулятора

сравнительно невелики.

7. Заключение

В статье показано, что максимальные уклонения выходов линейной неста-

ционарной системы на конечном временном горизонте при внешнем и/или

начальном возмущениях, а также максимальные уклонения выходов стацио-

нарной системы на бесконечном горизонте при внешнем возмущении можно

характеризовать в терминах решений дифференциальных или алгебраиче-

ских матричных уравнений и, как следствие, в терминах линейных матрич-

ных неравенств. Это позволяет синтезировать оптимальные по максимально-

му уклонению выхода законы управления, в том числе и многокритериаль-

ные. Результаты численных экспериментов, проведенных для задачи актив-

ной виброзащиты, демонстрируют эффективность предлагаемого подхода.

Авторы признательны Б.Т. Поляку за обсуждения, которые инициировали

проведение исследований, изложенных в данной статье.

ПРИЛОЖЕНИЕ

Доказательство теоремы 2.1. С целью нахождения величины J0,v

рассмотрим вспомогательную вариационную задачу: для системы (2.1) найти

наихудшее возмущение v = v_∗(t) и наихудший начальный вектор x∗0, достав-

ляющие максимум функционалу

(Π.1)

J (v) = |z(T )|² = x^T(T )C^T

(T )C(T )x(T )

при ограничении

∫T

(Π.2)

x^T0R-1x₀ +

|v(t)|²

dt = 1

t₀

в произвольный, но фиксированный момент времени T ∈ (t₀, T₀]. Введем

функцию Гамильтона

H = ψ^T[A(t)x + B(t)v] - μv^Tv,

применим стандартную процедуру решения вариационных задач и придем к

следующей краевой задаче:

x = A(t)x + (2μ)-1B(t)B^T(t)ψ,

ψ=-AT(t)ψ,

ψ(t₀) = 2μR-1x(t₀),

ψ(T ) = 2C^T(T )C(T )x(T ).

В этих уравнениях искомое наихудшее возмущение для вспомогательной за-

дачи имеет вид

v_∗(t) = (2μ)-1B^T(t)ψ(t),

где положительный параметр μ, являющийся множителем Лагранжа, пока

неизвестен и подлежит в дальнейшем определению.

Далее, исключая вспомогательную переменную ψ и связывая переменные

ψ и x линейным преобразованием ψ(t) = 2X(t)x(t), получим:

(X˙ + XA(t) + AT(t)X + μ-1XB(t)BT(t)X)x(t) = 0,

(Π.3)

X(t₀)x(t₀) = μR-1x(t₀),

X(T )x(T ) = C^T(T )C(T )x(T ).

При такой замене наихудшее возмущение имеет вид

v_∗(t) = μ-1B^T(t)X(t)x(t).

Определим теперь значение параметра μ. Вычисляя производную по времени

от квадратичной формы x^T(t)X(t)x(t) вдоль оптимальной траектории, отве-

чающей наихудшему возмущению v_∗(t), с учетом первого равенства в (Π.3)

получаем

x^T(t)X(t)x(t) = μvT∗(t)v_∗(t).

Интегрируя это равенство в пределах от t₀ до T с учетом двух последних

равенств в (Π.3), имеем

⎛

⎞

∫

J (v^∗) = x^T(T )C^T(T )C(T )x(T ) = μ ⎝x^T0R-1x₀ +

|v_∗(t)|²dt⎠ .

t₀

С учетом ограничения типа равенства (Π.2) в рассматриваемой вариационной

задаче получаем искомое значение параметра μ, совпадающее с оптимальным

значением функционала (Π.1):

(Π.4)

J (v_∗

Сделаем далее замену Q = X/μ в соотношениях (Π.3):

(Q˙ + QA(t) + A^T(t)Q + QB(t)B^T(t)Q)x(t) = 0,

(Π.5)

Q(t₀)x(t₀) = R-1x(t₀),

μQ(T)x(T) = C^T(T)C(T)x(T).

Наконец, введем матрицу Y = Q-1, которая удовлетворяет матричному диф-

ференциальному уравнению

(Π.6)

= A(t)Y + Y A^T(t) + B(t)B^T(t), Y (t₀

)=R.

Если матрица Y = Y (t) является решением задачи Коши (Π.6), то для лю-

бого вектора x(t) справедливы первые два уравнения (Π.5). Заметим так-

же, что матрица Y (t) является положительно определенной для всех значе-

ний t ∈ [t₀, T ], поскольку решение матричного дифференциального уравне-

ния (Π.6) может быть представлено в виде

∫^t

Y (t) = Φ(t, t₀)Y (t₀)Φ^T(t, t₀) + Φ(t, τ)B(τ)B^T(τ)Φ^T(t, τ)dτ ,

t₀

где Φ(t, τ) - фундаментальная матрица решений уравнения

x = A(t)x.

Таким образом, матрица Y , а следовательно, и матрица Q являются невы-

рожденными для всех t ∈ [t₀, T ].

Обратимся теперь к последнему равенству в (Π.5), которое можно пере-

писать в виде

Y (T )C^T(T )C(T )x(T ) = μx(T ).

Данное соотношение можно рассматривать как задачу на собственные значе-

ния и собственные векторы матрицы Y (T )C^T(T )C(T ). Поскольку в исходной

вариационной задаче требуется найти максимальное значение функционала,

то с учетом (Π.4) получаем, что μ есть максимальное собственное значение

матрицы Y (T )C^T(T )C(T ) или равное ему максимальное собственное значе-

ние матрицы C(T )Y (T )C^T(T ) (см. [32], с. 71). Итак,

(

)

μ=λ_max

C(T )Y (T )C^T(T )

Осталось найти наихудший вектор начальных условий x₀. С этой целью за-

мкнем исходную систему (2.1) наихудшим возмущением

v_∗(t) = B^T(t)Y-1(t)x(t)

и рассмотрим задачу Коши

x = (A(t) + B(t)B^T(t)Y -1(t))x,

(Π.7)

x(T ) = ge_max(Y (T )C^T(T )C(T )),

где Y (t) есть решение матричного дифференциального уравнения (Π.6), а

свободный параметр g подлежит в дальнейшем определению. Обозначим че-

рез x = s(t) решение указанной задачи Коши при g = 1, тогда искомое зна-

чение параметра g определится из условия (Π.2):

⎛

⎞-1/2

∫

(Π.8) g =^⎝s^T(t₀)R-1s(t₀) + s^T(τ)Y-1(τ)B(τ)B^T(τ)Y-1(τ)s(τ)dτ ⎠

t₀

Таким образом, исходя из необходимых условий оптимальности функциона-

J (v), наихудшие возмущение v_∗(t) и вектор начальных условий x∗0 по от-

ношению к этому функционалу определяются так:

(Π.9)

v_∗(t) = gB^T(t)Y-1(t)s(t), x∗0 = gs(t₀), t ∈ [t₀

,T].

При этом оптимальное значение функционал

J (v) таково:

(

)

J (v_∗) = λ_max

C(T )Y (T )C^T(T )

Обратно: пусть Y (t) удовлетворяет (Π.6). Тогда для функции V (x) =

= x^TY -1x в силу системы (2.1) выполнено равенство

= |v|² - |v - B^TY -1x|².

Интегрируя это уравнение с учетом того, что Y-1(t₀) = R, получим

(Π.10)

x^T(T)Y-1(T)x(T) = x^T0R-1x₀ + ∥v∥2[t

- ∥v - B^TY -1x∥²².

0,T]

Отсюда следует, что при любых допустимых возмущениях и началь-

ных условиях, удовлетворяющих ограничению (Π.2), имеет место неравен-

ство x^T(T )Y-1(T )x(T ) ≤ 1. Это значит, что x(T )x^T(T ) ≤ Y (T ). Следова-

тельно,

J (v) = |z(T )|² ≤ λ_max(C(T )Y (T )C^T(T )) и максимум достигается при

v_∗(t) = B^T(t)Y-1(t)x(t), где x(t) - решение уравнения (Π.7), а g определено

в (Π.8).

Возвращаясь к исходной задаче нахождения максимального уклонения,

записанного в виде (2.3), получаем, что

(Π.11)

J0,v = sup λ1/2max(C(t)Y0,v(t)C^T

(t)),

t∈[t₀,T₀]

где Y0,v(t) - решение уравнения (Π.6). Пусть T_∗ - момент времени, в который

[

]

[

]

λ_max

C(T_∗)Y0,v(T_∗)C^T(T_∗)

= sup λ_max

C(t)Y0,v(t)C^T(t)

t∈[t₀,T₀]

Тогда наихудшие возмущение и начальное состояние по отношению к J0,v

определяются как в (Π.9) при T = T_∗.

Теперь обратимся к частным случаям. Так же как и выше, запишем, что

|z(T )|

J_v = sup sup

T ∈[t₀,T₀] v∈L2 ∥v∥[t0,T0]

При нулевых начальных условиях в системе (2.1) выражение для z(t) имеет

вид

∫t

z(t) = C(t) Φ(t, τ)B(τ)v(τ)dτ .

t₀

Записывая

|z(t)| = max e^Tz(t)

|e|=1

и используя неравенство Коши-Буняковского, оценим |z(t)|:

⎛

⎞1/2 ⎛

⎞1/2

∫

|z(t)| ≤ max^⎝

|B^T(τ)Φ^T(t, τ)C^T(t)e|²dτ⎠

⎝

|v(τ)|²dτ ⎠

|e|=1

t₀

Далее получаем, что

⎛

⎡

⎤

⎞1/2

∫

|z(t)|

sup

≤⎝maxe^TC(t)⎣

Φ(t, τ)B(τ)B^T(τ)Φ^T(t, τ)dτ ⎦ C^T(t)e⎠

v∈L₂ ∥v∥2

|e|=1

t₀

Из последнего неравенства следует, что

|z(T )|

[

]

sup

≤λ1/2max

C(T )Y_v(T )C^T(T )

v∈L₂ ∥v∥[t₀,T₀]

где

∫^t

Y_v(t) = Φ(t,τ)B(τ)B^T(τ)Φ^T(t,τ)dτ

t₀

- решение матричного уравнения

= A(t)Y + Y A^T(t) + B(t)B^T(t), Y (t₀) = 0.

Нетрудно проверить, что построенная оценка достигается точно при

[

]

v_∗(τ) = B^T(τ)Φ^T(T,τ)C^T(T)e_max

C(T )Y_v(T )C^T(T )

τ ∈ [t₀,T].

Таким образом,

|z(T )|

[

]

sup

=λ1/2max

C(T )Y_v(T )C^T(T )

v∈L₂ ∥v∥[t₀,T₀]

Возвращаясь наконец к исходной задаче, получаем

sup

|z(t)|

t∈[t₀,T₀]

[

]

J_v

= sup

= sup λ1/2max

C(T )Y_v(T )C^T(T )

v∈L₂

∥v∥[t0,T₀]

T ∈[t₀,T₀]

Представим теперь J₀ в виде

|z(t)|

J₀ = sup sup

t∈[t₀,T₀] x0=0 (x⁰R-1x0)1/2

Выражение для z(t) может быть представлено в виде

z(t) = Φ(t, t₀)x₀.

Рассмотрим отношение

|z(t)|²

x^T0Φ^T(t,t₀)C^T(t)C(t)Φ(t,t₀)x₀

x^T0R-1x₀

Произведем далее замену ξ₀ = R-1/2x₀ и получим

|z(t)|

ξ^T0R1/2Φ^T(t,t₀)C^T(t)C(t)Φ(t,t₀)R1/2ξ₀

sup

= sup

ξ^T0ξ₀

x₀=0 x⁰R-1x0 ξ0=0

откуда следует, что

[

]

|z(t)|

sup

= λ_max R1/2Φ^T(t,t₀)C^T(t)C(t)Φ(t,t₀)R1/2

x₀=0 x⁰R-1x0

[

]

=λ_max

C(t)Φ(t, t₀)RΦ^T(t, t₀)C^T(t)

Заметим далее, что

C(t)Φ(t, t₀)RΦ^T(t, t₀)C^T(t) = C(t)Y₀(t)C^T(t),

где матрица Y₀(t) есть решение дифференциального матричного уравнения

= A(t)Y + Y A^T(t), Y (t₀) = R.

Итак, окончательно имеем

[

]

J₀ = sup λ1/2max

C(t)Y₀(t)C^T(t)

t∈[t₀,T₀]

Для определения наихудшего вектора начальных условий x∗0 предлагается

следующий алгоритм. Сначала определим момент времени t_∗ такой, что

[

]

[

]

λ_max

C(t_∗)Y₀(t_∗)C^T(t_∗)

= sup λ_max

C(t)Y₀(t)C^T(t)

t∈[t₀,T₀]

затем найдем нормированный собственный вектор e∗max матрицы

R1/2Φ^T(t_∗,t₀)C^T(t_∗)C(t_∗)Φ(t_∗,t₀)R1/2, отвечающий максимальному соб-

ственному числу. В результате искомый вектор x∗0 = R1/2e∗max. Терема 2.1

доказана.

Доказательство теоремы 3.1. Если в определении максимального

уклонения, данного в (2.2), выбрать z = Γ1/2(t)x и R = Γ(t₀), то получим,

что выполнение (3.3) эквивалентно неравенству J20,v < s₂/s₁. Действительно,

если J20,v < s₂/s₁, то из определения J0,v непосредственно следует выполне-

ние (3.3). Для обоснования справедливости обратного утверждения предпо-

ложим, что при выполнении (3.3) имеем J20,v ≥ s₂/s₁. Так как

J20,v = s-11 sup

sup x^T(t)Γ(t)x(t) ≥ s₂/s₁,

t∈[t₀,T₀]

x^t0^,v∈L2

где sup берется по всем x^T(t₀)Γ(t₀)x(t₀) + ∥v∥²² = s₁, то sup x^T(t)Γ(t)x(t) ≥

t∈[t₀,T₀]

≥ s₂, что противоречит (3.3). Таким образом, применяя теорему 2.1, прихо-

дим к (3.4). Терема 3.1 доказана.

СПИСОК ЛИТЕРАТУРЫ

Фельдбаум A.A. О распределении корней характеристического уравнения си-

стем регулирования // АиТ. 1948. № 4. C. 253-279.

Измайлов P.Н. Эффект “всплеска"в стационарных линейных системах со ска-

лярными входами и выходами // АиТ. 1987. № 8. С. 56-62.

Izmailov R.N. The Peak Effect in Stationary Linear Systems with Scalar Inputs and

Outputs // Autom. Remote Control. 1987. V. 48. No. 8. P. 1018-1024.

Булгаков Б.В. О накоплении возмущений в линейных колебательных системах

с постоянными параметрами // ДАН СССР. 1946. Т. 51. № 5. С. 339-342.

Александров В.В. К задаче Булгакова о накоплении возмущений // Докл. АН

СССР. Сер. Кибернетика и теория регулирования. 1969. Т. 186. № 3. С. 526-528.

Жермоленко В.Н. О максимальном отклонении линейной системы // АиТ. 2012.

№ 7. С. 3-14.

Zhermolenko V.N. On Maximal Deviation of Linear System // Autom. Remote

Control. 2012. V. 73. No. 7. P. 1117-1125.

Moler C., Van Loan C. Nineteen Dubious Ways to Compute the Exponential of a

Matrix, Twenty-Five Years Later // SIAM Rev. 2003. V. 45. No. 1. P. 3-49.

Boyd S., El Ghaoui L., Feron E., Balakrishnan V. Linear Matrix Inequalities in

Systems and Control Theory. Philadelphia: SIAM, 1994.

Whidborne J.F., McKernan J. On Minimizing Maximum Transient Energy

Growth // IEEE Trans. Autom. Control. 2007. V. 52. No. 9. P. 1762-1767.

Поляк Б.Т., Тремба А.А., Хлебников М.В., Щербаков П.С., Смирнов Г.В. Боль-

шие отклонения в линейных системах при ненулевых начальных условиях //

АиТ. 2015. № 6. С. 18-41.

Polyak B.T., Tremba A., Khlebnikov M.V., Shcherbakov P.S., Smirnov G.V. Large

Deviations in Linear Control Systems with Nonzero Initial Conditions // Autom.

Remote Control. 2015. V. 76. No. 6. P. 957-976.

10.

Polyak B.T., Smirnov G. Large Deviations for Non-zero Initial Conditions in Linear

Systems // Automatica. 2016. V. 74. P. 297-307.

11.

Агиевич В.Н., Парсегов С.Э., Щербаков П.С. Верхние оценки всплеска в линей-

ных дискретных системах // АиТ. 2018. № 11. С. 32-46.

Ahiyevich U.M., Parsegov S.E., Shcherbakov P.S. Upper Bounds on Peaks in

Discrete-Time Linear Systems // Autom. Remote Control. 2018. V. 79. No. 11.

P. 1976-1988.

12.

Wilson D.A. Convolution and Hankel Operator Norms for Linear Systems // IEEE

Trans. Autom. Control. 1989. V. 34. P. 94-97.

13.

Wilson D.A. Extended Optimality Properties of the Linear Quadratic Regulator and

Stationary Kalman Filter // IEEE Trans. Autom. Control. 1990. V. 35. P. 583-585.

14.

Kim J.H., Hagiwara T. Upper/Lower Bounds of Generalized H₂ Norms in Sampled-

Data Systems with Convergence Rate Analysis and Discretization Viewpoint // Syst.

Control Lett. 2017. V. 107. P. 28-35.

15.

Rotea M.A. The Generalized H₂ Control Problem // Automatica. 1993. V. 29. No. 2.

P. 373-385.

16.

Wilson D.A., Nekoui M.A., Halikias G.D. An LQR Weight Selection Approach to

the Discrete Generalized H₂ Control Problem // Int. J. Control. 1998. V. 71. No. 1.

P. 93-101.

17.

Баландин Д.В., Коган М.М. Синтез линейных законов управления при фазовых

ограничениях // АиТ. 2009. № 6. С. 48-57.

Balandin D.V., Kogan M.M. Linear Control Design under Phase Constraints //

Autom. Remote Control. 2009. V. 70. No. 6. P. 958-966.

18.

Коган М.М., Кривдина Л.Н. Синтез многоцелевых линейных законов управ-

ления дискретными объектами при интегральных и фазовых ограничениях //

АиТ. 2011. № 7. С. 83-95.

Kogan M.M., Krivdina L.N. Synthesis of Multipurpose Linear Control Laws of

Discrete Objects under Integral and Phase Constraints // Autom. Remote Control.

2011. V. 72. No. 7. P. 1427-1439.

19.

Баландин Д.В., Коган М.М. Оптимальное по Парето обобщенное H₂-управление

и задачи виброзащиты // АиТ. 2017. № 8. С. 76-90.

Balandin D.V., Kogan M.M. Pareto Optimal Generalized H₂-control and

Vibroprotection Problems // Autom. Remote Control. 2017. V. 78. No. 8. P. 1417-

1429.

20.

Balandin D.V., Kogan M.M. Multi-Objective Generalized H₂ Control

Automatica. 2019. V. 99. No. 1. P. 317-322.

21.

Барабанов А.Е., Граничин О.Н. Оптимальный регулятор дискретного объекта с

ограниченной помехой // АиТ. 1984. № 5. С. 39-46.

Barabanov A.E., Granichin O.N. An Optimal Controller for a Linear Plant with

Bounded Noise // Autom. Remote Control. 1984. V. 45. Part 1. No. 5. P. 578-584.

22.

Dahleh M.A., Diaz-Bobillo I.J. Control of uncertain systems: a linear programming

approach. Englewood Cliffs. N.J.: Prentice-Hall, 1995.

23.

Amato F., Ariola M., Cosentino C., Abdallah C.T., Dorato P. Necessary and

Sufficient Conditions for Finite-Time Stability of Linear Systems // Proc. Amer.

Control Conf. Denver, USA. 2003. P. 4452-4456.

24.

Garcia G., Tarbouriech S., Bernussou J. Finite-Time Stabilization of Linear Time-

Varying Continuous Systems // IEEE Trans. Autom. Control. 2009. V. 54. No. 2.

P. 364-369.

25.

Amato F., Carannante G., De Tommasi G., Pironti A. Input-Output Finite-Time

Stability of Linear Systems: Necessary and Sufficient Conditions // IEEE Trans.

Autom. Control. 2012. V. 57. No. 12. P. 3051-3063.

26.

Amato F., Ariola M., Cosentino C. Finite-time Control of Linear Time-Varying

Systems via Output Feedback // Proc. Amer. Control Conf. Portland, USA. 2005.

P. 4722-4726.

27.

Khargonekar P.P., Nagpal K.M., Poolla K.R. H_∞ Control with Transients // SIAM

J. Control Optim. 1991. V. 29. No. 6. P. 1373-1393.

28. Lu W.W., Balas G.J., Lee E.B. A Variational Approach to H_∞ Control with

Transients // IEEE Trans. Autom. Control. 1999. V. 44. No. 10. P. 1875-1879.

29. Баландин Д.В., Коган М.М. Обобщенное H_∞-оптимальное управление как ком-

промисс между H_∞-оптимальным и γ-оптимальным управлениями // АиТ. 2010.

№ 6. С. 20-38.

Balandin D.V., Kogan M.M. Generalized H_∞-optimal Control as a Trade-off between

the H_∞-optimal and γ-optimal Controls // Autom. Remote Control. 2010. V. 71.

No. 6. P. 993-1010.

30. Balandin D.V., Kogan M.M. LMI Based H_∞-optimal Control with Transients //

Int. J. Control. 2010. V. 83. No. 8. P. 1664-1673.

31. Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971.

32. Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.

Статья представлена к публикации членом редколлегии А.В. Назиным.

Поступила в редакцию 13.07.2018

После доработки 05.09.2018

Принята к публикации 08.11.2018