Автоматика и телемеханика, № 10, 2019

(Вильнюсский университет),

Н.М. МАРКОВИЧ, д-р физ.-мат. наук (nat.markovich@gmail.com,

markovic@ipu.rssi.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

КЛАСС СЕМИПАРАМЕТРИЧЕСКИХ ОЦЕНОК

ТЯЖЕСТИ ХВОСТА РАСПРЕДЕЛЕНИЯ

И ЕГО ПРИМЕНЕНИЯ¹

Предлагается новый класс семипараметрических оценок хвостового ин-

декса, основанный на довольно общем классе семипараметрических ста-

тистик. Доказывается асимптотическая нормальность предлагаемых оце-

нок. Проводится их сравнение с несколькими ранее предложенными оцен-

ками хвостового индекса посредством асимптотической среднеквадрати-

ческой ошибки. Для вычисления оценок предлагается алгоритм, который

применяется к нескольким последовательностям реальных данных.

Ключевые слова: хвостовой индекс, оценка Хилла, нормальное распреде-

ление, асимптотическая средне-квадратическая ошибка.

DOI: 10.1134/S0005231019100039

1. Введение

Пусть X₁, X₂, . . . , Xn - выборка независимых одинаково распределен-

ных (н.о.р.) случайных чисел (сл.в.) с неизвестной функцией распределения

(ф.р.) F (x). В статье формулируются предположения авторов в терминах

квантильной функции U, связанной с F , которая определяется как

{

0 < t ≤ 1,

U (t) =

inf {x : F (x) ≥ 1 - (1/t)} , t > 1.

А именно предполагается, что

U (tx)

(1)

lim

=x^γ

t→∞ U(t)

для всех x > 0 и некоторого γ > 0. Напомним, что любая неотрицательная

функция U, удовлетворяющая соотношению (1) с γ ∈ R, принадлежит классу

функций c регулярно меняющимся правым хвостом, т.е. U ∈ RV_γ. В теории

экстремальных величин параметр γ > 0 называется хвостовым индексом.

Он показывает тяжесть правого хвоста распределения. Во многих областях,

¹ Работа выполнена при частичной финансовой поддержке Маркович Н.М. Российским

фондом фундаментальных исследований (проект № 19-01-00090).

таких как метереология, гидрология, климатология, экология, телекомму-

никации, страхование и финансы, распределения с функцией U, удовлетво-

ряющей (1), рекомендованы как реалистичные модели исследуемых данных.

Поэтому задача оценивания хвостового индекса распределения привлекает

много внимания последние годы. Большая часть предлагаемых в публикаци-

ях оценок хвостового индекса основана на порядковых статистиках X1,n ≤

≤ X2,n ≤ ... ≤ X_n,n наблюдений X₁,...,X_n, см. обзор в [1].

Несколько семипараметрических оценок хвостового индекса можно запи-

сать, используя статистики, предложенные в [2]:

)

∑

⁽X_n-i,n

(2)

Gn(k, r, v) =

g_r,v

g_r,v(x) := x^r ln^v

(x),

X_n-k,n

i=0

где r ∈ R, v > -1. Например, оценку Хилла [3] γnH)(k) = G_n(k, 0, 1) или оцен-

ку отношения моментов γnmr)(k) = G_n(k, 0, 2) (2G_n(k, 0, 1))-1, которая была

предложена в [4]. Отметим, что статистики G_n(k, r, v) являются частным слу-

чаям статистик, введенных в [5].

В настоящей статье предлагается новый класс семипараметрических оце-

нок хвостового индекса γ относительно параметра r, определяемых как

{

(Gn(k, r, 0) - 1 - r · Gn(k, 0, 1)) (r (Gn(k, r, 0) - 1))-1 , r = 0,

(3)

γn(k, r) =

γnmr)(k),

r = 0.

Параметризованная оценка γ_n(k, r), как и статистики G_n(k, r, v), зависит

от двух параметров: от числа наибольших порядковых статистик 1 ≤ k ≤

≤ n - 1, используемых в оценке, и от параметра настройки (регуляриза-

ции) r. Существует непрерывность в отношении r в (3), поскольку выполнено

limr→0 γ_n(k, r) = γnmr)(k). Более того, lim_r→-∞ γ_n(k, r) = γnH)(k). В этой свя-

зи класс оценок γ_n(k, r) обобщает две классические оценки. Отметим, что

оценки γ_n(k, r), так же как и статистики G_n(k, r, v), являются инвариант-

ными относительно масштаба, т.е. они не меняются при замене наблюдений

X₁,... ,X_n на cX₁,... ,cX_n, где c > 0.

Цели статьи следующие: (a) исследовать асимптотические свойства, вклю-

чая слабую сходимость и асимптотическую нормальность новых оценок;

(b) сравнить предлагаемые оценки с некоторыми другими оценками хвосто-

вого индекса; (c) предложить алгоритм для адаптивного оценивания γ по

выборке с помощью новых оценок и применить этот алгоритм к нескольким

выборкам реальных данных.

Содержание статьи следующее. В разделе 2 формулируются основные

асимптотические результаты. Кроме того, используя ту же методологию, что

и в [6], проводится сравнение параметризованной оценки γ_n(k,r) с другими

параметризованными оценками хвостового индекса. В разделе 3 обсуждают-

ся некоторые вопросы, относящиеся к практическому применению введенной

оценки. В разделе 4 содержатся выводы. В Приложении приводятся доказа-

тельства основных результатов.

2. Основные результаты

Перед формулировкой результатов введем несколько обозначений. Пусть

→ - сходимость по распределению,

= - равенство по распределению.

Первый результат непосредственно вытекает из теоремы 1.1 в [2].

Теорема 1. Предположим, что X₁,...,Xn - независимые одинаково

распределенные случайные величины с функцией распределения F такой, что

ее функция квантилей U удовлетворяет условию (1). Пусть γr < 1. Пусть

последовательность k = k_n такова, что

(4)

k_n → ∞,

n/k_n

→ ∞, n → ∞.

→ γ, n → ∞.

Чтобы доказать асимптотическую нормальность любой оценки параметра

γ > 0 одного предположения (1) недостаточно. А именно, нужна дополни-

тельная информация о скорости сходимости U(tx)/U(t) к x^γ , см. гл. 2.3 в [7].

Поэтому предположим, что существует измеримая функция A(t), не меняю-

щая знак при больших t, не равная нулю и такая, что A(t) → 0 при t → ∞

так, что

U (tx)/U(t) - x

x^ρ - 1

(5)

lim

= f_ρ(x), f_ρ(x) =

t→∞

A(t)

для каждого x > 0, где ρ < 0 называется параметром второго порядка.

Главным результатом статьи является следующая теорема.

Теорема 2. Предположим, что X₁,...,X_n - н.о.р. сл.в. с ф.р. F, функ-

ция квантилей которой U удовлетворяет условию (5). Пусть γr < 1/2.

Пусть последовательность k = k_n удовлетворяет условиям (4) и

√

)

⁽n

(6)

lim

=μ

n→∞

с конечным μ.

Тогда

√

(

)

(7)

→ N

μν(r),γ²σ²(r)

n → ∞,

где N (·, ·) обозначает нормальное распределение и

1-γr

2(1 - γr)

(8)

ν(r) =

σ²(r) =

(1 - ρ)(1 - γr - ρ)

1 - 2γr

Напомним, что асимптотическая среднеквадратичная ошибка для γ_n(k, r)

определяется соотношением

)

⁽n

γ²σ² (r)

(9)

E(γ_n(k,r) - γ)² ∼ A²

ν² (r) +

n → ∞,

где последовательность целых чисел k = k_n удовлетворяет (4). Пусть μ = 0

в (6). Приведенная в [8] (см. также [9]) двухступенчатая процедура позволяет

минимизировать правую часть (9) по k = k_n и r. Применив эту процедуру,

получаем, что r^∗ = ρ/γ является оптимальным выбором параметра r, в то

время как оптимальный выбор k^∗n(r^∗) для последовательности k = k_n удовле-

творяет асимптотическому соотношению

)1/(1-2ρ)

⁽γ²σ²(r^∗)

(10)

k^∗n(r^∗) ∼

n → ∞.

ν²(r^∗)

a^←(1/n)

Здесь a^← обозначает функцию, обратную к функции a, которая определяется

так:

∫∞

(11)

A²(t) ∼

a(x)dx, t → ∞.

Теперь сравним γ_n(k, r) с несколькими параметризованными оценками:

{

(Gn(k, r, 0) - 1) / (rGn(k, r, 0)) , r = 0,

γ(1)n(k,r) =

γnH)(k),

r = 0,

γ(2)n(k,r) = (G_n(k,0,r)/Γ(r + 1))1/r ,

2G_n(k, r, 1)

γ(3)n(k,r) =

√

2rG_n(k, r, 1) + 1 +

4rG_n(k, r, 1) + 1

{

(rGn(k, r, 1) - Gn(k, r, 0) + 1)(r2Gn(k, r, 1))-1, r = 0,

γ(4)n(k,r) =

γnmr)(k),

r = 0,

где Γ(·) обозначает гамма-функцию. Параметризованная оценка γn1)(k, r) вве-

дена независимо в [8-10]. Она совпадает с оценкой Хилла [3] при r = 1. Пара-

метризованная оценка γn2)(k, r) введена в [11]. Следует отметить, что класс

оценок γn2)(k, r) обобщает оценку Хилла γn2)(k, 1) и оценку γn2)(k, 2), приве-

денную в [12]. Параметризованные оценки γnℓ)(k, r), ℓ = 3, 4, были представ-

лены в [2]. Оценка γn3)(k, 0) совпадает с оценкой Хилла [3], в то время как

оценка γn4)(k, 0) - с оценкой отношения моментов.

В следующей теореме собраны результаты об асимптотической нормаль-

ности оценок γnℓ)(k, r), ℓ = 1, 2, 3, 4. Соответствующие доказательства можно

найти в [8] (см. также [9, 10]), [2, 11].

Теорема 3. Пусть выполнены условия теоремы 2 (ограничение γr < 1/2

для γn2)(k, r) не требуется).

Тогда

√ (

)

(

)

γ(ℓ)n(k,r) - γ

→ N

μν_ℓ(r),γ²σ2ℓ(r)

n → ∞, ℓ = 1,2,3,4,

где

1-γr

(1 - γr)

ν₁(r) =

σ²¹(r) =

1-γr-ρ

1 - 2γr

(

)

1 - (1 - ρ)

Γ(2r + 1)

ν₂(r) =

σ²²(r) =

-1

rρ(1 - ρ)^r

r²

Γ²(r + 1)

(1 - γr)(1 - ρ - γ²r²)

(1 - γr)²(1 - 2γr + 2γ⁴r⁴)

ν₃(r) =

σ²³(r) =

(1 + γr)(1 - ρ - γr)²

(1 + γr)²(1 - 2γr)³

(1 - γr)

2(1 - γr)⁴

ν₄(r) =

σ²⁴(r) =

(1 - ρ - γr)²

(1 - 2γr)³

Более того,

(

√

)-1

(

√

)-1

r∗1 = γ-1 2-ρ+

(2 - ρ)² - 2

r∗3

= 2ργ-1 2-ρ+

(2 - ρ)² - 4ρ

— оптимальные значения параметра r для параметризованных оценок

γn1)(k,r) и γn3)(k,r) соответственно. В то же время решение r∗2 уравнения

)

d (

(

)-2ρ

(ν₂(r))²

σ²²(r)

является оптимальным значением параметра r для γn2)(k, r), а r∗4 = R^∗/γ -

оптимальным значением параметра r для γn4)(k,r), где R^∗ - решение урав-

нения

)

d (

(

)-2ρ

(ν₄ (R/γ))²

σ²⁴

(R/γ)

= 0.

Пусть k^∗n,ℓ(r^∗ℓ), ℓ = 1, 2, 3, 4, обозначает последовательности, удовлетворяю-

щие соотношению (10), где величины ν(r^∗) и σ²(r^∗) заменены на ν_ℓ(r^∗ℓ) и

σ2ℓ(r^∗ℓ) соответственно. Следуя [6], будем считать, что оценка γ_n (kn )((r∗),r∗)

превосходит оценку

γnℓ) k^∗n,ℓ(r^∗ℓ),r^∗

на луче {(γ, ρ): ρ = ρ₀, γ > 0}, если

ℓ

ψ_ℓ(ρ₀) > 1, где

(

)

)₂

E γnℓ)

k^∗n,ℓ(r^∗ℓ),r^∗

-γ

ℓ

ψ_ℓ(ρ) = lim

^n→∞ E(γ_n (k^∗n(r^∗),r^∗) - γ)²

Легко проверить, что

(

ν2ℓ(r^∗ℓ)

⁽σ2ℓ(r^∗ℓ))-2ρ)1/(1-2ρ)

(12)

ψ_ℓ(ρ) =

ν²(r^∗) σ²(r^∗)

Предполагаем, что оценка γ_n(k^∗n(r^∗), r^∗) превосходит оценки γnℓ)(k^∗n,ℓ(r^∗ℓ), r^∗ℓ),

ℓ = 1,2,3,4, в области {(γ,ρ): ρ<0, γ>0}, но доказать неравенства ψ_ℓ(ρ)>1,

1,05

1,04

1,03

1,02

1,01

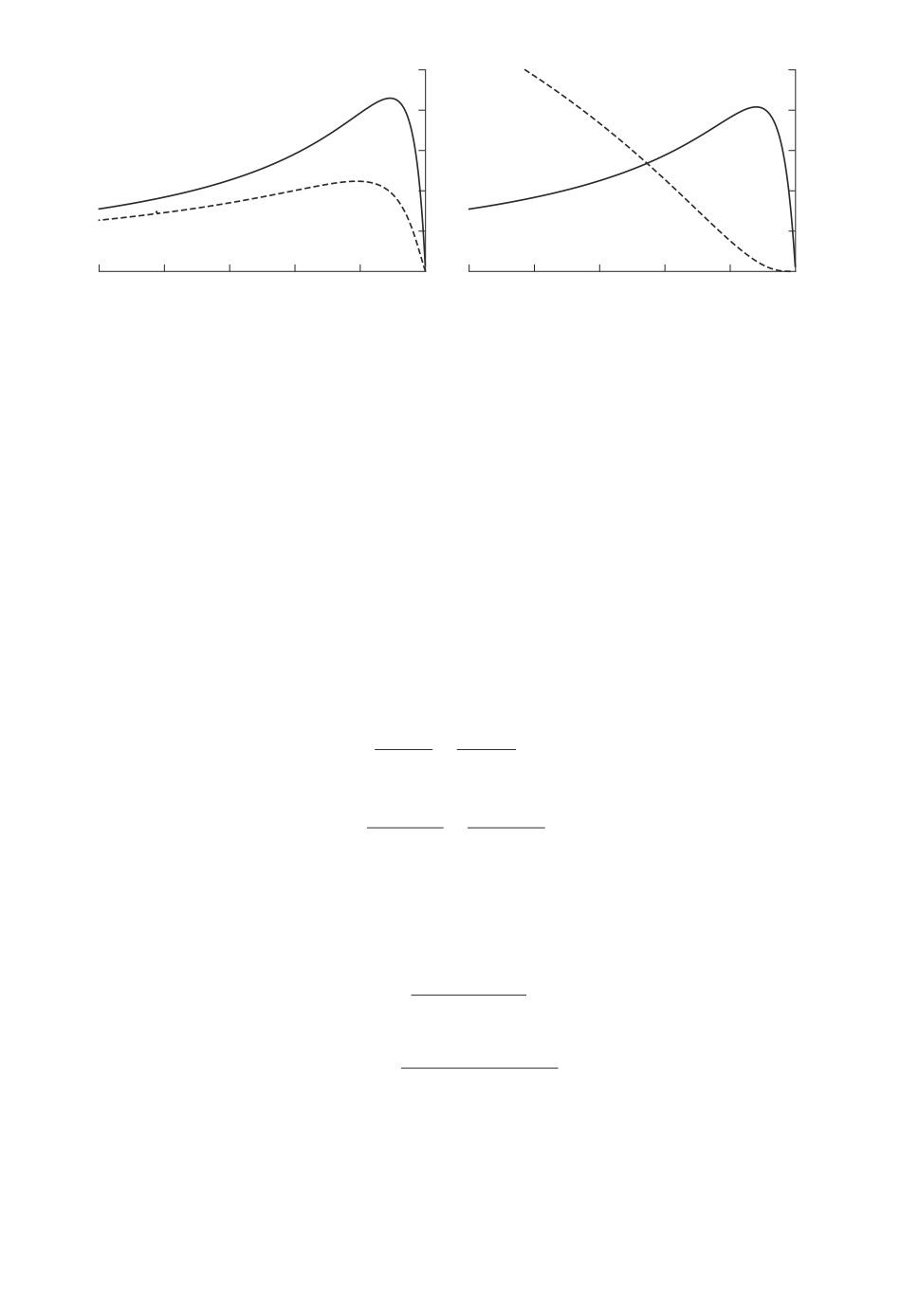
Рис. 1. а - Графики функций ψ₁(ρ) (сплошная линия) и ψ₂(ρ) (точечная ли-

ния); б - ψ₃(ρ) (сплошная линия), ψ₄(ρ) (штриховая линия).

ℓ = 1,2,3,4, для всех ρ < 0 представляется серьезной проблемой. Поэтому

здесь приводим лишь графики функций ψ_ℓ(ρ), ℓ = 1, 2, на рис. 1,а и ψ_ℓ(ρ), ℓ =

= 3, 4, - на рис. 1,б соответственно. Отсюда можно заключить, что ψ_ℓ(ρ) > 1,

ℓ = 1,2,3,4, для -10 ≤ ρ < 0, т.е. оценка γ_n(k^∗n(r^∗),r^∗) превосходит оценки

γnℓ)(k^∗n,ℓ(r^∗ℓ),r^∗ℓ), ℓ = 1,2,3,4, в области {(γ,ρ) : -10 ≤ ρ < 0, γ > 0}.

Во введении было замечено, что класс оценок γ_n (k_n(r), r) обобщает две

классические оценки: оценку отношения моментов γnmr)(k) и оценку Хилла

γnH)(k) . Поэтому сравним предложенную оценку γ_n (k^∗n(r^∗),r^∗) с этими оцен-

ками (при оптимальном выборе последовательности k = k_n для каждой). Как

и в (12), определим

(

ν²(0)

( σ²(0) )-2ρ)1/(1-2ρ)

(13)

ψ⁽⁰⁾(ρ) =

ν²(r^∗) σ²(r^∗)

(

ν²(-∞)

⁽σ²(-∞))-2ρ)1/(1-2ρ)

ψ(-∞)(ρ) =

ν²(r^∗)

σ²(r^∗)

где ν(-∞) = lim_r→-∞ ν²(r) и σ²(-∞) = lim_r→-∞ σ²(r). Подставляя парамет-

ры нормального закона (8) и r^∗ = ρ/γ в (13), получим

)1/(1-2ρ)

2-2ρ

⁽ (1 - 2ρ)

ψ⁽⁰⁾(ρ) =

(1 - ρ)4-2ρ

)1/(1-2ρ)

2+2ρ

⁽2-2ρ(1 - 2ρ)

ψ(-∞)(ρ) =

(1 - ρ)2+2ρ

Легко проверить, что выполнено ψ⁽⁰⁾(ρ) → 1, ψ(-∞)(ρ) → 1, ρ ↑ 0 и ψ⁽⁰⁾(ρ) →

→ 2, ψ(-∞)(ρ) → 1, ρ → -∞. Более того, выполнены неравенства

(14)

ψ⁽⁰⁾(ρ) > 1, ψ(-∞)

(ρ) > 1

1,6

1,5

1,4

1,3

1,2

1,1

Рис. 2. Графики функций ψ⁽⁰⁾(ρ) (сплошная линия), ψ(-∞)(ρ) (штриховая

линия).

для всех ρ < 0. Доказательство неравенств (14) приведено в разделе

Неравенствa (14) позволяют заключить, что оценка γ_n(k^∗n(r^∗), r^∗) превос-

ходит оценки отношения моментов и Хилла на всей области параметров

{(γ, ρ) : ρ < 0, γ > 0}. Для наглядности приведем графики функций ψ⁽⁰⁾(ρ)

и ψ(-∞)(ρ), -10 ≤ ρ < 0, на рис. 2.

3. Предлагаемый алгоритм и примеры его применения

Как правило, в приложениях используется более ограничительное, чем (5),

условие. А именно предполагается, что функция квантилей U принадлежит

классу Холла (см. [13, 14]), т.е.

(

)

A(t)

(15)

U (t) = Ct^γ

(1 + o(1))

t → ∞,

где C > 0, β = 0, ρ < 0 и A(t) = γβt^ρ. Используя (11), находим a^←(t) =

(

)1/(1-2ρ)

-2ργ²β²

t1/(2ρ-1). Теперь, используя правую часть (10), можно по-

строить оценки для k^∗n(0) и k^∗n(r^∗):

⎤

⎡(

)1/(1-2ˆρn)

(1 - ρ_n)

k∗

⎦_,

=^⎣

-ρ

β2nn2ρn

⎤

⎡(

)1/(1-2ˆρn)

k∗

⎦_,

=⎣(1-ρn)(1-2ρn)

-ρ

β2nn2ρn

где [·] обозначает целую часть числа. Оценим параметр ρ с помощью оценки

ρn = ρn(k), предложенной в [15]. Оценка ρn(k) задается как



 Gn(k, 0, 1) - 2 (Gn(k, 0, 2)/2)¹

/2 + (G_n(k, 0, 3)/6)1/3



(16)

ρn(k) = -3

,

Gn(k,0,1) - 4(G_n(k,0,2)/2)1/2 + 3(G_n(k,0,3)/6)1/3

где статистики G_n(k, r, v) определены в (2).

0,40

0,35

0,30

0,25

0,20

0,15

0,10

0,05

200

400

600

800

1000

200

400

600

800

1000

1200

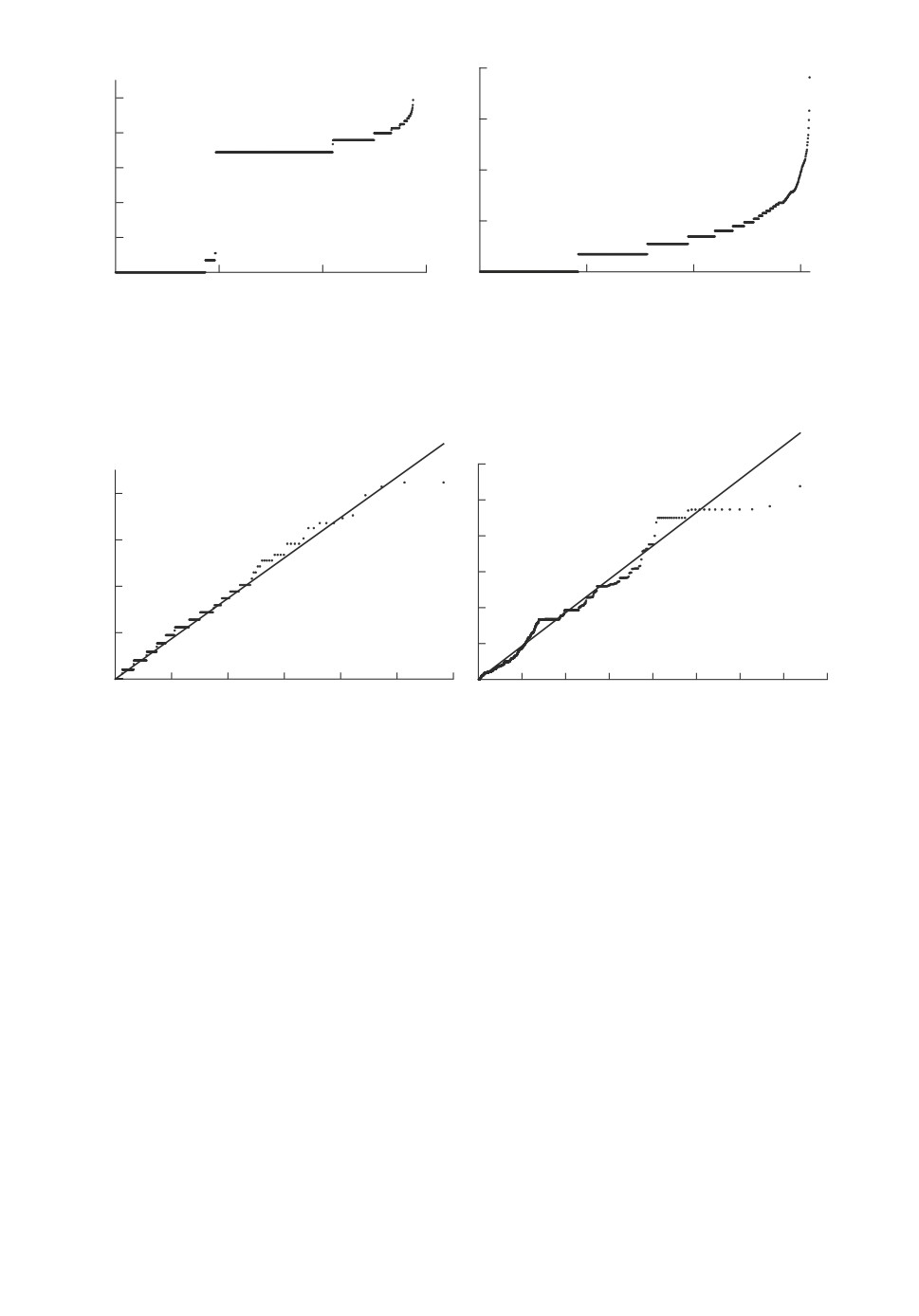
Рис. 3. а - График {(k, R^-k,n

1 ≤ k ≤ n₁}; б - график {(k,R+k,n

), 1 ≤ k ≤ n2}.

Чтобы оценить параметр β, используем оценк

β_n

β_n(k, ρ_n), которая вве-

дена в [16] и определяется как

(

)(

)

∑

(

)_-ρ

∑

(_k)-ρ

)_ρ

U_i

-¹

U_i

⁽k

i=1

(17)

β_n(k,ρ) =

(

)(

)

∑

(_k )_-ρ

∑

(_k

)-ρ

∑

(_k)-2ρ

U_i

-¹

U_i

i=1

где U_i = i ln (Xn-i+1,n/X_n-i,n). Применяя оценки (16), (17), использовали k =

= [n0,995]. Такой выбор последовательности k = k_n рекомендуется в [17], см.

также [15].

Теперь приступим к описанию алгоритма для адаптивного оценивания γ.

Напомним, что r^∗ = ρ/γ является оптимальным значением параметра r для

γn (kⁿ(r^∗), r^∗). Поэтому, чтобы оценить r^∗, нужна не только оценка парамет-

ра ρ, но и предварительная оценка хвостового индекса γ. Для этого включаем

классическую оценку γ_n(k, 0) в предлагаемый алгоритм.

Алгоритм 1.

1. Вычислить оценки ρ_n

β_n, используя (16) и (17) соответственно.

2. Вычислить оценкуk∗n, используя (16).

(

)

3. Вычислить предварительную оценку γ_n

k∗

(

)

k∗

4. Вычислить r^∗ = ρ_n/γ_n

5. Вычислить оценкуk∗n, используя (16).

(

)

k∗

6. Вычислить γ_n

,r^∗

Опишем применение приведенного алгоритма к нескольким наборам ре-

альных данных.

i. Проанализируем ежедневные цены отношения Биткоин/Доллар США

(Bitcoin/USD) с размером выборки n = 2043 в период с 28 апреля 2013 г. до

30 ноября 2018 г. Пусть R_t = ln(x_t/xt-1), 2 ≤ t ≤ n, обозначает так называе-

мые лог-возвраты (the log-returns) заданного временного ряда X_t, 1 ≤ t ≤ n.

Оценим левый хвост F (-x), x > 0, и правый хвост 1 - F (x), x > 0, отдель-

но. Пусть R-1,n

≤ ... ≤ R-n1,n₁, n1 = 936, обозначают порядковые статисти-

2,0

1,5

1,0

0,5

ln(k/j), k = 117

ln(k/j), k = 119

Рис. 4. а - График Sn1 (R^-;k∗n

+1) с линией (x, γn1 (k∗n

, r^∗)x), б - Sn2(R⁺; k∗ +1)_n

с линией (x, γn2 (k∗ , r^∗)x)._n

ки абсолютных величин отрицательных лог-возвратов, а R+1,n

≤...≤R⁺

n₂,n₂

n₂ {(1106, - )орядковые с}ти{(ики по )жительных }ог-возвратов. Графи-

ки k, R^-k,n

, 1≤k≤n1

и k,R+k,n

, 1≤k≤n2

довольно близки, см.

рис. 3.

Представленный алгоритм дает следующие оценки:

γn₁ (kn1 , r^∗) = 0,39

(r^∗ = -1,90,k∗n

= 116) и γn2 (k∗n

, r^∗) = 0,38 (r^∗ = -1,78,k∗

= 118). Чтобы

n₂

продемонстрировать, насколько хорошо полученные оценки параметра γ при-

ближают данные, используем предложение 4.1 из [18]. Оно утверждает в

предположениях теоремы 1, что

{(

}

⁽j⁾

⁽Xn+1-j,n))

(18)

S_n (X;k) =

- ln

, ln

, 1≤j ≤k

Xn+1-k,n

сходится по вероятности к множеству {(x, γx) , 0 ≤ x < ∞}. На рис. 4,а по-₍

)

(

) )

казан график Sn1 R^-;k∗n

и линия x, γn1

k^∗ , r^∗ x

. В (18) выбрано

n₁

k=k∗n

+ 1, поскольку отношения R^-n

/R^-n

, 0≤i≤k-1=k∗n

, бы-

1-i,n1

(

1-k,n1

)

ли использованы для вычисления оценки γn1

k∗

,r∗ . Можно заметить, что

n₁

(

) )

(

)

k∗

линия x, γn1

,r^∗

x отражает график Sn1 R^-;k∗n

довольно хо-

n₁

рошо. Аналогичное заключение можно сделать, анализируя положительные

лог-возвраты, см. рис. 4,б . Стоит отметить, что полученные оценки не проти-

воречат стилизованному факту финансовой доходности: распределение лог-

возвратов принадлежит классу RV-1/γ (или эквивалентно U ∈ RV_γ) с хвосто-

вым индексом 0,2 < γ < 0,5 для многих изученных наборов данных.

ii. Оценим хвостовой индекс γ распределения временных промежутков

(the inter-arrivals) между появлениями пакетов информации в потоках TСP

(Transmision Control Protocol). Используем трассировки (traces), содержа-

щие измерения одночасового трафика, передаваемого на большие расстояния,

между Digital Equipment Corporation и остальным миром с 8 марта 1995 г.

(см. http://ita.ee.lbl.gov/html/contrib/dec-pkt.html). Данные включают n₃ =

1 000 000

2 000 000

3 000 000

200 000

400 000

600 000

(

)

Рис. 5. a - График {k, ln

Xk,nj

,1 ≤ k ≤ n_j} для временных промежутков

между появлениями пакетов (j = 3); б - график для числа входящих связей

(in-degrees) узлов сети (j = 4).

0,8

0,6

0,4

0,2

ln(k/j), k = 339

ln(k/j), k = 1596

(

)

(

)

Рис. 6. a - График Snj X;k∗n

с линией (x, γnj

k^∗ x, r^∗ для временных_n

промежутков между появлениями пакетов (j = 3); б - график числа входящих

связей (in-degrees) для узлов (j = 4).

= 2873588 временных промежутков между появлениями пакетов, см. рис. 5,а,

где представлена зависимость {k, ln (Xk,n3 ) , 1 ≤ k ≤ n₃}.

(

)

k∗

Применяя предложенный алгоритм, получим оценку γn3

n₃

,r^∗

= 0,17

(

) )

k∗

(r^∗ = -1,2;k∗n

= 338). Линия x, γn3

, r^∗ x хорошо соответствует гра-

n₃

(

)

фику Sn3

X;k∗n

+ 1 , см. рис. 6,а. Оценка оптимального выбора k∗n3 состав-

ляет только 0,011 % от n₃, что несколько странно. Следует отметить, что

те же данные временных промежутков между пакетами были рассмотрены

в [19]. В [19] было найдено, что 3 % от наибольшей порядковой статистики хо-

рошо описываются распределением Парето с γ = 1,05. К сожалению, авторы

не нашли объяснения, как было оценено γ в [19]. Анализ трафика, полученно-

го при TCP соединениях, содержится в [20]. Применяя технику QQ-графика,

в [20] было замечено, что распределение временных промежутков между па-

кетами принадлежит классу распределений RV-1/γ с γ = 0,57.

3,5

0,10

3,0

0,08

2,5

2,0

0,06

1,5

0,04

1,0

0,02

0,5

5000

10 000

15 000

ln(k/j), k = 2998

Рис. 7. Графики для лог-возвратов индекса S&P 500.

iii. Многие авторы (см., например, [21] и библиографию в ней) согласны

с тем, что распределение числа входящих связей (in-degrees) узлов принад-

лежит классу RV_γ с γ = 0,91. Здесь используем данные Беркли-Стенфорд

(Berkley-Stanford data) [22] с числом Веб страниц n₄ = 617094, см. рис. 5,б .

(

)

k∗

Найдено, что γn4

,r^∗

= 0,93 (r^∗ = -0,32, k∗n

= 1595). Таким образом, по-

n₄

лученная в статье оценка γ согласуется с результатами статьи [21]. На рис. 6,б₍₎₍

(

) )

k∗

показан график Sn4 X;k∗n

и линия x, γn4

, r^∗ x как показатель

n₄

хорошей точности полученной в статье оценки хвостового индекса γ.

iv. Исследуем ещe один набор лог-возвратов. Известные данные ин-

декса S&P 500 взяты из https://finance.yahoo.com. За период 1950/01/03-

2018/12/21 этот набор данных содержит n₅ = 17356 абсолютных величин_{

(

)

}

лог-возвратовRk = |R_k|, см. рис. 7,а для графика k, ln

k,n₅

,1≤k≤n₅

(

)

Предложенный в статье алгоритм дает оценку γn5

k^∗ , r^∗

= 0,39 (r^∗ = 4,61,

n₅

k∗

= 2997). В статистической литературе нет единого мнения о тяжести хво-

n₅

ста для распределения набора

R_k, 1 ≤ k ≤ n₅. Например, в [23], используя

оценку Хилла и выбирая значение, соответствующее интервалу постоянства

графика зависимости оценки Хилла от числа наибольших порядковых стати-

стик k, получена оценка γn5 = 0,27, а в статье [24] показано, что исследуемый

набор лог-возвратов состоит из трех подвыборок, для которых оценки хво-

стового индекса(ледующие)γ = 0,22, γ (0,28, γ ( 0,21.)) рис. 7,б представ-

лен график Sn5

^R;k∗n

+ 1 , где линия x,xγn5

k^∗ , r^∗

показана черным

n₅

цветом, а соответствующая оценка Хилла (x, xγn5 ) - серым цветом. Таким

образом, полученная в статье оценка лучше приближает данные, чем оценка

Хилла.

4. Заключение

В статье предложен новый класс семипараметрических оценок хвостового

индекса. Этот класс получен путем использования параметризованных ста-

тистик G_n(k, r).

Доказаны слабая сходимость и асимптотическая нормальность введенных

оценок при классических условиях на функцию квантилей U и последова-

тельность k = k_n, а также при дополнительном условии на параметр на-

стройки r. Теорема 2 является главным результатом статьи. Имея асимпто-

тическую нормальность, становится возможным (i) сравнить оценки γ_n(k, r)

с другими асимптотически нормально распределенными оценками хвостово-

го индекса; (ii) построить оценки оптимального выбора последовательности

k = k_n и параметра настройки r. В разделе 3 продемонстрировано, что па-

раметризованная оценка γ_n(k, r) превосходит классические оценки отноше-

ния моментов γnmr)(k) и Хилла γnH)(k) (при соответствующем оптимальном

выборе последовательности k = k_n и параметра настройки r) в области из-

менения параметров {(γ, ρ) : ρ < 0, γ > 0}. Доминирование предложенного в

настоящей статье нового класса оценок над некоторыми недавно получен-

ными оценками позволяет надеяться на полезность предложенных оценок в

оценивании хвостового индекса.

Основываясь на r^∗ = ρ/γ и соотношении (10), построены оценки оптималь-

ного выбора параметра настройки r и последовательности k = k_n. Предло-

женный алгоритм для оценивания γ является адаптивной процедурой. Мож-

но заметить, что предложенный алгоритм детализирует классическую(ценк)

k∗

отношения моментов γnmr)(k). Очевидно, что сначала оцениваются γ_n

(

,0)

(шаг 3 в алгоритме), а после оценивания r^∗ считается оценка γ_n

k∗

,r^∗

(шаг 6 в алгоритме). Предложенный алгоритм легко реализуем. Его работо-

способность продемонстрирована на нескольких наборах реальных данных.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. По теореме 1.1 из [2] имеем, что

γ^vΓ(1 + v)

(Π.1)

→

n → ∞.

(1 - γr)1+v

Остается применить теорему о непрерывном отображении (the continuous

mapping theorem) ( [25]; теорема 12.5.1 (iv) в [26]).

Доказательство теоремы 2. Случай r = 0 исследован в [6], и поэто-

му в статье нужно рассмотреть только случай γr < 1/2, r = 0.

Имеем γ_n(k, r) - γ = S_n(k, r)/ (G_n(k, r, 0) - 1), где

(1 - γr) (G_n(k, r, 0) - 1)

S_n(k,r) =

- G_n(k,0,1).

Имея в виду (Π.1), отношение (7) будет доказано, если показать, что

(

)

√

γrμ

2γ⁴r²

(Π.2)

→N

n → ∞.

(1 - ρ)(1 - γr - ρ)

(1 - γr)(1 - 2γr)

Пусть Y₁, . . . , Y_n - н.о.р. сл.в. с хвостовой функцией IP(Y₁ > x) = 1/x, x ≥ 1.

= X_i, 1 ≤ i ≤ n. Это дает, что

{

∑

( U (Y_n-i,n) ⁾

( U (Y_n-i,n) ^)}

(1 - γr)f_r

- ln

U (Y_n-k,n)

i=0

где f_r(x) = r-1 (x^r - 1), x ≥ 1, - та же, что в (5), функция.

В [8] получены следующие неравенства. Для функции

A(t) такой, что

A(t) ∼ A(t) при t → ∞, при любых ε > 0 и 0 < δ < min{1 - γr - ρ, 1 - ρ} су-

ществует t₀ = t₀(ε, δ), что для t > t₀ и x > 1 выполнено неравенство



)



⁽U(tx)



(Π.3)

-f_r(x^γ)

A(t)x^γrf_ρ(x)

A(t)xγr+ρ+δ.

^f

≤

^r U(t)

Неравенство (Π.3) выполнено также для случая r = 0, см. например, с. 74

в [7]. Таким образом, из (Π.3) получим, что



)



⁽U(tx)

⁽U(tx)⁾



1 - γr)f_r

- ln

- (1 - γr)f_r (x^γ) + ln (x^γ) -

⁽

U (t)



(Π.4)

-A˜(t)f_ρ(x) ((1 - γr)x^γr - 1) ≤ ε

A(t)xρ+δ (xγr

+ 1) .

По лемме 3.2.1 из [7] в предположении k = o(n) имеем, что Y_n-k,n → ∞ по-

чти наверное. Подставляя x = Y_n-i,n/Y_n-k,n и t = Y_n-k,n в (Π.4) и производя

суммирование по i = 0, 1, . . . , k - 1, получим



(Π.5)

S_n(k, r) - S(1)n(k, r)

A (Y_n-k,n) S(2)n(k, r)≤ε

A (Y_n-k,n)S(3)n

(k, r),

где

{

)_γ)

∑

⁽⁽ Y_n-i,n

⁽⁽ Y_n-i,n )^γ)},

S(1)n(k,r) =

(1 - γr)f_r

- ln

Y_n-k,n

i=0

){

}

∑

⁽Y_n-i,n

⁽Y_n-i,n)^γr

S(2)n(k,r) =

f_ρ

(1 - γr)

-1

Y_n-k,n

i=0

}

∑

⁽Y_n-i,n)ρ+δ{(Y_n-i,n)^γr

S(3)n(k,r) =

Y_n-k,n

i=0

Далее, отношение (Π.2) следует из

(

)

√

2γ⁴r²

(Π.6)

→ N 0,

(1 - γr)(1 - 2γr)

√

γrμ

(Π.7)

→

(1 - ρ)(1 - γr - ρ)



√



|μ|

(Π.8)

A (Y_n-k,n)

→

1-γr-ρ-δ

1-ρ-δ

при n → ∞.

Пусть Z₁, . . . , Z_n - н.о.р. сл.в. с хвостовой функцией IP(Z₁ > x) = 1/x,

x ≥ 1. По представлению Реньи (Rényi) имеем для фиксированного k < n:

(

)

Y_n-i,n

(Π.9)

0≤i≤k-1

= (Z_k-i,k

0 ≤ i ≤ k - 1).

Y_n-k,n

Используя (Π.9), получим, что

∑

(Π.10)

{(1 - γr)f_r (Z^γi) - ln (Z^γi

)} .

i=0

Слагаемые в правой части (Π.10) - н.о.р. сл.в. с нулевым средним. Более того,

в предположении γr < 1/2 получим равенство

2γ⁴r

Var {(1 - γr)f_r (Zγ1) - ln (Zγ1)} =

(1 - γr)(1 - 2γr)

Тогда, применяя центральную предельную теорему Линдеберга - Леви (Lin-

deberg - Lévy), получим соотношение (Π.6).

Применяя (Π.9) еще раз, имеем

∑

(Π.11)

f_ρ (Z_i) {(1 - γr)Z^γri

− 1} .

i=0

Правая часть (Π.11) представляет собой сумму н.о.р. сл.в. с

γr

IE {f_ρ (Zγ1) {(1 - γr)Zγr1 - 1}} =

(1 - ρ)(1 - γr - ρ)

Из слабого закона больших чисел Хинчина следует соотношение

γr

→

n → ∞.

(1 - ρ)(1 - γr - ρ)

Последнее соотношение и

A(t) ∼ A(t), t → ∞, вместе с предположением (6)

и фактом, чт

A(Y_n-k,n)

→ 1, n → ∞, дают (Π.7). Доказательство

последнего соотношения может быть найдено на с. 75 в [7].

Доказательство (Π.8) подобно доказательству (Π.7), поэтому опускаем его.

Доказательство. Приведем доказательство неравенств (14).

Начнем с неравенства ψ⁽⁰⁾(ρ) > 1. Достаточно доказать, что (1 - 2ρ)1-ρ >

(1 - ρ)2-ρ для ρ < 0 или, эквивалентно, b(ρ) > 0, где b(ρ) = (1 - ρ) ln(1 - 2ρ) -

- (2 - ρ) ln(1 - ρ). Имеем

(

)

db(ρ)

-ρ

- ln

dρ

(1 - ρ)(1 - 2ρ)

1-ρ

Используя неравенство ln(1 + x) ≥ x/(x + 1), x > -1 (см., например, с. 67

в [27]) с x = -ρ/(1 - ρ), получим

db(ρ)

-ρ²

≤

dρ

(1 - ρ)(1 - 2ρ)

для ρ < 0. Отсюда следует, что функция b(ρ) строго убывает на интервале

(-∞, 0). Это вместе с b(0) = 0 доказывает, что b(ρ) > 0, ρ < 0.

Для проверки неравенства ψ(-∞)(ρ) > 1 достаточно его переписать в виде

((2 - 2ρ)-2ρ (1 - 2ρ)2)1/(1-2ρ)

1 - 2ρ

1-ρ

и заметить, что (2 - 2ρ)/(1 - 2ρ) > 1 и (1 - 2ρ)/(1 - ρ) > 1 при ρ < 0.

СПИСОК ЛИТЕРАТУРЫ

Gomes M.I., Guillou A. Extreme Value Theory and Statistics of Univariate

Extremes: A Review // Int. Stat. Rev. 2015. No. 83. P. 263-292.

Paulauskas V., Vaičiulis M. Several New Tail Index Estimators // Ann. Inst. Stat.

Math. 2017. No. 69. P. 461-487.

Hill B.M. A Simple General Approach to Inference about the Tail of a Distri-

bution // Ann. Stat. 1975. No. 3. P. 1163-1174.

Danielsson J., Jansen D.W., de Vries C.G. The Method of Moments Ratio

Estimator for the Tail Shape Parameter // Commun. Stat. Theory. 1986. No. 25.

P. 711-720.

Segers J. Residual Estimators // J. Stat. Plan. Inf. 2001. No. 98. P. 15-27.

De Haan L., Peng L. Comparison of Tail Index Estimators // Stat. Nederl. 1998.

No. 52. P. 60-70.

De Haan L., Ferreira A. Extreme Value Theory: An Introduction, N.Y.: Springer,

2006.

Paulauskas V., Vaičiulis M. On the Improvement of Hill and Some Other

Estimators // Lith. Math. J. 2013. No. 53. P. 336-355.

Brilhante F., Gomes M.I., Pestana D. A Simple Generalization of the Hill

Estimator // Comput. Stat. Data Anal. 2013. No. 57. P. 518-535.

10.

Beran J., Schell D., Stehlik M. The Harmonic Moment Tail Index Estimator:

Asymptotic Distribution and Robustness // Ann. Inst. Stat. Math. 2014. No. 66.

P. 193-220.

11.

Gomes M.I., Martins M.J. Eficient Alternatives to the Hill Estimator // Proc.

Workshop V.E.L.A. Extreme Values and Additive Laws. C.E.A.U.L. Ed. 1999.

No. 9. P. 40-43.

12.

Gomes M.I., Martins M.J., Neves M. Alternatives to a Semi-parametric Estimator

of Parameters of Rare Events - the Jackknife Methodology // Extremes. 2000.

No. 3. P. 207-229.

13.

Hall P., Welsh A.H. Adaptive Estimates of Parameters of Regular Variation //

Ann. Statist. 1985. No. 13. P. 331-341.

14.

Hall P. On Some Simple Estimates of an Exponent of Regular Variation // J. Royal

Statist. Soc. B. 1982. No. 44. P. 37-42.

15.

Fraga Alves M.I., Gomes M.I., de Haan L. A New Class of Semi-parametric

Estimators of the Second Order Parameter // Portugaliae Mathematica. 2003.

No. 60. P. 193-214.

16.

Gomes M.I., Martins M.J. Asymptotically Unbiased Estimators of the Tail Index

Based on External Estimation of the Second Order Parameter // Extremes. 2002.

No. 5. P. 5-31.

17.

Caeiro F., Gomes M.I. Minimum-variance Reduced-bias Tail Index and High

Quantile Estimation // Revstat. 2008. No. 6. P. 1-20.

18.

Das B., Resnick S. QQ Plots, Random Sets and Data from a Heavy Tailed

Distribution // Stochast. Models. 2008. No. 24. P. 103-132.

19.

Paxson V., Floyd S. Wide-area Traffic: the Failure of Poisson Modeling //

IEEE/ACM Trans. Networking. 1995. No. 3. P. 226-244.

20.

Guo L., Crovella M., Matta I. TCP Congestion Control and Heavy Tails, Technical

Report BUCS-2000-017, Computer Science Department. Boston University, 2000.

21.

Volkovich Y.V., Litvak N. Asymptotic Analysis for Personalized Web Search //

Adv. Appl. Prob. 2010. No. 42 (2). P. 577-604.

22.

Leskovec J., Krevl A. SNAP Datasets: Stanford Large Network Dataset Collection.

2014.

23.

Mikosch T.V. Modeling dependence and tails of financial time series. H.C.O.-Tryk,

Kobenhavns Univ. 2002. P. 1-75.

24.

Galbraith J.W. Circuit Breakers and the Tail Index of Equity Returns // J. Financ.

Economet. 2004. No. 2(1). P. 109-129.

25.

Resnick S.I. Heavy-Tail Phenomena. Probabilistic and Statistical Modeling. N.Y.:

Springer, 2006.

26.

Whitt W. Stochastic-Process Limits. An Introduction to Stochastic-Process Limits

and their Application to Queues. N.Y.: Springer, 2002.

27.

Mitrinović D.S. Elementary Inequalities. P. Noordhoff Ltd, Groningen, 1964.

Статья представлена к публикации членом редколлегии А.В. Назиным.

Поступила в редакцию 19.07.2018

После доработки 02.10.2018

Принята к публикации 08.11.2018